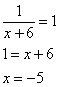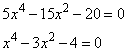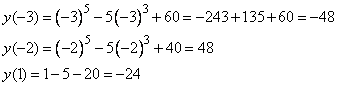12 задание егэ математика профиль примеры с решением

Задание 12 Профильного ЕГЭ по математике – это решение уравнений. Чаще всего, конечно, это тригонометрические уравнения. Но встречаются и другие типы – показательные, логарифмические, комбинированные.

Сейчас задание 12 Профильного ЕГЭ на решение уравнения состоят из двух пунктов: собственно решения и отбора корней на определенном отрезке.

Что нужно знать, чтобы справиться с этой задачей на ЕГЭ? Вот необходимые темы для повторения.

Задачи из сборников Ященко, 2021 год

Квадратные уравнения

Показательные уравнения

Логарифмические уравнения

Модуль числа

Уравнения с модулем

Тригонометрический круг

Формулы тригонометрии

Формулы приведения

Простейшие тригонометрические уравнения 1

Простейшие тригонометрические уравнения 2

Тригонометрические уравнения

Что необходимо помнить при решении уравнений?

1) Помним про область допустимых значений уравнения! Если в уравнении есть дроби, корни, логарифмы или арксинусы с арккосинусами — сразу записываем ОДЗ. А найдя корни, проверяем, входят они в эту область или нет. Есть в уравнении есть tg x — помним, что он существует, только если {cos xne 0}.

2) Стараемся записывать решение в виде цепочки равносильных переходов.

3) Если есть возможность сделать замену переменной — делаем замену переменной! Уравнение сразу станет проще.

4) Если еще не выучили формулы тригонометрии — пора это сделать! Много формул не нужно. Самое главное — тригонометрический круг, формулы синусов и косинусов двойных углов, синусов и косинусов суммы (разности), понижения степени. Формулы приведения не надо зубрить наизусть! Надо знать, как они получаются.

5) Как отбирать решения с помощью тригонометрического круга? Вспомним, что крайняя правая точка тригонометрического круга соответствует числам -4 pi , -2 pi , 0, 2 pi , 4 pi dots Дальше всё просто. Смотрим, какая из точек этого типа попадает в указанный в условии промежуток. И к ней прибавляем (или вычитаем) нужные значения.

Например, вы нашли серию решений x=frac{pi}{3}+2pi n , где n — целое, а найти надо корни на отрезке left [frac{5 pi}{2};frac{9 pi}{2} right ]. На указанном промежутке лежит точка 4 pi. От нее и будем отсчитывать. Получим: x=4 pi +frac{pi}{3}=frac{13 pi}{3}.

6) Получив ответ, проверьте его правильность. Просто подставьте найденные решения в исходное уравнение!

Давайте потренируемся.

а) Решите уравнение 2{{sin}^2 left(frac{pi }{2}+xright)}=-sqrt{3}{cos x}

б) Найдите все корни этого уравнения, принадлежащие промежутку left[-3pi right.;left.-frac{3pi }{2}right]

2{{sin}^2 left(frac{pi }{2}+xright)}=-sqrt{3}{cos x}

Упростим левую часть по формуле приведения.

2{{cos}^2 x+sqrt{3}{cos x}=0}

Вынесем {cos x} за скобки. Произведение двух (или нескольких) множителей равно нулю тогда и только тогда, когда хотя бы один из них равен нулю.

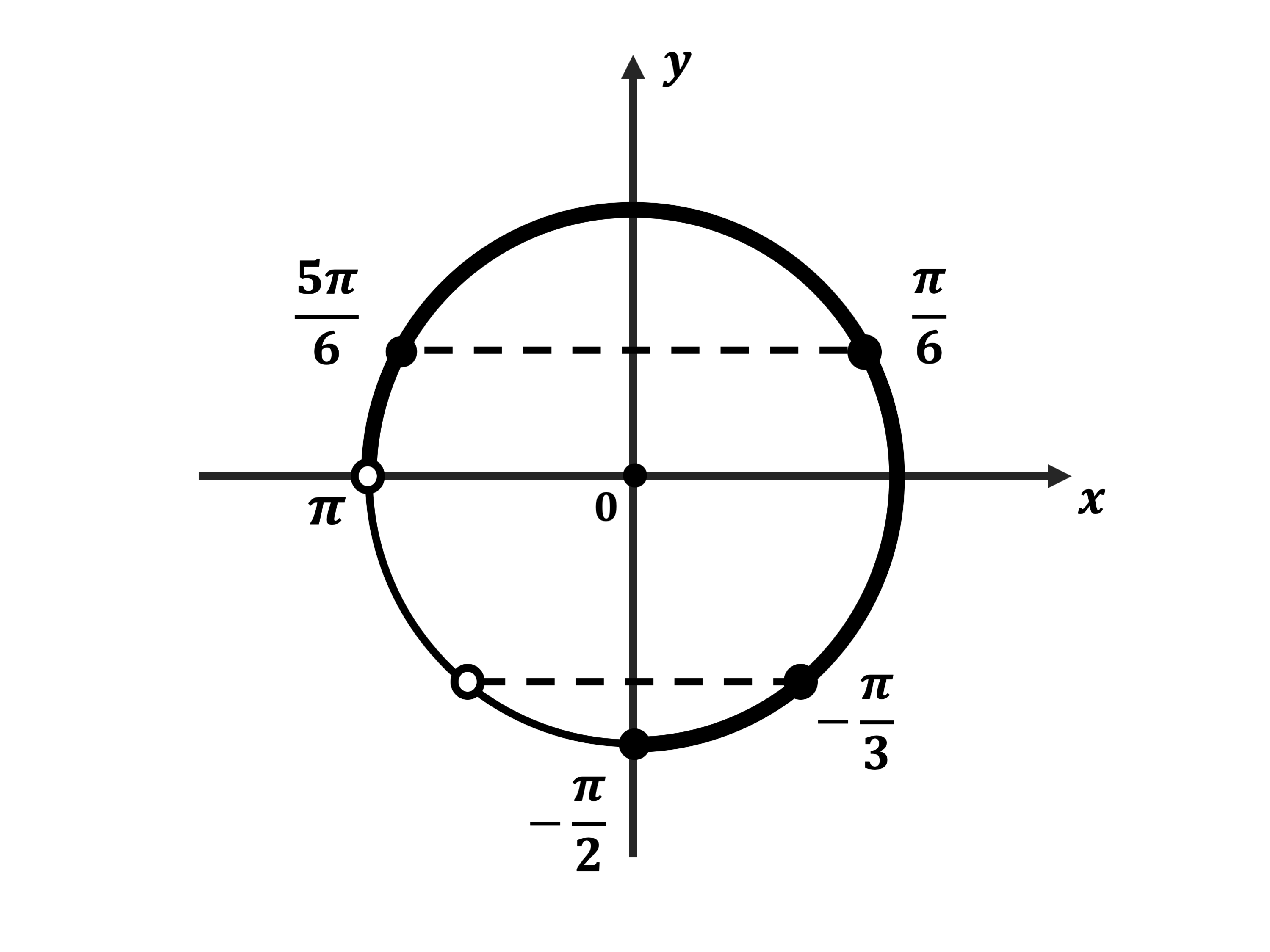
б) Отметим на тригонометрическом круге найденные серии решений и отрезок left[-3pi right.;left.-frac{3pi }{2}right].

Видим, что указанному отрезку принадлежат решения -frac{17pi }{6};-frac{5pi }{2};-frac{3pi }{2}.

Ответ: -frac{17pi }{6};-frac{5pi }{2};-frac{3pi }{2}.

Как отбирать решения с помощью тригонометрического круга? Вспомним, что крайняя правая точка тригонометрического круга соответствует числам -4 pi , -2 pi , 0, 2 pi , 4 pi dots Дальше всё просто. Смотрим, какая из точек этого типа попадает в указанный в условии промежуток. И к ней прибавляем (или вычитаем) нужные значения.

Например, вы нашли серию решений x=frac{pi }{3}+2pi n, где n — целое, а найти надо корни на отрезке [frac{5pi }{2};frac{9pi }{2}]. На указанном промежутке лежит точка 4 pi. От нее и отсчитываем.

Получим: x=4pi +frac{pi }{3}=frac{13pi }{3}.

2. а) Решите уравнение {({27}^{{cos x}})}^{{sin x}}=3^{frac{3{cos x}}{2}}

б) Найдите все корни этого уравнения, принадлежащие отрезку left[-pi ;frac{pi }{2}right].

Это уравнение — комбинированное. Кроме тригонометрии, применяем свойства степеней.

а) 3^{3{cos x{sin x}}}=3^{frac{3{cos x}}{2}}

Степени равны, их основания равны. Значит, равны и показатели.

3{cos x{sin x}}=frac{3{cos x}}{2}

2{cos x{sin x-{cos x=0}}}

{cos x({sin x-frac{1}{2})=0}}

Это ответ в пункте (а).

б) Отберем корни, принадлежащие отрезку left[-pi ;frac{pi }{2}right].

Отметим на тригонометрическом круге отрезок left[-pi ;frac{pi }{2}right] и найденные серии решений.

Видим, что указанному отрезку принадлежат точки x=-frac{pi }{2} и x=frac{pi }{2} из серии x=frac{pi }{2}+pi n,nin z.

Точки серии x=frac{5pi }{6}+2pi n,nin z не входят в указанный отрезок.

А из серии x=frac{pi }{6}+2pi n,nin z в указанный отрезок входит точка x=frac{pi }{6}.

Ответ в пункте (б): -frac{pi }{2},frac{pi }{6} , frac{pi }{2}.

3. а) Решите уравнение {cos 2x}+{{sin}^2 x=0,5}

б) Найдите все корни этого уравнения, принадлежащие отрезку left[-frac{7pi }{2}right.;left.-2pi right].

а)
{cos 2x}+{{sin}^2 x=0,5}

Применим формулу косинуса двойного угла: boldsymbol{cos2alpha =1-{2sin}^2alpha }

1-2{{sin}^2 x}+{{sin}^2 x}=0,5

{{-sin}^2 x=-0,5}

{{sin}^2 x=0,5}

Перенесем всё в левую часть уравнения и разложим по формуле разности квадратов.

Обратите внимание: мы отметили серии решений на тригонометрическом круге. Это помогло нам увидеть, как их записать одной формулой.

б) Для разнообразия отберем корни на отрезке left[-frac{7pi }{2}right.;left.-2pi right] с помощью двойного неравенства.

Сначала серия x=frac{pi }{4}+pi n,nin Z.

-frac{7pi }{2}le frac{pi }{4}+pi nle -2pi

-frac{7}{2}le frac{1}{4}+nle -2

-3,75le nle -2,25

n=-3, x_1=frac{pi }{4}-3pi =-frac{11pi }{4}

Теперь серия x=-frac{pi }{4}+pi n,nin Z

-frac{7pi }{2}le -frac{pi }{4}+pi nle -2pi

-frac{7}{2}le -frac{1}{4}+nle -2

-3,25le nle -1,75

n=-3, x_2=-frac{pi }{4}-3pi =-frac{13pi }{4}

n=-2, x_3=-frac{pi }{4}-2pi =-frac{9pi }{4}

Ответ: -frac{13pi }{4};-frac{11pi }{4};-frac{9pi }{4} .

Какой способ отбора корней лучше — с помощью тригонометрического круга или с помощью двойного неравенства? У каждого из них есть «плюсы» и «минусы».

Пользуясь тригонометрическим кругом, вы не ошибетесь. Вы видите и интервал, и сами серии решений. Это наглядный способ.

Зато, если интервал больше, чем один круг, удобнее отбирать корни с помощью двойного неравенства. Например, надо найти корни из серии x=-frac{pi }{4}+2pi n,nin Z на отрезке left[-frac{pi }{2}right.;left.20pi right]. Это больше 10 кругов! Конечно, в таком случае лучше решить двойное неравенство.

4. а) Решите уравнение left({tg}^2x-3right)sqrt{11{cos x}}=0.

б) Найдите все корни этого уравнения, принадлежащие отрезку left[-frac{5pi }{2};-pi right].

Самое сложное здесь — область допустимых значений (ОДЗ). Условие {11cos x}ge 0 заметно сразу. А условие {cos x}ne 0 появляется, поскольку в уравнении есть {tg x=frac{{sin x}}{{cos x}}}.

ОДЗ:

Уравнение равносильно системе:

Отберем решения с помощью тригонометрического круга. Нам нужны те серии решений, для которых , то есть те, что соответствуют точкам справа от оси Y.

Ответ в пункте а) x=pm frac{pi }{3}+2pi n, nin z

б) Отметим на тригонометрическом круге найденные серии решений и отрезок left[-frac{5pi }{2};-pi right].

Как обычно, ориентируемся на начало круга. Видим, что указанному промежутку принадлежат точки

x=frac{pi }{3}-2pi =-frac{5pi }{3} и x=-frac{pi }{3}-2pi =-frac{7pi }{3}.

5. а) Решите уравнение sqrt{{cos x+{sin x}}}({{cos}^2 x-frac{1}{2})=0}

б) Найдите корни, принадлежащие отрезку [-pi ;4pi ].

Выражение под корнем должно быть неотрицательно, а произведение двух множителей равно нулю тогда и только тогда, когда хотя бы один из них равен нулю.

Это значит, что уравнение равносильно системе:

Решим эту систему с помощью тригонометрического круга. Отметим на нем углы, для которых {cos x}=frac{sqrt{2}}{2} или {cos x}=-frac{sqrt{2}}{2}. Заметим, что среди них находятся и углы, для которых tgx=-1.

Числа серии x=-frac{3pi }{4}+2pi n не могут быть корнями исходного уравнения, т.к. для этих чисел не выполнено условие {cos x+{sin x}}ge 0. Остальные серии решений нас устраивают.

Тогда в ответ в пункте (а) войдут серии решений:

б) Отберем корни, принадлежащие отрезку [-pi ;4pi ] любым способом — с помощью тригонометрического круга или с помощью двойного неравенства.

На отрезке left[-pi ;0right] нам подходит корень x =-frac{pi }{4}.

На отрезке left[0;2pi right] нам подходят корни x=frac{pi }{4};frac{3pi }{4};frac{7pi }{4}.

На отрезке left[2pi ;4pi right] — корни x= frac{9pi }{4} ; frac{11pi }{4};frac{15pi }{4}.

Ответ в пункте б): -frac{pi }{4};frac{3pi }{4};frac{7pi }{4};frac{pi }{4};frac{9pi }{4} ; frac{11pi }{4};frac{15pi }{4}.

Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Задание №12. Уравнения u0026#8212; профильный ЕГЭ по математике» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
09.03.2023

Источник
Skip to content

Всё варианты 12 задания математика ЕГЭ Профиль 2022

Всё варианты 12 задания математика ЕГЭ Профиль 2022admin2022-08-03T22:19:54+03:00

Скачать задания в формате pdf.

Задания 12 ЕГЭ по математике профильного уровня 2022 год (уравнения)

1) (28.03.2022 досрочная волна) а) Решите уравнение    ({4^{sin x}} + {4^{sin left( {pi  + x} right)}} = frac{5}{2}.)

б) Найдите все корни этого уравнения, принадлежащие промежутку (left[ {frac{{{text{5}}pi }}{2};;4pi } right]).

ОТВЕТ: а) ( pm frac{pi }{6} + pi k;;;k in Z;)  б) (frac{{17pi }}{6};,,,,,frac{{19pi }}{6};,,,,,frac{{{text{23}}pi }}{6}.)

2) (28.03.2022 досрочная волна) а) Решите уравнение     ({81^{cos x}} — 12 cdot {9^{cos x}} + 27 = 0.)

б) Найдите все корни этого уравнения, принадлежащие промежутку (left[ { — ,4pi ;,,, — frac{{{text{5}}pi }}{2}} right]).

ОТВЕТ: а) ( pm frac{pi }{3} + 2pi k;;;2pi k;;;k in Z;)  б) ( — frac{{11pi }}{3};,,,, — 4pi .)

3) (28.03.2022 досрочная волна) а) Решите уравнение     ({16^{sin x}} — 1,5 cdot {4^{sin x + 1}} + 8 = 0.)

б) Найдите все корни этого уравнения, принадлежащие промежутку (left[ { — ,5pi ;,,, — frac{{{text{7}}pi }}{2}} right]).

ОТВЕТ:  а) (frac{pi }{6} + 2pi k;,,;frac{{{text{5}}pi }}{6} + 2pi k;;;frac{pi }{2} + 2pi k;;;k in Z;)  б) ( — frac{{{text{23}}pi }}{6};,,,, — frac{{7pi }}{2}.)

4) (02.06.2022 основная волна) а) Решите уравнение      (2{sin ^2}x — cos left( { — x} right) — 1 = 0.)

б) Найдите все корни этого уравнения, принадлежащие промежутку (left[ { — ,pi ;,,,frac{pi }{2}} right]).

ОТВЕТ:  а) ( pm frac{pi }{3} + 2pi k;,,;pi  + 2pi k;;;k in Z;)  б) ( — pi ;,,, — frac{pi }{3};,,,,frac{pi }{3}.)

5) (06.2022 основная волна) а) Решите уравнение      (2{cos ^2}x — 3sinleft( { — x} right) — 3 = 0.)

б) Найдите все корни этого уравнения, принадлежащие промежутку (left[ {frac{{{text{5}}pi }}{2};,,4pi } right]).

ОТВЕТ:  а) (frac{pi }{6} + 2pi k;,,;frac{{{text{5}}pi }}{6} + 2pi k;;;frac{pi }{2} + 2pi k;;;k in Z;)  б) (frac{{{text{17}}pi }}{6};,,,,frac{{{text{5}}pi }}{2}.)

6) (06.2022 основная волна) а) Решите уравнение     (cos 2x + sinleft( { — x} right) — 1 = 0.)

б) Найдите все корни этого уравнения, принадлежащие промежутку (left[ {frac{pi }{2};,,2pi } right]).

ОТВЕТ:  а) ( — frac{pi }{6} + 2pi k;,,; — frac{{{text{5}}pi }}{6} + 2pi k;;;pi k;;;k in Z;)  б) (pi ;,,,,frac{{{text{7}}pi }}{6};,,,,frac{{{text{11}}pi }}{6};,,,2pi .)

7) (06.2022 основная волна) а) Решите уравнение     (cos 2x + 3sinleft( { — x} right) — 2 = 0.)

б) Найдите все корни этого уравнения, принадлежащие промежутку (left[ {frac{{{text{3}}pi }}{2};,,3pi } right]).

ОТВЕТ:  а) ( — frac{pi }{6} + 2pi k;,,; — frac{{{text{5}}pi }}{6} + 2pi k;;; — frac{pi }{{text{2}}}{text{ + 2}}pi k;;;k in Z;)  б) (frac{{{text{3}}pi }}{2};,,,,frac{{{text{11}}pi }}{6}.)

8) (06.2022 основная волна) а) Решите уравнение     (sin 2x — 2sin x + 2cos x — 2 = 0.)

б) Найдите все корни этого уравнения, принадлежащие промежутку (left[ {{text{3}}pi ;,,frac{{{text{9}}pi }}{2}} right]).

ОТВЕТ:  а) ( — frac{pi }{2} + 2pi k;,,;2pi k;;;;k in Z;)  б) (frac{{{text{7}}pi }}{2};,,,4pi .)

9) (06.2022 основная волна) а) Решите уравнение     (sin 2x + 2sin left( { — x} right) + cos left( { — x} right) — 1 = 0.)

б) Найдите все корни этого уравнения, принадлежащие промежутку (left[ {{text{2}}pi ;,,frac{{{text{7}}pi }}{2}} right]).

ОТВЕТ:  а) ( — frac{pi }{6} + 2pi k;,,; — frac{{{text{5}}pi }}{6} + 2pi k;;;2pi k;;;k in Z;)  б) (frac{{{text{19}}pi }}{6};,,,2pi .)

10) (27.06.2022 резервная волна) а) Решите уравнение     ({log _{11}}left( {2{{sin }^2}x + 7sqrt 3 sin x — 11} right) = 0.)

б) Найдите все корни этого уравнения, принадлежащие промежутку (left[ {frac{{{text{3}}pi }}{2};,,3pi } right]).

ОТВЕТ:  а) (frac{pi }{3} + 2pi k;,,;frac{{{text{2}}pi }}{3} + 2pi k;;;k in Z;)  б) (frac{{{text{7}}pi }}{3};,,,frac{{{text{8}}pi }}{3}.)

11) (27.06.2022 резервная волна) а) Решите уравнение    ({log _9}left( {sqrt 2 sin x + sin 2x + 9} right) = 1.)

б) Найдите все корни этого уравнения, принадлежащие промежутку (left[ { — frac{{{text{7}}pi }}{2};,, — 2pi } right]).

ОТВЕТ:  а) ( pm frac{{{text{3}}pi }}{4} + 2pi k;,,;;pi k;;;k in Z;)  б) ( — frac{{{text{13}}pi }}{4};,, — 3pi ;,,, — frac{{{text{11}}pi }}{4};,, — 2pi .)

Источник


Пройти тестирование по 10 заданиям
Пройти тестирование по всем заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

1

а)  Решите уравнение логарифм по основанию 5 левая круглая скобка 2 минус x правая круглая скобка = логарифм по основанию левая круглая скобка 25 правая круглая скобка x в степени 4 .

б)  Укажите корни этого уравнения, принадлежащие отрезку левая квадратная скобка логарифм по основанию 9 дробь: числитель: 1, знаменатель: { конец дроби 82; логарифм по основанию 9 8 правая квадратная скобка .

Источник: Задания 13 (С1) ЕГЭ 2014, Задания 13 (С1) ЕГЭ 2019

2

а)  Решите уравнение логарифм по основанию 2 левая круглая скобка x в квадрате минус 14x правая круглая скобка =5.

б)  Укажите корни этого уравнения, принадлежащие отрезку левая квадратная скобка логарифм по основанию 3 0,1; 5 корень из 10 правая квадратная скобка .

Источник: ЕГЭ по математике 28.06.2017. Резервный день. Вариант 501 (C часть), Задания 13 (С1) ЕГЭ 2017

3

а)  Решите уравнение 9 в степени левая круглая скобка x минус дробь: числитель: 1, знаменатель: 2 конец дроби правая круглая скобка минус 8 умножить на 3 в степени левая круглая скобка x минус 1 правая круглая скобка плюс 5=0.

б)  Найдите все корни этого уравнения, принадлежащие промежутку левая круглая скобка 1, дробь: числитель: 7, знаменатель: 3 конец дроби правая круглая скобка .

Источник: ЕГЭ по математике 19.06.2013. Основная волна, резервная волна. Центр. Вариант 502, Задания 13 (С1) ЕГЭ 2013

4

а)  Решите уравнение: 4 в степени левая круглая скобка x правая круглая скобка минус 2 в степени левая круглая скобка x плюс 3 правая круглая скобка плюс 15=0.

б)  Определите, какие из его корней принадлежат отрезку левая квадратная скобка 2; корень из 10 правая квадратная скобка .

Источник: Пробный экзамен Санкт-Петербург, 11.04.2017. Вариант 1., Пробный экзамен Санкт-Петербург, 11.04.2017. Вариант 1. (C часть).

5

а)  Решите уравнение 6 логарифм по основанию 8 в квадрате x минус 5 логарифм по основанию 8 x плюс 1=0.

б)  Найдите все корни этого уравнения, принадлежащие отрезку левая квадратная скобка 2;2,5 правая квадратная скобка .

Источник: Задания 13 (С1) ЕГЭ 2016, ЕГЭ по математике 06.06.2016. Основная волна. Вариант 701 (C часть).

Пройти тестирование по этим заданиям

Источник
ЕГЭ по математике профиль

Прототипы задания №12 ЕГЭ по математике профильного уровня — уравнения. Практический материал для подготовки к экзамену в 11 классе.

Для успешного выполнения задания №12 необходимо уметь решать уравнения и неравенства.

Практика

Коды проверяемых элементов содержания (по кодификатору) — 2.1, 2.2

Уровень сложности задания — повышенный.

Максимальный балл за выполнение задания — 2

Примерное время выполнения задания выпускником, изучавшим математику на профильном уровне (в мин.) — 10

Связанные страницы:

Источник

Значения функции: наибольшее и наименьшее

В задании №12 ЕГЭ по математике профильного уровня нам необходимо найти наибольшее или наименьшее значение функции. Для этого необходимо воспользоваться, очевидно, производной. Посмотрим на типовом примере.

Разбор типовых вариантов заданий №12 ЕГЭ по математике профильного уровня

Первый вариант задания (демонстрационный вариант 2018)

[su_note note_color=”#defae6″]

Найти точку максимума функции y = ln(x+4)2+2x+7.

[/su_note]

Алгоритм решения:
  1. Определяем область определения функции.
  2. Находим производную.
  3. Определяем, в каких точках производная равна 0.
  4. Исключаем точки, не принадлежащие области определения.
  5. Среди оставшихся точек ищем значения х, в которых функция имеет максимум.
  6. Записываем ответ.
Решение:

1. Ищем значения х, при которых логарифм имеет смысл. Для этого решаем неравенство:

(x+4)2 > 0

Поскольку квадрат любого числа неотрицателен. Решением неравенства будет лишь то значение х, при котором х+4≠ 0, т.е. при х≠-4.

2. Находим производную:

у’=(ln(x+4)2 + 2x + 7)’

По свойству логарифма получаем:

у’=(ln(x+4)2 )’+(2x)’+(7)’.

По формуле производной сложной функции:

(lnf)’=(1/f)∙f’. У нас f=(x+4)2

у, = (ln(x+4)2 )’+ 2 + 0 = (1/(x+4)2 )∙((x+4)2)’ + 2=(1/(x+4)2 2)∙(х2 + 8х + 16)’ +2=2(х + 4) /((х + 4)2) + 2

у’= 2/(х + 4) + 2

3. Приравниваем производную к нулю:

у, = 0 → (2+2∙(х + 4))/(х + 4)=0,

2 +2х +8 =0, 2х + 10 = 0,

2х = -10,

х = -5

Ответ: -5.

Второй вариант задания (из Ященко, №1)

[su_note note_color=”#defae6″]

Найдите точку минимума функции y = x – ln(x+6) + 3.

[/su_note]

Алгоритм решения:
  1. Определяем область определения функции.
  2. Находим производную.
  3. Определяем, в каких точках производная равна 0.
  4. Исключаем точки, не принадлежащие области определения.
  5. Среди оставшихся точек ищем значения х, в которых функция имеет минимум.
  6. Записываем ответ.
Решение:

1. ОДЗ: .

2. Найдем производную функции:

3. Приравниваем полученное выражение к нулю:

4. Получили одну точку x=-5, принадлежащую области определения функции.

5. В этой точке функция имеет экстремум. Проверим, минимум ли это. При х=-4

При х=-5,5 производная функции отрицательна, так как

Значит, точка х=-5 является точкой минимума.

Ответ: -5.

Третий вариант задания (из Ященко, №12)

[su_note note_color=”#defae6″]

Найдите наибольшее значение функции http://self-edu.ru/htm/ege2016_36/files/6_12.files/image001.gif  на отрезке [-3; 1].

[/su_note]

Алгоритм решения:.
  1. Находим производную.
  2. Определяем, в каких точках производная равна 0.
  3. Исключаем точки, не принадлежащие заданному отрезку.
  4. Среди оставшихся точек ищем значения х, в которых функция имеет максимум.
  5. Находим значения функции на концах отрезка.
  6. Ищем среди полученных значений наибольшее.
  7. Записываем ответ.
Решение:

1. Вычисляем производную от функции, получим

2. Приравниваем производную к нулю:

Решение уравнения дает два корня

 – не принадлежит множеству действительных чисел

.

3. Значение  и остается одна точка .

4. Вычисляем значения функции в точке -2 и на концах отрезка -3 и 1, получим:

Наибольшее значение функции на заданном отрезке равно 48 в точке х=-2.

Ответ: 48.

Даниил Романович | Просмотров: 11.8k

Источник

За это задание ты можешь получить 2 балла. На решение дается около 10 минут. Уровень сложности: повышенный.
Средний процент выполнения: 45.3%
Ответом к заданию 12 по математике (профильной) может быть развернутый ответ (полная запись решения с обоснованием выполненных действий).

Разбор сложных заданий в тг-канале

Задачи для практики

Задача 1

а) Решите уравнение $11cos 2x=7sin (x-{π} / {2})-9$.

б) Укажите корни этого уравнения, принадлежащие отрезку $[-π;0]$.

Решение

а) $11cos 2x=7sin (x-{π} / {2})-9$,

$11(2cos^2 x-1)=-7cos x-9$,

$22cos^2 x -11+7cos x +9=0$,

$22cos^2 x+7cos x -2=0$.

Обозначим $cos x=t$, $|t|⩽1$.

Тогда уравнение примет вид: $22t^2+7t-2=0$.

Решим его. $22t^2+7t-2=0$,

$D=49+2⋅ 4⋅ 22=225$. $t_{1,2}={-7±15} / {44}$,

$t_1=-{1} / {2}$, $t_2={8} / {44}={2} / {11}$.

$1$. $cos x=-{1} / {2}$, $x=±(π-{π} / {3})+2π n$;

$x=± {2π} / {3}+2π n$, $n∈ Z$.

$2$. $cos x={2} / {11}$, $x=± arccos {2} / {11}+2π k$, $k∈ Z$.

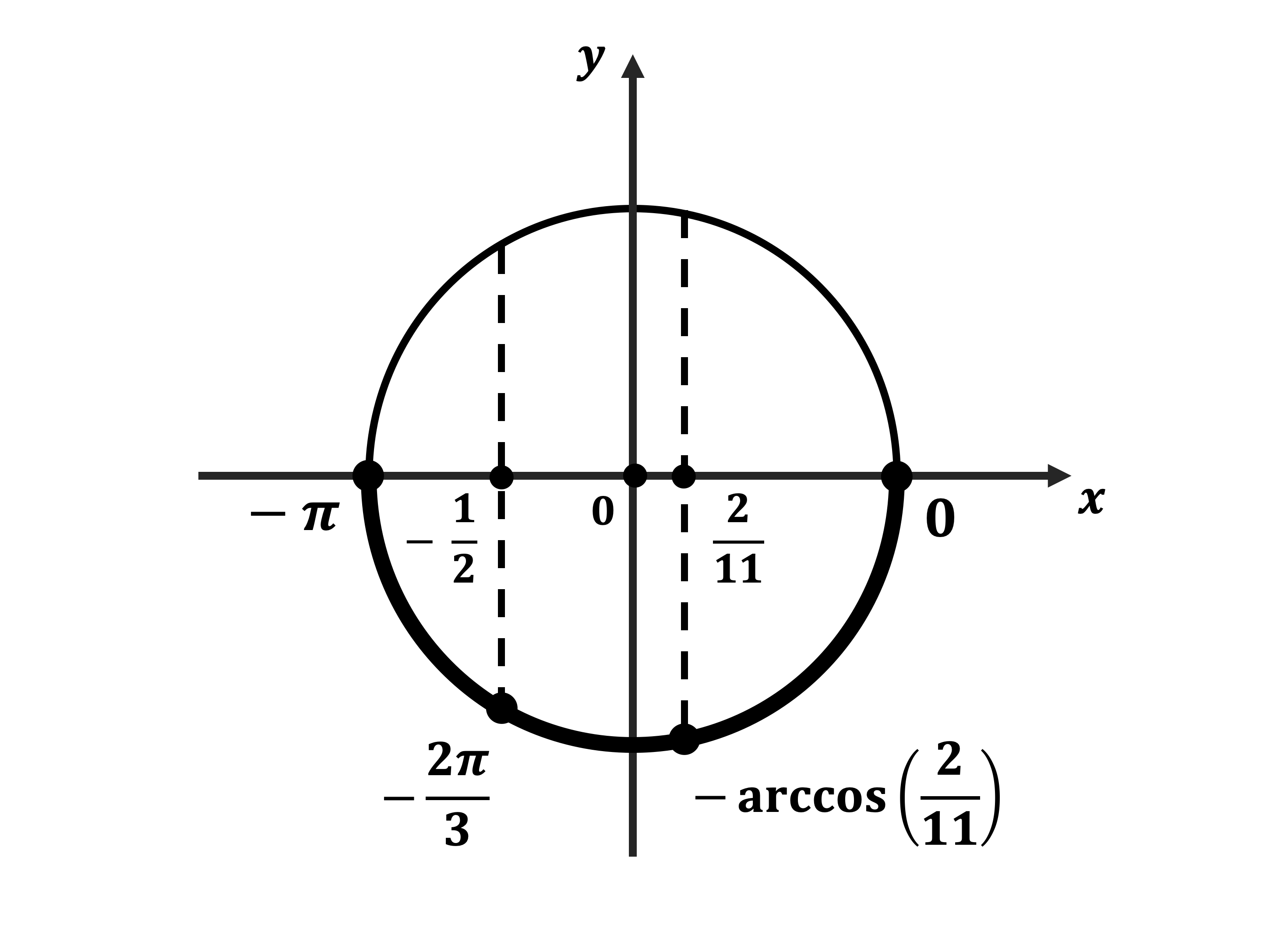
б) Найдём корни этого уравнения, принадлежащие промежутку $[-π;0]$.

$x_1=-π+{π} / {3}=-{2π} / {3}$

$x_2=-arccos {2} / {11}$.

Ответ: а)$± {2π} / {3}+2πn, n∈ Z; ± arccos {2} / {11}+2π k, k∈ Z;б)-{2π}/{3}, -arccos{2}/{11}$

Задача 2

а) Решите уравнение $2 sin^2 x — 7 cos(x + {π}/{2})- 4 = 0$.

б) Найдите все корни этого уравнения, принадлежащие промежутку $[-2π;-{π}/{2}]$.

Решение

а) Преобразуем уравнение, согласно формуле приведения:

$cos(x+{π}/{2})=-sinx,$

$2sin^2x + 7sinx -4 = 0$

Обозначим $sin x = t, −1 ≤ t ≤ 1$, получим

$2t^2 + 7t -4 = 0.$

$t_1 = {−7 − 9}/{2·2} = −4$ — не удовлетворяет условию $−1 ≤ t ≤ 1. $

$t_2 = {−7 + 9}/{2·2} = {1}/{2}$.

Вернёмся к исходной переменной:

$sinx ={1}/{2}$,

$x = {π}/{6} + 2πn, n ∈ Z$

$x = {5π}/{6} + 2πk, k ∈ Z$

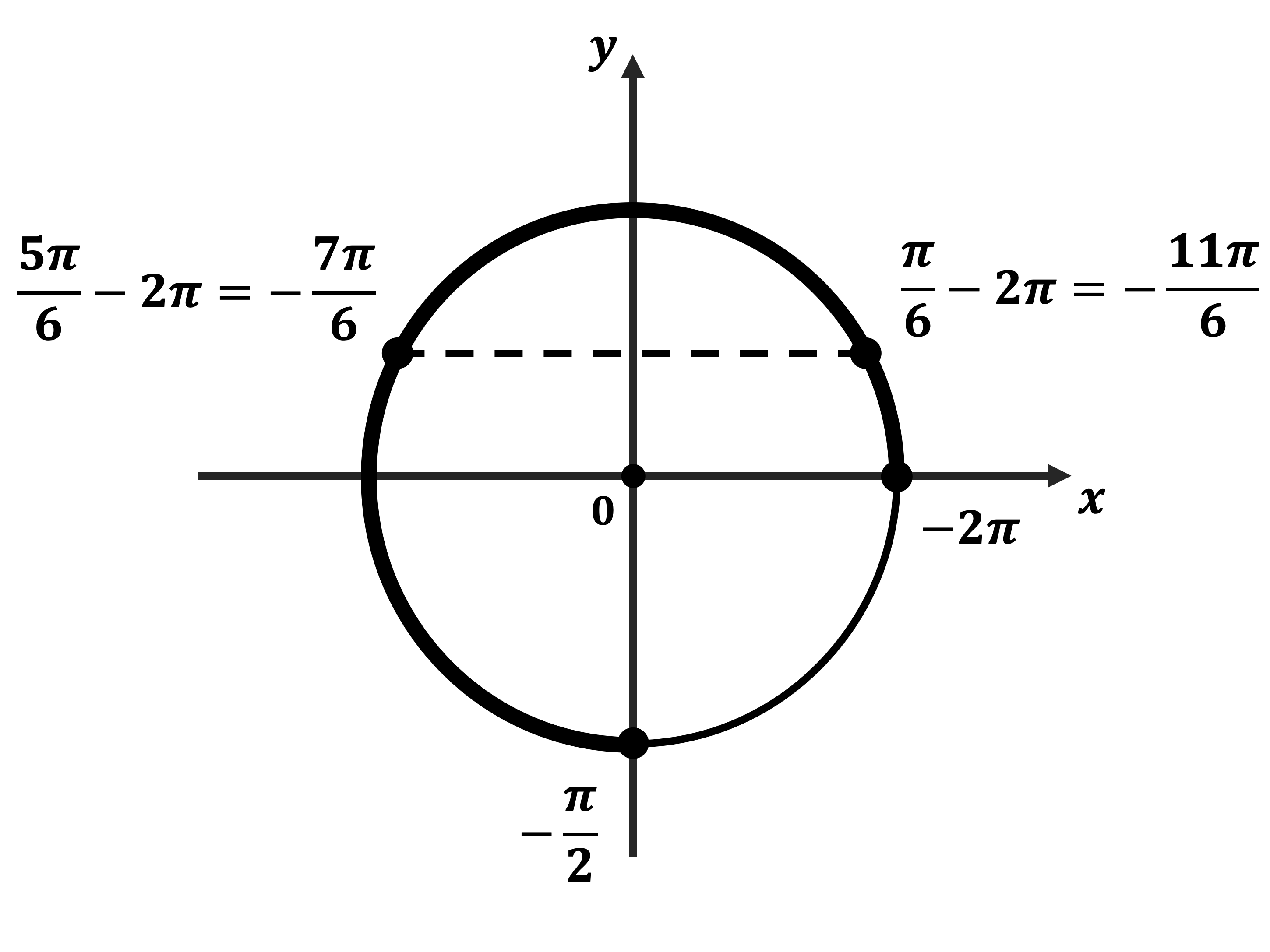
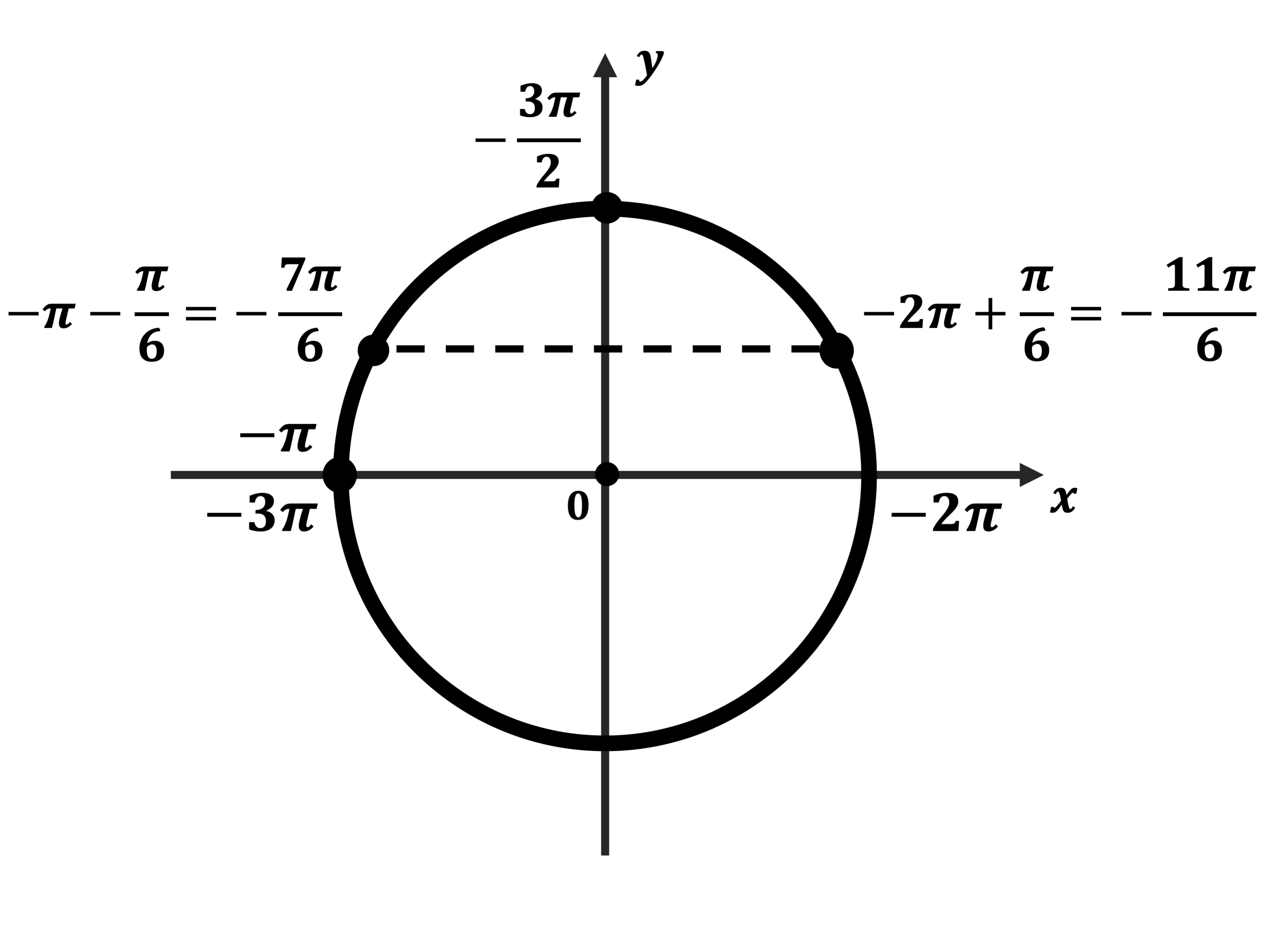
б) Корни, принадлежащие отрезку $[-2π; -{π}/{2}]$, найдём с помощью единичной окружности. Получим: ${π}/{6}-2π=-{11π}/{6}; {5π}/{6}-2π=-{7π}/{6}$.

Ответ: а) $ {π}/{6} + 2πn, n ∈ Z$; $ {5π}/{6} + 2πk, k ∈ Z$ б) $-{11π}/{6};-{7π}/{6}$

Задача 3

а) Решите уравнение $2 cos^2 x — 5 sin(x + {3π}/{2})+ 2 = 0$.

б) Найдите все корни этого уравнения, принадлежащие промежутку $[{π}/{2};{3π}/{2}]$.

Решение

а) Преобразуем уравнение, согласно формуле приведения:

$sin(x+{3π}/{2})=-cosx,$

$2cos^2x + 5 cos x + 2 = 0$

Обозначим $cos x = t, −1 ≤ t ≤ 1$, получим $2t^2 + 5t + 2 = 0. t_1 = {−5 − 3}/{2·2} = −2$ — не удовлетворяет условию $−1 ≤ t ≤ 1. t_2 = {−5 + 3}/{2· 2} = −{1}/{2}$.

Вернёмся к исходной переменной: $cos x = − {1}/{2}$,

$x = ±(π − {π}/{3}) + 2πn, n ∈ Z , x = ±{2π}/{3} + 2πn, n ∈ Z.$

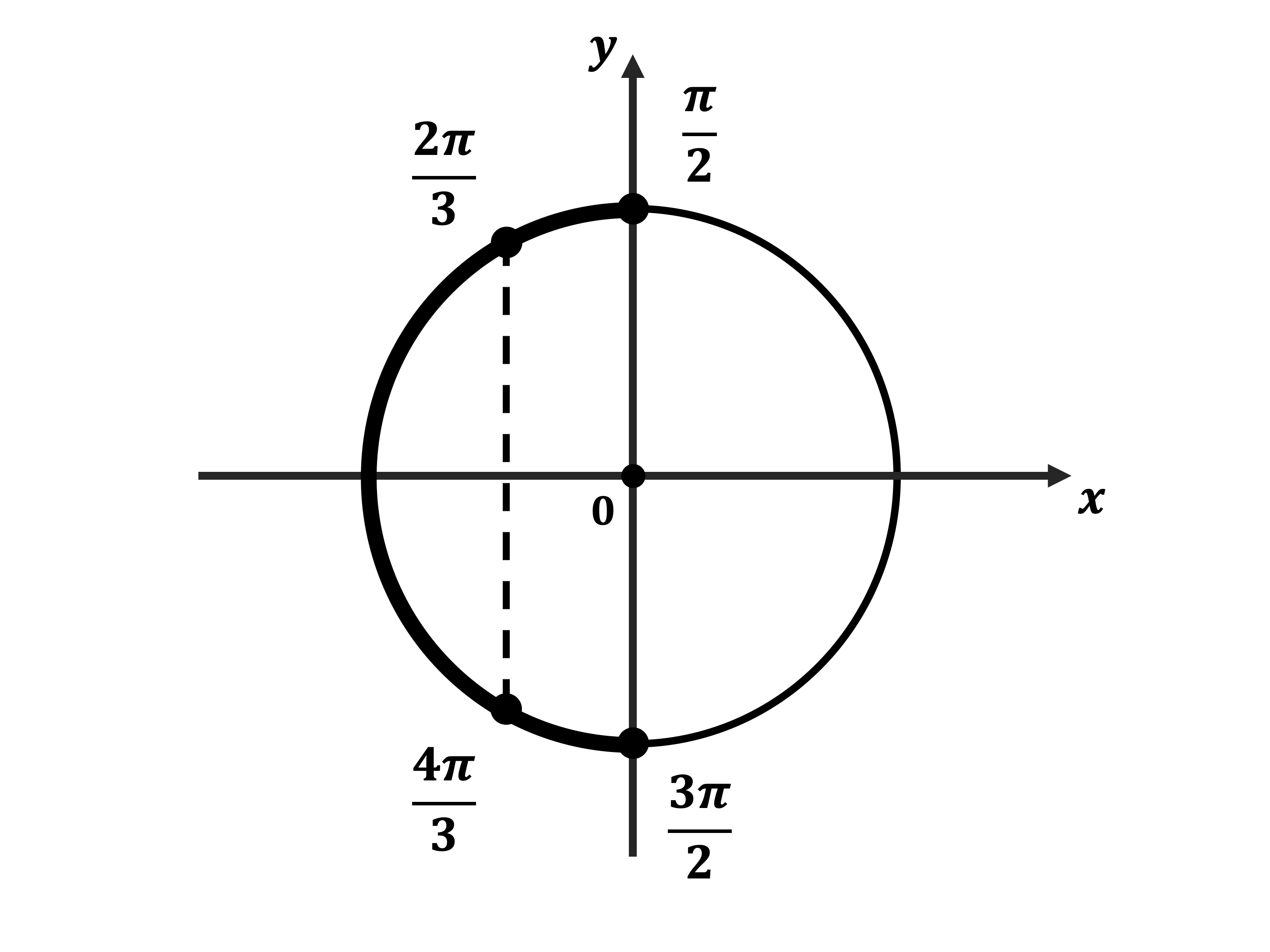
б) Корни, принадлежащие отрезку $[{π}/{2}; {3π}/{2}]$, найдём с помощью единичной окружности. Получим числа ${2π}/{3}; {4π}/{3}$.

Ответ: а)$±{2π}/{3}+2πn,n∈Z;$ б) ${2π}/{3};{4π}/{3}$

Задача 4

а) Решите уравнение $cos(x — {3π}/{2})= sin 2x$.

б) Найдите все корни этого уравнения, принадлежащие промежутку $[-{3π}/{2};0]$.

Решение

а) Преобразуем уравнение:

$−sin x = sin 2x,$

$sinx + 2 sin x cos x = 0,$

$sinx(1 + 2 cos x) = 0,$

$sin x = 0;x = πn, n ∈ Z,$

$cosx = -{1}/{2}; x = ±{2π}/{3} + 2πk, k ∈ Z .,$

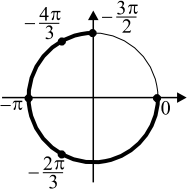
б) Корни, принадлежащие отрезку $[-{3π}/{2};0]$, найдём с помощью единичной окружности. Получим числа $−{4π}/{3}; −π; −{2π}/{3}; 0$.

Ответ: а) $x=±{2π}/{3}+2πk;x=πn,k,n∈Z$ б) $-{4π}/{3};-π;-{2π}/{3};0$.

Задача 5

а) Решите уравнение $sin({π}/{2}+ x)= sin (-2x)$.

б) Найдите все корни этого уравнения, принадлежащие промежутку $[0; π]$.

Решение

а) Преобразуем уравнение:

$cos x = − sin 2x,$

$cos x + 2 sin x cos x = 0,$

$cos x(1 + 2 sin x) = 0,$

$cos x = 0;$

$x = {π}/{2} + πn, n ∈ Z$

$sin x = −{1}/{2},$

$x = (−1)^{k+1}·{π}/{6} + πk, k ∈ Z$

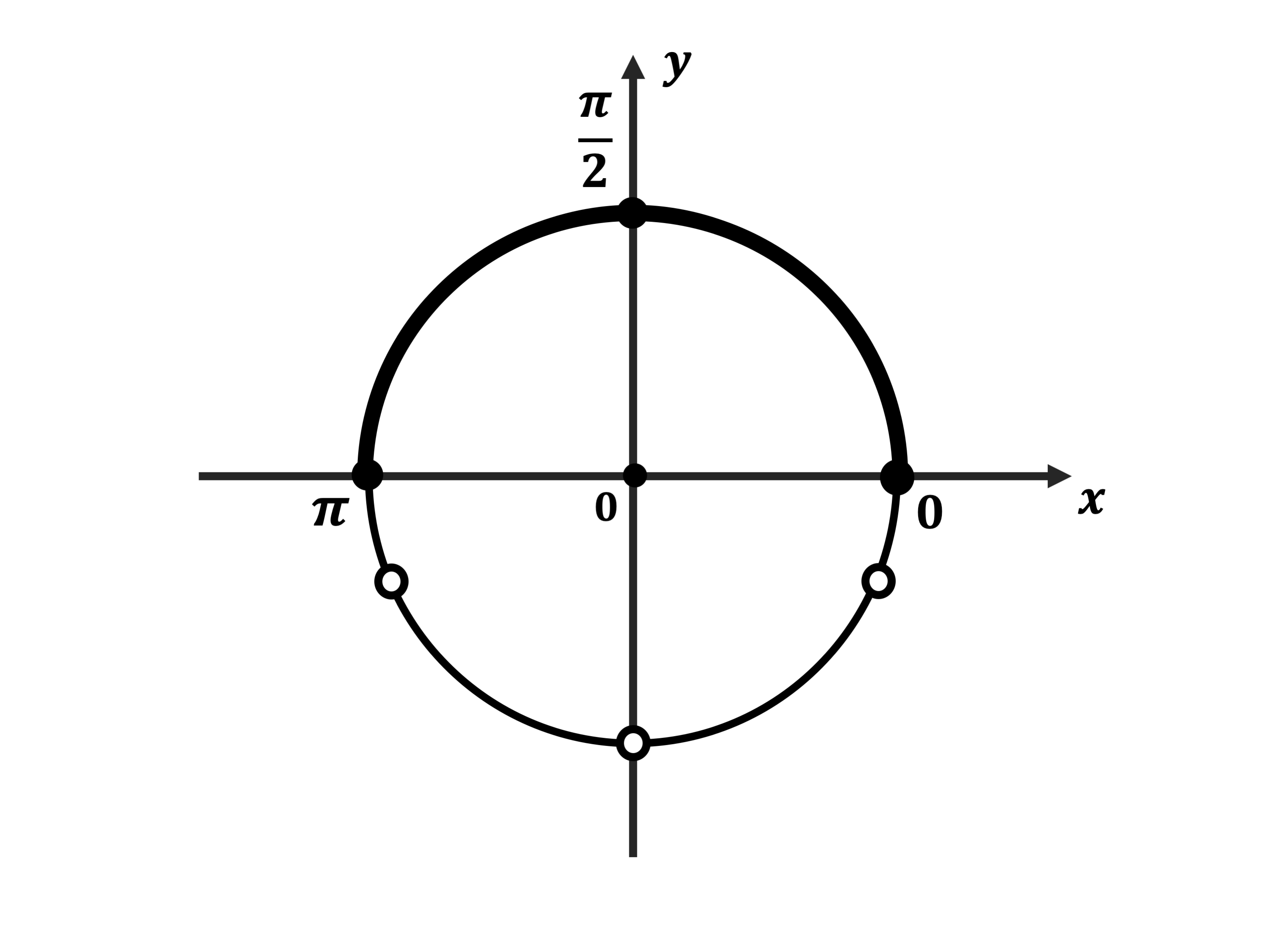
б) Корни, принадлежащие отрезку $[0; π]$, найдём с помощью единичной окружности.

Указанному промежутку принадлежит единственное число ${π}/{2}$.

Ответ: а) ${π}/{2}+πn,n∈Z;(-1)^{k+1}{π}/{6}+πk,k∈Z$; б) ${π}/{2}$

Задача 6

а) Решите уравнение $sin x(2 sin x — 1) + √3 sin x + sin {4π}/{3}= 0$.

б) Найдите все корни этого уравнения, принадлежащие промежутку $[-{π}/{2};π]$.

Решение

а) Решим уравнение $sinx(2sinx-1) +√3sinx + sin{4π}/{3} = 0$.

Так как $sin{4π}/{3} = sin(π +{π}/{3}) = − sin{π}/{3} = −{√3}/{2}$, то уравнение примет вид $sin x(2 sin x-1) +√3 sin x-{√3}/{2} = 0$. Отсюда $2 sin x(sin x-{1}/{2})+ √3(sin x-{1}/{2}) = 0; (2sinx+√3)(sin x-{1}/{2}) = 0$.

Тогда $sin x = {1}/{2}; x = (−1)^n{π}/{6} + πn$ или $sin x = −{√3}/{2}; x = (−1)^{n+1}{π}/{3} + πn$, где $n ∈ Z.$

б) Корни, принадлежащие промежутку $[−{π}/{2}; π]$, найдём с помощью числовой окружности: $−{π}/{3}; {π}/{6}; {5π}/{6}$.

Ответ: а)$(-1)^{n}{π}/{6}+πn;(-1)^{n+1}{π}/{3}+πn,n∈Z$; б) $-{π}/{3};{π}/{6};{5π}/{6}$

Задача 7

а) Решите уравнение $4cos^{2}x = 3cos2x + 1$.

б) Найдите корни уравнения, принадлежащие отрезку $[-4π;-{5π}/{4})$.

Решение

a) $4cos^{2}x = 3cos2x+1$,

$4cos^{2}x = 3(2cos^{2}x-1)+1$,

$4cos^{2}x=6cos^{2}x-3+1$,

$cos^{2}x=1, [tablecosx=1; cosx=-1;$ $[tablex=2πn, n ∈ Z; x=π+2πk, k ∈ Z;$ $x=πk, k ∈ Z$

б) Корни, принадлежащие промежутку $[-4π;-{5π}/{4})$, найдем из неравенства $-4π ≤ πk < -{5π}/{4}; k=-4, -3, -2$

$x_1=-4π, x_2=-3π, x_3=-2π$.

Ответ: а)$πn,n∈Z$;б)$-4π;-3π;-π$

Задача 8

а) Решите уравнение $cos (2x) + 3 sin x — 2 = 0$.

б) Найдите корни уравнения, принадлежащие отрезку $[-3π;-π]$.

Решение

a) $cos(2x) + 3sinx-2=0$,

$1 — 2sin^{2}x + 3 sin x -2 = 0$,

$2 sin^{2}x — 3sin x +1 = 0$,

Пусть $sin x = y, |sinx| ≤ 1$, уравнение примет вид

$2y^2 — 3y + 1 = 0$,

$y_{1,2} = {3±√{9-8}}/{4} = {3±1}/{4};$

$ y_1=1, y_2={1}/{2}$.

$sin x = 1, x = {π}/{2}+2πn, n ∈ Z; sinx={1}/{2}, x=(-1)^{k}{π}/{6} + πk, k ∈ Z$.

б) Найдём корни уравнения на отрезке $[-3π;-π]$.

С помощью числовой окружности отберём корни уравнения, принадлежащие $[-3π;-π]$.

Это числа $-{11π}/{6}, -{3π}/{2}, -{7π}/{6}$.

Ответ: а)${π}/{2}+2πn,n∈Z;(-1)^{k}{π}/{6}+πk,k∈Z$;б)$-{11π}/{6};-{3π}/{2};-{7π}/{6}$

Задача 9

а) Решите уравнение $2 cos^2 x + 19 sin x + 8 = 0$.

б) Найдите корни уравнения, принадлежащие отрезку $[-π;{π}/{2}]$.

Решение

a) $2 cos^{2}x + 19sinx+8=0$,

$2(1 — sin^{2}x) + 19 sin x +8 = 0$,

$-2 sin^{2}x + 19 sin x +10 = 0$,

$2 sin^{2}x — 19 sin x -10 = 0$.

Пусть $sin x = y, |y| ≤ 1$, уравнение примет вид $2y^2 — 19y -10 = 0$, решим его: $y_{1,2} = {19±√{361 + 80}}/{4} = {19±21}/{4}$.

$y_1 = 10$ или $y_2 = -{1}/{2}$. $y_1=10$ не удовлетворяет условию $|y| ≤ 1$. $sin x = -{1}/{2}, x = (-1)^{n+1}{π}/{6} + πn, n ∈ Z$.

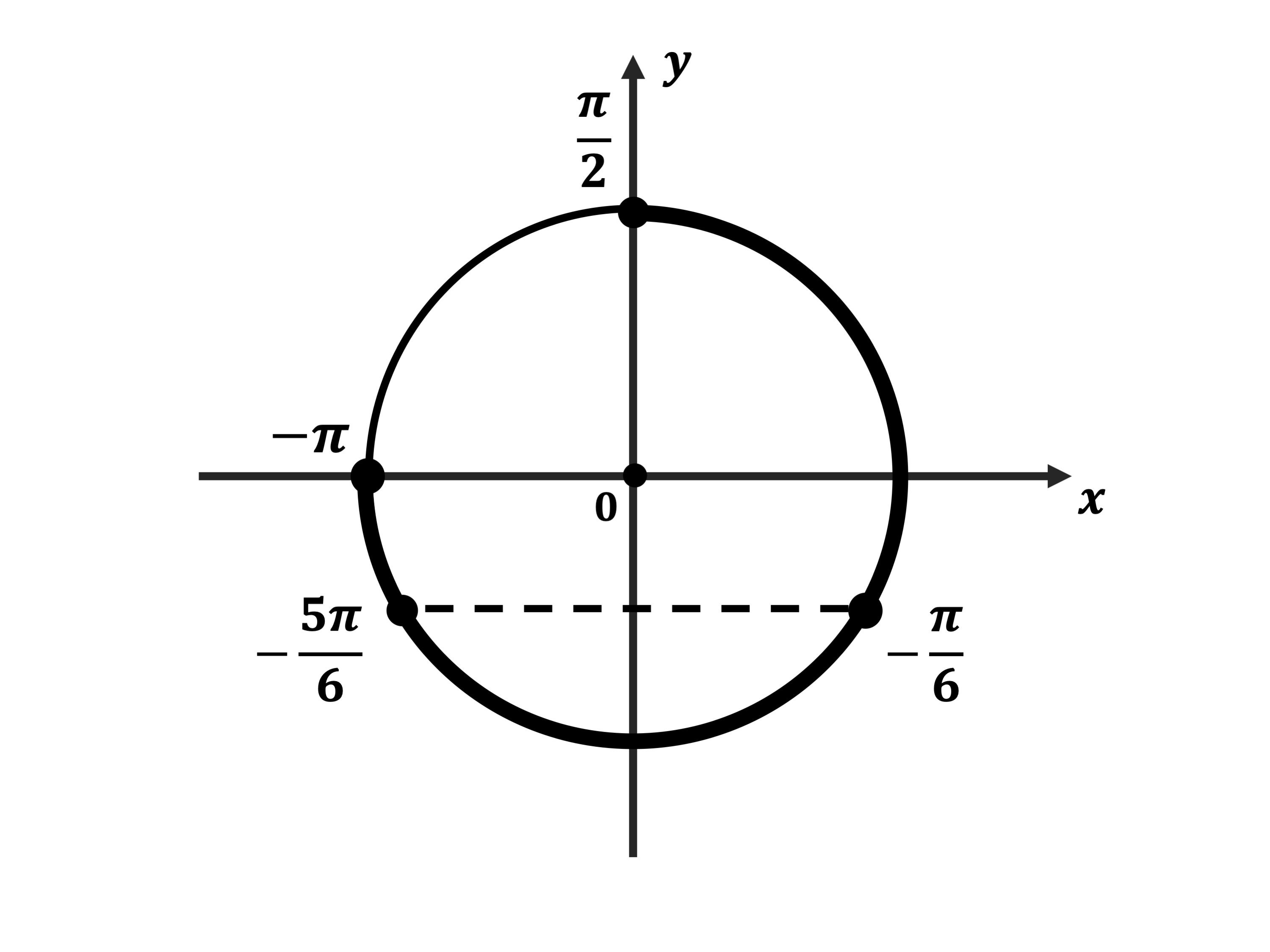
б) Найдём корни уравнения на отрезке $[-π;{π}/{2}]$.

Это числа $-{5π}/{6}$ и $-{π}/{6}$.

Ответ: а)$(-1)^{n+1}{π}/{6}+πn,n∈Z$; б) $-{5π}/{6},-{π}/{6}$

Задача 10

а) Решите уравнение $8sin x + 4 cos^2 x = 7$.

б) Найдите корни уравнения, принадлежащие отрезку $[-{3π}/{2};-{π}/{2}]$.

Решение

a) $8 sin x + 4 cos^{2} x = 7$,

$4(1 — sin^{2}x) + 8 sin x — 7 = 0$,

$-4 sin^{2}x + 8 sin x — 3 = 0$,

$4 sin^{2}x — 8 sin x + 3 = 0$.

Пусть $sin x = t, |t| ≤ 1$, уравнение примет вид $4t^2 — 8t + 3 = 0$, решим его: $t_{1,2} = {8±√{64 — 48}}/{8} = {8±√{16}}/{8} = {8±4}/{8} = 1±{1}/{2}$.

$t_1 = {1}/{2}$ или $t_2 = {3}/{2}$. $t_2$ не удовлетворяет условию $|t| ≤ 1$. $sin x = {1}/{2}, x = (-1)^{n}{π}/{6} + πn, n ∈ Z$.

б) Найдём корни уравнения на отрезке $[-{3π}/{2};-{π}/{2}]$.

Это число ${5π}/{6} — 2π = -{7π}/{6}$.

Ответ: а)$(-1)^{n}{π}/{6}+πn,n∈Z$;б)$-{7π}/{6}$

Задача 11

а) Решите уравнение ${sin 2x}/{sin({3π}/{2}+ x)}= 1$.

б) Укажите корни этого уравнения, принадлежащие промежутку $(3π;{9π}/{2})$.

Решение

а) ${{sin2x}/{sin({3π}/{2} + x)} = 1$.

Зная, что $sin2x = 2sinxcosx$ и $sin({3π}/{2}+ x)= −cosx$, получим: ${2sinxcosx}/{−cosx}= 1$, где $cosx≠0, x≠{π}/{2}+ πm, m ∈ Z$.

$−2sinx = 1, sinx =−{1}/{2}$.

$x=−{π}/{6}+2πn, n ∈ Z;$

$x=-{5π}/{6}+ 2πk, k ∈ Z$.

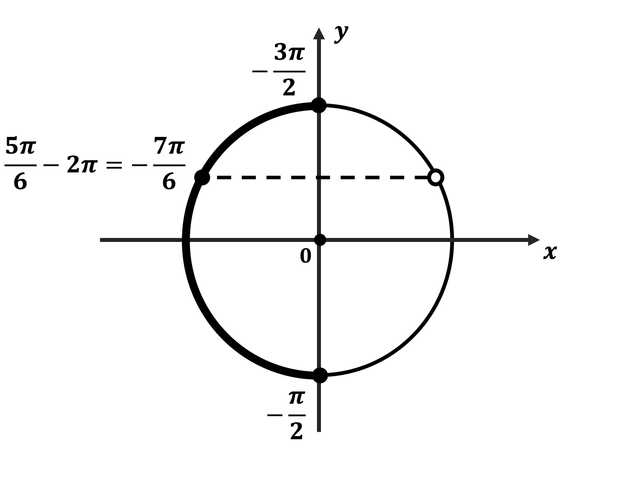
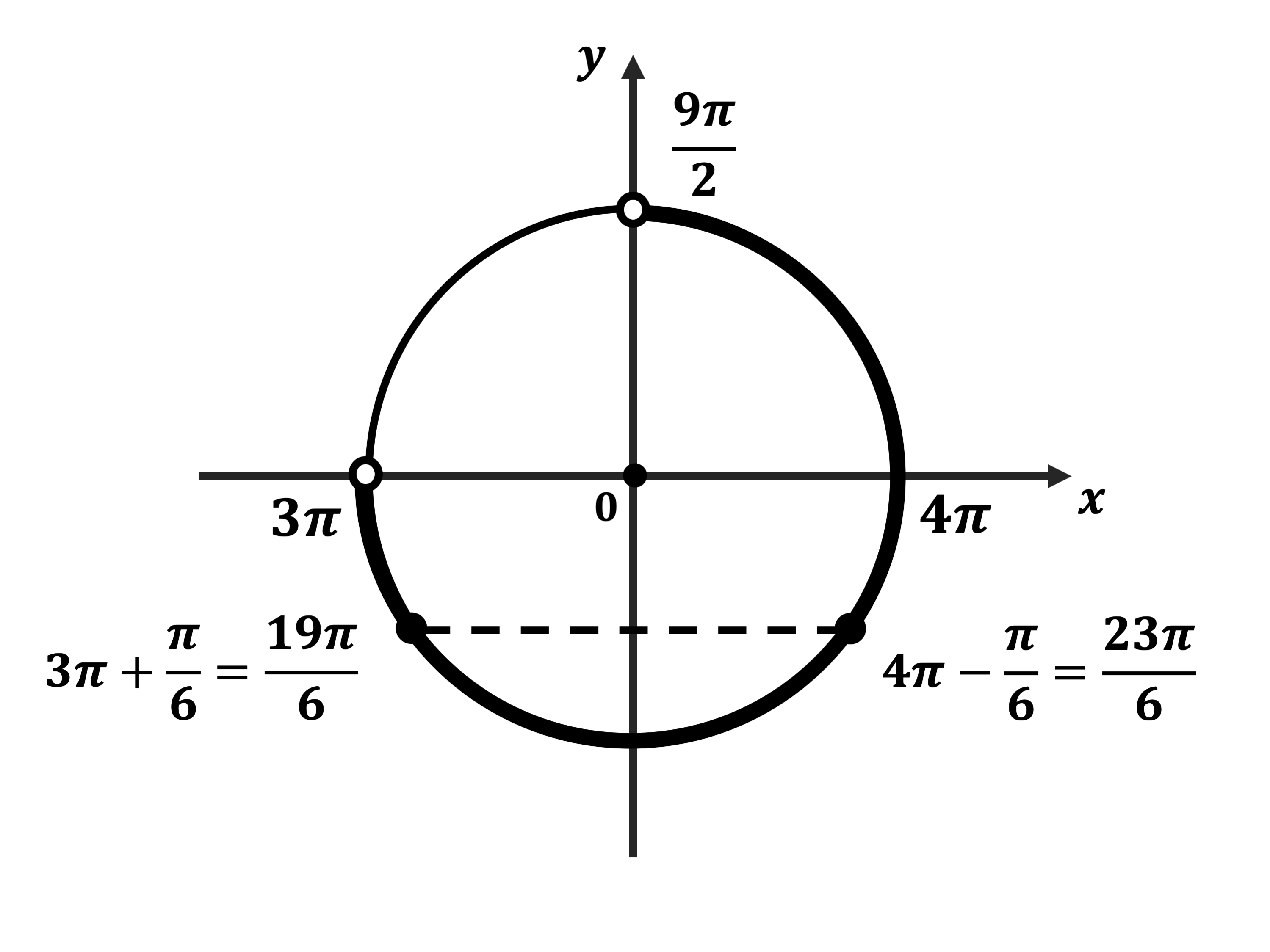
б) Отберём корни уравнения, принадлежащие промежутку $(3π; {9π}/{2})$,с помощью числовой окружности.

$x_1=3π+{π}/{6}={19π}/{6}$,

$x_2=4π−{π}/{6}={23π}/{6}$.

Ответ: а)$-{π}/{6}+2πn,-{5π}/{6}+2πk,n,k∈Z$;б)${19π}/{6};{23π}/{6}$

Задача 12

а) Решите уравнение ${sin 2x}/{sin(π — x)}= √2$.

б) Укажите корни этого уравнения, принадлежащие промежутку $[-{5π}/{2};-π)$.

Решение

а)${sin2x}/{sin(π — x)}=√2$.

а) Применим формулу синуса двойного аргумента $sin2x = 2sinxcosx$ и формулу приведения $sin(π — x) = sin x$.

Уравнение примет вид: ${2sinxcosx}/{sinx} = √2$.

Учитывая, что $sinx≠0, x≠πn, n∈Z$, получим:

$2cosx=√2$,

$cosx = {√2}/{2}$,

$x = ±{π}/{4} + 2πk, k∈Z$;

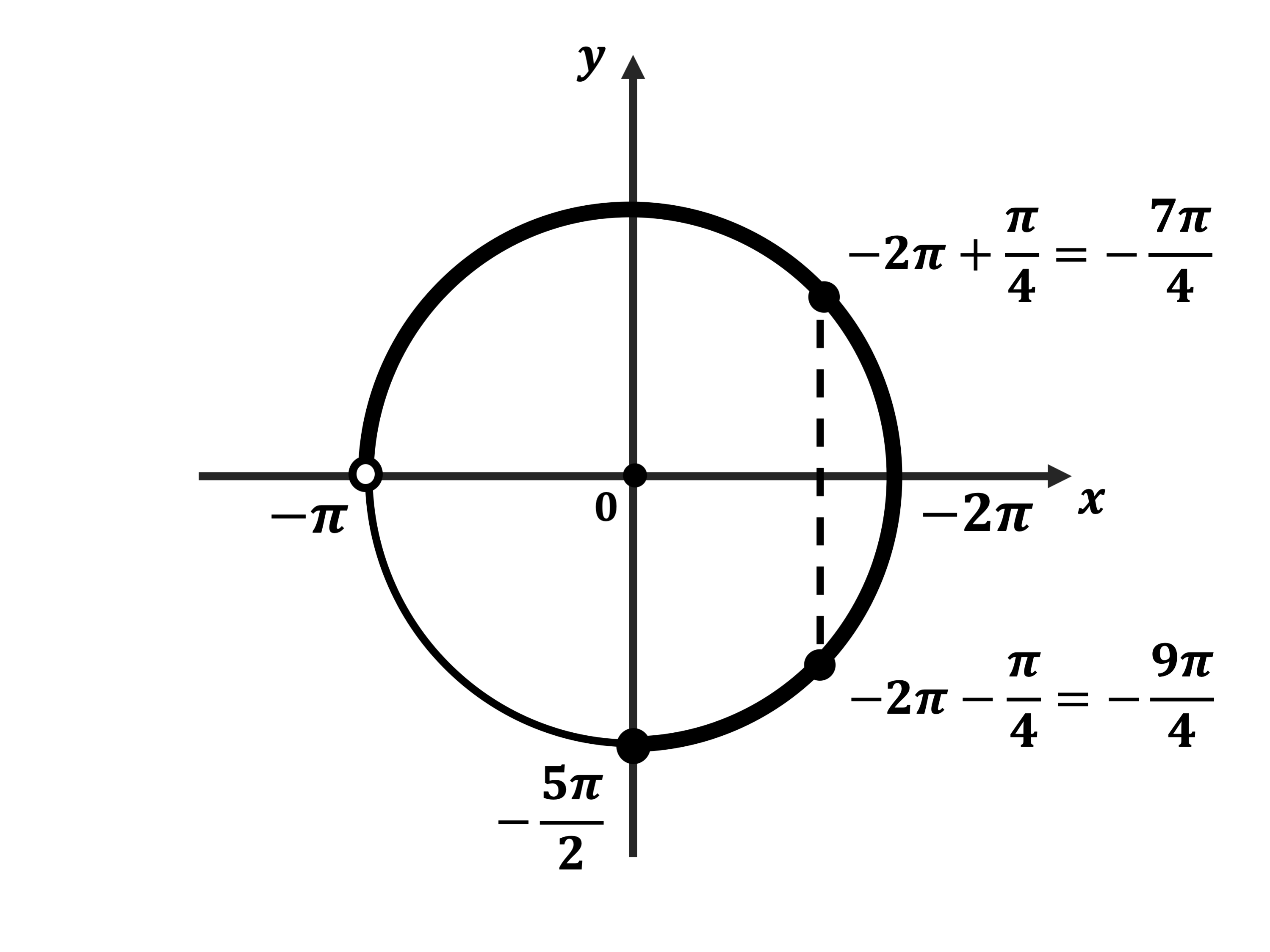
б) Отберём корни уравнения, принадлежащие промежутку $[-{5π}/{2};-π)$, с помощью окружности.

$x_1=-2π+{π}/{4}=-{7π}/{4}$

$x_2=-2π-{π}/{4}=-{9π}/{4}$

Ответ: а)$±{π}/{4}+2πk,k∈Z$;б)$-{9π}/{4};-{7π}/{4}$

Задача 13

а) Решите уравнение ${sin 2x}/{cos(π + x)}= -√2$.

б) Укажите корни этого уравнения, принадлежащие промежутку $(-2π;-{π}/{2})$.

Решение

а)${sin2x}/{cos(π + x)}=-√2$.

Зная, что $sin2x = 2sinxcosx, cos(π + x)=-cosx$, получим: ${2sinxcosx}/{-cosx}=-√2$.

Учитывая, что $cosx≠0, x≠{π}/{2} + πm, m∈Z$, имеем:

$2sinx=√2$,

$sinx = {√2}/{2}$,

$x = {π}/{4} + 2πn, n∈Z$;

$x = {3π}/{4} + 2πk, k∈Z$.

б) Отберём корни уравнения, принадлежащие промежутку $(-2π;-{π}/{2})$.

1. $x = {π}/{4} + 2πn, n∈Z$.

$-2π < {π}/{4} + 2πn < -{π}/{2},$

$-2 < {1}/{4} + 2n < -{1}/{2},$

$-2-{1}/{4} < 2n < -{1}/{2}-{1}/{4},$

$-{9}/{4} < 2n < -{3}/{4},$

$-{9}/{8} < n < -{3}/{8},$

$n = -1$.

При $n =-1$

$x = {π}/{4}-2π=-{7π}/{4}$.

2. $x = {3π}/{4} + 2πk, k∈Z$.

$-2π < {3π}/{4} + 2πk < -{π}/{2}$,

$-2 < {3}/{4} + 2k < -{1}/{2}$,

$-2-{3}/{4} < 2k < -{1}/{2}-{3}/{4}$,

$-{11}/{4} < 2k < -{5}/{4}$,

$-{11}/{8} < k < -{5}/{8}$,

$k = -1$.

При $k = -1$

$x = {3π}/{4}-2π = -{5π}/{4}$.

Ответ: а)${π}/{4}+2πn,{3π}/{4}+2πk,n,k∈Z$;б)$-{7π}/{4};-{5π}/{4}$

Задача 14

а) Решите уравнение $9·3^{2 cos x} — 10√3·3^{cos x} + 3 = 0$.

б) Укажите корни этого уравнения, принадлежащие отрезку $[{3π}/{2};4π]$.

Решение

а) После замены $t = 3^{cosx}$ исходное уравнение примет вид $9t^2 — 10√3t + 3 = 0$. Корни этого уравнения $t = √3; t = {√3}/{9}$. Возвращаясь к переменной $x$, получим

$[table3^{cosx}=√3; 3^{cosx}={√3}/{9};$ $[table3^{cosx}=3^{{1}/{2}}; 3^{cosx}=3^{-{3}/{2}};$ $[tablecosx={1}/{2}; cosx=-{3}/{2};$

Второе уравнение совокупности не имеет корней. Решая первое уравнение, получим $x =±{π}/{3} + 2πn; n ∈ Z$.

б) Запишем решение уравнения в виде $x =-{π}/{3} + 2πn; n ∈ Z$ или $x ={π}/{3} + 2πk; k ∈ Z$ и выясним, для каких целых значений $n$ и $k$ справедливы неравенства ${3π}/{2}≤-{π}/{3}+2πn≤4π$ и ${3π}/{2}≤{π}/{3}+2πk≤4π$.

Получим ${11}/{12} ≤ n ≤ {26}/{12}$ и ${7}/{12} ≤ k ≤{22}/{12}$.

Откуда следует, что два целых значения $n = 1$ и $n = 2$ удовлетворяют неравенству ${11}/{12} ≤ n ≤ {26}/{12}; k = 1$ — единственное целое $k$, удовлетворяющее неравенству ${7}/{12} ≤ k ≤{22}/{12}$.

При $n = 1$ $x = -{π}/{3} + 2π·1 = {5π}/{3}$.

При $n = 2$ $x = -{π}/{3} + 2π·2 = {11π}/{3}$.

При $k = 1$ $x = {π}/{3} + 2π·1 = {7π}/{3}$. Итак, ${5π}/{3}; {7π}/{3}; {11π}/{3}$ — корни уравнения, принадлежащие промежутку $[{3π}/{2};4π]$.

Ответ: а)$x=±{π}/{3}+2πn,n∈Z$;б)${5π}/{3};{7π}/{3};{11π}/{3}$

Задача 15

а) Решите уравнение $log_2^2(2 sin x + 1) — 17 log_2(2 sin x + 1) + 16 = 0$.

б) Укажите корни этого уравнения, принадлежащие отрезку $[{π}/{4};2π]$.

Решение

а) После замены $t = log_2(2 sin x+1)$ исходное уравнение примет вид $t^2-17t+16 = 0$. Корни этого уравнения $t = 1, t = 16$. Возвращаясь к переменной $x$, получим:

$[tablelog_2(2 sin x + 1) = 1; log_2(2 sin x + 1) = 16;$ $[table2 sin x + 1 = 2;; 2sin x + 1 = 2^{16};$

Второе уравнение совокупности не имеет корней. Решая первое уравнение, получим: $sin x = {1}/{2}; x = (-1)^n{π}/{6} + πn; n ∈ Z$.

б) Запишем решение уравнения в виде $x = {π}/{6} + 2πn; n ∈ Z$ или $x = {5π}/{6} + 2πk; k ∈ Z$ и выясним, для каких целых значений $n$ и $k$ справедливы неравенства ${π}/{4}≤{π}/{6}+2πn≤2π$ и ${π}/{4}≤{5π}/{6}+2πk≤2π$.

Получим: ${1}/{24}≤n≤{11}/{12}$ и $-{7}/{24}≤k≤{7}/{12}$, откуда следует, что нет целых значений $n$, удовлетворяющих неравенству ${1}/{24}≤n≤{11}/{12}; k = 0$ — единственное целое $k$, удовлетворяющее неравенству $-{7}/{24}≤k≤{7}/{12}$.

При $k = 0$ $x = {5π}/{6} + 2π·0 = {5π}/{6}$. Итак, ${5π}/{6}$ — корень уравнения, принадлежащий отрезку $[{π}/{4};2π]$.

Ответ: а)$(-1)^{n}{π}/{6}+πn,n∈Z$;б)${5π}/{6}$

Задача 16

а) Решите уравнение $6 log_2^2(2 cos x) — 9 log_2(2 cos x) + 3 = 0$.

б) Найдите все корни этого уравнения, принадлежащие отрезку $[-{π}/{2};π]$.

Решение

а) Решим уравнение $6log_2^2(2 cos x)-9 log_2(2 cos x)+3 = 0$. Обозначим $log_2(2 cos x) = t$ и решим получившееся квадратное уравнение.

$6t^2 — 9t + 3 = 0, t = {9±3}/{12}; t_1 = {1}/{2}; t_2 = 1$.

$[tablelog_2(2 cos x) ={1}/{2}; log_2(2 cos x) = 1;$ $[table2 cos x = √2; 2 cos x = 2;$

$[tablecos x = {√2}/{2}; cos x= 1;$ $[tablex = ±{π}/{4}+ 2π n; n ∊ Z; x = 2πk; k ∊ Z;$

б) Корни, принадлежащие отрезку $[-{π}/{2};π]$, найдём с помощью числовой окружности:

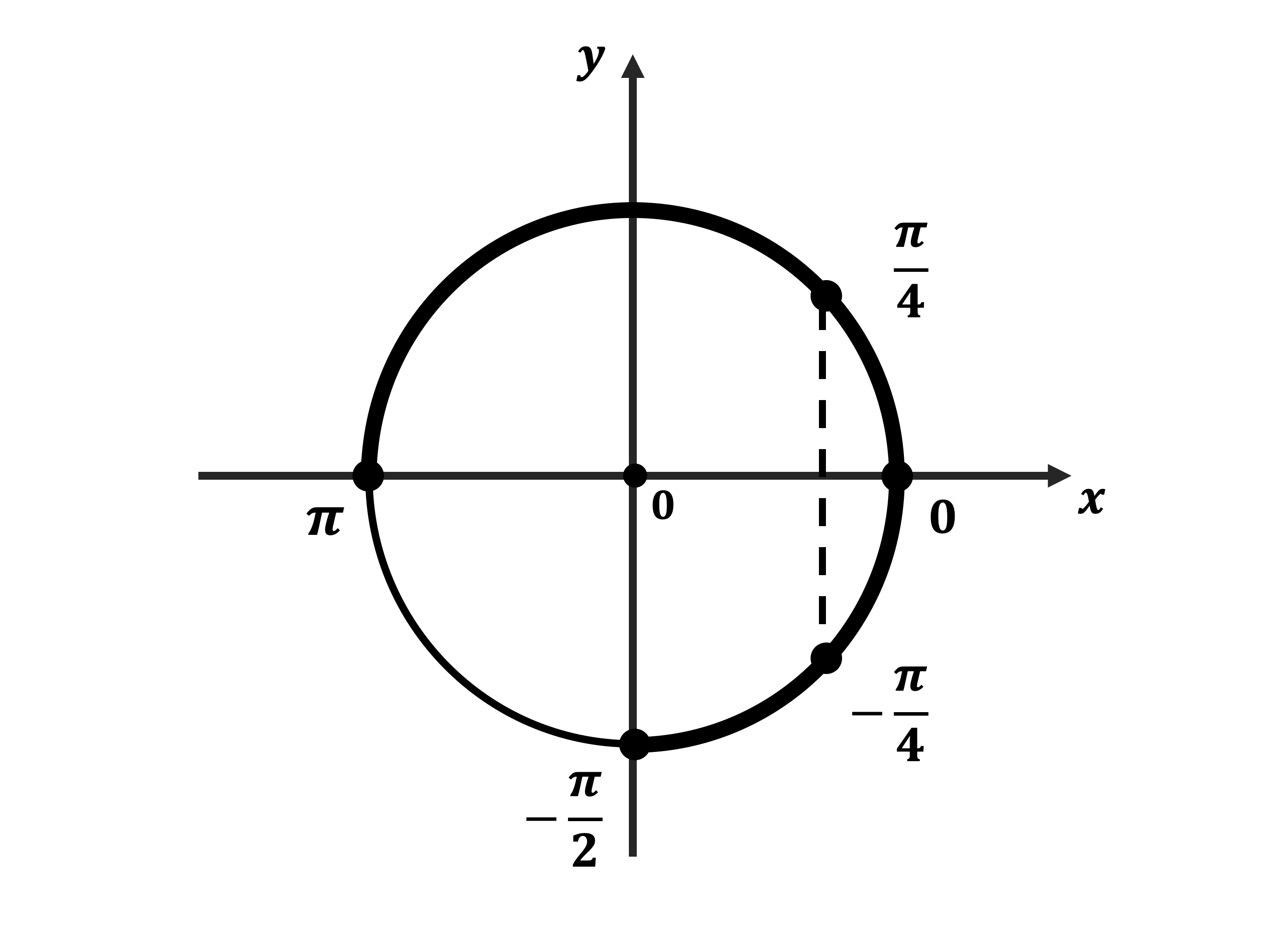
$x_1 = -{π}/{4}; x_2 = 0; x_3 ={π}/{4}$.

Ответ: а)$±{π}/{4}+2πn,n∈Z;2πk,k∈Z$;б)$-{π}/{4};0;{π}/{4}$

Задача 17

а) Решите уравнение $2log_2^2(2 sin x) — 3 log_2(2 sin x) + 1 = 0$.

б) Найдите все корни этого уравнения, принадлежащие отрезку $[{3π}/{2}; 3π]$.

Решение

а) Решим уравнение $2log_2^2(2 sin x) — 3 log_2(2 sin x) + 1 = 0$. Обозначим $log_2(2 sin x) = t$ и решим получившееся уравнение. $2t^2 — 3t + 1 = 0, t = {3±1}/{4}; t_1 = 1; t_2 ={1}/{2}$

$[tablelog_2(2 sin x) = 1; log_2(2 sin x) ={1}/{2};$ $[table2 sin x = 2; 2 sin x=√2;$

$[tablesin x = 1; sin x = {√2}/{2};$ $[tablex={π}/{2}+2πn; x=(-1)^k{π}/{4}+πk;$ $n,k∈Z$

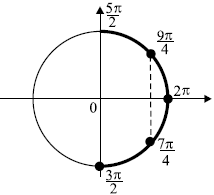
б) Корни, принадлежащие отрезку $[{3π}/{2}; 3π]$, найдём с помощью числовой окружности:

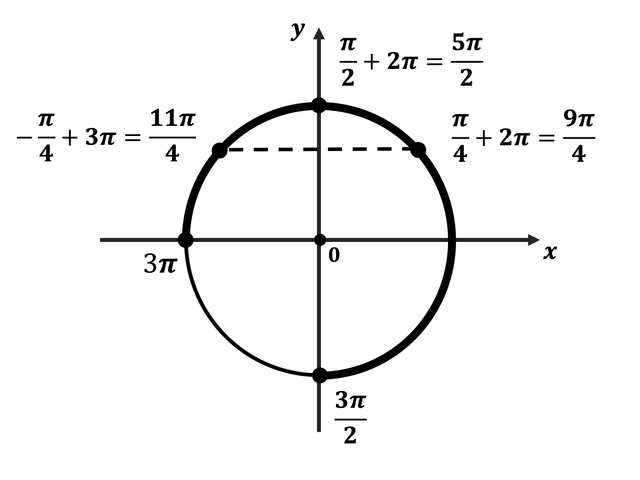
$x_1 = 2π + {π}/{4} = {9π}/{4}; x_2 = 2π + {π}/{2} ={5π}/{2}; x_3 = 3π -{π}/{4} = {11π}/{4}$.

Ответ: а)${π}/{2}+2πn,n∈Z;(-1)^k{π}/{4}+πk,k∈Z$;б)${9π}/{4};{5π}/{2};{11π}/{4}$

Задача 18

а) Решите уравнение $27^{x} — 5·9^{x} — 3^{x+4} + 405 = 0$.

б) Укажите все корни этого уравнения, принадлежащие отрезку $[log_{3}6; log_{3}10]$.

Решение

а) Преобразуем исходное уравнение и разложим на множители его левую часть.

$3^{3x} — 5·3^{2x} — 81·3^x + 405 = 0$,

$3^{2x}(3^x — 5) — 81(3^x — 5) = 0$,

$(3^{2x} — 81)(3^x — 5) = 0$.

Получаем: $3^{2x} -81 = 0$ или $3^x -5 = 0$. Значит, $3^{2x} = 81$, откуда $x = 2$ или $3^x = 5$, откуда $x = log_{3}5$.

б) Нам нужно выбрать те корни уравнения, которые принадлежат отрезку $[log_{3}6; log_{3}10]$. Заметим, что $2 = log_{3}9$. Тогда $log_{3}5 < log_{3}6 < 2 < log_{3}10$. Значит, указанному отрезку принадлежит корень $x = 2$.

Ответ: а)$2;log_{3}5$; б)$2$

Задача 19

а) Решите уравнение $3√{2}sin({π}/{2}+x)-2=2cos^{2}x$.

б) Укажите корни этого уравнения, принадлежащие отрезку $[{3π}/{2};{5π}/{2}]$.

Решение

а) Запишем исходное уравнение в виде $2 cos^2 x — 3√2 cos x + 2 = 0$.

Решая это уравнение как квадратное относительно $cos x$, получим $(cos x)_{1,2} ={3√2±√{18 — 16}}/{4}={3√2± √2}/{4}$.

Значит, $(cos x)_1 = {√2}/{2}$, откуда $x =π/4 + 2πn, n ∈ Z$ или $x =-π/4 + 2πn, n ∈ Z$.

Уравнение $(cosx)_2 = √2$ корней не имеет.

б) Отберём корни, принадлежащие отрезку $[{3π}/{2};{5π}/{2}]$ с помощью числовой окружности.

Получим числа

$2π -{π}/{4} ={7π}/{4}$;

$2π + {π}/{4} = {9π}/{4}$.

Ответ: а)$±{π}/{4}+2πn,n∈Z$;б)${7π}/{4},{9π}/{4}$

Задача 20

а) Решите уравнение $3√{3}cos({3π}/{2}+x)-3=2sin^{2}x$.

б) Укажите корни этого уравнения, принадлежащие отрезку $[2π; 3π]$.

Решение

а) Запишем исходное уравнение в виде $2sin^2 x — 3√3 sin x + 3 = 0$.

Решая это уравнение как квадратное относительно $sin x$, получим $(sin x)_{1,2} = {3√3±√{27-24}}/{4}= {3√3±√3}/{4}$.

Значит,$(sin x)_1 ={√3}/{2}$, откуда $x ={π}/{3} +2πn, n ∈ Z$ или $x ={2π}/{3}+2πm, m ∈ Z$.

Уравнение $(sin x)_2 = √3$ корней не имеет.

б) С помощью числовой окружности отберём корни, принадлежащие отрезку: $[2π; 3π]$

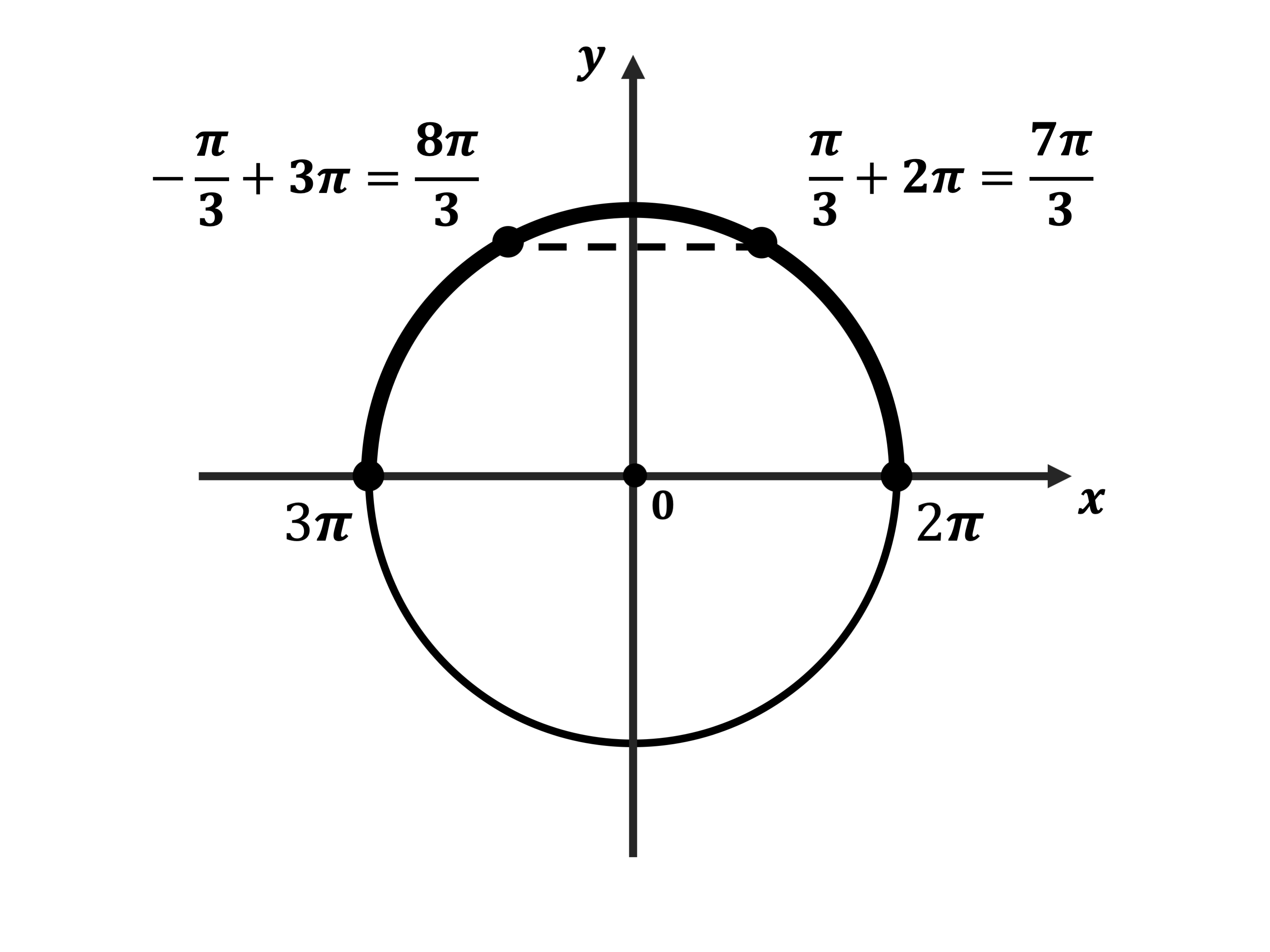
Получим числа:

$2π +{π}/{3}={7π}/{3}$;

$3π -{π}/{3}={8π}/{3}$.

Ответ: а)${π}/{3}+2πn,n∈Z;{2π}/{3}+2πm,m∈Z$;б)${7π}/{3},{8π}/{3}$

Рекомендуемые курсы подготовки

Источник

Уважаемый посетитель!

Если у вас есть вопрос, предложение или жалоба, пожалуйста, заполните короткую форму и изложите суть обращения в текстовом поле ниже. Мы обязательно с ним ознакомимся и в  30-дневный срок ответим на указанный вами адрес электронной почты

Статус Абитуриент Студент Родитель Соискатель Сотрудник Другое

Филиал Абакан Актобе Алагир Алматы Алушта Анапа Ангарск Архангельск Армавир Асбест Астана Астрахань Атырау Баку Балхаш Барановичи Барнаул Белая Калитва Белгород Бельцы Берлин Бишкек Благовещенск Бобров Бобруйск Борисов Боровичи Бронницы Брянск Бузулук Чехов Челябинск Череповец Черкесск Дамаск Дербент Димитровград Дмитров Долгопрудный Домодедово Дубай Дубна Душанбе Екатеринбург Электросталь Елец Элиста Ереван Евпатория Гана Гомель Гродно Грозный Хабаровск Ханты-Мансийск Хива Худжанд Иркутск Истра Иваново Ижевск Калининград Карабулак Караганда Каракол Кашира Казань Кемерово Киев Кинешма Киров Кизляр Королев Кострома Красноармейск Краснодар Красногорск Красноярск Краснознаменск Курган Курск Кызыл Липецк Лобня Магадан Махачкала Майкоп Минеральные Воды Минск Могилев Москва Моздок Мозырь Мурманск Набережные Челны Нальчик Наро-Фоминск Нижневартовск Нижний Новгород Нижний Тагил Ногинск Норильск Новокузнецк Новосибирск Новоуральск Ноябрьск Обнинск Одинцово Омск Орехово-Зуево Орел Оренбург Ош Озёры Павлодар Пенза Пермь Петропавловск Подольск Полоцк Псков Пушкино Пятигорск Радужный Ростов-на-Дону Рязань Рыбинск Ржев Сальск Самара Самарканд Санкт-Петербург Саратов Сергиев Посад Серпухов Севастополь Северодвинск Щербинка Шымкент Слоним Смоленск Солигорск Солнечногорск Ставрополь Сургут Светлогорск Сыктывкар Сызрань Тамбов Ташкент Тбилиси Терек Тихорецк Тобольск Тольятти Томск Троицк Тула Тверь Тюмень Уфа Ухта Улан-Удэ Ульяновск Ургенч Усть-Каменогорск Вёшенская Видное Владимир Владивосток Волгодонск Волгоград Волжск Воркута Воронеж Якутск Ярославль Юдино Жлобин Жуковский Златоуст Зубова Поляна Звенигород

Тип обращения Вопрос Предложение Благодарность Жалоба

Тема обращения Поступление Трудоустройство Обучение Оплата Кадровый резерв Внеучебная деятельность Работа автоматических сервисов университета Другое

* Все поля обязательны для заполнения

Я даю согласие на обработку персональных данных, согласен на получение информационных рассылок от Университета «Синергия» и соглашаюсь c  политикой конфиденциальности

Источник

Понравилась статья? Поделить с друзьями:
  • 12 баллов по математике егэ какая оценка профиль
  • 12 sin 150 cos 120 решу егэ
  • 119977 решу егэ математика профиль
  • 119973 решу егэ математика профиль
  • 119972 решу егэ математика профиль