Для какого наибольшего целого числа А формула
((x ≤ 9) →(x ⋅ x ≤ A)) ⋀ ((y ⋅ y ≤ A) → (y ≤ 9))
тождественно истинна, то есть принимает значение 1 при любых целых неотрицательных x и y?
Спрятать решение
Решение.
Раскрывая импликацию по правилу A → B = ¬A + B, заменяя логическую сумму совокупностью, а логическое произведение системой соотношений, определим значения параметра А, при котором система совокупностей
будет иметь решения для любых целых неотрицательных чисел.
Заметим, что переменные не связаны между собой уравнением или неравенством, поэтому необходимо и достаточно, чтобы решениями первой совокупности были все неотрицательные х, а решениями второй совокупности были все неотрицательные y.
Решениями неравенства являются числа 10, 11, 12, … Чтобы совокупность выполнялась для всех целых неотрицательных чисел, числа 0, 1, 2, … 9 должны быть решениями неравенства
Значит,
Аналогично, решениями неравенства являются числа 0, 1, … 9. Следовательно, числа 10, 11, 12, … должны быть решениями неравенства
Поэтому
Тем самым, Искомое наибольшее целое значение параметра равно 99.
Ответ: 99.
Приведём другое решение на языке Python.
for a in range(300, 1, -1):
k = 0
for x in range(0, 300):
for y in range(0, 300):
if ((x <= 9) <= (x * x <= a)) and ((y*y <= a) <= (y <= 9)):
k += 1
if k == 90_000:
print(a)
break
Источник: Демонстрационная версия ЕГЭ—2018 по информатике.
Тип 1 № 26975
На рисунке слева изображена схема дорог Н-ского района, в таблице звёздочкой обозначено наличие дороги из одного населённого пункта в другой. Отсутствие звёздочки означает, что такой дороги нет. Определите, какие номера населённых пунктов в таблице могут соответствовать населённым пунктам Б и В на схеме. В ответ запишите без разделителей сначала номер пункта Б, потом номер пункта В.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| 1 | * | * | * | |||||
| 2 | * | * | ||||||
| 3 | * | * | * | |||||
| 4 | * | * | * | |||||
| 5 | * | * | * | |||||
| 6 | * | * | * | |||||
| 7 | * | * | ||||||
| 8 | * | * | * |
2. Тип 2 № 15814
Логическая функция F задаётся выражением (x ≡ ( w ∨ y)) ∨ ((w → z ) ∧ (y → w)).
Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности функции F.
Определите, какому столбцу таблицы истинности соответствует каждая из переменных x, y, z, w.
| Переменная 1 | Переменная 2 | Переменная 3 | Переменная 4 | Функция |
|---|---|---|---|---|
| ??? | ??? | ??? | ??? | F |
| 1 | 1 | 0 | ||
| 1 | 0 | |||
| 1 | 1 | 0 |
В ответе напишите буквы w, x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала — буква, соответствующая первому столбцу; затем — буква, соответствующая второму столбцу, и т. д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Пример. Пусть задано выражение x → y, зависящее от двух переменных x и y, и фрагмент таблицы истинности:
| Переменная 1 | Переменная 2 | Функция |
|---|---|---|
| ??? | ??? | F |
| 0 | 1 | 0 |
Тогда первому столбцу соответствует переменная y, а второму столбцу соответствует переменная x. В ответе нужно написать: yx.
3. Тип 3 № 37507
В файле приведён фрагмент базы данных «Продукты» о поставках товаров в магазины районов города. База данных состоит из трёх таблиц.
3.xlsx
Таблица «Движение товаров» содержит записи о поставках товаров в магазины в течение первой декады июня 2021 г., а также информацию о проданных товарах. Поле Тип операции содержит значение Поступление или Продажа, а в соответствующее поле Количество упаковок, шт. занесена информация о том, сколько упаковок товара поступило в магазин или было продано в течение дня. Заголовок таблицы имеет следующий вид.
| ID операции | Дата | ID магазина | Артикул | Тип операции | Количество упаковок, шт. |
Цена, руб./шт. |
Таблица «Товар» содержит информацию об основных характеристиках каждого товара. Заголовок таблицы имеет следующий вид.
| Артикул | Отдел | Наименование | Ед. изм. | Количество в упаковке |
Поставщик |
Таблица «Магазин» содержит информацию о местонахождении магазинов. Заголовок таблицы имеет следующий вид.
На рисунке приведена схема указанной базы данных.
Используя информацию из приведённой базы данных, определите, сколько рублей выручили магазины Октябрьского района от продажи риса (всех видов) за период с 1 по 10 июня включительно.
В ответе запишите только число.
4. Тип 4 № 18553
По каналу связи передаются сообщения, содержащие только восемь букв: А, В, Е, З, И, Н, О, Р. Для передачи используется двоичный код, удовлетворяющий условию Фано. Кодовые слова для некоторых букв известны: А — 101, В — 010, И — 00. Какое наименьшее количество двоичных знаков потребуется для кодирования слова НЕВЕЗЕНИЕ?
Примечание. Условие Фано означает, что ни одно кодовое слово не является началом другого кодового слова.
5. Тип 5 № 18785
На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом.
1. Строится двоичная запись числа N.
2. Далее эта запись обрабатывается по следующему правилу:
а) если число чётное, то к двоичной записи числа слева дописывается 1, а справа 0. Например, для исходного числа 1002 результатом будет являться число 11000;
б) если число нечётное, то к двоичной записи числа слева дописывается 11 и справа дописывается 11.
Полученная таким образом запись является двоичной записью искомого числа R.
Укажите минимальное число N, после обработки которого с помощью этого алгоритма получается число, большее, чем 52. В ответе запишите это число в десятичной системе счисления.
6. Тип 6 № 47248
Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует две команды: Вперёд n (где n — целое число), вызывающая передвижение Черепахи на n единиц в том направлении, куда указывает её голова, и Направо m (где m — целое число), вызывающая изменение направления движения на m градусов по часовой стрелке. Запись
Повтори k [Команда1 Команда2 … КомандаS]
означает, что последовательность из S команд повторится k раз. Черепахе был дан для исполнения следующий алгоритм:
Повтори 4 [Вперёд 10 Направо 90]
Определите, сколько точек с целочисленными координатами будут находиться внутри области, ограниченной линией, заданной данным алгоритмом. Точки на линии учитывать не следует.
7. Тип 7 № 18557
Для хранения в информационной системе документы сканируются с разрешением 600 dpi и цветовой системой, содержащей 224 = 16 777 216 цветов. Методы сжатия изображений не используются. Средний размер отсканированного документа составляет 12 Мбайт. В целях экономии было решено перейти на разрешение 300 dpi и цветовую систему, содержащую 216 = 65 536 цветов. Сколько Мбайт будет составлять средний размер документа, отсканированного с изменёнными параметрами?
8. Тип 8 № 18558
Иван составляет 5-буквенные коды из букв И, В, А, Н. Буквы в коде могут повторяться, использовать все буквы не обязательно, но букву И нужно использовать хотя бы один раз. Сколько различных кодов может составить Иван?
9. Тип 9 № 35467
Электронная таблица содержит результаты ежечасного измерения температуры воздуха на протяжении трёх месяцев. Определите, сколько раз за время измерений результат очередного измерения оказывался выше результата предыдущего на 2 и более градусов.
Задание 9
10. Тип 10 № 35468
Определите, сколько раз в тексте произведения А. С. Пушкина «Дубровский» встречается существительное «ключ» в любом числе и падеже.
Задание 10
11. Тип 11 № 18819
Сотрудникам компании выдают электронную карту, на которой записаны их личный код, номер подразделения (целое число от 1 до 1200) и дополнительная информация. Личный код содержит 17 символов и может включать латинские буквы из 26-символьного латинского алфавита (заглавные и строчные буквы различаются), десятичные цифры и специальные знаки из набора @#$%^&*(). Для хранения кода используется посимвольное кодирование, все символы кодируются одинаковым минимально возможным количеством битов, для записи кода отводится минимально возможное целое число байтов. Номер подразделения кодируется отдельно и занимает минимально возможное целое число байтов. Известно, что на карте хранится всего 48 байтов данных. Сколько байтов занимает дополнительная информация?
12. Тип 12 № 16443
Исполнитель Редактор получает на вход строку цифр и преобразует её. Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки цифр.
А) заменить (v, w).
Эта команда заменяет в строке первое слева вхождение цепочки v на цепочку w. Например, выполнение команды
заменить (111, 27)
преобразует строку 05111150 в строку 0527150.
Если в строке нет вхождений цепочки v, то выполнение команды заменить (v, w) не меняет эту строку.
Б) нашлось (v).
Эта команда проверяет, встречается ли цепочка v в строке исполнителя Редактор. Если она встречается, то команда возвращает логическое значение «истина», в противном случае возвращает значение «ложь». Строка исполнителя при этом не изменяется.
Цикл
ПОКА условие
последовательность команд
КОНЕЦ ПОКА
выполняется, пока условие истинно.
Какая строка получится в результате применения приведённой ниже программы к строке, состоящей из 84 единиц?
НАЧАЛО
ПОКА нашлось (11111)
заменить (222, 1)
заменить (111, 2)
КОНЕЦ ПОКА
КОНЕЦ
13. Тип 13 № 27300
На рисунке — схема дорог, связывающих пункты А, Б, В, Г, Д, Е, Ж, И, К, Л, М, Н, П. Сколько существует различных путей из пункта А в пункт П, проходящих через пункт Г или через пункт Е, но не через оба этих пункта?
14. Тип 14 № 13362
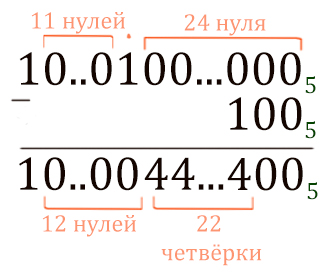
Значение арифметического выражения: 125 + 253 + 59 – записали в системе счисления с основанием 5. Сколько значащих нулей содержит эта запись?
15. Тип 15 № 13745
Для какого наибольшего целого числа А формула
((x ≤ 9) →(x ⋅ x ≤ A)) ⋀ ((y ⋅ y ≤ A) → (y ≤ 9))
тождественно истинна, то есть принимает значение 1 при любых целых неотрицательных x и y?
16. Тип 16 № 4657
Алгоритм вычисления значения функции F(n) и G(n), где n – натуральное число, задан следующими соотношениями:
F(1) = 1
F(n) = 2 * G(n–1) + 5 * n, при n >1
G(1) = 1
G(n) = F(n–1) + 2 * n, при n >1
Чему равно значение функции F(4) + G(4)?
В ответе запишите только натуральное число.
17. Тип 17 № 39763
Файл содержит последовательность неотрицательных целых чисел, не превышающих 10 000. Назовём тройкой три идущих подряд элемента последовательности. Определите количество троек чисел таких, которые могут являться сторонами остроугольного треугольника. В ответе запишите два числа: сначала количество найденных троек, а затем — максимальную сумму элементов таких троек. Если таких троек не найдётся — следует вывести 0 0.
Задание 17
Ответ:
18. Тип 18 № 35476
Дан квадрат 15 × 15 клеток, в каждой клетке которого записано целое число. В левом верхнем углу квадрата стоит робот. За один ход робот может переместиться на одну клетку вправо, вниз или по диагонали вправо вниз. Выходить за пределы квадрата робот не может. Необходимо переместить робота в правый нижний угол так, чтобы сумма чисел в клетках, через которые прошёл робот (включая начальную и конечную), была максимальной. В ответе запишите максимально возможную сумму.
Исходные данные записаны в электронной таблице.
Задание 18
Пример входных данных (для таблицы размером 4 × 4):
| 4 | 21 | −36 | 11 |
| 37 | −12 | 29 | 7 |
| −30 | 24 | −1 | −5 |
| 8 | −8 | 9 | 21 |
Для указанных входных данных ответом будет число 95 (робот проходит через клетки с числами 4, 37, 24, 9, 21).
19. Тип 19 № 27768
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч один камень, увеличить количество камней в первой куче в два раза или увеличить количество камней во второй куче в три раза. Например, пусть в одной куче 6 камней, а в другой 9 камней; такую позицию мы будем обозначать (6, 9). За один ход из позиции (6, 9) можно получить любую из четырёх позиций: (7, 9), (12, 9), (6, 10), (6, 27). Чтобы делать
ходы, у каждого игрока есть неограниченное количество камней.
Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 84. Победителем считается игрок, сделавший последний ход, то есть первым получивший позицию, в которой в кучах будет 84 или больше камней.
В начальный момент в первой куче было 16 камней, во второй куче — S камней, 1 ≤ S ≤ 67.
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока — значит, описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника. В описание выигрышной стратегии не следует включать ходы играющего по ней игрока, которые не являются для него безусловно выигрышными, т.е не гарантирующие выигрыш независимо от игры противника.
Известно, что Ваня выиграл своим первым ходом после неудачного первого хода Пети. Укажите минимальное значение S, когда такая ситуация возможна.
20. Тип 20 № 27769
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч один камень, увеличить количество камней в первой куче в два раза или увеличить количество камней во второй куче в три раза. Например, пусть в одной куче 6 камней, а в другой 9 камней; такую позицию мы будем обозначать (6, 9). За один ход из позиции (6, 9) можно получить любую из четырёх позиций: (7, 9), (12, 9), (6, 10), (6, 27). Чтобы делать
ходы, у каждого игрока есть неограниченное количество камней.
Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 84. Победителем считается игрок, сделавший последний ход, то есть первым получивший позицию, в которой в кучах будет 84 или больше камней.
В начальный момент в первой куче было 16 камней, во второй куче — S камней, 1 ≤ S ≤ 67.
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока — значит, описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника. В описание выигрышной стратегии не следует включать ходы играющего по ней игрока, которые не являются для него безусловно выигрышными, т.е не гарантирующие выигрыш независимо от игры противника.
Найдите два таких значения S, при которых у Пети есть выигрышная стратегия, причём одновременно выполняются два условия:
— Петя не может выиграть за один ход;
— Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.
Найденные значения запишите в ответе в порядке возрастания без разделительных знаков.
21. Тип 21 № 27770
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч один камень, увеличить количество камней в первой куче в два раза или увеличить количество камней во второй куче в три раза. Например, пусть в одной куче 6 камней, а в другой 9 камней; такую позицию мы будем обозначать (6, 9). За один ход из позиции (6, 9) можно получить любую из четырёх позиций: (7, 9), (12, 9), (6, 10), (6, 27). Чтобы делать
ходы, у каждого игрока есть неограниченное количество камней.
Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 84. Победителем считается игрок, сделавший последний ход, то есть первым получивший позицию, в которой в кучах будет 84 или больше камней.
В начальный момент в первой куче было 16 камней, во второй куче — S камней, 1 ≤ S ≤ 67.
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока — значит, описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника. В описание выигрышной стратегии не следует включать ходы играющего по ней игрока, которые не являются для него безусловно выигрышными, т.е не гарантирующие выигрыш независимо от игры противника.
Найдите минимальное значение S, при котором одновременно выполняются два условия:
— у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;
— у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
22. Тип 22 № 47583
В файле 22_3.xlsx содержится информация о совокупности N вычислительных процессов, которые могут выполняться параллельно или последовательно. Будем говорить, что процесс B зависит от процесса A, если для выполнения процесса B необходимы результаты выполнения процесса A. В этом случае процессы могут выполняться только последовательно.
Информация о процессах представлена в файле в виде таблицы. В первой строке таблицы указан идентификатор процесса (ID), во второй строке таблицы — время его выполнения в миллисекундах, в третьей строке перечислены с разделителем «;» ID процессов, от которых зависит данный процесс. Если процесс является независимым, то в таблице указано значение 0.
Определите минимальное время, через которое завершится выполнение всей совокупности процессов, при условии, что все независимые друг от друга процессы могут выполняться параллельно.
Типовой пример организации данных в файле:
| ID процесса B | Время выполнения процесса B (мс) | ID процесса(ов) A |
|---|---|---|
| 1 | 4 | 0 |
| 2 | 3 | 0 |
| 3 | 1 | 1;2 |
| 4 | 7 | 3 |
В данном случае независимые процессы 1 и 2 могут выполняться параллельно, при этом процесс 1 завершится через 4 мс, а процесс 2 — через 3 мс с момента старта. Процесс 3 может начаться только после завершения обоих процессов 1 и 2, то есть, через 4 мс после старта. Он длится 1 мс и закончится через 4 + 1 = 5 мс после старта. Выполнение процесса 4 может начаться только после завершения процесса 3, то есть, через 5 мс. Он длится 7 мс, так что минимальное время завершения всех процессов равно 5 + 7 = 12 мс.
23. Тип 23 № 15932
Исполнитель РазДваТри преобразует число на экране.
У исполнителя есть три команды, которым присвоены номера:
1. Прибавить 1
2. Умножить на 2
3. Умножить на 3
Первая команда увеличивает число на экране на 1, вторая умножает его на 2, третья умножает его на 3.
Программа для исполнителя РазДваТри — это последовательность команд.
Сколько существует программ, которые преобразуют исходное число 2 в число 44 и при этом траектория вычислений содержит число 13 и не содержит числа 29?
Траектория вычислений — это последовательность результатов выполнения всех команд программы. Например, для программы 312 при исходном числе 6 траектория будет состоять из чисел 18, 19, 38.
24. Тип 24 № 35482
Текстовый файл содержит строки различной длины. Общий объём файла не превышает 1 Мбайт. Строки содержат только заглавные буквы латинского алфавита (ABC…Z).
Необходимо найти строку, содержащую наименьшее количество букв G (если таких строк несколько, надо взять ту, которая находится в файле раньше), и определить, какая буква встречается в этой строке чаще всего. Если таких букв несколько, надо взять ту, которая позже стоит в алфавите.
Пример. Исходный файл:
GIGA
GABLAB
AGAAA
В этом примере в первой строке две буквы G, во второй и третьей — по одной. Берём вторую строку, т. к. она находится в файле раньше. В этой строке чаще других встречаются буквы A и B (по два раза), выбираем букву B, т. к. она позже стоит в алфавите. В ответе для этого примера надо записать B.
Для выполнения этого задания следует написать программу. Ниже приведён файл, который необходимо обработать с помощью данного алгоритма.
Задание 24
25. Тип 25 № 35483
Найдите все натуральные числа, принадлежащие отрезку [35 000 000; 40 000 000], у которых ровно пять различных нечётных делителей (количество чётных делителей может быть любым). В ответе перечислите найденные числа в порядке возрастания.
Ответ:
26. Тип 26 № 27885
Системный администратор раз в неделю создаёт архив пользовательских файлов. Однако объём диска, куда он помещает архив, может быть меньше, чем суммарный объём архивируемых файлов. Известно, какой объём занимает файл каждого пользователя.
По заданной информации об объёме файлов пользователей и свободном объёме на архивном диске определите максимальное число пользователей, чьи файлы можно сохранить в архиве, а также максимальный размер имеющегося файла, который может быть сохранён в архиве, при условии, что сохранены файлы максимально возможного числа пользователей.
Входные данные.
Задание 26
В первой строке входного файла находятся два числа: S — размер свободного места на диске (натуральное число, не превышающее 10 000) и N — количество пользователей (натуральное число, не превышающее 3000). В следующих N строках находятся значения объёмов файлов каждого пользователя (все числа натуральные, не превышающие 100), каждое в отдельной строке.
Запишите в ответе два числа: сначала наибольшее число пользователей, чьи файлы могут быть помещены в архив, затем максимальный размер имеющегося файла, который может быть сохранён в архиве, при условии, что сохранены файлы максимально возможного числа пользователей.
Пример входного файла:
100 4
80
30
50
40
При таких исходных данных можно сохранить файлы максимум двух пользователей. Возможные объёмы этих двух файлов 30 и 40, 30 и 50 или 40 и 50. Наибольший объём файла из перечисленных пар — 50, поэтому ответ для приведённого примера:
2 50
Ответ:
27. Тип 27 № 35485
В текстовом файле записан набор натуральных чисел, не превышающих 108. Гарантируется, что все числа различны. Из набора нужно выбрать три числа, сумма которых делится на 3. Какую наибольшую сумму можно при этом получить?
Входные данные.
Файл A
Файл B
Первая строка входного файла содержит целое число N — общее количество чисел в наборе. Каждая из следующих N строк содержит одно число.
Пример входного файла:
4
5
8
14
11
В данном случае есть четыре подходящие тройки: 5, 8, 11 (сумма 24); 5, 8 14 (сумма 27); 5, 14 11 (сумма 30) и 8, 14, 11 (сумма 33). В ответе надо записать число 33.
Вам даны два входных файла (A и B), каждый из которых имеет описанную выше структуру. В ответе укажите два числа: сначала значение искомой суммы для файла A, затем для файла B.
Ответ:
Просмотр содержимого документа
«ЕГЭ 2023 Январь Информатика Вариант 1»
ЕГЭ информатика 24 задание разбор, теория, как решать.
Создание программы для обработки символьной информации, (В) — 1 балл
Е24.35 сколько раз буква, образующая самую длинную цепочку в файле, встречается в строке
Текстовый файл содержит строки различной длины, содержащие только заглавные буквы латинского алфавита (ABC…Z). Будем называть цепочкой группу идущих подряд одинаковых букв в одной строке. Определите, сколько раз буква, образующая самую длинную цепочку в файле, встречается в строке, содержащей эту цепочку. Если в файле есть несколько цепочек одинаковой максимальной длины, нужно выбрать ту из них, для …
Читать далее
Е24.34 Определите максимальное количество идущих подряд пар символов вида согласная + гласная
Текстовый файл состоит из символов A, C, D, F и O. Определите максимальное количество идущих подряд пар символов вида согласная + гласная в прилагаемом файле. Для выполнения этого задания следует написать программу. Ответ: TXT ZIP Демонстрационный вариант ЕГЭ 2023 г. – задание №24
Читать далее
Е24.33 Определите количество групп из идущих подряд не менее 10 символов
Текстовый файл содержит только заглавные буквы латинского алфавита (ABC…Z). Определите количество групп из идущих подряд не менее 10 символов, которые начинаются и заканчиваются буквой D, не содержат других букв D (кроме первой и последней) и содержат не меньше двух букв C. Ответ: TXT ZIP СтатГрад Вариант ИН2110402 30.03.2022 – задание №24
Читать далее
Е24.32 Определите максимальное количество идущих подряд пар символов AB или CB в прилагаемом файле
Текстовый файл состоит из символов A, B и C. Определите максимальное количество идущих подряд пар символов AB или CB в прилагаемом файле. Искомая подпоследовательность должна состоять только из пар AB, или только из пар CB, или только из пар AB и CB в произвольном порядке следования этих пар. Для выполнения этого задания следует написать программу. …
Читать далее
Е24.31 Определите максимальное количество идущих подряд пар символов АВ или АС
Текстовый файл состоит из символов А, В и С. Определите максимальное количество идущих подряд пар символов АВ или АС в прилагаемом файле. Для выполнения этого задания следует написать программу. TXT ZIP Апробация ЕГЭ по информатике 19 февраля 2022 – задание №24 Тренировочный экзамен по информатике и ИКТ (КЕГЭ) в компьютерной форме
Читать далее
Е24.30 не содержат других букв E (кроме первой и последней) и букв F
Текстовый файл содержит только заглавные буквы латинского алфавита (ABC…Z). Определите количество групп из идущих подряд не менее 12 символов, которые начинаются и заканчиваются буквой E и не содержат других букв E (кроме первой и последней) и букв F. TXT СтатГрад Вариант ИН2110301 08.02.2022 – задание №24
Читать далее
Е24.29 максимальное количество идущих подряд символов, среди которых не более двух букв D
Текстовый файл содержит только заглавные буквы латинского алфавита(ABC…Z). Определите максимальное количество идущих подряд символов, среди которых не более двух букв D. Ответ: TXT «Некрыловские варианты» от Евгения Джобса — Вариант 5
Читать далее
Е24.28 среди которых нет ни одной буквы B и при этом не менее трёх букв A.
Текстовый файл содержит только заглавные буквы латинского алфавита (ABC…Z). Определите максимальное количество идущих подряд символов, среди которых нет ни одной буквы B и при этом не менее трёх букв A. Ответ: TXT informatikaexpert.ru
Читать далее
Е24.27 Необходимо найти строку, содержащую наименьшее количество букв N
Текстовый файл содержит строки различной длины. Общий объём файла не превышает 1 Мбайт. Строки содержат только заглавные буквы латинского алфавита (ABC…Z). Необходимо найти строку, содержащую наименьшее количество букв N (если таких строк несколько, надо взять ту, которая находится в файле раньше), и определить, какая буква встречается в этой строке чаще всего. Если таких букв несколько, …
Читать далее
Е24.26 максимальное расстояние между одинаковыми буквами в одной строке
Текстовый файл содержит строки различной длины. Общий объём файла не превышает 1 Мбайт. Строки содержат только заглавные буквы латинского алфавита (ABC…Z). В строках, содержащих менее 25 букв A, нужно определить и вывести максимальное расстояние между одинаковыми буквами в одной строке. Пример. Исходный файл: GIGA GABLAB NOTEBOOK AGAAA В этом примере во всех строках меньше 25 …
Читать далее
Решу егэ информатика 13745
ИНФОРМАТИКА
Демонстрационная версия ЕГЭ по информатике 2022 года с решениями.
2020—2021 УЧЕБНЫЙ ГОД
Демонстрационная версия ЕГЭ по информатике 2021 года с решениями.
ЕГЭ по информатике 24.06.2021. Основная волна. Разные задачи.
2019—2020 УЧЕБНЫЙ ГОД
Демонстрационная версия ЕГЭ по информатике 2020 года с решениями.
ЕГЭ по информатике. Досрочная волна. Вариант 1.
ЕГЭ по информатике. Досрочная волна. Вариант 2.
ЕГЭ по информатике 03.07.2020. Основная волна. Вариант 1 (Имаева−Зубовой).
ЕГЭ по информатике 03.07.2020. Основная волна. Вариант 2.
2018—2019 УЧЕБНЫЙ ГОД
ЕГЭ по информатике 3.04.2019. Досрочная волна. Вариант 1.
ЕГЭ по информатике 3.04.2019. Досрочная волна. Вариант 2.
2017—2018 УЧЕБНЫЙ ГОД
ЕГЭ по информатике 21.03.2018. Досрочная волна. Вариант.
ЕГЭ по информатике 28.05.2018. Основная волна. Вариант.
2016—2017 УЧЕБНЫЙ ГОД
ЕГЭ по информатике 23.03.2017. Досрочная волна. Вариант.
2015—2016 УЧЕБНЫЙ ГОД
Демонстрационная версия ЕГЭ по информатике 2016 года с решениями.
ЕГЭ по информатике 23.03.2016. Досрочная волна. Вариант.
ЕГЭ по информатике 16.06.2016. Основная волна. Вариант 41 (Часть С).
ЕГЭ по информатике 16.06.2016. Основная волна. Вариант 52 (Часть С).
ЕГЭ по информатике 16.06.2016. Основная волна. Вариант 66 (Часть С).
ЕГЭ по информатике 16.06.2016. Основная волна. Вариант 77 (Часть С).
2014—2015 УЧЕБНЫЙ ГОД
Демонстрационная версия ЕГЭ по информатике 2015 года с решениями.
ЕГЭ по информатике 05.05.2015. Досрочная волна. Вариант.
2013—2014 УЧЕБНЫЙ ГОД
Демонстрационная версия ЕГЭ по информатике 2014 года с решениями.
ЕГЭ по информатике 05.05.2014. Досрочная волна. Вариант 1.
ЕГЭ по информатике 05.05.2014. Досрочная волна. Вариант 2.
ЕГЭ по информатике 08.05.2014. Досрочная волна, резервный день. Вариант 201.
ЕГЭ по информатике 08.05.2014. Досрочная волна, резервный день. Вариант 202.
2012—2013 УЧЕБНЫЙ ГОД
Демонстрационная версия ЕГЭ по информатике 2013 года с решениями.
ЕГЭ по информатике 30.05.2013. Основная волна. Дальний Восток. Вариант 1.
ЕГЭ по информатике 30.05.2013. Основная волна. Дальний Восток. Вариант 2.
ЕГЭ по информатике 30.05.2013. Основная волна. Дальний Восток. Вариант 3.
ЕГЭ по информатике 30.05.2013. Основная волна. Дальний Восток. Вариант 4.
ЕГЭ по информатике 30.05.2013. Основная волна. Дальний Восток. Вариант 5.
2016 2017 УЧЕБНЫЙ ГОД.
Inf-ege. sdamgia. ru
08.06.2018 14:34:25
2018-06-08 14:34:25
Источники:
Https://inf-ege. sdamgia. ru/methodist
ЕГЭ–2022, информатика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword { color: red; } Решу егэ информатика 13745
Решу егэ информатика 13745
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
—>
Задание 15 № 13745
Для какого наибольшего целого числа А формула
((x ≤ 9) →(x ⋅ x ≤ A)) ⋀ ((y ⋅ y ≤ A) → (y ≤ 9))
Тождественно истинна, то есть принимает значение 1 при любых целых неотрицательных x и y?
Раскрывая импликацию по правилу A → B = A + B, заменяя логическую сумму совокупностью, а логическое произведение системой соотношений, определим значения параметра А, при котором система совокупностей
Будет иметь решения для любых целых неотрицательных чисел.
Заметим, что переменные не связаны между собой уравнением или неравенством, поэтому необходимо и достаточно, чтобы решениями первой совокупности были все неотрицательные Х, а решениями второй совокупности были все неотрицательные Y.
Решениями неравенства являются числа 10, 11, 12, . Чтобы совокупность выполнялась для всех целых неотрицательных чисел, числа 0, 1, 2, . 9 должны быть решениями неравенства. Значит, .
Аналогично, решениями неравенства являются числа 0, 1, . 9. Следовательно, числа 10, 11, 12, . должны быть решениями неравенства. Поэтому.
—>
Задание 15 № 13745
Уско рен ная под го тов ка к ЕГЭ с ре пе ти то ра ми Учи.
Inf-ege. sdamgia. ru
27.04.2017 9:37:21
2017-04-27 09:37:21
Источники:
Https://inf-ege. sdamgia. ru/problem? id=13745
Информатика 11 класс пробный вариант №13 решу ЕГЭ 2022 задания с ответами | ЕГЭ ОГЭ СТАТГРАД ВПР 100 баллов » /> » /> .keyword { color: red; } Решу егэ информатика 13745
Информатика 11 класс пробный вариант №13 решу ЕГЭ 2022 задания с ответами
Информатика 11 класс пробный вариант №13 решу ЕГЭ 2022 задания с ответами
1)На рисунке справа схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведения о длинах этих дорог (в километрах). Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Выпишите последовательно, без пробелов и знаков препинания, указанные на графе буквенные обозначения пунктов от П1 до П7: сначала букву, соответствующую П1, затем букву, соответствующую П2, и т. д.
Правильный ответ: ЕЖГБАДВ
2)Логическая функция F задаётся выражением w ∨ (x → y) ∧ (z → x). На рисунке приведён частично заполненный фрагмент таблицы истинности функции F, содержащий неповторяющиеся строки. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.
Правильный ответ: wzyx
3)В файле 3-5.xls приведён фрагмент базы фрагмент базы данных «Аудиотека». База данных состоит из четырёх таблиц. Таблица «Альбомы» содержит записи о записанных альбомах, а также информацию о исполнителях. Таблица «Артисты» содержит записи о названии исполнителей. Таблица «Треки» содержит записи о записанных композициях, а также информацию о альбомах и жанрах. Поле Длительность содержит длительность аудиозаписи в миллисекундах, поле Размер содержит размер аудиозаписи в байтах, а поле Стоимость содержит стоимость аудиозаписи в рублях. Таблица «Жанры» содержит данные о названии жанров. На рисунке приведена схема указанной базы данных. Используя информацию из приведённой базы данных, найдите исполнителя в жанре Rock с наименьшей суммарной длительностью песен в этом жанре. В ответе укажите целую часть длительности его песен в секундах.
Правильный ответ: 310
4)По каналу связи передаются сообщения, содержащие только семь букв: А, Б, В, Г, Д, Е и Ж. Для передачи используется двоичный код, удовлетворяющий условию Фано. Для буквы А используется кодовое слово 10; для буквы Б используется кодовое слово 011. Какова минимальная общая длина кодовых слов для всех семи букв?
Правильный ответ: 20
5)На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом. 1) Строится двоичная запись числа N. 2) Затем справа дописываются два разряда: символы 01, если число N чётное, и 10, если нечётное. Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью искомого числа R. Укажите минимальное число N, после обработки которого автомат получает число, большее 73. В ответе это число запишите в десятичной системе.
Правильный ответ: 19
6)Определите наименьшее и наибольшее введённое значение переменной s, при котором программа выведет число 42. В ответ запишите оба числа в порядке возрастания без пробелов и других разделителей.
Правильный ответ: 1122
7)Геннадий создает мультипликационный ролик, где каждый кадр – отдельно отрисованная картинка. Известно, что каждая картинка имеет разрешение 640х480 пикселей и цветовую палитру в 216 = 65536 цветов. Каждый пиксель кодируется с помощью минимально возможного и одинакового для всех пикселей количества бит. Картинки записываются одна за другой без разделителей и заголовков файла. Частота смены кадров в конечном ролике – 24 кадра/сек. В качестве звукового сопровождения выбран формат стерео с глубиной кодирования 10 бит и частотой дискретизации 40 кГц. Найдите размер мультфильма в МБайтах, если известно, что его длительность 5 минут. В качестве ответа укажите число – минимальное целое количество Мбайт достаточное для хранения такого файла.
Правильный ответ: 4248
8)Лиза составляет слова из букв О, Н, И, К, С, причём буква С должна встречаться в этих словах ровно 3 раза, а буква О — ровно 1 раз. Длина слова составляет от 4 до 6 букв. Сколько различных слов может составить Лиза?
Правильный ответ: 604
9)Откройте файл электронной таблицы 9-119.xls, содержащей в каждой строке четыре натуральных числа, являющиеся последовательностью длин отрезков ломаной. Выясните, какое количество четверок чисел может являться сторонами описанного четырехугольника. В ответе запишите только число.
Правильный ответ: 787
10)В файле 10-141.docx приведена книга Н. В. Гоголя «Вечера на хуторе близ Диканьки». Сколько раз слово «Нет» (с заглавной буквы) встречается в тексте повести «Страшная месть» (не считая сносок)? В ответе укажите только число.
Правильный ответ: 21
11)Каждый сотрудник предприятия получает электронный пропуск, на котором записаны личный код, состоящий из двух частей. Первая часть кода содержит 10 символов, каждый из которых может быть одной из 26 заглавных латинских букв. Вторая часть кода содержит 5 символов, каждый из которых может быть одной из десятичных цифр. При этом в базе данных сервера формируется запись, содержащая этот код и дополнительную информацию о пользователе. Для представления кода используют посимвольное кодирование, все символы в пределах одной части кода кодируют одинаковым минимально возможным для этой части количеством битов, а для кода в целом выделяется минимально возможное целое количество байтов. Для хранения данных о 40 пользователях потребовалось 1800 байт. Сколько байтов выделено для хранения дополнительной информации об одном пользователе? В ответе запишите только целое число – количество байтов.
Правильный ответ: 36
12)Исполнитель Редактор получает на вход строку цифр и преобразовывает её. Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки символов. 1. заменить (v, w) 2. нашлось (v) Первая команда заменяет в строке первое слева вхождение цепочки v на цепочку w. Если цепочки v в строке нет, эта команда не изменяет строку. Вторая команда проверяет, встречается ли цепочка v в строке исполнителя Редактор. Дана программа для исполнителя Редактор: НАЧАЛО ПОКА нашлось(АА) ИЛИ нашлось(ВВ) ИЛИ нашлось(АВ) заменить(АА, В) заменить(ВВ, А) заменить(АВ, ВА) КОНЕЦ ПОКА КОНЕЦ Известно, что на вход программы поступила строка из 52 подряд идущих комбинаций «АВ» (все буквы заглавные, латинские). Какая строка получится после выполнения алгоритма?
Правильный ответ: ВА
13)На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К, Л. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей, ведущих из города А в город Л и проходящих через город Ж, но НЕ проходящих через город Д?
Правильный ответ: 9
14)Значение выражения 41503 + 3∙4244 – 2∙41444 – 96 записали в системе счисления с основанием 4. Найдите сумму цифр получившегося числа и запишите её в ответе в десятичной системе счисления.
Правильный ответ: 902
15)Элементами множества А являются натуральные числа. Известно, что выражение ((x ∈ ) ≡ (x ∈ A)) → ((x ∈ ) ≡ (x ∈ A)) истинно (т. е. принимает значение 1 при любом значении переменной х. Определите наименьшее возможное значение произведения элементов множества A.
Правильный ответ: 90
Правильный ответ: 1288
17)В файле 17-7.txt содержится последовательность целых чисел. Элементы последовательности могут принимать значения от 0 до 200 включительно. Рассматривается множество элементов последовательности, для которых сумма цифр кратна 3. Найдите количество таких чисел и максимальное из них.
Правильный ответ: 54 138
Правильный ответ: 2263, 587
22)Ниже записана программа, которая вводит натуральное число x, выполняет преобразования, а затем выводит два числа. Укажите наименьшее возможное значение x, при вводе которого программа выведет числа 3 и 10. x = int(input()) k = x % 5 a = 0 b = 0 while x > 0: d = x % 5 if d == k: a += 1 b += d x //= 5 print(a, b).
Правильный ответ: 218
23)Исполнитель Нолик преобразует число, записанное на экране в четверичной системе счисления. У исполнителя есть три команды, которым присвоены номера: 1. Прибавить 2 2. Прибавить 3 3. Добавить справа 0 Первая команда увеличивает число на 2. Вторая команда увеличивает число на 3. Третья команда приписывает к записи числа справа 0, например, для числа 123 результатом работы данной команды будет являться число 1230. Сколько существует программ, которые число 1, записанное в четверичной системе счисления, преобразуют в четверичную запись 100?
Правильный ответ: 43
24)Текстовый файл 24-164.txt состоит не более чем из 106 символов и содержит только заглавные буквы латинского алфавита (ABC…Z). Текст разбит на строки различной длины. В строках, содержащих менее 20 букв E, нужно определить и вывести максимальное расстояние между одинаковыми буквами в одной строке. Пример. Исходный файл: VOVA ZAEALE QRAEQT В этом примере во всех строках меньше 20 букв E. Самое большое расстояние между одинаковыми буквами – в третьей строке между буквами Q, расположенными в строке на 1-й и 5-й позициях. В ответе для данного примера нужно вывести число 4.
Правильный ответ: 974
25)Напишите программу, которая ищет среди целых чисел, принадлежащих числовому отрезку [3; 1000000] последовательности подряд идущих составных чисел длиной не менее 90. Для каждой найденной последовательности запишите в порядке возрастания простые числа, стоящие на границах данных последовательностей. В ответе запишите эти пары простых чисел в порядке возрастания первого числа в паре.
26)В текстовом файле записан набор натуральных чисел. Гарантируется, что все числа различны. Необходимо определить, сколько в наборе троек чисел с суммой, кратной трём, таких что их среднее арифметическое тоже присутствует в файле, и чему равно наименьшее из средних арифметических таких троек. Входные данные представлены в файле 26-46.txt следующим образом. Первая строка содержит целое число N – общее количество чисел в наборе. Каждая из следующих N строк содержит одно число, не превышающее 109. В ответе запишите два целых числа: сначала количество троек, затем наименьшее среднее арифметическое.
Сколько существует различных путей, ведущих из города А в город Л и проходящих через город Ж, но НЕ проходящих через город Д.
100ballnik. com
05.07.2019 6:06:01
2019-07-05 06:06:01
Источники:
Https://100ballnik. com/%D0%B8%D0%BD%D1%84%D0%BE%D1%80%D0%BC%D0%B0%D1%82%D0%B8%D0%BA%D0%B0-11-%D0%BA%D0%BB%D0%B0%D1%81%D1%81-%D0%BF%D1%80%D0%BE%D0%B1%D0%BD%D1%8B%D0%B9-%D0%B2%D0%B0%D1%80%D0%B8%D0%B0%D0%BD%D1%82-%E2%84%9613/
Мы подошли к 14 заданию из ЕГЭ по информатике 2022. Оно связано с различными системами счисления. Что такое различные системы счисления, мы рассматривали в этой статье. Так же будет полезно посмотреть эту статью.
Переходим к первому тренировочному 14-ому заданию из ЕГЭ по информатике. Раньше это задание было под номером 16.
Задача (ЕГЭ по информатике, 2019, Москва)
Значение выражения 536 + 524 — 25 записали в системе счисления с основанием 5. Сколько цифр «4» содержится в этой записи?
Решение:
Первый способ. (С помощью Питона)
f = 5**36 + 5**24 - 25 s='' while f>0: s = s + str(f%5) f = f // 5 print(s.count('4'))
В переменную f записываем функцию. Две звёздочки подряд обозначают возведение в степень. Заводим строчку s, где и будет сформировано число в пятеричной системе.
Сам перевод числа f в пятеричную систему происходит в цикле WHILE.
Записываем остатки от деления на 5 в строку s. Делаем так же, как если бы переводили в ручную. И так же производим само целочисленное деление. Это мы тоже делаем, когда переводим на листке бумаги.
В строке s получается число в пятеричной системе, но в цифры в этой записи стоят в обратном порядке. Ведь, когда мы переводим в ручную, остатки должны записать задом наперёд.
Здесь и не важен порядок цифр, важно количество четвёрок!
С помощью функции count находим количество четвёрок в строке s.
В ответе напишем 22.
Второй способ. (Классический)
Сформулируем главное правило, на которое будем опираться при решении подобного типа задач.
Примеры:
54 (в десятичной системе) — это 100005 (в пятеричной системе)
72 (в десятичной системе) — это 1007 (в семеричной системе)
29 (в десятичной системе) — это 10000000002 (в двоичной системе)
Перепишем наше выражение, чтобы все числа были в виде степени представлены.
536 + 524 — 52
Посчитаем 536 + 524 в пятеричной системе столбиком, используя основное правило.
Здесь всё просто: ноль прибавить ноль, будет ноль. Единица плюс ноль, будет один.
Теперь от получившегося числа нужно отнять 52 (1005).
Первые два разряда посчитать легко. Ноль минус ноль, будет ноль.
Третий разряд: из нуля отнять единицу мы не можем, поэтому занимаем у более старших разрядов.
В более старших разрядах тоже нули, поэтому идём до единицы, у которой можно занять. Получается 22 четвёрки.
Вот как было бы, если бы считали в нашей родной десятичной системе счисления в аналогичной ситуации.
Здесь мы считаем в десятичной системе, поэтому получаются девятки. В нашей задаче считали в пятеричной системе, поэтому получаются четвёрки.
В ответе напишем 22 четвёрки.
Ответ: 22
Задача (ЕГЭ по информатике, 2020, Москва)
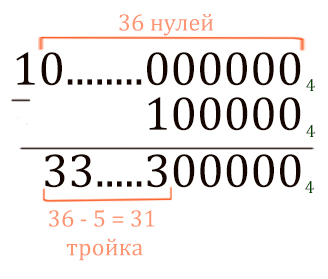
Значение выражения 168 × 420 — 45 — 64 записали в системе счисления с основанием 4. Сколько цифр «3» содержится в этой записи?
Решение:
Первый способ. (С помощью Питона)
f = 16**8 * 4**20 - 4**5 - 64 s='' while f>0: s = s + str(f%4) f = f // 4 print(s.count('3'))
Второй способ. (Классический)
Преобразуем наше выражение. Приведём всё к 4-ам.
168 × 420 — 45 — 64 =
= (42)8 × 420 — 45 — 43 =
= 416 × 420 — 45 — 43 =
= 436 — 45 — 43
Здесь не можем применить технику устного счёта, потому что стоят два минуса. Значит, будем решать с помощью столбиков.
Сначала посчитаем 436 — 45.
Теперь от этого числа нужно отнять 43 (10004)
Получается 32 тройки.
В последнем вычислении нет ничего сложно. В десятичной системе вы бы легко вычислили в аналогичной ситуации.
Ответ: 32
Задача (Тренировочная)
Укажите через запятую в порядке возрастания все десятичные натуральные числа, не превосходящие 17, запись которых в троичной системе счисления оканчивается на две одинаковые цифры.
Решение:
1) Переведём число 17 в троичную систему.
Получилось 1223.
2) Теперь выпишем все числа, которые не превосходят 1223 (Т.е. 1223 тоже подходит!), запись которых в троичной системе счисления оканчивается на две одинаковые цифры. В троичной системе могут применяться цифры 0, 1, 2.
1223
1223
1113
1003
223
113
Теперь переведём эти числа в десятичную систему.
1223 = 2 × 30 + 2 × 31 + 1 × 32 = 1710
1113 = 1 × 30 + 1 × 31 + 1 × 32 = 1310
1003 = 0 × 30 + 0 × 31 + 1 × 32 = 910
223 = 2 × 30 + 2 × 31 = 810
113 = 1 × 30 + 1 × 31 = 410
Ответ: 4, 8, 9, 13, 17
Ещё один интересный тип задания номер 14, который вполне может быть на реальном ЕГЭ по информатике 2022.
Задача (Уравнение)
Чему равно наименьшее основание позиционной системы счисления x, при котором 225x = 405y?
Ответ записать в виде целого числа.
Решение:
Переведём каждое из чисел 225x и 405y в десятичную систему счисления и приравняем, т.к. эти числа равны.
5 × x0 + 2 × x1 + 2 × x2 = 5 × y0 + 0 × y1 + 4 × y2
Любое число в нулевой степени — это 1. Значит, 5 × x0 = 5 × y0 = 5. Эти два выражения равны одному и тому же значению, следовательно, их можно убрать и слева, и справа.
2x + 2x2 = 4y2
x + x2 = 2y2
x(1 + x) = 2y2
Получили уравнение в целых числах. Слева умножение двух последовательных чисел. Нужно начать подбирать целые числа.
При y = 6 :
x (1 + x) = 2 × 62 = 72 ; Произведение двух последовательных чисел 8 * 9 = 72. Значит, x = 8.
Мы начали проверку с числа 6, потому что у нас в уравнении присутствуют цифра 5. Значит, система счисления может быть минимум с основанием 6.
Получается, что наименьшее значение x равно 8.
В подобных задач нужно знать, что числа обязательно найдутся, нужно их просто хорошо поискать.
Для качественной проработки 14 задания из ЕГЭ по информатике 2022 разберём ещё некоторые задачи.
Задача (Основание системы)
Запись числа 338 в системе счисления с основанием N содержит 3 цифры и оканчивается на 2. Чему равно максимально возможное основание системы счисления?
Решение:
В этой задаче применим формулу:
Примером для данной формулы можно взять два разряда в двоичной системе. Максимальное число в двоичной системе равно 112. А в десятичной системе это число равно 310. Т.е. 22 — 1.
338 число будет точно больше, чем двухзначное число с основанием N.
Получается неравенство:
338 > N2 — 1
N2 < 339
N — положительное целое число. Тогда:
N < √339 ≈ 18
N ≤ 18
Сказано, что число в системе с основанием N оканчивается на 2. Поэтому первый остаток должен быть равен 2!
Будем идти вниз от числа 18 и проверять, на что делится 336.
Число 336 должно делится на N.
Подошло число 16 (16 * 21 = 336!)
Ответ: 16
Продолжаем подготовку к 14 заданию из ЕГЭ по информатике 2022
Задача (На понимание)
Запись числа в девятеричной системе счисления заканчивается цифрой 4. Какой будет последняя цифра в записи этого числа в троичной системе счисления?
Решение:
Подберём такие числа в десятичной системе, которые в остатке при первом делении на 9 дадут 4!
Посмотрим, какой остаток будет при делении этого же числа на 3 при первом делении. Получается 1. Это и будет ответ.
Ответ: 1
Задача (Закрепление материала)
Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 23 оканчивается на 2.
Решение:
Нужно перебрать все числа от 3 до 23 и определить, какие из них при делении числа 23 дадут остаток 2.
23 : 3 = 7 (ост. 2) +
23 : 4 = 5 (ост. 3) —
23 : 5 = 4 (ост. 3) —
23 : 6 = 3 (ост. 5) —
23 : 7 = 3 (ост. 2) +
23 : 8 = 2 (ост. 7) —
23 : 9 = 2 (ост. 5) —
23 : 10 = 2 (ост. 3) —
23 : 11 = 2 (ост. 1) —
23 : 12 = 1 (ост. 11) —
23 : 13 = 1 (ост. 10) —
23 : 14 = 1 (ост. 9) —
23 : 15 = 1 (ост. 
23 : 16 = 1 (ост. 7) —
23 : 17 = 1 (ост. 6) —
23 : 18 = 1 (ост. 5) —
23 : 19 = 1 (ост. 4) —
23 : 20 = 1 (ост. 3) —
23 : 21 = 1 (ост. 2) +
23 : 22 = 1 (ост. 1) —
23 : 23 = 1 (ост. 0) —
Подходят числа 3, 7, 21.
Здесь можно и написать программу:
for i in range(3, 24): if 23%i==2: print(i)
Ответ: 3, 7, 21
Задача (Добьём 14 задание из ЕГЭ по информатике 2022)
В некоторой системе счисления записи десятичных чисел 66 и 40 заканчиваются на 1. Определите основание системы счисления.
Решение:
Нужно найти такое число, чтобы числа 66 и 40 при делении на это число давали остаток 1.
Т.е. искомое число должно быть делителем чисел 65 (66-1) и 39 (40-1). У числа 39 не так много делителей: 1, 3, 13, 39
Видим, что число 65 делится на 13 (65 : 13 = 5). Поэтому искомое число равно 13.
Ответ: 13
Задача (Для чемпионов!)
В какой системе счисления выполняется равенство 12 · 13 = 222?
В ответе укажите число – основание системы счисления.
Решение:
Если бы мы находились в десятичной системе, то последней цифрой была бы 6 (2 * 3). Но у нас 2! Т.е. Система счисления меньше или равна 6, т.к. если бы система счисления была больше 6, то у нас была бы 6 последняя цифра.
Шестёрка не «поместилась» в младший разряд, от неё осталось только 2. Остальные 4 единицы ушли в более старший разряд. Если 4 единицы составляют единицу более старшего разряда, то значит, мы находимся в четверичной системе.
Ответ: 4
Задача (Новый тип, Статград окт 2022)
В выражении 1xBAD16 + 2CxFE16 x обозначает некоторую цифру из алфавита шестнадцатеричной системы счисления. Определите наименьшее значение x, при котором значение данного выражения кратно 15. Для найденного x вычислите частное от деления данного выражения на 15 и запишите его в ответе в десятичной системе счисления.
Решение:
Здесь дана сумма чисел, которые написаны в шестнадцатеричной системе счисления.
Мы будем перебирать каждую цифру из шестнадцатеричной системы (0-15) с помощью цикла. Нас будут интересовать те значения x, при котором сумма этих чисел будет делится на 15.
for x in range(0, 16): a=13*16**0 + 10*16**1 + 11*16**2 + x*16**3 + 1*16**4 b=14*16**0 + 15*16**1 + x*16**2 + 12*16**3 + 2*16**4 if (a+b)%15==0: print(x, (a+b)//15)
Чтобы проверить, делится ли данное выражение на 15, переводим оба слагаемых в нашу родную десятичную систему. Переводим стандартным образом, об этом можно прочитать здесь.
В задаче нужно написать для наименьшего найденного значения x результат от деления данной суммы на 15.
Получается 18341
Ответ: 18341
Задача(Новый тип, закрепление)
(Богданов) Операнды арифметического выражения записаны в системе счисления с основанием 17:
9759x17 + 3×10817
В записи чисел переменной x обозначена неизвестная цифра из алфавита 17-ричной системы счисления. Определите наименьшее значение x, при котором значение данного арифметического выражения кратного 11. Для найденного значения x вычислите частное от деления значения арифметического выражения на 11 и укажите его в ответе в десятичной системе счисления. Основание системы счисления в ответе указывать не нужно.
Решение:
Решим задание с помощью предыдущего шаблона на языке Python.
for x in range(0, 17): a=x*17**0 + 9*17**1 + 5*17**2 + 7*17**3 + 9*17**4 b=8*17**0 + 0*17**1 + 1*17**2 + x*17**3 + 3*17**4 if (a+b)%11==0: print(x, (a+b)//11)
Ответ: 95306
Задача (Новый тип, две переменные)
(В. Шубинкин) Числа M и N записаны в системах счисления с основаниями 15 и 13 соответственно.
M = 2y23x515, N = 67x9y13
В записи чисел переменными x и y обозначены допустимые в данных системах счисления неизвестные цифры. Определите наименьшее значение натурального числа A, при котором существуют такие x, y, что M + A кратно N.
Решение:
Принцип решения данной задачи похож на решение 15 задания из ЕГЭ по информатике.
for A in range(1, 5000): for x in range(0, 13): for y in range(0, 13): M=5*15**0 + x*15**1 + 3*15**2 + 2*15**3 + y*15**4 + 2*15**5 N=y*13**0 + 9*13**1 + x*13**2 + 7*13**3 + 6*13**4 if (M+A)%N==0: print(A)
Нужно найти A, значит, начинаем перебирать A. Идём от 1, т.к. речь идёт о натуральных числах. Перебираем x и y. Они могут принимать значения из алфавита в 13-ой системе. Берём меньшую, т.к. эти переменные и в первом числе, и во втором одинаковые.
Если выполняется условие задачи, то нам интересно такое A при котором это произошло.
В этой задаче A получается достаточно большим, поэтому перебираем эту переменную до 5000.
Ответ: 1535
На этом всё! Вы прошли чемпионскую тренировку по подготовке 14 задания из ЕГЭ по информатике 2022. Успехов на экзамене!
«В переменную f записываем функцию». В переменную f мы записываем не функцию, а выражение
Господа, вот это я понимаю, по-настоящему чемпионская подготовка. Тут же и язык свой придумали, и решение на нём сделали. Скажите, зачем над змеёй то издеваться? Очень уж режет слух неправильное произношение. «Пайтон» — вот как должно быть. Я бы промолчал, увидев это раз, но видя подобное насилие над словом постоянно — молчать более не могу
Для ласт задачи модно сделать код куда проще и короче
for a in range(1, 10000):
for x in ‘0123456789ABC’:
for y in ‘0123456789ABC’:
M = int(f’2{y}23{x}5′, 15)
N = int(f’67{x}9{y}’, 13)
if (M + a) % N == 0:
print(a)
break
Первое задание, первое решение, очепятка: «В ответе напишем 4»,
вместо: «В ответе напишем 22».
И спасибо Вам за этот сайт!)
Примерное время на чтение статьи: 13 минут
Рассмотрим решение некоторых задач из варианта ИН2010401 (Статград 2021 № 4).
Задача 2
Логическая функция F задаётся выражением ¬((?∨?)→(?∧?))∧(?→?). Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности функции F. Определите, какому столбцу таблицы истинности соответствует каждая из переменных x, y, z, w.
| Переменная 1 | Переменная 2 | Переменная 3 | Переменная 4 | Функция |
| ??? | ??? | ??? | ??? | F |
| 1 | 1 | 1 | 1 | |
| 1 | 1 | 1 | ||
| 1 | 1 | 1 |
В ответе напишите буквы x, y, z, w; в том порядке, в котором идут соответствующие им столбцы (сначала — буква, соответствующая первому столбцу; затем — буква, соответствующая второму столбцу, и т. д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Пример. Пусть задано выражение x → y, зависящее от двух переменных x и y, и фрагмент таблицы истинности:
| Переменная 1 | Переменная 1 | Функция |
| ??? | ??? | F |
| 0 | 1 | 0 |
Тогда первому столбцу соответствует переменная y, а второму столбцу соответствует переменная x. В ответе нужно написать: yx.
Решение. Поскольку пока не известно, в каком столбце заголовка стоит какая переменная, дадим им произвольные имена по порядку, например a, b, c, d. После чего подставим их в функцию F и отобразим только строки, соответствующие значению F=1. Рассмотрим два варианта решения:
# Способ 1 (без использования библиотеки itertools)
print('a b c d')
for a in range(2):
for b in range(2):
for c in range(2):
for d in range(2):
if (not ((a or b) <= (c and d))) and (a <= d):
print(a, b, c, d)# Способ 2 (с использованием функции product библиотеки itertools)
from itertools import product
def condition(x, y, z, w):
return (not ((x or y) <= (z and w))) and (x <= w)
print('a b c d')
rec = list(product('01', repeat=4))
for a in rec:
if condition(int(a[0]), int(a[1]), int(a[2]), int(a[3])) == 1:
print(int(a[0]), int(a[1]), int(a[2]), int(a[3]))Результат работы программы:
a b c d
0 1 0 0
0 1 0 1
0 1 1 0
1 0 0 1
1 1 0 1Ответ: zxy
Задача 5
Алгоритм получает на вход натуральное число ?>1 и строит по нему новое число ? следующим образом:
- Строится двоичная запись числа ?.
- Подсчитывается количество нулей и единиц в полученной записи. Если их количество одинаково, в конец записи добавляется её последняя цифра. В противном случае в конец записи добавляется та цифра, которая встречается реже.
- Шаг 2 повторяется ещё два раза.
- Результат переводится в десятичную систему счисления.
Пример. Дано число ?=19. Алгоритм работает следующим образом:
- Двоичная запись числа N: 10011.
- В полученной записи нулей меньше, чем единиц, в конец записи добавляется 0. Новая запись: 100110.
- В текущей записи нулей и единиц поровну, в конец записывается последняя цифра, это 0. Получается 1001100. В этой записи единиц меньше, в конец добавляется 1: 10011001.
- Результат работы алгоритма ?=153.
При каком наименьшем исходном числе ?>99 в результате работы алгоритма получится число, кратное 4?
def modify(st):
(k0, k1) = (st.count('0'), st.count('1'))
if k0 == k1:
st = st + st[-1]
elif k0 > k1:
st = st + '1'
else:
st = st + '0'
return st
N = 99
while True:
strN = bin(N)[2:]
for _ in range(3):
strN = modify(strN)
R = int(strN, 2)
if N > 99 and R % 4 == 0:
print(N);
break
N += 1Ответ: 103
Задание 6
Определите, при каком наименьшем введённом значении переменной ? программа выведет число 11. Для Вашего удобства программа представлена на двух языках программирования.

def alg(s):
s = 10 * s + 5
n = 1
while s < 2021:
s = s + 2 * n
n = n + 1
return n == 11
s = 1
while True:
if alg(s):
print(s);
break;
s += 1Ответ: 191
Задание 7
В информационной системе хранятся изображения размером 1024×768 пикселей. Методы сжатия изображений не используются. Каждое изображение дополняется служебной информацией, которая занимает 1280 Кбайт. Для хранения 2048 изображений потребовалось 4 Гбайт. Сколько цветов использовано в палитре каждого изображения?
for B in range(1, 24):
v = 2048 * (1024 * 768 * B + 1280 * 2**13) / (2 ** 33)
if v == 4:
print(2**B)Ответ: 256
Задача 8
Вероника составляет 3-буквенные коды из букв В,Е,Р,О,Н,И,К,А, причём буква В должна входить в код ровно один раз. Все полученные коды Вероника записала в алфавитном порядке и пронумеровала. Начало списка выглядит так:
- ААВ
- АВА
- АВЕ
- …
На каком месте будет записан первый код, не содержащий ни одной буквы А?
from itertools import product
lstAll = list(product('ВЕРОНИКА', repeat=3))
lst = []
for item in lstAll:
if item.count('В') == 1:
lst.append(''.join(item))
lst.sort()
for i in range(0, len(lst)-1):
if not 'А' in lst[i]:
print(i + 1)
breakОтвет: 23
Задание 11
Каждый объект, зарегистрированный в информационной системе, получает уникальный код из 14 символов, каждый из которых может быть одной из 26 заглавных латинских букв или одной из 10 цифр. Для представления кода используют посимвольное кодирование, все символы кодируют одинаковым минимально возможным количеством битов, а для кода в целом выделяется минимально возможное целое количество байтов. Кроме того, для каждого объекта в системе выделено 79 байт для хранения содержательной информации. Сколько байтов потребуется для хранения данных (код и содержательная информация) о 30 объектах? В ответе запишите только целое число – количество байтов.
part_1 = 14 * 6 # 26 заглавных латинских букв и 10 цифр (36 комбинаций) потребуют 6 бит
if part_1 / 8 == part_1 // 8:
kod = part_1 // 8
else:
kod = part_1 // 8 + 1
v = (kod + 79) * 30
print(v)Ответ: 2700
Задание 14
Значение выражения 7297+316–18 записали в системе счисления с основанием 9. Сколько раз в этой записи встречается цифра 0?
N = 729**7 + 3**16 - 18
k = 0
while N > 0:
if N % 9 == 0:
k += 1
N = N // 9
print(k)Ответ: 14
Задание 15
Для какого наименьшего натурального числа ? формула ДЕЛ(?,45)∧(ДЕЛ(750,?)→(¬ДЕЛ(?,?)→¬ДЕЛ(120,?))) тождественно истинна, то есть принимает значение 1 при любом натуральном ??
def Del(n, m):
return n % m == 0
def condition(x, A):
return Del(A, 45) and (Del(750, x) <= ((not Del(A, x)) <= (not Del(120, x))))
for A in range(1, 10000):
Ok = True # для этого А все x хорошие
for x in range(1, 1000000+1):
if not(condition(x, A)):
Ok = False
break
if Ok:
print(A)
breakОтвет: 90
Задача 16
Обозначим через ???(?,?) остаток от деления натурального числа ? на натуральное число ?. Алгоритм вычисления значения функции ?(?), где ? – целое неотрицательное число, задан следующими соотношениями:
- ?(0)=0;
- ?(?)=?(?/3), если ?>0 и при этом ???(?,3)=0;
- ?(?)=???(?,3)+?(?–???(?,3)), если ???(?,3)>0.
Назовите минимальное значение ?, для которого ?(?)=11.
def F(n):
if n == 0:
return 0
elif n > 0 and n % 3 == 0:
return F(n // 3)
elif n % 3 > 0:
return n % 3 + F(n - (n % 3))
n = 0 # n — целое неотрицательное число
while True:
if F(n) == 11:
print(n)
break
n += 1Ответ: 485
Задача 17
Назовём натуральное число подходящим, если у него ровно 3 различных простых делителя. Например, число 180 подходящее (его простые делители – 2, 3 и 5), а число 12 – нет (у него только два различных простых делителя). Определите количество подходящих чисел, принадлежащих отрезку [10001;50000], а также наименьшее из таких чисел. В ответе запишите два целых числа: сначала количество, затем наименьшее число.
def PrimeDelThree(n):
SetPrimeDel = set()
prime = True
for d in range(2, n+1):
while n % d == 0:
SetPrimeDel.add(d)
prime = False
n = n // d
if n == 1:
break
else:
if (d*d>n) and prime:
break
if prime:
SetPrimeDel.add(n)
return len(SetPrimeDel)==3
(count, mn) = (0, 50_000)
for n in range (50_000, 10001-1, -1):
if PrimeDelThree(n):
count += 1
mn = n
print(count, mn)Ответ: 15652 10002
Задача 22
Ниже записана программа, которая вводит натуральное число ?, выполняет преобразования, а затем выводит два числа. Укажите наименьшее возможное значение ?, при вводе которого программа выведет числа 3 и 10.

def alg(x):
k = x % 9
a, b = 0, 0
while x > 0:
d = x % 9
if d == k:
a = a + 1
b = b + d
x = x // 9
return (a, b)
x = 1
while True:
if alg(x) == (3, 10):
print(x)
break
x += 1Ответ: 874
Задача 23
Исполнитель преобразует число на экране. У исполнителя есть три команды, которым присвоены номера:
- Прибавить 1
- Умножить на 2
- Умножить на 3
Первая команда увеличивает число на экране на 1, вторая умножает его на 2, третья – умножает на 3. Программа для исполнителя – это последовательность команд.
Сколько существует программ, которые преобразуют исходное число 2 в число 36, и при этом траектория вычислений содержит число 12 и не содержит числа 30?
def numProg(start, x):
if x < start or x == 30:
return 0
if x == start:
return 1
k = numProg(start, x-1)
if x % 2 == 0:
k += numProg(start, x//2)
if x % 3 == 0:
k += numProg(start, x//3)
return k
# Умножаем количество маршрутов 2->12 на 12->36 (комбинаторика)
print(numProg(2, 12) * numProg(12, 36))Ответ: 60
Задача 24
Текстовый файл содержит строки различной длины. Общий объём файла не превышает 1 Мбайт. Строки содержат только заглавные буквы латинского алфавита (???…?).
Необходимо найти строку, содержащую наименьшее количество букв ? (если таких строк несколько, надо взять ту, которая находится в файле раньше), и определить, какая буква встречается в этой строке чаще всего. Если таких букв несколько, надо взять ту, которая позже стоит в алфавите.
Пример. Исходный файл:
GIGA
GABLAB
AGAAAВ этом примере в первой строке две буквы G, во второй и третьей – по одной. Берём вторую строку, т. к. она находится в файле раньше. В этой строке чаще других встречаются буквы A и B (по два раза), выбираем букву B, т. к. она позже стоит в алфавите. В ответе для этого примера надо записать B.
# С помощью списка
f = open('./Data/24/ИН2010401.txt')
minG = 1_000_000_000
for stroka in f:
kcurrG = stroka.count('G')
if kcurrG < minG:
minG, s = kcurrG, stroka
f.close()
cnt = [0]*26
for i in range(0, len(s) - 1):
cnt[ord(s[i]) - ord('A')] += 1
maxCount = 0
maxi = 0
for i in range(len(cnt)):
if cnt[i] >= maxCount:
maxCount = cnt[i]
maxi = i
print(chr(maxi + ord('A')))# С помощью словаря
f = open('./Data/24/ИН2010401.txt')
minG = 1_000_000_000
for stroka in f:
kcurrG = stroka.count('G')
if kcurrG < minG:
minG, s = kcurrG, stroka
f.close()
D = {}
for c in s:
if c in D:
D[c] += 1
else:
D[c] = 1
mx = max(D.values())
ans = []
for key, value in D.items():
if mx == value:
ans.append(key)
ans.sort()
print(ans[-1])Ответ: T
Задача 25
Найдите все натуральные числа, принадлежащие отрезку [35000000;40000000], у которых ровно пять различных нечётных делителей (количество чётных делителей может быть любым). В ответе перечислите найденные числа в порядке возрастания.
Идея. Нас интересуют числа, являющиеся четвертой степенью простого числа, возможно умноженные на некоторую степень двойки.
def isPrime(n):
d = 2
while d * d <= n:
if n % d == 0:
return False
d += 1
return True
(a, b) = (35_000_000, 40_000_000)
for n in range (a, b+1):
x = n
while x % 2 == 0:
x = x // 2 # Убираем все четные делители
if x ** 0.25 == int(x ** 0.25) and isPrime(x ** 0.25):
print(n)
n += 1Ответ: 35819648; 38950081; 39037448; 39337984
Задача 26
В текстовом файле записан набор натуральных чисел, не превышающих 109. Гарантируется, что все числа различны. Необходимо определить, сколько в наборе таких пар чётных чисел, что их среднее арифметическое тоже присутствует в файле, и чему равно наибольшее из средних арифметических таких пар.
Входные данные Первая строка входного файла содержит целое число ? – общее количество чисел в наборе. Каждая из следующих ? строк содержит одно число.
Пример входного файла
6
3
8
14
11
2
17В данном случае есть две подходящие пары: 8 и 14 (среднее арифметическое 11), 14 и 2 (среднее арифметическое 8). В ответе надо записать числа 2 и 11. В ответе запишите два целых числа: сначала количество пар, затем наибольшее среднее арифметическое.
# Линейный поиск (работает долго)
data = list(map(int, open(r'./Data/26/ИН2010401.txt').read().splitlines()))[1:]
k, mx = 0, 0
for i in range(len(data)-1):
if data[i] % 2 == 0:
for j in range(i + 1, len(data)):
if data[j] % 2 == 0:
sr = (data[i] + data[j]) // 2
if sr in data:
k, mx = k + 1, max(mx, sr)
print(k, mx)# Бинарный поиск
a = list(map(int, open(r'./Data/26/ИН2010401.txt').read().splitlines()))[1:]
a.sort()
lsts = []
for i in range(len(a) - 1):
for j in range(i + 1, len(a)):
if a[i] % 2 == 0 and a[j] % 2 == 0:
s = (a[i] + a[j]) // 2
L = i
R = j + 1
while L < R - 1:
C = ( R + L) // 2
if s < a[C]:
R = C
else:
L = C
if a[L] == s:
lsts.append(s)
print(len(lsts), max(lsts))Ответ: 15; 976339247
Задача 27
В текстовом файле записан набор натуральных чисел, не превышающих 108. Гарантируется, что все числа различны. Из набора нужно выбрать три числа, сумма которых делится на 3. Какую наибольшую сумму можно при этом получить?
Входные данные Первая строка входного файла содержит целое число ? – общее количество чисел в наборе. Каждая из следующих ? строк содержит одно число.
4
5
8
14
11В данном случае есть две подходящие тройки: 5,14,11 (сумма 30) и 8,14,11 (сумма 33). В ответе надо записать число 33.
Вам даны два входных файла (? и ?), каждый из которых имеет описанную выше структуру. В ответе укажите два числа: сначала значение искомой суммы для файла ?, затем для файла ?.
data = sorted(list(map(int, open(r'./Data/27/ИН2010401-B.txt').read().splitlines()))[1:])
m01, m02, m03, m11, m12, m13, m21, m22, m23 = 0, 0, 0, 0, 0, 0, 0, 0, 0
for a in data:
if a % 3 == 0:
m03, m02, m01 = m02, m01, a
if a % 3 == 1:
m13, m12, m11 = m12, m11, a
if a % 3 == 2:
m23, m22, m21 = m22, m21, a
print(max(m01 + m02 + m03, m11 + m12 + m13, m01 + m11 + m21, m21 + m22 + m23))Ответ: 2697; 299986167
Содержание:
- Решение 8 задания
- Сколько вариантов шифра или кодовых слов
- Сколько существует n-значных чисел, записанных в m-ной системе счисления
- Список в алфавитном порядке
- Вероятность событий
8-е задание: «Измерение количества информации»
Уровень сложности
— базовый,
Требуется использование специализированного программного обеспечения
— нет,
Максимальный балл
— 1,
Примерное время выполнения
— 4 минуты.
Проверяемые элементы содержания: Знание о методах измерения количества информации
До ЕГЭ 2021 года — это было задание № 10 ЕГЭ
Плейлист видеоразборов задания на YouTube:
Задание демонстрационного варианта 2022 года ФИПИ
Сколько вариантов шифра или кодовых слов
8_1:
Шифр кодового замка представляет собой последовательность из пяти символов, каждый из которых является цифрой от 1 до 6.
Сколько различных вариантов шифра можно задать, если известно, что цифра 1 должна встречаться в коде ровно 1 раз, а каждая из других допустимых цифр может встречаться в шифре любое количество раз или не встречаться совсем?
Типовые задания для тренировки
Ответ: 3125
✍ Показать решение:
-
✎ Решение теоретическое:
- Формула нахождения количества различных сообщений:
- Итак, что у нас дано из этой формулы:
- Длина сообщения (L) = 5 символов
- Мощность алфавита (N) = 6 (цифры от 1 до 6).
- Но так как цифра 1 встречается по условию ровно один раз, а остальные 5 цифр — любое количество раз, то будем считать, что N = 5 (цифры от 2 до 6, исключая 1).
Найдем количество вариантов для одного случая, а именно: когда единица стоит на первом месте, а остальные 5 цифр размещаем на четыре позиции:
Q = NL
1 5 5 5 5 - 1 * Q = 54 = 625
Найдем количество вариантов двумя разными способами (можно выбрать любой из них):
✎ 1 способ. Найдем количество вариантов методом перебора:
1 5 5 5 5 -1 * Q=54= 625 5 1 5 5 5 -1 * Q=54= 625 5 5 1 5 5 -1 * Q=54= 625 5 5 5 1 5 -1 * Q=54= 625 5 5 5 5 1 -1 * Q=54= 625
✎ 2 способ. Найдем количество вариантов при помощи формулы комбинаторики:
[ C{binom{4}{5}}= frac{5!}{4!(5-4)!} = 5 ]
625 * 5 = 3125
✎ Решение с использованием программирования:
PascalABC.net (приближенный к традиционному, долгое решение):
|
||
PascalABC.net (использование LINQ, быстрое решение):
* LINQ (Language Integrated Query) — язык интегрированных запросов |
||
Python:
|
||
| С++: |
📹 Видео (теоретическое решение)
📹 Видеорешение на RuTube здесь (теоретическое решение)
8_2:
Шифр кодового замка представляет собой последовательность из пяти символов, каждый из которых является либо буквой (A или B) или цифрой (1, 2 или 3).
Сколько различных вариантов шифра можно задать, если известно, что в коде присутствует ровно одна буква, а все другие символы являются цифрами?
Ответ: 810
✍ Показать решение:
-
✎ Решение теоретическое:
- Формула нахождения количества различных сообщений:
- Посчитаем количество возможных шифров для одного из вариантов (например, когда буквы находятся на первой позиции). Так как цифры (1, 2, 3) могут занимать 4 позиции из пяти, а две буквы (А и В) одну из позиций, значит:
Q = NL
Q = 2 * 34 = 162
AB 123 123 123 123 = 162
"2" означает одна из двух букв: А или B, "3" - одна из трех цифр: 2 3 3 3 3 -> Q = 2 * 34 = 162 3 2 3 3 3 -> Q = 2 * 34 = 162 3 3 2 3 3 -> Q = 2 * 34 = 162 3 3 3 2 3 -> Q = 2 * 34 = 162 3 3 3 3 2 -> Q = 2 * 34 = 162
5 * 162 = 810
✎ Решение с использованием программирования:
PascalABC.net (приближенный к традиционному, долгое решение):
|
||
PascalABC.net (использование LINQ, быстрое решение):
Cartesian(5) — метод расширения последовательности, возвращающий декартову степень множества символов, т.е. в нашем случае перебор 5-знаковых слов из заданных символов * LINQ (Language Integrated Query) — язык интегрированных запросов |
||
Python:
|
||
| С++: |
📹 Видео (теоретическое решение)
📹 Видеорешение на RuTube здесь (теоретическое решение)
8_3:
Олег составляет таблицу кодовых слов для передачи сообщений, каждому сообщению соответствует своё кодовое слово. В качестве кодовых слов Олег использует 4-буквенные слова, в которых есть только буквы A, Б, В, Г, Д и Е, причём буква Г появляется ровно 1 раз и только на первом или последнем месте. Каждая из других допустимых букв может встречаться в кодовом слове любое количество раз или не встречаться совсем.
Сколько различных кодовых слов может использовать Олег?
Ответ: 250
✍ Показать решение:
-
✎ Решение теоретическое:
- Вспомним формулу получения количества возможных вариантов слов:
- где n1 — количество вариантов выбора первой буквы, n2 — количество вариантов выбора второй буквы и т.п.
- Рассмотрим варианты, когда буква Г встречается на первом или последнем месте:
N = n1 * n2 * n3 * … * nL = nL
Г ? ? ? = 1 * 5 * 5 * 5 = 53 = 125 ? ? ? Г = 5 * 5 * 5 * 1 = 53 = 125
125 + 125 = 250
✎ Решение с использованием программирования:
PascalABC.net (приближенный к традиционному, долгое решение):
|
||
PascalABC.net (использование LINQ, быстрое решение):
Cartesian(4) — метод расширения последовательности, возвращающий декартову степень множества символов, т.е. в нашем случае перебор 4-знаковых слов из заданных символов * LINQ (Language Integrated Query) — язык интегрированных запросов |
||
Python:
|
||
| С++: |
📹 Видео (теоретическое решение)
📹 Видеорешение на RuTube здесь (теоретическое решение)
8_4:
Шифр кодового замка представляет собой последовательность из пяти символов, каждый из которых является одной из букв X, Y или Z.
Сколько различных вариантов шифра можно задать, если известно, что буква X должна встречаться в коде ровно 2 раза, а каждая из других допустимых букв может встречаться в шифре любое количество раз или не встречаться совсем?
Типовые задания для тренировки
Ответ: 80
✍ Показать решение:
-
✎ Решение теоретическое:
- Формула нахождения количества различных сообщений:
- Итак, что у нас дано из этой формулы:
- Начальная мощность алфавита (N) = 3 (буквы X, Y, Z). Но так как буква X встречается ровно два раза, то мы ее рассмотрим отдельно, а остальные 2 буквы — встречаются любое количество раз, значит, будем считать, что:
Q = NL
N = 3 - 1 = 2 (Y и Z)
(L) = 5 - 2 = 3 символа (остальные два символа отведем на размещение X)
X X ? ? ? -> 12 * Q = 23 = 8
✎1 способ. Перебор всех вариантов:
X X ? ? ? - 12 * Q = 23 = 8 X ? X ? ? - 12 * Q = 23 = 8 X ? ? X ? - 12 * Q = 23 = 8 X ? ? ? X - 12 * Q = 23 = 8 ? X X ? ? - 12 * Q = 23 = 8 ? X ? X ? - 12 * Q = 23 = 8 ? X ? ? X - 12 * Q = 23 = 8 ? ? X X ? - 12 * Q = 23 = 8 ? ? X ? X - 12 * Q = 23 = 8 ? ? ? X X - 12 * Q = 23 = 8
✎ 2 способ. При помощи формулы поиска числа сочетаний:
[ C{binom{k}{n}}= frac{n!}{k!(n-k)!} ]
Число сочетаний из n элементов по k элементов:
[ C{binom{2}{5}}= frac{5!}{2!(5-2)!} = frac{120}{12} = 10 ]
* Факториал числа: n! = 0 * 1 * 2 * 3 * .. * n
8 * 10 = 80
✎ Решение с использованием программирования:
PascalABC.net (приближенный к традиционному, долгое решение):
|
||
PascalABC.net (использование LINQ, быстрое решение):
Cartesian(5) — метод расширения последовательности, возвращающий декартову степень множества символов, т.е. в нашем случае перебор 5-знаковых слов из заданных символов * LINQ (Language Integrated Query) — язык интегрированных запросов |
||
Python:
|
||
| С++: |
📹 Видео (теоретическое решение)
📹 Видеорешение на RuTube здесь (теоретическое решение)
8_5:
Сколько слов длины 5, начинающихся с согласной буквы и заканчивающихся гласной буквой, можно составить из букв ОСЕНЬ? Каждая буква может входить в слово несколько раз. Слова не обязательно должны быть осмысленными словами русского языка.
Типовые задания для тренировки
Ответ: 500
✍ Показать решение:
-
✎ Решение теоретическое:
- Из букв слова ОСЕНЬ имеем 2 гласных буквы (О, Е) и 2 согласных буквы (С, Н). Буква мягкий знак «нейтральна».
- Подсчитаем количество букв на каждой из 5 позиций:
2 5 5 5 2 СН все все все ОЕ
N = n1 * n2 * n3 * … * nL = nL
N = 2 * 5 * 5 * 5 * 2 = 500
✎ Решение с использованием программирования:
PascalABC.net (приближенный к традиционному, долгое решение):
|
||
PascalABC.net (использование LINQ, быстрое решение):
* LINQ (Language Integrated Query) — язык интегрированных запросов |
||
Python:
|
||
| С++: |
📹 Видео (теоретическое решение)
📹 Видеорешение на RuTube здесь (теоретическое решение)
8_6:
Вася составляет 4-буквенные слова, в которых есть только буквы Л, Е, Т, О, причём буква Е используется в каждом слове хотя бы 1 раз. Каждая из других допустимых букв может встречаться в слове любое количество раз или не встречаться совсем.
Ответ: 175
✍ Показать решение:
-
✎ Решение теоретическое:
- Количество вариантов различных слов вычислим по формуле:
- n1 — количество вариантов выбора первой буквы и т.п.
- Рассмотрим все варианты расположения буквы Е:
✎ 1 способ:
N = n1 * n2 * n3 * …
где
1. Е ? ? ? или 2. ? Е ? ? или 3. ? ? Е ? или 4. ? ? ? Е Где вопросительный знак означает любую букву из Л, Е, Т, О.
Е ? ? ? = 1 * 4 * 4 * 4 = 64 т.е. на первой позиции - только 1 буква - Е, на каждой последующей - одна из четырех букв Л, Е, Т, О.
? Е ? ? = 3 * 1 * 4 * 4 = 48
? ? Е ? = 3 * 3 * 1 * 4 = 36
? ? ? Е = 3 * 3 * 3 * 1 = 27
64 + 48 + 36 + 27 = 175
Результат: 175
✎ 2 способ:
- Так как по условию буква Е встретится хотя бы 1 раз, значит, можно утверждать, что не может быть такого, чтобы буква Е не встретилась бы ни одного раза.
- Таким образом, рассчитаем случай, когда буква Е встречается все 4 раза (т.е. все случаи) и отнимем от результата невозможный случай: когда буква Е не встретится ни одного раза:
1. Буква Е используется 4 раза (т.е. на всех позициях): 4 * 4 * 4 * 4 = 256 2. Буква Е не используется совсем (т.е. только 3 буквы): 3 * 3 * 3 * 3 = 81
256 - 81 = 175
✎ Решение с использованием программирования:
PascalABC.net (приближенный к традиционному, долгое решение):
|
||
PascalABC.net (использование LINQ, быстрое решение):
## var d:='лето'.Cartesian(4).where(w->w.countOf('е')>=1).count.print Cartesian(4) — метод расширения последовательности, возвращающий декартову степень множества символов, т.е. в нашем случае перебор 4-знаковых слов из заданных символов * LINQ (Language Integrated Query) — язык интегрированных запросов |
||
Python:
|
||
| С++: |
📹 Видео (теоретическое решение)
📹 Видеорешение на RuTube здесь (теоретическое решение)
8_7:
Вася составляет 4-буквенные слова, в которых есть только буквы К, А, Т, Е, Р, причём буква Р используется в каждом слове хотя бы 2 раза. Каждая из других допустимых букв может встречаться в слове любое количество раз или не встречаться совсем.
Ответ: 113
✍ Показать решение:
-
✎ Решение теоретическое:
- Количество возможных вариантов слов вычислим по формуле:
- где n1 — количество вариантов выбора первой буквы, n2 — количество вариантов выбора второй буквы и т.п.
- Сначала по формуле получим все варианты для всех пяти букв, включая букву Р:
N = n1 * n2 * n3 * … * nL = nL
5 * 5 * 5 * 5 = 54 = 625
4 * 4 * 4 * 4 = 44 = 256
р ? ? ? = 1 * 4 * 4 * 4 = 43 ? р ? ? = 4 * 1 * 4 * 4 = 43 ? ? р ? = 4 * 4 * 1 * 4 = 43 ? ? ? р = 4 * 4 * 4 * 1 = 43 Получим 43 * 4 = 256
625 - 256 - 256 = 113
✎ Решение с использованием программирования:
PascalABC.net (традиционный):
|
||
PascalABC.net (LINQ):
|
||
Python:
|
||
| С++: |
📹 Видео (теоретическое решение)
📹 Видеорешение на RuTube здесь (теоретическое решение)
8_8:
Вася составляет 4-буквенные слова, в которых есть только буквы К, О, М, А, Р, причём буква А используется в них не более 3-х раз. Каждая из других допустимых букв может встречаться в слове любое количество раз или не встречаться совсем. Словом считается любая допустимая последовательность букв, необязательно осмысленная.
Ответ: 624
✍ Показать решение:
-
✎ Решение теоретическое:
- Вспомним формулу получения количества возможных вариантов слов:
- где n1 — количество вариантов выбора первой буквы,
- n2 — количество вариантов выбора второй буквы и т.п.
- Так как буква А по условию используется не более 3-х раз, это значит, что она используется либо 3 раза, либо 2 раза, либо 1 раз, либо не используется совсем. Рассмотрим все эти варианты отдельно.
- 1. Буква А используется 3 раза:
N = n1 * n2 * n3 * … * nL = nL
А А А _ -> 1 * 1 * 1 * 4 = 4 А А _ А -> 1 * 1 * 4 * А = 4 А _ А А -> 1 * 4 * 1 * 1 = 4 _ А А А -> 4 * 1 * 1 * 1 = 4
_ может быть любая из 4 букв: К О М Р. Значит, имеем:4 * 4 = 16 вариантов
А А _ _ -> 1 * 1 * 4 * 4 = 16 А _ А _ -> 1 * 4 * 1 * 4 = 16 А _ _ А -> 1 * 4 * 4 * 1 = 16 _ А А _ -> 4 * 1 * 1 * 4 = 16 _ А _ А -> 4 * 1 * 4 * 1 = 16 _ _ А А -> 4 * 4 * 1 * 1 = 16
_ может быть любая из 4 букв: К О М Р. Значит имеем:16 * 6 = 96 вариантов
А _ _ _ -> 1 * 4 * 4 * 4 = 64 _ А _ _ -> = 64 _ _ А _ -> = 64 _ _ _ А -> = 64
64 * 4 = 256 вариантов
_ _ _ _ -> 44 = 256
16 + 96 + 256 + 256 = 624
✎ Решение с использованием программирования:
PascalABC.net (приближенный к традиционному, долгое решение):
|
||
PascalABC.net (использование LINQ, быстрое решение):
Cartesian(4) — метод расширения последовательности, возвращающий декартову степень множества символов, т.е. в нашем случае перебор 4-знаковых слов из заданных символов * LINQ (Language Integrated Query) — язык интегрированных запросов |
||
Python:
|
||
| С++: |
📹 Видео (теоретическое решение)
📹 Видеорешение на RuTube здесь (теоретическое решение)
8_10:
Сколько существует различных символьных последовательностей длины 3 в четырёхбуквенном алфавите {A,B,C,D}, если известно, что одним из соседей A обязательно является D, а буквы B и C никогда не соседствуют друг с другом?
Ответ: 29
✍ Показать решение:
-
✎ Решение теоретическое:
- Вспомним формулу получения количества возможных вариантов слов:
- где n1 — количество вариантов выбора первой буквы,
- n2 — количество вариантов выбора второй буквы и т.п.
- Будем рассматривать варианты, расставляя каждую букву последовательно по алфавиту, начиная с первой буквы. При этом будем учитывать указанные ограничения для букв А, B и С:
N = n1 * n2 * n3 * … * nL = nL
Начинаем с A: A D 4ABCD = 1 * 1 * 4 = 4 Начинаем с B: B A D, B B 2BD, B D 4ABCD = 7 Начинаем с C: C A D, C C 2CD, C D 4ABCD = 7 Начинаем с D: D A 3BCD, D B 2BD, D C 2CD, D D 4ABCD = 11
4 + 7 + 7 + 11 = 29
📹 Видео (теоретическое решение)
📹 Видеорешение на RuTube здесь (теоретическое решение)
8_22:
Лена составляет 5-буквенные слова из букв Я, С, Н, О, В, И, Д, Е, Ц, причём слово должно начинаться с согласной и заканчиваться гласной. Первая и последняя буквы слова встречаются в нем только один раз; остальные буквы могут повторяться.
Сколько слов может составить Лена?
Ответ: 6860
✍ Показать решение:
✎ Решение с использованием программирования:
PascalABC.net (использование LINQ, быстрое решение):
|
||
PascalABC.net (приближенный к традиционному, долгое решение):
|
||
| Python: | ||
| С++: |
Результат: 6860
- Рассмотрим два варианта: когда слово начинается с гласной буквы, и когда оно начинается с согласной.
- Подсчитаем общее количество вариантов:
- Учтем, что в слове КОРАБЛИКИ две буквы К и две И.
- Всего в слове 4 гласных, но поскольку две буквы
И, то необходимо считать только 3 гласных. - Всего в слове 5 согласных, однако две из них — буквы
К, поэтому считать следует 4 согласных. - Посчитаем количество согласных и гласных для каждой из 5 позиций слова, учитывая, что с каждой последующей буквой количество используемых гласных/согласных уменьшается. Под позициями приведем пример букв:
- Количество слов вычисляется как произведение полученных чисел:
- Посчитаем количество слов без двух подряд одинаковых букв. Будем считать относительно буквы А, которых две в заданном слове АДЖИКА. Буквы не могут повторяться, поэтому их кол-во в каждом варианте будет уменьшается:
- Получили 10 вариантов, и в каждом из них можно составить по 24 слова.
- Таким образом, получим общее количество слов:
- Выполним задание следующим образом: 1. посчитаем общее количество слов, не учитывая никакие ограничения. 2. Затем посчитаем случаи, которые необходимо исключить. 3. Вычтем из результата пункта 1 результат пункта 2.
- Общее количество независимо от ограничений (учтем, что буквы не должны повторяться):
- Посчитаем варианты, которые необходимо исключить. Их будет несколько:
- а) буква ь — на последнем месте:
- б) буква ь — между гласными:
- Посчитаем количество слов, согласно условию задачи:
- Выпишем все четные и нечетные цифры, которые могут использоваться в 8-й с.с.:
- Рассмотрим два случая построения числа по заданию: 1) начиная с четной цифры и 2) начиная с нечетной цифры. Изобразим схематично числа, указывая сверху возможное количество цифр на разряд:
- Сложим количество вариантов в обеих случаях:
- Данное задание лучше решать следующим образом. Подставим вместо букв цифры (А -> 0, О -> 1, У -> 2):
- Видим, что каждая последующее число получается путем прибавления в столбик единицы к предыдущему числу. В троичной системе счисления! Т.к. цифр всего три.
- Порядковый номер, написанный рядом с пунктом, всегда на единицу больше располагающейся рядом цифры в троичной системе счисления.
- Значит, пункту под номером 242 будет соответствовать число 241 в троичной системе счисления.
- Переведем 241 в 3-ю систему делением на 3:
- Перепишем остатки снизу вверх: 22221, им соответствуют буквы УУУУО
- Подставим вместо букв цифры (Д -> 0, Е -> 1, К -> 2, О -> 3, Р -> 4):
- Видим, что каждое последующее число получается путем прибавления единицы в столбик к предыдущему (в пятеричной системе счисления! т.к. цифр всего пять).
- Порядковый номер, написанный рядом с пунктом, всегда на единицу больше располагающейся рядом цифры в пятеричной системе счисления.
- Определим число, которое получится, если мы в начале слова поставим букву К (остальные должны остаться нулями, т.к. числа идут по порядку, а нам необходимо первое, начинающееся с К):
- Полученное число — 2000 — необходимо перевести из пятеричной системы счисления в десятичную, чтобы узнать порядковый номер:
- Поскольку порядковый номер числа всегда на единицу больше самого числа, то имеем 251.
- Пронумерованный список начинается со всех букв А. Представим, что А — 0, В — 1, Г — 2, Е — 3, Н — 4. Получим следующий список:
- Такой список представляет из себя увеличивающиеся числа 5-й системы счисления.
- Так как букве А соответствует 0, то первое (самое младшее) четырехзначное число без нуля — это 1111.
- Чтобы вычислить под каким номером стоит данное число, переведем его в 10-ю систему и прибавим к результату единицу (так как порядковые номера в списке на единицу больше самих чисел):
- Для решения данного задания необходимо вспомнить две формулы:
- Подставим в первую формулу известное значение — вероятность того, что Василий получил четверку:
- Затем подставим известное по условию значение в формулу вероятности случайного события:
- Поскольку p мы уже нашли, подставим найденное значение и найдем искомое число — количество четверок за четверть:
8_11:
Из букв С, Р, Е, Д, А составляются трехбуквенные комбинации по следующему правилу – в комбинации не может быть подряд идущих гласных и одинаковых букв.
Например, комбинации ААР или ЕСС не являются допустимыми.
Сколько всего комбинаций можно составить, используя это правило?
Ответ: 66
✍ Показать решение:
-
✎ Решение теоретическое:
1. С гласной:
1.1 2 3 2 = 2 * 3 * 2 = 12 гл с с 1.2 2 3 2 = 2 * 3 * 2 = 12 гл с гл
2. С согласной:
2.1 3 2 2 = 3 * 2 * 2 = 12 с с с 2.2 3 2 3 = 3 * 2 * 3 = 18 с гл с 2.3 3 2 2 = 3 * 2 * 2 = 12 с с гл
12 + 12 + 12 + 18 + 12 = 66
✎ Решение с использованием программирования:
PascalABC.net (использование LINQ, быстрое решение):
|
||
PascalABC.net (приближенный к традиционному, долгое решение):
|
||
Python:
|
||
| С++: |
8_12:
Дано слово КОРАБЛИКИ. Таня решила составлять новые 5-буквенные слова из букв этого слова по следующим правилам:
1) слово начинается с гласной буквы;
2) гласные и согласные буквы в слове должны чередоваться;
3) буквы в слове не должны повторяться.
Ответ: 72
✍ Показать решение:
-
✎ Решение теоретическое:
гл с гл с гл 3 4 2 3 1 оаи крбл оа крб и
3 * 4 * 2 * 3 * 1 = 72
✎ Решение с использованием программирования:
PascalABC.net (использование LINQ, быстрое решение):
|
||
| Python: | ||
| С++: |
Результат: 72
8_21:
Ксюша составляет слова, меняя местами буквы в слове МИМИКРИЯ.
Сколько различных слов, включая исходное, может составить Ксюша?
Ответ: 3360
Показать решение:
✎ Решение с использованием программирования:
PascalABC.net (приближенный к традиционному, долгое решение):
Смысл решения в использовании типа множества ( |
||
PascalABC.net (использование LINQ, быстрое решение):
* LINQ (Language Integrated Query) — язык интегрированных запросов |
||
| Python: | ||
| С++: |
📹 Видео (программный способ)
📹 Видеорешение на RuTube здесь (программное решение)
8_19:
Петя составляет шестибуквенные слова
перестановкой букв
слова АДЖИКА. При этом он избегает слов с двумя подряд одинаковыми буквами. Сколько всего различных слов может составить Петя?
Типовые задания для тренировки
Ответ: 240
✍ Показать решение:
-
✎ Решение теоретическое:
А*А*** = 4*3*2*1 = 24 слова с данным расположением буквы А. А**А** = 4*3*2*1 = 24 А***А* = 4*3*2*1 А****А = ... *А*А** *А**А* *А***А **А*А* **А**А ***А*А
10 * 24 = 240
✎ Решение с использованием программирования:
PascalABC.net (приближенный к традиционному, долгое решение):
Смысл решения в использовании типа — множества ( |
||
PascalABC.net (использование LINQ, быстрое решение):
|
||
| Python: | ||
| С++: |
8_20:
Маша составляет 7-буквенные коды из букв В, Е, Н, Т, И, Л, Ь. Каждую букву нужно использовать
ровно 1 раз
, при этом код буква Ь не может стоять на последнем месте и между гласными. Сколько различных кодов может составить Маша?
Типовые задания для тренировки
Ответ: 4080
Показать решение:
✎ Решение теоретическое:
7 6 5 4 3 2 1 - количество возможных вариантов букв на семи позициях ИТОГО: 7! = 5040 слов
6 5 4 3 2 1 Ь = 6! = 720
И Ь Е 4 3 2 1 = 24 варианта Так как буквы смещаются по всем позициям, то получим (4 И Ь Е 3 2 1, ...): 24 * 5 = 120 Е Ь И 4 3 2 1 = 24 варианта 24 * 5 = 120
5040 - 720 - 120 - 120 = 4080
✎ Решение с использованием программирования:
Стоит заметить, что теоретическое решение занимает меньше времени, чем программный способ!
PascalABC.net (приближенный к традиционному, долгое решение):
|
||
PascalABC.net (использование LINQ, быстрое решение):
|
||
| Python: | ||
| С++: |
8_23:
Артур составляет 6-буквенные коды перестановкой букв слова ВОРОТА. При этом нельзя ставить рядом две гласные.
Сколько различных кодов может составить Артур?
Ответ: 72
✍ Показать решение:
✎ Решение с использованием программирования:
PascalABC.net (использование LINQ, спортивное прогр-е):
* LINQ (Language Integrated Query) — язык интегрированных запросов |
||
| Python: | ||
| С++: |
Ответ: 72
Сколько существует n-значных чисел, записанных в m-ной системе счисления
Разбор 8 задания экзамена ЕГЭ 2020 г. (со слов учащегося):
Сколько существует восьмизначных чисел, записанных в восьмеричной системе счисления, в которых все цифры различны и рядом не могут стоять 2 чётные или 2 нечётные цифры?
Типовые задания для тренировки
Ответ: 1008
✍ Показать решение:
-
✎ Решение теоретическое:
четные: 0, 2, 4, 6 - итого 4 цифры нечетные: 1, 3, 5, 7 - итого 4 цифры
1) с четной цифры: 3 4 3 3 2 2 1 1 = 3*4*3*3*2*2*1*1 = 432 ч н ч н ч н ч н
Самый старший разряд не может быть равен 0 (поэтому 3 цифры из 4 возможных), так как разряд просто потеряется, и число станет семизначным). Каждый последующий разряд включает на одну цифру меньше, так как по заданию цифры не могут повторяться.
2) с нечетной цифры: 4 4 3 3 2 2 1 1 = 4*4*3*3*2*2*1*1 = 576 н ч н ч н ч н ч
Каждый последующий разряд включает на одну цифру меньше, так как по заданию цифры не могут повторяться.
432 + 576 = 1008
✎ Решение с использованием программирования:
PascalABC.net (использование LINQ, быстрое решение):
* LINQ (Language Integrated Query) — язык интегрированных запросов |
||
| Python: | ||
| С++: |
Список в алфавитном порядке
8_13:
Все 5-буквенные слова, составленные из букв А, О, У, записаны в алфавитном порядке. Ниже приведено начало списка:
1. ААААА
2. ААААО
3. ААААУ
4. АААОА
…
Запишите слово, которое стоит под номером 242 от начала списка.
Ответ: УУУУО
✍ Показать решение:
-
✎ Решение теоретическое:
1. 00000 2. 00001 3. 00002 4. 00010 ...
остатки 241 | 3 | 1 80 | 3 | 2 26 | 3 | 2 8 | 3 | 2 2 | |
✎ Решение с использованием программирования:
PascalABC.net (использование LINQ, быстрое решение):
Смотрим слова и находим по номеру нужное слово: … (241,[У,У,У,У,А]) (242,[У,У,У,У,О]) (243,[У,У,У,У,У])
* LINQ (Language Integrated Query) — язык интегрированных запросов |
||
| Python: | ||
| С++: |
📹 Видео (теоретический способ)
📹 Видеорешение на RuTube здесь (теоретическое решение)
8 (10) задание. Демоверсия ЕГЭ 2018 информатика:
Все 4-буквенные слова, составленные из букв Д, Е, К, О, Р, записаны в алфавитном порядке и пронумерованы, начиная с 1.
Ниже приведено начало списка.
1. ДДДД 2. ДДДЕ 3. ДДДК 4. ДДДО 5. ДДДР 6. ДДЕД …
Под каким номером в списке идёт первое слово, которое начинается с буквы K?
Ответ: 251
✍ Показать решение:
-
✎ Решение теоретическое:
1. 0000 2. 0001 3. 0002 4. 0003 5. 0004 6. 0010 ...
K -> 2 -> 2000
По формуле разложения числа по степеням основания: 20005 = 2 * 53 + 0 * 22 + 0 + 0 = 2 * 125 = 25010
✎ Решение с использованием программирования:
PascalABC.net (использование LINQ, быстрое решение):
* LINQ (Language Integrated Query) — язык интегрированных запросов |
||
| Python: | ||
| С++: |
📹 Видео (теоретическое решение)
📹 Видеорешение на RuTube здесь (теоретическое решение)
8_15:
Все 4-буквенные слова, составленные из букв П, Р, С, Т, записаны в алфавитном порядке.
Вот начало списка:
1. ПППП 2. ПППР 3. ПППС 4. ПППТ 5. ППРП ... ...
Ответ: 65
📹 Видео
📹 Видеорешение на RuTube здесь (теоретическое решение)
8_16:
Все четырёхбуквенные слова, составленные из букв В, Е, Г, А, Н записаны в алфавитном порядке и пронумерованы, начиная с 1. Начало списка выглядит так:
1. АААА 2. АААВ 3. АААГ 4. АААЕ 5. АААН 6. ААВА …
Под каким номером в списке идёт первое слово, в котором нет буквы А?
Ответ: 157
✍ Показать решение:
-
✎ Решение теоретическое:
1. 0000 2. 0001 3. 0002 4. 0003 5. 0004 6. 0010
11115 = 1 * 53 + 1 * 52 + 1 * 51 + 1 * 50 = 156
156 + 1 = 157
✎ Решение с использованием программирования:
PascalABC.net (использование LINQ, быстрое решение):
* LINQ (Language Integrated Query) — язык интегрированных запросов |
||
| Python: | ||
| С++: |
📹 Видео (теоретическое решение)
📹 Видеорешение на RuTube здесь (теоретическое решение)
Вероятность событий
8_17:
За четверть Василий Пупкин получил 20 оценок. Сообщение о том, что он вчера получил четверку, несет 2 бита информации.
Сколько четверок получил Василий за четверть?
Ответ: 5
✍ Показать решение:
1. Формула Шеннона:
x = log2(1/p)
x - количество информации в сообщении о событии p - вероятность события
2. Формула вероятности случайного события:
p(A) = m/n
m - число случаев, способствующих событию А n - общее число равновозможных случаев
2 = log2(1/p);
=>
1/p = 4;
=>
p = 1/4
p = ?/20
1/4 = ?/20
? = 1/4 * 20 = 5
📹 Видео
📹 Видеорешение на RuTube здесь (теоретическое решение)