Задание 17 Профильного ЕГЭ по математике — это уравнение, система уравнений или неравенство с параметром. Или несколькими параметрами.
Конечно, за один день научиться решать такие задачи невозможно. И все-таки мы немного расскажем о том, как научиться решать задачи с параметрами. С чего начать. И какие вообще есть методы решения задач с параметрами.
Начнем с хорошей новости. Задача 17 (с параметром) оценивается в целых 4 первичных балла ЕГЭ, которые отлично пересчитываются в тестовые.
Если вы полны решимости получить на ЕГЭ заветные 4 первичных балла за задачу 17 (с параметром), не стоит начинать с реальных экзаменационных задач. Ведь мы хотим получить результат, а не разочарование! Поэтому сначала необходимо повторить следующие темы:
1. Элементарные функции и их графики. Парабола, синус, логарифм, арктангенс и все остальные — всех их надо знать «в лицо».
2. Преобразование графиков функций.
3. Построение графиков функций.
4. Базовые элементы для решения задач с параметрами. Да, мы будем рисовать не только привычные функции. Но еще и окружности, ромбики, полуплоскости и всевозможные их комбинации.
5. Что такое параметр. Простые задачи с параметрами.
Только после этого можно переходить к самому простому и наглядному способу решения задач с параметрами — графическому.
Читайте статью, смотрите видеокурс. И помните, что графический метод — хороший, но не единственный.
Потому что, кроме него, есть и другие:
— Квадратные уравнения и неравенства с параметрами.
— Задачи с параметрами. Условия касания.
— Метод оценки в задачах с параметрами.
— Использование четности функций в задачах с параметрами.
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 1, задача 17.
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 5, задача 17.
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 11, задача 17.
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 26, задача 17.
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 36, задача 17.
И не думайте, что это все возможные методы решения задач с параметрами. Их намного больше! Мы дали ссылки на те, которые встречаются чаще всего в задачах ЕГЭ.
Несколько мудрых советов о том, как и зачем решать задачи с параметрами.
1. Чтобы на ЕГЭ уверенно справиться с заданием 17, нужно решить не менее 50 задач с параметрами.
2. Настанет момент, когда вы увидите, что задача с параметром похожи на конструктор, где вы собираете решение из знакомых элементов.
3. Два самых главных секрета решения задач с параметрами. Готовы узнать? Вот они:
— Если в задаче с параметром можно сделать замену переменной — сделайте замену.
— Если задачу с параметром можно решить графически — решите графически.
4. Сколько бы вы ни занимались задачами с параметрами, каким бы отличником ни стали — всегда найдется задача, над которой вы задумаетесь. Вот такая, например:
Задача 1. При каких значениях a системы и
равносильны?
Две системы уравнений с двумя переменными называются равносильными, если они имеют одни и те же решения, или обе системы не имеют решений.
1) При — системы равносильны, так как обе не имеют решений.
2) При — второе уравнение имеет решение
которое является решением первой системы.
3) При
Система уравнений
Уравнение задает окружность с центром в начале координат и радиусом
Решениями системы:
являются две точки, в которых прямая пересекает окружность, заданную уравнением
А вот уравнение задает семейство параллельных прямых
Мы хотим, чтобы две системы были равносильны, то есть чтобы окружность, заданная уравнением , пересекала только одну из этого семейства прямых, а именно прямую
, и не имела общих точек с другими прямыми из этого семейства.
Меняя параметр а, мы можем менять радиус окружности. Мы хотим, чтобы окружность радиуса не имела общих точек с прямыми, параллельными прямой
, то есть лежала ниже прямой, проходящей через точку А на рисунке, и выше прямой, проходящей через точку В.
Когда же происходит касание в точках A и B?
В случае касания радиус окружности Мы легко находим это из прямоугольного треугольника СОА, где О — начало координат.
Значит, в случае касания , а если
— касания не происходит.
Объединяя случаи, получим, что системы равносильны, если
Легко? Если справились — вот еще одна интересная задача:
Задача 2. При каких значениях параметра a найдется такое значение параметра , что система уравнений
имеет ровно три различных решения?
Вот решение этой задачи.
Лучше всего осваивать эту непростую тему на нашем Онлайн-курсе подготовки к ЕГЭ на 100 баллов. Или на интенсивах ЕГЭ-Студии в Москве. Удачи, друзья!
Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Задание 17. Задача с параметрами u0026#8212; профильный ЕГЭ по математике» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
09.03.2023
| 3644 | При каких значениях параметра a уравнение (a^2-6a+8)x^2+. (a^2-4)x+10-3a-a^2=0. имеет более двух корней |
При каких значениях параметра a уравнение (a2-6a+8)x2 +(a2-4)x + 10-3a-a2 =0 имеет более двух корней | |
| 3591 | Найдите все значения a при каждом из которых уравнение a(a+3)x^2+(2a+6)x-3a-9=0 имеет более одного корня |
Найдите все значения a при каждом из которых уравнение a(a+3)x2 +(2a+6)x -3a -9 =0 имеет более одного корня | |
| 3585 | Найдите все значения a при каждом из которых уравнение 2sqrt(x^4+(a-3)^4)=abs(x+a-3)+abs(x-a+3) имеет единственное решение |
Найдите все значения a при каждом из которых уравнение 2sqrt(x4 +(a-3)4) = abs(x+a-3) +abs(x-a+3) имеет единственное решение ! Тренировочная работа по математике №2 СтатГрад 11 класс 13.12.2022 Задание 17 Вариант МА2210209 #Задачи — аналоги 621 104 | |
| 3544 | Найдите все значения a, при которых система уравнений {(abs(y+x^3)-abs(y+3x)=2y+x^3+3x), (abs(-y-3x+1)-abs(y+x^3-a)=), (= -3y-6x-x^3+a+2) :} имеет единственное решение |
Найдите все значения a, при которых система уравнений {|y+x^3|-|y+3x| = 2y+x^3+3x), |-y-3x+1| -|y+x^3-a| =-3y-6x-x3+a+2 имеет единственное решение ! математика 50 вариантов ЕГЭ 2022 профильный уровень Ященко Вариант 6 Задание 17 |
|
| 3434 | Найдите все значения параметра a, b при которых неравенство a^3x^4+2ax^3+b <= 2bx^2+b^3x+a выполняется для всех x из отрезка [0; 1] |
Найдите все значения параметра a, b при которых неравенство выполняется для всех x из отрезка [0; 1] ! ДВИ в МГУ 2022 — 5 поток, Вариант 225 Задание 6 # Решение Натальи Яковлевны Захаровой youtube видео разбор | |
| 3405 | Найдите все значения a, при которых система уравнений {(abs(y+1/2x^3)-abs(y+3/2x)=2y+1/2x^3+3/2x), (abs(-y-3/2x+1)-abs(y+1/2x^3-a)=), (-4 y-9/2x-1/2x^3+a+3) :}. имеет единственное решение |
Найдите все значения a, при которых система уравнений { |y+1/2×3| -|y+3/2x| = 2y + 1/2×3 +3/2x |-y-3/2x+1| — |y+1/2×3 -a| = -4y -9/2x -1/2×3 +a +3 имеет единственное решение ! математика 50 вариантов ЕГЭ 2022 профильный уровень Ященко Вариант 8 Задание 17 # Ошибка в ответе пособия у Ященко ? : color{red}{a > -1 ?} |
|
| 3404 | Найдите все значения параметра a, при которых уравнение x^2+(1-a+root(4)(abs(x)))^2=a^2/4. имеет ровно три решения |
Найдите все значения параметра a, при которых уравнение x2 + (1-a+ корень 4 степени из |x|) 2 = a 2/4 имеет ровно три решения ! ДВИ в МГУ 2022 — 1 поток, Вариант 1 Задание 6 | |
| 3391 | Найдите все значения параметра a, при каждом из которых уравнение sqrt(15x^2+6ax+9)=x^2+ax+3 имеет три различных решения |
Найдите все значения параметра a, при каждом из которых уравнение корень из 15×2 +6ax+9 =x2 +ax+3 имеет три различных решения ! ЕГЭ 2022 по математике 27.06.2022 резервный день Задание 17 | |
| 3379 | Найдите все значения параметра a, при каждом из которых уравнение x^2+a^2+2x-4a=abs(4x+2a). имеет более двух различных корней |
Найдите все значения параметра a, при каждом из которых уравнение x2 +a2 +2x -4a = |4x+2a| имеет более двух различных корней ! ЕГЭ 2022 по математике 02.06.2022 основная волна Задание 17 Санкт-Петербург | |
| 3368 | Оценки экспертов решений задания 17 ЕГЭ по математике профильного уровня. Задание № 17 — это уравнение, неравенство или их системы с параметром. Задачи с параметром допускают весьма разнообразные способы решения. Наиболее распространёнными из них являются: – чисто алгебраический способ решения; – способ решения, основанный на построении и исследовании геометрической модели данной задачи; – функциональный способ, в котором могут быть и алгебраические, и геометрические элементы, но базовым является исследование некоторой функции. Зачастую (но далеко не всегда) графический метод более ясно ведёт к цели. Кроме того, в конкретном тексте решения вполне могут встречаться элементы каждого из трёх перечисленных способов |
Критерии оценивания решений задания 17 ЕГЭ по математике профильного уровня ! Примеры оценивания реальных работ 2016-2021 гг # Приведены типы заданий с развёрнутым ответом, используемые в КИМ ЕГЭ по математике и критерии оценки выполнения заданий с развёрнутым ответом, приводятся примеры оценивания выполнения заданий и даются комментарии, объясняющие выставленную оценку | |

Показана страница 1 из 55
17 задание егэ математика профиль
Линейные уравнения, неравенства и системы линейных уравнений относятся к числу самых простых задач с параметрами. Поэтому задачи этого раздела являются подготовительными заданиями к решению реальных задач с параметрами, предлагаемых на ЕГЭ.
- Исследование дискриминанта и применение теоремы Виета
Решение многих задач с параметрами сводится к исследованию квадратного трехчлена. Для решение некоторых задач этого вида достаточно исследования дискриминанта и применение теоремы Виета.
- Расположение корней квадратного трёхчлена относительно данных чисел
Решение многих задач с параметрами сводится к исследованию квадратного трехчлена. Для решения некоторых задач этого вида достаточно исследования дискриминанта и применение теоремы Виета. В данном разделе будут рассмотрены задачи связанные с исследованием расположения корней квадратного трехчлена относительно заданных чисел, для решения которых будут использованы материалы, изученные в предыдущем разделе: Исследование дискриминанта и применение теоремы Виета.
В данном разделе будут рассмотрены квадратные неравенства с параметрами, для решения которых будут использованы материалы, изученные в предыдущих разделах: Исследование дискриминанта и применение теоремы Виета; Расположение корней квадратного трехчлена относительно данных чисел.
Также для решения задач этого раздела необходимо уметь «легко» решать квадратные неравенства. В целом решение квадратных неравенств с параметрами вызывают больше трудностей, нежели решений квадратных уравнений с параметрами. Это связано с тем, при решении неравенств приходится разбирать больше случаев и проводить более тонкие логические рассуждения, чем при решении уравнений.
Задачи для самостоятельного решения разбиты на два уровня сложности А и В. Уровень А представляет собой простейшие квадратные неравенства с параметрами. Уровень В по сложности максимально приближен к 17 заданиям ЕГЭ по профильной математике.
- Задачи сводящиеся к исследованию квадратного трехчлена
В этом разделе будут рассмотрены задачи с параметрами, решение которых сводится к исследованию расположения корней квадратных уравнений и неравенств относительно некоторых чисел только после определенных предварительных действий: замены переменной, алгебраических действий и т. д. В основном это будут показательные, логарифмические, алгебраические и тригонометрические уравнения и неравенства, которые после замены переменной приводятся к квадратным. Для этого необходимо хорошо знать свойства показательной, логарифмической и тригонометрических функций. В частности, необходимо знать область определения, множество значений, промежутки возрастания и убывания этих функций, а также уметь решать простейшие уравнения и неравенства, содержащие эти функции.
- Применение монотонности и ограниченности функций к решению уравнений и неравенств
В этом разделе будут рассмотрены уравнения и неравенства с параметрами (и не только), решение которых будет опираться на свойства элементарных функций, изучаемых в школьном курсе математики, такие как монотонность и ограниченность.
В этом разделе будут рассмотрены уравнения и системы уравнений с параметрами, ключевым признаком которых является инвариантность. Типичные формулировки таких задач следующие: «Найдите все значения параметра а, при которых уравнение (или система уравнений) имеет единственное решение». Слово «единственное» в формулировке таких задач является ключевым. Оно, как правило, служит сигналом для проверки уравнения, неравенства или системы уравнений на инвариантность. Слово «инвариантность» означает «неизменность». В математике под инвариантностью понимается неизменяемость каких-либо выражений с переменными или функций по отношению к каким-либо преобразованиям над этими самыми переменными.
- Графический метод, преобразование и построение графиков в системе
Ещё одним основным методом решений заданий с параметрами является графический метод. В этом разделе рассмотрим задачи для решения которых потребуется построить график некоторой функции на плоскости ; , при этом в большинстве случаев придется прибегнуть к элементарным преобразованиям заданных функций. На плоскости; задает семейство кривых, зависящих от параметра a. Естественно, для решения задач этого раздела, необходимо знать и уметь строить графики основных элементарных функций. Напомним основные способы преобразования элементарных функций, которые потребуется для построения их графиков.
Рассмотрим задачи для решения которых потребуется строить не только графики функций, но и отмечать области удовлетворяющие определенным условиям, как правило, некоторым неравенствам или системам неравенств. Функции y f x удовлетворяют все точки плоскости Oxy принадлежащие графику этой функции. Тогда, очевидно, что все точки, удовлетворяющие неравенству, y f x расположены выше графика функции y f x, а все точки, удовлетворяющие неравенству, y f x расположены ниже графика функции y f x.
- Уравнение, неравенства и системы с параметрами
В этом разделе представлены уравнения, неравенства и системы с параметрами которые не предлагались в предыдущих разделах.
Слово единственное в формулировке таких задач является ключевым.
100ballnik. com
17.01.2017 5:09:10
2018-06-18 14:40:38
Источники:
Https://100ballnik. com/17-%D0%B7%D0%B0%D0%B4%D0%B0%D0%BD%D0%B8%D0%B5-%D0%B5%D0%B3%D1%8D-2022-%D0%BF%D1%80%D0%BE%D1%84%D0%B8%D0%BB%D1%8C-%D0%BC%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D0%BA%D0%B0-11-%D0%BA%D0%BB%D0%B0/
Онлайн-школа Турбо ЕГЭ » /> » /> .keyword { color: red; } 17 задание егэ математика профиль
17 задание егэ математика профиль
17 задание егэ математика профиль
Найдите все значения параметра $p$, при каждом из которых система неравенств $;
$<tablep ≥ /; p 0$, при каждом из которых система
Имеет ровно $2$ решения.
Решение
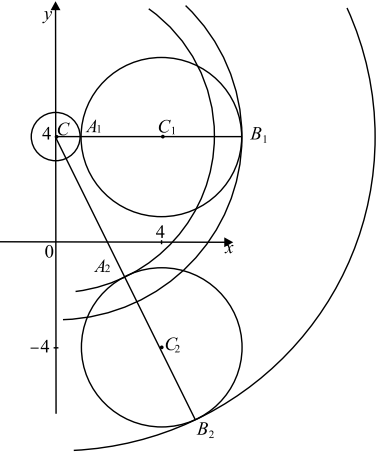
Если $y ≥ 0$, то первое уравнение задаёт окружность $∅_1$ с центром в точке $C_1(4; 4)$ радиуса $3$, а если $y 0$ второе уравнение задаёт окружность $∅$ с центром в точке $C (0; 4)$ радиуса $a$. Поэтому задача состоит в том, чтобы найти все значения параметра $a$, при каждом из которых окружность $∅$ имеет ровно две общие точки с объединением окружностей $∅_1$ и $∅_2$.
Координаты точки касания окружностей $∅$ и $∅_2$ явно видны на чертеже: это точки $A_1(1; 4)$ и $B_1(7; 4)$. То есть при $a = CA_1=1$ и $a = CB_1=7$ окружности $∅$ и $∅_2$ касаются. При $a > 7$ и $a CB_2$ окружности $∅$ и $∅_2$ не пересекаются. При $CA_2 0$, при каждом из которых система
Имеет единственное решение.
Решение
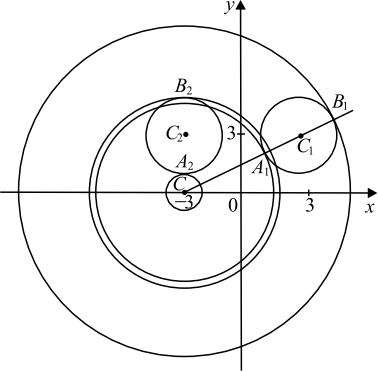
Если $x ≥ 0$, то первое уравнение задаёт окружность $∅_1$ с центром в точке $C_1(3; 3)$ радиуса $2$, а если $x 0$ второе уравнение задаёт окружность $∅$ с центром в точке $C (−3; 0)$ радиуса $a$. Поэтому задача состоит в том, чтобы найти все значения параметра $a$, при каждом из которых окружность $∅$ имеет единственную общую точку с объединением окружностей $∅_1$ и $∅_2$.
Из точки $C$ проведём луч $CC_1$ и обозначим $A_1$ и $B_1$ точки его пересечения с окружностью $∅_1$, где $A_1$ лежит между $C$ и $C_1$.
Так как $CC_1 = √ = √ = 3√5$, то $CA_1 = 3√5 − 2, CB_1 = 3√5 + 2$.
При $a CB_1$ окружности $∅$ и $∅_1$ не пересекаются. При $CA_1 0;$. Второе неравенство системы преобразуем так, чтобы получить неравенство для внутренней части круга. Первое неравенство преобразуем так, чтобы скобки выглядели симметрично $/$ решением является промежуток $[/; √)$.
Отсюда решение содержит отрезок длиной не менее $/$, если
Решив системы, получим: $a ∈[2-√2; /]$ или $a ∈ (/; √2)$, отсюда $a ∈ [2 — √2; √2)$.
Замечание. Задачу можно решить и другими способами, например аналитически. Получив систему, можно заметить, что первое неравенство системы при $a 4$). Решением второго неравенства будут $x$, удовлетворяющие неравенству $x 4$ не возможен.
Несложно убедиться, что при ограничениях $0 ≤ a ≤ √3$ для решения задачи достаточно решить систему $/a^2 ≥ 0.5; √-/ > 0.5;$
Задача 11
Найдите все значения параметра a, при каждом из которых система уравнений $<tabley=√<-8-6x-x^2>; y+ax=a+1;$ имеет единственное решение.
Решение
Построим график уравнения $y = √$.
Преобразовав подкоренное выражение, получим: $y = √, y =√$.
Если $y ≥ 0$, то $y^2 = 1−(x + 3)^2, (x + 3)^2 + y^2 = 1$.
Если $y 0$ для любого $a$).
Указанные окружности будут иметь ровно три общие точки с парой указанных выше пересекающихся прямых в том и только том случае, когда окружность проходит через точку пересечения этих прямых.
В таком случае точка $(-1; 2)$ лежит на окружности, значит, верно равенство $(-1 + 1)^2 + (2 — a)^2 = 3a^2 — 2a + 4$.
Отсюда получаем: $4 — 4a + a^2 = 3a^2 — 2a + 4; 2a^2 + 2a = 0; 2a ·(a + 1) = 0; $
Задача 14
Найдите все значения $a$, при которых система уравнений
Имеет ровно три решения.
Решение
Уравнение $(x — 3)^2 = (y — 1)^2$ равносильно совокупности двух уравнений
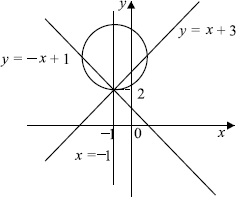
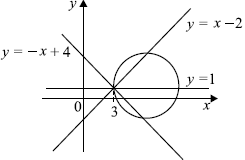
Множество решений этой совокупности совпадает с множеством всех точек, лежащих на двух прямых: $y = x — 2$ и $y = — x + 4$. Заметим, что эти прямые проходят через точку $(3; 1)$, так как система $
При каждом значении $a$ множеством решений второго уравнения системы $(x — a)^2 + (y — 1)^2 = 3a^2 — 8a + 9$ будет множество всех точек окружности с центром в точке $(a; 1)$, лежащей на прямой $y = 1$, и радиусом $√$ (заметим, что $3a^2 — 8a + 9 > 0$ для любого $a$).
Указанные окружности будут иметь ровно три общие точки с парой указанных выше пересекающихся прямых в том и только том случае, когда окружность проходит через точку пересечения этих прямых.
В таком случае точка $(3; 1)$ лежит на окружности, значит, верно равенство $(3 — a)^2 + (1 — 1)^2 = 3a^2 — 8a + 9$.
Отсюда получаем: $9 — 6a + a^2 = 3a^2 — 8a + 9; 2a^2 — 2a = 0; 2a ·(a — 1) = 0; a = 0$ или $a = 1$.
Задача 15
Найдите все значения $a$, при каждом из которых уравнение $/ = 1$ имеет единственный корень.
Решение
В левой части уравнения выделим целую часть
Тогда уравнение примет вид $/x — x^3> = 0$. Оно равносильно системе
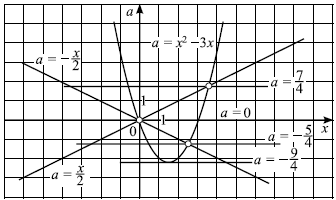
Решим систему графически в системе координат $xOa$. Для этого строим графики функций $a = x^2 — 3x$ и $a = ±/$.
Графиком функции $a = x^2 — 3x$ является парабола, ветви которой направлены вверх. Вершина параболы — точка $(/; -/)$, точки $(0; 0)$ и $(3; 0)$ принадлежат параболе. Графиками функций $a = ±/$ являются прямые.
Решая уравнение $x^2 — 3x = /$, находим точки пересечения прямой $a = /$ и параболы $a = x^2 — 3x: x = 0, x = /$, откуда $a = 0, a = /$. Аналогично, решая уравнение $x^2 — 3x = — /$, находим $x = 0, x = /$. Тогда $a = 0, a = — /$. Выкалываем эти точки.
По рисунку видим, что ровно одна точка пересечения параболы с каждой из прямых при $a = — /, a = — /, a = 0, a = /$.
Задача 16
Найдите все значения $a$, при каждом из которых уравнение $/= 1$ имеет единственный корень.
Решение
В левой части уравнения выделим целую часть
Тогда уравнение примет вид $/ = 0$.
Оно равносильно системе
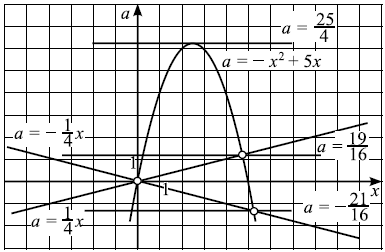
Решим систему графически в системе координат $xOa$. Для этого построим графики функций $a = — x^2 + 5x$ и $a =±/$.
Графиком функции $a = — x^2+5x$ является парабола, ветви которой направлены вниз. Вершина параболы — точка $(/; /)$, точки (0; 0) и (5; 0) принадлежат параболе. Графиками функций $a =±/$ являются прямые.
Решая уравнение $-x^2 + 5x = /$, находим точки пересечения прямой $a =/$ и параболы $a = — x^2 + 5x: x = 0, x = /$, откуда $a = 0, a = /$. Аналогично, решая уравнение $-x^2 + 5x = -/$, находим $a = 0, a = -/$. Выкалываем эти точки.
По рисунку видим, что ровно одна точка пересечения параболы с каждой из прямых будет при $a = -/, a = 0, a = /; a = /$.
Задача 17
Найдите все значения параметра $а$, при которых уравнение $√+/<√>=1$ имеет ровно два различных корня.
Решение
После приведения к общему знаменателю уравнение примет вид $/> = 1$ или $/> = 1$. Пусть $3^x = t, t > 0$. Заметим, что после замены каждому положительному корню уравнения $/> = 1$ соответствует единственный корень исходного уравнения (это следует из монотонности функции $3^x = t$). Уравнение $/> = 1$ равносильно системе
Возведём в квадрат обе части первого уравнения, учитывая, что $t ≥ 1$.
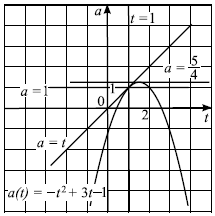
Решим систему графически в системе координат $tOa$.
Вершина параболы $a = — t^2 + 3t — 1$ — точка с координатами $(/;/)$.
Графики функций $a = — t^2 + 3t — 1$ и $a = t$ имеют единственную общую точку $t = 1$. Множество точек, удовлетворяющих неравенству $a 0$. Числа $x_2 = — a + 2√3$ и $x_3 = — a — 2√3$ будут корнями исходного уравнения, если выполняются условия:
Задача 19
Найдите все значения параметра a, при каждом из которых уравнение $x^2 + ax + 4 = √$ имеет ровно три различных корня.
Решение
Уравнение $x^2 + ax + 4 = √$ при $x^2 + ax + 4 0$. Числа $x_2 = — a + √$ и $x_3 = — a — √$ будут корнями исходного уравнения, если выполняются условия:
Задача 20
Найдите все значения $a$, при каждом из которых система уравнений $<table(xy^2-5xy-5y+25)/<√>=0; y=ax;$ имеет ровно два различных решения.
Решение
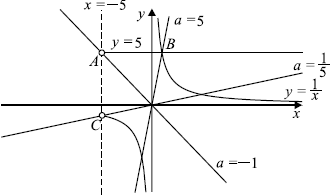
Решим задачу графически. Построим графики первого и второго уравнения и определим, сколько точек пересечения они имеют при различных значениях параметра.
Первое уравнение $/>= 0$ параметра не содержит и представляет собой равенство дроби нулю. Это выполняется, если числитель равен нулю, а знаменатель не равен нулю, при этом оба выражения имеют смысл.
Запишем уравнение в виде $<(y — 5)(xy — 5)>/> = 0$, разложив числитель на множители.
При $x ≤ -5$ первое уравнение системы не имеет смысла. При $x > -5$ уравнение задаёт прямую $y = 5$ и гиперболу $y =/$.
Число решений исходной системы равно числу точек пересечения прямой $y = 5$ и гиперболы $y =/$ с прямой $y = ax$ при условии $x>-5$.
Найдём координаты точек $A, B$ и $C$.
$B$ — точка пересечения прямой $y = 5$ и гиперболы $y =/$, чтобы найти её координаты, нужно решить систему уравнений $<tabley = 5; y =/;$
Получаем $B(1; 5)$.
У точек $A$ и $C$ абсцисса равна $-5$, ординаты находим из уравнений прямой и гиперболы. $A(-5; 5)$ и $C(-5;-1)$.
При каждом значении $a$ уравнение $y = ax$ задаёт прямую с угловым коэффициентом $a$, проходящую через начало координат. Чтобы найти значение $a$, при котором такая прямая проходит через точку с указанными координатами, нужно подставить координаты в уравнение прямой.
Например, для точки $A(-5; 5)$ получаем $x = -5; y = 5; 5 = a·(-5); a = -1$. Аналогично для $B(1; 5)$ получим $a = 5$. Для $C(-5;-1)$ получим $a =/$.
При $x>-5$ прямая $y = ax$ пересекает прямую $y = 5$ при $a 0$, пересекает правую ветвь гиперболы $y =/$ при $a>0$, пересекает левую ветвь гиперболы $y =/$ при $a>/$. При этом прямая $y = ax$ проходит через точку пересечения прямой $y = 5$ и гиперболы $y =/$ при $a = 5$.
Таким образом, исходная система имеет ровно два решения при $0 ×
Для доступа к решениям необходимо включить уведомления от группы Турбо в вк — это займет буквально 10 секунд. Никакого спама, только самое важное и полезное для тебя. Ты всегда можешь запретить уведомления.
Статистика
В задании №17 требуется решить текстовую задачу. Наиболее часто встречаются задачи экономического содержания на кредиты, вклады и оптимальный выбор.
Получить за решение этого задания можно 3 первичных балла, если обоснованно получен верный ответ. Если математическая модель построена верно, но решение недостаточно обоснованно, или допущена вычислительная ошибка – вы получите 2 первичных балла. А вот если решение не завершено, при правильно построенной математической модели, то вам достанется 1 первичный балл.
Виды платежей
1. Аннуитетный платеж — вариант ежемесячного платежа по кредиту, когда размер ежемесячного платежа остаётся постоянным на всём периоде кредитования.
- известно, что кредит был выплачен тремя равными платежами (за 3 года) он будет платить каждый год по 2 073 600 рублей кредит можно выплатить за четыре года равными платежами по 56 507 рублей
2. Дифференцированный платеж — вариант ежемесячного платежа по кредиту, когда сумма долга каждый год уменьшается на одну и ту же сумму, а размер ежемесячного платежа по погашению кредита постепенно уменьшается к концу периода кредитования.
- должен быть на X тысяч рублей меньше долга на n-е число предыдущего месяца n-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на n-е число предыдущего месяца
3. Фиксированные платежи — долг уменьшается по заданным в таблице или в условии задачи параметрам.
- выплатили за 2 года платежами 130 000 рублей в первый год и 150 000 рублей во второй 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей
Пример
- каждый январь долг возрастает на 20% по сравнению с концом предыдущего года; с февраля по июнь каждого года необходимо выплатить некоторую часть долга.
Сколько рублей необходимо будет отдать, если кредит будет погашен 4 равными платежами.
Решение:
- $x$ — ежегодный платеж $s$ — сумма кредита $r$ — процентная ставка $k=1+r/100$ — коэффициент.
Мы знаем, что после последнего платежа долг должен быть полностью погашен:
Сразу отмечу, что обычно вместо 1,2 удобнее было бы подставить как дробь 6/5. Но в данном примере нам повезло и расчеты оказались относительно простые.
После того как мы нашли x — ежегодный платеж, необходимо ответить на вопрос задачи, то есть найти общую сумму выплат за все 4 года, то есть 4x.
Еще больше крутых лайфхаков, разборов, ловушек ЕГЭ и теории в нашей группе вконтакте и инсте преподавателей @turboegemath и @turbomath
При x -5 первое уравнение системы не имеет смысла.
Egeturbo. ru
29.08.2019 18:35:11
2019-08-29 18:35:11
Источники:
Https://egeturbo. ru/ege/math/tasks/17
Задание 17 ЕГЭ по математике профильного уровня 2022 — теория и практика: Бингоскул » /> » /> .keyword { color: red; } 17 задание егэ математика профиль
Задание 17. Финансовая математика
Задание 17. Финансовая математика
За правильное выполненное задание без ошибок получишь 3 балла.
На решение отводится примерно 35 минут.
Чтобы решить задание 17 по математике профильного уровня нужно знать:
Задание подразделяется на несколько видов:
- задачи, связанные с банками, вкладами и кредитами; задачи на оптимальный выбор.
Формула расчета ежемесячного платежа: Sкредит = S/12 t Формула расчета простых процентов: S =α(1 + t p/m) Формула расчета сложных процентов: С = x (1 + a%)n
Процент – это одна сотая часть какой-либо величины.
- x*(1 + p/100) — величина x увеличилась на p% x*(1 — k/100) — величина x уменьшилась на k% x*(1 + p/100) k — величина x увеличилась на p% k раз x*(1 + p/100)*(1 — k/100) – величина х сначала увеличилась на p%, а потом уменьшилась на k%
Задачи на погашение кредита равными платежами:
Размер кредита принимается за х. Процента банка – а. Выплата по кредиту – S.
Через год после начисления процентов и выплаты суммы S размер долга — x * (1 + a/100), p = 1 + a/100
- Размер долга через 2 года: (xp – S)p – S Размер долга через 3 года: ((xp – S)p – S)p – S Размер долга через n лет: xp n – S(p n-1 + … + p 3 + p 2 + p + 1)
Задачи для тренировки
В 2014 году стандартная заработная плата на человека в месяц по Приморскому краю составляла 23040 рублей. Каждый год процент повышения дохода составлял 50. А в Хабаровском крае стандартная заработная плата на человека в месяц в 2014 году составляла 45000 рублей. Каждый год процент общего дохода жителей Хабаровского края повышался на 44 в течение трёх лет, каждый год процент населения возрастал на q. Стандартная месячная заработная плата по Приморскому краю и Хабаровскому краю сравнялась в 2017 году. Найдите q.
У компании по производству глазированных сырков существует 2 фабрики в Новосибирске и Магадане, где идентичным способом создают однотипный товар. За неделю на одной из фабрик рабочие изготавливают глазированных сырков, если общее время их труда составляет n 2 часов в неделю. Компания осуществляет оплату каждый час по 500 рублей на первой фабрике в Новосибирске, и по 300 рублей на второй в Магадане, причём компания на заработные платы рабочих выделяет 1200000 рублей. Найдите максимальное количество глазированных сырков, которое можно изготовить за неделю на двух фабриках.
В банковской ячейке семьи Сладковых, к которой доступ имели жена Людмила и муж Валентин, находился 1000000 рублей наличными. Процент фальшивых банкнот составлял 20. Каждый месяц Валентин вносил 100000 рублей, 10 процентов из которых были фальшивыми. Также каждый месяц Людмила забирала 50000 рублей, где процент фальшивых купюр являлся 30. Сколько месяц должно пройти, пока содержание фальшивых банкнот в банковской ячейке составит 5 процентов от всей суммы.
Маркиз обратился в банк, чтобы открыть счет, банковский процент которого составлял 10 Но спустя год мужчина взял деньги со счета в размере 2000 тыс. рублей. По прошествии еще одного года, Маркиз положил денежные средства обратно. Спустя 3 года с момента внесения изначальной суммы, мужчина получил начисления, которые были ниже прогнозируемого итога. Какое количество денег потерял Маркиз из-за операций со вкладом?
В доме Персивальды живет три различных животных: кролик, кот и лошадь. Женщина каждый месяц покупает им корм. Если бы цены на корм для лошадей повысились на 50%, то итоговая сумма оплаты увеличилась бы на 35%. Если бы цены на корм для кота поднялись, на 50%, то итоговая сумма оплаты повысилась бы на 10%.Сколько процентов от общих расходов на корм приходится на кролика?
Если бы цены на корм для лошадей повысились на 50 , то итоговая сумма оплаты увеличилась бы на 35.
Bingoschool. ru
08.11.2020 22:29:44
2020-11-08 22:29:44
Источники:
Https://bingoschool. ru/ege/maths-profile/tasks/17/
Задание 17 (№15 ЕГЭ-2022) профильного уровня
Это второе издание книги. От первой она отличается объёмом, разнообразием формулировок, полезностью (в эту книгу вошли задачи реальных вариантов ЕГЭ-2015 и задачи пробных вариантов 2016 года), многообразием методов решения и серьёзностью в оформлении.
Из спецификации к демоверсии:
→ Уметь использовать приобретённые знания и умения в практической деятельности и повседневной жизни.
Из кодификатора к демоверсии (требования к уровню подготовки выпускников):
→ Анализировать реальные числовые данные, информацию статистического характера; осуществлять практические расчёты по формулам; пользоваться оценкой и прикидкой при практических расчетах.
→ Решать прикладные задачи, в том числе социально-экономического и физического характера, на наибольшие и наименьшие значения, на нахождение скорости и ускорения.
4. Вся сумма выплат равна: 

Задание 17. Финансовая математика
За правильное выполненное задание без ошибок получишь 3 балла.
На решение отводится примерно 35 минут.
Чтобы решить задание 17 по математике профильного уровня нужно знать:
- Задание подразделяется на несколько видов:
- задачи, связанные с банками, вкладами и кредитами;
- задачи на оптимальный выбор.
- Формула расчета ежемесячного платежа: Sкредит = S/12 t
- Формула расчета простых процентов: S =α(1 + t p/m)
- Формула расчета сложных процентов: С = x (1 + a%)n
Процент – это одна сотая часть какой-либо величины.
- x*(1 + p/100) — величина x увеличилась на p%
- x*(1 — k/100) — величина x уменьшилась на k%
- x*(1 + p/100) k — величина x увеличилась на p% k раз
- x*(1 + p/100)*(1 — k/100) – величина х сначала увеличилась на p%, а потом уменьшилась на k%
Задачи на погашение кредита равными платежами:
Размер кредита принимается за х. Процента банка – а. Выплата по кредиту – S.
Через год после начисления процентов и выплаты суммы S размер долга — x * (1 + a/100), p = 1 + a/100
- Размер долга через 2 года: (xp – S)p – S
- Размер долга через 3 года: ((xp – S)p – S)p – S
- Размер долга через n лет: xp n – S(p n-1 + … + p 3 + p 2 + p + 1)
Задачи для тренировки
В 2014 году стандартная заработная плата на человека в месяц по Приморскому краю составляла 23040 рублей. Каждый год процент повышения дохода составлял 50. А в Хабаровском крае стандартная заработная плата на человека в месяц в 2014 году составляла 45000 рублей. Каждый год процент общего дохода жителей Хабаровского края повышался на 44 в течение трёх лет, каждый год процент населения возрастал на q. Стандартная месячная заработная плата по Приморскому краю и Хабаровскому краю сравнялась в 2017 году. Найдите q.
У компании по производству глазированных сырков существует 2 фабрики в Новосибирске и Магадане, где идентичным способом создают однотипный товар. За неделю на одной из фабрик рабочие изготавливают глазированных сырков, если общее время их труда составляет n 2 часов в неделю. Компания осуществляет оплату каждый час по 500 рублей на первой фабрике в Новосибирске, и по 300 рублей на второй в Магадане, причём компания на заработные платы рабочих выделяет 1200000 рублей. Найдите максимальное количество глазированных сырков, которое можно изготовить за неделю на двух фабриках.
В банковской ячейке семьи Сладковых, к которой доступ имели жена Людмила и муж Валентин, находился 1000000 рублей наличными. Процент фальшивых банкнот составлял 20. Каждый месяц Валентин вносил 100000 рублей, 10 процентов из которых были фальшивыми. Также каждый месяц Людмила забирала 50000 рублей, где процент фальшивых купюр являлся 30. Сколько месяц должно пройти, пока содержание фальшивых банкнот в банковской ячейке составит 5 процентов от всей суммы.
Маркиз обратился в банк, чтобы открыть счет, банковский процент которого составлял 10 Но спустя год мужчина взял деньги со счета в размере 2000 тыс. рублей. По прошествии еще одного года, Маркиз положил денежные средства обратно. Спустя 3 года с момента внесения изначальной суммы, мужчина получил начисления, которые были ниже прогнозируемого итога. Какое количество денег потерял Маркиз из-за операций со вкладом?
В доме Персивальды живет три различных животных: кролик, кот и лошадь. Женщина каждый месяц покупает им корм. Если бы цены на корм для лошадей повысились на 50%, то итоговая сумма оплаты увеличилась бы на 35%. Если бы цены на корм для кота поднялись, на 50%, то итоговая сумма оплаты повысилась бы на 10%.Сколько процентов от общих расходов на корм приходится на кролика?
Задание 17. Задача с параметром. ЕГЭ 2022 по математике профильного уровня
Для того, чтобы решить задачу необходимо составить математическую модель (уравнение, неравенство или функцию, которую нужно исследовать).
Для решения задач на кредиты, необходимо разобраться в основных схемах кредитования с дифференцированными и аннуитетными платежами. Часто для преобразования уравнения нужно знать формулы алгебраической и геометрической прогрессий.
В задачах на оптимизацию нужно уметь работать с функциями: брать производную, находить точки экстремумов.
Задачи для практики
Задача 1
При каком значении $a$ множеством решений неравенства
$ <1+3^x>/ <1+3^<-x>>> <3>/ <|x+a|>$ является множество всех положительных чисел?
Решение
Сократив левую часть неравенства на $1 + 3^x$, получим равносильное неравенство $3^x > <3>/<|x + a|>$ или $3^ > <1>/<|x + a|>$. Так как обе части неравенства положительны, то $<1>/<3^> <4>/ <√ >$ является множество всех отрицательных чисел?
Решение
Сократив левую часть неравенства на $1+2^x$ и применив свойство квадратного корня $√ =|m|$, получим равносильное неравенство $ <1>/ <2^x>> <4>/ <|x+a|>$ или $ <1>/ <2^>> <1>/ <|x+a|>$. Так как обе части неравенства положительны, то $2^ 0$ уравнение имеет два корня.
Проверим при каких значениях $a$ значения $x = -4$ и $x = a$ являются корнями уравнения $x^2 — x(4a + 1) + 4a^2 + 4a — 4 = 0$.
При $x = -4$ должно выполняться равенство $16 + 4(4a + 1) + 4a^2 + 4a — 4 = 0, a^2 + 5a + 4 = 0, a = -4, a = -1$.
При $x = a$ должно выполняться равенство $a^2 — 4a^2 — a + 4a^2 + 4a — 4 = 0, a^2 + 3a — 4 = 0, a = 1, a = -4$.
При $a = -1, a = 1$ исходное уравнение имеет единственный корень.
При $а=-4$, $D>0$ и корни $х=-4$ и $х=а$ совпадают, поэтому это значение параметра также подходит
Задача 5
Найдите все значения параметра $p$, при каждом из которых система неравенств $<<table ;
$<tablep ≥ <5>/; p 0$, при каждом из которых система
имеет ровно $2$ решения.
Решение
Если $y ≥ 0$, то первое уравнение задаёт окружность $∅_1$ с центром в точке $C_1(4; 4)$ радиуса $3$, а если $y 0$ второе уравнение задаёт окружность $∅$ с центром в точке $C (0; 4)$ радиуса $a$. Поэтому задача состоит в том, чтобы найти все значения параметра $a$, при каждом из которых окружность $∅$ имеет ровно две общие точки с объединением окружностей $∅_1$ и $∅_2$.
Координаты точки касания окружностей $∅$ и $∅_2$ явно видны на чертеже: это точки $A_1(1; 4)$ и $B_1(7; 4)$. То есть при $a = CA_1=1$ и $a = CB_1=7$ окружности $∅$ и $∅_2$ касаются. При $a > 7$ и $a CB_2$ окружности $∅$ и $∅_2$ не пересекаются. При $CA_2 0$, при каждом из которых система
имеет единственное решение.
Решение
Если $x ≥ 0$, то первое уравнение задаёт окружность $∅_1$ с центром в точке $C_1(3; 3)$ радиуса $2$, а если $x 0$ второе уравнение задаёт окружность $∅$ с центром в точке $C (−3; 0)$ радиуса $a$. Поэтому задача состоит в том, чтобы найти все значения параметра $a$, при каждом из которых окружность $∅$ имеет единственную общую точку с объединением окружностей $∅_1$ и $∅_2$.
Из точки $C$ проведём луч $CC_1$ и обозначим $A_1$ и $B_1$ точки его пересечения с окружностью $∅_1$, где $A_1$ лежит между $C$ и $C_1$.
Так как $CC_1 = √ <6^2 + 3^2>= √ <45>= 3√5$, то $CA_1 = 3√5 − 2, CB_1 = 3√5 + 2$.
При $a CB_1$ окружности $∅$ и $∅_1$ не пересекаются. При $CA_1 0;$. Второе неравенство системы преобразуем так, чтобы получить неравенство для внутренней части круга. Первое неравенство преобразуем так, чтобы скобки выглядели симметрично $<table (2√x — a)(a — x) ≤ 0; a^2+x^2 <√3>/<√2>$ решением является промежуток $[/<4>; √<3 — a^2>)$.
Отсюда решение содержит отрезок длиной не менее $<1>/<2>$, если
Решив системы, получим: $a ∈[2-√2; <√3>/<√2>]$ или $a ∈ (<√3>/<√2>; √2)$, отсюда $a ∈ [2 — √2; √2)$.
Замечание. Задачу можно решить и другими способами, например аналитически. Получив систему, можно заметить, что первое неравенство системы при $a 4$). Решением второго неравенства будут $x$, удовлетворяющие неравенству $x 4$ не возможен.
Несложно убедиться, что при ограничениях $0 ≤ a ≤ √3$ для решения задачи достаточно решить систему $<table a-<1>/<4>a^2 ≥ 0.5; √<3-a^2>—/ <4>> 0.5;$
Задача 11
Найдите все значения параметра a, при каждом из которых система уравнений $<tabley=√<-8-6x-x^2>; y+ax=a+1;$ имеет единственное решение.
Решение
Построим график уравнения $y = √<−8−6x−x^2>$.
Преобразовав подкоренное выражение, получим: $y = √<1−(x^2 + 6x + 9)>, y =√<1−(x + 3)^2>$.
Если $y ≥ 0$, то $y^2 = 1−(x + 3)^2, (x + 3)^2 + y^2 = 1$.
Если $y 0$ для любого $a$).
Указанные окружности будут иметь ровно три общие точки с парой указанных выше пересекающихся прямых в том и только том случае, когда окружность проходит через точку пересечения этих прямых.
В таком случае точка $(-1; 2)$ лежит на окружности, значит, верно равенство $(-1 + 1)^2 + (2 — a)^2 = 3a^2 — 2a + 4$.
Отсюда получаем: $4 — 4a + a^2 = 3a^2 — 2a + 4; 2a^2 + 2a = 0; 2a ·(a + 1) = 0; $
Задача 14
Найдите все значения $a$, при которых система уравнений
имеет ровно три решения.
Решение
Уравнение $(x — 3)^2 = (y — 1)^2$ равносильно совокупности двух уравнений
Множество решений этой совокупности совпадает с множеством всех точек, лежащих на двух прямых: $y = x — 2$ и $y = -x + 4$. Заметим, что эти прямые проходят через точку $(3; 1)$, так как система $<table y = x — 2; y = -x + 4;$ имеет единственное решение $(3; 1)$.
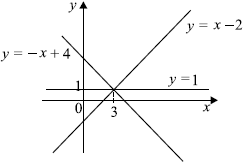
При каждом значении $a$ множеством решений второго уравнения системы $(x — a)^2 + (y — 1)^2 = 3a^2 — 8a + 9$ будет множество всех точек окружности с центром в точке $(a; 1)$, лежащей на прямой $y = 1$, и радиусом $√<3a^2 — 8a + 9>$ (заметим, что $3a^2 — 8a + 9 > 0$ для любого $a$).
Указанные окружности будут иметь ровно три общие точки с парой указанных выше пересекающихся прямых в том и только том случае, когда окружность проходит через точку пересечения этих прямых.
В таком случае точка $(3; 1)$ лежит на окружности, значит, верно равенство $(3 — a)^2 + (1 — 1)^2 = 3a^2 — 8a + 9$.
Отсюда получаем: $9 — 6a + a^2 = 3a^2 — 8a + 9; 2a^2 — 2a = 0; 2a ·(a — 1) = 0; a = 0$ или $a = 1$.
Задача 15
Найдите все значения $a$, при каждом из которых уравнение $<3x + a — x^2 + 4a^2x — x^3>/ <4a^2x — x^3>= 1$ имеет единственный корень.
Решение
В левой части уравнения выделим целую часть
Тогда уравнение примет вид $<-x^2 + 3x + a>/<4a^<2>x — x^3> = 0$. Оно равносильно системе
Решим систему графически в системе координат $xOa$. Для этого строим графики функций $a = x^2 — 3x$ и $a = ±/<2>$.
Графиком функции $a = x^2 — 3x$ является парабола, ветви которой направлены вверх. Вершина параболы — точка $(<3>/<2>; —<9>/<4>)$, точки $(0; 0)$ и $(3; 0)$ принадлежат параболе. Графиками функций $a = ±/<2>$ являются прямые.
Решая уравнение $x^2 — 3x = /<2>$, находим точки пересечения прямой $a = /<2>$ и параболы $a = x^2 — 3x: x = 0, x = <7>/<2>$, откуда $a = 0, a = <7>/<4>$. Аналогично, решая уравнение $x^2 — 3x = — /<2>$, находим $x = 0, x = <5>/<2>$. Тогда $a = 0, a = — <5>/<4>$. Выкалываем эти точки.
По рисунку видим, что ровно одна точка пересечения параболы с каждой из прямых при $a = — <9>/<4>, a = — <5>/<4>, a = 0, a = <7>/<4>$.
Задача 16
Найдите все значения $a$, при каждом из которых уравнение $/= 1$ имеет единственный корень.
Решение
В левой части уравнения выделим целую часть
Тогда уравнение примет вид $/ = 0$.
Оно равносильно системе
Решим систему графически в системе координат $xOa$. Для этого построим графики функций $a = -x^2 + 5x$ и $a =±/<4>$.
Графиком функции $a = -x^2+5x$ является парабола, ветви которой направлены вниз. Вершина параболы — точка $(<5>/<2>; <25>/<4>)$, точки (0; 0) и (5; 0) принадлежат параболе. Графиками функций $a =±/<4>$ являются прямые.
Решая уравнение $-x^2 + 5x = /<4>$, находим точки пересечения прямой $a =/<4>$ и параболы $a = -x^2 + 5x: x = 0, x = <19>/<4>$, откуда $a = 0, a = <19>/<16>$. Аналогично, решая уравнение $-x^2 + 5x = —/<4>$, находим $a = 0, a = —<21>/<16>$. Выкалываем эти точки.
По рисунку видим, что ровно одна точка пересечения параболы с каждой из прямых будет при $a = —<21>/<16>, a = 0, a = <19>/<16>; a = <25>/<4>$.
Задача 17
Найдите все значения параметра $а$, при которых уравнение $√<3^x-a>+/<√<3^x-a>>=1$ имеет ровно два различных корня.
Решение

После приведения к общему знаменателю уравнение примет вид $<3x — a + a — 1>/<√<3^x — a>> = 1$ или $<3^x — 1>/<√<3^x — a>> = 1$. Пусть $3^x = t, t > 0$. Заметим, что после замены каждому положительному корню уравнения $/<√> = 1$ соответствует единственный корень исходного уравнения (это следует из монотонности функции $3^x = t$). Уравнение $/<√> = 1$ равносильно системе
Возведём в квадрат обе части первого уравнения, учитывая, что $t ≥ 1$.
Решим систему графически в системе координат $tOa$.
Вершина параболы $a = -t^2 + 3t — 1$ — точка с координатами $(<3>/<2>;<5>/<4>)$.
Графики функций $a = -t^2 + 3t — 1$ и $a = t$ имеют единственную общую точку $t = 1$. Множество точек, удовлетворяющих неравенству $a 0$. Числа $x_2 = -a + 2√3$ и $x_3 = -a — 2√3$ будут корнями исходного уравнения, если выполняются условия:
Задача 19
Найдите все значения параметра a, при каждом из которых уравнение $x^2 + ax + 4 = √<20x^2 + 8ax + 16>$ имеет ровно три различных корня.
Решение
Уравнение $x^2 + ax + 4 = √<20x^2 + 8ax + 16>$ при $x^2 + ax + 4 0$. Числа $x_2 = -a + √<12>$ и $x_3 = -a — √<12>$ будут корнями исходного уравнения, если выполняются условия:
Задача 20
Найдите все значения $a$, при каждом из которых система уравнений $<table(xy^2-5xy-5y+25)/<√>=0; y=ax;$ имеет ровно два различных решения.
Решение
Решим задачу графически. Построим графики первого и второго уравнения и определим, сколько точек пересечения они имеют при различных значениях параметра.
Первое уравнение $/<√>= 0$ параметра не содержит и представляет собой равенство дроби нулю. Это выполняется, если числитель равен нулю, а знаменатель не равен нулю, при этом оба выражения имеют смысл.
Запишем уравнение в виде $<(y — 5)(xy — 5)>/<√> = 0$, разложив числитель на множители.
При $x ≤ -5$ первое уравнение системы не имеет смысла. При $x > -5$ уравнение задаёт прямую $y = 5$ и гиперболу $y =<5>/$.
Число решений исходной системы равно числу точек пересечения прямой $y = 5$ и гиперболы $y =<5>/$ с прямой $y = ax$ при условии $x>-5$.
Найдём координаты точек $A, B$ и $C$.
$B$ — точка пересечения прямой $y = 5$ и гиперболы $y =<5>/$, чтобы найти её координаты, нужно решить систему уравнений $<tabley = 5; y =<5>/;$
Получаем $B(1; 5)$.
У точек $A$ и $C$ абсцисса равна $-5$, ординаты находим из уравнений прямой и гиперболы. $A(-5; 5)$ и $C(-5;-1)$.
При каждом значении $a$ уравнение $y = ax$ задаёт прямую с угловым коэффициентом $a$, проходящую через начало координат. Чтобы найти значение $a$, при котором такая прямая проходит через точку с указанными координатами, нужно подставить координаты в уравнение прямой.
Например, для точки $A(-5; 5)$ получаем $x = -5; y = 5; 5 = a·(-5); a = -1$. Аналогично для $B(1; 5)$ получим $a = 5$. Для $C(-5;-1)$ получим $a =<1>/<5>$.
При $x>-5$ прямая $y = ax$ пересекает прямую $y = 5$ при $a 0$, пересекает правую ветвь гиперболы $y =<5>/$ при $a>0$, пересекает левую ветвь гиперболы $y =<5>/$ при $a><1>/<5>$. При этом прямая $y = ax$ проходит через точку пересечения прямой $y = 5$ и гиперболы $y =<5>/$ при $a = 5$.
Таким образом, исходная система имеет ровно два решения при $0 ×
Для доступа к решениям необходимо включить уведомления от группы Турбо в вк — это займет буквально 10 секунд. Никакого спама, только самое важное и полезное для тебя. Ты всегда можешь запретить уведомления.
Статистика
В задании №17 требуется решить текстовую задачу. Наиболее часто встречаются задачи экономического содержания на кредиты, вклады и оптимальный выбор.
Получить за решение этого задания можно 3 первичных балла, если обоснованно получен верный ответ. Если математическая модель построена верно, но решение недостаточно обоснованно, или допущена вычислительная ошибка – вы получите 2 первичных балла. А вот если решение не завершено, при правильно построенной математической модели, то вам достанется 1 первичный балл.
Виды платежей
1. Аннуитетный платеж — вариант ежемесячного платежа по кредиту, когда размер ежемесячного платежа остаётся постоянным на всём периоде кредитования.
- известно, что кредит был выплачен тремя равными платежами (за 3 года)
- он будет платить каждый год по 2 073 600 рублей
- кредит можно выплатить за четыре года равными платежами по 56 507 рублей
2. Дифференцированный платеж — вариант ежемесячного платежа по кредиту, когда сумма долга каждый год уменьшается на одну и ту же сумму, а размер ежемесячного платежа по погашению кредита постепенно уменьшается к концу периода кредитования.
- должен быть на X тысяч рублей меньше долга на n-е число предыдущего месяца
- n-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на n-е число предыдущего месяца
3. Фиксированные платежи — долг уменьшается по заданным в таблице или в условии задачи параметрам.
- выплатили за 2 года платежами 130 000 рублей в первый год и 150 000 рублей во второй
- 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей
Пример
- каждый январь долг возрастает на 20% по сравнению с концом предыдущего года;
- с февраля по июнь каждого года необходимо выплатить некоторую часть долга.
Сколько рублей необходимо будет отдать, если кредит будет погашен 4 равными платежами.
Решение:
- $x$ — ежегодный платеж
- $s$ — сумма кредита
- $r$ — процентная ставка
- $k=1+r/100$ — коэффициент.
Мы знаем, что после последнего платежа долг должен быть полностью погашен:
Сразу отмечу, что обычно вместо 1,2 удобнее было бы подставить как дробь 6/5. Но в данном примере нам повезло и расчеты оказались относительно простые.
После того как мы нашли x — ежегодный платеж, необходимо ответить на вопрос задачи, то есть найти общую сумму выплат за все 4 года, то есть 4x.
Еще больше крутых лайфхаков, разборов, ловушек ЕГЭ и теории в нашей группе вконтакте и инсте преподавателей @turboegemath и @turbomath