Диагностический вариант СтатГрад ЕГЭ Профиль по математике 2110209-15.12.2021 с ответами и критериями
А. Ларин: Тренировочный вариант № 209.
При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
Версия для печати и копирования в MS Word
1
Дано уравнение
а) Решите уравнение.
б) Найдите корни этого уравнения, принадлежащие отрезку
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
2
Внутри куба расположены два равных шара, касающихся друга. При этом один шар касается трех граней куба, имеющих общую вершину, а другой касается трех оставшихся граней.
а) Докажите, что центры шаров принадлежат диагонали куба, исходящей из общей для граней вершины.
б) Найдите радиусы этих шаров, если ребро куба равно 13.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
3
Решите неравенство:
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
4
Точка E — середина боковой стороны CD трапеции ABCD. На стороне AB взяли точку K так, что прямые CK и AE параллельны. Отрезки CK и BE пересекаются в точке O.
а) Докажите, что CO = KO.
б) Найдите отношение оснований трапеции BC и AD, если площадь треугольника BCK составляет 0,09 площади трапеции ABCD.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
5
Иван Петрович получил кредит в банке под определенный процент годовых. Через год в счет погашения кредита он вернул в банк 1/6 от всей суммы, которую он должен банку к этому времени. А еще через год в счет полного погашения кредита Иван Петрович внес в банк сумму, на 20% превышающую величину полученного кредита. Каков процент годовых по кредиту в данном банке?
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
6
При каких значениях параметра система уравнений имеет единственное решение?
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
7
Натуральные числа от 1 до 12 разбивают на четыре группы, в каждой из которых есть по крайней мере два числа. Для каждой группы находят сумму чисел этой группы. Для каждой пары групп находят модуль разности полученных сумм и полученные 6 чисел складывают.
а) Может ли в результате получиться 0?
б) Может ли в результате получиться 1?
в) Какое наименьшее возможное значение полученного результата?
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
Завершить тестирование, свериться с ответами, увидеть решения.
Задание 13
Внутри куба расположены два равных шара, касающихся друга. При этом один шар касается трех граней куба, имеющих общую вершину, а другой касается трех оставшихся граней.
а) Докажите, что центры шаров принадлежат диагонали куба, исходящей из общей для граней вершины.
б) Найдите радиусы этих шаров, если ребро куба равно 13.
Ответ: $$frac{13sqrt{3}}{2+2sqrt{3}}$$
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
a) Пусть шар с центром в точке $$O_1$$ касается граней $$ABCD,AA_1D_1D,AA_1B_1B$$, соответственно шар с центром в точке $$O_2$$ касается граней $$A_1B_1C_1D_1,BB_1C_1C,DD_1C_1C$$.
Так как первый шар касается граней $$AA_1B_1B,AA_1D_1D$$, то его центр $$O_1$$ равноудален от указанных граней, то есть лежит на биссекторной плоскости двугранного угла c ребром $$AA_1$$, то есть на плоскости $$AA_1C_1C$$ (с учетом того, что $$ABCDA_1B_1C_1D_1$$ – куб).
Так первый шар касается граней $$ABCD,AA_1D_1D$$, то его центр $$O_1$$ равноудален от указанных граней, то есть лежит на биссекторной плоскости двугранного угла c ребром $$AD$$, то есть на плоскости $$AB_1C_1D$$ (с учетом того, что $$ABCDA_1B_1C_1D_1$$ – куб).
Но тогда точка $$O_1$$ лежит на прямой пересечения плоскостей $$AA_1C_1C,AB_1C_1D$$, то есть на $$AC_1$$ (естественно, раз шар находится внутри куба, то $$O_1$$ – точка отрезка $$AC_1$$).
Рассуждая аналогичным образом, приходим к тому, что и точка $$O_2$$ лежит на отрезке $$AC_1$$.
б) Очевидно, $$A_1C_1=13sqrt2$$, $$AC_1=13sqrt3$$. Очевидно, в силу симметрии, $$AO_1=C_1O_2$$ и $$AO_1=C_1O_2=frac{13sqrt3-2r}{2}$$, где $$r$$ – радиусы шаров.
Пусть, например, $$K_2$$ – точка касания второго шара с гранью $$A_1B_1C_1D_1$$ ($$K_2$$ принадлежит $$A_1C_1$$).
Треугольники $$AA_1C_1,O_2K_2C_1$$ подобны по двум углам, тогда $$frac{AA_1}{O_2K_2}=frac{AC_1}{O_2C_1}$$; $$frac{13}{r}=frac{13sqrt2}{frac{13sqrt3-2r}{2}}$$; $$frac{1}{r}=frac{2sqrt2}{13sqrt3-2r}$$; $$2sqrt2 r=13sqrt3-2r$$; $$r(2sqrt2+2)=13sqrt3$$; $$r=frac{13sqrt3}{2sqrt2+2}$$.
Решение и ответы заданий варианта 2210209 СтатГрад 13 декабря ЕГЭ 2023 по математике (профильный уровень). ГДЗ профиль для 11 класса. +Задания №1, №4, №6 из варианта 2210211.


Задание 1.
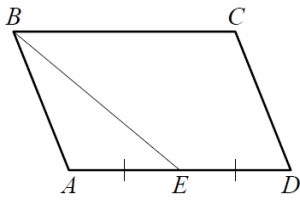
Площадь параллелограмма ABCD равна 96. Точка Е – середина стороны AD. Найдите площадь треугольника ABE.
Задание 1 из варианта 2210211.
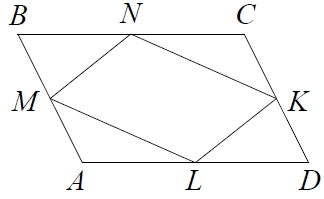
Площадь параллелограмма ABCD равна 26. Найдите площадь параллелограмма MNKL , вершинами которого являются середины сторон данного параллелограмма.
Задание 2.
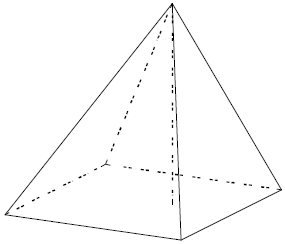
Основанием пирамиды является прямоугольник со сторонами 2 и 7. Её объём равен 14. Найдите высоту этой пирамиды.
Задание 3.
На чемпионате по прыжкам в воду выступают 30 спортсменов, среди них 3 прыгуна из Польши и 4 прыгуна из Дании. Порядок выступлений определяется жеребьёвкой. Найдите вероятность того, что четвёртым будет выступать прыгун из Польши.
Задание 4.
Игральную кость бросили один или несколько раз. Оказалось, что сумма всех выпавших очков равна 4. Какова вероятность того, что был сделан один бросок? Ответ округлите до сотых.
Задание 4 из варианта 2210211.
Игральную кость бросали до тех пор, пока сумма всех выпавших очков не превысила число 4. Какова вероятность того, что для этого потребовалось два броска?
Задание 5.
Решите уравнение sqrt{-35-12x}=-x. Если уравнение имеет больше одного корня, в ответе запишите больший из корней.
Задание 6.
Найдите значение 13cos(frac{pi}{2} − α), если cosα = −frac{12}{13} и α∈ (frac{pi}{2}; π).
Задание 6 из варианта 2210211.
Найдите значение frac{4cos(–pi–beta)+3sin(frac{3pi}{2}+beta)}{cos(beta+3pi)}.
Задание 7.
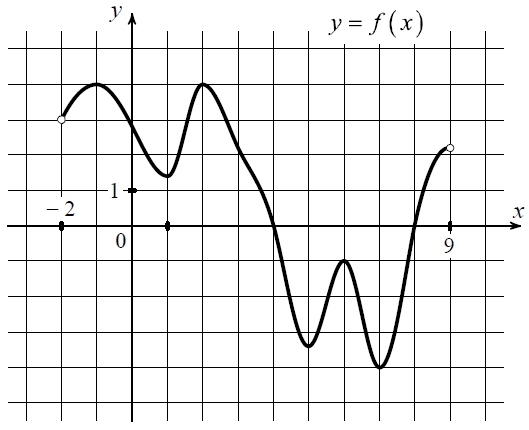
На рисунке изображён график функции y = f(x), определённой на интервале (−2; 9). Определите количество точек, в которых производная функции f(x) равна 0.
Задание 8.
Если достаточно быстро вращать ведёрко с водой на верёвке в вертикальной плоскости, то вода не будет выливаться. При вращении ведёрка сила давления воды на дно не остаётся постоянной: она максимальна в нижней точке и минимальна в верхней. Вода не будет выливаться, если сила её давления на дно будет положительной во всех точках траектории кроме верхней, где она может быть равной нулю. В верхней точке сила давления, выраженная в ньютонах, равна P=m(frac{v^{2}}{L}-g), где m – масса воды в килограммах, v – скорость движения ведёрка в м/с, L – длина верёвки в метрах, g – ускорение свободного падения (считайте g = 10 м/с2). С какой наименьшей скоростью надо вращать ведёрко, чтобы вода не выливалась, если длина верёвки равна 90 см? Ответ дайте в м/с.
Задание 9.
Первый садовый насос перекачивает 6 литров воды за 2 минуты, второй насос перекачивает тот же объём воды за 3 минуты. Сколько минут эти два насоса должны работать одновременно, чтобы перекачать 5 литров воды?
Задание 10.
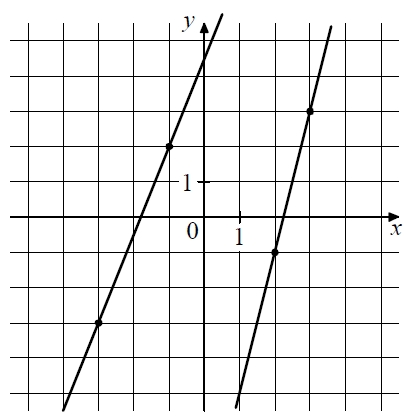
На рисунке изображены графики линейных функций, которые пересекаются в точке A. Найдите абсциссу точки A.
Задание 11.
Найдите наименьшее значение функции y = 10x − 10ln(x + 4) + 23 на отрезке [−3,5; 0].
Задание 12.
а) Решите уравнение 15sinx = 3sinx·5–cosx.
б) Найдите все корни этого уравнения, принадлежащие отрезку [frac{3pi}{2};3pi].
Задание 13.
В основании четырёхугольной пирамиды SABCD лежит прямоугольник ABCD со сторонами AB = 5 и BC = √23 . Длины боковых рёбер пирамиды SA = 2√15, SB = √85, SD = √83.
а) Докажите, что SA – высота пирамиды SABCD.
б) Найдите угол между прямыми SC и BD.
Задание 14.
Решите неравенство
(3x3 – 18x2 + 27x)·(x – 3)–1 – (6x3 – 11x2 – 44x – 30)·(2x + 3)–1 ≤ 11.
Задание 15.
15 января планируется взять кредит в банке на 9 месяцев. Условия его возврата таковы:
– 1-го числа каждого месяца долг возрастает на 3 % по сравнению с концом предыдущего месяца;
– со 2-го по 14-е число каждого месяца необходимо оплатить часть долга одним платежом;
– 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца.
Какую сумму следует взять в кредит, чтобы общая сумма платежей после полного погашения равнялась 4,6 млн рублей?
Задание 16.
Высоты BB1 и CC1 остроугольного треугольника ABC пересекаются в точке H.
а) Докажите, что ∠BB1C1 = ∠BAH.
б) Найдите расстояние от центра окружности, описанной около треугольника ABC, до стороны BC, если B1C1 = 9 и ∠BAC = 60°.
Задание 17.
Найдите все значения a, при каждом из которых уравнение
2sqrt{x^{4}+(a-3)^{4}}=|x+a-3|+|x-a+3|
имеет единственное решение.
Задание 18.
Сначала Маша написала на доске 15 натуральных чисел (необязательно различных), каждое из которых не превосходит 30. Затем вместо некоторых из чисел (возможно, одного) она написала на доске числа, меньшие первоначальных на единицу. Числа, которые после этого оказались равными 0, она с доски стёрла.
а) Могло ли оказаться так, что среднее арифметическое чисел на доске увеличилось?
б) Среднее арифметическое первоначально написанных чисел равнялось 25. Могло ли среднее арифметическое оставшихся на доске чисел оказаться равным 32?
в) Среднее арифметическое первоначально написанных чисел равнялось 25. Найдите наибольшее возможное значение среднего арифметического чисел, которые остались на доске.
Источник варианта: СтатГрад/statgrad.org.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 4.4 / 5. Количество оценок: 7
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
| Автор | Сообщение | |||
|---|---|---|---|---|
|
Заголовок сообщения: Тренировочный вариант №209
|
||||
|
http://alexlarin.net/ege/2018/trvar209.html |
|||
  |
||||
|
|
||||
|
Ege2018 |
Заголовок сообщения: Re: Тренировочный вариант №209
|
|||
|
Всем привет, я новичок у вас. Подробности: Последний раз редактировалось Ege2018 28 окт 2017, 10:31, всего редактировалось 3 раз(а). |
|||
  |
||||
|
ГОРЕВАВГ |
Заголовок сообщения: Re: Тренировочный вариант №209
|
|||
|
Спасибо за новый вариант _________________ |
|||
  |
||||
|
Andreymath |
Заголовок сообщения: Re: Тренировочный вариант №209
|
|||
|
18) сверим? Подробности: |
|||
  |
||||
|
olka-109 |
Заголовок сообщения: Re: Тренировочный вариант №209
|
|||
|
19 Подробности: _________________ |
|||
  |
||||
|
khazh |
Заголовок сообщения: Re: Тренировочный вариант №209
|
|||
|
Andreymath писал(а): 18) сверим? Подробности: Почему `a=1` не вошло в ответ? |
|||
  |
||||
|
Andreymath |
Заголовок сообщения: Re: Тренировочный вариант №209
|
|||
|
khazh писал(а): Andreymath писал(а): 18) сверим? Подробности: Почему `a=1` не вошло в ответ? Потому что я записал недостаточно условий… Моя вина. |
|||
  |
||||
|
netka |
Заголовок сообщения: Re: Тренировочный вариант №209
|
|||
|
Ege2018 писал(а): Всем привет, я новичок у вас. Добро пожаловать! Ege2018 писал(а): Мои ответы Подробности: согласна Подробности: Ege2018 писал(а): 15) Подробности: не согласна Подробности: |
|||
  |
||||
|
Kirill Kolokolcev |
Заголовок сообщения: Re: Тренировочный вариант №209
|
|||
|
Ege2018 писал(а): Всем привет, я новичок у вас. Подробности: У меня в 15 другой ответ Подробности: |
|||
  |
||||
|
Николай99 |
Заголовок сообщения: Re: Тренировочный вариант №209
|
|||
|
Планиметрия в этом варианте довольно простая. Подробности: |
|||
  |
||||
| Показать сообщения за: Сортировать по: |
Кто сейчас на форуме
|
Сейчас этот форум просматривают: нет зарегистрированных пользователей и гости: 1 |
|
Вы не можете начинать темы |
|
|
Ответы, решения и задания для 4 вариантов МА2210209, МА2210210, МА2210211, МА2210212 тренировочная работа №2 статград ЕГЭ 2023 профильный уровень (ПРОФИЛЬ) по математике 11 класс в формате реального экзамена ЕГЭ 2023 года, которая прошла 13 декабря 2022 года.
статград-егэ2023-профиль
Вариант МА2210209 и ответы
1. Площадь параллелограмма ABCD равна 96. Точка E — середина стороны AD . Найдите площадь треугольника ABE .
2. Основанием пирамиды является прямоугольник со сторонами 2 и 7. Её объём равен 14. Найдите высоту этой пирамиды.
3. На чемпионате по прыжкам в воду выступают 30 спортсменов, среди них 3 прыгуна из Польши и 4 прыгуна из Дании. Порядок выступлений определяется жеребьёвкой. Найдите вероятность того, что четвёртым будет выступать прыгун из Польши.
4. Игральную кость бросили один или несколько раз. Оказалось, что сумма всех выпавших очков равна 4. Какова вероятность того, что был сделан один бросок? Ответ округлите до сотых.
9. Первый садовый насос перекачивает 6 литров воды за 2 минуты, второй насос перекачивает тот же объём воды за 3 минуты. Сколько минут эти два насоса должны работать одновременно, чтобы перекачать 5 литров воды?
10. На рисунке изображены графики линейных функций, которые пересекаются в точке A. Найдите абсциссу точки A.
15. 15 января планируется взять кредит в банке на 9 месяцев. Условия его возврата таковы: — 1-го числа каждого месяца долг возрастает на 3 % по сравнению с концом предыдущего месяца; — со 2-го по 14-е число каждого месяца необходимо оплатить часть долга одним платежом; — 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца. Какую сумму следует взять в кредит, чтобы общая сумма платежей после полного погашения равнялась 4,6 млн рублей?
18. Сначала Маша написала на доске 15 натуральных чисел (необязательно различных), каждое из которых не превосходит 30. Затем вместо некоторых из чисел (возможно, одного) она написала на доске числа, меньшие первоначальных на единицу. Числа, которые после этого оказались равными 0, она с доски стёрла. а) Могло ли оказаться так, что среднее арифметическое чисел на доске увеличилось? б) Среднее арифметическое первоначально написанных чисел равнялось 25. Могло ли среднее арифметическое оставшихся на доске чисел оказаться равным 32? в) Среднее арифметическое первоначально написанных чисел равнялось 25. Найдите наибольшее возможное значение среднего арифметического чисел, которые остались на доске.
Вариант МА2210210 и ответы
1. Площадь параллелограмма ABCD равна 68. Точка E — середина стороны AD . Найдите площадь треугольника ABE .
2. Основанием пирамиды является прямоугольник со сторонами 2 и 4. Её объём равен 16. Найдите высоту этой пирамиды.
3. На чемпионате по прыжкам в воду выступают 25 спортсменов, среди них 3 прыгуна из Голландии и 7 прыгунов из Бразилии. Порядок выступлений определяется жеребьёвкой. Найдите вероятность того, что седьмым будет выступать прыгун из Бразилии.
4. Игральную кость бросили один или несколько раз. Оказалось, что сумма всех выпавших очков равна 3. Какова вероятность того, что было сделано три броска? Ответ округлите до сотых.
9. Первый садовый насос перекачивает 6 литров воды за 2 минуты, второй насос перекачивает тот же объём воды за 5 минут. Сколько минут эти два насоса должны работать одновременно, чтобы перекачать 42 литра воды?
10. На рисунке изображены графики линейных функций, которые пересекаются в точке A. Найдите абсциссу точки A.
15. 15 января планируется взять кредит в банке на 9 месяцев. Условия его возврата таковы: — 1-го числа каждого месяца долг возрастает на 4 % по сравнению с концом предыдущего месяца; — со 2-го по 14-е число каждого месяца необходимо оплатить часть долга одним платежом; — 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца. Какую сумму следует взять в кредит, чтобы общая сумма платежей после полного погашения равнялась 3,6 млн рублей?
18. Сначала Маша написала на доске 20 натуральных чисел (необязательно различных), каждое из которых не превосходит 30. Затем вместо некоторых из чисел (возможно, одного) она написала на доске числа, меньшие первоначальных на единицу. Числа, которые после этого оказались равными 0, она с доски стёрла. а) Могло ли оказаться так, что среднее арифметическое чисел на доске увеличилось? б) Среднее арифметическое первоначально написанных чисел равнялось 24. Могло ли среднее арифметическое оставшихся на доске чисел оказаться равным 30? в) Среднее арифметическое первоначально написанных чисел равнялось 24. Найдите наибольшее возможное значение среднего арифметического чисел, которые остались на доске.
Вариант МА2210211 и ответы
1. Площадь параллелограмма ABCD равна 26. Найдите площадь параллелограмма MNKL, вершинами которого являются середины сторон данного параллелограмма.
2. В правильной четырёхугольной пирамиде высота равна 5, боковое ребро равно 10. Найдите её объём.
3. На рок-фестивале выступают группы — по одной от каждой из заявленных стран, в том числе группы из Швеции, России и Вьетнама. Порядок выступления определяется жребием. Какова вероятность того, что группа из Швеции будет выступать позже групп из России и Вьетнама? Ответ округлите до сотых.
4. Игральную кость бросали до тех пор, пока сумма всех выпавших очков не превысила число 4. Какова вероятность того, что для этого потребовалось два броска?
9. Первый и второй насосы наполняют бассейн за 42 минуты, второй и третий — за 48 минут, а первый и третий — за 56 минут. За сколько минут эти три насоса заполнят бассейн, работая вместе?
10. На рисунке изображены графики двух линейных функций. Найдите ординату точки пересечения графиков.
15. 15 января планируется взять кредит в банке на 15 месяцев. Условия его возврата таковы: — 1-го числа каждого месяца долг возрастает на 2 % по сравнению с концом предыдущего месяца; — со 2-го по 14-е число каждого месяца необходимо оплатить часть долга одним платежом; — 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца. Какую сумму следует взять в кредит, чтобы общая сумма платежей после полного погашения равнялась 2,9 млн рублей?
18. Сначала Маша написала на доске 15 натуральных чисел (необязательно различных), каждое из которых не превосходит 40. Затем вместо некоторых из чисел (возможно, одного) она написала на доске числа, меньшие первоначальных на единицу. Числа, которые после этого оказались равными 0, она с доски стёрла. а) Могло ли оказаться так, что среднее арифметическое чисел на доске увеличилось? б) Среднее арифметическое первоначально написанных чисел равнялось 26. Могло ли среднее арифметическое оставшихся на доске чисел оказаться равным 33? в) Среднее арифметическое первоначально написанных чисел равнялось 26. Найдите наибольшее возможное значение среднего арифметического чисел, которые остались на доске.
Вариант МА2210212 и ответы
1. Площадь параллелограмма ABCD равна 68. Найдите площадь параллелограмма MNKL, вершинами которого являются середины сторон данного параллелограмма.
2. В правильной четырёхугольной пирамиде высота равна 3, боковое ребро равно 9. Найдите её объём.
3. На рок-фестивале выступают группы — по одной от каждой из заявленных стран, в том числе группы из Канады, Англии и Вьетнама. Порядок выступления определяется жребием. Какова вероятность того, что группа из Канады будет выступать позже групп из Англии и Вьетнама? Ответ округлите до сотых.
4. Игральную кость бросали до тех пор, пока сумма всех выпавших очков не превысила число 5. Какова вероятность того, что для этого потребовалось два броска? Ответ округлите до сотых.
9. Первый и второй насосы наполняют бассейн за 1 час 30 минут, второй и третий — за 1 час 50 минут, а первый и третий — за 2 часа 12 минут. За сколько минут эти три насоса заполнят бассейн, работая вместе?
10. На рисунке изображены графики двух линейных функций. Найдите ординату точки пересечения графиков.
15. 15 января планируется взять кредит в банке на 13 месяцев. Условия его возврата таковы: — 1-го числа каждого месяца долг возрастает на 5 % по сравнению с концом предыдущего месяца; — со 2-го по 14-е число каждого месяца необходимо оплатить часть долга одним платежом; — 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца. Какую сумму следует взять в кредит, чтобы общая сумма платежей после полного погашения равнялась 2,7 млн рублей?
18. Сначала Маша написала на доске 20 натуральных чисел (необязательно различных), каждое из которых не превосходит 50. Затем вместо некоторых из чисел (возможно, одного) она написала на доске числа, меньшие первоначальных на единицу. Числа, которые после этого оказались равными 0, она с доски стёрла. а) Могло ли оказаться так, что среднее арифметическое чисел на доске увеличилось? б) Среднее арифметическое первоначально написанных чисел равнялось 29. Могло ли среднее арифметическое оставшихся на доске чисел оказаться равным 34? в) Среднее арифметическое первоначально написанных чисел равнялось 29. Найдите наибольшее возможное значение среднего арифметического чисел, которые остались на доске.
- Статград математика 11 класс ЕГЭ 2023 варианты и ответы
- 13 декабря 2022 Математика 11 класс база ЕГЭ 2023