Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Спрятать решение
Решение.
Площадь четырёхугольника равна разности площади большого прямоугольника, маленького прямоугольника и двух прямоугольных треугольников, гипотенузы которых являются сторонами исходного четырёхугольника. Поэтому
Примечание.
Заданный четырёхугольник можно рассматривать как два прямоугольных треугольника с катетами 1 и 2, которые, приложив их гипотенузы друг к другу, можно сложить в прямоугольник со сторонами 1 и 2, площадь которого равна 2.
Каталог заданий
Версия для печати и копирования в MS Word
1
Задания Д4 № 245004
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Аналоги к заданию № 245004: 261419 261421 261423 261425 261427 261429 261431 261433 261435 261437 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 5.5.5 Площадь треугольника, параллелограмма, трапеции, круга, сектора
Решение
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь

4 вариант с ответами и решением из нового сборника Ященко И.В ЕГЭ 2023 профильный уровень математика 11 класс 36 тренировочных вариантов с полным видео разбором варианта, данный вариант вы можете скачать или решать онлайн.
Скачать 4 вариант Ященко
4 вариант Ященко ЕГЭ 2023 профиль с ответами
4вариант-егэ2023-ященко-профиль
Полное видео решение заданий варианта
Задания и ответы с варианта
1.Площадь ромба равна 9. Одна из его диагоналей в 8 раз больше другой. Найдите меньшую диагональ.
Ответ: 1,5
2.Длина окружности основания конуса равна 6, образующая равна 4. Найдите площадь боковой поверхности конуса.
Ответ: 12
3.Из районного центра в деревню ежедневно ходит автобус. Вероятность того, что в понедельник в автобусе окажется меньше 18 пассажиров, равна 0,9. Вероятность того, что окажется меньше 9 пассажиров, равна 0,66. Найдите вероятность того, что число пассажиров будет от 9 до 17 включительно.
Ответ: 0,24
4.Перед началом волейбольного матча капитаны команд тянут честный жребий, чтобы определить, какая из команд начнёт игру с мячом. Команда «Стартер» по очереди играет с командами «Ротор», «Мотор» и «Монтёр». Найдите вероятность того, что «Стартер» будет начинать только вторую игру.
Ответ: 0,125
9.Заказ на изготовление 216 деталей первый рабочий выполняет на 6 часов быстрее, чем второй. Сколько деталей за час изготавливает первый рабочий, если известно, что он за час изготавливает на 6 деталей больше второго?
Ответ: 18
15.В июле Борис планирует взять кредит в банке на некоторую сумму. Банк предложил Борису два варианта кредитования.
- 1-й вариант; — кредит предоставляется на 3 года; — в январе каждого года действия кредита долг увеличивается на 10 % от суммы долга на конец предыдущего года; — в период с февраля по июнь каждого года действия кредита выплачиваются равные суммы, причём последний платёж должен погасить долг по кредиту полностью.
- 2-й вариант: — кредит предоставляется на 2 года; — в январе каждого года действия кредита долг увеличивается на 16 % от суммы долга на конец предыдущего года; — в период с февраля по июнь каждого года действия кредита выплачиваются равные суммы, причём последний платёж должен погасить долг по кредиту полностью. Когда Борис подсчитал, то выяснил, что по 1-му варианту кредитования ему придётся выплачивать на 353 740 рублей меньше, чем по 2-му варианту. Какую сумму Борис планирует взять в кредит?
Ответ: 8937 тыс. рублей
16.Четырёхугольник АВСР со сторонами ВС =14 и AB=CD=40 вписан в окружность радиусом В=25. а) Докажите, что прямые ВС и AD параллельны. 6) Найдите AD.
Ответ: 42,16
18.Все члены конечной последовательности являются натуральными числами. Каждый член этой последовательности, начиная со второго, либо в 8 раз больше, либо в 8 раз меньше предыдущего. Сумма всех членов последовательности равна 4040.
- а) Может ли последовательность состоять из трёх членов?
- б) Может ли последовательность состоять из четырёх членов?
- в) Какое наибольшее количество членов может быть в последовательности?
Ответ: а-да, б-нет, в-897
- Вариант 1 Ященко ЕГЭ 2023 математика профиль с ответами
- Вариант 2 Ященко ЕГЭ 2023 математика профиль с ответами
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
Задание 1
Площадь ромба равна 9. Одна из его диагоналей в 8 раз больше другой. Найдите меньшую диагональ.
Ответ: 1,5
Скрыть
Задание 2
Длина окружности основания конуса равна 6, образующая равна 4. Найдите площадь боковой поверхности конуса.
Ответ: 12
Скрыть
Задание 3
Из районного центра в деревню ежедневно ходит автобус. Вероятность того, что в понедельник в автобусе окажется меньше 18 пассажира, равна 0,9. Вероятность того, что окажется меньше 9 пассажиров, равна 0,66. Найдите вероятность того, что число пассажиров будет от 9 до 17 включительно.
Ответ: 0,24
Скрыть
Задание 4
Перед началом волейбольного матча капитаны команд тянут честный жребий, чтобы определить, какая из команд начнёт игру с мячом. Команда «Стартер» по очереди играет с командами «Ротор», «Мотор» и «Монтёр». Найдите вероятность того, что «Стартер» будет начинать только вторую игру.
Ответ: 0,125
Скрыть
Задание 5
Решите уравнение $$cos frac{pi(8x+8)}{3}=frac{1}{2}$$. В ответе запишите наибольший отрицательный корень.
Ответ: 0,375
Скрыть
Задание 6
Найдите значение выражения $$frac{125^{3,2}}{25^{3,3}}$$
Ответ: 125
Скрыть
Задание 7
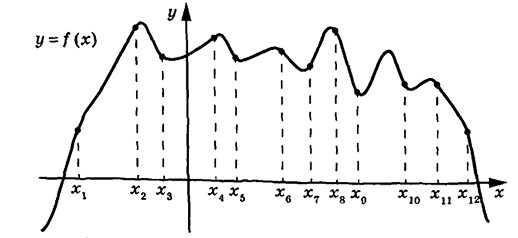
На рисунке изображён график функции $$y=f(x)$$. На оси абсцисс отмечено двенадцать точек: $$x_1$$, $$x_2$$, $$x_3$$, $$x_4$$, $$x_5$$, $$x_6$$, $$x_7$$, $$x_8$$, $$x_9$$, $$x_{10}$$, $$x_{11}$$, $$x_{12}$$. В ответе укажите количество точек (из отмеченных), в которых производная функции $$f(x)$$ отрицательна.
Ответ: 8
Скрыть
Задание 8
Наблюдатель находится на высоте $$h$$, выраженной в метрах. Расстояние от наблюдателя до наблюдаемой им линии горизонта, выраженное в километрах, вычисляется по формуле $$l=sqrt{frac{Rh}{500}}$$, где $$R=6400$$ км — радиус Земли. На какой высоте находится наблюдатель, если он видит линию горизонта на расстоянии 60 километров? Ответ дайте в метрах.
Ответ: 281,25
Скрыть
Задание 9
Заказ на изготовление 216 деталей первый рабочий выполняет на 6 часов быстрее, чем второй. Сколько деталей за час изготавливает первый рабочий, если известно, что он за час изготавливает на 6 деталей больше?
Ответ: 18
Скрыть
Задание 10
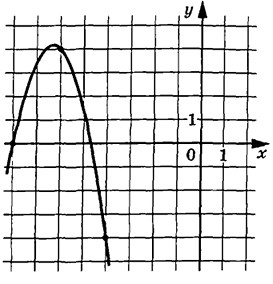
На рисунке изображён график функции $$f(x)=ax^2+bx+c$$. Найдите ординату точки пересечения графика функции $$y=f(x)$$ с осью ординат.
Ответ: -56
Скрыть
Задание 11
Найдите точку минимума функции $$y=10x-ln (x+11)+3$$.
Ответ: -10,9
Скрыть
Задание 12
а) Решите уравнение $$5^{x+sqrt{x}-1}+6cdot 5^{x-sqrt{x}+1}-5^{x+1}=0$$
б) Найдите все корни этого уравнения, принадлежащие отрезку $$[1;2,56]$$
Ответ: а)$$log^{2}_{5}10;log^{2}_{5}15$$ б)$$log^{2}_{5}10$$
Скрыть
Задание 13
В прямой пятиугольной призме $$ABCDEA_1B_1C_1D_1E_1$$ высота равна $$2sqrt{3}$$ , треугольник $$BCD$$ — правильный, со стороной 6, а четырёхугольник $$ABDE$$ — равнобедренная трапеция со сторонами $$AB=DE=2$$, $$BD=6$$ и $$AE=4$$.
а) Докажите, что плоскости $$CA_1E_1$$ и $$AED_1$$ перпендикулярны.
б) Найдите объём многогранника $$CAED_1B_1$$.
Ответ: 40
Скрыть
Задание 14
Решите неравенство $$log_{tg 0,9}(log_{frac{1}{4}}(x^2-2))leq 0$$
Ответ: $$(-sqrt{3};-1,5];[1,5;sqrt{3})$$
Скрыть
Задание 15
В июле Борис планирует взять кредит в банке на некоторую сумму. Банк предложил Борису два варианта кредитования.
1-й вариант:
— кредит предоставляется на 3 года;
— в январе каждого года действия кредита долг увеличивается на 10 % от суммы долга на конец предыдущего года;
— в период с февраля по июнь каждого года действия кредита выплачиваются равные суммы, причём последний платёж должен погасить долг по кредиту полностью,
2-й вариант:
— кредит предоставляется на 2 года; — в январе каждого года действия кредита долг увеличивается на 16 %;
— в период с февраля по июнь каждого года действия кредита выплачиваются равные суммы, причём последний платёж должен погасить долг по кредиту полностью.
Когда Борис подсчитал, то выяснил, что по 1-му варианту кредитования ему придётся выплачивать на 353 740 рублей меньше, чем по 2-му варианту. Какую сумму Борис планирует взять в кредит?
Ответ: 8937 тыс. руб.
Скрыть
Задание 16
Четырёхугольник $$ABCD$$ со сторонами $$BC=14$$ и $$AB=CD=40$$ вписан в окружность радиусом $$R=25$$.
а) Докажите, что прямые $$BC$$ и $$AD$$ параллельны.
б) Найдите $$AD$$.
Ответ: 42,16
Скрыть
Задание 17
Найдите все значения $$а$$, при каждом из которых уравнение $$frac{log_{0,2}(6x^2+13ax+7x+8a^2+2a-2)}{sqrt{4-3a-2x}}=0$$ имеет единственный корень.
Ответ: $$(-infty;-7];[2;+infty);-frac{11}{8}$$
Скрыть
Задание 18
Все члены конечной последовательности являются натуральными числами. Каждый член этой последовательности, начиная со второго, либо в 8 раз больше, либо в 7 раз меньше предыдущего. Сумма всех членов последовательности равна 4040.
а) Может ли последовательность состоять из трёх членов?
б) Может ли последовательность состоять из пяти членов?
в) Какое наибольшее количество членов может быть в последовательности?
Ответ: а)да б)нет в)897
Скрыть
ЕГЭ по математике — Профиль 2023. Открытый банк заданий с ответами.
Решение и ответы заданий варианта МА2210309 СтатГрад 28 февраля ЕГЭ 2023 по математике (профильный уровень). Тренировочная работа №3. ГДЗ профиль для 11 класса.
+Задания №1, №4, №6, №10 из варианта МА2210311.


Задание 1.
В треугольнике ABC угол C равен 90°, CH – высота, BC = 5, cosA=frac{2sqrt{6}}{5}. Найдите длину отрезка AH.
Задание 1 из варианта 2210311.
Найдите периметр прямоугольника, если его площадь равна 12, а отношение соседних сторон равно 1:3.
Задание 2.
Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 2. Объём параллелепипеда равен 3,2. Найдите высоту цилиндра.
Задание 3.
В группе 16 человек, среди них – Анна и Татьяна. Группу случайным образом делят на 4 одинаковые по численности подгруппы. Найдите вероятность того, что Анна и Татьяна окажутся в одной подгруппе.
Задание 4.
Агрофирма закупает куриные яйца только в двух домашних хозяйствах. Известно, что 40 % яиц из первого хозяйства – яйца высшей категории, а из второго хозяйства – 60 % яиц высшей категории. В этой агрофирме 50 % яиц высшей категории. Найдите вероятность того, что яйцо, купленное у этой агрофирмы, окажется из первого хозяйства.
Задание 4 из варианта 2210311.
Игральный кубик бросают дважды. Известно, что в сумме выпало 11 очков. Найдите вероятность того, что во второй раз выпало 5 очков.
Задание 5.
Решите уравнение frac{x–1}{5x+11}=frac{x–1}{3x-7}. Если уравнение имеет больше одного корня, в ответе запишите больший из корней.
Задание 6.
Найдите значение выражения frac{(4^{frac{3}{5} }cdot7^{frac{2}{3}})^{15}}{28^{9}} .
Задание 6 из варианта 2210311.
Найдите 98cos2α, если cosα = frac{4}{7}.
Задание 7.
На рисунке изображён график y = f’(x) – производной функции f(x), определённой на интервале (−5; 5). В какой точке отрезка [−4; −1] функция f(x) принимает наибольшее значение?
Задание 8.
На верфи инженеры проектируют новый аппарат для погружения на небольшие глубины. Конструкция имеет кубическую форму, а значит, действующая на аппарат выталкивающая (архимедова) сила, выражаемая в ньютонах, будет определяться по формуле FA = ρgl3, где l – длина ребра куба в метрах, ρ = 1000 кг/м3 – плотность воды, а g – ускорение свободного падения (считайте, что g = 9,8 Н/кг). Какой может быть максимальная длина ребра куба, чтобы обеспечить его эксплуатацию в условиях, когда выталкивающая сила при погружении будет не больше чем 2116800 Н? Ответ дайте в метрах.
Задание 9.
Пристани A и B расположены на озере, расстояние между ними равно 280 км. Баржа отправилась с постоянной скоростью из A в B. На следующий день после прибытия она отправилась обратно со скоростью на 4 км/ч больше прежней, сделав по пути остановку на 8 часов. В результате она затратила на обратный путь столько же времени, сколько на путь из A в B. Найдите скорость баржи на пути из A в B. Ответ дайте в км/ч.
Задание 10.
На рисунке изображён график функции f(x) = ax2 + bx + c. Найдите значение f(−1).
Задание 10 из варианта 2210311.
На рисунке изображены графики функций f(x) = frac{k}{x} и g(x) = ax + b, которые пересекаются в точках A и B. Найдите абсциссу точки B.
Задание 11.
Найдите точку минимума функции y = x3 − 27x2 + 13.
Задание 12.
а) Решите уравнение 2cos3x = –sin(frac{3pi}{2} + x)
б) Найдите все корни этого уравнения, принадлежащие отрезку [3π; 4π]
Задание 13.
Основанием правильной пирамиды PABCD является квадрат ABCD. Сечение пирамиды проходит через вершину В и середину ребра PD перпендикулярно этому ребру.
а) Докажите, что угол наклона бокового ребра пирамиды к её основанию равен 60°.
б) Найдите площадь сечения пирамиды, если AB = 30.
Задание 14.
Решите неравенство frac{9^{x}–13cdot 3^{x}+30}{3^{x+2}–3^{2x+1}}ge frac{1}{3^{x}}.
Задание 15.
По вкладу «А» банк в конце каждого года планирует увеличивать на 13 % сумму, имеющуюся на вкладе в начале года, а по вкладу «Б» – увеличивать эту сумму на 7 % в первый год и на целое число n процентов за второй год. Найдите наименьшее значение n, при котором за два года хранения вклад «Б» окажется выгоднее вклада «А» при одинаковых суммах первоначальных взносов.
Задание 16.
В треугольнике ABC медианы AA1, BB1 и CC1 пересекаются в точке M. Известно, что AC = 3MB.
а) Докажите, что треугольник ABC прямоугольный.
б) Найдите сумму квадратов медиан AA1 и CC1, если известно, что AC = 22.
Задание 17.
Найдите все значения a, при каждом из которых система уравнений
begin{cases} (x-5a+1)^{2}+(y-2a-1)^{2}=a-2 \ 3x-4y=2a+3 end{cases}
не имеет решений.
Задание 18.
У Ани есть 800 рублей. Ей нужно купить конверты (большие и маленькие). Большой конверт стоит 32 рубля, а маленький – 25 рублей. При этом число маленьких конвертов не должно отличаться от числа больших конвертов больше чем на пять.
а) Может ли Аня купить 24 конверта?
б) Может ли Аня купить 29 конвертов?
в) Какое наибольшее число конвертов может купить Аня?
Источник варианта: СтатГрад/statgrad.org.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 5 / 5. Количество оценок: 3
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
- ОГЭ по математике
Подборка тренировочных вариантов по математике для 9 класса в формате ОГЭ 2023 с ответами и критериями оценивания.
Изменений относительно 2022 года нет, потому актуальны и варианты прошлого года.
Тренировочные варианты ОГЭ 2023 по математике
| alexlarin.net | уровень 1 | уровень 2 |
| вариант 327 | larin22-oge-327-1 | larin22-oge-327 |
| вариант 328 | larin22-oge-328-1 | larin22-oge-328 |
| вариант 329 | larin23-oge-329-1 | larin23-oge-329 |
| вариант 330 | larin23-oge-330-1 | larin23-oge-330 |
| вариант 331 | larin23-oge-331-1 | larin23-oge-331 |
| вариант 332 | larin23-oge-332-1 | larin23-oge-332 |
| вариант 333 | larin23-oge-333-1 | larin23-oge-333 |
| вариант 334 | larin23-oge-334-1 | larin23-oge-334 |
| вариант 335 | larin23-oge-335-1 | larin23-oge-335 |
| вариант 336 | larin23-oge-336-1 | larin23-oge-336 |
| вариант 337 | larin23-oge-337-1 | larin23-oge-337 |
| вариант 338 | larin23-oge-338-1 | larin23-oge-338 |
| вариант 339 | larin23-oge-339-1 | larin23-oge-339 |
| вариант 340 | larin23-oge-340-1 | larin23-oge-340 |
| вариант 341 | larin23-oge-341-1 | larin23-oge-341 |
| вариант 342 | larin23-oge-342-1 | larin23-oge-342 |
| вариант 343 | larin23-oge-343-1 | larin23-oge-343 |
| вариант 344 | larin23-oge-344-1 | larin23-oge-344 |
| вариант 345 | larin23-oge-345-1 | larin23-oge-345 |
| вариант 346 | larin23-oge-346-1 | larin23-oge-346 |
| вариант 347 | larin23-oge-347-1 | larin23-oge-347 |
| вариант 348 | larin23-oge-348-1 | larin23-oge-348 |
| вариант 349 | larin23-oge-349-1 | larin23-oge-349 |
| вариант 350 | larin23-oge-350-1 | larin23-oge-350 |
| вариант 351 | larin23-oge-351-1 | larin23-oge-351 |
| вариант 352 | larin23-oge-352-1 | larin23-oge-352 |
| math100.ru | |
| Вариант 54 | math100-oge-54 |
| Вариант 55 | math100-oge-55 |
| Вариант 56 | math100-oge-56 |
| Вариант 57 | math100-oge-57 |
| Вариант 58 | math100-oge-58 |
| Вариант 59 | math100-oge-59 |
| Вариант 60 | math100-oge-60 |
| Вариант 61 | math100-oge-61 |
| Вариант 62 | math100-oge-62 |
| Вариант 63 | math100-oge-63 |
| Вариант 64 | math100-oge-64 |
| Вариант 65 | math100-oge-65 |
| Вариант 66 | math100-oge-66 |
| Вариант 67 | math100-oge-67 |
| Вариант 68 | math100-oge-68 |
| Вариант 69 | math100-oge-69 |
| Вариант 70 | math100-oge-70 |
| Вариант 71 | math100-oge-71 |
| Вариант 72 | math100-oge-72 |
| Вариант 73 | math100-oge-73 |
| Вариант 74 | math100-oge-74 |
| Вариант 75 | math100-oge-75 |
| Вариант 76 | math100-oge-76 |
| Вариант 77 | math100-oge-77 |
| Вариант 78 | math100-oge-78 |
| Вариант 79 | math100-oge-79 |
| Вариант 80 | math100-oge-80 |
| time4math.ru | |
| Варианты 1-2 | ответы |
| Варианты 3-4 | ответы |
| Варианты 5-6 | ответы |
| Варианты 7-8 | ответы |
| Варианты 9-10 | ответы |
| Варианты 11-12 | ответы |
| Варианты 13-14 | ответы |
| Варианты 15-16 | ответы |
| vk.com/pezhirovschool | |
| Вариант 1 (с решением) | скачать |
| Вариант 2 (с решением) | скачать |
| Вариант 3 (с решением) | скачать |
| Вариант 4 (с решением) | скачать |
| Вариант 5 (с ответами) | скачать |
| Вариант 6 | скачать |
| vk.com/oge100ballov | |
| variant 1 | скачать |
| variant 2 | скачать |
| variant 3 | скачать |
| variant 4 | скачать |
| yagubov.ru | |
| вариант 33 (сентябрь) | скачать |
| вариант 34 (октябрь) | скачать |
| вариант 35 (ноябрь) | скачать |
| вариант 36 (декабрь) | скачать |
| вариант 37 (январь) | скачать |
| вариант 38 (февраль) | скачать |
| вариант 39 (март) | скачать |
| vk.com/math.studying | |
| вариант 1 | ответы |
| вариант 2 | ответы |
| vk.com/matematicalate | |
| variant 1 | скачать |
| variant 2 | скачать |
| variant 3 | скачать |
Характеристика структуры и содержания КИМ ОГЭ 2023 по математике
Работа содержит 25 заданий и состоит из двух частей.
Часть 1 содержит 19 заданий с кратким ответом; часть 2 – 6 заданий с развёрнутым ответом. При проверке базовой математической компетентности экзаменуемые должны продемонстрировать владение основными алгоритмами, знание и понимание ключевых элементов содержания (математических понятий, их свойств, приёмов решения задач и проч.), умение пользоваться математической записью, применять знания к решению математических задач, не сводящихся к прямому применению алгоритма, а также применять математические знания в простейших практических ситуациях.
Задания части 2 направлены на проверку владения материалом на повышенном и высоком уровнях. Их назначение – дифференцировать хорошо успевающих школьников по уровням подготовки, выявить наиболее подготовленных обучающихся, составляющих потенциальный контингент профильных классов.
Эта часть содержит задания повышенного и высокого уровней сложности из различных разделов математики.
Все задания требуют записи решений и ответа. Задания расположены по нарастанию трудности: от относительно простых до сложных, предполагающих свободное владение материалом и высокий уровень математической культуры.
Связанные страницы: