Егэ по математике 27115
ЗАРЕГИСТРИРУЙТЕСЬ и ПОЛУЧИТЕ:
1. Прототипы заданий с ответами — более 1614 задач 1-11 профиль.
2. Решение 75 заданий ЕГЭ по теории вероятноcтей /файл PDF/.
3. ДЕМО-вариант книги «Самые хитрые задачи на ЕГЭ по математике».
4. Доступ к закрытому контенту сайта — всё самое «сладкое» — фишки и лайфхаки.
Чем вам это будет полезно?
Многие задачи научитесь решать всего за одну минуту.
С уважением, Александр Крутицких
Подготовка к ЕГЭ по математике Подробные решения заданий ЕГЭ по математике
ДЕМО-вариант книги Самые хитрые задачи на ЕГЭ по математике.
Matematikalegko. ru
19.10.2018 23:43:39
2018-10-19 23:43:39
Источники:
Https://matematikalegko. ru/ege/zadachi-b11/zadacha-27115-iz-edinogo-banka-zadach-ege-po-matematike
ЕГЭ–2022, математика базовый уровень: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword { color: red; } Егэ по математике 27115
Егэ по математике 27115
Егэ по математике 27115
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
—>
Задания Д13 № 75109
От треугольной пирамиды, объем которой равен 100, отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания. Найдите объем отсеченной треугольной пирамиды.
Объем пирамиды Исходная и отсеченная пирамиды имеют общую высоту, поэтому их объемы относятся как площади их оснований. Площадь основания отсеченной части в 4 раза меньше площади основания исходной пирамиды, так как средняя линия отсекает от треугольника подобный с коэффициентом подобия 0,5. Поэтому объем отсеченной пирамиды в 4 раза меньше объема исходной. Тем самым, он равен 25.
—>
Задания Д13 № 75109
Егэ по математике 27115.
Mathb-ege. sdamgia. ru
14.01.2017 20:12:19
2017-01-14 20:12:19
Источники:
Https://mathb-ege. sdamgia. ru/problem? id=75109
ЕГЭ–2022, математика базовый уровень: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword { color: red; } Егэ по математике 27115
Егэ по математике 27115
Егэ по математике 27115
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
—>
Задания Д13 № 27115
От треугольной пирамиды, объем которой равен 12, отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания. Найдите объем отсеченной треугольной пирамиды.
Объем пирамиды Площадь основания отсеченной части меньше в 4 раза (так как высота и сторона треугольника в основании меньше исходных в 2 раза), поэтому и объем оставшейся части меньше в 4 раза. Тем самым, он равен 3.
—>
Задания Д13 № 27115
Уско рен ная под го тов ка к ЕГЭ с ре пе ти то ра ми Учи.
Mathb-ege. sdamgia. ru
23.10.2017 7:09:32
2017-10-23 07:09:32
Источники:
Https://mathb-ege. sdamgia. ru/problem? id=27115
Тренажер задания 5 профильного ЕГЭ по математике-2022 (с ответами). Здесь приведены прототипы задания 5 — задачи на определение объемов. Это задание на стереометрию. Номер заданий соответствует номеру заданий в базе mathege.ru.
ОБЪЕМ
Параллелепипед
27041. Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 1. Найдите объем параллелепипеда.
27042. Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 4. Объем параллелепипеда равен 16. Найдите высоту цилиндра.
27079. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2 и 6. Объем параллелепипеда равен 48. Найдите третье ребро параллелепипеда, выходящее из той же вершины.
27074. Объем параллелепипеда ABCDA1B1C1D1 равен 9. Найдите объем треугольной пирамиды ABDA1.
77154. Найдите объем параллелепипеда ABCDA1B1C1D1, если объем треугольной пирамиды ABDA1 равен 3.
Куб
27043. Куб описан около сферы радиуса 1. Найдите объём куба.
27105. Объём куба, описанного около сферы, равен 216. Найдите радиус сферы.
324449. Шар, объём которого равен 6π, вписан в куб. Найдите объём куба.
27141. Площадь поверхности куба равна 24. Найдите его объем.
27099. Объем куба равен Найдите его диагональ.
27081. Во сколько раз увеличится объем куба, если все его ребра увеличить в три раза?
27102. Если каждое ребро куба увеличить на 1, то его объем увеличится на 19. Найдите ребро куба.
27075. Из единичного куба вырезана правильная четырехугольная призма со стороной основания 0,5 и боковым ребром 1. Найдите площадь поверхности оставшейся части куба.
324459. Объём треугольной призмы, отсекаемой от куба плоскостью, проходящей через середины двух рёбер, выходящих из одной вершины, и параллельной третьему ребру, выходящему из этой же вершины, равен 2. Найдите объём куба.
Многогранник
27117. Найдите объем пространственного креста, изображенного на рисунке и составленного из единичных кубов.
27214. Объём тетраэдра равен 19. Найдите объём многогранника, вершинами которого являются середины рёбер данного тетраэдра.
Цилиндр
27045. В цилиндрический сосуд налили 2000см3 воды. Уровень жидкости оказался равным 12 см. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 9 см. Чему равен объем детали? Ответ выразите в cм3.
27118. Одна цилиндрическая кружка вдвое выше второй, зато вторая в полтора раза шире. Найдите отношение объема второй кружки к объему первой.
27053. Дано два цилиндра. Объём первого цилиндра равен 12. У второго цилиндра высота в три раза больше, а радиус основания в два раза меньше, чем у первого. Найдите объём второго цилиндра.
27050. В основании прямой призмы лежит квадрат со стороной 2. Боковые ребра призмы равны 2/π. Найдите объём цилиндра, описанного около этой призмы.
Призма
27047. В сосуд, имеющий форму правильной треугольной призмы, налили 2300 см3 воды и полностью в нее погрузили деталь. При этом уровень жидкости в сосуде поднялся с отметки 25 см до отметки 27 см. Чему равен объем детали? Ответ выразите в см3.
27106. Через среднюю линию основания треугольной призмы, объём которой равен 32, проведена плоскость, параллельная боковому ребру. Найдите объём отсеченной треугольной призмы.
27107. Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Найдите объём этой призмы, если объём отсеченной треугольной призмы равен 5.
27082. Основанием прямой треугольной призмы является прямоугольный треугольник с катетами 6 и 8, боковое ребро призмы равно 5. Найдите объём призмы.
27083. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 3 и 5, объём призмы равен 30. Найдите боковое ребро призмы.
27112. От треугольной призмы, объем которой равен 6, отсечена треугольная пирамида плоскостью, проходящей через сторону одного основания и противоположную вершину другого основания. Найдите объем оставшейся части.
Пирамида
27086. Основанием пирамиды является прямоугольник со сторонами 3 и 4. Ее объем равен 16. Найдите высоту этой пирамиды.
27087. Найдите объем правильной треугольной пирамиды, стороны основания которой равны 1, а высота равна
27088. Найдите высоту правильной треугольной пирамиды, стороны основания которой равны 2, а объем равен
27085. Во сколько раз увеличится объем правильного тетраэдра, если все его ребра увеличить в два раза?
27089. Во сколько раз увеличится объем шестиугольной пирамиды, если ее высоту увеличить в четыре раза?
27113. Объем треугольной пирамиды SABC, являющейся частью правильной шестиугольной пирамиды SABCDEF, равен 1. Найдите объем шестиугольной пирамиды.
27114. Объем правильной четырехугольной пирамиды SABCD равен 12. Точка E — середина ребра SB. Найдите объем треугольной пирамиды EABC.
27115. От треугольной пирамиды, объем которой равен 12, отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания. Найдите объем отсеченной треугольной пирамиды.
27182. Объем параллелепипеда ABCDA1B1C1D1 равен 12. Найдите объем треугольной пирамиды B1ABC.
27209. Объем параллелепипеда ABCDA1B1C1D1 равен 4.5. Найдите объем треугольной пирамиды AD1CB1.
27184. Объем куба равен 12. Найдите объем четырехугольной пирамиды, основанием которой является грань куба, а вершиной — центр куба.
27109. В правильной четырехугольной пирамиде высота равна 6, боковое ребро равно 10. Найдите ее объем.
27181. Сторона основания правильной шестиугольной пирамиды равна 4, а угол между боковой гранью и основанием равен 45º. Найдите объем пирамиды.
Конус
27052. Объем конуса равен 16. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.
Шар
27097. Во сколько раз увеличится объем шара, если его радиус увеличить в три раза?
27162. Объем одного шара в 27 раз больше объема второго. Во сколько раз площадь поверхности первого шара больше площади поверхности второго?
Задать свой вопрос
*более 50 000 пользователей получили ответ на «Решим всё»
Задача 27115 Л8. Боковые ребра треугольной пирамиды…
Условие
slava191
05.05.2018
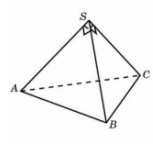
Л8. Боковые ребра треугольной пирамиды взаимно перпендикулярны, каждое из них равно 3. Найдите объем пирамиды.
математика 10-11 класс
2353
Решение
SOVA
05.05.2018
★
Пусть прямоугольный треугольник SBC- основание пирамиды, AS ⊥ пл SBC .
Значит AS — высота пирамиды
H=AS=3
S( Δ SBC) = (1/2) SB*SC=(1/2)*3*3=9/2
V ( пирамиды SABC)=(1/3)*S(осн.)*H=
=(1/3)*S ( Δ SBC)* H=(1/3)*(9/2)*3=9/2=4,5
О т в е т. 4,5
Написать комментарий
Меню
- Решим всё
- Найти задачу
- Категории
- Статьи
- Тесты
- Архив задач





















