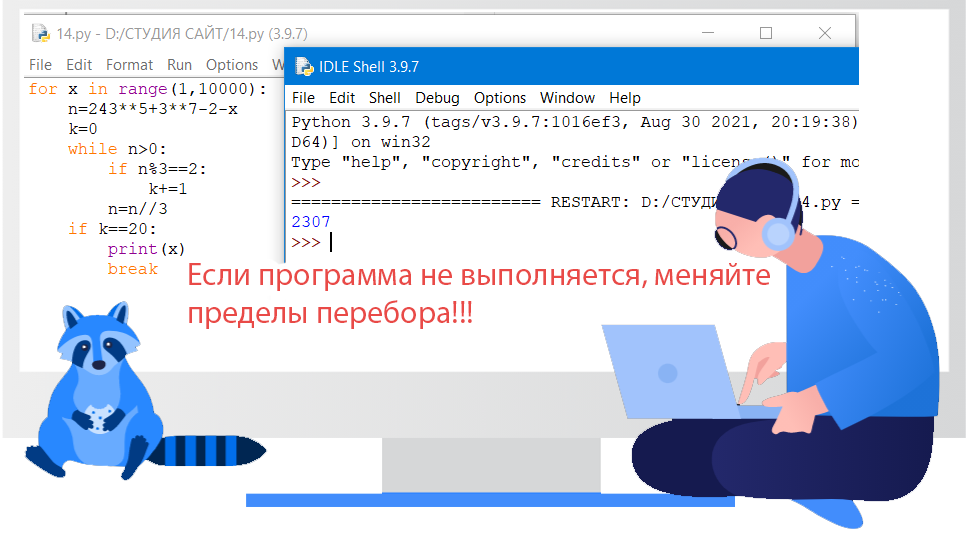
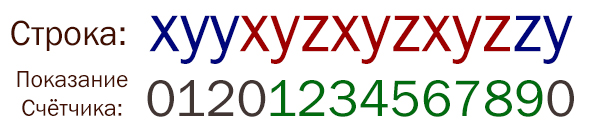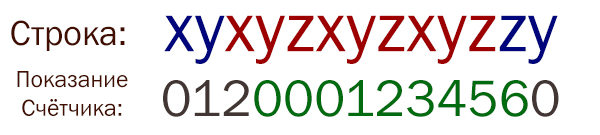37417 егэ информатика - Помощь в подготовке к экзаменам и поступлению

(№ 4127) (А. Богданов) Исполнитель Редактор получает на вход строку цифр и преобразовывает её. Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки символов.

1. заменить (v, w)

2. нашлось (v)

Первая команда заменяет в строке первое слева вхождение цепочки v на цепочку w. Если цепочки v в строке нет, эта команда не изменяет строку. Вторая команда проверяет, встречается ли цепочка v в строке исполнителя Редактор.
Дана программа для исполнителя Редактор:

ПОКА нашлось(43) ИЛИ нашлось(53)

ЕСЛИ нашлось(43)

ТО заменить(43, 33)

ИНАЧЕ заменить(53, 433)

КОНЕЦ ПОКА

Определите максимально возможное количество цифр 3, которое может получиться в результате применения этой программы к строке, состоящей из 17 цифр «3», 23 цифр «4» и 29 цифр «5», идущих в произвольном порядке.

Решение:

Максимально возможное количество цифр 3 может получиться в результате применения программы к строке, состоящей из 17 цифр «3», 23 цифр «4» и 29 цифр «5», идущих в произвольном порядке, только в том случае, когда программа осуществит максимальное число замен:

«43» на «33» и
«53» на «433».

А это возможно только в том случае, когда все цифры будут расположены попарно определенным образом (учтите, что замена происходит только тогда, когда цифра «3» стоит после цифры «4» или после цифры «5»).

Давайте рассмотрим некоторые возможные варианты:

Вариант 1:

Вариант 2 (максимальное количество цифр «3»):

Решение на Pyton:

«Зададим исходную строку рациональным образом»

s = ‘5’ * 12 + ‘4’ * 23 + ’53’ * 17

«Зададим цикл перебора и замены значений в соответствии с условиями задачи»

while (’43’ in s) or (’53’ in s):

if (’43’ in s):

s = s.replace(’43’, ’33’, 1)

print(s)

else:

s = s.replace(’53’, ‘433’, 1)

print(s)

«Посчитаем количество цифр 3»

n = 0

for i in range(0,len(s)):

if s[i] == ‘3’:

n = n + 1

print(«Количество цифр 3 в строке: «, n)

Источник

В решение заданий демо-версии используется язык программирования Python.

Задание 1. Анализ информационных моделей

На рисунке схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведения о протяжённости каждой из этих дорог (в километрах).

Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите, какова сумма протяжённостей дорог из пункта D в пункт В и из пункта F в пункт A. В ответе запишите целое число.

На графе расставим веса вершин.
Мы видим, что вершина В уникальна, имеет вес 2 и связана с двумя «тройками по весу».
Из таблицы видим, В это 4, далее видим, что «тройки по весу» это вершины 2 и 7.
7 вершина связана кроме В, еще с двумя «тройками по весу», значит D это 7, а F это 2.

Далее 2 и 7 вершины ведут нас к 5, значит А это 5, оставшаяся «тройка» это вершина Е под номером 6.
Рассуждая дальше видим, что С это 1, G это 2.

Сумма дорог BD + AF = 53 + 5 = 58

Ответ: 58

Задание 2. Построение таблиц истинности логических выражений

Миша заполнял таблицу истинности логической функции F

F= ¬(y → x) v (z→ w) v ¬z , но успел заполнить лишь фрагмент из трёх различных её строк, даже не указав, какому столбцу таблицы соответствует каждая из переменных w, x, y, z.

Определите, какому столбцу таблицы соответствует каждая из переменных w, x, y, z. В ответе напишите буквы w, x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала буква, соответствующая первому столбцу; затем буква, соответствующая второму столбцу, и т.д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.

Пример. Функция задана выражением ¬x v y, зависящим от двух переменных, а фрагмент таблицы имеет следующий вид. В этом случае первому столбцу соответствует переменная y, а второму столбцу – переменная x. В ответе следует написать yx.

¬(y → x) v (z→ w) v ¬z=0. Следовательно y → x =1, z→ w=0, z=1. Значит третий столбец z. z→ w=0, значит w=0, и это может быть только 4 столбец. y → x =1, следовательно из второй строки мы видим, что первый столбец может быть только у, а второй х.

y	x	z	w
0	0	1	0
0	1	1	0
1	1	1	0

Решение на Python

Ответ: YXZW

Задание выполняется с использованием прилагаемых файлов

Задание 3. Базы данных. Файловая система

В прикрепленном файле приведён фрагмент базы данных «Продукты» о поставках товаров в магазины районов города. База данных состоит из трёх таблиц. Таблица «Движение товаров» содержит записи о поставках товаров в
магазины в течение первой декады июня 2021 г., а также информацию о проданных товарах. Поле Тип операции содержит значение Поступление или Продажа, а в соответствующее поле Количество упаковок, шт. занесена информация о том, сколько упаковок товара поступило в магазин или было продано в течение дня.

На рисунке приведена схема указанной базы данных.

Используя информацию из приведённой базы данных, определите общий вес
(в кг) крахмала картофельного, поступившего в магазины Заречного района
за период с 1 по 8 июня включительно. В ответе запишите только число.

На третьем листе книги применим фильтр по району и получим ID четырех магазинов.

На втором листе применим фильтр по товару и получим ID товара.

На первом листе применим фильтры по ID товара и ID магазинов и типу операции. Все даты попадают в интервал от 1 до 8 июня. Получим:

Поступило в продажу 710 упаковок. В упаковке 0,5 кг. Получим 355 кг.

Ответ: 355

Задание 4. Кодирование и декодирование информации

По каналу связи передаются сообщения, содержащие только буквы из набора: А, З, К, Н, Ч. Для передачи используется двоичный код,удовлетворяющий прямому условию Фано, согласно которому никакое кодовое слово не является началом другого кодового слова. Это условие обеспечивает возможность однозначной расшифровки закодированных сообщений.

Кодовые слова для некоторых букв известны: Н – 1111, З – 110. Для трёх оставшихся букв А, К и Ч кодовые слова неизвестны. Какое количество двоичных знаков потребуется для кодирования слова КАЗАЧКА, если известно, что оно закодировано минимально возможным количеством двоичных знаков?

Ответ: 14

Задание 5. Анализ и построение алгоритмов для исполнителей

На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему
новое число R следующим образом.

1. Строится двоичная запись числа N.
2. Далее эта запись обрабатывается по следующему правилу:
а) если сумма цифр в двоичной записи числа чётная, то к этой записи справа дописывается 0, а затем два левых разряда заменяются на 10;
б) если сумма цифр в двоичной записи числа нечётная, то к этой записи справа дописывается 1, а затем два левых разряда заменяются на 11.

Полученная таким образом запись является двоичной записью искомого числа R.Например, для исходного числа 610 = 1102 результатом является число
10002 = 810, а для исходного числа 410 = 1002 результатом является число 11012 = 1310.
Укажите минимальное число N, после обработки которого с помощью этого алгоритма получается число R, большее 40. В ответе запишите это число в десятичной системе счисления.

Минимальное R, большее 40, это 41.
В результате выполнения алгоритма число R должно либо начинаться на 10 и оканчиваться 0, либо начинаться на 11 и оканчиваться 1.
Из чисел, больших 41, это 42, 44, 46, 49, и т.д.
Мы должны найти минимальное N, из которого данное число получено.
Поскольку первые цифры заменялись, то мы видим, что данные числа могли быть получены из чисел 29, 30, 23, 16.
Из которых 16 минимальное, и меньше уже быть не может.

ИЛИ программное решение

Ответ: 16

Задание 6. Определение результатов работы простейших алгоритмов

Исполнитель Черепаха действует на плоскости с декартовой системой координат.
В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует две команды:
Вперёд n (где n–целое число), вызывающая передвижение Черепахи на n единиц в том направлении, куда указывает её голова, и Направо m (где m – целое число), вызывающая изменение направления движения на m градусов по часовой стрелке.
Запись Повтори k [Команда1 Команда2 … КомандаS] означает, что последовательность из S команд повторится k раз.

Черепахе был дан для исполнения следующий алгоритм:
Повтори 7 [Вперёд 10 Направо 120].
Определите, сколько точек с целочисленными координатами будут находиться внутри области, ограниченной линией, заданной данным алгоритмом. Точки на линии учитывать не следует.

ИЛИ

Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует 5 команд: Поднять хвост, означающая переход к перемещению без рисования; Опустить хвост, означающая переход в режим рисования; Вперёд n (где n– целое число), вызывающая передвижение Черепахи на n единиц в том направлении, куда указывает её голова; Назад n (где n– целое число), вызывающая передвижение в противоположном голове направлении; Направо m (где m – целое число), вызывающая изменение направления движения на m градусов по часовой стрелке, Налево m (где m– целое число), вызывающая изменение направления движения на m градусов против часовой стрелки.

Запись Повтори k [Команда1 Команда2 … КомандаS] означает, что последовательность из S команд повторится k раз.

Черепахе был дан для исполнения следующий алгоритм:
Повтори 2 [Вперёд 10 Направо 90 Вперёд 20 Направо 90]
Поднять хвост
Вперёд 3 Направо 90 Вперёд 5 Налево 90
Опустить хвост
Повтори 2 [Вперёд 70 Направо 90 Вперёд 80 Направо 90]

Определите, сколько точек с целочисленными координатами будут находиться внутри пересечения фигур, ограниченных заданными алгоритмом линиями, включая точки на границах этого пересечения.

Сначала нужно построить фигуру.
Это можно сделать к примеру, на тетрадном листе, при помощи библиотеки Turtle или в Excel.

Далее мы находим уравнения прямых, которыми ограничена фигура и решаем
систему уравнений программно.

ИЛИ
Фигуру можно построить программно или к примеру, в Excel.
Далее анализируем и считаем точки.

Ответ: 1 задание — 38, 2 задание — 128

Задание 7. Кодирование и декодирование информации. Передача информации

Музыкальный фрагмент был записан в формате моно, оцифрован и сохранён в виде файла без использования сжатия данных. Размер полученного файла – 28 Мбайт. Затем тот же музыкальный фрагмент был записан повторно в формате стерео (двухканальная запись) и оцифрован с разрешением в 3,5 раза выше и частотой дискретизации в 2 раза меньше, чем в первый раз. Сжатие данных не производилось. Укажите размер полученного при повторной записи файла в Мбайт. В ответе запишите только целое число, единицу измерения писать не нужно.

I = ν ⋅ i ⋅ t ⋅ k, где ν — частота дискретизации (Гц),

i — разрешение (бит), t — время (с), k — количество дорожек (1 -моно, 2- стерео, 4 — квадро)

I₁ = ν ⋅ i ⋅ t
I₂ = ν/2 ⋅ 3,5 ⋅ i ⋅ t ⋅ 2 = 3,5 ⋅ I₁

I₂ = 3,5 · 28 = 98

Ответ: 98

Задание 8. Перебор слов и системы счисления

Определите количество пятизначных чисел, записанных в восьмеричной системе счисления, в записи которых только одна цифра 6, при этом никакая нечётная цифра не стоит рядом с цифрой 6.

* * * * * — пятизначное число.
В восьмеричной системе счисления в алфавите 8 цифр: 0..7.
Первая цифра 0 быть не может.
Цифра 6 — одна, при этом стоит рядом только с четными цифрами — 0, 2 или 4.
Получим:

6 * * * * — вариантов 3 ⋅ 7 ⋅ 7 ⋅ 7 = 1029
* 6 * * * — вариантов 2 ⋅ 3 ⋅ 7 ⋅ 7 = 294
* * 6 * * — вариантов 6 ⋅ 3 ⋅ 3 ⋅ 7 = 378
* * * 6 * — вариантов 6 ⋅ 7 ⋅ 3 ⋅ 3 = 378
* * * * 6 — вариантов 6 ⋅ 7 ⋅ 7 ⋅ 3 = 882

Ответ: 2961

Задание выполняется с использованием прилагаемых файлов

Задание 9. Работа с таблицами

Файл с данными

Откройте файл электронной таблицы, содержащей в каждой строке шесть натуральных чисел. Определите количество строк таблицы, содержащих числа, для которых выполнены оба условия:
– в строке только одно число повторяется дважды;
– среднее арифметическое неповторяющихся чисел строки не больше суммы повторяющихся чисел.
В ответе запишите только число.

Для решения этой задачи понадобится 10 вспомогательных столбцов. Сначала мы посчитаем количество повторяющихся чисел в каждой строке.

Затем сумму каждой строки диапазона H:M. Если повторений нет, то эта сумма равна 6.

Далее мы найдем среднее арифметическое неповторяющихся значений.

Затем найдем сумму повторяющихся значений.

Затем проверим соблюдение двух условий. И подсчитаем количество строк, в которых соблюдаются оба условия.

Ответ: 2241

Задание выполняется с использованием прилагаемых файлов

Задание 10. Поиск символов в текстовом редакторе

Файл с данными

Текст произведения Льва Николаевича Толстого «Севастопольские рассказы» представлен в виде файлов различных форматов. Откройте один из файлов и определите, сколько раз встречается в тексте отдельное слово «теперь» со строчной буквы. Другие формы этого слова учитывать не следует.
В ответе запишите только число.

В текстовом редакторе используем инструмент найти (по умолчанию он не учитывает регистр, в расширенном поиске есть кнопка больше, где можно проверить настройки). Ищем слово целиком. Ставим галочку учитывать регистр. Слово теперь со строчной буквы встречается 45 раз.

Ответ: 45

Задание 11. Вычисление количества информации

При регистрации в компьютерной системе каждому объекту присваивается идентификатор, состоящий из 250 символов и содержащий только десятичные цифры и символы из 1650-символьного специального алфавита. В базе данных для хранения каждого идентификатора отведено одинаковое и минимально возможное целое число байт. При этом используется посимвольное кодирование идентификаторов, все символы кодируются одинаковым и минимально возможным количеством бит. Определите объём памяти (в Кбайт), необходимый для хранения 65 536 идентификаторов. В ответе запишите только целое число – количество Кбайт.

I = K · i, N = 2 ⁱ

ID : ****….**** – всего 250 различных символов в наборе

N = 10 + 1650 = 1660, 1024<1660<2048, 2048 = 2¹¹, значит для кодирования одного символа нужно 11 бит.

I_ID = 250 · 11 = 2750 бит = 343,75 байт ≈ 344 байт – отводится на идентификатор целое число байт

I₆₅₅₃₆ = 65536 ⋅ 344 = 22544384 байта = 22016 Кбайт– всего

Ответ: 22016

Задание 12. Выполнение алгоритмов для исполнителей

Исполнитель Редактор получает на вход строку цифр и преобразовывает её. Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки цифр.

А) заменить (v, w). Эта команда заменяет в строке первое слева вхождение цепочки v на цепочку w.
Например, выполнение команды заменить (111, 27) преобразует строку 05111150 в строку 0527150.
Если в строке нет вхождений цепочки v, то выполнение команды заменить (v, w) не меняет эту строку.

Б) нашлось (v). Эта команда проверяет, встречается ли цепочка v в строке исполнителя Редактор. Если она встречается, то команда возвращает логическое значение «истина», в противном случае возвращает значение «ложь». Строка исполнителя при этом не изменяется.

Цикл
    ПОКА условие
        последовательность команд
    КОНЕЦ ПОКА

выполняется, пока условие истинно.

В конструкции

    ЕСЛИ условие
        ТО команда 1
    КОНЕЦ ЕСЛИ

выполняется команда 1 (если условие истинно).

В конструкции

    ЕСЛИ условие
        ТО команда 1
        ИНАЧЕ команда 2
    КОНЕЦ ЕСЛИ

выполняется команда 1 (если условие истинно) или команда 2 (если условие ложно).

Дана программа для Редактора:
НАЧАЛО
ПОКА нашлось (>1) ИЛИ нашлось (>2) ИЛИ нашлось (>0)
ЕСЛИ нашлось (>1)
ТО заменить (>1, 22>)
КОНЕЦ ЕСЛИ
ЕСЛИ нашлось (>2)
ТО заменить (>2, 2>)
КОНЕЦ ЕСЛИ
ЕСЛИ нашлось (>0)
ТО заменить (>0, 1>)
КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
КОНЕЦ
На вход приведённой выше программе поступает строка, начинающаяся с символа «>», а затем содержащая 39 цифр «0», n цифр «1» и 39 цифр «2», расположенных в произвольном порядке. Определите наименьшее значение n, при котором сумма числовых значений цифр строки, получившейся в результате выполнения программы, является простым числом.

def pr(n): #функция определяет простое ли число
for i in range(2,int(n**0.5)+1):
if (n%i) == 0:
return False
return True

for n in range(100): #перебираем n
s=’>’ + 39*’0′ + n*’1′ + 39*’2′
while ‘>1’ in s or ‘>2’ in s or ‘>0’ in s:
if ‘>1’ in s:
s=s.replace(‘>1′,’22>’,1)

if ‘>2’ in s:
s=s.replace(‘>2′,’2>’,1)

if ‘>0’ in s:
s=s.replace(‘>0′,’1>’,1)

sum_s = 0
for i in s[:-1]: #считаем сумму цифр в строке
sum_s += int(i)
if pr(sum_s): #проверяем на простоту
print(n)
break

Ответ: 5

Задание 13. Поиск путей в графе

На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К, Л. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой.
Определите количество различных путей ненулевой длины, которые начинаются и заканчиваются в городе Е, не содержат этот город в качестве промежуточного пункта и проходят через промежуточные города не более одного раза.

Начнем подсчет из вершины Е налево через В и возвращаемся в Е через Л.

Ответ: 21

Задание 14. Кодирование чисел. Системы счисления

Операнды арифметического выражения записаны в системе счисления с основанием 15.
123x515 + 1x23315
В записи чисел переменной x обозначена неизвестная цифра из алфавита 15-ричной системы счисления. Определите наименьшее значение x, при котором значение данного арифметического выражения кратно 14. Для найденного значения x вычислите частное от деления значения арифметического выражения на 14 и укажите его в ответе в десятичной системе счисления. Основание системы счисления в ответе указывать не нужно.

for x in range(15):
s1=’123’+ str(x) +’5′
s2=’1’+ str(x) +’233′
n= int(s1,15)+ int(s2,15)

if n%14 == 0:
print(n//14)
break

Ответ: 8767

Задание 15. Преобразование логических выражений

На числовой прямой даны два отрезка: D = [17; 58] и C = [29; 80]. Укажите наименьшую возможную длину такого отрезка A, для которого логическое выражение
(x ∈ D) → ((¬(x ∈ C) & ¬(x ∈ A)) → ¬(x ∈ D)) истинно (т.е. принимает значение 1) при любом значении переменной х.

def deli(n,m):
if n%m == 0:
return True

for A in range(1,1000):
Ok = True
for x in range(1,10000):
Ok*=( (not(deli(x,2)) or (not(deli(x,3)))) or ((x+A)>=100) )

if Ok:
print(A)
break

Ответ: 94

Задание 16. Рекурсивные алгоритмы

Алгоритм вычисления значения функции F(n), где n – натуральное число,
задан следующими соотношениями:
F(n) = 1 при n = 1;
F(n) = n × F(n — 1), если n > 1.
Чему равно значение выражения F(2023) / F(2020)?

F(2023) = 2023! = 2023 ⋅ 2022!

F(2023)/F(2020) = (2023 ⋅ 2022 ⋅ 2021 ⋅ 2020!)/2020! = 2023 ⋅ 2022 ⋅ 2021 =

= 8266912626

Ответ: 8266912626

Задание выполняется с использованием прилагаемых файлов

Задание 17. Проверка на делимость

Файл с данными

В файле содержится последовательность целых чисел. Элементы последовательности могут принимать целые значения от –10 000 до 10 000 включительно. Определите количество пар последовательности, в которых
только одно число оканчивается на 3, а сумма квадратов элементов пары не меньше квадрата максимального элемента последовательности, оканчивающегося на 3. В ответе запишите два числа: сначала количество найденных пар, затем максимальную из сумм квадратов элементов таких пар. В данной задаче под парой подразумевается два идущих подряд элемента последовательности.

f= open(’17.txt’)
p=[int(i) for i in f]
f.close()

k = 0
PP = 0
M3 = 0

for i in p:
if (abs(i))%10 == 3:
M3 = max(i, M3)

for i in range(1,len(p)): #Осторожно, скобки!
if ( ((abs(p[i-1])%10 == 3) + ((abs(p[i])% 10 == 3)) ==1 ) and ((p[i-1]**2 + p[i]**2) >= M3**2) ):
k+=1
PP = max(PP, p[i-1]**2 + p[i]**2)

print(k,PP)

Ответ: 180 190360573

Задание выполняется с использованием прилагаемых файлов

Задание 18. Робот-сборщик монет

Файл с данными

Квадрат разлинован на N×N клеток (1 < N < 17). Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: вправо или вниз. По команде вправо Робот перемещается в соседнюю правую клетку, по команде вниз — в соседнюю нижнюю. При попытке выхода за границу квадрата Робот разрушается. Перед каждым запуском Робота в каждой клетке квадрата лежит монета достоинством от 1 до 100. Посетив клетку, Робот забирает монету с собой; это также относится к начальной и конечной клетке маршрута Робота.

Откройте файл. Определите максимальную и минимальную денежную сумму, которую может собрать Робот, пройдя из левой верхней клетки в правую нижнюю. В ответ запишите два числа друг за другом без разделительных знаков — сначала максимальную сумму, затем минимальную.

Исходные данные представляют собой электронную таблицу размером N×N, каждая ячейка которой соответствует клетке квадрата.Пример входных данных:

1	8	8	4
10	1	1	3
1	3	12	2
2	3	5	6

Для указанных входных данных ответом должна быть пара чисел 41 и 22.

Сначала скопируем таблицу рядом, начиная со столбца АА, можно уменьшить ширину столбца до 4-5. Ячейка АА1=А1. Ячейка АВ1 = АА1+В1, протягиваем ее до АТ1. Ячейка АА2 = АА1 + А2, протягиваем ее до АА20. Далее ячейка АВ2 = В2+МАКС(АА2;АВ1), протягиваем ее на весь оставшийся диапазон, копируем только значения, не трогая стен.

Справа от стен формулы повторяют крайний левый рял, столбец АА, снизу от стен формулы копируют верхнюю строку 1.

Далее делаем замену всех формул МАКС на МИН.

Ответ: 1099 1026

Задание 19. Выигрышная стратегия. Задание 1

Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один камень или увеличить количество камней в куче в два раза. Для того чтобы делать ходы, у каждого игрока есть неограниченное количество камней.

Игра завершается в тот момент, когда количество камней в куче становится не менее 129. Победителем считается игрок, сделавший последний ход, т.е. первым получивший кучу из 129 или больше камней.

В начальный момент в куче было S камней, 1 ≤ S ≤ 128. Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Укажите такое значение S, при котором Петя не может выиграть за один ход, но при любом ходе Пети Ваня может выиграть своим первым ходом.

При значениях S < 64 у Пети есть возможность сделать такой ход, что Ваня не сможет выиграть своим первым ходом. При значении S = 64 Петя своим первым ходом может получить 65 или 128 камней в куче. Во всех случаях Ваня увеличивает количество камней в куче в два раза и выигрывает своим первым ходом.

Ответ: 64

Задание 20. Выигрышная стратегия. Задание 2

Для игры, описанной в задании 19, найдите два таких значения S, при которых у Пети есть выигрышная стратегия, причем одновременно выполняются два условия:

Петя не может выиграть за один ход;
Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.

Найденные значения запишите в порядке возрастания.

Значение S должно быть меньше 64, поскольку иначе Ваня сможет выиграть своим первым ходом.

Ответ: 32 63

Задание 21. Выигрышная стратегия. Задание 3

Для игры, описанной в задании 19, найдите значение S, при котором одновременно выполняются два условия:

у Вани есть выигрышная стратегия, позволяющая ему выиграть
первым или вторым ходом при любой игре Пети;
у Вани нет стратегии, которая позволит ему гарантированно выиграть
первым ходом.

Если найдено несколько значений S, в ответе запишите минимальное из них.

Ответ: 62

Задание 22. Многопроцессорные системы

В файле содержится информация о совокупности N вычислительных процессов, которые могут выполняться параллельно или последовательно. Будем говорить, что процесс B зависит от процесса A, если для выполнения процесса B необходимы результаты выполнения процесса A. В этом случае процессы могут выполняться только последовательно.
Информация о процессах представлена в файле в виде таблицы. В первой строке таблицы указан идентификатор процесса (ID), во второй строке таблицы – время его выполнения в миллисекундах, в третьей строке перечислены с разделителем «;» ID процессов, от которых зависит данный процесс. Если процесс является независимым, то в таблице указано значение 0.
Типовой пример организации данных в файле:

Определите минимальное время, через которое завершится выполнение всей совокупности процессов, при условии, что все независимые друг от друга процессы могут выполняться параллельно.
Типовой пример имеет иллюстративный характер. Для выполнения задания используйте данные из прилагаемого файла.

В независимых процессах время считается от 0,
в зависимых прибавляется к времени процесса, от которого зависит.

Ответ: 17

Задание 23. Анализ программы с циклами и условными операторами

Исполнитель преобразует число на экране.
У исполнителя есть две команды, которые обозначены латинскими буквами:
A. Прибавить 1
B. Умножить на 2
Программа для исполнителя – это последовательность команд. Сколько существует программ, для которых при исходном числе 1 результатом является число 35, при этом траектория вычислений содержит число 10 и не содержит 17?
Траектория вычислений программы – это последовательность результатов
выполнения всех команд программы. Например, для программы ABA при
исходном числе 7 траектория будет состоять из чисел 8, 16, 17.

def f(x, y):
if x == y:
return 1
if x > y or x == 17:
return 0
else:
return f(x + 1, y) + f (2 * x, y)

print (f(1,10) * f(10, 35))

Ответ: 98

Задание выполняется с использованием прилагаемых файлов

Задание 24. Анализ программы с циклами и условными операторами

Файл с данными

Текстовый файл состоит из символов A, C, D, F и O. Определите максимальное количество идущих подряд пар символов вида согласная + гласная
в прилагаемом файле. Для выполнения этого задания следует написать программу.

f=open(’24.txt’)
p= f.readline()
f.close()

PP = [‘CA’, ‘CO’, ‘DA’, ‘DO’, ‘FA’, ‘FO’]
M=k=0

for i in range(1, len(p), 2):
x = p[i-1] + p[i]
if x in PP:
k += 1
else:
k = 0
M=max(M,k)
print(M)

Ответ: 95

Задание 25. Анализ программы с циклами и условными операторами

Назовём маской числа последовательность цифр, в которой также могут
встречаться следующие символы:
– символ «?» означает ровно одну произвольную цифру;
– символ «*» означает любую последовательность цифр произвольной длины;
в том числе «*» может задавать и пустую последовательность.

Например, маске 123*4?5 соответствуют числа 123405 и 12300405.

Среди натуральных чисел, не превышающих 10¹⁰, найдите все числа, соответствующие маске 1?2139*4, делящиеся на 2023 без остатка.
В ответе запишите в первом столбце таблицы все найденные числа в порядке возрастания, а во втором столбце – соответствующие им результаты деления этих чисел на 2023. Количество строк в таблице для ответа избыточно.

Самый простой способ использовать библиотеку fnmatch.
Функция fnmatch() проверяет, соответствует ли строка шаблонной строке, возвращая True или False

или так полным перебором:

y = {»,’0′,’00’,’000′}
for x in y:
for j in range(10):
s = ‘1’ + str(j) + ‘2139’ + x + ‘4’
if int(s) % 2023 == 0:
print (s, int(s)//2023)

for x in range (1000):
for j in range(10):
s = ‘1’ + str(j) + ‘2139’ + str(x) + ‘4’
if int(s) % 2023 == 0:
print (s, int(s)//2023

Ответ: 162139404 80148
1321399324 653188
1421396214 702618
1521393104 752048

Задание выполняется с использованием прилагаемых файлов

Задание 26. Анализ программы с циклами и условными операторами

В магазине для упаковки подарков есть N кубических коробок. Самой интересной считается упаковка подарка по принципу матрёшки – подарок упаковывается в одну из коробок, та в свою очередь в другую коробку и т.д.
Одну коробку можно поместить в другую, если длина её стороны хотя бы на 3 единицы меньше длины стороны другой коробки. Определите наибольшее количество коробок, которое можно использовать для упаковки одного подарка, и максимально возможную длину стороны самой маленькой коробки, где будет находиться подарок. Размер подарка позволяет поместить его в самую маленькую коробку.
Входные данные
В первой строке входного файла находится число N – количество коробок в магазине (натуральное число, не превышающее 10 000). В следующих N строках находятся значения длин сторон коробок (все числа натуральные, не превышающие 10 000), каждое – в отдельной строке.
Запишите в ответе два целых числа: сначала наибольшее количество коробок, которое можно использовать для упаковки одного подарка, затем максимально возможную длину стороны самой маленькой коробки в таком наборе.
Типовой пример организации данных во входном файле
5
43
40
32
40
30
Пример входного файла приведён для пяти коробок и случая, когда минимальная допустимая разница между длинами сторон коробок, подходящих для упаковки «матрёшкой», составляет 3 единицы. При таких исходных данных условию задачи удовлетворяют наборы коробок с длинами сторон 30, 40 и 43 или 32, 40 и 43 соответственно, т.е. количество коробок равно 3, а длина стороны самой маленькой коробки равна 32.
Типовой пример имеет иллюстративный характер. Для выполнения задания используйте данные из прилагаемых файлов.

Задание выполняется с использованием прилагаемых файлов

Задание 27. Анализ программы с циклами и условными операторами

У медицинской компании есть N пунктов приёма биоматериалов на анализ. Все пункты расположены вдоль автомагистрали и имеют номера, соответствующие расстоянию от нулевой отметки до конкретного пункта. Известно количество пробирок, которое ежедневно принимают в каждом из пунктов. Пробирки перевозят в специальных транспортировочных контейнерах вместимостью не более 36 штук. Каждый транспортировочный контейнер упаковывается в пункте приёма и вскрывается только в лаборатории.
Стоимость перевозки биоматериалов равна произведению расстояния от пункта до лаборатории на количество контейнеров с пробирками. Общая стоимость перевозки за день равна сумме стоимостей перевозок из каждого пункта в лабораторию. Лабораторию расположили в одном из пунктов приёма биоматериалов таким образом, что общая стоимость доставки биоматериалов из всех пунктов минимальна.
Определите минимальную общую стоимость доставки биоматериалов из всех пунктов приёма в лабораторию.
Входные данные

Файл А
Файл В

Дано два входных файла (файл A и файл B), каждый из которых в первой строке содержит число N (1 ≤ N ≤ 10 000 000) – количество пунктов приёма биоматериалов. В каждой из следующих N строк находится два числа: номер пункта и количество пробирок в этом пункте (все числа натуральные, количество пробирок в каждом пункте не превышает 1000). Пункты перечислены в порядке их расположения вдоль дороги, начиная от нулевой отметки.
В ответе укажите два числа: сначала значение искомой величины для файла А, затем – для файла B.
Типовой пример организации данных во входном файле
6
1 100
2 200
5 4
7 3
8 2
10 190
При таких исходных данных и вместимости транспортировочного контейнера, составляющей 96 пробирок, компании выгодно открыть лабораторию в пункте 2. В этом случае сумма транспортных затрат составит: 1 ∙ 2 + 3 ∙ 1 + 5 ∙ 1 + 6 ∙ 1 + 8 ∙ 2.

Типовой пример имеет иллюстративный характер. Для выполнения задания используйте данные из прилагаемых файлов.
Предупреждение: для обработки файла B не следует использовать переборный алгоритм, вычисляющий сумму для всех возможных вариантов, поскольку написанная по такому алгоритму программа будет выполняться слишком долго.

Ответ: 51063 5634689219329

Источник

Сегодня посмотрим одно из самых интересных заданий из ЕГЭ по информатике 2023. Будем решать 24 задание. В этом задании нужно работать с файлами.

Все решения задач из задания 24 ЕГЭ по информатике 2023 будут приведены на языке программирования Python (Питон).

Поехали!

Задача (Самая простая)

Текстовый файл состоит не более чем из 10⁶ символов A, B и C. Определите максимальное количество идущих подряд символов B. Для выполнения этого задания следует написать программу. Ниже приведён файл, который необходимо обработать с помощью данного алгоритма.

Решение:

Решим данную задачу на языке Python.

f=open('24_1.txt')
s=f.read()
k=0
kmax=0

for i in range(0, len(s)):
    if s[i]=='B':
        k=k+1
        kmax=max(k, kmax)
    else:
        k=0

print(kmax)

С помощью команды open() подвязываемся к файлу. Чтобы не прописывать полный путь, файл должен лежать в той же папке, что и программа.

С помощью команды .read() зачитываем в переменную s всё содержимое файла.

Переменная k — это текущий счётчик символов «B». Задача переменной kmax сохранить максимальное значение k.

С помощью цикла for перебираем все символы из строки s. Переменная i пробегается по номерам всех симолов. Счёт символов начинается в строке с нуля. В начале берём нулевой символ, потом первый и т.д. Конструкция for i in range(0, len(s)) позволяет пройтись по всем символам строки до конца.

Если нам встретился нужный символ «B», то мы счётчик прибавляем на 1. Это значит, что мы подсчитываем текущую цепочку. Если будет стоять 3 символа «B» подряд, значит, счёт k покажет значение 3. Как только встретится дургой символ, то это означает, что цепочка прервалась и счётчик переводится в первоначальное положение 0.

При любом увеличении счётчика происходит анализ этого счётчика на максимальность. Функция max выбирает максимальное значение из старого значения kmax и нового показания счётчика k. Если счётчику k удалось победить kmax, то его значение будет считаться максимальным на данный момент времени.

В ответ идёт значение kmax. Это и есть длина максимальной цепочки. В этой задачке ответ получается 11.

Ответ: 11

Закрепим это простое задание из ЕГЭ по информатике 2023.

Задача (Простая, закрепление)

Текстовый файл состоит не более чем из 10⁶ символов X, Y и Z. Определите максимальное количество идущих подряд символов, среди которых нет символа Z. Для выполнения этого задания следует написать программу.

Решение:

Решение похоже на предыдущее.

f=open('24_2.txt')
s=f.read()
k=0
kmax=0

for i in range(0, len(s)):
    if s[i]!='Z':
        k=k+1
        kmax=max(k, kmax)
    else:
        k=0

print(kmax)

Если нет символов «Z», то подсчитываем, иначе сбрасываем.

Задача (Обращаемся к соседу)

Текстовый файл состоит не более чем из 10⁶ символов X, Y и Z. Определите максимальное количество идущих подряд символов, расположенных в алфавитном порядке (возможно с повторением симолов). Для выполнения этого задания следует написать программу.

Решение:

f=open('24_2.txt')
s=f.read()
k=1
kmax=0

for i in range(0, len(s)-1):
    if s[i]<=s[i+1]:
        k=k+1
        kmax=max(k, kmax)
    else:
        k=1

print(kmax)

В ответе получается 15. Символы можно сравнивать между собой с помощью знаков «>» или меньше «<» ( а так же «>=» или «<=»), причём это сравнение происходит в алфавитном порядке. Например, символ «B» будет больше, чем «A» и т.п. Теперь нам нужно уже обратится к соседу, уже важна связь между соседними символами. Раз мы обращаемся к следующему символу, то должны пробегать до len(s)-1, иначе куда мы будем обращаться, когда дойдём до последнего символа?

В самом начале цепочки мы анализируем два символа, а к счётчику прибавляем всего лишь 1. Чтобы это учесть, в начале счётчику (переменной k) присваиваем 1. Затем, по мере продвижения по цепочке, мы добавляем в наш анализ 1 новый символ, и к счётчику добавляется одна 1. Дальше уже таких проблем нет.

Раз мы присвоили в переменную k единицу, то и сбрасывать в ветке else мы тоже должны на 1. Эти значения обычно взаимосвязаны.

Если мы обращаемся к соседнему символу, как правило, счётчик и сброс устанавливаются в 1. Это не стопроцентная истина, но иметь ввиду это нужно.

Ответ: 15

Задача (Обращаемся к соседу, закрепление)

Текстовый файл состоит не более чем из 10⁶ символов арабских цифр (0, 1, …,9). Определите максимальное количество идущих подряд цифр, среди которых каждые две соседние различны. Для выполнения этого задания следует написать программу.

Решение:

f=open('24_3.txt')
s=f.read()
k=1
kmax=0

for i in range(0, len(s)-1):
    if s[i]!=s[i+1]:
        k=k+1
        kmax=max(k, kmax)
    else:
        k=1

print(kmax)

Если соседи различны, мы подсчитываем, иначе сбрасываем.

Ответ: 120

Задача (Обращаемся к соседу, ещё сложнее)

Текстовый файл состоит не более чем из 10⁶ символов арабских цифр (0, 1, …,9). Определите максимальное количество идущих подряд нечётных цифр, расположенных в неубывающем порядке. Для выполнения этого задания следует написать программу.

Решение:

f=open('24_3.txt')
s=f.read()
k=1
kmax=0

for i in range(0, len(s)-1):
    if s[i]<=s[i+1] and s[i] in '13579' and s[i+1] in '13579' :
        k=k+1
        kmax=max(k, kmax)
    else:
        k=1

print(kmax)

Здесь опять можно применить знаки сравнения прям к символам. Удобно проверить принадлежность к нечётным цифрам конструкцией s[i] in ‘13579’. Нечётной цифрой должна быть как текущая, так и следующая.

Ответ: 8

Решим ещё одну тренировочную задачу из ЕГЭ по информатике 2023.

Задача (Обращаемся к соседу, ещё сложнее, закрепление)

Текстовый файл состоит не более чем из 10⁶ символов 1, 2, 3, A, B, С. Определите максимальное количество идущих подряд символов, среди которых никакие две буквы и никакие две цифры не стоят рядом. Для выполнения этого задания следует написать программу.

Решение:

f=open('24_4.txt')
s=f.read()
k=1
kmax=0

for i in range(0, len(s)-1):
    if (s[i] in '123' and s[i+1] in 'ABC') or (s[i] in 'ABC' and s[i+1] in '123') :
        k=k+1
        kmax=max(k, kmax)
    else:
        k=1

print(kmax)

В этой задаче цифры и буквы должны чередоваться. Если у нас цифра, то следующая должны быть буква, или наоборот, если у нас буква, то следующая должна быть цифра. В этих двух случаях прибавляем к счётчику 1.

Ответ: 20

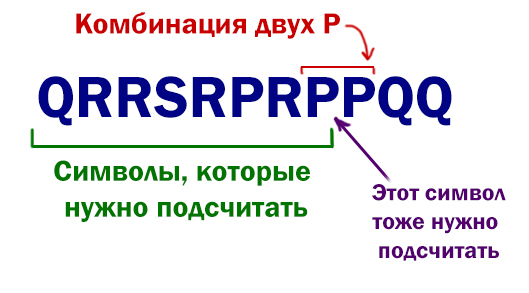
Задача (Исключаем строку из 2-х символов, демо 2022)

Текстовый файл состоит из символов P, Q, R и S.

Определите максимальное количество идущих подряд символов
в прилагаемом файле, среди которых нет идущих подряд символов P.
Для выполнения этого задания следует написать программу.

Решение:

Напишем решение на языке Python.

f=open('24_5.txt')
s=f.read()
k=1
kmax=0

for i in range(0, len(s)-1):
    if s[i]=='P' and s[i+1]=='P':
        k=1
    else:
        k=k+1
        kmax = max(k, kmax)

print(kmax)

Подсчитываем символы, пока не встретилась комбинация двух P подряд. Как только встретилась данная комбинация, сбрасываем счётчик на 1. Здесь мы сбрасываем счётчик на значение 1, чтобы учесть один символ, которые находится в самой комбинации PP. И в начале мы тоже устанавливаем счётчик в значение 1 по этой же причине.

Мы проходим в цикле for до длины строки минус один. Значение 1 в счётчике при сбросе и в начале программы так же компенсирует и тот момент, что мы не подсчитываем последний символ!

При изменении счётчика, сохраняем максимальное значение в переменной mx

Если бы у нас была вместо PP другая комбинация, состоящая к примеру из 5 символов, то мы бы тогда в начале и при сбросе писали в счётчик значение 5-1=4.

Здесь тоже работает негласное правило, обращаемся к соседу, значит, счётчик устанавливаем в 1.

В этой задаче получается ответ 188.

Ответ: 188

Задача (Исключаем подстроку из 3-х символов)

Текстовый файл состоит из символов арабских цифр(0, 1, …,9).

Определите максимальное количество идущих подряд символов
в прилагаемом файле, среди которых нет трёх символов 0, стоящих рядом.
Для выполнения этого задания следует написать программу.

Решение:

Напишем решение на языке Python.

f=open('24_6.txt')
s=f.read()
k=2
kmax=0

for i in range(0, len(s)-2):
    if s[i]=='0' and s[i+1]=='0' and s[i+2]=='0':
        k=2
    else:
        k=k+1
        kmax = max(k, kmax)

print(kmax)

Чтобы понять это решение, нужно посмотреть предыдущую задачу. Мы здесь обращаемся к двум соседям, значит, счётчик устанавливаем в 2. Так же проходим в цикле до len(s)-2. Нежелательная строка может состоять не только из одинаковых символов. Может быть строка «XYYZ», к примеру.

Ответ: 7684

Задача (Не более одного символа Z)

Текстовый файл состоит не более чем из 10⁶ символов X, Y и Z. Определите максимальное количество идущих подряд символов, среди которых символ Z встречается не более одного раза.

Решение:

В нашей цепочке один раз можно встретиь символ Z, а два раза уже нельзя. Здесь мы применим функцию .split(). Как работает эта фнкция? Напишем тестовую программу.

s='sadqttqtreq'
a=s.split('q')
print(a)

Результат данной программы будет следующим:

[‘sad’, ‘tt’, ‘tre’, »]

Команда split «разрезает» строку по символу «q». В результате мы получаем массив с кусочками этой строки.

Решение нашей задачи.

f=open('24_7.txt')
s=f.read()
a=s.split('Z')
k=0
kmax=0

for i in range(0, len(a)-1):
  k = len(a[i]) + 1 + len(a[i+1])
  kmax = max(k, kmax)

print(kmax)

Разрезаем нашу строку по символу «Z». Пробегаемся уже по массиву a. Цепочка-кандидат это текущий кусочек (a[i]), символ Z (1) и следующий кусочек (a[i+1]).

Каждого кандитата проверяем сразу на максимальность.

Ответ: 43

Задача (Не более двух символов Z)

Текстовый файл состоит не более чем из 10⁶ символов X, Y и Z. Определите максимальное количество идущих подряд символов, среди которых символ Z встречается не более двух раз.

Решение:

Решение аналогично предыдущему.

f=open('24_7.txt')
s=f.read()
a=s.split('Z')
k=0
kmax=0

for i in range(0, len(a)-2):
  k = len(a[i]) + 1 + len(a[i+1]) + 1 + len(a[i+2])
  kmax = max(k, kmax)

print(kmax)

Ответ: 50

Задача (Звенья)

Текстовый файл состоит не более чем из 10⁶ символов X, Y и Z. Определите максимальную длину цепочки символов, состоящей из повторяющихся фрагментов XYZ. Цепочка должна начинаться с символа X и заканчиваться символом Z. Например, для строки ZZZXYZXYZXZZZ длина цепочки равна 6: XYZ+XYZ

Решение:

Если мы подсчитаем количество идущих подряд звеньев XYZ, то, можно сказать, дело сделано.

f=open('24_8.txt')
s=f.read()
s=s.replace('XYZ', '1')
k=0
kmax=0

for i in range(0, len(s)):
    if s[i]=='1':
        k=k+1
        kmax=max(k, kmax)
    else:
        k=0

print(kmax*3)

Мы с помощью команды replace заменили звенья на «1» (на символ, которого точно нет в файле). Теперь задача свелась к самой простой, которую мы рассматривали в начале статьи. Нужно просто подсчитать количество идущих поряд единиц.

В ответе нас просили указать количество символов, а не звеньев, поэтому переменную kmax умножаем на 3.

Ответ: 66

Задача (Звенья, закрепление)

Текстовый файл состоит не более, чем из 10⁶ символов из набора A, B, С. Найдите максимальное количество идущих пар символов AC или AB. Искомая подстрока может включать только пары AB, только пары AC или содержать одновременно как пары AC, так и пары AB.

Решение:

f=open('24_9.txt')
s=f.read()
s=s.replace('AB', '1')
s=s.replace('AC', '1')
k=0
kmax=0

for i in range(0, len(s)):
    if s[i]=='1':
        k=k+1
        kmax=max(k, kmax)
    else:
        k=0

print(kmax)

Здесь нам подходит звено, как и AB, так и AC. В ответе нужно указать количество пар, поэтому не на что умножать переменную kmax не нужно.

Ответ: 19

Задача (Звенья, основная волна 20.06.22)

Текстовый файл состоит из символов A, B, C, D и O. Определите максимальное количество идущих подряд пар символов вида согласная + гласная в прилагаемом файле. Для выполенения этого задания следует написать программу.

Решение:

f=open('24_10.txt')
s=f.read()
s=s.replace('BA', '1')
s=s.replace('CA', '1')
s=s.replace('DA', '1')
s=s.replace('BO', '1')
s=s.replace('CO', '1')
s=s.replace('DO', '1')
k=0
kmax=0

for i in range(0, len(s)):
    if s[i]=='1':
        k=k+1
        kmax=max(k, kmax)
    else:
        k=0

print(kmax)

Ответ: 174

Задача (Звенья, последнее звено неполное)

Текстовый файл состоит не более чем из 10⁶ символов X, Y и Z. Определите максимальную длину цепочки вида XYZXYZXYZ… (составленной из фрагментов XYZ, последний фрагмент может быть неполным). Для выполнения этого задания следует написать программу. Ниже приведён файл, который необходимо обработать с помощью данного алгоритма.

Решение:

Т.к. последнее звено может быть неполным, здесь удобно применить другой алгоритм.

Пусть в начале показания счётчика равно нулю. Если мы находим нужный нам символ в нужной последовательности, то прибавляем к счётчику 1. Если последовательность сбивается, то ставим счётчик в ноль.

На рисунке представлен данный алгоритм. В нижней строке указано показание счётчика в момент анализа символа.

На данном рисунке максимальная длина цепочки нужных символов равна 9.

Видим, что для символа X, когда он находится на своём месте, остаток от деления значения счётчика на 3 равен 0.

Для символа Y, когда данный символ находится на своём месте, остаток от деления значения счётчика на 3 равен 1.

Для символа Z, когда данный символ находится на своём месте, остаток от деления значения счётчика на 3 равен 2.

Мы смотрим остаток от деления на 3, потому что у нас длина звена равна трём (XYZ).

Таким образом, мы и наш анализ очередного символа привяжем к показанию счётчика:

f=open('24_11.txt')
s=f.read()
k=0
kmax=0

for i in range(0, len(s)):
    if (s[i]=='X' and k%3==0) or  (s[i]=='Y' and k%3==1) or (s[i]=='Z' and k%3==2):
        k=k+1
        kmax = max(k, kmax)
    else:
        if s[i]=='X': k=1
        else: k=0


print(kmax)

Важный момент: Если нужную цепочку прервал символ X, то нужно счётчик сразу выставить в 1, иначе может произойти такая ошибка:

Т.е. первые три нужных символа в цепочке алгоритм не засчитал.

Поэтому мы не просто сбрасываем счётчик в ноль, а прописываем условие:

if s[i]=='X': k=1
else: k=0

Ответ: 13

Задача (Полезный приём)

Текстовый файл 24-157.txt состоит не более чем из 10⁶ символов и содержит только заглавные буквы латинского алфавита (ABC…Z). Определите символ, который чаще всего встречается в файле между двумя одинаковыми символами. Например, в тексте CCBAABABCBC есть комбинации ABA, BAB, BCB и CBC. Чаще всего – 2 раза – между двумя одинаковыми символами стоит B, в ответе для этого случая надо написать B2 (без пробелов и других разделителей). Если таких символов несколько, выведите тот, который стоит раньше в алфавите.

Решение:

f=open('24-157.txt')
s=f.read()
a=[0]*150

for i in range(0, len(s)-2):
    if s[i]==s[i+2]:
        a[ord(s[i+1])] = a[ord(s[i+1])] + 1

ch=''
mx=0
for i in range(0, 150):
    if a[i]>mx:
        mx=a[i]
        ch=chr(i)


print(ch, mx)

Здесь мы заводим массив a. Индексы этого массива — это коды ANSI всех букв латинского алфавита (ABC…Z). Ведь, как мы знаем, каждая буква кодируется определённым числом (кодом ANSI). Вот часть этой таблицы.

Например, буква A кодируется кодом 65. Коды увеличиваются в алфавитном порядке на 1. Буква Z кодируется числом 90. Таким образом, 150 ячеек точно хватит для нашего алфавита. Здесь берём с запасом, потому что на экзамене можно точно не вспомнить коды, но достаточно запомнить, что 150 ячеек вполне хватит для заглавных и строчных букв латинского алфавита.

Значит, ячейка 65 отвечает за букву A, ячейка 66 отвечает за букву B и т.д. Если мы встретили букву между двумя одинаковыми буквами, то её ячейка увеличивается на 1.

Функция ord() превращает символ в код ANSI.

После того, как мы прошли всю строку и собрали информацию о наших буквах, нужно пройти массив a и найти наибольшее число в нём.

Здесь мы уже не пользуемся функцией max, а используем условие, потому что нужно кроме максимального числа тянуть ещё один параметр — сам код (переменную i). Функция chr() превращает код ANSI обратно в символ.

Ответ: W1608

Задача (Строки различной длины)

Текстовый файл 24-164.txt состоит не более чем из 10⁶ символов и содержит только заглавные буквы латинского алфавита (ABC…Z). Текст разбит на строки различной длины. Необходимо найти строку, содержащую самую длинную цепочку стоящих подряд одинаковых букв. Если таких строк несколько, надо взять ту, которая в файле встретилась раньше. Определите, какая буква встречается в этой строке чаще всего. Если таких букв несколько, надо взять ту, которая стоит раньше в алфавите. Запишите в ответе эту букву, а затем – сколько раз она встречается во всем файле.

Пример. Исходный файл:

ZZQABA
ZALAAC
QRAQUT

В этом примере в первой и второй строках наибольшая длина цепочек одинаковых буквы равна 2 (ZZ в первой строке, AA во второй), в третьей – 1. Берём первую строку, т.к. она находится в файле раньше. В этой строке чаще других встречаются буквы Z и A (по 2 раза), выбираем букву A, т. к. она стоит раньше в алфавите. В ответе для этого примера надо записать A6, так как во всех строках файла буква A встречается 6 раз.

Решение:

Для считывания построчно файла, будем использовать конструкцию, как в задании 17. В начале найдём строчку, содержащую самую длинную цепочку стоящих подряд одинаковых букв.

f=open('24-164.txt')
kmax=0
count=0
n=-1
for s in f.readlines():
    count=count+1
    k=1
    for i in range(0, len(s)-1):
       if s[i]==s[i+1]:
           k=k+1
           if k>kmax:
               kmax=k
               n=count
       else:
           k=1

print(n)

Получается строка под номером 162. Переменная count считает строки по порядку. В переменную n сохраняем номер нужной строки. Опять пользуемся условием, а не функцией max, т.к. здесь нужно и обновлять kmax, и сохранять значение n. У нас условие строгое k>kmax, значит, сохранится первая строка с наибольшей искомой цепочкой.

f=open('24-164.txt')

count=0
a=[0]*150

for s in f.readlines():
    count=count+1
    k=1
    if count==162:
        for i in range(0, len(s)):
            a[ord(s[i])] = a[ord(s[i])] + 1
       
ch=''
mx=0
for i in range(0, 150):
    if a[i] > mx:
        mx=a[i]
        ch=chr(i)

print(ch)

Теперь нас интересует только строка под номером 162. Далее используем приём из прошлой задачи. Заводим массив a из 150 ячеек и используем таблицу кодов ANSI. Так определяем какая буква встретилась чаще всего в строке под номером 162. Получается буква K.

f=open('24-164.txt')
s=f.read()
print(s.count('K'))

Осталось найти количестов букв K во всём файле. Для этого используем функцию .count()

Ответ: K36582

В задаче 15 «Задача (Полезный приём)», созданы переменные k и kmax — напрасно, они не используются.

Убрал, по привычке написал.

Источник

14-е задание: «Операции в системах счисления»

Уровень сложности

— повышенный,

Требуется использование специализированного программного обеспечения

— нет,

Максимальный балл

— 1,

Примерное время выполнения

— 5 минут.

Проверяемые элементы содержания: Знание позиционных систем счисления

До ЕГЭ 2021 года — это было задание № 16 ЕГЭ

Плейлист видеоразборов задания на YouTube:
Задание демонстрационного варианта 2022 года ФИПИ

Содержание:

Определите наибольшее/наименьшее значение x, y
Сколько цифр и сумма цифр
Найти основание системы счисления и уравнения

Определите наибольшее/наименьшее значение x, y

14_14:

Операнды арифметического выражения записаны в системе счисления с основанием 15.

82x19₁₅ – 6x073₁₅

В записи чисел переменной x обозначена неизвестная цифра из алфавита 15-ричной системы счисления. Определите наименьшее значение x, при котором значение данного арифметического выражения кратно 11. Для найденного значения x вычислите частное от деления значения арифметического выражения на 11 и укажите его в ответе в десятичной системе счисления. Основание системы счисления в ответе указывать не нужно.

Ответ: 7806

Показать решение:

✎ Решение с использованием программирования:

PascalABC.net:

uses school;
begin
  foreach var x in '0123456789abcde' do
  begin
    var a := dec('82'+ x +'19', 15);
    var b :=dec('6' + x +'073', 15);
    var sum := a - b;
    if sum mod 11 = 0 then
    begin
      print(sum / 11);
      break;
    end
  end;
end.

Python:

С++:

Сколько цифр и сумма цифр

14_12:

Значение арифметического выражения

43∙7¹⁰³ – 21∙7⁵⁷ + 98

записали в системе счисления с основанием 7.
Найдите сумму цифр получившегося числа и запишите её в ответе в десятичной системе счисления.

Ответ: 276

Показать решение:

✎ Решение с использованием программирования:

PascalABC.net, Решение 1:

begin
  var x,s: Biginteger;
  x := 43*Biginteger.Pow(7, 103) - 21*Biginteger.Pow(7, 57) + 98;
  // в получившемся числе рассматриваем каждую цифру в 7-й системе сч.
  s:=0;
  while x > 0 do
  begin
    s:=s+ x mod 7; // добавляем цифру правого разряда
    x := x div 7; // убираем разряд числа в 7-й системе сч.
  end;
  println(s);
end.

PascalABC.net, Решение 2:

uses school;
 
begin
  var n: bigInteger;
  n := 43 * Biginteger.Pow(7, 103) - 21 * Biginteger.Pow(7, 57) + 98;
  print(n.ToString.ToBase(7).CountOf('1') +
    n.ToString.ToBase(7).CountOf('2') * 2 + 
    n.ToString.ToBase(7).CountOf('3') * 3 +
    n.ToString.ToBase(7).CountOf('4') * 4 +
    n.ToString.ToBase(7).CountOf('5') * 5 +
    n.ToString.ToBase(7).CountOf('6') * 6);
end.

Python:

x = 43*7**103 - 21*7**57 + 98
s = 0
# в получившемся числе рассматриваем каждую цифру в 7-й системе сч.
while x: 
    s+= x % 7 # добавляем цифру к сумматору
    x //= 7 # убираем разряд числа в 7-й системе сч.
print( s )

С++:

14_1:

Значение арифметического выражения:
2¹⁰²⁴ + 4⁶⁴ — 64
записали в системе счисления с основанием 2.

Ответ: 123

✍ Показать решение:

✎ Решение с использованием программирования:

PascalABC.net, Решение 1:

begin
  var k := 0;
  var x: Biginteger;
  x := Biginteger.Pow(2, 1024) + Biginteger.Pow(4, 64) - 64;
  // в получившемся числе рассматриваем каждую цифру в 2-й системе сч.
  while x > 0 do
  begin
    if x mod 2 = 1 then k += 1; // если цифра = 1, то считаем ее
    x := x div 2; // убираем разряд числа в 2-й системе сч.
  end;
  println(k);
end.

PascalABC.net, Решение 2:

uses school;
 
begin
  var x: bigInteger;
  x := Biginteger.Pow(2, 1024) + Biginteger.Pow(4, 64) - 64;
  print(x.ToString.ToBase(2).CountOf('1'));
end.

Python:

x = 2**1024 + 4**64 - 64
k = 0
# в получившемся числе рассматриваем каждую цифру в 2-й системе сч.
while x: 
    if x % 2 == 1: # если цифра = 1, то считаем ее
        k += 1
    x //= 2 # убираем разряд числа в 2-й системе сч.
print( k )

С++:

✎ Решение теоретическое:

Существует правило:

2^N = 10..0₂(1 единица и N нулей)

Чтобы воспользоваться этим правилом, преобразуем общее выражение к степеням двойки:

2¹⁰²⁴ + (2²)⁶⁴ - 2⁶ = 2¹⁰²⁴ + 2¹²⁸ - 2⁶

При переводе в двоичную систему получим:

10...0 (1024 нуля) + 10...0 (128 нулей) - 10...0 (6 нулей)

Обратим внимание, что разница между числами большая. Т.е. при выполнении сложения в столбик, единицы в одном и том же разряде быть не могут. Так:

 10....00000  - 1024 нуля
+
       10..0  - 128 нулей
_________________________
 10....10..0

Из первого слагаемого 10…0 (1024 нуля) запомним одну единицу в старшем бите, остальные нули нас не интересуют, так как далее мы воспользуемся другим правилом — для разницы:

 10....00000  - 1024 нуля
+
       10..0  - 128 нулей
_________________________
 10....10..0  - запомним единицу

Существует также правило:

2^N — 2^K = 1…1 (N - K единиц)0…0(K нулей)

По формуле выполним вычитание 2¹²⁸ — 2⁶: получим 1..1 (122 единицы) 0..0(6 нулей):

 10..0000000  - 128 нулей
-
     1000000  
_________________________
 11..1000000  - 122 единицы и 6 нулей

Прибавим к 122 получившимся единицам еще одну из первого слагаемого (10…0 (1024 нуля)) и получим:

122 + 1 = 123 единицы

📹 Видео (аналитическое решение)
📹 Видеорешение на RuTube здесь

14 задание. Демоверсия ЕГЭ 2018 информатика:

Значение арифметического выражения:
49¹⁰ + 7³⁰ – 49
записали в системе счисления с основанием 7.

Сколько цифр «6» содержится в этой записи?

Типовые задания для тренировки

Ответ: 18

✍ Показать решение:

✎ Решение с использованием программирования:

PascalABC.net, решение 1:

begin
  var x: Biginteger;
  x := Biginteger.Pow(49, 10) + Biginteger.Pow(7, 30) - 49;
  // в получившемся числе рассматриваем каждую цифру в 7-й системе сч.
  var k:=0;
  while x > 0 do
  begin
    if x mod 7 = 6 then k+=1; // если цифра = 6, то считаем ее
    x := x div 7; // убираем разряд числа в 7-й системе сч.
  end;
  println(k);
end.

PascalABC.net, решение 2:

uses school;
 
begin
  var x: bigInteger;
  x := Biginteger.Pow(49, 10) + Biginteger.Pow(7, 30) - 49;
  print(x.ToString.ToBase(7).CountOf('6'));
end.

Python:

x = 49**10 + 7**30 - 49
k = 0
# в получившемся числе рассматриваем каждую цифру в 7-й системе сч.
while x: 
    if x % 7 == 6: # если цифра = 6, то считаем ее
        k += 1
    x //= 7 # убираем разряд числа в 7-й системе сч.
print( k )

С++:

✎ Решение теоретическое:

Приведем все числа к степеням 7:

7²⁰ + 7³⁰ - 7²

Расставим операнды выражения в порядке убывания степеней:

7³⁰ + 7²⁰ - 7²

Вспомним две формулы для работы со системами счисления:

1.
aⁿ = 10..0_a
       ⁿ
2.
aⁿ - a^m = (a-1)..(a-1)0..0_a
              ^n-m       ^m

Переведем первое число согласно формуле 1:

7³⁰ = 10..0
        ³⁰

В данном числе нет цифры 6, как и в остальных числах.
Цифра 6 появляется при выполнении вычитания.
Подсчитаем все «6», используя формулу 2:

0 + (20 - 2) = 18

Получаем шестерок: 18

Результат: 18

📹 Видео (аналитическое решение)
📹 Видеорешение на RuTube здесь

14_2:

Значение арифметического выражения:
4⁵⁰⁰ + 3*4²⁵⁰⁰ + 16⁵⁰⁰ — 1024
записали в системе счисления с основанием 4.

Сколько цифр «3» содержится в этой записи?

Типовые задания для тренировки

Ответ: 496

✍ Показать решение:

✎ Решение с использованием программирования:

PascalABC.net:

uses school;
 
begin
  var x: bigInteger;
  x := Biginteger.Pow(4,500) + 3*Biginteger.Pow(4,2500) + Biginteger.Pow(16,500) - 1024;
  print(x.ToString.ToBase(4).CountOf('3'));
end.

Python:

x = 4**500 + 3*4**2500 + 16**500 - 1024
k = 0
# в получившемся числе рассматриваем каждую цифру в 4-й системе сч.
while x: 
    if x % 4 == 3: # если цифра = 3, то считаем ее
        k += 1
    x //= 4 # убираем разряд числа в 4-й системе сч.
print( k )

С++:

Результат: 496

📹 Видео (аналитическое решение)
📹 Видеорешение на RuTube здесь

14_5:

Значение арифметического выражения: 8¹⁰²⁴ + 8³² – 65 – записали в системе счисления с основанием 8. Сколько цифр «7» содержится в этой записи?

Типовые задания для тренировки

Ответ: 31

✍ Показать решение:

✎ Решение с использованием программирования:

PascalABC.net:

uses school;
 
begin
  var x: bigInteger;
  x := Biginteger.Pow(8,1024) + Biginteger.Pow(8,32) - 65;
  print(x.ToString.ToBase(8).CountOf('7'));
end.

Python:

x = 8**1024 + 8**32 - 65
k = 0
# в получившемся числе рассматриваем каждую цифру в 8-й системе сч.
while x: 
    if x % 8 == 7: # если цифра = 7, то считаем ее
        k += 1
    x //= 8 # убираем разряд числа в 8-й системе сч.
print( k )

С++:

✎ Решение теоретическое:

Приведем все числа к степеням восьмерки:

65 = 64 + 1 = 8² + 8⁰;

Получаем:

8¹⁰²⁴ + 8³² - (8² + 8⁰);
8¹⁰²⁴ + 8³² - 8² - 8⁰

Вспомним две формулы для работы с системами счисления:

1.
aⁿ = 10..0_a
       ⁿ
2.
aⁿ - a^m = (a-1)..(a-1)0..0_a
              ^n-m       ^m

Переведем первое число согласно формуле 1:

8¹⁰²⁴ = 10..0
        ¹⁰²⁴

В данном числе нет цифры 7, как и в остальных числах.
Цифра 7 появляется при выполнении вычитания. У нас два таких действия, идущих подряд. Это неудобно. Необходимо, чтобы действия чередовались (a + b — c + d — e…)
Вспомним еще одну формулу:

-2ⁿ = -2ⁿ⁺¹ + 2ⁿ

! Формула предназначена для чисел в двоичной системе счисления, но для подсчета цифр "7" в 8-й (или "6" в 7-й и т.п.) ее можно использовать (для поиска единиц или нулей она не подходит!!!)

В нашем случае заменим часть выражения:

-8² = -8³ + 8²
! обратите внимание, что тождество неверно, но
при поиске количества "7" этой формулой можно воспользоваться
(для поиска единиц или нулей она не подходит!)


Получаем:

8¹⁰²⁴ + 8³² - 8³ + 8²- 8⁰

Получили чередование операций «+» и «-«.
Теперь посчитаем все «7», используя формулу 2:

0 + (32 - 3) + (2 - 0) = 31

Получаем семерок: 31

14_13:

Сколько значащих нулей в двоичной записи числа 4³⁵⁰ + 8³⁴⁰ – 2³²⁰ – 12?

Ответ: 324

Показать решение:

✎ Решение с использованием программирования:

PascalABC.net:

begin
  var b2 := biginteger(2);
  var numb := (2 * b2) ** 350 + (4 * b2) ** 340 - (1 * b2) ** 320 - 12;
  var digit: biginteger;
  var n := 0;
  while numb > 0 do
  begin
    digit := numb mod 2;
    if digit = 0 then n += 1;
    numb := numb div 2
  end;
  print(n)
 end.

PascalABC.net, решение 2:

uses school;
 
begin
  var x: bigInteger;
  x := Biginteger.Pow(4,350) + Biginteger.Pow(8,340) - Biginteger.Pow(2,320) - 12;
  print(x.ToString.ToBase(2).CountOf('0'));
end.

Python:

x = 4**350 + 8**340 - 2**320 - 12
print(x)
k = 0
while x:
  if x % 2 == 0: k += 1
  x //= 2
     print( k )

С++:

✎ Решение теоретическое:
4³⁵⁰ + 8³⁴⁰ – 2³²⁰ – 12

По возможности приведем каждое слагаемое к степеням 2. Получим:

(2²)³⁵⁰ + (2³)³⁴⁰ - 2³²⁰ - 3*2² =
(2²)³⁵⁰ + (2³)³⁴⁰ - 2³²⁰ - 12 =
2⁷⁰⁰ + 2¹⁰²⁰ - 2³²⁰ - (2³ + 2²)

Далее рассуждаем так: количество нулей можно найти, если из общего количества цифр в результирующем числе вычесть количество не нулей (любых других цифр).

Расположим операнды по убыванию:

2¹⁰²⁰ + 2⁷⁰⁰ - 2³²⁰ - 2³ - 2²

Наибольшее число 2¹⁰²⁰, в нем 1021 разряд в двоичной с.с. (одна единица и 1020 нулей). То есть всего 1021 знаков.

Для того, чтобы избежать два подряд идущих минуса, воспользуемся правилом -2ⁿ = -2ⁿ⁺¹+2ⁿ и преобразуем выражение:

2¹⁰²⁰ + 2⁷⁰⁰ - 2³²¹+ 2³²⁰- 2⁴ + 2³ - 2²

Посчитаем количество не нулей в каждом операнде:

2¹⁰²⁰ -> один не ноль
2⁷⁰⁰ - 2³²¹ -> 379 не нулей
2³²⁰- 2⁴ -> 316 не нулей 
2³ - 2² -> один не ноль
Итого: 1+ 379+316 +1 = 697

Получаем нулей:

1021 - 697 = 324

Результат: 324

Найти основание системы счисления и уравнения

14_7:

Укажите, сколько всего раз встречается цифра 2 в записи чисел 13, 14, 15, …, 23 в системе счисления с основанием 3.

Типовые задания для тренировки

Ответ: 13

Показать решение:

Для начала достаточно перевести первое и последнее число предложенного интервала в троичную систему счисления. Сделаем это:

1.
 13 | 3 
 12   4 | 3 
  1   3   1   
      1
131₀ = 111₃

2.
23 | 3 
21   7 | 3 
2    6   2
     1
23₁₀ = 212₃

Теперь добавим промежуточные числа в троичной системе счисления (прибавляя единицу к каждому очередному полученному числу), не забывая, что в троичной системе всего три цифры (0, 1 и 2):

111, 112, 120, 121, 122, 200, 201, 202, 210, 211, 212

На всякий случай стоит посчитать количество полученных чисел и сравнить их с количеством чисел в исходной последовательности.
Теперь осталось посчитать количество цифр 2 в полученной последовательности. Их 13:

111, 112, 120, 121, 122, 200, 201, 202, 210, 211, 212

Ответ: 9

Показать решение:

Разделим уравнение на три части и вычислим каждую часть отдельно (выделим части разным цветом):

204_N+1 = 204_N + 26₁₆
 1       2     3

Используем формулу разложения числа по степеням основания:

1. 
₂₁₀
204_N+1

По формуле получаем:
2*(N+1)² + 0*(N+1)¹ + 4*(N+1)⁰ =
= 2*(N² + 2N + 1) + 0 + 4 = 2N² + 4N + 6

Выполним то же самое для остальных двух частей:

2.
₂₁₀
204_N

По формуле получаем:
2*N² + 0*N¹ + 4*N⁰ =
= 2N2 + 4

3.
26₁₆ = 38₁₀

Подставим результаты всех частей в уравнение:

2N² + 4N + 6 = 2N² + 4 + 38;
4N = 36;
N = 9

Ответ: 7

Показать решение:

Вместо обозначения искомой системы счисления введем неизвестное x:

144_x + 24_x = 201_x

Запишем формулу перевода в десятичную систему счисления каждого из слагаемых и сумму исходного равенства:

144 + 24 = 201
1*x² + 4*x¹ + 4*x⁰ + 2*x¹ + 4*x⁰ = 2*x² + 0*x¹ + 1*x⁰

Упростим полученное уравнение:

x² - 6x - 7 = 0

Решим уравнение:

D = b² - 4ac = 36 - 4*1*(-7) = 64
x = (-b ± √D)/2a
x1 = (6 + 8)/2 = 7
x2 = (6 - 8)/2 - не подходит
x = 7

14_9:

В некоторой системе счисления записи десятичных чисел 68 и 94 заканчиваются на 3. Определите основание системы счисления.

Типовые задания для тренировки

Ответ: 13

Показать решение:

Вспомним правило:

Последняя цифра записи числа в системе счисления с основанием X — это остаток от деления этого числа на X

Примем искомую систему счисления за x. Тогда, исходя из приведенного правила имеем:

94 / x = некоторое число и остаток 3
и
68 / x = некоторое число и остаток 3

Поскольку x должно быть целым числом, то следующее деление должно выполняться без остатка:

91/x 
65/x

Иными словами x — наибольший общий делитель чисел 91 и 65.
Найдем НОД, например, по алгоритму Евклида:

91 - 65 = 26
65 - 26 = 39
39 - 26 = 13
26 - 13 = 13

Получаем результат 13.

14_10:

Некоторое число X из десятичной системы счисления перевели в системы счисления с основаниями 16, 8. Часть символов при записи утеряна. Позиции утерянных символов обозначены *:

X = *5₁₆ = *0*₈

Сколько чисел соответствуют условию задачи?

Типовые задания для тренировки

Ответ: 3

Показать решение:

Данные числа с утерянными символами переведем из 16-й и из 8-й системы счисления в двоичную. Перевод будем делать триадами и тетрадами, неизвестные позиции оставим пустыми:

1. *5₁₆
    *   |    5  ₁₆

* * * * | 0 1 0 1 ₂

2. *0*₈
  *  |  0  |  *  ₈
* * *|0 0 0|* * * ₂

Сопоставим известные и неизвестные биты в обеих получившихся масках:

* * 0 0 0 1 0 1

Неизвестными остались 7-й и 8-й бит. Они не могут быть одновременно нулями, так как для *0*₈ тогда исчезнет старший разряд. Поэтому оставшиеся варианты будут такими:

1. 01000101
2. 10000101
3. 11000101

Итого 3 варианта.

📹 Видео (аналитическое решение
📹 Видеорешение на RuTube здесь)

14_4:

Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 75 оканчивается на 13.

Типовые задания для тренировки

Ответ: 8,72

✍ Показать решение:

Так как 75 должно оканчиваться на 13, то имеем два общих случая:

1. 75₁₀ = 13_N 
2. 75₁₀ = ...13_N (число оканчивается на 13)

Рассмотрим подробно каждый случай.

1 случай:

Остаток должен быть равен 3 (последнее число в неизвестной системе), а частное должно равняться 1 (предпоследнее число в неизвестной системе):

 75|N 
  N|1  отсюда имеем => 75 - N = 3; т.е. N = 72
  3

Таким образом, мы получили одно из искомых оснований (72).

2 случай:

Искомое оканчивается на цифру 3, значит:

 75|N 
 72|y  отсюда имеем => 75 = Ny + 3, где N - целое, неотриц.
  3

и далее, частное от деления — 1 (предпоследнее число):

 75|N  
 72|  y |N   => y = Nz + 1, где z - целое, неотриц.
  3  y-1|z
       1

Получаем два равенства (систему уравнений):

75 = Ny + 3
y = Nz + 1

Подставим y из второго равенства в первое:

75 = N (Nz + 1) + 3;
75 = N²z + N + 3;
75 = N²z + N

Выразим z:

z = (72 - N)/N²

Учитывая то, что z — целое неотрицательное число, то 72 — N должно быть кратно N², т.е. в числителе не может быть простого числа.
Простое число 67 получается путем вычитания из 72 числа 5. Соответственно, 5 нам не подходит: N ≠ 5:

72 - 5 / 5² = 67 / 25  не делится, - не подходит!

Еще одно простое число — 71 получится при вычитании 72 — 1. Единица не подходит, так как при переводе в конце числа никак не останется 13: N ≠ 1.
Раз в знаменателе N², то отбросим все числа, квадрат которых больше 72: 9, 10, … и т.д. до бесконечности: N < 9
Раз в итоговом числе есть число 13, значит основание системы счисления больше 3 (т.е. цифра три присутствует в системах, начиная с 4-й): N >= 4
Проверим оставшиеся варианты — 4, 6, 7, 8:

 75 | 4 
 72 | 18| 4 
  3   16| 2
       2  => не подходит! должна быть единица

 75 | 6 
 72 | 12| 6 
  3   12| 1
       0  => не подходит! должна быть единица

 75 | 7 
 70 
  5 => не подходит! должна быть 3

 75 | 8 
 72 | 9| 8 
  3   8| 1
       1  => подходит!

📹 Видео (аналитический способ)
📹 Видеорешение на RuTube здесь

14_11:

Выражение 2⁵*3²⁵ записано в троичной системе счисления. Определите, сколько в этой записи цифр 0, 1 и 2.

Ответ: «0»=26, «1»=2, «2»=1

Показать решение:

Первый сомножитель:

2⁵ = 32

Переведем в троичную систему счисления (делением на 3, переписываем остатки).
Результат:
32₁₀= 1012₃

Для рассмотрения второго сомножителя будем использовать правило:

Получим:

3²⁵ = 10..0{25 нулей}₃

Выполним произведение, но для простоты счета, представим, что нулей не 25, а только 3:

В исходном числе было 3 нуля, стало 4. Значит если было 25 нулей, то станет 25 + 1 = 26.
Единиц = 2, двоек = 1.

📹 Видео (аналитическое решение)
📹 Видеорешение на RuTube здесь

Источник

Рубрика «ЕГЭ»

Е25.22 которые соответствуют маске 1?7246*1 и при этом без остатка делятся на 4173

Маска числа – это последовательность цифр, в которой могут встречаться специальные символы «?» и «*». Символ «?» означает ровно одну произвольную цифру, символ «*» означает произвольную (в том числе пустую) последовательность цифр. Пример. Маске 123*4?5 соответствуют числа 123405 и 12376415. Найдите все натуральные числа, не превышающие 1010, которые соответствуют маске 1?7246*1 и при этом без …

Е24.35 сколько раз буква, образующая самую длинную цепочку в файле, встречается в строке

Текстовый файл содержит строки различной длины, содержащие только заглавные буквы латинского алфавита (ABC…Z). Будем называть цепочкой группу идущих подряд одинаковых букв в одной строке. Определите, сколько раз буква, образующая самую длинную цепочку в файле, встречается в строке, содержащей эту цепочку. Если в файле есть несколько цепочек одинаковой максимальной длины, нужно выбрать ту из них, для …

Е23.33 число 1 в число 11 и при этом содержат ровно одну команду умножения

Исполнитель преобразует число на экране. У исполнителя есть четыре команды, которым присвоены номера: 1. Прибавить 1 2. Прибавить 2 3. Умножить на 2 4. Умножить на 3 Первая команда увеличивает число на экране на 1, вторая увеличивает его на 2, третья – умножает на 2, четвёртая – умножает на 3. Программа для исполнителя – это …

Е17.44 запись элементов пары заканчивается одной и той же цифрой

Файл содержит последовательность целых чисел, по модулю не превышающих 10 000. Назовём парой два идущих подряд элемента последовательности. Определите количество пар, для которых выполняются следующие условия: – запись элементов пары заканчивается одной и той же цифрой; – ровно один элемент из пары делится без остатка на 3; – сумма квадратов элементов пары не превышает квадрат …

для которых можно подобрать такое b, что F(a, b) = 1 048 576

Алгоритм вычисления значения функции F(a, b), где a и b – целые неотрицательные числа, задан следующими соотношениями: F(0, 0) = 0; F(a, b) = F(a–1, b) + b, если a > b; F(a, b) = F(a, b–1) + a, если a ≤ b и b > 0. Укажите количество таких целых неотрицательных чисел a, для …

Е15.43 формула (x&35 ≠ 0 ∨ x&22 ≠ 0) → (x&15 = 0 → x&А ≠ 0) тождественно истинна

Обозначим через m&n поразрядную конъюнкцию неотрицательных целых чисел m и n. Например, 14&5 = 11102&01012 = 01002 = 4. Для какого наименьшего неотрицательного целого числа А формула (x&35 ≠ 0 ∨ x&22 ≠ 0) → (x&15 = 0 → x&А ≠ 0) тождественно истинна (т. е. принимает значение 1 при любом неотрицательном целом значении переменной …

Е14.56 В системе счисления с основанием p выполняется равенство 32×8 + xxx9 = yy02.

В системе счисления с основанием p выполняется равенство 32×8 + xxx9 = yy02. Буквами x и y обозначены некоторые цифры из алфавита системы счисления с основанием p. Определите значение числа yyxp и запишите это значение в десятичной системе счисления. Ответ: СтатГрад Вариант ИН22110301 14.02.2023 – задание №14

Е13.27 Определите количество различных путей ненулевой длины, которые начинаются

На рисунке представлена схема дорог, связывающих пункты А, Б, В, Г, Д, Е, Ж, И , К , Л , М , Н . П о каждой д ороге можно передвигаться только в направлении, указанном стрелкой. Определите количество различных путей ненулевой длины, которые начинаются и заканчиваются в пункте Е, не содержат этот пункт в качестве …

Е11.31 Сколько Кбайт потребуется для хранения 65 536 описаний, построенных по такой схеме

В базе данных хранится информация об объектах определённой структуры. Каждый объект описывается как последовательность из 404 простых элементов, при этом всего используется 2023 различных простых элемента. Каждое описание объекта записывается как последовательность кодов простых элементов, при этом код каждого элемента содержит одинаковое для всех элементов минимально возможное число битов, а для описания в целом отводится …

Е10.13 «Мастер и Маргарита» встречается числительное «двадцать» в любом падеже.

Определите, сколько раз в тексте романа Михаила Булгакова «Мастер и Маргарита» встречается числительное «двадцать» в любом падеже. Слово «двадцать» как часть составных числительных (например, «двадцать один») учитывать не надо. DOCX Ответ: СтатГрад Вариант ИН22110301 14.02.2023 – задание №10

Источник

Разбор варианта ЕГЭ информатика 2022
Кулабухов (Вариант 1)

Задание 7
Задание 8
Задание 9
Задание 10
Задание 11
Задание 12
Задание 13
Задание 14

Задание 1

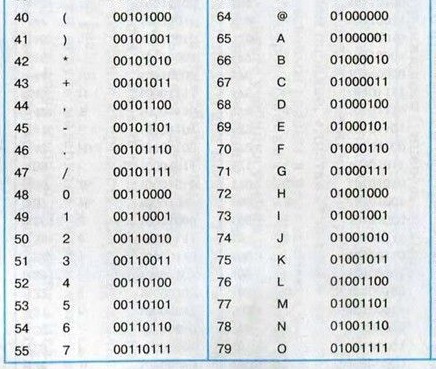
На рисунке схема дорог изображена в виде графа, в таблице звездочками отображено наличие дорог между населеными пунктами. Отсутствие звездочки означает, что такой дороги нет.
Так как таблицу и схему рисовали независимо друг от друга, то нумерация населенных пунктов в таблице никак не связана с буквенными обозначениями на графе.
Выпишите последовательно, без пробелов и знаков препинания указанные на графе буквенные обозначения пунктов от П2 до П5, сначала букву, соответствующую П2, затем букву, соответствующую П3, и т.д.

Решение:

Ответ: ГАДБ

Задание 2

Олег заполнял таблицу истинности функции (¬ х ∨ y)  ∧ (x ≡ ¬z) ∧ w, но успел заполнить лишь фрагмент из трёх различных её строк, даже не указав, какому столбцу таблицы соответствует каждая из переменных w, x, y, z.

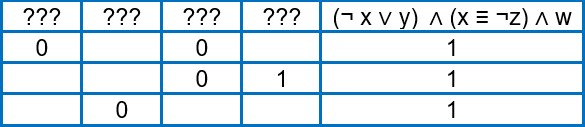
Определите, какому столбцу таблицы соответствует каждая из переменных w, x, y, z.

В ответе напишите буквы w, x, y, z. В том порядке, в котором идут соответствующие им столбцы (сначала буква, соответствующая первому столбцу, затем буква, соответствующая второму столбцу, и т.д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.

Решение:

Составить таблицу истинности для выражения (¬ х ∨ y)  ∧ (x ≡ ¬z) ∧ w нам поможет Python.

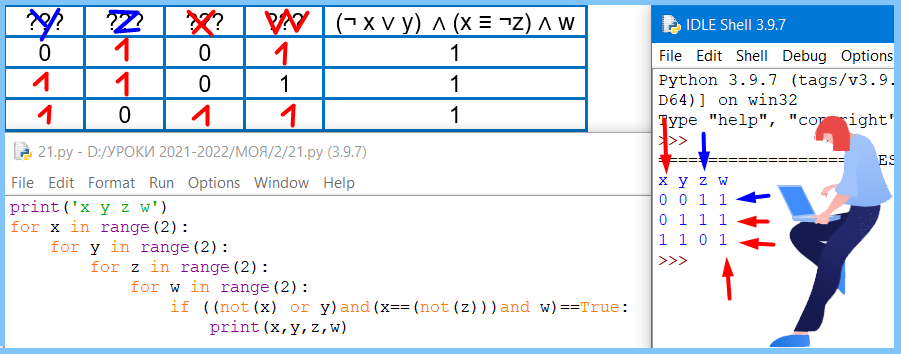
Phyton построил нам таблицу для функции, при которых данное выражение равно 1. Получили следующие наборы (см. рисунок). Сопоставим эти наборы с приведенным в задании фрагментом таблицы истинности.

Можем смело поставить единицы в пустые ячейки таблицы. Три единицы по вертикали имеет переменная w. Два нуля по вертикали только у переменной х. По горизонтали, в строке с двумя единицами, одна для w, вторая для z, а y определился сам. ВСЁ!

Ответ: yzxw

Задание 3

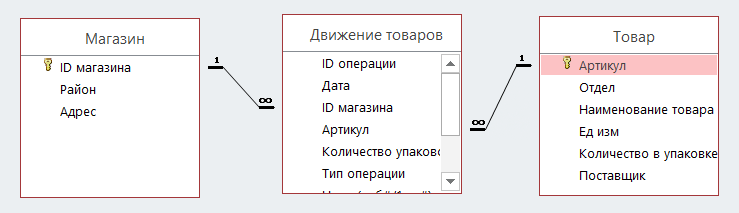
В файле приведен фрагмент базы данных «Стройматериалы» о поставках товаров в магазины некоторой торговой сети в нескольких районах города. База данных состоит из трех таблиц.

Таблица «Движение товаров» содержит записи о поставках товаров в магазины в течение первой декады сентября 2021г., а также информацию о проданных товарах. Поле Тип операции содержит значение Поступление или Продажа, а в соответствующее поле Количество упаковок занесена информация о том, сколько упаковок товара поступило в магазин или было продано в течение дня. Заголовок таблицы имеет следующий вид.

Таблица «Товар» содержит информацию об основных характеристиках каждого товара. Заголовок имеет следующий вид.

Таблица «Магазин» содержит информацию о местонахождении магазинов. Заголовок таблицы имеет следующий вид.

На рисунке изображена схема указанной базы данной

Используя информацию из приведенной базы данных, определите, на сколько уменьшилось количество упаковок свёрл по дереву диаметром 8 мм, имеющихся в наличии в магазинах Утреннего района, за период с 1 по 10 сентября включительно. В ответе запишите только число.
Скачать файл БД

Решение:

Решить задание нам помогут возможности табличного процессора Excel. Подключаем ко всем листам ФИЛЬТР.

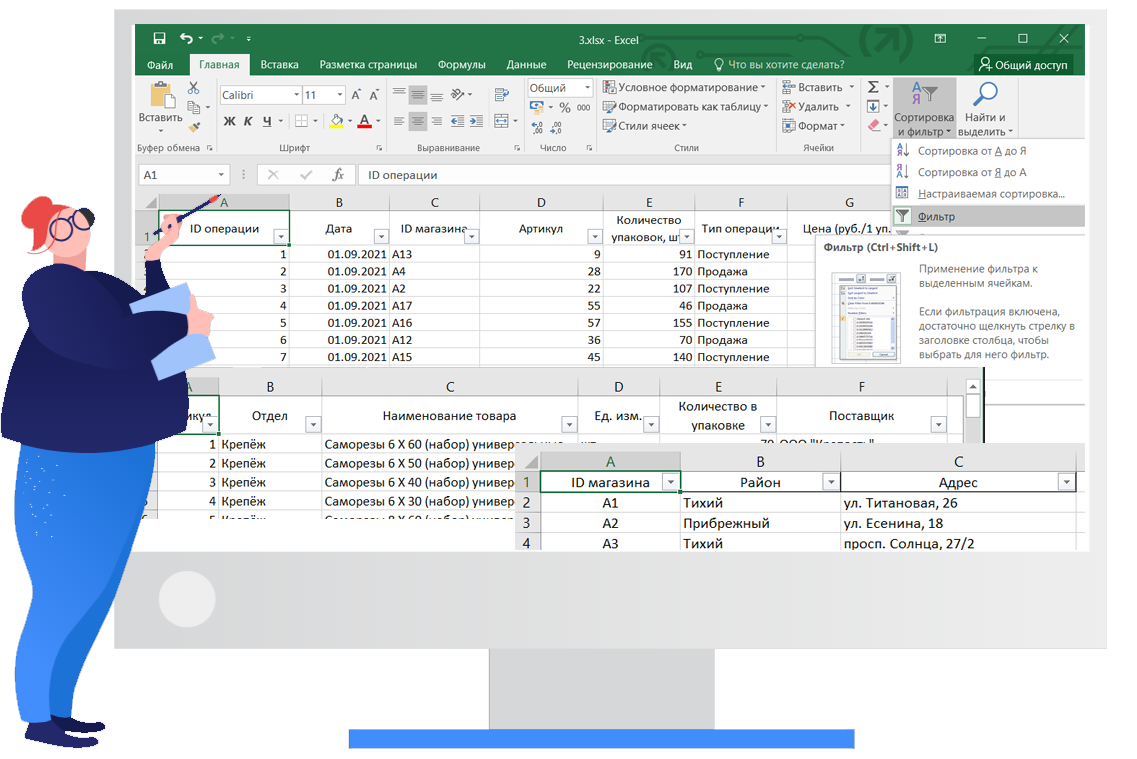
Перейдём на лист «Магазин». Требуется отфильтровать записи в таблице, оставив только записи для магазинов Утреннего района.

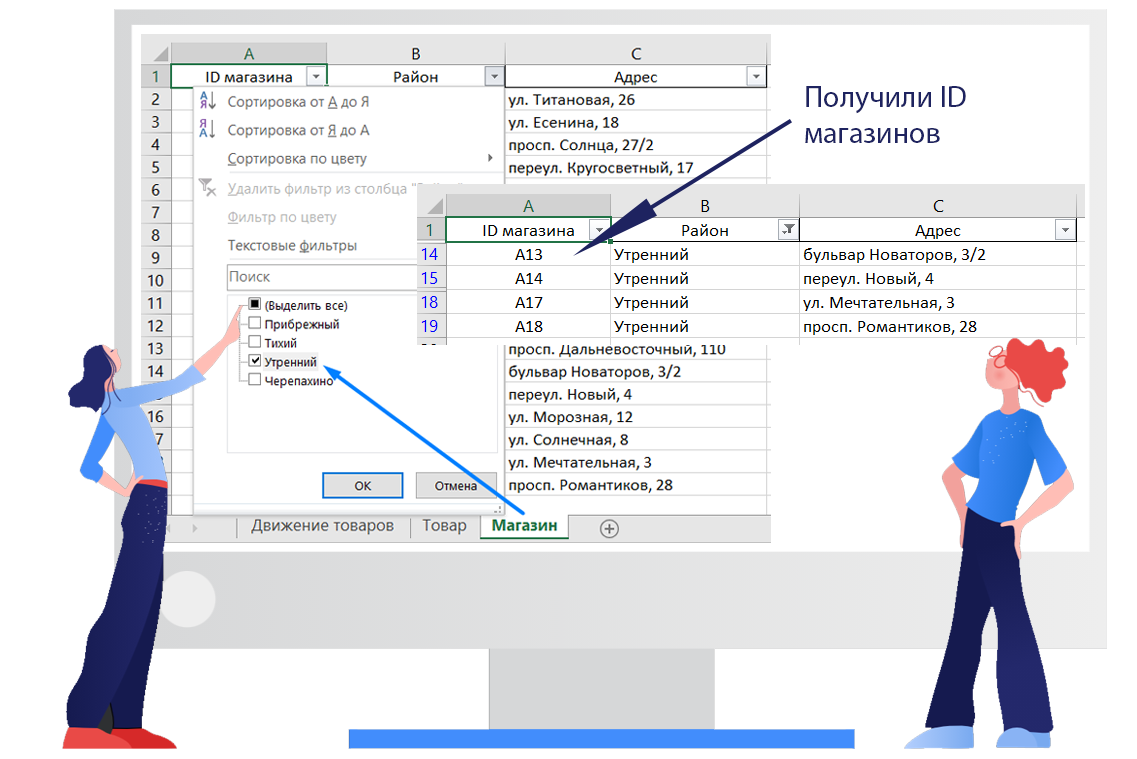
Перейдём на лист «Товар». В этой таблице, воспользовавшись средствами поиска, найдём строку с товаром «Свёрло по дереву диаметром 8 мм». Артикул товара — 31:

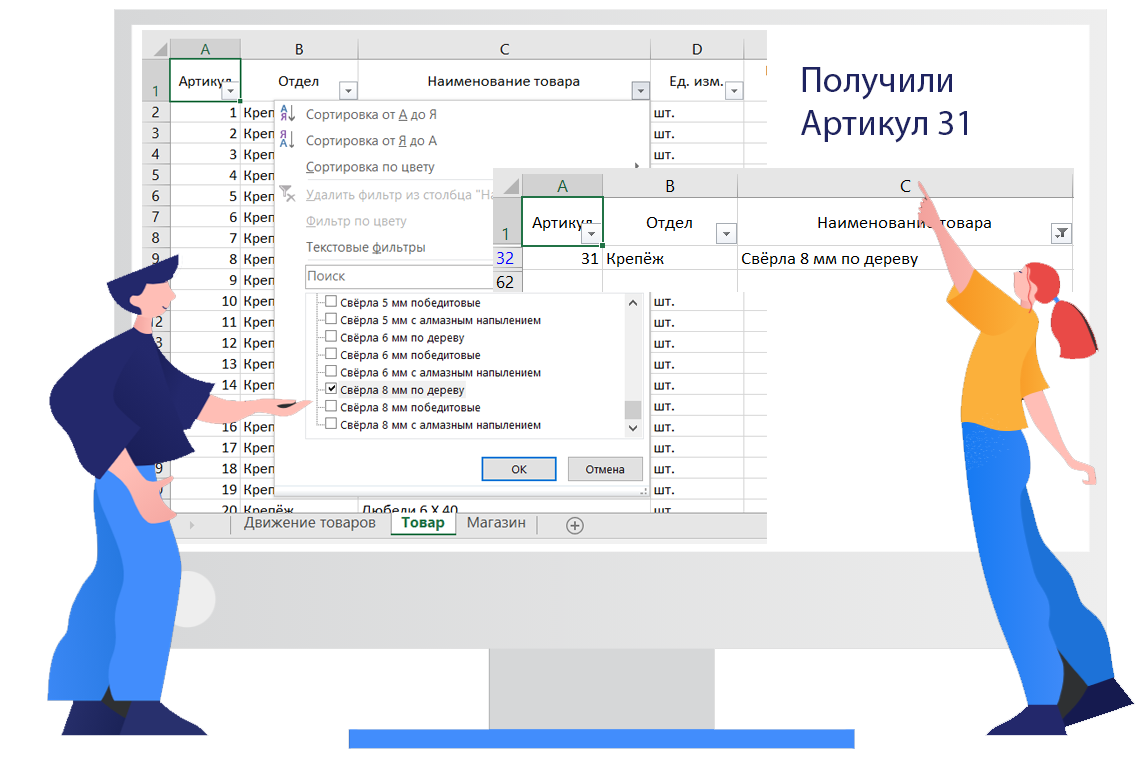
Перейдём на лист «Движение товаров». Снова воспользуемся фильтром по столбцу «ID магазина», в фильтре отметим те ID магазинов, которые были найдены в таблице «Магазин» — А13, А14, А17 и А18. В столбце «Артикул» оставим только записи о движении товаров по артикулу 31. Проверим столбец с датами, всё в порядке, с 1 по 10 сентября. Что бы найти остаток, отсортируем столбец Тип операции во возрастанию, что бы отделить Поступление от Продажи. Скопируем полученную таблицу на отдельный лист. В результате получим следующую таблицу:

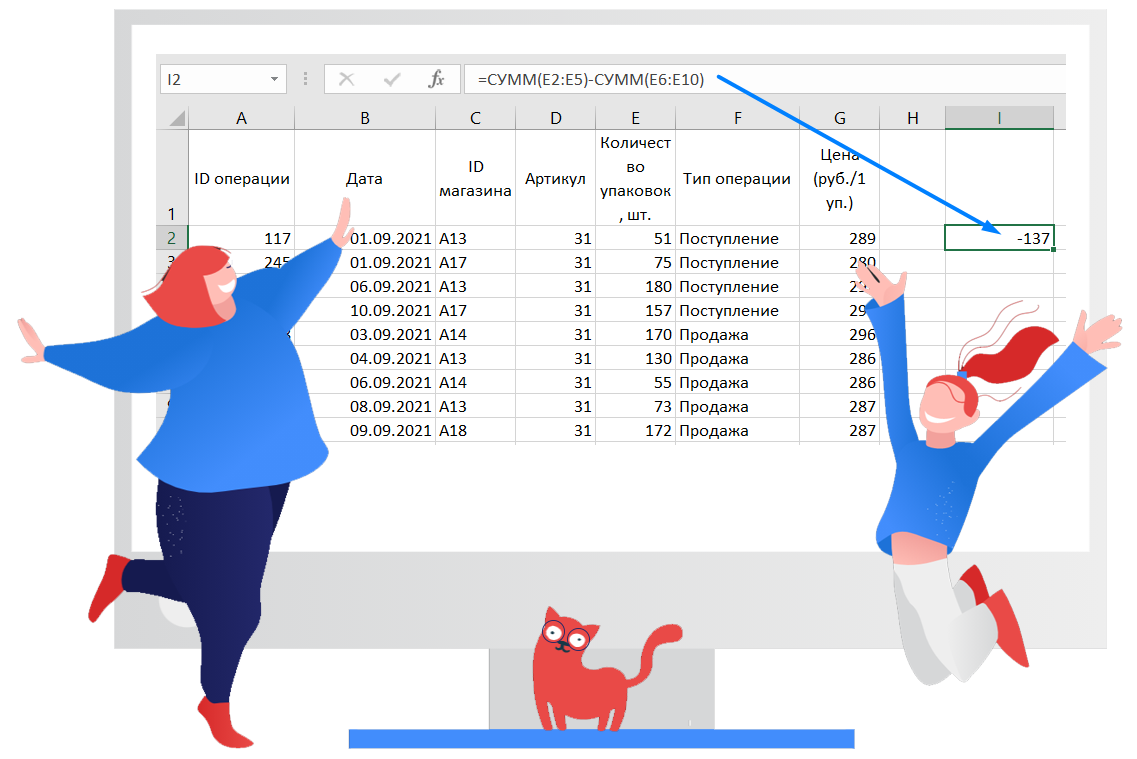
Ответ: -137

Задание 4

Для кодирования некоторой последовательности, состоящей из букв А, К, С, У, Ф, Ч, решили использовать неравномерный двоичный код, удовлетворяющий условию, что никакое кодовое слово не является началом другого кодового слова. Это условие обеспечивает возможность однозначной расшифровки закодированных сообщений. Для букв А, К, С, У использовали соответствиенно кодовые слова 00, 010, 10, 11. Для оставшихся букв – Ф и Ч – кодовые слова неизвестны.

Укажите кратчайшее возможное кодовое слово для буквы Ф, при котором код будет удовлетворять указанному условию. Если таких кодов несколько, укажите код с минимальным числовым значением.

Решение:

Используем приём Дерево Фано. Расставим на этом дереве те буквы, для которых уже известны кодовые слова.

Дерево рисуется обычно сверху вниз. В начале от дерева рисуются две ветки: ветка 0 и ветка 1. От каждой ветки можно нарисовать ещё две ветки, так же 0 и 1, и т. д.

Для удобства ветки с 1 будем направлять вправо, а ветки с 0 будем направлять влево.

В конце каждой ветки можно размещать буквы, но если мы разместили букву, то эта ветка блокируется, и от этой ветки больше нельзя делать новые ответвления.

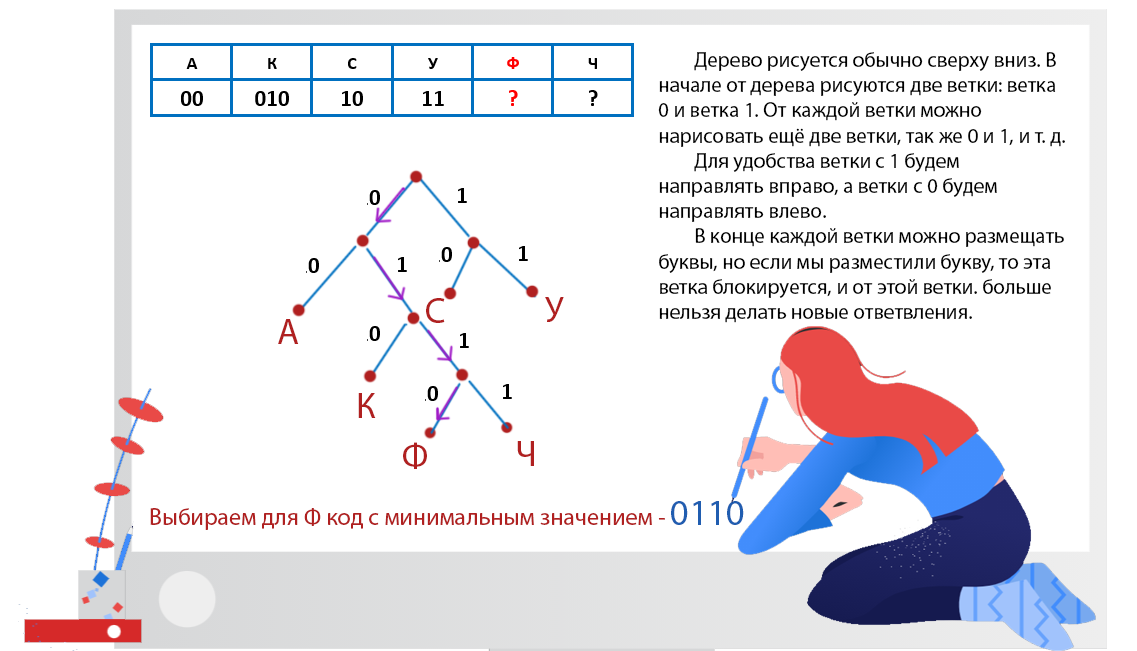
Ответ: 0110

Задание 5

На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом.

Строится двоичная запись числа N.
К этой записи дописывается справа ещё три разряда по следующему правилу:

а) если число четное, то в конце числа (справа) дописывается 00, в противном случае дописывается 10.
б) если в полученном числе количество единиц чётное, то справа дописывается 0, в противном случае дописывается 1.

Укажите количество чисел R, которые принадлежат диапазону [130;350] и могут являться результатом работы алгоритма.

Решение:

Ответ: 27

Задание 6

Определите, при каком наименьшем значении переменной а программа выведет число 19. Для вашего удобства программа представлена на четырех языках программирования.

x = 0
p = 0
a = int(input())
while p + x < 1050:
p = p + a
x = x + 1
print(x)

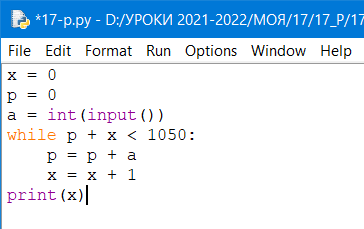
Составим программу на языке Phyton для перебора возможных значений переменной a и выполнения для каждого значения заданного алгоритма. Выведем первое значение, при котором получится 19.

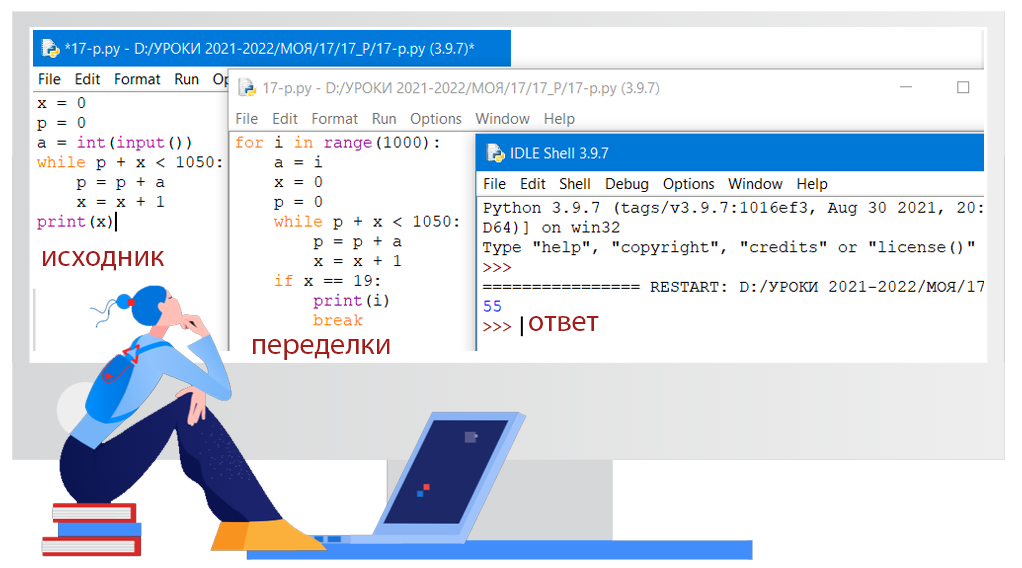
Ответ: 55

Задание 7

В графическом редакторе была создана картина с цветовой системой, содержащей 2¹² = 4096 цветов. Размер такой картинки – 24 Мбайта (без учета размера заголовка). В целях уменьшения объёма изображения и длину, и высоту рисунка уменьшили вдвое, а цветовую систему изменили до 2¹⁰ = 1024 цветов. Для кодирования цвета каждого пикселя используется одинаковое наименьшее возможное число битов, коды пикселей записываются в файл один за другим без промежутков. Сколько Мбайт будет составлять картинка с изменёнными параметрами без учета размера заголовка?

Решение:

Ответ: 5

Задание 8

Саша составляет слова, переставляя буквы из слова «ИДИЛЛИЯ». Словом, считается любая допустимая последовательность букв, не обязательно осмысленная.

Сколько существует различных слов, которые может написать Саша?

Решение:

Ответ: 420

Задание 9

Откройте файл электронной таблицы Скачать 9.xlsx, содержащей вещественные числа — результаты измерения средней месячной влажности воздуха в период с 1935 по 2020 год. Найдите количество лет, в которые среднее арифметическое значение влажности воздуха за зимние месяцы (декабрь, январь, февраль) было больше среднего арифметического значения влажности воздуха за летние месяцы (июнь, июль, август).

Решение:

Ответ: 15

Задание 10

С помощью текстового редактора определите, сколько раз встречается слово “господ” или “Господ” в тексте произведения Н. А. Некрасова “Необыкновенный завтрак”. Другие формы слова “господ”, такие как “господа”, “господами” и т.д., учитывать не следует. В ответе укажите только число. Скачать 10.docx

Решение:

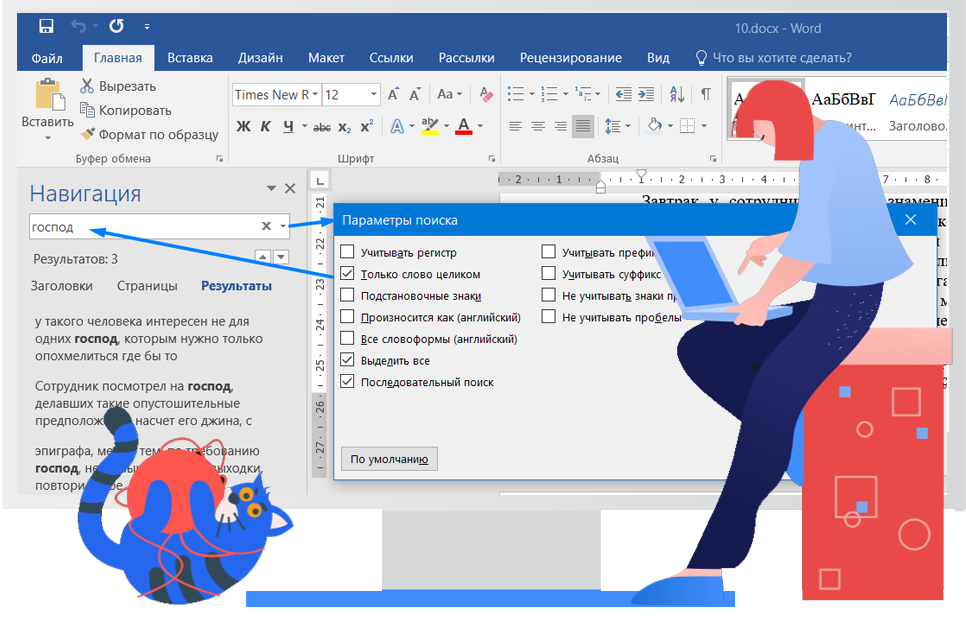
Ответ: 3

Задание 11

Запись для каждого пользователя при регистрации состоит из идентификатора, логина и пароля. Идентификатор представляет собой пятизначное (в десятичной системе счисления) натуральное число, которое кодируется минимальным количеством бит, одинаковым для всех пятизначных чисел, и занимает в компьютерной системе минимально возможное целое число байт. Логин состоит из 17 символов, которые пользователь придумывает сам, и содержит только символы из 11-символьного набора: A, B, C, D, E, F, G, H, K, L, M. Каждый такой логин в компьютерной программе записывается минимально возможным и одинаковым целым количеством байт (при этом используют посимвольное кодирование, все символы кодируются одинаковым и минимально возможным количеством бит). Далее к логину каждого пользователя дописывается пароль, автоматически сгенерированный системой, под которую отводится 9 байт.

Определите наибольшее количество пользователей, которых можно зарегистрировать в компьютерной системе, если для хранения сведений об этих пользователях выделено 6 Кбайт.

Решение:

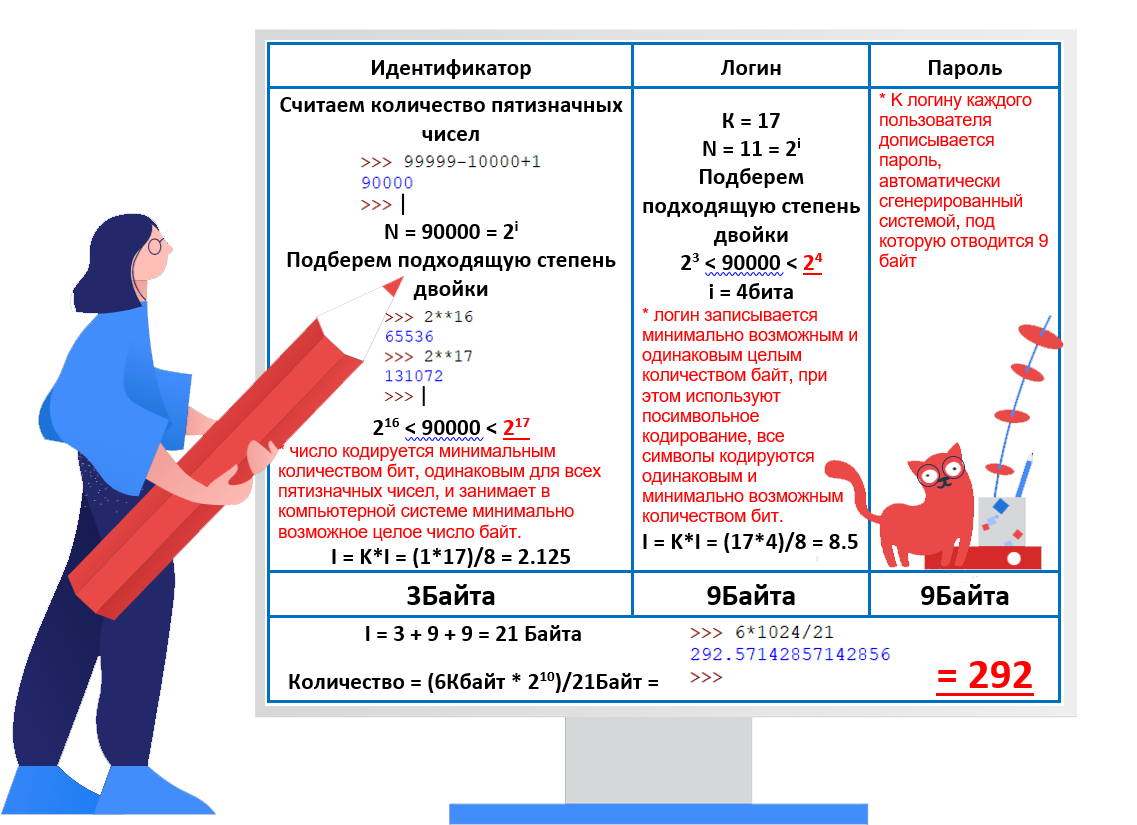
Ответ: 292

Задание 12

А) заменить (v, w).

Эта команда заменяет в строке первое слева вхождение цепочки v на цепочку w.

Например, выполнение команды

Заменить (222, 58)

Преобразует строку 45222222234 в строку 4558222234.

Если в строке нет вхождений цепочки v, то выполнение команды

заменить (v, w)

не меняет эту строку.

Б) нашлось (v).

Эта команда проверяет, встречается ли цепочка v в строке исполнителя Редактор. Если она встречается, то команда возвращает логическое значение “истина”, в противном случае возвращает значение “ложь”. Строка исполнителя при этом не меняется.

Цикл

ПОКА условие

последовательность команд

КОНЕЦ ПОКА

означает, что последовательность команд выполняется, пока условие истинно.

В конструкции

ЕСЛИ условие

ТО команда

КОНЕЦ ЕСЛИ

команда выполняется, если условие истинно.

Решение:

Проверим решение программой:

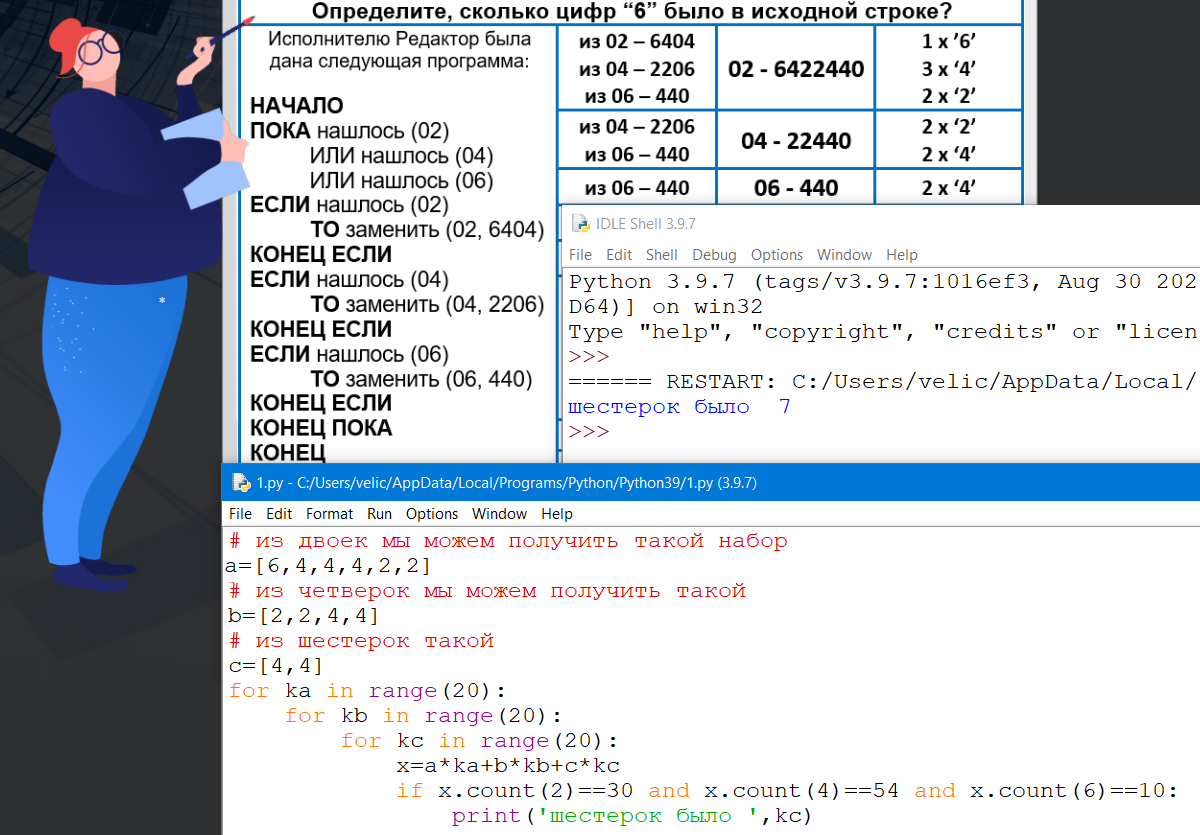
Ответ: 7

Задание 13

На рисунке 3 представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К, Л, М. По каждой дороге можно двигаться в одном направлении, указанном стрелкой.

Сколько существует различных путей из города А в город М, проходящих через город Ж и не проходящих через город В?

Решение:

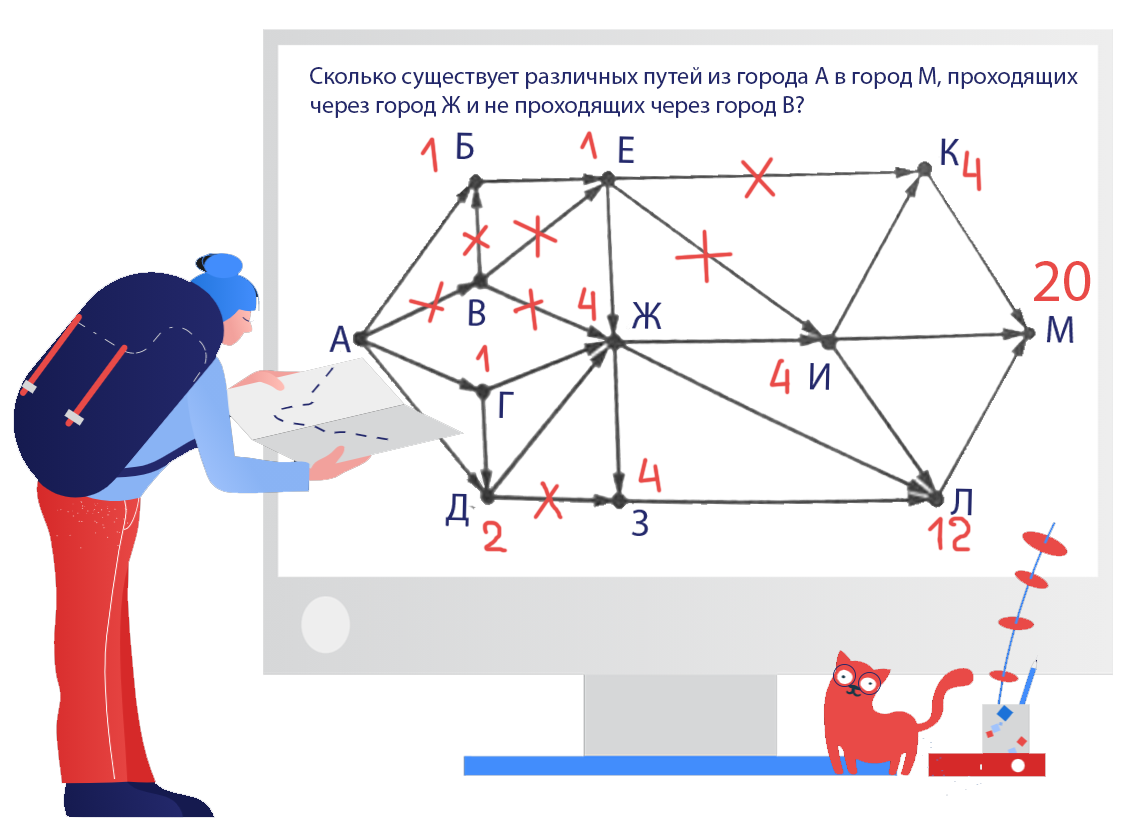
Ответ: 20

Задание 14

Значение выражения 243⁵ + 3⁷ — 2 — X записали в системе счисления с основанием 3, при этом в записи оказалось ровно 20 цифр “2”.

Решение:

Ответ: 2307

Источник

Решение:

Вариант 1:

Вариант 2 (максимальное количество цифр «3»):

Решение на Pyton:

Определите наибольшее/наименьшее значение x, y

Сколько цифр и сумма цифр

Найти основание системы счисления и уравнения

Е25.22 которые соответствуют маске 1?7246*1 и при этом без остатка делятся на 4173

Е24.35 сколько раз буква, образующая самую длинную цепочку в файле, встречается в строке

Е23.33 число 1 в число 11 и при этом содержат ровно одну команду умножения

Е17.44 запись элементов пары заканчивается одной и той же цифрой

для которых можно подобрать такое b, что F(a, b) = 1 048 576

Е15.43 формула (x&35 ≠ 0 ∨ x&22 ≠ 0) → (x&15 = 0 → x&А ≠ 0) тождественно истинна

Е14.56 В системе счисления с основанием p выполняется равенство 32×8 + xxx9 = yy02.

Е13.27 Определите количество различных путей ненулевой длины, которые начинаются

Е11.31 Сколько Кбайт потребуется для хранения 65 536 описаний, построенных по такой схеме

Е10.13 «Мастер и Маргарита» встречается числительное «двадцать» в любом падеже.

Разбор варианта ЕГЭ информатика 2022Кулабухов (Вариант 1)

Задание 1

Решение:

Ответ: ГАДБ

Задание 2

Решение:

Ответ: yzxw

Задание 3

Решение:

Ответ: -137

Задание 4

Решение:

Ответ: 0110

Задание 5

Решение:

Ответ: 27

Задание 6

x = 0 p = 0 a = int(input()) while p + x < 1050: p = p + a x = x + 1 print(x)

Ответ: 55

Задание 7

Решение:

Ответ: 5

Задание 8

Решение:

Ответ: 420

Задание 9

Решение:

Ответ: 15

Задание 10

Решение:

Ответ: 3

Задание 11

Решение:

Ответ: 292

Задание 12

Решение:

Проверим решение программой:

Ответ: 7

Задание 13

Решение:

Ответ: 20

Задание 14

Решение:

Ответ: 2307

Разбор варианта ЕГЭ информатика 2022
Кулабухов (Вариант 1)

x = 0
p = 0
a = int(input())
while p + x < 1050:
p = p + a
x = x + 1
print(x)