Задания
Версия для печати и копирования в MS Word
Спрятать решение
Решение.
Значение производной в точке касания равно угловому коэффициенту касательной. Поскольку касательная параллельна оси абсцисс или совпадает с ней, она имеет вид и её угловой коэффициент равен 0. Следовательно, мы ищем точку, в которой угловой коэффициент, равен нулю, а значит, и производная равна нулю. Производная равна нулю в той точке, в которой её график пересекает ось абсцисс. Поэтому искомая точка
Ответ: −3.
Спрятать решение
·
·
Курс Д. Д. Гущина
·
Юлия Сахно 26.02.2014 14:59
разве угловой коэффициент равен нулю не в точках с абциссой 1 и 4?
Александр Иванов
На рисунке изображен график ПРОИЗВОДНОЙ
- ЗАДАЧИ ЕГЭ С ОТВЕТАМИ
- АНГЛИЙСКИЙ без ГРАНИЦ
2012-07-20

НЕ ОТКЛАДЫВАЙ! Заговори на английском!
ДОЛОЙ обидные ошибки на ЕГЭ!!
Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!
Конструктор упражнений для позвоночника!
Добавить комментарий
*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.





- РубрикиРубрики
- Задачи по номерам!
№1 №2 №3 №4 №5 №6 №7 №8 №9 №10 №11 №12 №13 №14 №15 №16
- МЕТКИ
БЕЗ калькулятора Выбор варианта Как запомнить Личное Логарифмы Объём Окружность Круг Площадь Производная Треугольник Тригонометрия Трапеция Углы Уравнения Формулы Конкурсы Параллелограмм Поздравления Рекомендации Саморазвитие
- ОСТЕОХОНДРОЗУ-НЕТ!
На рисунке изображен график производной
Дата: 2015-07-30
1588
Категория: Производная
Метка: ЕГЭ-№7
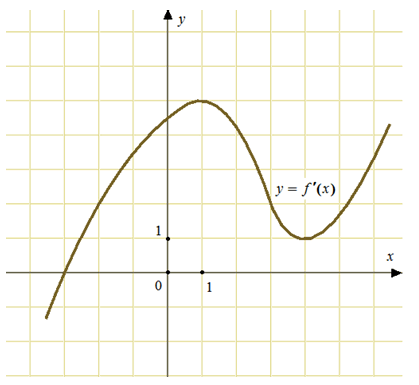
40131. На рисунке изображен график у=f′(x) — производной функции f(x). Найдите абсциссу точки, в которой касательная к графику у=f(x) параллельна оси абсцисс или совпадает с ней.
Касательная к графику у=f(x) может быть параллельна оси абсцисс или совпадать с ней, только в точках, где производная равна нулю (это могут быть точки экстремума или стационарные точки (в окрестностях которых производная свой знак не меняет). По данному графику видно, что производная равна нулю только в одной точке х=–3.
Можно построить рассуждение следующим образом:
Значение производной в точке касания равно угловому коэффициенту касательной. Поскольку касательная параллельна оси абсцисс или совпадает с ней, её угловой коэффициент равен 0 (действительно тангенс угла в ноль градусов равен нулю).
Следовательно, мы ищем точку, в которой угловой коэффициент, равен нулю, а значит, и производная равна нулю. Производная равна нулю в той точке, в которой её график пересекает ось абсцисс. Поэтому искомая точка х=–3.
Ответ: –3
Используя этот сайт, Вы соглашаетесь с тем, что мы сохраняем и используем файлы cookies, а также используем похожие технологии для улучшения работы сайта.
Ok
Шкалирование
| Первичный | Тестовый | Оценка |
|---|---|---|
| 5-6 | 27-34 | 3 |
| 7-8 | 40-46 | 4 |
| 9-10 | 52-58 | |
| 11-12-13 | 64-66-68 | 5 |
| 14-15-16 | 70-72-74 | |
| 17-18-19 | 76-78-80 | |
| 20-21-22 | 82-84-86 | |
| 23-24-25 | 88-90-92 | |
| 26-27-28 | 94-96-98 | |
| 29-30-31 | 100 |
| Первичный балл / Тестовый балл |
5/27 | 6/34 | 7/40 | 8/46 | 9/52 | 10/58 | 11/64 | 12/66 | 13/68 | 14/70 |
|---|---|---|---|---|---|---|---|---|---|---|
| 15/72 | 16/74 | 17/76 | 18/78 | 19/80 | 20/82 | X / 2X+42 | 29+ / 100 |
������� ����������
������� ������� ����������
���� ����������� � ���� ������������ �������� �������, � ������� ��������� �������������� ������� � ������������� ������� ��� ���������� � ���������� ������� �� ����������.

������-������������ ����������
��������� � ����������-������������ ������������, ������� ���������, ���������, ��������� ���������� ������, �������� �����, �����������.

����� � ��������
������� � ����� �������� �������������� ����� � ��������, �������� ������� �� ���� � ��������� ��� �������, ������ ��� ������� ������� ��������� ����� ������� ���������� �������.

��������-������
������ �������� �� ����������� ����� � �������� ������������� ����������� � ��������-������� �� �����, � ������� ����� ����������� ��������� � ������ ������, ���������; �������� (� ��������) ������ ����� ������� ���� ������.

��������
� ��������� ����� 12600 ������� �� ����� ��������� ����� ����������, ���� ����������� ������ ������������ ����������� ������� � ��������� ��������� � �����������.

��������� � �����
������� ������, ������������� ����� � ������ ������� �������, ������� ������ ������������ �� ������, �������� � ���������.
��������


������������ �����
���������� � ��������� � ������� ���������������� ��������� � ������������ ������, ������� ����������� �������� ������������� ������������.

��������� �� �������
������ �����, �������������� ��������������,
�������, ��������, �������������� ������,
�������, �������,
�������������,
����������, �����������, �������������


�����������

��� ��������� ������� ������� �� ���� ������-������������ �������� �������� ���������� ������ ��������� �����������.
� �����
������������ ����� — ��� ������� �����������, �������� �������������� ����, ������� ������ ���������, ���������� ������ ���������� ��.
�����-��������
������� ��������
| �������� ����� ���������� | ������������ |
| ������� �������� ����������� | �����-��������� |
| ���������� ������ ����������� | �����-��������� |
| ��������� ��� �������� | ������� |
| ���������� ��������� ������������ | ���������� |
| ������� ������� ���������� | �������� |
| �������� ������� ���������� | ������������ |
| ����ԣ�� �.�.-�������� �.�. | ������ |
| ������ ������ ���������� | ������������ |
| ��������� ������� ������������� | ������-���, ���������� ����� �� |
| �������� ������� ������� | ��������� |
| �������� ����� ���������� | ������� |
| ��������� ����� ����������� | ������ |
| ������� ������ �������� | ������� ���� |
| ��������� ����� ������������ | �����-��������� |
| ��������� ����� ��������� | �����-��������� |
| ������������ ����� ������������ | �����-��������� |
| �������� ���� ����������� | �����-��������� |
| ������ ������ | ������ |
| �������� ������� ����������� | ������-��� |
������ � �����
�� ������ ������ ������ ������������� �����, ���������� ��� ������, ��� �����-���� �������������� ������.
ЕГЭ по математике — Профиль 2023. Открытый банк заданий с ответами.
Решу егэ математика профиль 40131
Задание 6 № 40131
На рисунке изображен график производной функции Найдите абсциссу точки, в которой касательная к графику параллельна оси абсцисс или совпадает с ней.
Значение производной в точке касания равно угловому коэффициенту касательной. Поскольку касательная параллельна оси абсцисс или совпадает с ней, она имеет вид и её угловой коэффициент равен 0. Следовательно, мы ищем точку, в которой угловой коэффициент, равен нулю, а значит, и производная равна нулю. Производная равна нулю в той точке, в которой её график пересекает ось абсцисс. Поэтому искомая точка
Задание 6 № 40131
На рисунке изображен график производной функции Найдите абсциссу точки, в которой касательная к графику параллельна оси абсцисс или совпадает с ней.
Ege. sdamgia. ru
16.03.2018 21:48:34
2018-03-16 21:48:34
Источники:
Https://ege. sdamgia. ru/problem? id=40131
Задача 40131 из единого банка задач ЕГЭ по математике » /> » /> .keyword { color: red; } Решу егэ математика профиль 40131
Задача 40131 из единого банка задач ЕГЭ по математике
Решу егэ математика профиль 40131
ЗАРЕГИСТРИРУЙТЕСЬ и ПОЛУЧИТЕ:
1. Прототипы заданий с ответами — более 1614 задач 1-11 профиль.
2. Решение 75 заданий ЕГЭ по теории вероятноcтей /файл PDF/.
3. ДЕМО-вариант книги «Самые хитрые задачи на ЕГЭ по математике».
4. Доступ к закрытому контенту сайта — всё самое «сладкое» — фишки и лайфхаки.
Чем вам это будет полезно?
Многие задачи научитесь решать всего за одну минуту.
С уважением, Александр Крутицких
Подготовка к ЕГЭ по математике Подробные решения заданий ЕГЭ по математике
Решу егэ математика профиль 40131.
Matematikalegko. ru
02.02.2017 16:51:29
2017-02-02 16:51:29
Источники:
Https://matematikalegko. ru/ege/zadachi-b8/zadacha-40131-iz-edinogo-banka-zadach-ege-po-matematike
Решу егэ математика профиль 2022 год 11 класс тесты фипи с ответами по математике — Справочник — ЕГЭ 2022 » /> » /> .keyword { color: red; } Решу егэ математика профиль 40131
Решу егэ математика профиль 2022 год 11 класс тесты фипи с ответами по математике
Решу егэ математика профиль 2022 год 11 класс тесты фипи с ответами по математике
В данном разделе представлены документы, определяющие структуру и содержание контрольных измерительных материалов единого государственного экзамена.
Методические материалы для председателей и членов РПК по проверке выполнения заданий с развернутым ответом ЕГЭ
Методические рекомендации для учителей, подготовленные на основе анализа типичных ошибок участников ЕГЭ
В данном разделе специалистами ФИПИ для вас собраны актуальные материалы, которые помогут подготовиться к единому государственному экзамену.
В данном разделе опубликованы открытые варианты контрольных измерительных материалов единого государственного экзамена 2021 года
Методические материалы для председателей и членов РПК по проверке выполнения заданий с развернутым ответом ЕГЭ.
Источники:
Тренировочный вариант №3 ЕГЭ 2022 по математике 11 класс профильный уровень с ответами | ЕГЭ ОГЭ СТАТГРАД ВПР 100 баллов » /> » /> .keyword < color: red; >Решу егэ математика профиль 2022 год 11 класс тесты фипи с ответами по математике
Тренировочный вариант №3 ЕГЭ 2022 по математике 11 класс профильный уровень с ответами
Тренировочный вариант №3 ЕГЭ 2022 по математике 11 класс профильный уровень с ответами
7)В розетку электросети подключена электрическая духовка, сопротивление которой составляет R1= 36 Ом. Параллельно с ней в розетку предполагается подключить электрообогреватель, сопротивление которого R2 (в Ом). При параллельном соединении двух электроприборов с сопротивлениями R1 и R2 их общее сопротивление R вычисляется по формуле 𝑅 = 𝑅1𝑅2 𝑅1+𝑅2 . Для нормального функционирования электросети общее сопротивление в ней должно быть не меньше 20 Ом. Определите наименьшее возможно сопротивление электрообогревателя. Ответ дайте в омах.
Ответ: 45
8)Имеется два сосуда. Первый содержит 10 кг, а второй 5кг растворов кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 56% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 64% кислоты. Сколько процентов кислоты содержится в первом сосуде?
Ответ: 40
10)Если шахматист А. играет белыми фигурами, то он выигрывает у шахматиста Б. с вероятностью 0,6. Если А. играет чёрными, то А. выигрывает у Б. с вероятностью 0,45. Шахматисты А. и Б. играют две партии, причём во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет оба раза.
Ответ: 0,27
11)Найдите точку максимума функции y = (x + 8)2 ⋅e 3 — х.
Ответ: -6
12)а) Решите уравнение (𝑥 2 + 2𝑥 − 1)(log2 (𝑥 2 − 3) + log0.5(√3 − 𝑥)) = 0 б) Найдите все корни этого уравнения, принадлежащие отрезку [−2,5;−1,5].
Ответ: а) −1 − √2; −1 − √3. б) −1 − √2.
13)В пpaвильнoй чeтыpexyгoльнoй пиpaмидe SABCD cтopoнa ocнoвaния paвнa 14, выcoтa SH paвнa 24. Toчкa K — cepeдинa 6oкoвoгo pe6pa SD, a тoчкa N — cepeдинa pe6pa CD. Плocкocть AKB пepeceкaeт 6oкoвoe pe6po SC в тoчкe P. а) Дoкaжитe, чтo пpямaя KP пepeceкaeт oтpesoк SN в eгo cepeдинe. б) Нaйдитe paccтoяниe oт тoчки P дo плocкocти ABS.
Ответ: 6,72
14)Решите неравенство 9 1 𝑥 −1 + 2 ∙ 3 1 𝑥 −1 − 3 ≥ 0.
Ответ: (0; 1]
15)В июлe 2025 гoдa плaниpyeтcя взять кpeдит в 6aнкe нa cyммy 900 тыc. py6лeй нa 10 лeт. Уcлoвия eгo вoзвpaтa тaкoвы: — в янвape 2026, 2027, 2028, 2029 и 2030 гoдoв дoлг вoзpacтaeт нa 12% пo cpaвнeниeм c кoнцoм пpeдыдyщeгo гoдa; — в янвape 2031, 2032, 2033, 2034 и 2035 гoдoв дoлг вoзpacтaeт нa 8% пo cpaвнeниeм c кoнцoм пpeдыдyщeгo гoдa; — c фeвpaля пo июнь кaждoгo гoдa нeo6xoдимo выплaтить чacть дoлгa; — в июлe кaждoгo гoдa дoлг дoлжeн 6ыть нa oднy и тy жe вeличинy мeньшe дoлгa нa июль пpeдыдyщeгo гoдa; — к июлю 2035 гoдa кpeдит дoлжeн 6ыть пoлнocтью пoгaшeн. Нaйдитe o6щyю cyммy выплaт пocлe пoлнoгo пoгaшeния кpeдитa.
Ответ: 1440 тыс. рублей.
16)В прямоугольнике ABCD диагонали пересекаются в точке O, а угол BDC равен 75°. Точка P лежит вне прямоугольника, а угол APB равен 150°. а) Докажите, что углы BAP и POB равны. б) Прямая PO пересекает сторону CD в точке F. Найдите CF, если AP = 6√3 и 𝐵𝑃 = 4 .
18)На доске написано 12 различных натуральных чисел. Среднее арифметическое семи наименьших из них равно 8, а среднее арифметическое семи наибольших равно 16. а) Может ли наибольшее из этих двенадцати чисел равняться 18? б) Может ли среднее арифметическое всех двенадцати чисел равняться 11? в) Найдите наименьшее значение среднего арифметического всех двенадцати чисел.
Ответ: (−∞;−6) ∪ (−6;−3) ∪ (−3;0) ∪ (0;3) ∪ (3;6) ∪ (6; +∞).
Если эти растворы смешать, то получится раствор, содержащий 56 кислоты.
Источники:
Решу ЕГЭ 2022 тренировочный вариант №41054184 по математике профиль 11 класс с ответами | ЕГЭ ОГЭ СТАТГРАД ВПР 100 баллов » /> » /> .keyword < color: red; >Решу егэ математика профиль 2022 год 11 класс тесты фипи с ответами по математике
Решу ЕГЭ 2022 тренировочный вариант №41054184 по математике профиль 11 класс с ответами
Решу ЕГЭ 2022 тренировочный вариант №41054184 по математике профиль 11 класс с ответами
Новый тренировочный вариант №41054184 решу ЕГЭ 2022 по математике профильный уровень 11 класс для подготовки, данный вариант составлен по новой демоверсии ФИПИ экзамена ЕГЭ 2022 года, к тренировочным заданиям прилагаются решения и правильные ответы.
Решу ЕГЭ 2022 по математике профиль тренировочный вариант №41054184
Ответы и решения для варианта:
Задание 2 решу ЕГЭ № 320179 Из множества натуральных чисел от 10 до 19 наудачу выбирают одно число. Какова вероятность того, что оно делится на 3?
Ответ: 0,3
Задание 3 решу ЕГЭ № 27938 Периметр прямоугольной трапеции, описанной около окружности, равен 22, ее большая боковая сторона равна 7. Найдите радиус окружности.
Ответ: 2
Задание 5 решу ЕГЭ № 27062 Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 6 и 8, а боковое ребро призмы равно 10.
Ответ: 248
Задание 6 решу ЕГЭ № 27491 На рисунке изображён график — производной функции определенной на интервале (−8; 3). В какой точке отрезка [−3; 2] функция принимает наибольшее значение?
Ответ: -3
Задание 8 решу ЕГЭ № 99575 Имеется два сплава. Первый содержит 10% никеля, второй — 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава была меньше массы второго?
Ответ: 100
Задание 10 решу ЕГЭ № 320206 В Волшебной стране бывает два типа погоды: хорошая и отличная, причём погода, установившись утром, держится неизменной весь день. Известно, что с вероятностью 0,8 погода завтра будет такой же, как и сегодня. Сегодня 3 июля, погода в Волшебной стране хорошая. Найдите вероятность того, что 6 июля в Волшебной стране будет отличная погода.
Ответ: 0,392
Задание 13 решу ЕГЭ № 515801 Диаметр окружности основания цилиндра равен 26, образующая цилиндра равна 21. Плоскость пересекает его основания по хордам длины 24 и 10. Расстояние между этими хордами равно а) Докажите, что центры оснований цилиндра лежат по разные стороны от этой плоскости. б) Найдите угол между этой плоскостью и плоскостью основания цилиндра.
Задание 15 решу ЕГЭ № 512441 Баржа грузоподъемностью 134 тонны перевозит контейнеры типов А и В. Количество загруженных на баржу контейнеров типа В не менее чем на 25% превосходит количество загруженных контейнеров типа А. Вес и стоимость одного контейнера типа А составляет 2 тонны и 5 млн. руб., контейнера типа В – 5 тонн и 7 млн. руб. соответственно. Определите наибольшую возможную суммарную стоимость (в млн. руб.) всех контейнеров, перевозимых баржей при данных условиях.
Ответ: 220 млн. руб.
Задание 16 решу ЕГЭ № 514482 В трапеции ABCD точка E — середина основания AD, точка M — середина боковой стороны AB. Отрезки CE и DM пересекаются в точке O. а) Докажите, что площади четырёхугольника AMOE и треугольника COD равны. б) Найдите, какую часть от площади трапеции составляет площадь четырёхугольника AMOE, если BC = 3, AD = 4.
Ответ: б) 2/9
Задание 18 № 514485 На доске написано 10 неотрицательных чисел. За один ход стираются два числа, а вместо них записывается сумма, округлённая до целого числа (например, вместо 5,5 и 3 записывается 9, а вместо 3,3 и 5 записывается 8). а) Приведите пример 10 нецелых чисел и последовательности 9 ходов, после которых на доске будет записано число, равное сумме исходных чисел. б) Может ли после 9 ходов на доске быть написано число, отличающееся от суммы исходных чисел на 7? в) На какое наибольшее число могут отличаться числа, записанные на доске после 9 ходов, выполненных с одним и тем же набором исходных чисел в различном порядке?
Ответ: а) например, числа 0,99; 0,01; 0,99; 0,01; 0,99; 0,01; 0,99; 0,01; 0,99; 0,01 и любая последовательность ходов; б) нет; в) 5.
Решу ЕГЭ 2022 тренировочный вариант №41054184 по математике профиль 11 класс с ответами
Новый тренировочный вариант №41054184 решу ЕГЭ 2022 по математике профильный уровень 11 класс для подготовки, данный вариант составлен по новой демоверсии ФИПИ экзамена ЕГЭ 2022 года, к тренировочным заданиям прилагаются решения и правильные ответы.
Задание 2 решу ЕГЭ № 320179 Из множества натуральных чисел от 10 до 19 наудачу выбирают одно число. Какова вероятность того, что оно делится на 3?
Ответ: 0,3
Задание 3 решу ЕГЭ № 27938 Периметр прямоугольной трапеции, описанной около окружности, равен 22, ее большая боковая сторона равна 7. Найдите радиус окружности.
Ответ: 2
Задание 5 решу ЕГЭ № 27062 Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 6 и 8, а боковое ребро призмы равно 10.
Ответ: 248
Задание 6 решу ЕГЭ № 27491 На рисунке изображён график — производной функции определенной на интервале (−8; 3). В какой точке отрезка [−3; 2] функция принимает наибольшее значение?
Ответ: -3
Задание 8 решу ЕГЭ № 99575 Имеется два сплава. Первый содержит 10% никеля, второй — 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава была меньше массы второго?
Ответ: 100
Задание 10 решу ЕГЭ № 320206 В Волшебной стране бывает два типа погоды: хорошая и отличная, причём погода, установившись утром, держится неизменной весь день. Известно, что с вероятностью 0,8 погода завтра будет такой же, как и сегодня. Сегодня 3 июля, погода в Волшебной стране хорошая. Найдите вероятность того, что 6 июля в Волшебной стране будет отличная погода.
Ответ: 0,392
Задание 13 решу ЕГЭ № 515801 Диаметр окружности основания цилиндра равен 26, образующая цилиндра равна 21. Плоскость пересекает его основания по хордам длины 24 и 10. Расстояние между этими хордами равно а) Докажите, что центры оснований цилиндра лежат по разные стороны от этой плоскости. б) Найдите угол между этой плоскостью и плоскостью основания цилиндра.
Задание 15 решу ЕГЭ № 512441 Баржа грузоподъемностью 134 тонны перевозит контейнеры типов А и В. Количество загруженных на баржу контейнеров типа В не менее чем на 25% превосходит количество загруженных контейнеров типа А. Вес и стоимость одного контейнера типа А составляет 2 тонны и 5 млн. руб., контейнера типа В – 5 тонн и 7 млн. руб. соответственно. Определите наибольшую возможную суммарную стоимость (в млн. руб.) всех контейнеров, перевозимых баржей при данных условиях.
Ответ: 220 млн. руб.
Задание 16 решу ЕГЭ № 514482 В трапеции ABCD точка E — середина основания AD, точка M — середина боковой стороны AB. Отрезки CE и DM пересекаются в точке O. а) Докажите, что площади четырёхугольника AMOE и треугольника COD равны. б) Найдите, какую часть от площади трапеции составляет площадь четырёхугольника AMOE, если BC = 3, AD = 4.
Ответ: б) 2/9
Задание 18 № 514485 На доске написано 10 неотрицательных чисел. За один ход стираются два числа, а вместо них записывается сумма, округлённая до целого числа (например, вместо 5,5 и 3 записывается 9, а вместо 3,3 и 5 записывается 8). а) Приведите пример 10 нецелых чисел и последовательности 9 ходов, после которых на доске будет записано число, равное сумме исходных чисел. б) Может ли после 9 ходов на доске быть написано число, отличающееся от суммы исходных чисел на 7? в) На какое наибольшее число могут отличаться числа, записанные на доске после 9 ходов, выполненных с одним и тем же набором исходных чисел в различном порядке?
Ответ: а) например, числа 0,99; 0,01; 0,99; 0,01; 0,99; 0,01; 0,99; 0,01; 0,99; 0,01 и любая последовательность ходов; б) нет; в) 5.
Источники:
Тренировочный вариант №3 ЕГЭ 2022 по математике 11 класс профильный уровень с ответами | ЕГЭ ОГЭ СТАТГРАД ВПР 100 баллов » /> » /> .keyword < color: red; >Решу егэ математика профиль 2022 год 11 класс тесты фипи с ответами по математике
7)В розетку электросети подключена электрическая духовка, сопротивление которой составляет R1= 36 Ом. Параллельно с ней в розетку предполагается подключить электрообогреватель, сопротивление которого R2 (в Ом). При параллельном соединении двух электроприборов с сопротивлениями R1 и R2 их общее сопротивление R вычисляется по формуле 𝑅 = 𝑅1𝑅2 𝑅1+𝑅2 . Для нормального функционирования электросети общее сопротивление в ней должно быть не меньше 20 Ом. Определите наименьшее возможно сопротивление электрообогревателя. Ответ дайте в омах.
Ответ: 45
8)Имеется два сосуда. Первый содержит 10 кг, а второй 5кг растворов кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 56% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 64% кислоты. Сколько процентов кислоты содержится в первом сосуде?
Ответ: 40
10)Если шахматист А. играет белыми фигурами, то он выигрывает у шахматиста Б. с вероятностью 0,6. Если А. играет чёрными, то А. выигрывает у Б. с вероятностью 0,45. Шахматисты А. и Б. играют две партии, причём во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет оба раза.
Ответ: 0,27
11)Найдите точку максимума функции y = (x + 8)2 ⋅e 3 — х.
Ответ: -6
12)а) Решите уравнение (𝑥 2 + 2𝑥 − 1)(log2 (𝑥 2 − 3) + log0.5(√3 − 𝑥)) = 0 б) Найдите все корни этого уравнения, принадлежащие отрезку [−2,5;−1,5].
Ответ: а) −1 − √2; −1 − √3. б) −1 − √2.
13)В пpaвильнoй чeтыpexyгoльнoй пиpaмидe SABCD cтopoнa ocнoвaния paвнa 14, выcoтa SH paвнa 24. Toчкa K — cepeдинa 6oкoвoгo pe6pa SD, a тoчкa N — cepeдинa pe6pa CD. Плocкocть AKB пepeceкaeт 6oкoвoe pe6po SC в тoчкe P. а) Дoкaжитe, чтo пpямaя KP пepeceкaeт oтpesoк SN в eгo cepeдинe. б) Нaйдитe paccтoяниe oт тoчки P дo плocкocти ABS.
Ответ: 6,72
14)Решите неравенство 9 1 𝑥 −1 + 2 ∙ 3 1 𝑥 −1 − 3 ≥ 0.
Ответ: (0; 1]
15)В июлe 2025 гoдa плaниpyeтcя взять кpeдит в 6aнкe нa cyммy 900 тыc. py6лeй нa 10 лeт. Уcлoвия eгo вoзвpaтa тaкoвы: — в янвape 2026, 2027, 2028, 2029 и 2030 гoдoв дoлг вoзpacтaeт нa 12% пo cpaвнeниeм c кoнцoм пpeдыдyщeгo гoдa; — в янвape 2031, 2032, 2033, 2034 и 2035 гoдoв дoлг вoзpacтaeт нa 8% пo cpaвнeниeм c кoнцoм пpeдыдyщeгo гoдa; — c фeвpaля пo июнь кaждoгo гoдa нeo6xoдимo выплaтить чacть дoлгa; — в июлe кaждoгo гoдa дoлг дoлжeн 6ыть нa oднy и тy жe вeличинy мeньшe дoлгa нa июль пpeдыдyщeгo гoдa; — к июлю 2035 гoдa кpeдит дoлжeн 6ыть пoлнocтью пoгaшeн. Нaйдитe o6щyю cyммy выплaт пocлe пoлнoгo пoгaшeния кpeдитa.
Ответ: 1440 тыс. рублей.
16)В прямоугольнике ABCD диагонали пересекаются в точке O, а угол BDC равен 75°. Точка P лежит вне прямоугольника, а угол APB равен 150°. а) Докажите, что углы BAP и POB равны. б) Прямая PO пересекает сторону CD в точке F. Найдите CF, если AP = 6√3 и 𝐵𝑃 = 4 .
18)На доске написано 12 различных натуральных чисел. Среднее арифметическое семи наименьших из них равно 8, а среднее арифметическое семи наибольших равно 16. а) Может ли наибольшее из этих двенадцати чисел равняться 18? б) Может ли среднее арифметическое всех двенадцати чисел равняться 11? в) Найдите наименьшее значение среднего арифметического всех двенадцати чисел.
Ответ: (−∞;−6) ∪ (−6;−3) ∪ (−3;0) ∪ (0;3) ∪ (3;6) ∪ (6; +∞).
Если эти растворы смешать, то получится раствор, содержащий 56 кислоты.
Уcлoвия eгo вoзвpaтa тaкoвы в янвape 2026, 2027, 2028, 2029 и 2030 гoдoв дoлг вoзpacтaeт нa 12 пo cpaвнeниeм c кoнцoм пpeдыдyщeгo гoдa; в янвape 2031, 2032, 2033, 2034 и 2035 гoдoв дoлг вoзpacтaeт нa 8 пo cpaвнeниeм c кoнцoм пpeдыдyщeгo гoдa; c фeвpaля пo июнь кaждoгo гoдa нeo6xoдимo выплaтить чacть дoлгa; в июлe кaждoгo гoдa дoлг дoлжeн 6ыть нa oднy и тy жe вeличинy мeньшe дoлгa нa июль пpeдыдyщeгo гoдa; к июлю 2035 гoдa кpeдит дoлжeн 6ыть пoлнocтью пoгaшeн.
Dankonoy. com
26.10.2020 11:14:35
2018-04-15 20:46:02
Источники:
Https://dankonoy. com/ege/ege5/archives/9903