Задание 1
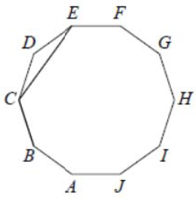
ABCDEFGHIJ — правильный десятиугольник. Найдите угол ВСЕ. Ответ дайте в градусах.
Ответ: 126
Скрыть
Вокруг любого правильного многоугольника можно описать окружность.
Центральный угол EOB равен $$frac{360^{circ}}{10}cdot3=108^{circ}$$.
Тогда большая дуга EB равна $$360^{circ}-108^{circ}=252^{circ}$$.
Угол BCE опирается на ту же дугу EB, но является вписанным, поэтому равен половине дуги EB, т. е. $$126^{circ}$$.
Задание 2
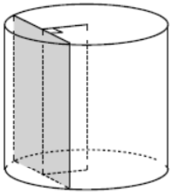
Радиус основания цилиндра равен 10, а его образующая равна 18. Сечение, параллельное оси цилиндра, удалено от неё на расстояние, равное 8. Найдите площадь этого сечения.
Ответ: 216
Скрыть
Для удобства введем буквенные обозначения: О – центр основания цилиндра, DA и СВ – образующие цилиндра, ОН – расстояние от оси до сечения.
Сечение представляет собой прямоугольник, площадь которого равна произведению двух его смежных сторон, а именно:
S = АВ · DA
DA – образующая цилиндра, следовательно DA = 18,
Найдем АВ. Для этого рассмотрим треугольник ОНА. Данный треугольник прямоугольный (с прямым углом Н). Так же в треугольнике известны катет ОН = 8 и гипотенуза OA = 10 (ОА – радиус основания).
По теореме Пифагора найдем катет, АН:
АН2 = ОА2 — ОН2 = 102 – 82 = 36
АН = 6
АВ = АН + ВН, так как АН = ВН = 6, то
АВ = 6 + 6 = 12
Осталось найти площадь сечения:
S = АВ · DA = 12 · 18 = 216 – площадь сечения
Задание 3
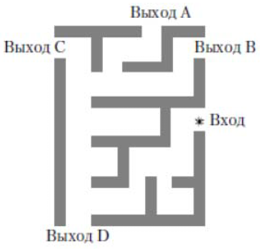
На рисунке изображён лабиринт. Паук заползает в лабиринт в точке «Вход». Развернуться и ползти назад паук не может. На каждом разветвлении паук выбирает путь, по которому ещё не полз. Считая выбор дальнейшего пути случайным, определите, с какой вероятностью паук придёт к выходу D.
Ответ: 0,25
Скрыть
$$P(A)=frac{1}{2}cdotfrac{1}{2}=frac{1}{4}=0,25$$
Задание 4
Турнир по настольному теннису проводится по олимпийской системе в несколько туров: если в туре участвует чётное число игроков, то они разбиваются на случайные игровые пары. Если число игроков нечётно, то с помощью жребия выбираются случайные игровые пары, а один игрок остаётся без пары и не участвует в туре. Проигравший в каждой паре (ничья невозможна) выбывает из турнира, а победители и игрок без пары, если он есть, выходят в следующий тур, который проводится по таким же правилам. Так продолжается до тех пор, пока не останутся двое, которые играют между собой финальный тур, то есть последнюю партию, которая выявляет победителя турнира. Всего в турнире участвует 25 игроков, все они играют одинаково хорошо, поэтому в каждой встрече вероятность выигрыша и поражения у каждого игрока равна 0,5. Среди игроков два друга — Иван и Алексей. Какова вероятность того, что этим двоим в каком-то туре придётся сыграть друг с другом?
Ответ: 0,08
Скрыть
Пусть $$n$$ — число участников.
Всего возможных пар игроков:
$$binom{2}{n}=frac{n!}{2!cdot(n-1)!}=frac{n(n-1)}{2}$$.
Значит, вероятность, что в какой-то одной любой игре будет нужная нам пара игроков:
$$(frac{n(n-1)}{2})^{-1}=frac{2}{n(n-1)}$$.
Так как изначально было $$n$$ игроков и ровно один после каждой игры выбывает, то всего игр будет:
$$n-1$$.
Так как во всех играх вероятность выпадения нужной нам пары игроков одинакова, то искомая вероятность:
$$frac{2}{n(n-1)}cdot(n-1)=frac{2}{n}$$.
$$P(A)=frac{2}{25}=0,08$$
Задание 5
Решите уравнение $$tgfrac{pi(x+1)}{3}=-sqrt{3}$$. В ответе укажите наименьший положительный корень.
Ответ: 1
Скрыть
$$tgfrac{pi(x+1)}{3}=-sqrt{3}Rightarrowfrac{pi(x+1)}{3}=-frac{pi}{3}+pi nRightarrow x+1=-1+3nRightarrow x=-2+3n$$
$$left{begin{matrix} -2+3n>0\ nto min \ nin Z end{matrix}right.Rightarrowleft{begin{matrix} n>frac{2}{3}\ nto min\ nin Z end{matrix}right.Rightarrow n=1:quad x=-2+3cdot1=1$$
Задание 6
Найдите значение выражения $$7cos(pi+beta)-2sin(frac{pi}{2}+beta)$$, если $$cosbeta=-frac{1}{3}$$.
Ответ: 3
Скрыть
$$7cos(pi+beta)-2sin(frac{pi}{2}+beta)=-7cosbeta-2cosbeta=-9cosbeta=-9cdot(-frac{1}{3})=3$$
Задание 7
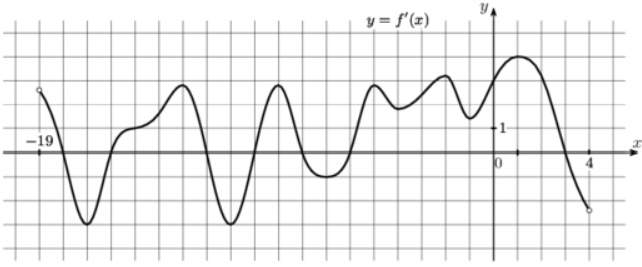
На рисунке изображен график $$y=f'(x)$$ — производной функции $$f(x)$$, определенной на интервале (-19;4). Найдите количество точек минимума функции $$f(x)$$, принадлежащих отрезку [-17;-1].
Ответ: 3
Скрыть
На графике производной точка минимума — точка пересечения оси Ox при возрастании графика.
$$-16; -10; -6Rightarrow 3$$ точки
Задание 8
Скорость колеблющегося на пружине груза меняется по закону $$v(t)=5sin(pi t)$$ (см/с), где $$t$$ — время в секундах. Какую долю времени из первой секунды скорость движения превышала 2,5 см/с? Ответ выразите десятичной дробью, если нужно, округлите до сотых.
Ответ: 0,67
Скрыть
$$5sinpi tgeq2,5$$
$$sinpi tgeq0,5$$
$$frac{pi}{6}+2pi nleqpi tleqfrac{5pi}{6}+2pi n$$
Так как просят в течении первой секунды, то $$n=0$$
$$frac{1}{6}leq tleqfrac{5}{6}$$
$$tau=frac{frac{5}{6}-frac{1}{6}}{1}=frac{2}{3}approx0,67$$
Задание 9
Учебный самолет летел со скоростью 800 км/час. Когда ему осталось пролететь на 90 км больше, чем он пролетел, пилот увеличил скорость до 900 км/час. Средняя скорость на всем пути оказалась равной 850 км/час. Какое расстояние (в км) пролетел самолет всего?
Ответ: 1530
Скрыть
Решение сводится к составлению линейного уравнения. Если принять за $$x$$ расстояние полета с начальной скоростью, тогда:
$$frac{x+x+90}{850}=frac{x}{800}+frac{x+90}{900}$$, т.е. мы уравняли время полета всего расстояния.
Решение (без вычислений НОЗ) приводит нас к такому «упрощенному» виду уравнения:
$$1440000x + 64800000 = 1445000x + 61200000$$ или
$$3600000 = 5000x$$ откуда
имеем $$x = 720, x + 90 = 810$$, а весь путь самолета $$= 1530$$ км.
Задание 10
На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков.
Ответ: 10
Скрыть
Верхний проходит через $$(-1;4)$$ и $$(-3;3)$$. Тогда:
$$left{begin{matrix} 4=-1k+b\ 3=-3k+b end{matrix}right.Leftrightarrowleft{begin{matrix} 1=2k\ 4=-0,5+b end{matrix}right.Leftrightarrowleft{begin{matrix} k=0,5\ b=4,5 end{matrix}right.$$
$$y=0,5x+4,5$$
Нижний через $$(1;-4)$$ и $$(3;-1)$$. Тогда:
$$left{begin{matrix} -4=k+b\ -1=3k+b end{matrix}right.Leftrightarrowleft{begin{matrix} 3=2k\ -4=1,5+b end{matrix}right.Leftrightarrowleft{begin{matrix} k=1,5\ b=-5,5 end{matrix}right.$$
$$y=1,5x-5,5$$
Тогда:
$$0,5x+4,5=1,5x-5,5Rightarrow x=10$$
Задание 11
Найдите наименьшее значение функции $$y=x^5-80x$$ на отрезке [-4;-1].
Ответ: -704
Скрыть
$$y’=5x^4-80$$
$$5x^4-80=0$$
$$5x^4=80$$
$$x^4=16$$
$$x=pm2$$
$$x=2$$ — точка минимума по методу интервалов, но она не попадает в отрезок, проверяем значения концов отрезка.
$$y(-1)=79$$
$$y(-4)=-1024+320=-704$$
Задание 12
А) Решите уравнение $$tg2x=2cos2xcdotctg x$$
Б) Найдите все корни уравнения, принадлежащие отрезку $$[-pi;frac{pi}{2}]$$
Ответ: А)$$pmfrac{pi}{6}+frac{2pi n}{3},nin Z$$ Б)$$-frac{5pi}{6};-frac{pi}{2};-frac{pi}{6};frac{pi}{6};frac{pi}{2}$$
Задание 13
Дан куб ABCDA1B1C1D1 с ребром длины 1. Точка Р — середина A1D1, точка Q делит отрезок АВ1 в отношении 2:1, считая от вершины А, R — точка пересечения отрезков ВС1 и В1С.
А) Найдите площадь сечения куба плоскостью PQR.
Б) Найдите отношение, в котором плоскость сечения делит диагональ АС1 куба.
Ответ: А) $$frac{sqrt{5}}{2}$$ Б) $$frac{2}{1}$$
Задание 14
Решите неравенство: $$8+log_{sqrt{x}}8leq4log_xsqrt{17x^2-2}$$
Ответ: $$(sqrt{frac{2}{17}};frac{1}{2sqrt{2}}],(1;sqrt{2}]$$
Задание 15
В июне 2025 года Анна Михайловна планирует взять кредит в банке на 3 года. Условия его. возврата таковы:
— в январе каждого года долг увеличивается на 10 % от суммы долга на конец предыдущего года;
— в период с февраля по июнь каждого из 2026 и 2027 годов необходимо выплатить часть долга, причём платёж 2027 года в 1,5 раза больше платежа предыдущего года;
— в период с февраля по июнь 2028 года выплачивается оставшаяся сумма по кредиту, равная 2 679 600 рублей.
Найдите сумму кредита, если сумма всех платежей составит 9 179 600 рублей.
Ответ: 7,6 млн
Задание 16
Первая окружность проходит через вершины А и В треугольника АВС и пересекает стороны АС и ВС в точках D и Е соответственно. Вторая окружность проходит через точки D и Е и пересекает продолжения сторон ВС и АС за вершину С в точках М и N соответственно.
А) Докажите, что прямая MN параллельна прямой АВ.
Б) Прямые MD и NE вторично пересекают первую окружность в точках Х и Y соответственно. Найдите ее радиус, если AX=XY=2, а АВ=4.
Ответ: 2
Задание 17
Найдите все значения параметра $$a$$, при каждом из которых неравенство
$$-1leqsin xcdot(a-cos2x)leq1$$
верно при всех действительных значениях $$x$$.
Ответ: $$[1-frac{3}{sqrt[3]{2}};0]$$
Задание 18
В записи натурального числа $$n$$ сделаем замену цифр. Если цифра $$a > 0$$, то заменяем её на цифру $$(10 — a)$$, а если $$a = 0$$, то её не меняем. Обозначим полученное число через $$n^*$$.
А) Может ли быть $$n=10n^*$$?
Б) Какое наибольшее значение может принимать отношение $$frac{n}{n^*}$$?
В) Если $$n$$ делится на $$n^*$$, то чему может быть равно отношение $$frac{n}{n^*}$$?
Ответ: А) нет, Б) 9, В) 1;4;5;9
А. Ларин. Тренировочный вариант № 410.
При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
Версия для печати и копирования в MS Word
1
а) Решите уравнение
б) Найдите все корни уравнения, принадлежащие отрезку
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
2
Дан куб ABCDA1B1C1D1 с ребром длины 1. Точка Р — середина A1D1, точка Q делит отрезок AB1 в отношении 2 : 1, считая от вершины A, R — точка пересечения отрезков BC1 и B1C.
а) Найдите площадь сечения куба плоскостью PQR.
б) Найдите отношение, в котором плоскость сечения делит диагональ AC1 куба.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
3
Решите неравенство:
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
4
В июне 2025 года Анна Михайловна планирует взять кредит в банке на 3 года. Условия его возврата таковы:
— в январе каждого года долг увеличивается на 10% от суммы долга на конец предыдущего года;
— в период с февраля по июнь каждого из 2026 и 2027 годов необходимо выплатить часть долга, причём платёж 2027 года в 1,5 раза больше платежа предыдущего года;
— в период с февраля по июнь 2028 года выплачивается оставшаяся сумма по кредиту, равная 2 679 600 рублей.
Найдите сумму кредита, если сумма всех платежей составит 9 179 600 рублей.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
5
Первая окружность проходит через вершины А и В треугольника ABC и пересекает стороны AC и BC в точках D и E соответственно. Вторая окружность проходит через точки D и E и пересекает продолжения сторон BC и AC за вершину C в точках M и N соответственно.
а) Докажите, что прямая MN параллельна прямой AB.
б) Прямые MD и NE вторично пересекают первую окружность в точках X и Y соответственно. Найдите ее радиус, если a AB = 4.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
6
Найдите все значения параметра a, при каждом из которых неравенство
верно при всех действительных значениях x.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
7
В записи натурального числа n сделаем замену цифр. Если цифра то заменяем её на цифру (10 – a), а если a = 0, то её не меняем. Обозначим полученное число через n*.
а) Может ли быть n = 10n*?
б) Какое наибольшее значение может принимать отношение
в) Если n делится на то чему может быть равно отношение
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
Завершить тестирование, свериться с ответами, увидеть решения.
Вариант 410 Алекса Ларина ЕГЭ 2023 по математике профильный уровень 11 класс с ответами и решением, а также полным видео разбором, который опубликован на сайте 10 декабря 2022 года, по новой демоверсии ЕГЭ 2023 года ФИПИ.
var410
Видео решение заданий варианта
Ответы для варианта
1. ABCDEFGHIJ – правильный десятиугольник. Найдите угол ВСЕ. Ответ дайте в градусах.
2. Радиус основания цилиндра равен 10, а его образующая равна 18. Сечение, параллельное оси цилиндра, удалено от неё на расстояние, равное 8. Найдите площадь этого сечения.
3. На рисунке изображён лабиринт. Паук заползает в лабиринт в точке «Вход». Развернуться и ползти назад паук не может. На каждом разветвлении паук выбирает путь, по которому ещё не полз. Считая выбор дальнейшего пути случайным, определите, с какой вероятностью паук придёт к выходу D.
4. Турнир по настольному теннису проводится по олимпийской системе в несколько туров: если в туре участвует чётное число игроков, то они разбиваются на случайные игровые пары. Если число игроков нечётно, то с помощью жребия выбираются случайные игровые пары, а один игрок остаётся без пары и не участвует в туре. Проигравший в каждой паре (ничья невозможна) выбывает из турнира, а победители и игрок без пары, если он есть, выходят в следующий тур, который проводится по таким же правилам. Так продолжается до тех пор, пока не останутся двое, которые играют между собой финальный тур, то есть последнюю партию, которая выявляет победителя турнира. Всего в турнире участвует 25 игроков, все они играют одинаково хорошо, поэтому в каждой встрече вероятность выигрыша и поражения у каждого игрока равна 0,5. Среди игроков два друга — Иван и Алексей. Какова вероятность того, что этим двоим в каком‐то туре придётся сыграть друг с другом?
9. Учебный самолет летел со скоростью 800 км/час. Когда ему осталось пролететь на 90 км больше, чем он пролетел, пилот увеличил скорость до 900 км/час. Средняя скорость на всем пути оказалась равной 850 км/час. Какое расстояние (в км) пролетел самолет всего?
10. На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков.
15. В июне 2025 года Анна Михайловна планирует взять кредит в банке на 3 года. Условия его. возврата таковы: ‐ в январе каждого года долг увеличивается на 10 % от суммы долга на конец предыдущего года; ‐ в период с февраля по июнь каждого из 2026 и 2027 годов необходимо выплатить часть долга, причём платёж 2027 года в 1,5 раза больше платежа предыдущего года; ‐ в период с февраля по июнь 2028 года выплачивается оставшаяся сумма по кредиту, равная 2 679 600 рублей. Найдите сумму кредита, если сумма всех платежей составит 9 179 600 рублей.
16. Первая окружность проходит через вершины А и В треугольника АВС и пересекает стороны АС и ВС в точках D и Е соответственно. Вторая окружность проходит через точки D и Е и пересекает продолжения сторон ВС и АС за вершину С в точках М и N соответственно. А) Докажите, что прямая MN параллельна прямой АВ. Б) Прямые MD и NE вторично пересекают первую окружность в точках Х и Y соответственно. Найдите ее радиус, если AX=XY=2, а АВ=4.
- Сборник ЕГЭ 2023 Ященко математика 11 класс профиль
- Ларин вариант 409 ЕГЭ 2023 профиль по математике
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
Диагностический вариант СтатГрад ЕГЭ Профиль по математике 2110410-15.03.2022 с ответами и критериями
| Автор | Сообщение | |||||
|---|---|---|---|---|---|---|
|
Заголовок сообщения: Тренировочный вариант №410
|
||||||
|
https://alexlarin.net/ege/2023/trvar410.html |
|||||
  |
||||||
|
|
||||||
|
Kirill Kolokolcev |
Заголовок сообщения: Re: Тренировочный вариант №410
|
|||||
|
Спасибо за интересный вариант! Подробности: |
|||||
  |
||||||
|
OlegTheMath |
Заголовок сообщения: Re: Тренировочный вариант №410
|
|||||
|
Kirill Kolokolcev писал(а): Спасибо за интересный вариант! Подробности: Такой же ответ. 410.16 У меня так получилось: Подробности: 410.13 Подробности: |
|||||
  |
||||||
|
Kirill Kolokolcev |
Заголовок сообщения: Re: Тренировочный вариант №410
|
|||||
|
OlegTheMath писал(а): 410.16 У меня так получилось: Подробности: Также |
|||||
  |
||||||
|
vasikplay |
Заголовок сообщения: Re: Тренировочный вариант №410
|
|||||
|
Интересный варик , вот моя первая часть, только я 4 задание не понял
|
|||||
  |
||||||
|
спастбо |
Заголовок сообщения: Re: Тренировочный вариант №410
|
|||||
|
помогите с 16 задачей, как доказать параллельность? |
|||||
  |
||||||
|
antonov_m_n |
Заголовок сообщения: Re: Тренировочный вариант №410
|
|||||
|
спастбо писал(а): помогите с 16 задачей, как доказать параллельность? Подробные решения будут на сайте в четверг , на картинке подсказка ( докажите равенство накрест лежащих углов )
_________________ |
|||||
  |
||||||
|
Lucky_7_2006 |
Заголовок сообщения: Re: Тренировочный вариант №410
|
|||||
|
1) Сумма противоположных углов вписанного четырёхугольника равна 180 градусам. |
|||||
  |
||||||
|
hpbhpb |
Заголовок сообщения: Re: Тренировочный вариант №410
|
|||||
|
vasikplay писал(а): Интересный варик , вот моя первая часть, только я 4 задание не понял В чт напишу решение 4-й задачи. |
|||||
  |
||||||
|
Владимiръ |
Заголовок сообщения: Re: Тренировочный вариант №410
|
|||||
|
Задача 18 Подробности:
|
|||||
  |
||||||
| Показать сообщения за: Сортировать по: |
Кто сейчас на форуме
|
Сейчас этот форум просматривают: нет зарегистрированных пользователей и гости: 17 |
|
Вы не можете начинать темы |
|
|
Тренировочная работа №1 статград ЕГЭ 2022 по математике 10-11 класс задания и ответы для вариантов базового уровня и профильного уровня. Официальная дата проведения работы: 27.01.2022 (27 января 2022 год).
Скачать варианты базового уровня МА2100101-МА2100108
Скачать варианты профильного уровня МА2100109-МА2100110
Все ответы (решения) и задания (без водяного знака)
Тренировочные варианты базового уровня статград МА2100101 и МА2100102 ЕГЭ 2022 по математике 10-11 класс:
Тренировочные варианты профильного уровня статград МА2100109 МА2100110:
Сложные задания с варианта МА2100101:
2)В пачке 500 листов бумаги формата А4. За неделю в офисе расходуется 1200 листов. Какого наименьшего количества пачек бумаги хватит на 8 недель?
Правильный ответ: 20
4)Результаты соревнований по метанию молота представлены в таблице. Места распределяются по результату лучшей попытки каждого спортсмена: чем дальше он метнул молот, тем лучше. Каков результат лучшей попытки (в метрах) спортсмена, занявшего третье место?
Правильный ответ: 55
6)Футболка стоила 600 рублей. После повышения цены она стала стоить 660 рублей. На сколько процентов была повышена цена футболки?
Правильный ответ: 10
11)Конкурс исполнителей проводится в 5 дней. Всего заявлено 80 выступлений — по одному от каждой страны, участвующей в конкурсе. Исполнитель из России участвует в конкурсе. В первый день запланировано 32 выступления, остальные распределены поровну между оставшимися днями. Порядок выступлений определяется жеребьёвкой. Какова вероятность того, что выступление исполнителя из России состоится в третий день конкурса?
Правильный ответ: 0,15
12)Строительный подрядчик планирует купить 6 тонн облицовочного кирпича у одного из трёх поставщиков. Один кирпич весит 5 кг. Цена кирпича и условия доставки всей покупки приведены в таблице. Во сколько рублей обойдётся наиболее дешёвый вариант покупки с доставкой?
Правильный ответ: 22300
13)Деталь имеет форму изображённого на рисунке многогранника (все двугранные углы прямые). Числа на рисунке обозначают длины рёбер в сантиметрах. Найдите объём этой детали. Ответ дайте в кубических сантиметрах.
Правильный ответ: 21
18)Детям, отдыхающим в лагере, можно купаться на речке или плавать в бассейне. Утром некоторые дети ходили купаться на речку. Днём некоторые дети пойдут плавать в бассейн, причём среди них не будет тех, кто утром ходил купаться на речку. Выберите утверждения, которые будут верны при указанных условиях независимо от того, какие дети пойдут плавать в бассейн. 1) Каждый ребёнок, который не ходил купаться на речку, пойдёт плавать в бассейн. 2) Найдётся ребёнок, который не ходил купаться на речку и не пойдёт плавать в бассейн. 3) Среди детей в этом лагере, которые не пойдут плавать в бассейн, есть хотя бы один, который ходил купаться на речку. 4) В лагере нет ни одного ребёнка, который ходил купаться на речку и пойдёт плавать в бассейн.
Правильный ответ: 34
19)Найдите шестизначное натуральное число, которое записывается только цифрами 0 и 6 и делится на 90. В ответе укажите какое-нибудь одно такое число.
Правильный ответ: 666000
20)В четверг акции компании подорожали на некоторое число процентов, а в пятницу подешевели на то же самое число процентов. В результате они стали стоить на 9 % дешевле, чем при открытии торгов в четверг. На сколько процентов подорожали акции компании в четверг?
Правильный ответ: 30
21)Миша, Коля и Лёша играют в настольный теннис: игрок, проигравший партию, уступает место игроку, не участвовавшему в ней. В итоге оказалось, что Миша сыграл 9 партий, а Коля — 19. Сколько партий сыграл Лёша?
Правильный ответ: 10
Сложные задания с варианта МА2100102:
2)В пачке 500 листов бумаги формата А4. За неделю в офисе расходуется 900 листов. Какого наименьшего количества пачек бумаги хватит на 7 недель?
Правильный ответ: 13
6)Футболка стоила 450 рублей. После повышения цены она стала стоить 540 рублей. На сколько процентов была повышена цена футболки?
Правильный ответ: 20
11)Конкурс исполнителей проводится в 5 дней. Всего заявлено 50 выступлений — по одному от каждой страны, участвующей в конкурсе. Исполнитель из России участвует в конкурсе. В первый день запланировано 14 выступлений, остальные распределены поровну между оставшимися днями. Порядок выступлений определяется жеребьёвкой. Какова вероятность того, что выступление исполнителя из России состоится в третий день конкурса?
Правильный ответ: 0,18
12)Строительный подрядчик планирует купить 20 тонн облицовочного кирпича у одного из трёх поставщиков. Один кирпич весит 5 кг. Цена кирпича и условия доставки всей покупки приведены в таблице. Во сколько рублей обойдётся наиболее дешёвый вариант покупки с доставкой?
Правильный ответ: 212000
13)Деталь имеет форму изображённого на рисунке многогранника (все двугранные углы прямые). Числа на рисунке обозначают длины рёбер в сантиметрах. Найдите объём этой детали. Ответ дайте в кубических сантиметрах.
Правильный ответ: 24
18)Некоторые учащиеся школы съели за завтраком булочку. Некоторые учащиеся этой школы на обед получат пирожок, причём среди них не будет тех, кто съел за завтраком булочку. Выберите утверждения, которые будут верны при указанных условиях независимо от того, кому достанутся пирожки. 1) Нет ни одного учащегося этой школы, который съел булочку за завтраком и получит пирожок на обед. 2) Найдётся учащийся, который не съел булочку за завтраком и не получит пирожок на обед. 3) Каждый учащийся, который не съел булочку за завтраком, получит пирожок на обед. 4) Среди учащихся этой школы, которым не достанется пирожок на обед, есть хотя бы один, который съел булочку за завтраком.
Правильный ответ: 14
19)Найдите шестизначное натуральное число, которое записывается только цифрами 1 и 5 и делится на 45. В ответе укажите какое-нибудь одно такое число.
Правильный ответ: 111555
20)В четверг акции компании подорожали на некоторое число процентов, а в пятницу подешевели на то же самое число процентов. В результате они стали стоить на 36 % дешевле, чем при открытии торгов в четверг. На сколько процентов подорожали акции компании в четверг?
Правильный ответ: 60
21)Миша, Коля и Лёша играют в настольный теннис: игрок, проигравший партию, уступает место игроку, не участвовавшему в ней. В итоге оказалось, что Миша сыграл 13 партий, а Коля — 27. Сколько партий сыграл Лёша?
Правильный ответ: 14
Сложные задания с варианта МА2100105:
2)В летнем лагере на каждого участника полагается 35 г сахара в день. В лагере 205 человек. Какое наименьшее количество килограммовых упаковок сахара нужно на весь лагерь на 7 дней?
Правильный ответ: 51
6)Налог на доходы составляет 13 % от заработной платы. Заработная плата Ивана Кузьмича равна 8000 рублей. Какую сумму он получит после уплаты налога на доходы? Ответ дайте в рублях.
Правильный ответ: 6960
10)Два садовода, имеющие прямоугольные участки размерами 20 м на 30 м с общей границей, договорились и сделали общий круглый пруд площадью 140 квадратных метров (см. чертёж), причём граница участков проходит точно через центр пруда. Какова площадь (в квадратных метрах) оставшейся части участка каждого садовода?
Правильный ответ: 675
11)На чемпионате по прыжкам в воду выступают 25 спортсменов, среди них 8 прыгунов из России и 9 прыгунов из Китая. Порядок выступлений определяется жеребьёвкой. Найдите вероятность того, что первым будет выступать прыгун из Китая.
Правильный ответ: 0,36
13)В бак, имеющий форму правильной четырёхугольной призмы со стороной основания 30 см, налита жидкость. Чтобы измерить объём детали сложной формы, её полностью погружают в эту жидкость. Найдите объём детали, если после её погружения уровень жидкости в баке поднялся на 10 см. Ответ дайте в кубических сантиметрах.
Правильный ответ: 32000
16)Два ребра прямоугольного параллелепипеда равны 1 и 2, а объём параллелепипеда равен 6. Найдите площадь поверхности этого параллелепипеда.
Правильный ответ: 22
18)Тане на день рождения подарили 15 шариков, 8 из которых жёлтые, а остальные зелёные. Таня хочет на трёх шариках нарисовать рисунки маркером, чтобы подарить маме, папе и брату. Выберите утверждения, которые будут верны при указанных условиях независимо от того, на каких шариках Таня нарисует рисунки. 1) Найдётся 2 зелёных шарика без рисунков. 2) Не найдётся 5 жёлтых шариков с рисунками. 3) Если шарик жёлтый, то на нём Таня нарисует рисунок. 4) Найдётся 3 жёлтых шарика с рисунками.
Правильный ответ: 12
19)Найдите чётное четырёхзначное натуральное число, сумма цифр которого на 1 меньше их произведения. В ответе укажите какое-нибудь одно такое число.
Правильный ответ: 1152
20)Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 60 килограммов изюма, если виноград содержит 80 % воды, а изюм содержит 12 % воды?
Правильный ответ: 308
21)В обменном пункте можно совершить одну из двух операций: • за 3 золотые монеты получить 4 серебряные и одну медную; • за 7 серебряных монет получить 4 золотые и одну медную. У Николая были только серебряные монеты. После нескольких посещений обменного пункта серебряных монет у него стало меньше, золотых не появилось, зато появились 42 медные. На сколько уменьшилось количество серебряных монет у Николая?
Правильный ответ: 30
Сложные задания с варианта МА2100109:
2)В среднем из 2000 садовых насосов, поступивших в продажу, 12 подтекают. Найдите вероятность того, что один случайно выбранный для контроля насос не подтекает.
Правильный ответ: 0,99
5)Стороны основания правильной четырёхугольной пирамиды равны 24, боковые рёбра равны 37. Найдите площадь поверхности этой пирамиды.
Правильный ответ: 2256
8)Имеется два сплава. Первый содержит 10 % никеля, второй — 35 % никеля. Из этих двух сплавов получили третий сплав массой 175 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава была меньше массы второго?
Правильный ответ: 35
10)Если шахматист А. играет белыми фигурами, то он выигрывает у шахматиста Б. с вероятностью 0,5. Если А. играет чёрными, то А. выигрывает у Б. с вероятностью 0,3. Шахматисты А. и Б. играют две партии, причём во второй партии играют фигурами другого цвета. Найдите вероятность того, что А. выиграет оба раза.
Правильный ответ: 0,15
13)Точка S лежит вне плоскости прямоугольника АВСD . Известно, что АВ = 8, ВС =12 , SA = 6 , SB =10 , SD = 6 5 . а) Докажите, что прямая SA перпендикулярна плоскости АВС . б) Найдите расстояние от точки А до плоскости SCB.
15)В июле 2022 года планируется взять кредит в банке на четыре года в размере S млн рублей, где S — целое число. Условия его возврата таковы: — каждый январь долг увеличивается на 15 % по сравнению с концом предыдущего года; — с февраля по июнь каждого года необходимо выплатить одним платежом часть долга; — в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей. Найдите наибольшее значение S , при котором каждая из выплат будет меньше 3 млн рублей.
16)Дан треугольник АВС. Точка О — центр вписанной в него окружности. На стороне ВС отмечена такая точка M , что СM = АС и ВM = АО. а) Докажите, что прямые АВ и ОM параллельны. б) Найдите площадь четырёхугольника АВMО, если угол AСB прямой и АС = 4.
18)Юра записывает на доске n-значное натуральное число, не используя цифру 0. Затем он записывает рядом ещё одно число, полученное из исходного перемещением первой цифры на последнее место. (Например, если n =3 и исходное число равно 123, то второе число равно 231.) После этого Юра находит сумму этих двух чисел. а) Может ли сумма чисел на доске равняться 2728, если n = 4? б) Может ли сумма чисел на доске равняться 83 347, если n =5? в) При n =6 оказалось, что сумма чисел делится на 99. Сколько натуральных чисел от 925 111 до 925 999, которые Юра мог использовать в качестве исходного числа?
Сложные задания с варианта МА2100110:
2)В среднем из 1500 садовых насосов, поступивших в продажу, 12 подтекают. Найдите вероятность того, что один случайно выбранный для контроля насос не подтекает.
Правильный ответ: 0,99
5)Стороны основания правильной четырёхугольной пирамиды равны 22, боковые рёбра равны 61. Найдите площадь поверхности этой пирамиды
Правильный ответ: 3124
8)Имеется два сплава. Первый содержит 5 % никеля, второй — 30 % никеля. Из этих двух сплавов получили третий сплав массой 225 кг, содержащий 20% никеля. На сколько килограммов масса первого сплава была меньше массы второго?
Правильный ответ: 45
10)Если шахматист А. играет белыми фигурами, то он выигрывает у шахматиста Б. с вероятностью 0,5. Если А. играет чёрными, то А. выигрывает у Б. с вероятностью 0,34. Шахматисты А. и Б. играют две партии, причём во второй партии играют фигурами другого цвета. Найдите вероятность того, что А. выиграет оба раза.
Правильный ответ: 0.17
15)В июле 2022 года планируется взять кредит в банке на четыре года в размере S млн рублей, где S — целое число. Условия его возврата таковы: — каждый январь долг увеличивается на 12 % по сравнению с концом предыдущего года; — с февраля по июнь каждого года необходимо выплатить одним платежом часть долга; — в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей. Найдите наибольшее значение S , при котором каждая из выплат будет меньше 2 млн рублей.
Правильный ответ: 4
16)Дан треугольник АВС . Точка О — центр вписанной в него окружности. На стороне ВС отмечена такая точка M , что СM АС = и ВM АО = . а) Докажите, что прямые АВ и ОM параллельны. б) Найдите площадь четырёхугольника АВMО , если угол AСB прямой и АС = 6 .
18)Юра записывает на доске n -значное натуральное число, не используя цифру 0. Затем он записывает рядом ещё одно число, полученное из исходного перемещением первой цифры на последнее место. (Например, если n = 3 и исходное число равно 123, то второе число равно 231.) После этого Юра находит сумму этих двух чисел. а) Может ли сумма чисел на доске равняться 2640, если n = 4? б) Может ли сумма чисел на доске равняться 25 795, если n = 5? в) При n = 6 оказалось, что сумма чисел делится на 33. Сколько натуральных чисел от 525 111 до 525 799, которые Юра мог выбрать в качестве исходного числа?
Другие тренировочные варианты ЕГЭ 2022 по математике 11 класс:
Статград пробный ЕГЭ 2022 по математике 11 класс варианты МА2110201-МА2110212 с ответами
Работы СТАТГРАД по математике задания и ответы
Share the post «Варианты МА2100101-МА2100110 ЕГЭ 2022 работа статград математика 10-11 класс с ответами»
- VKontakte
Метки: ЕГЭ 2022заданияматематика 10-11 классответыстатградтренировочная работа