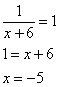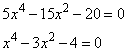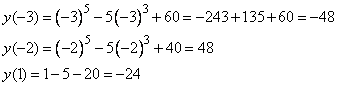500000 решу егэ математика профиль - Помощь в подготовке к экзаменам и поступлению

Образовательный портал для подготовки к экзаменам

Математика профильного уровня

Сайты, меню, вход, новости

Задания

Версия для печати и копирования в MS Word

Дано уравнение

а)  Решите данное уравнение.

б)  Укажите корни данного уравнения, принадлежащие промежутку

Спрятать решение

Решение.

а)  Сведем уравнение к квадратному относительно тангенса:

б)  С помощью числовой окружности находим, что из найденных решений промежутку принадлежат числа

Ответ: а) б)

Спрятать критерии

Критерии проверки:

Критерии оценивания выполнения задания	Баллы
Обоснованно получены верные ответы в обоих пунктах.	2
Обоснованно получен верный ответ в пункте а), ИЛИ получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения пункта а) и пункта б).	1
Решение не соответствует ни одному из критериев, перечисленных выше.	0
Максимальный балл	2

Спрятать решение

Курс Д. Д. Гущина

Андрей Анатольевич 28.09.2016 23:04

Как в пункте б) без калькулятора понять, что такое arctg(1/3)?

Служба поддержки

Угол, тангенс которого равен 1/3, меньше угла, тангенс которого равен 1, то есть меньше 45°.

Эля Газимова 10.04.2017 09:33

Когда сводят уравнение к квадратному относительно тангенса вроде на косинус в квадрате делят и я не понимаю,почему не учитывают,что он мог бы быть равным нулю и тогда делить нельзя..

Александр Иванов

В принципе Вы правы…

НО…

Уравнение вида , где является полным однородным уравнением второй степени и не имеет корней . Поэтому его свободно можно делить на и на , не боясь при этом потерять корни. И такой способ является стандартным для решения подобных уравнений.

Источник

Значения функции: наибольшее и наименьшее

В задании №12 ЕГЭ по математике профильного уровня нам необходимо найти наибольшее или наименьшее значение функции. Для этого необходимо воспользоваться, очевидно, производной. Посмотрим на типовом примере.

Разбор типовых вариантов заданий №12 ЕГЭ по математике профильного уровня

Первый вариант задания (демонстрационный вариант 2018)

Найти точку максимума функции y = ln(x+4)²+2x+7.

Алгоритм решения:

Определяем область определения функции.
Находим производную.
Определяем, в каких точках производная равна 0.
Исключаем точки, не принадлежащие области определения.
Среди оставшихся точек ищем значения х, в которых функция имеет максимум.
Записываем ответ.

Решение:

1. Ищем значения х, при которых логарифм имеет смысл. Для этого решаем неравенство:

(x+4)² > 0

Поскольку квадрат любого числа неотрицателен. Решением неравенства будет лишь то значение х, при котором х+4≠ 0, т.е. при х≠-4.

2. Находим производную:

у’=(ln(x+4)² + 2x + 7)’

По свойству логарифма получаем:

у’=(ln(x+4)² )’+(2x)’+(7)’.

По формуле производной сложной функции:

(lnf)’=(1/f)∙f’. У нас f=(x+4)²

у^, = (ln(x+4)² )’+ 2 + 0 = (1/(x+4)² )∙((x+4)²)’ + 2=(1/(x+4)² 2)∙(х² + 8х + 16)’ +2=2(х + 4) /((х + 4)²) + 2

у’= 2/(х + 4) + 2

3. Приравниваем производную к нулю:

у^, = 0 → (2+2∙(х + 4))/(х + 4)=0,

2 +2х +8 =0, 2х + 10 = 0,

2х = -10,

х = -5

Ответ: -5.

Второй вариант задания (из Ященко, №1)

Найдите точку минимума функции y = x – ln(x+6) + 3.

Алгоритм решения:

Определяем область определения функции.
Находим производную.
Определяем, в каких точках производная равна 0.
Исключаем точки, не принадлежащие области определения.
Среди оставшихся точек ищем значения х, в которых функция имеет минимум.
Записываем ответ.

Решение:

1. ОДЗ: .

2. Найдем производную функции:

3. Приравниваем полученное выражение к нулю:

4. Получили одну точку x=-5, принадлежащую области определения функции.

5. В этой точке функция имеет экстремум. Проверим, минимум ли это. При х=-4

При х=-5,5 производная функции отрицательна, так как

Значит, точка х=-5 является точкой минимума.

Ответ: -5.

Третий вариант задания (из Ященко, №12)

Найдите наибольшее значение функции 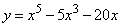на отрезке [-3; 1].

Алгоритм решения:.

Находим производную.
Определяем, в каких точках производная равна 0.
Исключаем точки, не принадлежащие заданному отрезку.
Среди оставшихся точек ищем значения х, в которых функция имеет максимум.
Находим значения функции на концах отрезка.
Ищем среди полученных значений наибольшее.
Записываем ответ.

Решение:

1. Вычисляем производную от функции, получим

2. Приравниваем производную к нулю:

Решение уравнения дает два корня

— не принадлежит множеству действительных чисел

3. Значение и остается одна точка .

4. Вычисляем значения функции в точке -2 и на концах отрезка -3 и 1, получим:

Наибольшее значение функции на заданном отрезке равно 48 в точке х=-2.

Ответ: 48.

Источник

Главная
Новости
ЕГЭ
- ЕГЭ Профиль 2023
- ЕГЭ Профиль 2022
- ЕГЭ Профиль 2016-2021
- Варианты профильного ЕГЭ
- ЕГЭ База 2023
- ЕГЭ База 2022
- ЕГЭ База 2016-2021
ОГЭ
- ОГЭ 2019
- ОГЭ 2023
ГВЭ
- ГВЭ 11 класс
ВПР
- ВПР 4 класс
- ВПР 5 класс
- ВПР 6 класс
- ВПР 7 класс
- ВПР 8 класс
Алгебра
- Алгебра 7-9
- Алгебра 10-11
Геометрия
- Геометрия 7-9
- Геометрия 10-11
YouTube
Прочее
- Class100
- Разработки
- Обо мне
- Репетитор

Тренировочные варианты профильного ЕГЭ 2023 по математике с ответами.

Тренировочные варианты профильного ЕГЭ 2023 по математике с ответами.admin2023-03-05T21:56:54+03:00

Используйте LaTeX для набора формулы

Источник

Новые тренировочные варианты ЕГЭ 2023 по математике базовый и профильный уровень с ответами и решением для 10 и 11 класса, больше 100 вариантов в формате реального экзамена ФИПИ вы можете решать онлайн или скачать.

Тренировочные варианты ЕГЭ 2023 по математике база и профиль

13.09.2022 Тренировочный вариант №1 ЕГЭ 2023 по математике профиль с ответами

20.09.2022 Тренировочный вариант №2 ЕГЭ 2023 по математике профиль с ответами

20.09.2022 Тренировочный вариант №2 ЕГЭ 2023 база по математике с ответами

27.09.2022 Математика 11 класс профиль входная мониторинговая работа 3 варианта с ответами

28.09.2022 Тренировочный вариант №3 ЕГЭ 2023 база по математике с ответами

28 сентября 2022 Статград математика 11 класс ЕГЭ 2023 база и профиль варианты и ответы

29 сентября 2022 Тренировочный вариант №3 ЕГЭ 2023 по математике профиль с ответами

1 октября 2022 Ларин вариант 399 ЕГЭ 2023 по математике профиль решение с ответами

6 октября Тренировочный вариант №4 ЕГЭ 2023 база по математике с ответами

6 октября Тренировочный вариант №4 ЕГЭ 2023 по математике профиль с ответами

8 октября Ларин вариант 400 ЕГЭ 2023 по математике профиль решение с ответами

12 октября Тренировочный вариант №5 ЕГЭ 2023 база по математике с ответами

12 октября Тренировочный вариант №5 ЕГЭ 2023 по математике профиль с ответами

14 октября Вариант 1 Ященко ЕГЭ 2023 математика профиль с ответами и решением

14 октября Вариант 2 Ященко ЕГЭ 2023 математика профиль с ответами и решением

15 октября Ларин вариант 401 ЕГЭ 2023 по математике профиль решение с ответами

15 октября Ларин вариант 402 ЕГЭ 2023 по математике профиль решение с ответами

16 октября Вариант 3 Ященко ЕГЭ 2023 математика профиль с ответами и решением

16 октября Вариант 4 Ященко ЕГЭ 2023 математика профиль с ответами и решением

23 октября Тренировочный вариант №6 ЕГЭ 2023 база по математике с ответами

24 октября Тренировочный вариант №6 ЕГЭ 2023 по математике профиль с ответами

25 октября Тренировочный вариант №7 ЕГЭ 2023 база по математике с ответами

26 октября Тренировочный вариант №7 ЕГЭ 2023 по математике профиль с ответами

28 октября Ларин вариант 403 ЕГЭ 2023 по математике профиль решение с ответами

29 октября Ларин вариант 404 ЕГЭ 2023 по математике профиль решение с ответами

1 ноября 2022 Тренировочный вариант №8 решу ЕГЭ 2023 база по математике с ответами

1 ноября 2022 Тренировочный вариант №8 решу ЕГЭ 2023 по математике профиль с ответами

5 ноября 2022 Вариант 1-2 распечатай и реши ЕГЭ 2023 база по математике 11 класс с ответами

6 ноября 2022 Ларин вариант 405 ЕГЭ 2023 профиль по математике решение с ответами

9 ноября 2022 Тренировочный вариант №9 решу ЕГЭ 2023 база по математике с ответами

12 ноября 2022 Тренировочный вариант №9 решу ЕГЭ 2023 по математике профиль с ответами

13 ноября 2022 Ларин вариант 406 ЕГЭ 2023 профиль по математике решение с ответами

15 ноября 2022 Тренировочный вариант №10 решу ЕГЭ 2023 база по математике 11 класс с ответами

15 ноября 2022 Тренировочный вариант №10 решу ЕГЭ 2023 по математике профиль с ответами

21 ноября 2022 Ларин вариант 407 ЕГЭ 2023 профиль по математике решение с ответами

23 ноября 2022 Тренировочный вариант №11 решу ЕГЭ 2023 база по математике 11 класс с ответами

23 ноября 2022 Тренировочный вариант №11 решу ЕГЭ 2023 по математике профиль с ответами

27 ноября 2022 Ларин вариант 408 ЕГЭ 2023 профиль по математике решение с ответами

28 ноября 2022 Вариант 3-4 распечатай и реши ЕГЭ 2023 база по математике 11 класс с ответами

30 ноября 2022 Мониторинговая работа по математике 11 класс ЕГЭ 2023 профиль 1 полугодие

3 декабря 2022 Тренировочный вариант №12 решу ЕГЭ 2023 база по математике 11 класс с ответами

3 декабря 2022 Тренировочный вариант №12 решу ЕГЭ 2023 по математике профиль с ответами

3 декабря 2022 Пробник ЕГЭ 2023 Москва по математике профиль задания и ответы

5 декабря 2022 Ларин вариант 409 ЕГЭ 2023 профиль по математике решение с ответами

9 декабря 2022 Тренировочный вариант №13 решу ЕГЭ 2023 база по математике 11 класс с ответами

10 декабря 2022 Тренировочный вариант №13 решу ЕГЭ 2023 профиль по математике 11 класс с ответами

12 декабря 2022 Ларин вариант 410 ЕГЭ 2023 профиль по математике решение с ответами

13 декабря 2022 Статград математика 11 класс профиль ЕГЭ 2023 варианты МА2210209-МА2210212 и ответы

13 декабря 2022 Математика 11 класс база ЕГЭ 2023 статград варианты и ответы

15 декабря 2022 Тренировочный вариант №14 решу ЕГЭ 2023 профиль по математике 11 класс с ответами

15 декабря 2022 Тренировочный вариант №14 решу ЕГЭ 2023 база по математике 11 класс с ответами

20 декабря 2022 Вариант 5-6 распечатай и реши ЕГЭ 2023 база по математике 11 класс с ответами

20 декабря 2022 Ларин вариант 411 ЕГЭ 2023 профиль по математике решение с ответами

3 января 2023 Ларин вариант 412 ЕГЭ 2023 профиль по математике решение с ответами

6 января 2023 Тренировочный вариант 1-2 ЕГЭ 2023 профиль математика задания и ответы

8 января 2023 Вариант 3-4 ЕГЭ 2023 профиль математика задания и ответы

9 января 2023 Вариант 7-8 распечатай и реши ЕГЭ 2023 база по математике 11 класс с ответами

10 января 2023 Тренировочный вариант №15 и №16 решу ЕГЭ 2023 профиль по математике 11 класс с ответами

11 января 2023 ЕГЭ 2023 математика тренировочные задания и ответы Ященко, Семенов

11 января 2023 Тренировочный вариант №15 и №16 база ЕГЭ 2023 по математике 11 класс с ответами

19 января 2023 Тренировочные варианты №17 и №18 решу ЕГЭ 2023 профиль по математике 11 класс с ответами

22 января 2023 Ларин вариант 413 и 414 ЕГЭ 2023 профиль по математике решение и ответы

22 января 2023 Тренировочный 19 вариант решу ЕГЭ 2023 профиль по математике 11 класс с ответами

22 января 2023 База ЕГЭ 2023 математика 11 класс тренировочный вариант 19 с ответами

25 января 2023 База ЕГЭ 2023 математика 11 класс тренировочный вариант 20 с ответами

27 января 2023 Тренировочный вариант №20 решу ЕГЭ 2023 профиль по математике 11 класс с ответами

28 января 2023 Вариант 415 Ларина ЕГЭ 2023 по математике 11 класс задания и ответы

2 февраля 2023 Вариант 21 база ЕГЭ 2023 математика 11 класс тренировочный вариант с ответами

2 февраля 2023 Тренировочный вариант №21 решу ЕГЭ 2023 профиль по математике 11 класс с ответами

8 февраля 2023 Математика 10-11 класс ЕГЭ 2023 статград варианты база и профиль МА2200101-МА2200110 и ответы

11 февраля 2023 Тренировочный вариант №22 решу ЕГЭ 2023 профиль по математике 11 класс с ответами

11 февраля 2023 Тренировочный вариант №22 решу ЕГЭ 2023 база по математике 11 класс с ответами

12 февраля 2023 Вариант 416 Ларина ЕГЭ 2023 по математике 11 класс задания и ответы

12 февраля 2023 Вариант 417 Ларина ЕГЭ 2023 по математике 11 класс задания и ответы

13 февраля 2023 Вариант 9 и вариант 10 ЕГЭ 2023 база математика распечатай и реши задания

13 февраля 2023 Вариант 11 и вариант 12 ЕГЭ 2023 база математика распечатай и реши

16 февраля 2023 Тренировочный вариант №23 решу ЕГЭ 2023 база по математике 11 класс с ответами

16 февраля 2023 Тренировочный вариант №23 решу ЕГЭ 2023 профиль по математике 11 класс с ответами

18 февраля 2023 Вариант 418 Ларина ЕГЭ 2023 по математике 11 класс задания и ответы

22 февраля 2023 Пробный ЕГЭ 2023 вариант 24 база по математике 11 класс с ответами

22 февраля 2023 Пробный ЕГЭ 2023 вариант 24 профиль по математике 11 класс с ответами

25 февраля 2023 Вариант 419 Ларина ЕГЭ 2023 по математике 11 класс задания и ответы

28 февраля 2023 Статград математика 11 класс ЕГЭ 2023 база и профиль и ответы

4 марта 2023 Пробник ЕГЭ 2023 вариант 25 база по математике 11 класс с ответами

4 марта 2023 Вариант 420 Ларин ЕГЭ 2023 по математике 11 класс задания и ответы

5 марта 2023 Пробник ЕГЭ 2023 вариант 25 профиль по математике 11 класс с ответами

8 марта 2023 Пробник ЕГЭ 2023 вариант 26 профиль по математике 11 класс с ответами

8 марта 2023 Пробник ЕГЭ 2023 вариант 26 база по математике 11 класс 100 баллов с ответами

Смотрите также на нашем сайте:

Сборник Ященко ЕГЭ 2023 математика профильный уровень 36 вариантов

ПОДЕЛИТЬСЯ МАТЕРИАЛОМ

Источник

Задание 12 Профильного ЕГЭ по математике – это решение уравнений. Чаще всего, конечно, это тригонометрические уравнения. Но встречаются и другие типы – показательные, логарифмические, комбинированные.

Сейчас задание 12 Профильного ЕГЭ на решение уравнения состоят из двух пунктов: собственно решения и отбора корней на определенном отрезке.

Что нужно знать, чтобы справиться с этой задачей на ЕГЭ? Вот необходимые темы для повторения.

^NewЗадачи из сборников Ященко, 2021 год

Квадратные уравнения

Показательные уравнения

Логарифмические уравнения

Модуль числа

Уравнения с модулем

Тригонометрический круг

Формулы тригонометрии

Формулы приведения

Простейшие тригонометрические уравнения 1

Простейшие тригонометрические уравнения 2

Тригонометрические уравнения

Что необходимо помнить при решении уравнений?

1) Помним про область допустимых значений уравнения! Если в уравнении есть дроби, корни, логарифмы или арксинусы с арккосинусами — сразу записываем ОДЗ. А найдя корни, проверяем, входят они в эту область или нет. Есть в уравнении есть tg x — помним, что он существует, только если

2) Стараемся записывать решение в виде цепочки равносильных переходов.

3) Если есть возможность сделать замену переменной — делаем замену переменной! Уравнение сразу станет проще.

4) Если еще не выучили формулы тригонометрии — пора это сделать! Много формул не нужно. Самое главное — тригонометрический круг, формулы синусов и косинусов двойных углов, синусов и косинусов суммы (разности), понижения степени. Формулы приведения не надо зубрить наизусть! Надо знать, как они получаются.

5) Как отбирать решения с помощью тригонометрического круга? Вспомним, что крайняя правая точка тригонометрического круга соответствует числам Дальше всё просто. Смотрим, какая из точек этого типа попадает в указанный в условии промежуток. И к ней прибавляем (или вычитаем) нужные значения.

Например, вы нашли серию решений $x=frac{pi}{3}+2pi n$ , где — целое, а найти надо корни на отрезке $left [frac{5 pi}{2};frac{9 pi}{2} right ].$ На указанном промежутке лежит точка 4 pi . От нее и будем отсчитывать. Получим: $x=4 pi +frac{pi}{3}=frac{13 pi}{3}.$

6) Получив ответ, проверьте его правильность. Просто подставьте найденные решения в исходное уравнение!

Давайте потренируемся.

а) Решите уравнение $2{{sin}^2 left(frac{pi }{2}+xright)}=-sqrt{3}{cos x}$

б) Найдите все корни этого уравнения, принадлежащие промежутку $left[-3pi right.;left.-frac{3pi }{2}right]$

$2{{sin}^2 left(frac{pi }{2}+xright)}=-sqrt{3}{cos x}$

Упростим левую часть по формуле приведения.

$2{{cos}^2 x+sqrt{3}{cos x}=0}$

Вынесем {cos x} за скобки. Произведение двух (или нескольких) множителей равно нулю тогда и только тогда, когда хотя бы один из них равен нулю.

б) Отметим на тригонометрическом круге найденные серии решений и отрезок $left[-3pi right.;left.-frac{3pi }{2}right].$

Видим, что указанному отрезку принадлежат решения $-frac{17pi }{6};-frac{5pi }{2};-frac{3pi }{2}.$

Ответ: $-frac{17pi }{6};-frac{5pi }{2};-frac{3pi }{2}.$

Как отбирать решения с помощью тригонометрического круга? Вспомним, что крайняя правая точка тригонометрического круга соответствует числам Дальше всё просто. Смотрим, какая из точек этого типа попадает в указанный в условии промежуток. И к ней прибавляем (или вычитаем) нужные значения.

Например, вы нашли серию решений $x=frac{pi }{3}+2pi n$ , где — целое, а найти надо корни на отрезке $[frac{5pi }{2};frac{9pi }{2}].$ На указанном промежутке лежит точка 4 pi. От нее и отсчитываем.

Получим: $x=4pi +frac{pi }{3}=frac{13pi }{3}.$

2. а) Решите уравнение ${({27}^{{cos x}})}^{{sin x}}=3^{frac{3{cos x}}{2}}$

б) Найдите все корни этого уравнения, принадлежащие отрезку $left[-pi ;frac{pi }{2}right].$

Это уравнение — комбинированное. Кроме тригонометрии, применяем свойства степеней.

а) $3^{3{cos x{sin x}}}=3^{frac{3{cos x}}{2}}$

Степени равны, их основания равны. Значит, равны и показатели.

$3{cos x{sin x}}=frac{3{cos x}}{2}$

${cos x({sin x-frac{1}{2})=0}}$

Это ответ в пункте (а).

б) Отберем корни, принадлежащие отрезку $left[-pi ;frac{pi }{2}right].$

Отметим на тригонометрическом круге отрезок $left[-pi ;frac{pi }{2}right]$ и найденные серии решений.

Видим, что указанному отрезку принадлежат точки $x=-frac{pi }{2}$ и $x=frac{pi }{2}$ из серии $x=frac{pi }{2}+pi n,nin z.$

Точки серии $x=frac{5pi }{6}+2pi n,nin z$ не входят в указанный отрезок.

А из серии $x=frac{pi }{6}+2pi n,nin z$ в указанный отрезок входит точка $x=frac{pi }{6}.$

Ответ в пункте (б): $-frac{pi }{2},frac{pi }{6} , frac{pi }{2}.$

3. а) Решите уравнение ${cos 2x}+{{sin}^2 x=0,5}$

б) Найдите все корни этого уравнения, принадлежащие отрезку $left[-frac{7pi }{2}right.;left.-2pi right].$

а)
${cos 2x}+{{sin}^2 x=0,5}$

Применим формулу косинуса двойного угла: $boldsymbol{cos2alpha =1-{2sin}^2alpha }$

$1-2{{sin}^2 x}+{{sin}^2 x}=0,5$

${{-sin}^2 x=-0,5}$

${{sin}^2 x=0,5}$

Перенесем всё в левую часть уравнения и разложим по формуле разности квадратов.

Обратите внимание: мы отметили серии решений на тригонометрическом круге. Это помогло нам увидеть, как их записать одной формулой.

б) Для разнообразия отберем корни на отрезке $left[-frac{7pi }{2}right.;left.-2pi right]$ с помощью двойного неравенства.

Сначала серия $x=frac{pi }{4}+pi n,nin Z.$

$-frac{7pi }{2}le frac{pi }{4}+pi nle -2pi$

$-frac{7}{2}le frac{1}{4}+nle -2$

$n=-3, x_1=frac{pi }{4}-3pi =-frac{11pi }{4}$

Теперь серия $x=-frac{pi }{4}+pi n,nin Z$

$-frac{7pi }{2}le -frac{pi }{4}+pi nle -2pi$

$-frac{7}{2}le -frac{1}{4}+nle -2$

$n=-3, x_2=-frac{pi }{4}-3pi =-frac{13pi }{4}$

$n=-2, x_3=-frac{pi }{4}-2pi =-frac{9pi }{4}$

Ответ: $-frac{13pi }{4};-frac{11pi }{4};-frac{9pi }{4}$ .

Какой способ отбора корней лучше — с помощью тригонометрического круга или с помощью двойного неравенства? У каждого из них есть «плюсы» и «минусы».

Пользуясь тригонометрическим кругом, вы не ошибетесь. Вы видите и интервал, и сами серии решений. Это наглядный способ.

Зато, если интервал больше, чем один круг, удобнее отбирать корни с помощью двойного неравенства. Например, надо найти корни из серии $x=-frac{pi }{4}+2pi n,nin Z$ на отрезке $left[-frac{pi }{2}right.;left.20pi right].$ Это больше 10 кругов! Конечно, в таком случае лучше решить двойное неравенство.

4. а) Решите уравнение $left({tg}^2x-3right)sqrt{11{cos x}}=0.$

б) Найдите все корни этого уравнения, принадлежащие отрезку $left[-frac{5pi }{2};-pi right].$

Самое сложное здесь — область допустимых значений (ОДЗ). Условие заметно сразу. А условие появляется, поскольку в уравнении есть ${tg x=frac{{sin x}}{{cos x}}}.$

ОДЗ:

Уравнение равносильно системе:

Отберем решения с помощью тригонометрического круга. Нам нужны те серии решений, для которых , то есть те, что соответствуют точкам справа от оси .

Ответ в пункте а) $x=pm frac{pi }{3}+2pi n, nin z$

б) Отметим на тригонометрическом круге найденные серии решений и отрезок $left[-frac{5pi }{2};-pi right].$

Как обычно, ориентируемся на начало круга. Видим, что указанному промежутку принадлежат точки

$x=frac{pi }{3}-2pi =-frac{5pi }{3}$ и $x=-frac{pi }{3}-2pi =-frac{7pi }{3}.$

5. а) Решите уравнение $sqrt{{cos x+{sin x}}}({{cos}^2 x-frac{1}{2})=0}$

б) Найдите корни, принадлежащие отрезку

Выражение под корнем должно быть неотрицательно, а произведение двух множителей равно нулю тогда и только тогда, когда хотя бы один из них равен нулю.

Это значит, что уравнение равносильно системе:

Решим эту систему с помощью тригонометрического круга. Отметим на нем углы, для которых ${cos x}=frac{sqrt{2}}{2}$ или ${cos x}=-frac{sqrt{2}}{2}$ . Заметим, что среди них находятся и углы, для которых tgx=-1.

Числа серии $x=-frac{3pi }{4}+2pi n$ не могут быть корнями исходного уравнения, т.к. для этих чисел не выполнено условие . Остальные серии решений нас устраивают.

Тогда в ответ в пункте (а) войдут серии решений:

б) Отберем корни, принадлежащие отрезку любым способом — с помощью тригонометрического круга или с помощью двойного неравенства.

На отрезке нам подходит корень $x =-frac{pi }{4}$ .

На отрезке нам подходят корни $x=frac{pi }{4};frac{3pi }{4};frac{7pi }{4}$ .

На отрезке — корни $x= frac{9pi }{4} ; frac{11pi }{4};frac{15pi }{4}.$

Ответ в пункте б): $-frac{pi }{4};frac{3pi }{4};frac{7pi }{4};frac{pi }{4};frac{9pi }{4} ; frac{11pi }{4};frac{15pi }{4}.$

Главная » Решенные примеры » Профиль » Примеры задания 12 (профиль)

В категории решенных примеров: 102
Показано примеров: 1-10

Страницы: 1 2 3 … 10 11 »

Сортировать по:
Дате ·
Названию ·
Рейтингу ·
Комментариям ·
Загрузкам ·
Просмотрам

Пример №102 из задания 12 (профильный уровень)

Найдите точку минимума функции `y=-x/(x^2+484)`.

Примеры задания 12 (профиль) |
Просмотров: 4058 |
Добавил: Администратор |
Дата: 19.08.2018
| Комментарии (0)

Пример №101 из задания 12 (профильный уровень)

Найдите наибольшее значение функции `y=ln(x+3)^2-2x` на отрезке `[-2,5;0]`.

Примеры задания 12 (профиль) |
Просмотров: 2982 |
Добавил: Администратор |
Дата: 19.08.2018
| Комментарии (0)

Пример №100 из задания 12 (профильный уровень)

Найдите точку максимума функции `y=-(x)/(x^2+729)`.

Примеры задания 12 (профиль) |
Просмотров: 5541 |
Добавил: Администратор |
Дата: 19.08.2018
| Комментарии (0)

Пример №99 из задания 12 (профильный уровень)

Найдите наибольшее значение функции `y=ln(x+8)^3-3x` на отрезке `[-7,5;0]`.

Примеры задания 12 (профиль) |
Просмотров: 1906 |
Добавил: Администратор |
Дата: 18.08.2018
| Комментарии (0)

Пример №98 из задания 12 (профильный уровень)

Найдите наибольшее значение функции `y=sqrt(-12-8x-x^2)`.

Примеры задания 12 (профиль) |
Просмотров: 4693 |
Добавил: Администратор |
Дата: 18.08.2018
| Комментарии (0)

Пример №97 из задания 12 (профильный уровень)

Найдите точку минимума функции `y=(6-4x)cosx+4sinx+6`, принадлежащую промежутку `(0;pi/2)`.

Примеры задания 12 (профиль) |
Просмотров: 2659 |
Добавил: Администратор |
Дата: 18.08.2018
| Комментарии (0)

Пример №96 из задания 12 (профильный уровень)

Найдите наибольшее значение функции `y=x^3-6x^2+9x+5` на отрезке `[0,5;2]`.

Примеры задания 12 (профиль) |
Просмотров: 2091 |
Добавил: Администратор |
Дата: 18.08.2018
| Комментарии (0)

Пример №95 из задания 12 (профильный уровень)

Найдите наименьшее значение функции `y=sqrt(x^2+12x+40)`.

Примеры задания 12 (профиль) |
Просмотров: 3599 |
Добавил: Администратор |
Дата: 18.08.2018
| Комментарии (0)

Пример №94 из задания 12 (профильный уровень)

Найдите точку максимума функции `y=(2x-3)cosx-2sinx+2`, принадлежащую промежутку `(0;pi/2)`.

Примеры задания 12 (профиль) |
Просмотров: 1733 |
Добавил: Администратор |
Дата: 18.08.2018
| Комментарии (0)

Пример №93 из задания 12 (профильный уровень)

Найдите наименьшее значение функции `y=sqrt(x^2-10x+29)`.

Примеры задания 12 (профиль) |
Просмотров: 3720 |
Добавил: Администратор |
Дата: 18.08.2018
| Комментарии (0)

1-10 11-20 21-30 … 91-100 101-102

Источник

Задача 31457 В июле планируется взять кредит в банке…

Условие

В июле планируется взять кредит в банке на сумму 500000 рублей. Условия возврата таковы:

• каждый январь долг увеличивается на 17 % по сравнению с концом предыдущего года;

• с февраля по июнь каждого года необходимо выплатить одном платежом часть долга.

Найдите сумму выплаты в первый год, если известно, что кредит будет полностью погашен за два года и во второй год будет выплачено 409500 рублей.

математика 10-11 класс
5742

Все решения

Написать комментарий

Источник