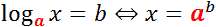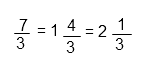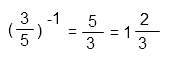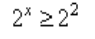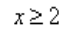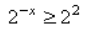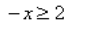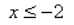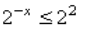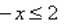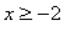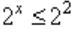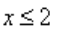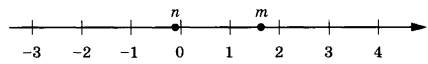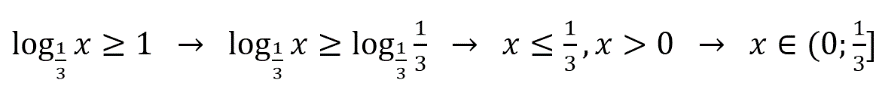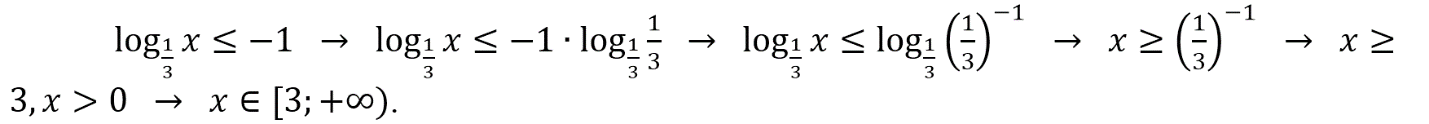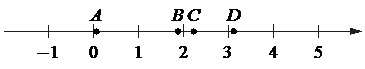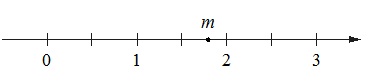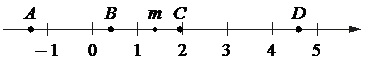Задания
Версия для печати и копирования в MS Word
Тип 1 № 500952
В треугольнике ABC угол C равен
Найдите
Спрятать решение
Решение.
Зная, что а
по определению косинуса имеем:
Тогда по теореме Пифагора
Приведем другое решение
Ответ: 6.
Аналоги к заданию № 27240: 26095 29575 29579 500952 29538 29539 29540 29541 29542 29543 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 1.2.1 Синус, косинус, тангенс, котангенс произвольного угла, 5.1.1 Треугольник
Спрятать решение
·
Прототип задания
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
Meet the Instructors
Course content
loading…
Price:
Free
Share this course
https://stepik.org/course/161885/promo
Price:
Free
На какие числа делится число онлайн калькулятор. Посчитать делители числа.
Какие числа делятся на 500952?
На число 500952 без остатка (нацело) делятся следующие числа: 500952, 1001904, 1502856, 2003808, 2504760, 3005712, 3506664, 4007616, 4508568, 5009520, 5510472, 6011424 и многие другие.
Какие четные числа делятся на 500952?
На число 500952 делятся следующие четные числа: 500952, 1001904, 1502856, 2003808, 2504760, 3005712, 3506664, 4007616, 4508568, 5009520, 5510472, 6011424 и многие други.
Какие нечетные числа делятся на 500952?
Таких чисел нет
На какое наибольшее число делится число 500952 без остатка?
Наибольшее число на которое делится число 500952 есть само число 500952. т.е делиться на само себя без остатка.
На какое наибольшее число делится число 500952 без остатка, не считая числа 500952 и 1?
Наибольшим делителем числа 500952 не считая самого числа 500952 является число 250476.
Какое наименьшее натуральное число делится на 500952?
Наименьшее натуральное число которое делиться на число 500952 является само число 500952.
На какое наименьшее натуральное число делится число 500952?
Наименьшее натуральное число на которое можно разделить число 500952 — это число 1.
Делители числа 500952.
(что бы не забыть запишите все делители числа 500952 в блокнот.)На какие целые и(или) натуральные числа делится число 500952?
Число 500952 делится на следующие целые, натуральные числа (все делители числа 500952): 1, 2, 3, 4, 6, 8, 12, 24, 20873, 41746, 62619, 83492, 125238, 166984, 250476, 500952
На какие четные числа делится число 500952?
Число 500952 делится на следующие четные числа (четные делители числа): 2, 4, 6, 8, 12, 24, 41746, 83492, 125238, 166984, 250476, 500952
На какие нечетные числа делится число 500952?
Число 500952 делится на следующие нечетные числа (нечетные делители числа): 1, 3, 20873, 62619
Сколько делителей имеет число 500952?
Число 500952 имеет 16 делителей
Сколько четных делителей имеет число 500952?
Число 500952 имеет 12 четных делителей
Сколько нечетных делителей имеет число 500952?
Число 500952 имеет 4 нечетных делителя
Число 500952 прописью, словами.
— пятьсот тысяч девятьсот пятьдесят два
(что бы не забыть запишите число 500952 прописью в блокнот.)
Числа кратные 500952.
— кратные числа, числу 500952 : 1001904, 1502856, 2003808, 2504760, 3005712, 3506664, 4007616, 4508568, 5009520, 5510472, 6011424 и многие другие.
Простые множители числа 500952.
У числа 500952 нет простых множителей кроме 1.
Сумма цифр числа 500952.
Сумма цифр числа 500952 равна 21
Произведение цифр числа 500952.
Произведение цифр числа 500952 равна 0
Квадрат числа 500952.
Квадрат числа 500952 равен 250952906304
Куб числа 500952.
Куб числа 500952 равен 125715360318801408
Квадратный корень числа 500952.
Квадратный корень числа 500952 равен 707.7796.
Число 500952 в двоичной системе счисления.
Запись числа 500952 в двоичной системе счисления выглядит так: 1111010010011011000
Количество значащих нулей в двоичной записи числа 500952 = 9
Количество едениц в двоичной записи числа 500952 = 10
(что бы не забыть запишите число 500952 в двоичной системе счисления в блокнот.)Число 500952 в шестнадцатеричной системе счисления.
Запись числа 500952 в шестнадцатеричной системе счисления выглядит так: 7a4d8
(что бы не забыть запишите число 500952 в шестнадцатеричной системе счисления в блокнот.)Число 500952 в восьмеричной системе счисления.
Запись числа 500952 в восьмеричной системе счисления выглядит так: 1722330
(что бы не забыть запишите число 500952 в восьмеричной системе счисления в блокнот.)Число 500952 не является простым!
Корни числа 500952.
Корень 3 степени из 500952.
Корень 3 (третьей) степени из 500952 равен 79.420394188502
Корень 4 степени из 500952.
Корень 4 (четвертой) степени из 500952 равен 26.604128001498
Корень 5 степени из 500952.
Корень 5 (пятой) степени из 500952 равен 13.802546628274
Корень 6 степени из 500952.
Корень 6 (шестой) степени из 500952 равен 8.911812059761
Корень 7 степени из 500952.
Корень 7 (седьмой) степени из 500952 равен 6.5201349984856
Корень 8 степени из 500952.
Корень 8 (восьмой) степени из 500952 равен 5.1579189603461
Корень 9 степени из 500952.
Корень 9 (девятой) степени из 500952 равен 4.2984381237301
Корень 10 степени из 500952.
Корень 10 (десятой) степени из 500952 равен 3.715177873033
Корень 11 степени из 500952.
Корень 11 (одиннадцатой) степени из 500952 равен 3.2973365995511
Корень 12 степени из 500952.
Корень 12 (двенадцатой) степени из 500952 равен 2.9852658273194
Корень 13 степени из 500952.
Корень 13 (тринадцатой) степени из 500952 равен 2.7443901694172
Корень 14 степени из 500952.
Корень 14 (четырнадцатой) степени из 500952 равен 2.5534555015675
Корень 15 степени из 500952.
Корень 15 (пятнадцатой) степени из 500952 равен 2.3987578426455
Степени числа 500952.
500952 в 3 степени.
500952 в 3 степени равно 125715360318801408.
500952 в 4 степени.
500952 в 4 степени равно 6.2977361182424E+22.
500952 в 5 степени.
500952 в 5 степени равно 3.1548635039058E+28.
500952 в 6 степени.
500952 в 6 степени равно 1.5804351820086E+34.
500952 в 7 степени.
500952 в 7 степени равно 7.9172216529758E+39.
500952 в 8 степени.
500952 в 8 степени равно 3.9661480215015E+45.
500952 в 9 степени.
500952 в 9 степени равно 1.9868497836672E+51.
500952 в 10 степени.
500952 в 10 степени равно 9.9531637282766E+56.
500952 в 11 степени.
500952 в 11 степени равно 4.9860572760076E+62.
500952 в 12 степени.
500952 в 12 степени равно 2.4977753645306E+68.
500952 в 13 степени.
500952 в 13 степени равно 1.2512655644123E+74.
500952 в 14 степени.
500952 в 14 степени равно 6.2682398702348E+79.
500952 в 15 степени.
500952 в 15 степени равно 3.1400872994739E+85.
Какое число имеет такую же сумму цифр как и число 500952?Математика. Найти сумму цифр числа 500952.
Число 500952 состоит из следующих цифр — 5, 0, 0, 9, 5, 2.
Определить сумму цифр числа 500952 не так уж и сложно.
Сумма цифр шестизначного числа 500952 равна 5 + 0 + 0 + 9 + 5 + 2 = 21.
Числа сумма цифр которых равна 21.
Следующие числа имеют такую же сумму цифр как и число 500952 — 399, 489, 498, 579, 588, 597, 669, 678, 687, 696, 759, 768, 777, 786, 795, 849, 858, 867, 876, 885.
Трехзначные числа сумма цифр которых равна 21 — 399, 489, 498, 579, 588, 597, 669, 678, 687, 696.
Четырехзначные числа сумма цифр которых равна 21 — 1299, 1389, 1398, 1479, 1488, 1497, 1569, 1578, 1587, 1596.
Пятизначные числа сумма цифр которых равна 21 — 10299, 10389, 10398, 10479, 10488, 10497, 10569, 10578, 10587, 10596.
Шестизначные числа сумма цифр которых равна 21 — 100299, 100389, 100398, 100479, 100488, 100497, 100569, 100578, 100587, 100596.
Квадрат суммы цифр числа 500952.
Квадрат суммы цифр шестизначного числа 500952 равен 5 + 0 + 0 + 9 + 5 + 2 = 21² = 441.
Сумма квадратов цифр шестизначного числа 500952.
Сумма квадратов цифр числа 500952 равна 5² + 0² + 0² + 9² + 5² + 2² = 25 + 0 + 0 + 81 + 25 + 4 = 135.
Сумма четных цифр числа 500952.
Сумма четных цифр шестизначного числа 500952 равна 2 = 2.
Квадрат суммы четных цифр шестизначного числа 500952.
Квадрат суммы четных цифр числа 500952 равна 2 = 2² = 4.
Сумма квадратов четных цифр шестизначного числа 500952.
Сумма квадратов четных цифр числа 500952 равна 2² = 4 = 4.
Сумма нечетных цифр числа 500952.
Сумма нечетных цифр шестизначного числа 500952 равна 5 + 9 + 5 = 19.
Квадрат суммы нечетных цифр шестизначного числа 500952.
Квадрат суммы нечетных цифр числа 500952 равна 5 + 9 + 5 = 19² = 361.
Сумма квадратов нечетных цифр шестизначного числа 500952.
Сумма квадратов нечетных цифр числа 500952 равна 5² + 9² + 5² = 25 + 81 + 25 = 131.
Произведение цифр числа 500952.
Какое число имеет такое же произведение цифр как и число 500952?Математика. Найти произведение цифр числа 500952.
Число 500952 состоит из следующих цифр — 5, 0, 0, 9, 5, 2.
Найти сумму цифр числа 500952 просто.
Решение:
Произведение цифр числа 500952 равно 5 * 0 * 0 * 9 * 5 * 2 = 0.
Числа произведение цифр которых равно 0.
Следующие числа имеют такое же произведение цифр как и число 500952 — 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 101, 102, 103, 104, 105, 106, 107, 108, 109, 110.
Двухзначные числа произведение цифр которых равно 0 — 10, 20, 30, 40, 50, 60, 70, 80, 90.
Трехзначные числа произведение цифр которых равно 0 — 100, 101, 102, 103, 104, 105, 106, 107, 108, 109.
Четырехзначные числа произведение цифр которых равно 0 — 1000, 1001, 1002, 1003, 1004, 1005, 1006, 1007, 1008, 1009.
Пятизначные числа произведение цифр которых равно 0 — 10000, 10001, 10002, 10003, 10004, 10005, 10006, 10007, 10008, 10009.
Шестизначные числа произведение цифр которых равно 0 — 100000, 100001, 100002, 100003, 100004, 100005, 100006, 100007, 100008, 100009.
Квадрат произведения цифр числа 500952.
Квадрат произведения цифр шестизначного числа 500952 равен 5 * 0 * 0 * 9 * 5 * 2 = 0² = 0.
Произведение квадратов цифр шестизначного числа 500952.
Произведение квадратов цифр числа 500952 равна 5² * 0² * 0² * 9² * 5² * 2² = 25 * 0 * 0 * 81 * 25 * 4 = 0.
Произведение четных цифр числа 500952.
Произведение четных цифр шестизначного числа 500952 равно 2 = 2.
Квадрат произведения четных цифр шестизначного числа 500952.
Квадрат произведения четных цифр числа 500952 равен 2 = 2² = 4.
Произведение квадратов четных цифр шестизначного числа 500952.
Произведение квадратов четных цифр числа 500952 равно 2² = 4 = 4.
Запишите числа которые в сумме дают число 500952.
Задача: Данно число 500952.Какие 2(два) числа дают в сумме число 500952?Решение:
1) 40685 + 460267 = 500952
2) 171555 + 329397 = 500952
3) 136889 + 364063 = 500952
4) 74891 + 426061 = 500952
5) 58557 + 442395 = 500952
Какие 3(три) числа дают в сумме число 500952?Решение:
1) 13031 + 151512 + 336409 = 500952
2) 125484 + 139280 + 236188 = 500952
3) 39124 + 151910 + 309918 = 500952
4) 10055 + 68979 + 421918 = 500952
5) 109642 + 51791 + 339519 = 500952
Какие 4(четыре) числа дают в сумме число 500952?Решение:
1) 34298 + 134880 + 80023 + 251751 = 500952
2) 8347 + 34628 + 124993 + 332984 = 500952
3) 52295 + 16618 + 130170 + 301869 = 500952
4) 42308 + 150760 + 65308 + 242576 = 500952
5) 82478 + 49386 + 928 + 368160 = 500952
Какие 5(пять) чисел дают в сумме число 500952?Решение:
1) 29731 + 77855 + 43221 + 82576 + 267569 = 500952
2) 72748 + 74040 + 11717 + 112306 + 230141 = 500952
3) 25669 + 90947 + 78021 + 114001 + 192314 = 500952
4) 61685 + 104219 + 121057 + 48004 + 165987 = 500952
5) 27400 + 28516 + 37843 + 36517 + 370676 = 500952
Неравенства и сравнения
В семнадцатом задании нам необходимо сравнить данные числа с положением на координатной прямой или решить и сопоставить решения неравенств с областью на прямой. В данном задании можно пользоваться правилом исключения, поэтому достаточно правильно определить три решения из четырех, выбирая в первую очередь простые. Итак, приступим к разбору 17 задания базового варианта ЕГЭ по математике.
Разбор типовых вариантов заданий №17 ЕГЭ по математике базового уровня
Вариант 17МБ1
На координатной прямой отмечены точки A, B, C и D.
Каждой точке соответствует одно из чисел в правом столбце. Установите соответствие между указанными точками и числами.
| ТОЧКИА
В С D |
ЧИСЛА1) log2 10
2) 7/3 3) √26 4) (3/5)-1 |
Алгоритм выполнения:
- Проанализировать рядом с каким из целых чисел стоит данная точка.
- Проанализировать на каком интервале лежат числа из правого столбца.
- Сравнить полученные интервалы и поставить в соответствие.
Решение:
- Рассмотрим точку А. Ее значение больше 1 и меньше 2.
- Рассмотрим точку B. Ее значение больше 2 и меньше 3.
- Рассмотрим точку С. Ее значение больше 3 и меньше 4.
- Рассмотрим точку D. Ее значение больше 5 и меньше 6.
- Вспомним что такое логарифм.
Логарифм по основанию a от аргумента x — это степень, в которую надо возвести число a, чтобы получить число x.
Обозначение: loga x = b, где a — основание, x — аргумент, b — собственно, чему равен логарифм.
В нашем случае а = 2, x = 10.
То есть нас интересует число 2b = 10. 23 = 8 и 24 = 16, следовательно, b лежит в промежутке от 3 до 4.
Следовательно, 7/3 больше 2 и меньше 3.
Рассмотрим √26. √25 = 5, √36 = 6. Значит, √26 больше 5 и меньше 6.
То есть (3/5)-1 больше 1 и меньше 2.
Поставим в соответствие полученные интервалы.
А — (3/5)-1 — 4
В — 7/3 – 2
С — log2 10 – 1
D — √26 – 3
Ответ: 4213.
Вариант 17МБ2
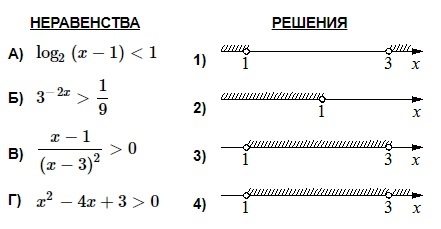
Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
Алгоритм выполнения:
- Представить правые и левые части неравенств в виде степени одного и того же числа.
- Сравнить степени, так как основания равны.
- Поставить в соответствие предложенные интервалы.
Решение:
А)
Представим 4 в виде степени с основанием 2. 22 = 4.
Неравенство примет вид:
Основания степеней одинаковы, следовательно, степени соотносятся так же.
то есть, 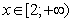
Б)
Число 0,5 можно представить как 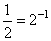
Неравенство примет вид:
Основания степеней одинаковы, следовательно, степени соотносятся так же.
Если умножить и правую и левую часть неравенства на -1, то знак изменится на противоположный.
то есть, 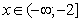
В)
Аналогично с вариантом Б.
Число 0,5 можно представить как 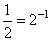
Неравенство примет вид:
Основания степеней одинаковы, следовательно, степени соотносятся так же.
Если умножить и правую и левую часть неравенства на -1, то знак изменится на противоположный.
то есть, 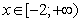
Г)
Представим 4 в виде степени с основанием 2. 22 = 4.
Неравенство примет вид:
Основания степеней одинаковы, следовательно, степени соотносятся так же.
и 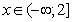
Ответ: 2143.
Вариант 17МБ3
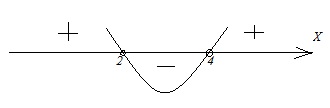
На прямой отмечены числа m и n.
Каждому из четырёх чисел в левом столбце соответствует отрезок, которому оно принадлежит. Установите соответствие между числами и отрезками из правого столбца.
Алгоритм выполнения:
- Найти промежутки в которых лежат числа m и n.
- Оценить интервалы, в которых лежат выражения в левом столбце.
- Поставить им в соответствие интервалы из правого столбца.
Решение:
Из рисунка видно, что число n немного меньше 0, а число m много больше отстоит от 1. Следовательно, их сумма m+n даст число в пределах [1; 2] – вариант ответа под номером 3.
Число m>1, следовательно, при делении на 1 получим положительное число меньше 1. Добавляя небольшое отрицательное значение n останемся в диапазоне [0; 1]. Вариант ответа 2.
Произведение mn положительного и отрицательного чисел дают отрицательное число. Подходит только один вариант [-1; 0] под номером 1.
Г) Квадрат числа m много больше квадрата числа n, поэтому их разница будет положительной и принадлежать диапазону [2; 3] – вариант под номером 4.
Ответ: 3214.
Вариант 17МБ4
Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
Рассмотрим первое неравенство:
2x≥4
представим 4 как 22, тогда:
2x ≥ 22
x ≥ 2
Остальные неравенства решаются аналогичным образом, достаточно вспомнить, что 0,5 = ½ = 2-1:
2-x ≥ 4
2-x ≥ 22
-x ≥ 2
x≤-2
Ответ: А-4, Б-3, В-2, А-1.
Вариант 17МБ5
Каждому из четырех неравенств в левом столбце соответствует одно из решений в правом столбце. Установить соответствие между неравенствами и их решениями.
Алгоритм выполнения
- Решаем по очереди каждое из неравенств (А–Г). При необходимости (для наглядности) отображаем полученное решение на координатной прямой.
- Записываем результаты в форме, которая предложена в столбце «Решения». Находим соответствующие пары «буква–число».
Решение:
А. 2–х+1 < 0,5 → 2–x+1 < 2–1 → –x+1 < –1 → –x < –2 → x > 2. Ответ: х ϵ (2; +∞). Получаем: А–3.
Б.
Неравенство преобразований не требует, поэтому сразу применяем метод интервалов, отобразив корни неравенства на координатной прямой.
Корни в данном случае – это х=4 и х=5. Имеем в виду, что неравенство строгое, т.е. значения корней в промежуток для ответа не включаем. В точке х=5 перехода знака не происходит, т.к. по условию (х–5) дано в квадрате. Поскольку нам нужен промежуток, где х<0, то ответ в данном случае: х ϵ (–∞; 4).
Соответственно, имеем: Б–4.
В. log4x > 1 → log4x > log44 → x > 4. Т.е.: х ϵ (4; +∞). Ответ: В–1.
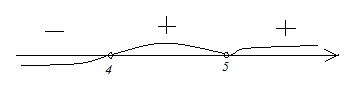
Г. (х–4)(х–2) < 0. Здесь так же, как и в неравенстве Б, нужно сразу отобразить решение на координатной прямой.
Неравенство дано квадратное, его корни – х=2 и х=4. Для получения промежутков с положительными и отрицательными значениями схематически изображаем параболу, пересекающую координатную прямую в точках корней. Промежуток «внутри» параболы отрицательный, промежутки «вне» ее положительны. Т.к. в неравенстве дано «<0», то для ответа следует взять промежуток отрицательных значений. Учитываем, что неравенство строгое. Получаем: х ϵ (2; 4).
Ответ: Г–2.
Вариант 17МБ6
На координатной прямой отмечены точки А, В, С и D.
Число m равно √2.
Каждой точке соответствует одно из чисел в правом столбце. Установите соответствие между указанными точками и числами.
Алгоритм выполнения
Для каждого из выражений правого столбца делаем следующее:
- Подставляем вместо m его числовое значение (√2). Вычисляем приблизительное значение.
- Ориентируясь на целую часть полученного числа, находим соответствующее значение на координатной прямой.
- Фиксируем пару «буква–число».
Решение:
Это значение на прямой находится между значениями –3 и –2 и соответствует точке А. Получили: А–1.
Число находится между значениями 2 и 3 и соответствует точке D. Имеем: D–2.
Число находится на прямой между 0 и 1. Это – точка С. Имеем: С–3.
Число размещается на прямой между значениями –1 и 0, что отображает т.В. Получаем: В–4.
Вариант 17МБ7
Каждому из четырех неравенств в левом столбце соответствует одно из решений в правом столбце. Установить соответствие между неравенствами и их решениями.
Алгоритм выполнения
- Последовательно решаем каждое неравенство (А–Г), получая в ответе промежуток значений. Находим соответствующее ему графическое отображение в правой колонке (Решения).
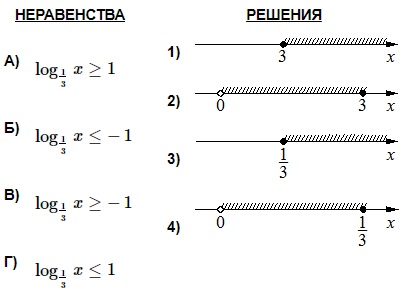
- При решении неравенств учитываем, что: 1) при снятии знаков логарифма с основанием, меньшим 1, знак неравенства меняется на противоположный; 2) выражение под знаком логарифма всегда больше 0.
Решение:
А.
Полученный промежуток-ответ отображен на 4-й координатной прямой. Поэтому имеем: А–4.
Б.
Полученный промежуток представлен на 1-й прямой. Отсюда имеем: Б–1.
В. Это неравенство аналогично предыдущему (Б) с разницей исключительно в знаке. Поэтому и ответ будет подобен с той только разницей, что в конечном неравенстве будет противоположный знак. Т.е. получим: х ≤ 3, х > 0 → x ϵ (0; 3]. Соответственно, получаем пару: В–2.
Г. Это неравенство аналогично 1-му (А), но с противоположным знаком. Поэтому ответ здесь будет таким: х ≥ 1/3, х > 0 → х ϵ [1/3; +∞). Т.о., ответ: Г–3.
Вариант 17МБ8
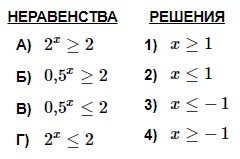
Каждому из четырех неравенств в левом столбце соответствует одно из решений в правом столбце. Установить соответствие между неравенствами и их решениями.
Алгоритм выполнения
- Решаем неравенство А. Находим номер соответствующего ответу решения из правой колонки.
- Рассматриваем неравенство Г как подобное неравенству А. Определяем для него номер решения из правого столбца.
- Решаем неравенство Б, перейдя к основанию 2. Определяем соответствующий для него номер варианта решения.
- По аналогии с неравенством Б решаем неравенство В.
Решение:
А. 2х ≥ 2 → 2х ≥ 21 → х ≥ 1. Имеем: А–1.
Г. По аналогии с неравенством А получаем в ответе: х ≤ 1. Имеем: Г–2.
Б. 0,5х ≥ 2 → (1/2)х ≥ 2 →2–х ≥ 21 х ≤ –1. Имеем: Б–3.
В. По аналогии с неравенством Б получаем в ответе: х ≥ –1. Имеем: В–4.
Вариант 17МБ9
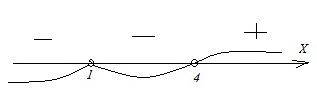
Каждому из четырех неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
Алгоритм выполнения
- Подобные неравенства решаются методом интервалов. На координатной прямой отмечаются точки, являющиеся корнями соответствующего кв.ур-ния; промежутки между этими точками имеют определенные знаки, причем 1-й из них справа (от +∞ до самого большого корня) всегда имеет знак «+». Далее, продвигаясь справа налево, знаки чередуем, т.е. 2-й справа промежуток будет иметь знак «–», 3-й – «+» и т.д.
- Если в неравенстве имеется выражение вида (х–а)2, то знак промежутка при прохождении точки а не меняется.
- Поскольку все неравенства строгие, то точки-корни в промежутки для ответов не включаются, что в результате фиксируется посредством круглых скобок.
- Знак «ᴗ» является объединяющим и должен прочитываться как «или».
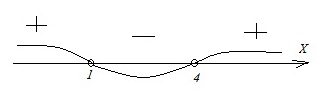
Решение:
Корнями в этих неравенствах являются х=1 и х=4.
Для неравенства А на прямой имеем:
Результатом здесь будут промежутки с отрицательным знаком, т.е. х < 1 или 1 < x < 4. Ответ: А–3.
Для неравенств Б и В получаем на прямой:
Для ответа в неравенстве Б следует взять промежутки со знаком «+». Получим: х < 1 или x > 4. Ответ: Б–1.
В неравенстве В нужно взять промежуток с отрицательным знаком. Тогда имеем: 1 < x < 4. Ответ: В–4.
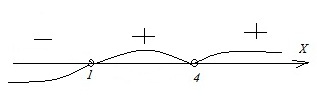
Б. Отмечаем на прямой корни и промежутки с соответствующими знаками:
Для неравенства Г на прямой получили:
Результат – промежутки с положительным знаком. Тогда имеем: 1 < x < 4 или x > 4. Ответ: Г–2.
Вариант 17МБ10
На координатной прямой отмечены точки А, В, С и D.
Каждой точке соответствует одно из чисел в правом столбце. Установите соответствие между указанными точками и числами.
Алгоритм выполнения
- Определяем приблизительное значение чисел, приведенных в правом столбце, или их целую часть, что позволит выяснить, между какими двумя целыми числами на координатной прямой они располагаются.
- Фиксируем пары «буква–число» для заполнения итоговой таблицы ответов.
Решение:
Число 1. log55=1, log525=log552=2log55=2·1=2. Т.к. 5<20<25, то 1<log520<2. Значит, на координатной прямой число log520 отображено точкой В. Ответ: В–1.
Число 2. . Это означает, что число отображено на прямой точкой С. Ответ: С–2.
Число 3. √10 совсем немного больше, чем √9=3. Это число точно меньше 4, поскольку 4=√16. Соответственно, √10 на прямой расположен между 3 и 4 и отображен точкой D. Ответ: D–3.
Число 4. 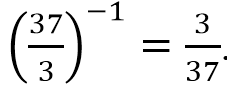
Вариант 17МБ11
Каждому из четырех неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
Алгоритм выполнения
- Решаем последовательно неравенства А–Г, учитывая ОДЗ.
- По результату (полученному простейшему неравенству) находим соответствующее графическое решение из правого столбца.
Решение:
- log2 (x–1) < 1 → log2 (x–1) < log2 2 → x–1 < 2 → x < 3. ОДЗ: х–1 > 0 → x > 1.
Объединяем полученный промежуток с ОДЗ, получаем: x ϵ (1; 3). Это соответствует решению №3. Ответ: А–3.
- . ОДЗ не дает ограничений
Тогда в результате имеем: х ϵ (1; +∞). Ответ: Б–2.
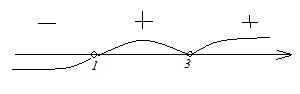
- Здесь не требуются преобразования. Решается неравенство методом интервалов. Точки пересечения с координатной прямой: х=1, х=3. Тогда имеем:
Для решения требуется взять промежутки с положительным знаком. ОДЗ: х≠3. Получаем: х ϵ (1; 3)ᴗ(3; +∞). Ответ: В–4.
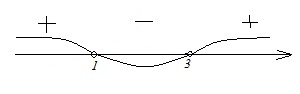
- х2 – 4х + 3 > 0 → (x–1)(x–3) > 0. Применив метод интервалов, получим:
ОДЗ не дает ограничений. Значит, х ϵ (–∞; 1)ᴗ(3; +∞). Ответ: Г–1.
Вариант 17МБ12
На координатной прямой отмечено число m.
Каждому из четырех чисел в левом столбце соответствует отрезок, которому оно принадлежит. Установите соответствие между числами и отрезками из правого столбца.
Алгоритм выполнения
- Определяем приблизительное значение для m.
- Подставляем найденное значение для m последовательно в каждое из выражений (А–Г), вычисляем их числовые значения.
- Сопоставляем полученные числа с отрезками, предложенными в правом столбце, находим пары «буква–число» для ответа.
Решение:
Число m располагается на прямой между 1,5 и 2 и немного смещено от середины этого отрезка к двойке. Следовательно, наиболее точным для него является 1,8.
Число А. Имеем: √1,8. Известно, что √1=1, √2≈1,4. Т.е. √1,8 наверняка располагается на отрезке между 1 и 2. Ответ: А–1.
Число Б. Оно равно: 1,83=5,832, т.е. это число принадлежит промежутку [5; 6]. Ответ: Б–4.
Число В. Это число равно: 1,8+1=2,8, что соответствует отрезку [2; 3]. Ответ: В–2.
Число Г. Тут получаем: 6/1,8≈3,33. Этому значению соответствует отрезок [3; 4]. Ответ: Г–3.
Вариант 17МБ13
Число m равно √0,15.
Каждому из четырех чисел в левом столбце соответствует отрезок, которому оно принадлежит. Установите соответствие между числами и отрезками из правого столбца.
Алгоритм выполнения
- Преобразуем число m так, чтобы вынести значение из-под корня.
- Подставляем последовательно полученную величину для m в каждое из выражений в левом столбце. Получаемые результаты соотносим с подходящим отрезком из правого.
Решение:
Число √0,15 очень немногим отличается от √0,16, а из 0,16 можно точно извлечь корень. Делая подобное приближение – всего на 0,01 – мы не выходим за пределы приемлемой абсолютной погрешности. Поэтому имеем право принять, что √0,15≈√0,16=0,4.
Находим значения выражений А–Г и определяем их соответствия отрезкам:
А. –1/0,4=–2,5. Результат соответствует отрезку [–3; –2]. Ответ: А–1.
Б. 0,42=0,16. Число входит в промежуток [0; 1]. Ответ: Б–3.
В. 4·0,4=1,6. Это число находится в интервале [1; 2]. Ответ: В–4.
Г. 0,4–1=–0,6. Результат попадает на отрезок [–1; 0]. Ответ: Г–2.
Вариант семнадцатого задания 2019 года (10)
На координатной прямой отмечено число m и точки А, В, С и D.
Каждой точке соответствует одно из чисел в правом столбце. Установите соответствие между указанными точками и числами.
Алгоритм выполнения
- Определяем приблизительное значение для m.
- Вычисляем значения выражений 1–4, находим соответствие между полученными результатами и точками А–D на координатной прямой.
Решение:
Точка m располагается почти посередине между 1 и 2, но немного ближе к 1, чем к 2. Максимально приближенным к реальному в данном случае следует считать значение m=1,4.
Определяем соответствие чисел и точек на прямой:
- 6–1,4=4,6. Это значение отображено точкой D. Ответ: D–1.
- 1,42=1,96. Такое число отображается в точке С. Ответ: С–2.
- 1,4–1=0,4. Это число соответствует точке В. Ответ: В–3.
- Здесь можно не вычислять результат, поскольку имеет место единственное отрицательное число, а на прямой обозначена единственная точка слева от 0 – т.А. Ответ: А–4.
Натуральное действительное
число 500952
является составным.
21 — сумма цифр числа.
У числа 16 делителей.
1252440 — сумма делителей.
0.000001996199236653412 является обратным числом к 500952.
Данное число можно представить произведением: 2 * 2 * 2 * 3 * 20873.
Представления числа 500952:
двоичная система счисления: 1111010010011011000, троичная система счисления: 221110011210, восьмеричная система счисления: 1722330, шестнадцатеричная система счисления: 7A4D8.
Конвертация из числа байтов это 489 килобайтов 216 байтов .
Число азбукой Морзе: ….. —— —— —-. ….. ..—
Число — не число Фибоначчи.
Синус: -0.0813, косинус: 0.9967, тангенс: -0.0815.
Логарифм натуральный числа: 13.1243.
Логарифм десятичный числа равен 5.6998.
707.7796 — квадратный корень из числа 500952, 79.4204 — кубический корень.
Число в квадрате это 2.5095e+11.
Конвертация из числа секунд — 5 дней 19 часов 9 минут 12 секунд .
Цифра 3 — это нумерологическое значение числа 500952.
Новые тренировочные варианты ЕГЭ 2023 по математике базовый и профильный уровень с ответами и решением для 10 и 11 класса, больше 100 вариантов в формате реального экзамена ФИПИ вы можете решать онлайн или скачать.
Тренировочные варианты ЕГЭ 2023 по математике база и профиль
13.09.2022 Тренировочный вариант №1 ЕГЭ 2023 по математике профиль с ответами
20.09.2022 Тренировочный вариант №2 ЕГЭ 2023 по математике профиль с ответами
20.09.2022 Тренировочный вариант №2 ЕГЭ 2023 база по математике с ответами
27.09.2022 Математика 11 класс профиль входная мониторинговая работа 3 варианта с ответами
28.09.2022 Тренировочный вариант №3 ЕГЭ 2023 база по математике с ответами
28 сентября 2022 Статград математика 11 класс ЕГЭ 2023 база и профиль варианты и ответы
29 сентября 2022 Тренировочный вариант №3 ЕГЭ 2023 по математике профиль с ответами
1 октября 2022 Ларин вариант 399 ЕГЭ 2023 по математике профиль решение с ответами
6 октября Тренировочный вариант №4 ЕГЭ 2023 база по математике с ответами
6 октября Тренировочный вариант №4 ЕГЭ 2023 по математике профиль с ответами
8 октября Ларин вариант 400 ЕГЭ 2023 по математике профиль решение с ответами
12 октября Тренировочный вариант №5 ЕГЭ 2023 база по математике с ответами
12 октября Тренировочный вариант №5 ЕГЭ 2023 по математике профиль с ответами
14 октября Вариант 1 Ященко ЕГЭ 2023 математика профиль с ответами и решением
14 октября Вариант 2 Ященко ЕГЭ 2023 математика профиль с ответами и решением
15 октября Ларин вариант 401 ЕГЭ 2023 по математике профиль решение с ответами
15 октября Ларин вариант 402 ЕГЭ 2023 по математике профиль решение с ответами
16 октября Вариант 3 Ященко ЕГЭ 2023 математика профиль с ответами и решением
16 октября Вариант 4 Ященко ЕГЭ 2023 математика профиль с ответами и решением
23 октября Тренировочный вариант №6 ЕГЭ 2023 база по математике с ответами
24 октября Тренировочный вариант №6 ЕГЭ 2023 по математике профиль с ответами
25 октября Тренировочный вариант №7 ЕГЭ 2023 база по математике с ответами
26 октября Тренировочный вариант №7 ЕГЭ 2023 по математике профиль с ответами
28 октября Ларин вариант 403 ЕГЭ 2023 по математике профиль решение с ответами
29 октября Ларин вариант 404 ЕГЭ 2023 по математике профиль решение с ответами
1 ноября 2022 Тренировочный вариант №8 решу ЕГЭ 2023 база по математике с ответами
1 ноября 2022 Тренировочный вариант №8 решу ЕГЭ 2023 по математике профиль с ответами
5 ноября 2022 Вариант 1-2 распечатай и реши ЕГЭ 2023 база по математике 11 класс с ответами
6 ноября 2022 Ларин вариант 405 ЕГЭ 2023 профиль по математике решение с ответами
9 ноября 2022 Тренировочный вариант №9 решу ЕГЭ 2023 база по математике с ответами
12 ноября 2022 Тренировочный вариант №9 решу ЕГЭ 2023 по математике профиль с ответами
13 ноября 2022 Ларин вариант 406 ЕГЭ 2023 профиль по математике решение с ответами
15 ноября 2022 Тренировочный вариант №10 решу ЕГЭ 2023 база по математике 11 класс с ответами
15 ноября 2022 Тренировочный вариант №10 решу ЕГЭ 2023 по математике профиль с ответами
21 ноября 2022 Ларин вариант 407 ЕГЭ 2023 профиль по математике решение с ответами
23 ноября 2022 Тренировочный вариант №11 решу ЕГЭ 2023 база по математике 11 класс с ответами
23 ноября 2022 Тренировочный вариант №11 решу ЕГЭ 2023 по математике профиль с ответами
27 ноября 2022 Ларин вариант 408 ЕГЭ 2023 профиль по математике решение с ответами
28 ноября 2022 Вариант 3-4 распечатай и реши ЕГЭ 2023 база по математике 11 класс с ответами
30 ноября 2022 Мониторинговая работа по математике 11 класс ЕГЭ 2023 профиль 1 полугодие
3 декабря 2022 Тренировочный вариант №12 решу ЕГЭ 2023 база по математике 11 класс с ответами
3 декабря 2022 Тренировочный вариант №12 решу ЕГЭ 2023 по математике профиль с ответами
3 декабря 2022 Пробник ЕГЭ 2023 Москва по математике профиль задания и ответы
5 декабря 2022 Ларин вариант 409 ЕГЭ 2023 профиль по математике решение с ответами
9 декабря 2022 Тренировочный вариант №13 решу ЕГЭ 2023 база по математике 11 класс с ответами
10 декабря 2022 Тренировочный вариант №13 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
12 декабря 2022 Ларин вариант 410 ЕГЭ 2023 профиль по математике решение с ответами
13 декабря 2022 Статград математика 11 класс профиль ЕГЭ 2023 варианты МА2210209-МА2210212 и ответы
13 декабря 2022 Математика 11 класс база ЕГЭ 2023 статград варианты и ответы
15 декабря 2022 Тренировочный вариант №14 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
15 декабря 2022 Тренировочный вариант №14 решу ЕГЭ 2023 база по математике 11 класс с ответами
20 декабря 2022 Вариант 5-6 распечатай и реши ЕГЭ 2023 база по математике 11 класс с ответами
20 декабря 2022 Ларин вариант 411 ЕГЭ 2023 профиль по математике решение с ответами
3 января 2023 Ларин вариант 412 ЕГЭ 2023 профиль по математике решение с ответами
6 января 2023 Тренировочный вариант 1-2 ЕГЭ 2023 профиль математика задания и ответы
8 января 2023 Вариант 3-4 ЕГЭ 2023 профиль математика задания и ответы
9 января 2023 Вариант 7-8 распечатай и реши ЕГЭ 2023 база по математике 11 класс с ответами
10 января 2023 Тренировочный вариант №15 и №16 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
11 января 2023 ЕГЭ 2023 математика тренировочные задания и ответы Ященко, Семенов
11 января 2023 Тренировочный вариант №15 и №16 база ЕГЭ 2023 по математике 11 класс с ответами
19 января 2023 Тренировочные варианты №17 и №18 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
22 января 2023 Ларин вариант 413 и 414 ЕГЭ 2023 профиль по математике решение и ответы
22 января 2023 Тренировочный 19 вариант решу ЕГЭ 2023 профиль по математике 11 класс с ответами
22 января 2023 База ЕГЭ 2023 математика 11 класс тренировочный вариант 19 с ответами
25 января 2023 База ЕГЭ 2023 математика 11 класс тренировочный вариант 20 с ответами
27 января 2023 Тренировочный вариант №20 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
28 января 2023 Вариант 415 Ларина ЕГЭ 2023 по математике 11 класс задания и ответы
2 февраля 2023 Вариант 21 база ЕГЭ 2023 математика 11 класс тренировочный вариант с ответами
2 февраля 2023 Тренировочный вариант №21 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
8 февраля 2023 Математика 10-11 класс ЕГЭ 2023 статград варианты база и профиль МА2200101-МА2200110 и ответы
11 февраля 2023 Тренировочный вариант №22 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
11 февраля 2023 Тренировочный вариант №22 решу ЕГЭ 2023 база по математике 11 класс с ответами
12 февраля 2023 Вариант 416 Ларина ЕГЭ 2023 по математике 11 класс задания и ответы
12 февраля 2023 Вариант 417 Ларина ЕГЭ 2023 по математике 11 класс задания и ответы
13 февраля 2023 Вариант 9 и вариант 10 ЕГЭ 2023 база математика распечатай и реши задания
13 февраля 2023 Вариант 11 и вариант 12 ЕГЭ 2023 база математика распечатай и реши
16 февраля 2023 Тренировочный вариант №23 решу ЕГЭ 2023 база по математике 11 класс с ответами
16 февраля 2023 Тренировочный вариант №23 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
18 февраля 2023 Вариант 418 Ларина ЕГЭ 2023 по математике 11 класс задания и ответы
22 февраля 2023 Пробный ЕГЭ 2023 вариант 24 база по математике 11 класс с ответами
22 февраля 2023 Пробный ЕГЭ 2023 вариант 24 профиль по математике 11 класс с ответами
25 февраля 2023 Вариант 419 Ларина ЕГЭ 2023 по математике 11 класс задания и ответы
28 февраля 2023 Статград математика 11 класс ЕГЭ 2023 база и профиль и ответы
4 марта 2023 Пробник ЕГЭ 2023 вариант 25 база по математике 11 класс с ответами
4 марта 2023 Вариант 420 Ларин ЕГЭ 2023 по математике 11 класс задания и ответы
5 марта 2023 Пробник ЕГЭ 2023 вариант 25 профиль по математике 11 класс с ответами
8 марта 2023 Пробник ЕГЭ 2023 вариант 26 профиль по математике 11 класс с ответами
8 марта 2023 Пробник ЕГЭ 2023 вариант 26 база по математике 11 класс 100 баллов с ответами
Смотрите также на нашем сайте:
Сборник Ященко ЕГЭ 2023 математика профильный уровень 36 вариантов
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
ЕГЭ по математике — Профиль 2022. Открытый банк заданий с ответами.