Образовательный портал для подготовки к экзаменам
Математика профильного уровня
Математика профильного уровня
Сайты, меню, вход, новости
Задания
Версия для печати и копирования в MS Word
а) Решите уравнение:
б) Найдите все корни этого уравнения, принадлежащие отрезку
Спрятать решение
Решение.
а) Запишем уравнение в виде:
б) С помощью числовой окружности отберём корни, принадлежащие отрезку Получим числа
Замечание. Отбор корней может быть обоснован и любым другим способом: с помощью графика, решения двойных неравенств и т. п.
Ответ: а) б)
Спрятать критерии
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получены верные ответы в обоих пунктах. | 2 |
| Обоснованно получен верный ответ в пункте а),
ИЛИ получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения пункта а) и пункта б). |
1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 2 |
Спрятать решение
·
·
Курс Д. Д. Гущина
·
Гость 19.04.2014 16:22
Здесь допущена ошибка в решении. Под буквой а). Там где соs квадрат х выносят за скобку, в скобке будет знак +. От этого изменится ответ и корни
Александр Иванов
ошибки нет.
Гость 09.11.2014 14:01
Ошибка:cosx=0 — верно,но sinx=1/корень из двух.
Александр Иванов
Ошибки нет.
Гость 07.03.2016 14:10
А если вынести V2 sinx , то уравнение принимает вид (V2sinx-1)*(Sin^2x-1)=0 , где выясняется , что sinx=+- 1 , т.е. корни будут p/2+2pn; и -p/2 +2pn , могли ли вы потерять корень?
Александр Иванов
Никита, а в решении эти корни есть и выглядят вот так:
Вы записали каждую точку на окружности отдельно, а в нашем решении две точки объединены.
Meet the Instructors
Course content
loading…
Price:
Free
Share this course
https://stepik.org/course/161885/promo
Price:
Free
Действующие депутаты разных уровней поделятся своим опытом с начинающими политиками
«ПолитСтарт» — это уникальная программа, позволяющая новым лицам попасть в серьёзные политические процессы, поскольку она даёт возможность обменяться опытом с такими мэтрами, как Александр Сидякин, руководитель Центрального исполнительного комитета партии «Единая Россия», как Евгений Минченко, президент Российской ассоциации по связям с общественностью. Проект позволяет использовать их опыт и навыки в реальной политической деятельности, проходить обучающие программы от компетентных специалистов, которые непосредственно связаны с текущими политическими процессами.
«Мы ждём в проекте активных и ярких людей, которые на деле хотят приносить пользу людям. Партия будет оказывать поддержку всем участникам «ПолитСтарта». Это позволит нам обновить депутатский корпус лидерами, которым доверяют люди», – отметил заместитель руководителя ЦИК «Единой России», директор Высшей партийной школы Роман Романов.
Участвовать в проекте могут кандидаты, которые официально зарегистрированы на предварительном голосовании партии, и политтехнологи, планирующие работать в региональных избирательных штабах. Приём заявок идёт на сайте politstart.er.ru.
«В этом году «ПолитСтарт» даёт особую возможность пройти обучение для тех участников, кто реализовал себя в новых территориях Российской Федерации, причём как в зоне СВО, так и в гуманитарных сферах. В Мурманской области официально старт предварительному голосованию был дан 1 марта. Праймериз – процедура уникальная. Только «Единая Россия» не просто предлагает своим избирателям проголосовать на тех или иных выборах, но и советуется с ними относительно кандидатур», – рассказала руководитель Мурманского регионального исполкома «Единой России» Эвелина Макарова.
В Абхазию с апреля можно будет доехать на поезде и автобусе по единому билету
Единый билет на два вида транспорта позволит пассажирам из России добраться до пяти населённых пунктов Абхазии.
Мультимодальные поездки между Россией и Абхазией будут осуществляться с 30 апреля по 30 сентября. В этот период пассажиры могут оформить для проезда «единый» билет на поезд и автобус. Для этого можно обратиться в кассу или купить на сайте. Обязательно при указании пункта отправления и пункта прибытия нужно выбирать кнопку «маршрут с пересадкой».
Таким образом, обладатели единого билета приезжают на поезде на ж/д вокзал Адлера, затем они переходят в комфортабельный автобус, который доставит их в Гагры, Пицунду, Гудауту, Новый Афон или Сухум. Такая же схема действует и на обратный путь из Абхазии. Стоимость проезда на автобусе варьируется от 600 до 800 рублей в зависимости от пункта назначения.
Уточняется, что на детей до 5 лет также оформляется талон на проезд на автобусе, проездной документ безденежный, но позволяет ребёнку занять отдельное место.
Также пассажирам по единому билету предоставляется право бесплатного провоза ручной клади весом не более 30 кг, а вот перевозка животных не допустима.
Информацию о расписании можно уточнить по телефонам круглосуточной бесплатной «горячей»линии:
8 (800) 600-10-06,
+7 (940) 744-00-00.
Ранее «Царьград-Юг» сообщал, что по одному вечернему рейсу добавилось на пригородном сообщении Сочи – Имеретинский курорт. Для удобства местных жителей и гостей курорта в Сочи с 1 марта по 30 ноября ввели дополнительный рейс на пригородном сообщении.
Уважаемые читатели «Царьграда»! Присоединяйтесь к нам в соцсетях «ВКонтакте«, в Одноклассники. Подписывайтесь на наш канал в Дзене и телеграм-канал. Там все самое интересное. Если вам есть чем поделиться с нами, присылайте свои наблюдения, вопросы, новости на электронную почту ug@Tsargrad.TV
Дзен
Телеграм
Подписывайтесь на наши каналы
и первыми узнавайте о главных новостях и важнейших событиях дня.
За это задание ты можешь получить 3 балла. На решение дается около 20 минут. Уровень сложности: повышенный.
Средний процент выполнения: 5.6%
Ответом к заданию 13 по математике (профильной) может быть развернутый ответ (полная запись решения с обоснованием выполненных действий).
Что нужно знать, чтобы решить задание 13:
В задании требуется решить уравнение одного из видов: тригонометрическое, рациональное, показательное, логарифмическое, уравнение с радикалом или смешанное уравнение, которое может содержать в себе несколько видов, например, логарифмы и тригонометрию. После решения уравнения, часто необходимо отобрать корни, которые принадлежат определенному промежутку.
Разбор сложных заданий в тг-канале
Задачи для практики
Задача 1
Дан куб $ABCDA_1B_1C_1D_1$. На ребре $AA_1$ отмечена точка $M$, причём $AM:MA_1=1:1$, на ребре $BB_1$ отмечена точка $N$,
причём $BN:NB_1=1:2$, на ребре $CC_1$ отмечена точка $K$, причём $CK:KC_1=1:3$.
а) В каком отношении, считая от точки $D$, плоскость $MNK$ делит ребро $DD_1$?
б) Найдите величину угла между плоскостями $MNK$ и $ABC$.
Решение
а) Пусть ребро куба равно $1$. Противоположные грани куба параллельны, поэтому плоскость $MNK$ пересекает их по параллельным отрезкам. Сечением куба плоскостью $MNK$ является параллелограмм $MNKF$, где $F$ — точка пересечения ребра $DD_1$ с плоскостью $MNK$. Рассмотрим проекцию куба на грань $CC_1D_1D$. $DM_1=AM$, $CN_1=BN$. Отрезки $M_1N_1$ и $FK$ параллельны, поэтому $N_1K={1} / {3}-{1} / {4}={1} / {12}$, и $FD=M_1D-M_1F={1} / {2}-{1} / {12}={5} / {12}$, значит, $DF:FD_1=5:7$. б) Прямая $FK$ пересекает плоскость основания куба в точке $L$, прямая $NK$ пересекает плоскость основания куба в точке $T$, поэтому плоскость $MNK$ пересекает плоскость $ABC$ по прямой $TL$. В прямоугольном треугольнике $CLT$ отрезок $CH$ — высота, по теореме о трёх перпендикулярах $KH⊥ TL$, поэтому линейный угол $CHK$ является углом между плоскостями $MNK$ и $ABC$. Треугольники $CLK$ и $DLF$ подобны, $CK={1} / {4}$, $FD={5} / {12}$, $DL=1+CL$, тогда из пропорции ${1} / {4}:{5} / {12}=CL:(1+CL)$, получим $CL={3} / {2}$. Аналогично из подобия треугольников $CTK$ и $BTN$ найдём $CT=3$. В прямоугольном треугольнике $CLT$ гипотенуза $LT$ вычисляется по теореме Пифагора:$LT={3√ 5} / {2}$, а высота $CH={CL⋅ CT} / {LT}={3} / {√ 5}$. В прямоугольном треугольнике $CHK$ вычисляем
$tg∠ CHK={CK} / {CH}={1} / {4}:{3} / {√ 5}={√ 5} / {12}$, значит, $∠ CHK=arctg{√ 5} / {12}$.
Ответ: begin{tabular}{c}а)$5:7$\б)$arctgfsm{sqrt5}{12}$end{tabular
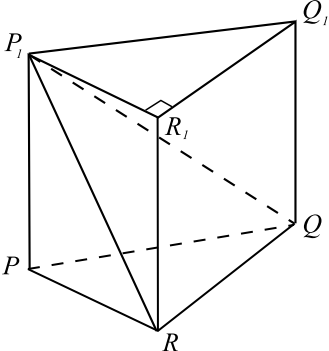
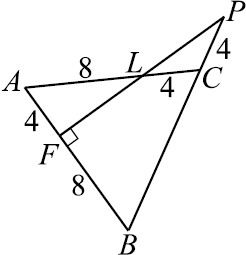
Задача 2
Основанием прямой треугольной призмы $PQRP_1Q_1R_1$ является прямоугольный треугольник $PQR$ с прямым углом $R$. Диагонали боковых граней $PP_1Q_1Q$ и $PP_1R_1R$ равны $17$ и $15$ соответственно, $PQ = 10$.
а) Докажите, что треугольник $P_1QR$ прямоугольный.
б) Найдите объём пирамиды $P_1QRR_1$.
Решение
По условию задачи сделаем чертёж.
а) Прямая $QR$ перпендикулярна плоскости $PP_1R_1R$, поскольку она перпендикулярна прямым $PR$ и $RR_1$. Значит, прямые $QR$ и $RP_1$ перпендикулярны, следовательно, в $△P_1QR$
$∠P_1RQ = 90°$.
б) Пусть $V$ — объём призмы $PQRP_1Q_1R_1$. Тогда объём треугольной пирамиды $PP_1QR$ равен ${V}/{3}$, поскольку её высота $PP_1$ и основание $PQR$ совпадают с высотой и основанием призмы соответственно. Аналогично, объём треугольной пирамиды $P_1Q_1R_1Q$ равен ${V}/{3}$. Призма $PQRP_1Q_1R_1$ составлена из трёх пирамид: $PP_1QR, P_1Q_1R_1Q$ и $P_1QRR_1$. Значит, объём пирамиды $P_1QRR_1$ равен ${V}/{3}$.
В призме $PQRP_1Q_1R_1 : QQ_1 = √{P_1Q^2 — P_1Q_1^2} = 3√21, QR = √{P_1Q^2 — P_1R^2} = 8, PR = √{PQ^2 — QR^2} = 6, V = PP_1 · {PR · QR}/{2} = 72√21$.
Таким образом, объём пирамиды $P_1QRR_1$ равен $24√21$.
Ответ: 24sqrt{21}
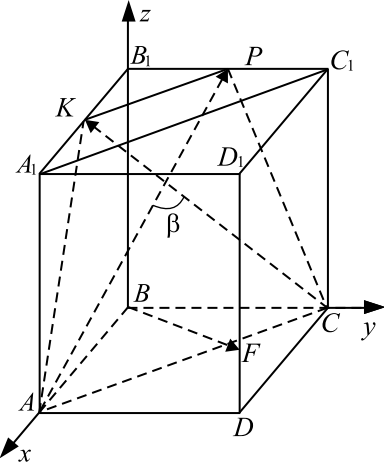
Задача 3
В правильной четырёхугольной пирамиде $SABCD$ боковое ребро $SA=12$, а высота равна $4$. На рёбрах $AB$, $CD$ и $AS$ отмечены точки $E$, $F$ и $K$ соответственно, причём $BE=CF=12$, $AK=3$.
а) Докажите, что плоскости $SBC$ и $KEF$ параллельны.
б) Найдите объём пирамиды $KSBC$.
Решение
а) Докажем, что плоскости $SBC$ и $KEF$ параллельны.
Введём прямоугольную систему координат, учитывая, что в основании правильной пирамиды квадрат $ABCD$ и угол между диагоналями квадрата прямой .
1. Найдём координаты точек $S, B, C , K , E, F$. В прямоугольном треугольнике $SOA$ по теореме Пифагора $OA^2 = SA^2 — SO^2, OA = √{12^2 — 4^2} = 8√2. OC = OB = OD = OA = 8√2$, тогда сторона квадрата $AB = {OA}/{sin 45°} = {8√2}/{{1}/{√2}} = 16, AE = AB — BE = 16 — 12 = 4$.
Проведём $KN ‖ SO, SO ⊥ (ABC)$, тогда $KN ⊥ (ABC)$ и $KN ⊥ OA, △SAO ∼ △KAN$ по первому признаку подобия $(∠SOA = ∠KNA = 90°, ∠A$ — общий) ${AS}/{AK} = {SO}/{KN}, {12}/{3} = {4}/{KN}, KN = 1$.
В прямоугольном треугольнике $ANK$ по теореме Пифагора $AN^2 = AK^2 — KN^2, AN = √{3^2 — 1^2} = 2√2$, тогда $ON = OA — AN = 8√2 — 2√2 = 6√2. EN$ — проекция $KE$ на плоскость $ABC$, значит $△ANE$ прямоугольный и равнобедренный $EN = AN = 2√2$.
Получим $S(0; 0; 4), B(0; -8√2; 0), C (-8√2; 0; 0), K (6√2; 0; 1), E(6√2; -2√2; 0), F (-2√2; 6√2; 0)$.
2. Докажем, что векторы нормали к плоскостям $SBC$ и $KEF$ коллинеарны. Для плоскости $SBC$, вектор нормали ${n_1}↖{→}(a_1; b_1; c_1)$ перпендикулярен к обеим прямым $SB$ и $SC$, поэтому он должен быть перпендикулярен к векторам ${SB}↖{→}(0; -8√2; -4)$ и ${SC}↖{→}(-8√2; 0; -4)$.
Получим систему ${table {n_1}↖{→} · {SB}↖{→} = 0; {n_1}↖{→} ·{SC}↖{→} = 0;$ ${table · a_1 — 8√2 · b_1 — 4c_1 = 0; -8√2a_1 + 0 · b_1 — 4 · c_1 = 0;$ ${table-2√2b_1 — c_1 = 0; -2√2a_1 — c_1 = 0;$
Пусть $c_1 = -1$, тогда система примет вид ${table-2√2b_1 + 1 = 0; -2√2a_1 + 1 = 0;$
Её решение $a_1 = {√2}/{4}; b_1 = {√2}/{4}$.
${n_1}↖{→}({√2}/{4}; {√2}/{4}; -1)$ — вектор нормали плоскости $SBC$ .
Для плоскости $KEF$, вектор нормали ${n_2}↖{→}(a_2; b_2; c_2)$ перпендикулярен к обеим прямым $KE$ и $KF$, поэтому он должен быть перпендикулярен к векторам ${KE}↖{→}(0; -2√2; -1)$ и ${KF}↖{→}(-8√2; 6√2; -1)$.
Получим систему ${table {n_2}↖{→} · {KE}↖{→} = 0; {n_2}↖{→} · {KF}↖{→} = 0;$ ${table · a_2 — 2√2 · b_2 — 1 · c_2 = 0; -8√2a_2 + 6√2 · b_2 — 1 · c_2 = 0;$ ${table-2√2b_2 — c_2 = 0; -8√2a_2 + 6√2b_2 — c_2 = 0$.
Пусть $c_2 = -1$, тогда система примет вид ${table-2√2b_2 + 1 = 0; 8√2a_2 + 6√2b_2 + 1 = 0;$
Её решение $a_2 = {√2}/{4}; b_2 = {√2}/{4}$.${n_2}↖{→}({√2}/{4}; {√2}/{4}; -1)$ — вектор нормали плоскости $KEF$.
Векторы ${n_1}↖{→}$ и ${n_2}↖{→}$ равны, значит коллинеарны, следовательно плоскости $SBC$ и $KEF$ параллельны.
б) Искомый объём $V = {1}/{3}S · h$, где $S$ — площадь треугольника $SBC$, а высота пирамиды $h$ — это расстояние от точки $K$ до плоскости $SBC$.
1. $S = {1}/{2}SB · SC · sin α$, где $α$ — угол между прямыми $SB$ и $SC$. $cos α ={{SB}↖{→} · {SC}↖{→}}/{|{SB}↖{→}| · |{SC}↖{→}|} = {0 · (-8√2) + (-8√2) · 0 + (-4)(-4)}/{12 · 12} = {16}/{144} = {1}/{9}$.
$sin α = √{1 — cos^2α} = √{1 — {1}/{81}} = {4√5}/{9} · S = {1}/{2} · 12 · 12 · {4√5}/{9} = 32√5$.
2. Чтобы найти $h$ необходимо найти уравнение плоскости $SBC$. Оно имеет вид $ax + by + cz + d = 0$, где ${n}↖{→}(a; b; c)$ — вектор нормали этой плоскости. Согласно пункту а), один из векторов нормали ${n_1}↖{→}({√2}/{4}; {√2}/{4}; -1)$. Значит, уравнение имеет вид ${√2}/{4}x + {√2}/{4}y — z + d = 0$. Чтобы найти значение $d$ подставим координаты точки $S(0; 0; 4)$ в это уравнение, получим $-4 + d = 0, d = 4$, тогда ${√2}/{4}x + {√2}/{4}y — z + 4 = 0$ — уравнение плоскости $SBC$. Расстояние от точки $K(6√2; 0; 1)$ до плоскости $SBC$
$h = {|ax_0+ by_0 + z_0 + d|}/{√{a_2 + b_2 + z_2}} ={|{√2}/{4} · 6√2 + {√2}/{4} · 0 + (-1) · 1 + 4|}/{√{({√2}/{4})^2 + ({√2}/{4})^2 + (-1)^2}} = {12√5}/{5}$, где $x_0, y_0, z_0$ — координаты точки $K$.
3. $V = {1}/{3} · 32√5 · {12√5}/{5} = 128$.
Ответ: 128
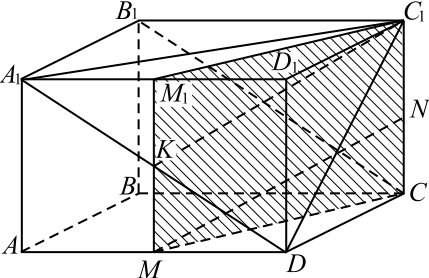
Задача 4
В правильной четырёхугольной призме $ABCDA_1B_1C_1D_1$ сторона основания $AB=8√ {2}$, а боковое ребро $AA_1=16$. Точка $K$ — середина ребра $A_1B_1$. На ребре $DD_1$ отмечена точка $F$ так, что $DF=4$. Плоскость $α$ параллельна прямой $A_1C_1$ и содержит точки $K$ и $A$.
а) Докажите, что прямая $BF$ перпендикулярна плоскости $α$.
б) Найдите объём пирамиды, вершина которой точка $B$, а основание — сечение данной призмы плоскостью $α$.
Решение
1. Построим сечение призмы плоскостью $α$.
Грани $ABCD$ и $A_1 B_1 C_1 D_1$ параллельны, значит плоскость α пересекает их по параллельным прямым.
По условию плоскость α параллельна прямой $A_1 C_1$, то есть содержит прямую, параллельную $A_1 C_1$. Поэтому, проведя через точку $K$ прямую $KP (P ∈ B_1 C_1)$, параллельную прямой $A_1 C_1$, и через точку $A$ — прямую $AC$, параллельную прямой $A_1 C_1$ (прямая $AC$ содержит диагональ нижнего основания) получим трапецию $AKPC$ — искомое сечение.
2. Выберем прямоугольную систему координат, как показано на рисунке. Найдём координаты нужных точек: $B(0; 0; 0), F (8√2; 8√2; 4), A(8√2; 0; 0), C (0; 8√2; 0), K (4√2; 0; 16), P (0; 4√2; 16)$.
3. Рассмотрим векторы ${BF}↖{→} (8√2; 8√2; 4), {AP}↖{→} (-8√2; 4√2; 16)$ и ${CK}↖{→} (4√2; -8√2; 16)$.
Так как ${BF}↖{→}· {AP}↖{→} = 8√2(-8√2) + 8√2 · 4√2 + 16 · 4 = 0$, то ${BF}↖{→} ⊥ {AP}↖{→}$.
Так как ${BF}↖{→} · {CK}↖{→} = 8√2 · 4√2 + 8√2 · (-8√2) + 4 · 16 = 0$, то ${BF}↖{→} ⊥ {CK}↖{→}$.
Отсюда следует, что $BF ⊥ α$ по признаку перпендикулярности прямой и плоскости ($BF$ перпендикулярна двум пересекающимся прямым плоскости).
б) Искомый объём $V = {1}/{3}S · h$, где $S$ — площадь четырёхугольника $AKPC$, а высота $h$ — расстояние от точки $B$ до плоскости $α$.
1. $S_{AKPC} = {1}/{2}AP · CK sin β$, где $β$ — угол между диагоналями $AP$ и $CK$ четырёхугольника $AKPC$.
$cos β = {{AP}↖{→} · {CK}↖{→}}/{|{AP}↖{→}| · |{CK}↖{→}|} = {-8√2 · 4√2 + 4√2(-8√2) + 16 · 16}/{√{(-8√2)^2 + (4√2)^2 + 16^2} · √{(4√2)^2 + (-8√2)^2 + 16^2}} = {-64 — 64 + 256}/{416} = {128}/{416} = {4}/{13}; |{AP}↖{→}| = |{CK}↖{→}| = √{416}$.
$sin β = √{1 — cos^2β} = √{1 — {16}/{169}} = {3√17}/{13}$.
Таким образом $S = {1}/{2} · √{416} · √{416} · {3√17}/{13} = 48√{17}$.
2. Чтобы найти $h$ необходимо найти уравнение плоскости $α$. Оно имеет вид $ax + by + cz + d = 0$, где ${n}↖{→}(a; b; c)$ — вектор нормали этой плоскости.
Согласно пункту а) одним из векторов нормали является вектор ${BF}↖{→}(8√2; 8√2; 4)$.
Значит, уравнение плоскости имеет вид $8√2x + 8√2y + 4z + d = 0 (1)$.
Чтобы найти значение $d$ подставим координаты точки $A(8√2; 0; 0)$ в уравнение (1) и получим $8√2 · 8√2 + d = 0, d = -128$.
Уравнение плоскости $α$ примет вид $8√2x + 8√2y + 4z — 128 = 0$.
Найдём расстояние $h$ от точки $B(0; 0; 0)$ до плоскости сечения.
$h = {|ax_0+ by_0 + cz_0 + d|}/{√{a^2 + b^2 + c^2}} = {|8√2 · 0 + 8√2 · 0 + 4 · 0 — 128|}/{√{(8√2)^2 + (8√2)^2 + 16}} = {32}/{√17}$, где ($x_0 ; y_0 ; z_0$ ) — координаты точки $B$.
$V = {1}/{3} · S · h = {1}/{3} · 48√{17} · {32}/{√17} = 512$.
Ответ: 512
Задача 5
В прямоугольном параллелепипеде $ABCDA_{1}B_{1}C_{1}D_{1}$ сторона $AB=AA_{1}=3$, $AD=6$. На рёбрах $AD$ и $CC_{1}$ взяты соответственно точки $M$ и $N$ — середины этих рёбер.
а) Постройте сечение параллелепипеда плоскостью, проходящей через вершину $D$, параллельно $MN$ и $B_{1}C$.
б) Найдите объём пирамиды, основание которой — построенное сечение, а вершина — точка $D_{1}$.
Решение
а) Искомое сечение проходит через вершину $D$ параллельно $B_1 C$, следовательно, пересекает грань $AA_1 D_1 D$ по диагонали $A_1 D$
Действительно, $A_1 D||B_1 C$ (плоскость пересекает две параллельные плоскости по параллельным прямым)
Рассмотрим прямоугольник $C C_1 M_1M$, где $M_1$ середина $A_1 D_1$
Проведём $C_1 K ||M N$. $K$ — середина отрезка $M M_1$ и середина отрезка $A_1 D$, значит, принадлежит искомому сечению, поэтому $C_1 K$ лежит в плоскости сечения
Таким образом, $A_1 C_1 D$ — искомое сечение.
б) Рассмотрим пирамиду $D_1A_1C_1D$ как пирамиду с основанием $D_1DC_1$ и высотой $A_1D_1 (A_1D_1 ⊥ D_1DC_1)$.
$V_{D_1A_1C_1D} = {1}/{3}S_{D_1DC_1} ·A_1D_1 = {1}/{3} · {1}/{2}D_1C_1 ·D_1D ·A_1D_1 = {1}/{6} ·3·3·6 = 9$.
Ответ: 9
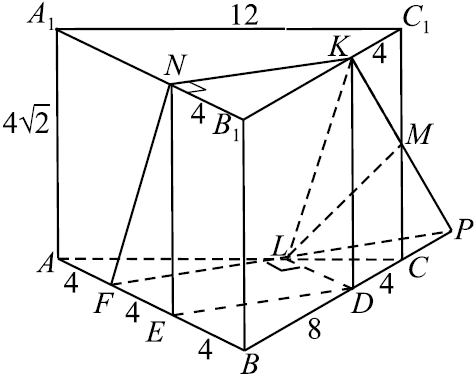
Задача 6
В правильной треугольной призме $ABCA_1 B_1 C_1$ сторона основания равна $12$, а боковое ребро равно $4√ {2}$. На рёбрах $AB$, $A_1 B_1$ и $B_1 C_1$ отмечены точки $F$, $N$ и $K$ соответственно, причём $AF=B_1 N=C_1 K =4$.
а) Пусть $L$ — точка пересечения плоскости $FNK$ с ребром $AC$. Докажите, что $FNKL$ — ромб.
б) Найдите площадь сечения призмы плоскостью $FNK$.
Решение
а) Докажем, что $FNKL$ — ромб.
1) Так как точка $L$ — точка пересечения плоскости $FNK$ с ребром $AC$, то (по свойству параллельных плоскостей) линии пересечения плоскости $FNK$ с основанием призмы параллельны, т.е $FL ‖ N K$.
2) В основаниях правильной треугольной призмы лежат правильные треугольники со стороной $12$.
В треугольнике $NB_1K$ $∠B1 = 60°, NB_1 = 4$ по условию, а $B_1 K = 12 — 4 = 8$. По теореме косинусов $N K = 4√3$, поэтому $N K^2 + NB_1^2 = KB_1^2$. Отсюда следует, что $∠N = 90°, ∠K = 30°$.
Значит, $N K ⊥ A_1B_1$ и $F L ⊥ AB$, т.к. $N K ‖ F L$, а $A_1B_1 ‖ AB$.
3) В $△AFL$ $∠A = 60°, ∠F = 90°, AF = 4$;
$AF$ в прямоугольном $△AFL$ лежит против $∠L = 30°$, следовательно, $AF = {1}/{2}AL, AL = AF · 2 = 4 · 2 = 8$;
$FL^2 = AL^2 — AF^2 = 8^2 — 4^2 = 64 — 16 = 48, F L = 4√3$.
Имеем $N K ‖ F L$ и $N K = F L$, следовательно $F N K L$ — параллелограмм.
Проведём $N E ⊥ F B$.
В $△NFE$ $∠E = 90°, N E = 4√2, F E = 12 — 8 = 4$.
$FN^2 = NE^2 + FE^2 = (4√2)^2 + 4^2 = 32 + 16 = 48$,
$FN = √48 = 4√3, KL = FN$ как противоположные стороны параллелограмма.
4) Имеем: $N K = K L = F N = F L$, следовательно, $F N K L$ — ромб.
б) $K N ⊥ A_1B_1 , K N ⊥ N E ⇒ K N ⊥ (AA_1B_1)$ и $K N ⊥ F N$, значит $K N F L$ — квадрат, $S_{KNFL} = FN^2 = 48$.
Построим сечение пирамиды плоскостью $FNK$ .
Продлим $FL$ до пересечения с $BC$, получим точку $P$.
Соединим точку $P$ с точкой $K$, $KP$ пересекает $CC_1$ в точке $M$. Соединим точку $M$ с точкой $L$.
Пятиугольник $F N K M L$ — искомое сечение.
В прямоугольном $△FBP$ $∠B = 60°$, значит $BP = 2FB = 16, PC = 16 — 12 = 4$.
$KC_1 = CP, ∠KC_1M = ∠MCP = 90°$, тогда $△KC_1M = △PCM$ и $C_1M = CM = 2√2. KM = √{4^2 + (2√2)^2} = √{24}$. В $△LMC$ $LM^2 = LC^2 + MC^2, LC = AC — AL = 12 — 8 = 4, MC = {1}/{2}CC_1 = 2√2, √{4^2 + (2√2)^2} = √{24}, K L = √{48}$, следовательно, $△KLM$ прямоугольный, $S_{KLM} = {1}/{2}(√{24})^2 = 12$.
$S_{сеч} = S_{KNFL} + S_{KLM} = 48 + 12 = 60$.
Ответ: 60
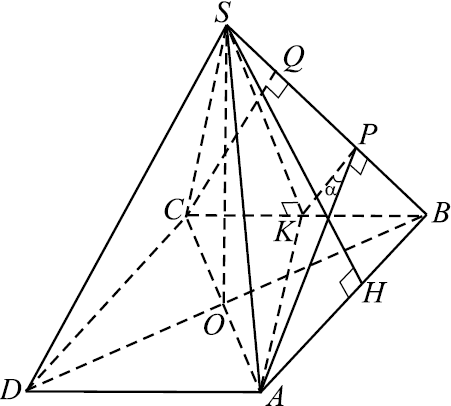
Задача 7
Дана четырёхугольная пирамида $SABCD$ с прямоугольником $ABCD$ в основании, $AB=6$, $BC=6√ {2}$. Высота пирамиды проектируется в точку пересечения диагоналей основания. Из вершин $A$ и $C$ на ребро $SB$ опущены перпендикуляры $AP$ и $CQ$.
а) Докажите, что точка $P$ является серединой отрезка $BQ$.
б) Найдите угол между плоскостями $SBA$ и $SBC$, если $SD=12$.
Решение
а) Пусть боковое ребро $SB$ равно $x$.
1) $△SHB∼△APB$ (прямоугольные с общим острым углом при вершине $B$). Тогда ${PB}/{BH} = {AB}/{SB}$. $H$ — середина $AB$. Тогда ${PB}/{3} = {6}/{x}; PB = {18}/{x}$.
2) $△SKB∼△CQB$ (прямоугольные с общим острым углом при вершине $B$). Тогда ${QB}/{BK} = {BC}/{SB}; {QB}/{3√2} = {6√2}/{x}; QB = {36}/{x}$.
3) Так как ${QB}/{PB} = {{36}/{x}}/{{18}/{x}} = 2$, то $PQ = PB$.
б) 1) Из пункта а) следует, что $PK$ — средняя линия $△BCQ$. Следовательно, $PK ‖ QC$. Но так как $QC ⊥ BS$, то и $PK ⊥ BS$. Значит, $∠APK$ — линейный угол двугранного угла между гранями $SBA$ и $SBC$. Пусть, $∠APK = α$.
2) $AK = √{AB^2 + BK^2} = √{6^2 + (3√2)^2} = 3√6$.
3) Так как по условию $SD = 12$ и $SB = SD$ (равным проекциям соответствуют равные наклонные), то $x = 12$, а $QB = {36}/{x} = {36}/{12}=3$.
Тогда $CQ = √{BC^2 — QB^2} = √{(6√2)^2 — 3^2} = 3√7$.
Так как $PK$ — средняя линия, то $PK = {1}/{2}CQ = {3√7}/{2}$.
4) $PB = {1}/{2}QB = {1}/{2}·3 = {3}/{2}$.
$AP = √{AB^2 — PB^2} = √{6^2 — ({3}/{2})^2} = {3}/{2}√{15}$.
5) По теореме косинусов для $△APK$:
$AK^2 = AP^2 + PK^2 — 2·AP·PK·cosα$;
$54 = {135}/{4} + {63}/{4} — 2·{3}/{2}√{15}·{3√7}/{2}·cosα$;
$cosα = — {1}/{√{105}}$;
Так как $cosα < 0$, то $α$ — тупой угол.
Значит, искомый угол между плоскостями $SBA$ и $SBC$ равен ($π-α$).
$cos(π-α) = -cosα = {1}/{√{105}}$.
Следовательно, искомый угол равен $arccos{1}/{√{105}}$.
Ответ:
Задача 8
Основанием прямой треугольной призмы $ABCA_1B_1C_1$ является прямоугольный треугольник $ABC$ с прямым углом $C$. Диагонали граней $AA_1B_1B$ и $BB_1C_1C$ равны $2√ {41}$ и $10$ соответственно, $AB=10$.
а) Докажите, что треугольник $A_1C_1B$ прямоугольный.
б) Найдите объём пирамиды $ACC_1B_1$.
Решение
а) Так как $A_1C_1 ⊥ B_1C_1$ и $A_1C_1 ⊥ CC_1$ по условию, то $A_1C_1 ⊥ BB_1C_1$ по признаку перпендикулярности прямой и плоскости.
Следовательно, $A_1C_1 ⊥ BC_1$, то есть треугольник $A_1C_1B$ прямоугольный.
б) 1) $AC = A_1C_1 = √{A_1B^2 — BC^2_1} = √{(2√{41})^2 — 10^2} = 8$.
2) $B_1C_1 = BC = √{AB^2 — AC^2} = √{10^2 — 8^2} = 6$.
3) $CC_1 = √{BC_1^2 — BC^2} = √{10^2 — 6^2} = 8$.
4) $V_{ACC_1B_1} = {1}/{3}·S_{ACC_1} ·B_1C_1 = {1}/{3} · {1}/{2} ·AC·CC_1 ·B_1C_1 = {1}/{6} ·8·8·6 = 64$.
Ответ: 64
Задача 9
В основании четырёхугольной пирамиды $PABCD$ лежит трапеция $ABCD$ с большим основанием $AD$. Известно, что сумма углов $BAD$ и $ADC$ равна $90^°$, плоскости $PAB$ и $PCD$ перпендикулярны основанию, прямые $AB$ и $CD$ пересекаются в точке $K$.
а) Докажите, что плоскость $PAB$ перпендикулярна плоскости $PDC$.
б) Найдите объём $PKBC$, если $AB=3$, $BC=5$, $CD=4$, а высота пирамиды $PABCD$ равна $7$.
Решение
а) 1) $∠AKD = 180° — (∠A + ∠D) = 180° — 90° = 90°$.
2) Если две пересекающиеся плоскости перпендикулярны третьей, то они пересекаются по прямой, также перпендикулярной этой плоскости. Отсюда следует, что так как $PAB ⊥ ABC$ и $PCD ⊥ ABC$, то $PK ⊥ ABC$.
3) Так как $PK ⊥ ABC$, то $PK ⊥ KA$ и $PK ⊥ KD$.
Значит, $∠AKD$ — линейный угол двугранного угла между плоскостями $PAB$ и $PCD$. Следовательно, $PAB ⊥ PCD$.
б) Обозначим $BK = x, CK = y$.
1) $△BKC∼ △AKD$, так как $AD ‖ BC$.
Тогда ${AK}/{BK} = {DK}/{CK}; {AB + BK}/{BK} = {CD + CK}/{CK}; {AB}/{BK} + 1 = {CD}/{CK} + 1; {AB}/{BK} = {CD}/{CK}; {3}/{x} = {4}/{y}; x = {3}/{4}y$.
2) По теореме Пифагора $BK^2 + CK^2 = BC^2; x^2 + y^2=5^2; ({3}/{4}y)^2+y^2=25; {25}/{16}y^2=25; y=4;x={3}/{4}y=3$.
3) $S_{KBC} = {1}/{2}BK·CK = {1}/{2}·3 ·4= 6$.
4) $V_{PKBC} = {1}/{3}S_{KBC}·PK = {1}/{3}·6·7 = 14$.
Ответ: 14
Задача 10
В основании четырёхугольной пирамиды $PABCD$ лежит трапеция $ABCD$ с большим основанием $AD$. Известно, что сумма углов $BAD$ и $ADC$ равна $90^°$, плоскости $PAB$ и $PCD$ перпендикулярны основанию, прямые $AB$ и $CD$ пересекаются в точке $K$.
а) Докажите, что плоскость $PAB$ перпендикулярна плоскости $PDC$.
б) Найдите объём $PKBC$, если $AB=BC=CD=4$, а высота пирамиды $PABCD$ равна $9$.
Решение
а) 1) $∠AKD = 180° — (∠A + ∠D) = 180° — 90° = 90°$.
2) Если две пересекающиеся плоскости перпендикулярны третьей, то они пересекаются по прямой, так же перпендикулярной этой плоскости. Отсюда следует, что так как $PAB ⊥ ABC$ и $PCD ⊥ ABC$, то $PK ⊥ ABC$.
3) Так как $PK ⊥ ABC$, то $PK ⊥ KA$ и $PK ⊥ KD$.
Значит, $∠AKD$ — линейный угол двугранного угла между плоскостями $PAB$ и $PCD$. Следовательно, $PAB ⊥ PCD$.
б) 1) Так как $ABCD$ — равнобедренная трапеция, то $∠A = ∠D$. Так как $BC ‖ AD$, то $∠A = ∠KBC, ∠D = ∠KCB$ как соответственные. Значит, $∠KBC = ∠KCB$, то есть $△KBC$ равнобедренный.
2) По теореме Пифагора $BK^2 + CK^2 = BC^2; 2BK^2 = BC^2; BK^2 = {BC^2}/{2} = {4^2}/{2} = 8$.
3) $S_{KBC} = {1}/{2}BK·CK = {1}/{2}BK^2 = {1}/{2}·8 = 4$.
4) $V_{PKBC} = {1}/{3}S_{KBC}·PK = {1}/{3}·4·9 = 12$.
Ответ: 12
Задача 11
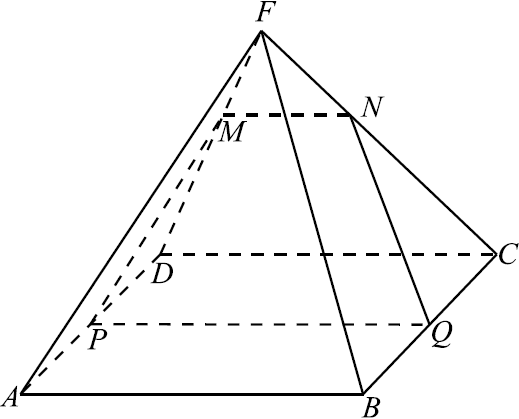
На боковом ребре $FD$ правильной четырёхугольной пирамиды ${FABCD}$ отмечена точка $M$ так, что $FM:FD=1:3$. Точки $P$и $Q$ — середины рёбер $AD$ и $BC$ соответственно.
а) Докажите, что сечение пирамиды плоскостью $MPQ$ есть равнобедренная трапеция.
б) Найдите отношение объёмов многогранников, на которые плоскость $MPQ$ разбивает пирамиду.
Решение
а) 1) Построим $MN ‖ CD$.
Так как и $PQ ‖ CD$, то $MN ‖ PQ$. Следовательно, точки $M, N, P$ и $Q$ лежат в одной плоскости. Таким образом, трапеция $MNQP$ является сечением пирамиды плоскостью $MPQ$.
2) $△FMN ∼△FDC$ (так как $MN ‖ CD$, то $∠FNM = ∠FCD$ и $∠FMN = ∠FDC$ как соответственные). Так как $△FCD$ равнобедренный, то и $△FNM$ тоже равнобедренный. Тогда $FM = FN; NC = FC — FN = FD — FM = MD$.
Кроме того, $PD = {1}/{2}AD = {1}/{2}BC = QC$. Так как $△FAD = △FBC$, то $∠MDP = ∠NCQ$. Отсюда $△PDM = △QCN$ по двум сторонам и углу между ними. Следовательно, $PM = NQ$, то есть $MNQP$ — равнобедренная трапеция.
б) 1) Пусть $MR ⊥ PQ, MS ⊥ CD, NX ⊥ PQ, NY ⊥ CD$.
Так как $MNQP$ и $MNCD$ — равнобедренные трапеции, то $V_1 = V_{PQCDMN} = V_{MRSNXY} + 2·V_{NXQCY}$ — объём первой части.
2) Пусть $a$ — сторона основания, $h$ — высота пирамиды. Тогда $QC = XY = RS = {a}/{2}; MN = {1}/{3}a; MO = {2}/{3}h(△FMN ∼△FDC$ и ${FM}/{FD} = {1}/{3}; QX = {PQ -MN}/{2} = {a -{1}/{3}a}/{2} = {1}/{3}a (MNQP$ — равнобедренная трапеция).
3) $S_{MRS} = {1}/{2}RS·MO = {1}/{2}·{a}/{2}·{2}/{3}h = {1}/{6}ah$. Объём прямой призмы $MRSNXY$ равен $V_{MRSNXY} = S_{MRS}·MN = {1}/{6}ah·{1}/{3}a = {1}/{18}a^2h$.
$V_{NXQCY} = {1}/{3}S_{XQCY}·MO = {1}/{3}·QX·QC·MO = {1}/{3}·{1}/{3}a·{a}/{2}·{2}/{3}h = {1}/{27}a^2h$.
$V_1 = V_{MRSNXY} + 2·V_{NXQCY} = {1}/{18}a^2h + 2·{1}/{27}a^2h = {7}/{54}a^2h$.
4) $V = V_{SABCD} = {1}/{3}S_{ABCD}·h = {1}/{3}a^2h$.
$V_2 = V — V_1 = ({1}/{3} — {7}/{54})a^2h = {11}/{54}a^2h$ — объём второй части.
5) ${V_1}/{V_2} ={{7}/{54}a^2h}/{{11}/{54}a^2h} = {7}/{11}$.
Ответ: 7:11
Задача 12
На боковом ребре $FD$ правильной четырёхугольной пирамиды ${FABCD}$ отмечена точка $M$ так, что $FM:FD=2:5$. Точки $P$ и $Q$ — середины рёбер $AD$ и $BC$ соответственно.
а) Докажите, что сечение пирамиды плоскостью $MPQ$ есть равнобедренная трапеция.
б) Найдите отношение объёмов многогранников, на которые плоскость $MPQ$ разбивает пирамиду.
Решение
а) 1) Построим $MN∥ CD$ (см. рис.).
Так как и $PQ∥ CD$, то $MN∥ PQ$. Следовательно, точки $M$, $N$, $P$ и $Q$ лежат в одной плоскости. Таким образом, трапеция $MNQP$ является сечением пирамиды плоскостью $MPQ$. 2) $▵ FMN∼ ▵ FDC$ (так как $MN∥ CD$, то $∠ FNM=∠ FCD$ и $∠ FMN=∠ FDC$ как соответственные). Так как $▵ FDC$ равнобедренный, то и $▵ FMN$ тоже равнобедренный. Тогда $FM=FN$; $NC=FC-FN=FD-FM=MD$. Кроме того, $PD={1} / {2}AD={1} / {2}BC=QC$. Так как $▵ FAD=▵ FBC$, то $∠ MDP=∠ NCQ$. Отсюда $▵ PDM=▵ QCN$ по двум сторонам и углу между ними. Следовательно, $PM=NQ$, то есть $MNQP$ — равнобедренная трапеция. б) 1) Пусть $MR⊥ PQ$, $MS⊥ CD$, $NX⊥ PQ$, $NY⊥ CD$ (см. рис.).
Так как $MNQP$ и $MNCD$ — равнобедренные трапеции, то $V_1=V_{PQCDMN}=V_{MRSNXY}+2⋅ V_{NXQCY}$ — объём первой части. 2) Пусть $a$ — сторона основания, $h$ — высота пирамиды. Тогда $QC=XY=RS={a} / {2}$; $MN={2} / {5}a$; $MO={3} / {5}h$ $(▵ FMN∼ ▵ FDC$ и ${FM} / {FD}={2} / {5})$; $QX={PQ-MN} / {2}={a-{2} / {5}a} / {2}={3} / {10}a$ ($MNQP$ — равнобедренная трапеция). 3) $S_{MRS}={1} / {2}RS⋅ MO={1} / {2}⋅ {a} / {2}⋅ {3} / {5}h={3} / {20}ah$. Объём прямой призмы $MRSNXY$ равен: $V_{MRSNXY}=S_{MRS}⋅ MN={3} / {20}ah⋅ {2} / {5}a={3} / {50}a^2h$. $V_{NXQCY}={1} / {3}S_{XQCY}⋅ MO={1} / {3}⋅ QX⋅ QC⋅ MO={1} / {3}⋅ {3} / {10}a⋅ {a} / {2}⋅ {3} / {5}h={3} / {100}a^2h$. $V_1=V_{MRSNXY}+2⋅ V_{NXQCY}={3} / {50}a^2h+2⋅ {3} / {100}a^2h={3} / {25}a^2h$. 4) $V=V_{SABCD}={1} / {3}S_{ABCD}⋅ h={1} / {3}a^2h$. $V_2=V-V_1=({1} / {3}-{3} / {25})a^2h={16} / {75}a^2h$ — объём второй части. 5) ${V_1} / {V_2}={{3} / {25}a^2h} / {{16} / {75}a^2h}={9} / {16}$.
Ответ: 9:16
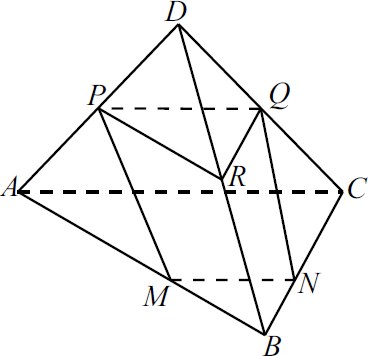
Задача 13
На рёбрах $AB$ и $BC$ треугольной пирамиды $DABC$ отмечены точки $M$ и $N$ так, что $AM:MB=CN:NB=2:1$. Точки $P$ и $Q$ — середины рёбер $DA$ и $DC$ соответственно.
а) Докажите, что точки $P$, $Q$, $M$ и $N$ лежат в одной плоскости.
б) Найдите отношение объёмов многогранников, на которые плоскость $PQM$ делит пирамиду.
Решение
а) 1) $△ABC ∼△MBN$ (угол $B$ общий, две пропорциональные стороны).
Значит $∠NMB = ∠CAB$. Следовательно, $MN ‖ AC$, так как равны соответствующие углы.
2) Так как $PQ$ — средняя линия $△ADC$, то $PQ ‖ AC$.
3) Так как $MN ‖ AC$ и $PQ ‖ AC$, то $MN ‖ PQ$. Следовательно, точки $P, Q, N$ и $M$ лежат в одной плоскости.
б) 1) Пусть $R$ — середина ребра $DB$. Тогда $PR$ — средняя линия $△ADB$. Следовательно, $PR ‖ AB$. Аналогично $QR ‖ BC$.
2) Обозначим через $V$ объём пирамиды $DABC, V_1 = V_{DPQR} + V_{MNBPQR}, V_2 = V — V_1, h$ — высота пирамиды $DABC, S$ — площадь $△ABC$.
Так как $△PQR∼ △ACB$ и ${PQ}/{AC} = {1}/{2}$, то $S_{PQR} ={S}/{4}$.
Так как ${DP}/{DA} = {1}/{2}$, то высота пирамиды $DPQR$ равна ${h}/{2}$.
Таким образом, $V_{DPQR} = {1}/{3}S_{PQR}· {h}/{2} = {1}/{3}· {S}/{4} ·{h}/{2} = {Sh}/{24}$.
3) Можно доказать, что $MNBPQR$ — усечёная пирамида. Её высота равна ${h}/{2}$.
Пусть $S_1 = S_{MNB}, S_2 = S_{PQR}$.
Так как $△BMN ∼ △BAC$ и ${BM}/{BA} = {1}/{3}$, то $S_1 = ({1}/{3})^2·S = {S}/{9}$.
Тогда $V_{MNBPQR} = {1}/{3}·{h}/{2}·(S_1 + √{S_1·S_2} + S_2)= {h}/{6}·({S}/{9} + √{{S}/{9}·{S}/{4}} + {S}/{4}) = {h}/{6}({S}/{9} + {S}/{6} + {S}/{4})= {19}/{216}Sh$.
4) $V_1 = V_{DPQR} + V_{MNBPQR} = {Sh}/{24} + {19}/{216}Sh = {7}/{54}Sh. V_2 = V — V_1 = {1}/{3}Sh — {7}/{54}Sh = {11}/{54}Sh$.
5) ${V_1}/{V_2} = {{7}/{54}Sh}/{{11}/{54}Sh} = {7}/{11}$.
Ответ: 7:11
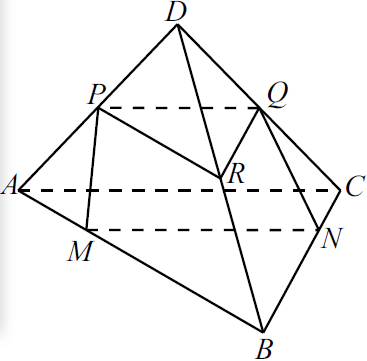
Задача 14
На рёбрах $AB$ и $BC$ треугольной пирамиды $DABC$ отмечены точки $M$ и $N$ так, что $AM:MB=CN:NB=1:3$. Точки $P$ и $Q$ — середины рёбер $DA$ и $DC$ соответственно.
а) Докажите, что точки $P$, $Q$, $M$ и $N$ лежат в одной плоскости.
б) Найдите отношение объёмов многогранников, на которые плоскость $PQM$ делит пирамиду.
Решение
а) 1) $△ABC ∼△MBN$ (угол $B$ общий, две пропорциональные стороны). $MB ={3}/{4}AB, BN ={3}/{4}BC$.
Следовательно, $MN ‖ AC$, так как равны соответствующие углы.
2) Так как $PQ$ — средняя линия $△ADC$, то $PQ ‖ AC$.
3) Так как $MN ‖ AC$ и $PQ ‖ AC$, то $MN ‖ PQ$. Следовательно, точки $P, Q, N$ и $M$ лежат в одной плоскости.
б) 1) Пусть $R$ — середина ребра $DB$. Тогда $PR$ — средняя линия $△ADB$. Следовательно, $PR ‖ AB, PR = {1}/{2}AB$. Аналогично $QR ‖ BC, QR = {1}/{2}BC$.
2) Обозначим через $V$ объём пирамиды $DABC, V_1 = V_{DPQR} + V_{MNBPQR}, V_2 = V — V_1, h$ — высота пирамиды $DABC, S$ — площадь $△ABC$.
Так как $△PQR∼ △ACB$ и ${PQ}/{AC} = {1}/{2}$, то $S_{PQR} ={S}/{4}$.
Так как ${DP}/{DA} = {1}/{2}$, то высота пирамиды $DPQR$ равна ${h}/{2}$.
Таким образом, $V_{DPQR} = {1}/{3}S_{PQR}· {h}/{2} = {1}/{3}· {S}/{4} ·{h}/{2} = {Sh}/{24}$.
3) Можно доказать, что $MNBPQR$ — усечёная пирамида. Её высота равна ${h}/{2}$.
Пусть $S_1 = S_{MNB}, S_2 = S_{PQR}$.
Так как $△BMN ∼ △BAC$ и ${BM}/{BA} = {3}/{4}$, то $S_1 = ({3}/{4})^2·S = {9}/{16}S$.
Тогда $V_{MNBPQR} = {1}/{3}·{h}/{2}·(S_1 + √{S_1·S_2} + S_2)= {h}/{6}·({9}/{16}S + √{{9}/{16}S·{S}/{4}} + {S}/{4}) = {h}/{6}({9}/{16}S + {3}/{8}S + {S}/{4})= {19}/{96}Sh$.
4) $V_1 = V_{DPQR} + V_{MNBPQR} = {Sh}/{24} + {19}/{96}Sh = {23}/{96}Sh. V_2 = V — V_1 = {1}/{3}Sh — {23}/{96}Sh = {3}/{32}Sh$.
5) ${V_1}/{V_2} = {{23}/{96}Sh}/{{3}/{32}Sh} = {23}/{9}$.
Ответ: 23:9
Задача 15
В правильной треугольной пирамиде $MNPQ$ с вершиной $M$ сторона основания равна $15$, высота равна $√ {6}$. На рёбрах $NP$, $NQ$ и $NM$ отмечены точки $E$, $F$, $K$ соответственно, причём $NE=NF=3$ и $NK={9} / {5}$. а) Докажите, что плоскости $EFK$ и $MPQ$ параллельны. б) Найдите расстояние от точки $K$ до плоскости $MPQ$.
Решение
а) Докажем, что $EFK ‖ MPQ$. Воспользуемся признаком параллельности плоскостей: если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то такие плоскости параллельны.
В плоскости $MPQ$ возьмём прямые $QP$ и $MQ$, а в плоскости $EFK$ — прямые $FE$ и $KF$. Пусть $O$ — центр основания.
В $△MNO: ∠NOM = 90°$ и по теореме Пифагора $NM = √{NO^2 +MO^2}$. Найдём $NO$: треугольник $NPQ$ — правильный, все его стороны равны, а высота $NA = {a√3}/{2}$, где $a$ — сторона треугольника $NPQ$. $NO = {2}/{3}NA = {2}/{3}·{a√3}/{2} = {a√3}/{3}$, то есть $NO = {15√3}/{3} = 5√3$. B $△NMO: ∠MON = 90°, NM = √{MO^2 + NO^2} = √{(5√3)^2 + 6} = √{75 + 6} = √{81} = 9$.
1) $△NKF∼△NMQ$, так как ${NK}/{NM} ={{9}/{5}}/{9} ={1}/{5}, {NF}/{NQ} = {3}/{15} = {1}/{5}$ и $∠MNQ$ — общий. Из подобия следует, что $∠NKF = ∠NMQ$. Это соответственные углы при прямых $KF$ и $MQ$ и секущей $NM$. Значит, $KF ‖ MQ$.
2) $△NEF∼△NPQ$, так как ${NE}/{NP} ={3}/{15} = {1}/{5}, {NF}/{NQ} ={3}/{15} = {1}/{5}$ и $∠PNQ$ — общий. Из подобия следует, что $∠NEF = ∠NPQ$. Это соответственные углы при прямых $EF$ и $PQ$ и секущей $NP$. Значит, $EF ‖ PQ$.
Итак, две пересекающейся прямые $KF$ и $FE$ плоскости $KFE$ соответственно параллельны двум пересекающимся прямым $MQ$ и $PQ$ плоскости $MPQ$, следовательно, $KFE ‖ MPQ$.
б) Найдём расстояние от точки $K$ до плоскости $MPQ$. Так как плоскость $KFE$ параллельна плоскости $MPQ$, то расстояние от точки $K$ до плоскости $MPQ$ равно расстоянию от точки $B$ до плоскости $MPQ$ и оно равно длине отрезка $BD$ ($BD$ — перпендикуляр к $AM$. Докажем это.
$NA ⊥ QP$ и $MA ⊥ QP$ (как высоты треугольников $NPQ$ и $MPQ$), значит, прямая $QP$ перпендикулярна плоскости $NMA$, и тогда прямая $PQ$ перпендикулярна любой прямой этой плоскости, в частности $BD$. С другой стороны $BD ⊥ AM$ по построению, значит, прямая $BD$ перпендикулярна двум пересекающимся прямым плоскости $MPQ$, и тогда отрезок $BD$ перпендикулярен плоскости $MPQ$ и равен расстоянию от $B$ до плоскости $MPQ$.
В $△BDA: ∠BDA = 90°; BD = BA · sin∠DAB; BA = NA — NB; NA = {15√3}/{2}; NB ={1}/{5}NA = {3√3}/{2}; BA = {15√3}/{2} — {3√3}/{2} = 6√3$.
Из $△MOA: sin∠MAO = sin∠DAB = {MO}/{MA} = {√6}/{√{MO^2 + OA^2}}={√6}/{√{6 +{75}/{4}}} = {√6·2}/{√{99}} = {2√6}/{3√{11}} ={2}/{3}√{{6}/{11}}$ (так как $AO ={1}/{3}NA = {5√3}/{2})$.
Из $△ABD:BD = AB·sin∠DAB = 6√3·{2}/{3}√{{6}/{11}} = 4√{{18}/{11}} = 12√{{2}/{11}} = {12√{22}}/{11}$.
Ответ:
Задача 16
В правильной треугольной пирамиде $DABC$ с вершиной $D$ сторона основания $AB$ равна $9$, высота равна $3$. На рёбрах $AB$, $AC$, $AD$ отмечены точки $P$, $K$, $F$ соответственно, причём $AP=AK=3$ и $AF=2$. а) Доказать, что плоскости $PKF$ и $DBC$ параллельны. б) Найти расстояние от точки $F$ до плоскости $DBC$.
Решение
Докажем, что плоскость $DBC$ параллельна плоскости $PKF$. Для этого в плоскости $PKF$ возьмём прямые $KP$ и $FP$, а в плоскости $DBC$ — прямые $CB$ и $DB$ (см. рис.). Пусть $O$ — центр основания.
В $▵ ADO$: $∠ DOA=90°$ и по теореме Пифагора $AD=√ {DO^2+AO^2}$. Найдём $AO$, треугольник $ABC$ — правильный, все его стороны равны, $AM$ — высота, $AM={a√ {3}} / {2}$, где $a$ — сторона $▵ ABC$, $AO={2} / {3} AM={2} / {3}⋅ {a√ {3}} / {2}={a√ {3}} / {3}$, то есть $AO={9√ {3}} / {3}=3√ {3}$, $AD=√ {3^2+(3√ {3})^2}=√ {9+27}=6$. $▵ APF∼ ▵ ABD$, так как ${AF} / {AD}={2} / {6}={1} / {3}$, ${AP} / {AB}={3} / {9}={1} / {3}$ и $∠ DAB$ — общий, то есть две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы между ними равны. Из подобия следует, что $∠ AFP=∠ ADB$. Это соответственные углы при прямых $FP$ и $DB$ и секущей $AD$. Значит, $FP∥ DB$. Аналогично рассуждая, получим, что $▵ AKP∼ ▵ ACB$, так как ${AK} / {AC}={3} / {9}={1} / {3}$, ${AP} / {AB}={3} / {9}={1} / {3}$ и $∠ BAC$ — общий, то есть две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы между ними равны. Из подобия следует, что $∠ APK=∠ ABC$. Это соответственные углы при прямых $KP$ и $BC$ и секущей $AB$. Значит, $KP∥ BC$. Итак, две пересекающиеся прямые $KP$ и $FP$ плоскости $PKF$ соответственно параллельны двум пересекающимся прямым $CB$ и $BD$ плоскости $DBC$. Следовательно, плоскости $DBC$ и $PKF$ параллельны по признаку параллельности плоскостей. б) Найдём расстояние от точки $F$ до плоскости $DBC$. Так как плоскость $KFP$ параллельна плоскости $DBC$, то расстояние от точки $F$ до плоскости $DBC$ равно расстоянию от точки $L$ до плоскости $DBC$ и равно длине отрезка $LN$ (см. рис.), где $LN$ — перпендикуляр к $MD$ в плоскости $AMD$.
Докажем это. $AM ⊥ BC$ и $DM⊥ BC$ (как высоты треугольников $ABC$ и $DBC$), значит, $BC⊥ MDA$ и тогда $BC$ перпендикулярен любой прямой этой плоскости, в частности, $LN$. С другой стороны, $LN ⊥ MD$ по построению, значит, $LN$ перпендикулярен двум пересекающимся прямым плоскости $DBC$, и тогда отрезок $LN$ перпендикулярен плоскости $DBC$ и равен расстоянию от точки $L$ до плоскости $DBC$. В $▵ LNM$: $∠ LNM=90°$, $LN=LM⋅ sin ∠ NML$. $ML=AM-LA$; $AM={9√ {3}} / {2}$;
$LA={1} / {3}⋅ AM={9√ {3}} / {6}={3√ {3}} / {2}$. $ML={9√ {3}} / {2}-{3√ {3}} / {2}=3√ {3}$. $sin ∠ NML={DO} / {DM}$; $DO=3$ (по условию). Из $▵ MDB$ найдём $DM$: $∠ DMB=90°$,
$MD=√ {BD^2-MB^2}=√ {36-({9} / {2})^2}={3√ {7}} / {2}$. $sin ∠ NML={2} / {√ {7}}$. $LN=LM⋅ sin ∠ NML=3√ {3}⋅{2} / {√ {7}}=6√ {{3} / {7}}$.
Ответ: 6sqrt{fsm{3}{7}}
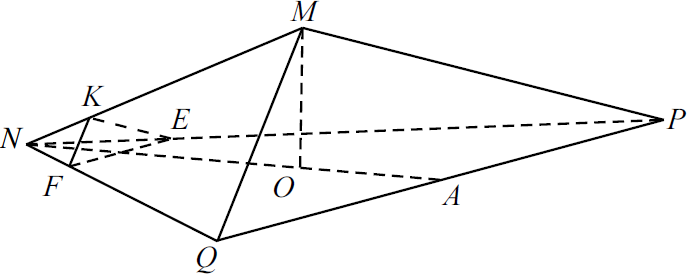
Задача 17
В правильной треугольной пирамиде $BMNK$ с основанием $MNK$ сторона основания равна $6$, а высота пирамиды равна $3$. На рёбрах $MN, MK$ и $MB$ соответственно отмечены точки $F, E$ и $P$, такие, что $MF = ME ={√{21}}/{2}$ и $MP ={7}/{4}$.
а) Докажите, что плоскости $FEP$ и $NBK$ параллельны.
б) Найдите расстояние от точки $P$ до плоскости $NBK$.
Решение
а) Пусть $BO -$ высота пирамиды. Чтобы доказать, что плоскости $FEP$ и $NKB$ параллельны, достаточно показать, что две пересекающиеся прямые $PF$ и $FE$ плоскости $FEP$ соответственно параллельны двум пересекающимся прямым $BN$ и $NK$ плоскости $BNK$. Покажем это.
Найдём боковое ребро $MB$ из треугольника $MBO$:
В $∆MKN:$ $MO_1 -$ высота, $MO_1 = {a√3}/{2}$, где $a -$ сторона $∆MNK$. $MO_1 = {6√3}/{2} = 3√3$.
$MO ={2}/{3} MO_1 = 2√3$,
$MB = √{OB^2 + OM^2} = √{3^2 + (2√3)^2} = √{21}$.
1. ${MP}/{MB} ={7}/{4·√{21}}={√{21}}/{12},{MF}/{MN} ={√{21}}/{2·6} = {√{21}}/{12}$. Отношения сторон равны. Используя условие, что $∠BMN$ общий, получим: $∆MPF∼∆MBN$. Из подобия треугольников следует, что $∠MPF = ∠MBN$. Эти углы — соответственные, образованные при пересечении двух прямых $PF$ и $BN$ прямой $MB$. Значит, $PF ‖ BN$.
2. Рассматривая треугольники $MEF$ и $MKN$, можно аналогично доказать, что $FE ‖ NK$.
Так как две пересекающиеся прямые $PF$ и $FE$ плоскости $PFE$ соответственно параллельны двум пересекающимся прямым $BN$ и $NK$ плоскости $NBK$, то эти плоскости параллельны.
б) Пусть $O_2$ — точка пересечения $MO_1$ и $FE$. Поскольку плоскость $PFE$ параллельна плоскости $BNK$, то расстояние от точки $P$ до плоскости $BNK$ равно расстоянию от точки $O_2$ до плоскости $BNK$, и оно равно длине отрезка $O_2H$, где точка $H$ лежит на $BO_1$ и $O_2H ⊥ BO_1$. Докажем, что $O_2H$ — расстояние от $O_2$ до плоскости $BNK$.
$NK ⊥ MO_1$ и $NK ⊥ BO_1$ ($MO_1$ и $BO_1$ — высоты $∆MNK$ и $∆NBK$), значит, $NK$ перпендикулярна плоскости $MBO_1$, и тогда $NK$ перпендикулярна любой прямой этой плоскости, в том числе $NK ⊥ O_2H$. По построению $O_2H ⊥ BO_1$. Прямая $O_2H$ перпендикулярна двум пересекающимся прямым плоскости $BNK$, значит, она перпендикулярна $BNK$, и отрезок $O_2H$ равен расстоянию от $O_2$ до плоскости $BNK$.
В треугольнике $O_2HO_1: O_2H = O_2O_1 sin∠HO_1O_2$.
$O_2O_1 = MO_1-MO_2$.
Из $∆MEO_2: ∠MO_2E = 90°, ∠EMO_2 = 30°$;
$MO_2 = MEcos30° = {√{21}}/{2}·{√3}/{2} = {3√7}/{4}$.
$O_2O_1 = 3√3 — {3√7}/{4} = {3(4√3 — √7)}/{4}$;
$sin ∠HO_1O_2 = {BO}/{BO_1} = {BO}/{√{BO^2 + OO_1^2}} = {3}/{√{3^2 + (√3)^2}} = {√3}/{2}$.
$O_2H = {3(4√3 — √7)}/{4}·{√3}/{2} = {3(12 — √{21})}/{8}$.
Ответ: ${3(12-√{21})}/{8}$
Задача 18
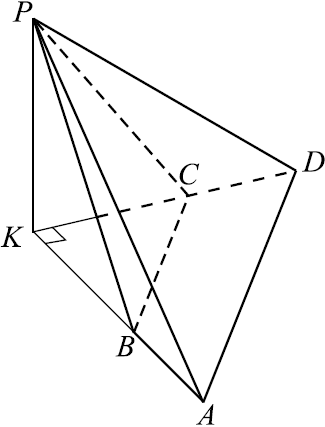
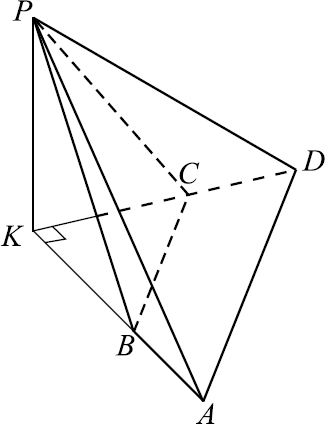
В прямоугольном параллелепипеде $ABCDA_{1}B_{1}C_{1}D_{1}$ стороны оснований $AB$ и $BC$ равны соответственно $8$ и $5$, а боковое ребро $AA_1$ равно $4$. На ребре $A_{1}B_1$ отмечена точка $K$, а на луче $BC$ — точка $F$, причём $A_{1}K = KB_1$ и $BF = AB$. Плоскость $AKF$ пересекает ребро $B_{1}C_1$ в точке $P$.
а) Докажите, что $B_{1}P : PC_1 = 4 : 1$.
б) Найдите площадь сечения параллелепипеда плоскостью $AKF$.
Решение
а) Построим сечение параллелепипеда плоскостью $AKF$.
$E$ — точка пересечения ребра $DC$ и отрезка $AF$.
$В$ плоскости $ABB_1$ проведём лучи $AK$ и $BB_1, AK$ пересекает $BB_1$ в точке $Q$. В плоскости $BCC_1$ проведём отрезок $FQ, FQ$ пересекает $B_1C_1$ в точке $P$, а $CC_1$ — в точке $R$. Пятиугольник $AKPRE$ — искомое сечение.
$KB_1 ‖ AB, KB_1 ={1}/{2}A_1B_1$, значит, $KB_1$ — средняя линия $△ABQ$, отсюда $BB_1 = QB_1$, а так как $BF ‖ B_1P$, то $B_1P$ — средняя линия $△FBQ, BF = 8, B_1P ={1}/{2}BF = 4. C_1P = B_1C_1 — B_1P = 5 — 4 = 1$, следовательно, $B_1P : PC_1 = 4 : 1$.
б) Прямоугольные треугольники $ABQ, FBQ$ и $ABF$ равны по двум катетам $AB = BF = BQ = 8$, отсюда $AQ = AF = QF = 8√2$. $S_{AQF} ={a^2√3}/{4}$ как площадь равностороннего треугольника со стороной $a$. $S_{AQF} = {(8√2)^2·√3}/{4} = 32√3, S_{KQP} ={1}/{4}S_{AQF}={32√3}/{4} = 8√3$.
$S_{AKPF} = S_{AQF} — S_{KQP} = 32√3 — 8√3 = 24√3$.
$△RCF~△RC_1P$ по первому признаку подобия $(∠C = ∠C_1 = 90°, ∠1 = ∠2$ как вертикальные). Из подобия следует ${CF}/{PC_1} ={FR}/{PR}$. По доказанному в а) $PC_1 = 1, BF = AB = 8$, тогда $CF = 8 — 5 = 3$ и ${FR}/{PR} ={3}/{1}$. Так как $KP$ средняя линия $△AQF$, то $PF ={1}/{2}QF = 4√2, FR = {3PF}/{4} = {4√2·3}/{4} = 3√2$.
В равнобедренном прямоугольном треугольнике $FCE$ $FC = EC = 3$, тогда $EF = 3√2$.
В $△REF$ $FR = EF = 3√2, ∠RFE = 60°$, отсюда $△REF$ — равносторонний. $S_{REF} ={(3√2)^2√3}/{4} = {9√3}/{2}$.
$S_{AKPRE} = S_{AKPF} — S_{REF} = 24√3 — {9√3}/{2} = {39√3}/{2}$.
Ответ: ${39√3}/{2}$