СДАМ ГИА:
РЕШУ ЕГЭ
Образовательный портал для подготовки к экзаменам
Математика профильного уровня
Математика профильного уровня
≡ Математика
Базовый уровень
Профильный уровень
Информатика
Русский язык
Английский язык
Немецкий язык
Французский язык
Испанский язык
Физика
Химия
Биология
География
Обществознание
Литература
История
Сайты, меню, вход, новости
СДАМ ГИАРЕШУ ЕГЭРЕШУ ОГЭРЕШУ ВПРРЕШУ ЦТ
Об экзамене
Каталог заданий
Варианты
Ученику
Учителю
Школа
Эксперту
Справочник
Карточки
Теория
Сказать спасибо
Вопрос — ответ
Чужой компьютер
Зарегистрироваться
Восстановить пароль
Войти через ВКонтакте
Играть в ЕГЭ-игрушку
Новости
10 марта
Как подготовиться к ЕГЭ и ОГЭ за 45 дней
6 марта
Изменения ВПР 2023
3 марта
Разместили утвержденное расписание ЕГЭ
27 января
Вариант экзамена блокадного Ленинграда
23 января
ДДОС-атака на Решу ЕГЭ. Шантаж.
6 января
Открываем новый сервис: «папки в избранном»
22 декабря
Открыли новый портал Решу Олимп. Для подготовки к перечневым олимпиадам!
4 ноября
Материалы для подготовки к итоговому сочинению 2022–2023
31 октября
Сертификаты для учителей о работе на Решу ЕГЭ, ОГЭ, ВПР
21 марта
Новый сервис: рисование
31 января
Внедрили тёмную тему!
НАШИ БОТЫ
Все новости
ЧУЖОЕ НЕ БРАТЬ!
Экзамер из Таганрога
10 апреля
Предприниматель Щеголихин скопировал сайт Решу ЕГЭ
Наша группа
Задания
Версия для печати и копирования в MS Word
Тип 2 № 501705
Найдите объём многогранника, вершинами которого являются точки
правильной треугольной призмы
площадь основания которой равна 9, а боковое ребро равно 8.
Спрятать решение
Решение.
Требуется найти объём пирамиды, основание и высота которой совпадают с основанием и высотой данной треугольной призмы. Поэтому
Ответ: 24.
Аналоги к заданию № 245340: 266513 266741 501705 501747 501980 519509 266515 266517 266519 266521 … Все
Источник: ЕГЭ по математике 03.06.2013. Основная волна. Сибирь. Вариант 302.
Кодификатор ФИПИ/Решу ЕГЭ: 5.5.7 Объём куба, прямоугольного параллелепипеда, пирамиды, призмы
Спрятать решение
·
Прототип задания
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
О проекте · Редакция · Правовая информация · О рекламе
© Гущин Д. Д., 2011—2023
Каталог заданий
Назад в каталог
Вернуться к списку прототипов этой категории
Версия для печати и копирования в MS Word
1
Тип 2 № 501705
Найдите объём многогранника, вершинами которого являются точки
правильной треугольной призмы
площадь основания которой равна 9, а боковое ребро равно 8.
Аналоги к заданию № 245340: 266513 266741 501705 501747 501980 519509 266515 266517 266519 266521 … Все
Источник: ЕГЭ по математике 03.06.2013. Основная волна. Сибирь. Вариант 302.
Кодификатор ФИПИ/Решу ЕГЭ: 5.5.7 Объём куба, прямоугольного параллелепипеда, пирамиды, призмы
Решение
·
Прототип задания
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
- ЕГЭ по математике профиль
Прототипы задания №12 ЕГЭ по математике профильного уровня — уравнения. Практический материал для подготовки к экзамену в 11 классе.
Для успешного выполнения задания №12 необходимо уметь решать уравнения и неравенства.
Практика
Коды проверяемых элементов содержания (по кодификатору) — 2.1, 2.2
Уровень сложности задания — повышенный.
Максимальный балл за выполнение задания — 2
Примерное время выполнения задания выпускником, изучавшим математику на профильном уровне (в мин.) — 10
Связанные страницы:
Решу егэ профиль математика 517739
Задание 12 № 517746
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
А) Из уравнения получаем:
Б) Заметим, что Значит, указанному отрезку принадлежит корень −3.
Ответ: а) −3 и 27; б) −3.
Аналоги к заданию № 517739: 517746 517747 Все
Задание 12 № 517747
Задание 12 № 517746
Задание 12 № 517747
Ответ а 3 и 27; б 3.
Ege. sdamgia. ru
12.01.2020 13:48:01
2020-01-12 13:48:01
Источники:
Https://ege. sdamgia. ru/test? likes=517739
Решу егэ профиль математика 517739 — Математика и Английский » /> » /> .keyword { color: red; } Решу егэ профиль математика 517739
Решу егэ профиль математика 517739
Решу егэ профиль математика 517739
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
Задание 12 № 517746
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
А) Из уравнения получаем:
Б) Заметим, что Значит, указанному отрезку принадлежит корень −3.
Ответ: а) −3 и 27; б) −3.
Аналоги к заданию № 517739: 517746 517747 Все
Задание 12 № 517747
Задание 12 № 517746
Б Заметим, что Значит, указанному отрезку принадлежит корень 3.
Источники:
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword < color: red; >Решу егэ профиль математика 517739
Решу егэ профиль математика 517739
Решу егэ профиль математика 517739
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
Задание 12 № 514082
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
А) Запишем исходное уравнение в виде:
Б) Поскольку отрезку принадлежит единственный корень −2.
Ответ: а) −2; 1, б) −2.
Почему такое странное ОДЗ?? Где 2-х>0, х>0, следовательно х0; тогда х (0;2)
Екатерина, в решении не находили ОДЗ.
В решении было использован равносильный переход, при котором условия достаточно для решения примера
А у Вас ОДЗ найдено с ошибкой.
Задание 12 № 517739
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
А) Из уравнения получаем:
Б) Заметим, что Значит, указанному отрезку принадлежит только корень −2.
Ответ: а) −2 и 16; б) −2.
В пункте «а» ответ только 16,вы не проверили ОДЗ
В этом уравнении не нужно искать ОДЗ. Это лишнее действие
Задание 12 № 502094
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие промежутку
А) Заметим, что преобразуем исходное уравнение:
Пусть тогда уравнение запишется в виде откуда или
При получим: откуда
При получим: откуда
Б) Корень не принадлежит промежутку Поскольку и корень принадлежит промежутку
Источник: ЕГЭ по математике 19.06.2013. Основная волна, резервный день. Центр. Вариант 502., Задания 13 (С1) ЕГЭ 2013
В строчке а) откуда-то взялась «3»
Путём каких преобразований мы получили ответ log(3)5 ?
1) Уравнение начинается с числе 9 в степени. Т. е. Мы раскладываем 9 как 3*3. Однако в первой строке решения мы видим 9*3. От туда и дальнейшее неверное вычисление.
2) Когда мы возвращаем замену (четвёртая строчка решения) вместо этого (если, допустим, t и правда равно 5/3) должно получиться Х-1= логорифм 5/3 по основанию 3. Верно?
Так ли это? Ибо мне свойственно ошибаться. Это правда ошибка, или я чего-то не понимаю? Если второе, то объясните, если можно.
Задание 12 № 517739
Задание 12 № 502094
Задание 12 502094.
Источники:
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword < color: red; >Решу егэ профиль математика 517739
Решу егэ профиль математика 517739
Решу егэ профиль математика 517739
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
Диагональ экрана телевизора равна 64 дюймам. Выразите диагональ экрана в сантиметрах, если в одном дюйме 2,54 см. Результат округлите до целого числа сантиметров.
Источники:
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword < color: red; >Решу егэ профиль математика 517739
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
Задание 12 № 514082
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
А) Запишем исходное уравнение в виде:
Б) Поскольку отрезку принадлежит единственный корень −2.
Ответ: а) −2; 1, б) −2.
Почему такое странное ОДЗ?? Где 2-х>0, х>0, следовательно х0; тогда х (0;2)
Екатерина, в решении не находили ОДЗ.
В решении было использован равносильный переход, при котором условия достаточно для решения примера
А у Вас ОДЗ найдено с ошибкой.
Задание 12 № 517739
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
А) Из уравнения получаем:
Б) Заметим, что Значит, указанному отрезку принадлежит только корень −2.
Ответ: а) −2 и 16; б) −2.
В пункте «а» ответ только 16,вы не проверили ОДЗ
В этом уравнении не нужно искать ОДЗ. Это лишнее действие
Задание 12 № 502094
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие промежутку
А) Заметим, что преобразуем исходное уравнение:
Пусть тогда уравнение запишется в виде откуда или
При получим: откуда
При получим: откуда
Б) Корень не принадлежит промежутку Поскольку и корень принадлежит промежутку
Источник: ЕГЭ по математике 19.06.2013. Основная волна, резервный день. Центр. Вариант 502., Задания 13 (С1) ЕГЭ 2013
В строчке а) откуда-то взялась «3»
Путём каких преобразований мы получили ответ log(3)5 ?
1) Уравнение начинается с числе 9 в степени. Т. е. Мы раскладываем 9 как 3*3. Однако в первой строке решения мы видим 9*3. От туда и дальнейшее неверное вычисление.
2) Когда мы возвращаем замену (четвёртая строчка решения) вместо этого (если, допустим, t и правда равно 5/3) должно получиться Х-1= логорифм 5/3 по основанию 3. Верно?
Так ли это? Ибо мне свойственно ошибаться. Это правда ошибка, или я чего-то не понимаю? Если второе, то объясните, если можно.
Задание 12 № 517739
Задание 12 № 502094
Задание 12 502094.
Уско рен ная под го тов ка к ЕГЭ с ре пе ти то ра ми Учи.
Dankonoy. com
16.06.2020 6:45:22
2020-06-16 06:45:22
Источники:
Https://dankonoy. com/ege/ege11/archives/10087
Материал для подготовки к экзамену по математике 1 курс. » /> » /> .keyword { color: red; } Решу егэ профиль математика 517739
Материал для подготовки к экзамену по математике 1 курс
Материал для подготовки к экзамену по математике 1 курс.
Материал для подготовки к экзамену по математике для 1 курса СПО.
Просмотр содержимого документа
«Материал для подготовки к экзамену по математике 1 курс.»
Логарифмические уравнения
1. Задание 5 № 26646
Найдите корень уравнения
2. Задание 5 № 26647
Найдите корень уравнения
3. Задание 5 № 26648
Найдите корень уравнения
4. Задание 5 № 26649
Найдите корень уравнения
5. Задание 5 № 26657
Найдите корень уравнения
6. Задание 5 № 26658
Найдите корень уравнения
7. Задание 5 № 26659
Найдите корень уравнения
8. Задание 5 № 77380
Решите уравнение
9. Задание 5 № 77381
Решите уравнение
10. Задание 5 № 77382
Решите уравнение Если уравнение имеет более одного корня, в ответе укажите меньший из них.
11. Задание 5 № 315120
Найдите корень уравнения
12. Задание 5 № 315535
Найдите корень уравнения
13. Задание 5 № 525399
Решите уравнение
Тригонометрические уравнения
1. Задание 5 № 26669
Найдите корни уравнения: В ответ запишите наибольший отрицательный корень.

Значениям соответствуют положительные корни.
Если, то и
Если, то и
Значениям соответствуют меньшие значения корней.
Следовательно, наибольшим отрицательным корнем является число
2. Задание 5 № 77376
Решите уравнение В ответе напишите наибольший отрицательный корень.
Значению соответствует Положительным значениям параметра соответствуют положительные значения корней, отрицательным значениям параметра соответствуют меньшие значения корней. Следовательно, наибольшим отрицательным корнем является число −1.
3. Задание 5 № 77377
Решите уравнение В ответе напишите наименьший положительный корень.
Значениям соответствуют отрицательные корни.
Если, то и
Если, то и
Значениям соответствуют большие положительные корни.
Наименьшим положительным решением является 0,5.
Преобразования числовых логарифмических выражений
1. Задание 9 № 26843
Найдите значение выражения
2. Задание 9 № 26844
Найдите значение выражения
3. Задание 9 № 26845
Найдите значение выражения
4. Задание 9 № 26846
Найдите значение выражения
5. Задание 9 № 26847
Найдите значение выражения
6. Задание 9 № 26848
Найдите значение выражения
7. Задание 9 № 26849
Найдите значение выражения
8. Задание 9 № 26850
Найдите значение выражения
9. Задание 9 № 26851
Найдите значение выражения
10. Задание 9 № 26852
Найдите значение выражения
11. Задание 9 № 26853
Найдите значение выражения
12. Задание 9 № 26854
Найдите значение выражения
13. Задание 9 № 26855
Найдите значение выражения
14. Задание 9 № 26856
Найдите значение выражения
15. Задание 9 № 26857
Найдите значение выражения
16. Задание 9 № 26858
Найдите значение выражения
17. Задание 9 № 26859
Найдите значение выражения
18. Задание 9 № 26860
Найдите значение выражения
19. Задание 9 № 26861
Найдите значение выражения
20. Задание 9 № 26862
Найдите значение выражения
21. Задание 9 № 26882
Найдите значение выражения
22. Задание 9 № 26883
Найдите значение выражения
23. Задание 9 № 26885
Найдите значение выражения
24. Задание 9 № 26889
Найдите значение выражения
25. Задание 9 № 26892
Найдите значение выражения
26. Задание 9 № 26893
Найдите значение выражения
27. Задание 9 № 26894
Найдите значение выражения
28. Задание 9 № 26896
Найдите значение выражения
29. Задание 9 № 77418
Вычислите значение выражения:
30. Задание 9 № 505097
Найдите значение выражения
31. Задание 9 № 509086
Найдите значение выражения
32. Задание 9 № 510939
Найдите значение выражения
33. Задание 9 № 525403
Найдите значение выражения
Вычисление значений тригонометрических выражений
1. Задание 9 № 26775
Найдите, если и
2. Задание 9 № 26776
Найдите, если и
3. Задание 9 № 26777
Найдите, если и
4. Задание 9 № 26778
Найдите, если и
5. Задание 9 № 26779
Найдите, если
6. Задание 9 № 26780
Найдите, если
7. Задание 9 № 26783
Найдите значение выражения, если
8. Задание 9 № 26784
Найдите, если и
9. Задание 9 № 26785
Найдите, если и
10. Задание 9 № 26786
Найдите, если
11. Задание 9 № 26787
Найдите, если
12. Задание 9 № 26788
Найдите, если
13. Задание 9 № 26789
Найдите, если
14. Задание 9 № 26790
Найдите, если
15. Задание 9 № 26791
Найдите, если
16. Задание 9 № 26792
Найдите значение выражения, если
17. Задание 9 № 26793
Найдите значение выражения, если
18. Задание 9 № 26794
Найдите, если
19. Задание 9 № 316350
Найдите, если
20. Задание 9 № 501598
Найдите значение выражения
21. Задание 9 № 502014
Найдите значение выражения
22. Задание 9 № 502045
Найдите значение выражения
23. Задание 9 № 502106
Найдите значение выражения
24. Задание 9 № 502285
Найдите значение выражения
25. Задание 9 № 502305
Найдите значение выражения если и
26. Задание 9 № 504410
Найдите значение выражения:
27. Задание 9 № 504824
Найдите значение выражения
28. Задание 9 № 508966
Найдите если
29. Задание 9 № 510424
Найдите если и
30. Задание 9 № 549336
Найдите если и
Преобразования числовых тригонометрических выражений
1. Задание 9 № 26755
Найдите значение выражения
2. Задание 9 № 26756
Найдите значение выражения
3. Задание 9 № 26757
Найдите значение выражения
4. Задание 9 № 26758
Найдите значение выражения
5. Задание 9 № 26759
Найдите значение выражения
6. Задание 9 № 26760
Найдите значение выражения
7. Задание 9 № 26761
Найдите значение выражения
8. Задание 9 № 26762
Найдите значение выражения
9. Задание 9 № 26763
Найдите значение выражения
10. Задание 9 № 26764
Найдите значение выражения
11. Задание 9 № 26765
Найдите значение выражения
12. Задание 9 № 26766
Найдите значение выражения
13. Задание 9 № 26767
Найдите значение выражения
14. Задание 9 № 26769
Найдите значение выражения
15. Задание 9 № 26770
Найдите значение выражения
16. Задание 9 № 26771
Найдите значение выражения
17. Задание 9 № 26772
Найдите значение выражения
18. Задание 9 № 26773
Найдите значение выражения
19. Задание 9 № 26774
Найдите значение выражения
20. Задание 9 № 77412
Найдите значение выражения
21. Задание 9 № 77413
Найдите значение выражения
22. Задание 9 № 77414
Найдите значение выражения:
23. Задание 9 № 245169
Найдите значение выражения
24. Задание 9 № 245170
Найдите значение выражения
25. Задание 9 № 245171
Найдите значение выражения
26. Задание 9 № 245172
Найдите значение выражения
27. Задание 9 № 501701
Найдите значение выражения
28. Задание 9 № 502994
Найдите значение выражения
29. Задание 9 № 503310
Найдите значения выражения
30. Задание 9 № 510013
Найдите если и
31. Задание 9 № 510312
Найдите значение выражения
32. Задание 9 № 510386
Найдите значение выражения
33. Задание 9 № 510405
Найдите значение выражения
34. Задание 9 № 510824
Найдите значение выражения
35. Задание 9 № 510843
Найдите значение выражения
36. Задание 9 № 525113
Найдите значение выражения
37. Задание 9 № 526009
Найдите значение выражения
Логарифмические и показательные уравнения
1. Задание 13 № 514082
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
2. Задание 13 № 517739
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
3. Задание 13 № 502094
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие промежутку
4. Задание 13 № 516760
А) Решите уравнение:
Б) Определите, какие из его корней принадлежат отрезку
5. Задание 13 № 514623
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие отрезку
6. Задание 13 № 502053
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие отрезку
7. Задание 13 № 525377
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие отрезку
8. Задание 13 № 513605
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
9. Задание 13 № 503127
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие отрезку
10. Задание 13 № 514081
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащего отрезку
11. Задание 13 № 502999
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие отрезку [−1; 2].
12. Задание 13 № 528517
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
13. Задание 13 № 550261
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие промежутку
14. Задание 13 № 555265
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
15. Задание 13 № 555583
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
16. Задание 13 № 561853
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие отрезку [−2,5; −1,5].
17. Задание 13 № 562032
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие отрезку [−0,5; 0,5].
18. Задание 13 № 562757
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие отрезку
б) Укажите корни этого уравнения, принадлежащие отрезку
Решите уравнение В ответе напишите наименьший положительный корень.
Просмотр содержимого документа «Материал для подготовки к экзамену по математике 1 курс.»
Б Укажите корни этого уравнения, принадлежащие отрезку.
Multiurok. ru
06.02.2020 18:29:01
2020-02-06 18:29:01
Источники:
Https://multiurok. ru/files/material-dlia-podgotovki-k-ekzamenu-po-matematike. html

Материалы и статьи
Пробник по профильной математике ЕГЭ 2023. Вариант и ответы с пробника ЕГЭ 2023 по математике профиль, который прошёл 3 декабря 2022 года у 11 класса школьников Москвы. Единая городская контрольная работа в формате ЕГЭ по математике профильный уровень.
скачать вариант №1
скачать вариант №2
Единая городская контрольная работа в формате ЕГЭ 2023 по математике профильный №1
Единая городская контрольная работа в формате ЕГЭ 2023 по математике профильный №2
1. Дан равнобедренный треугольник 𝐴𝐵𝐶 с основанием 𝐴𝐶 и боковой стороной длины 7. Точка 𝐾 на стороне 𝐵𝐶 такая, что 𝐾𝐶 = 3, 𝑆𝐴𝐵𝐶 = 14. Найдите площадь треугольника 𝐴𝐵𝐾.
2. Имеется банка в форме цилиндра. Из неё перелили сок в 40 цилиндрических стаканов. Диаметр одного стакана в 4 раза меньше диаметра банки. При этом уровень сока в каждом стакане оказался 8 см. Какой была высота уровня сока в банке? Ответ дайте в сантиметрах.
3. В сборнике 4 билета по теме «Механические колебания». Вероятность того, что ученику попадётся билет не по данной теме равна 0,9. Сколько всего билетов в сборнике?
4. Стрелок стреляет по мишеням 5 раз. Вероятность попадания каждым отдельным выстрелом равна 0,8. Во сколько раз вероятность события, что стрелок попадёт в цель 4 раза больше вероятности события, что он попадёт в цель 3 раза?
5. Найдите корень уравнения √3 34 − 3𝑥 = 4.
8. Полная энергия падающего тела вычисляется по формуле 𝐸пол = 𝑚𝑣2 2 +𝑚𝑔ℎ. С какой скоростью двигалось тело массой 3 кг в момент, когда оно находилось на высоте 1,5 м, если его полная энергия в этот момент составляла 68,1 Дж? Ускорение свободного падения 𝑔 = 9,8 м/c2 .
9. Из двух городов, расстояние между которыми 720 км, выехали навстречу друг другу два поезда. Второй поезд выехал на час позже первого и едет со скоростью на 4 км/ч больше скорости первого. Поезда встретились ровно в середине пути. Найдите скорость первого поезда.
10. Дан график 𝑓(𝑥) = ⃒ ⃒𝑎𝑥2 + 𝑏𝑥 + 𝑐 ⃒ ⃒ , где 𝑎, 𝑏, 𝑐 – целые числа. Найдите 𝑓(4).
13. В прямоугольном параллелепипеде 𝐴𝐵𝐶𝐷𝐴1𝐵1𝐶1𝐷1 на ребре 𝐴𝐴1 отмечена точка 𝐸 так, что 𝐴1𝐸 : 𝐸𝐴 = 3 : 2. Точка 𝑇 — середина ребра 𝐵1𝐶1, 𝐴𝐴1 = 10 и 𝐴𝐷 = 6. а) Докажите, что сечение параллелепипеда плоскостью 𝐸𝑇 𝐷1 – равнобедренная трапеция. б) Найдите площадь сечения параллелепипеда плоскостью 𝐸𝑇 𝐷1, если 𝐴𝐵 = 2√ 10.
15. В банке можно открыть один из двух вкладов. По вкладу А в конце каждого из трёх лет начисляется по 20% от суммы вклада в начале года. По вкладу Б в конце каждого из первых двух лет начисляется по 22% от суммы вклада в начале года. При каком наименьшем целом количестве начисляемых за третий год процентов по вкладу Б, вклад Б будет выгоднее вклада А?
16. Дан прямоугольный треугольник 𝐴𝐵𝐶. Квадрат 𝐶𝐾𝑁𝑀, такой, что точки 𝐾 и 𝑀 лежат на катетах 𝐴𝐶 и 𝐵𝐶 соответственно, а 𝑁 лежит на гипотенузе 𝐴𝐵. Квадрат 𝑃 𝑄𝑅𝑇 такой, что вершины 𝑃 и 𝑄 лежат на 𝐴𝐶 и 𝐵𝐶, а вершины 𝑇 и 𝑅 лежат на гипотенузе. а) Докажите, что точки 𝐶, 𝑁 и центры квадратов лежат на одной прямой. б) Найти сторону квадрата 𝑃 𝑄𝑅𝑇, если 𝐴𝐶 = 12 и 𝐵𝐶 = 5.
17. Найдите все значения а, при каждом из которых неравенство 𝑎(𝑎 − 7,5) − 2(𝑎 − 7,5) (2𝑥 + 2) 6 (︀ 2𝑥 2 − 3𝑥 )︀ (2𝑥 + 2) − 𝑎𝑥2 + 1,5𝑎𝑥 имеет хотя бы 1 решение на промежутке [−1; 0).
18. Пусть {𝑎𝑛} – последовательность натуральных чисел. Обозначим 𝑀<𝐶(𝑎𝑛) – среднее арифметическое всех членов последовательности {𝑎𝑛}, которые меньше некоторого числа 𝐶. Число 𝐶 лежит между наибольшим и наименьшим членами последовательности. Обозначим 𝑀>𝐶(𝑎𝑛) – среднее арифметическое всех членов последовательности {𝑎𝑛}, которые больше или равны 𝐶. Среднее арифметическое одного числа равно самому числу. Затем к каждому члену последовательности {𝑎𝑛} прибавили 4 и получили новую последовательность, которую обозначили {𝑎𝑛 + 4}.
- a) Существует ли последовательность {𝑎𝑛}, состоящая из трех членов, для которой 𝑀<79 (𝑎𝑛 + 4) < 𝑀<79 (𝑎𝑛)?
- б) Существует ли последовательность {𝑎𝑛}, состоящая из трех членов, для которой 𝑀<79 (𝑎𝑛 + 4) < 𝑀<79 (𝑎𝑛) и 𝑀>79 (𝑎𝑛 + 4) < 𝑀>79 (𝑎𝑛)?
- в) Известно, что среднее арифметическое всех членов последовательности {𝑎𝑛} равняется 84, 𝑀>79 (𝑎𝑎) = 94, 𝑀<79 (𝑎𝑛) = 70, 𝑀>79 (𝑎𝑛 + 4) = 96 и 𝑀<79 (𝑎𝑛 + 4) = 72. Какое наименьшее число членов может быть в последовательности {𝑎𝑛} ?
Вам будет интересно:
Тренировочный вариант №12 по профильной математике, решу ЕГЭ 2023 с ответами.
Метки: варианты и ответы ЕГЭ математика
ЕГЭ по математике — Профиль 2022. Открытый банк заданий с ответами.
За это задание ты можешь получить 2 балла. На решение дается около 10 минут. Уровень сложности: повышенный.
Средний процент выполнения: 45.3%
Ответом к заданию 12 по математике (профильной) может быть развернутый ответ (полная запись решения с обоснованием выполненных действий).
Разбор сложных заданий в тг-канале
Задачи для практики
Задача 1
а) Решите уравнение $11cos 2x=7sin (x-{π} / {2})-9$.
б) Укажите корни этого уравнения, принадлежащие отрезку $[-π;0]$.
Решение
а) $11cos 2x=7sin (x-{π} / {2})-9$,
$11(2cos^2 x-1)=-7cos x-9$,
$22cos^2 x -11+7cos x +9=0$,
$22cos^2 x+7cos x -2=0$.
Обозначим $cos x=t$, $|t|⩽1$.
Тогда уравнение примет вид: $22t^2+7t-2=0$.
Решим его. $22t^2+7t-2=0$,
$D=49+2⋅ 4⋅ 22=225$. $t_{1,2}={-7±15} / {44}$,
$t_1=-{1} / {2}$, $t_2={8} / {44}={2} / {11}$.
$1$. $cos x=-{1} / {2}$, $x=±(π-{π} / {3})+2π n$;
$x=± {2π} / {3}+2π n$, $n∈ Z$.
$2$. $cos x={2} / {11}$, $x=± arccos {2} / {11}+2π k$, $k∈ Z$.
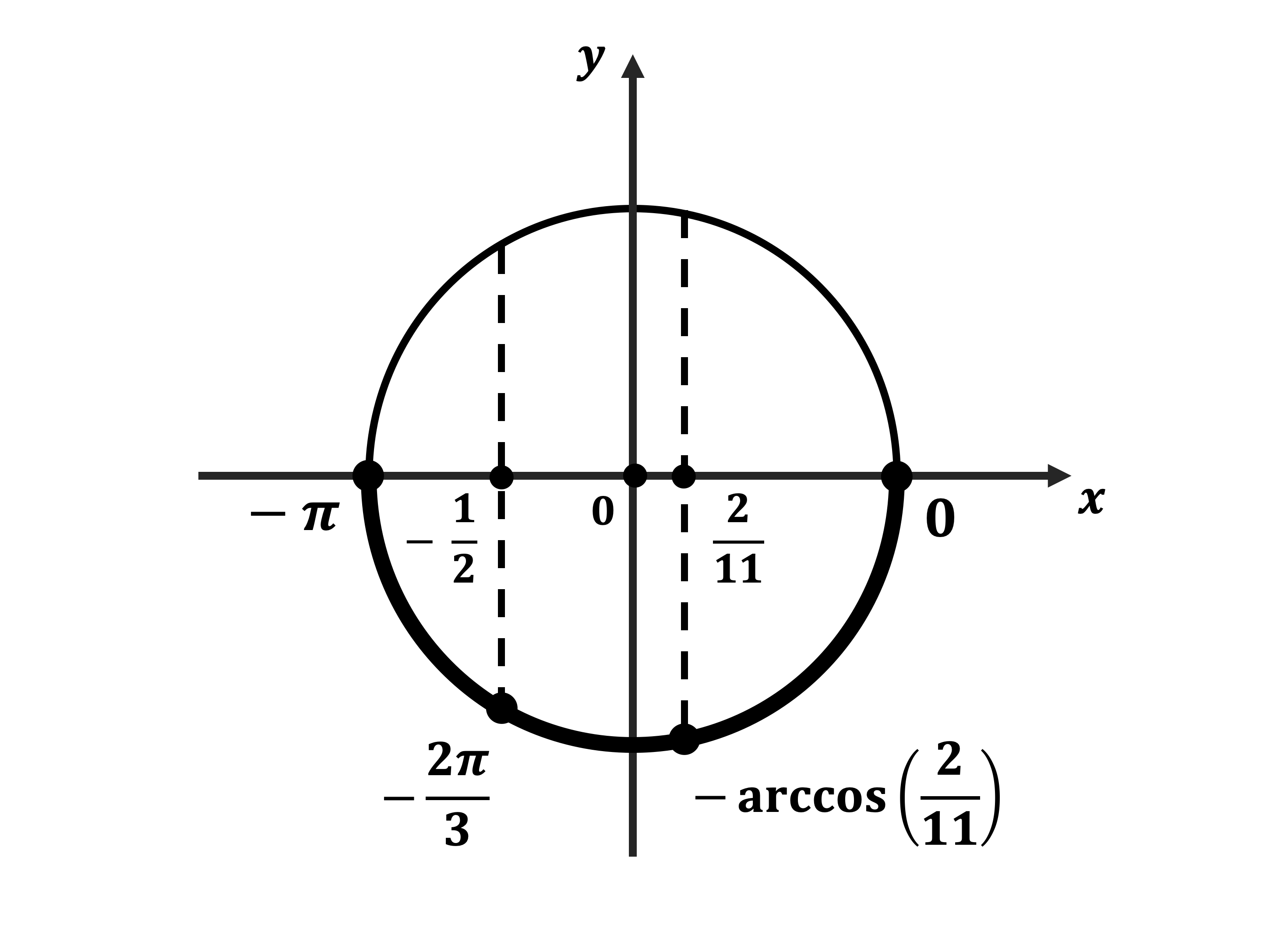
б) Найдём корни этого уравнения, принадлежащие промежутку $[-π;0]$.
$x_1=-π+{π} / {3}=-{2π} / {3}$
$x_2=-arccos {2} / {11}$.
Ответ: а)$± {2π} / {3}+2πn, n∈ Z; ± arccos {2} / {11}+2π k, k∈ Z;б)-{2π}/{3}, -arccos{2}/{11}$
Задача 2
а) Решите уравнение $2 sin^2 x — 7 cos(x + {π}/{2})- 4 = 0$.
б) Найдите все корни этого уравнения, принадлежащие промежутку $[-2π;-{π}/{2}]$.
Решение
а) Преобразуем уравнение, согласно формуле приведения:
$cos(x+{π}/{2})=-sinx,$
$2sin^2x + 7sinx -4 = 0$
Обозначим $sin x = t, −1 ≤ t ≤ 1$, получим
$2t^2 + 7t -4 = 0.$
$t_1 = {−7 − 9}/{2·2} = −4$ — не удовлетворяет условию $−1 ≤ t ≤ 1. $
$t_2 = {−7 + 9}/{2·2} = {1}/{2}$.
Вернёмся к исходной переменной:
$sinx ={1}/{2}$,
$x = {π}/{6} + 2πn, n ∈ Z$
$x = {5π}/{6} + 2πk, k ∈ Z$
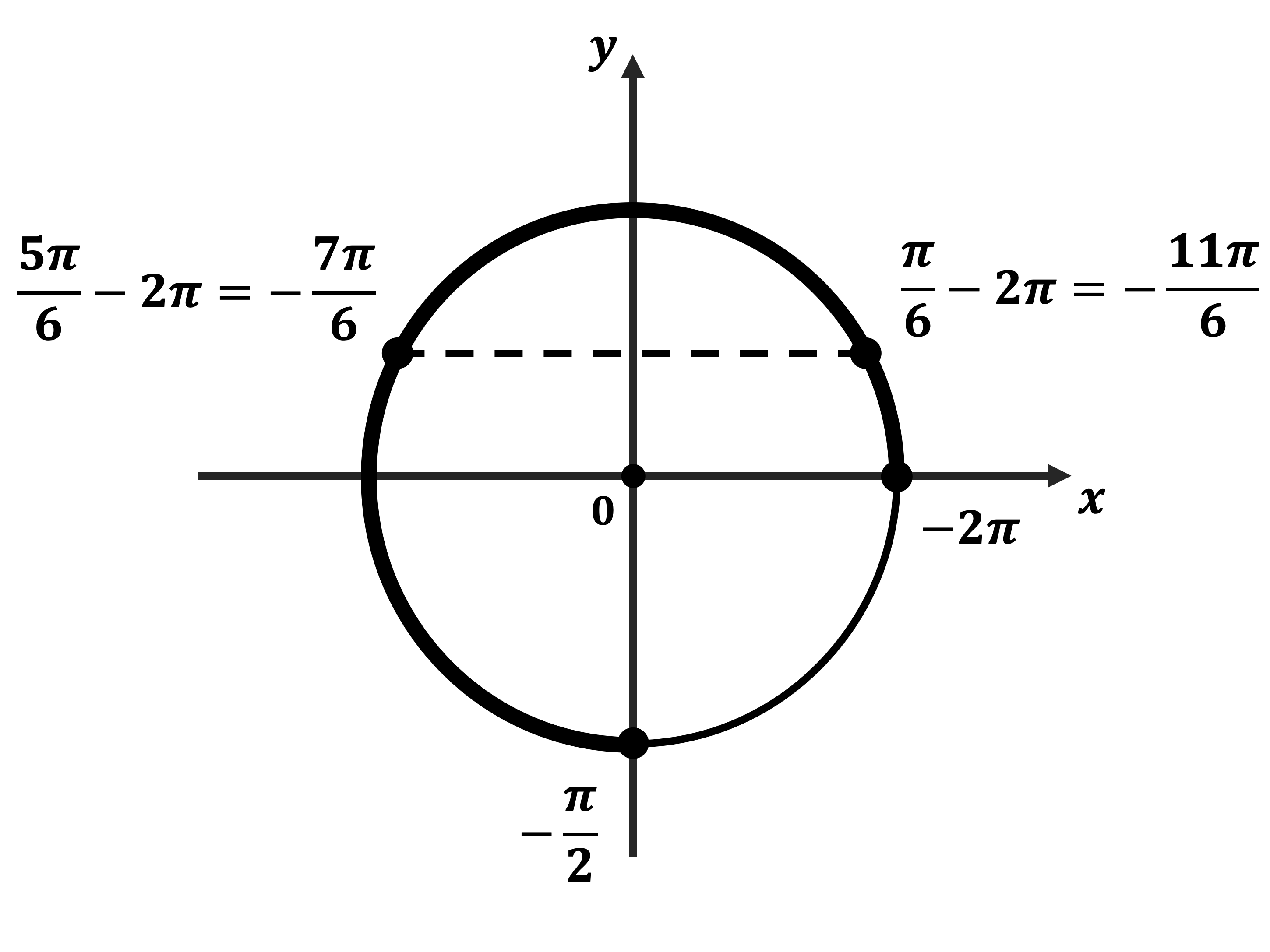
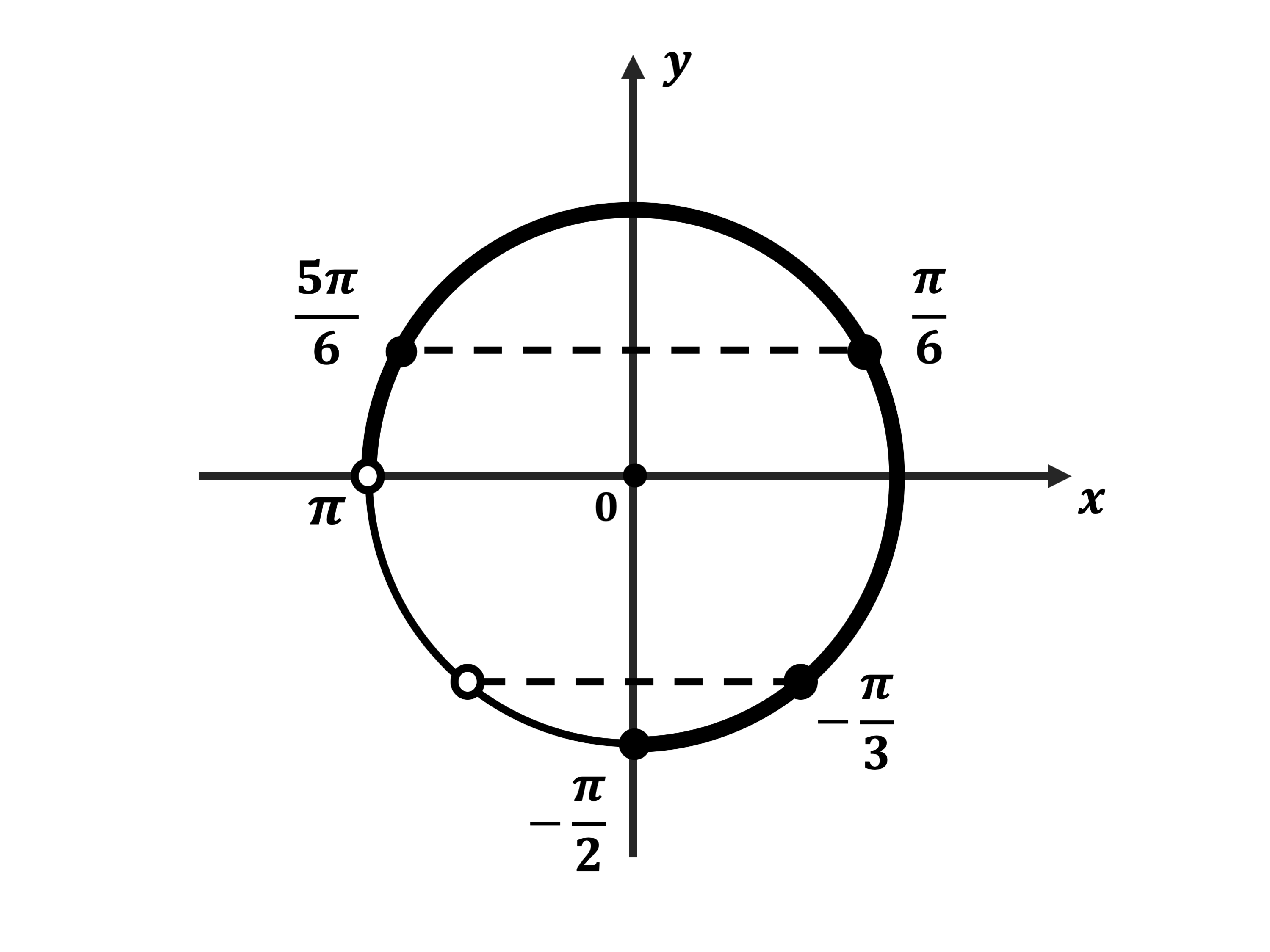
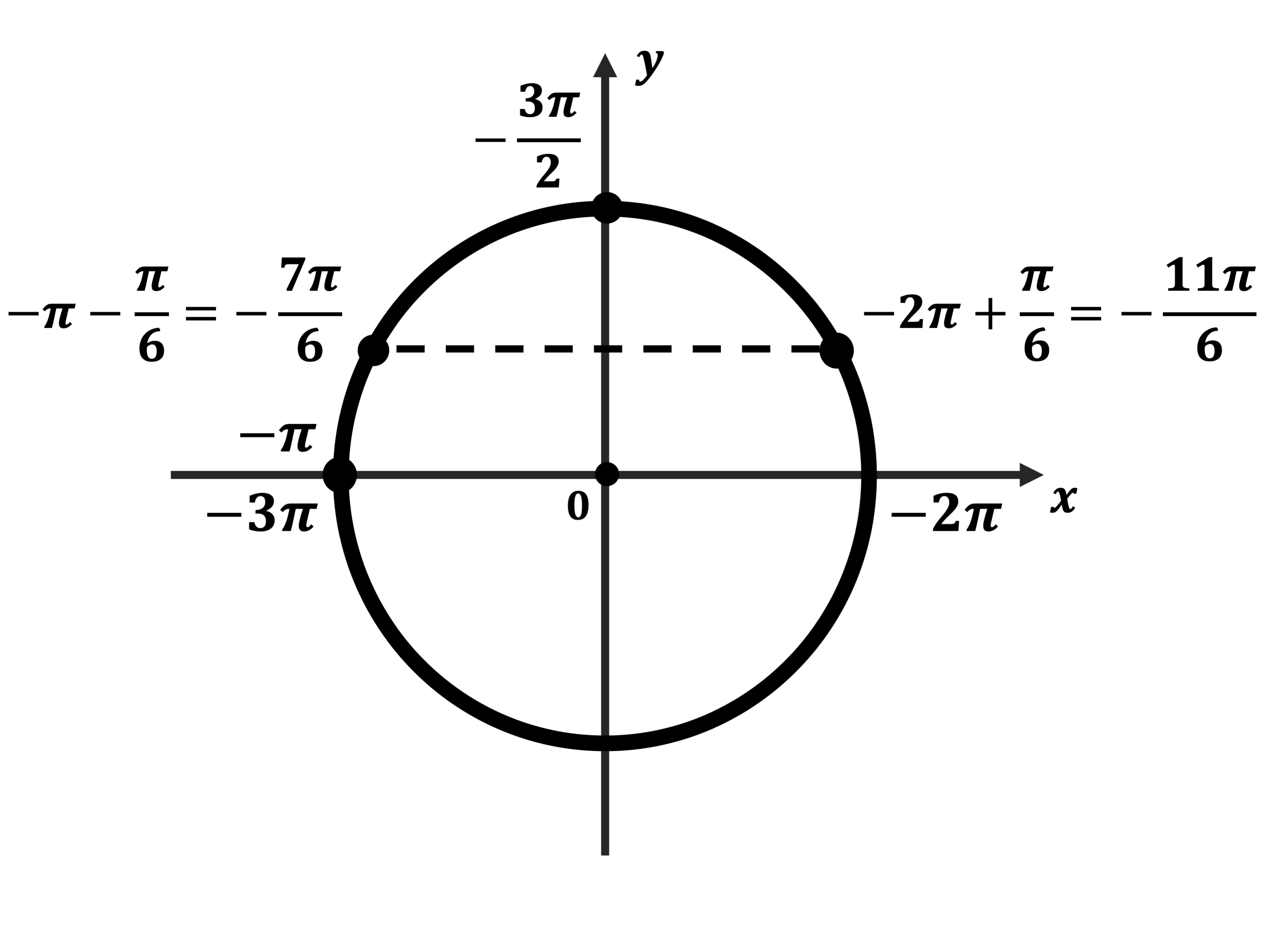
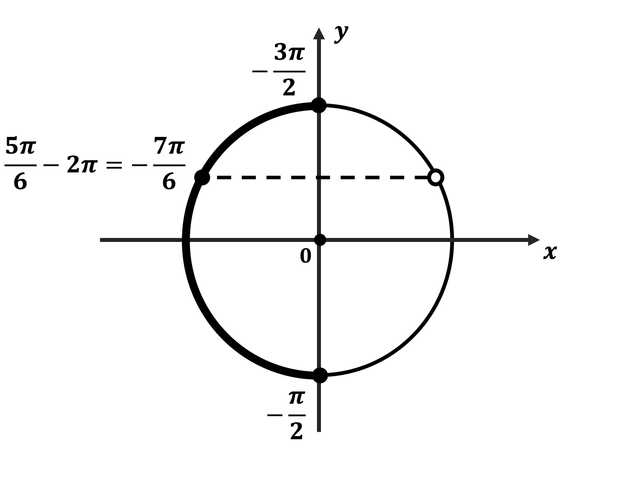
б) Корни, принадлежащие отрезку $[-2π; -{π}/{2}]$, найдём с помощью единичной окружности. Получим: ${π}/{6}-2π=-{11π}/{6}; {5π}/{6}-2π=-{7π}/{6}$.
Ответ: а) $ {π}/{6} + 2πn, n ∈ Z$; $ {5π}/{6} + 2πk, k ∈ Z$ б) $-{11π}/{6};-{7π}/{6}$
Задача 3
а) Решите уравнение $2 cos^2 x — 5 sin(x + {3π}/{2})+ 2 = 0$.
б) Найдите все корни этого уравнения, принадлежащие промежутку $[{π}/{2};{3π}/{2}]$.
Решение
а) Преобразуем уравнение, согласно формуле приведения:
$sin(x+{3π}/{2})=-cosx,$
$2cos^2x + 5 cos x + 2 = 0$
Обозначим $cos x = t, −1 ≤ t ≤ 1$, получим $2t^2 + 5t + 2 = 0. t_1 = {−5 − 3}/{2·2} = −2$ — не удовлетворяет условию $−1 ≤ t ≤ 1. t_2 = {−5 + 3}/{2· 2} = −{1}/{2}$.
Вернёмся к исходной переменной: $cos x = − {1}/{2}$,
$x = ±(π − {π}/{3}) + 2πn, n ∈ Z , x = ±{2π}/{3} + 2πn, n ∈ Z.$
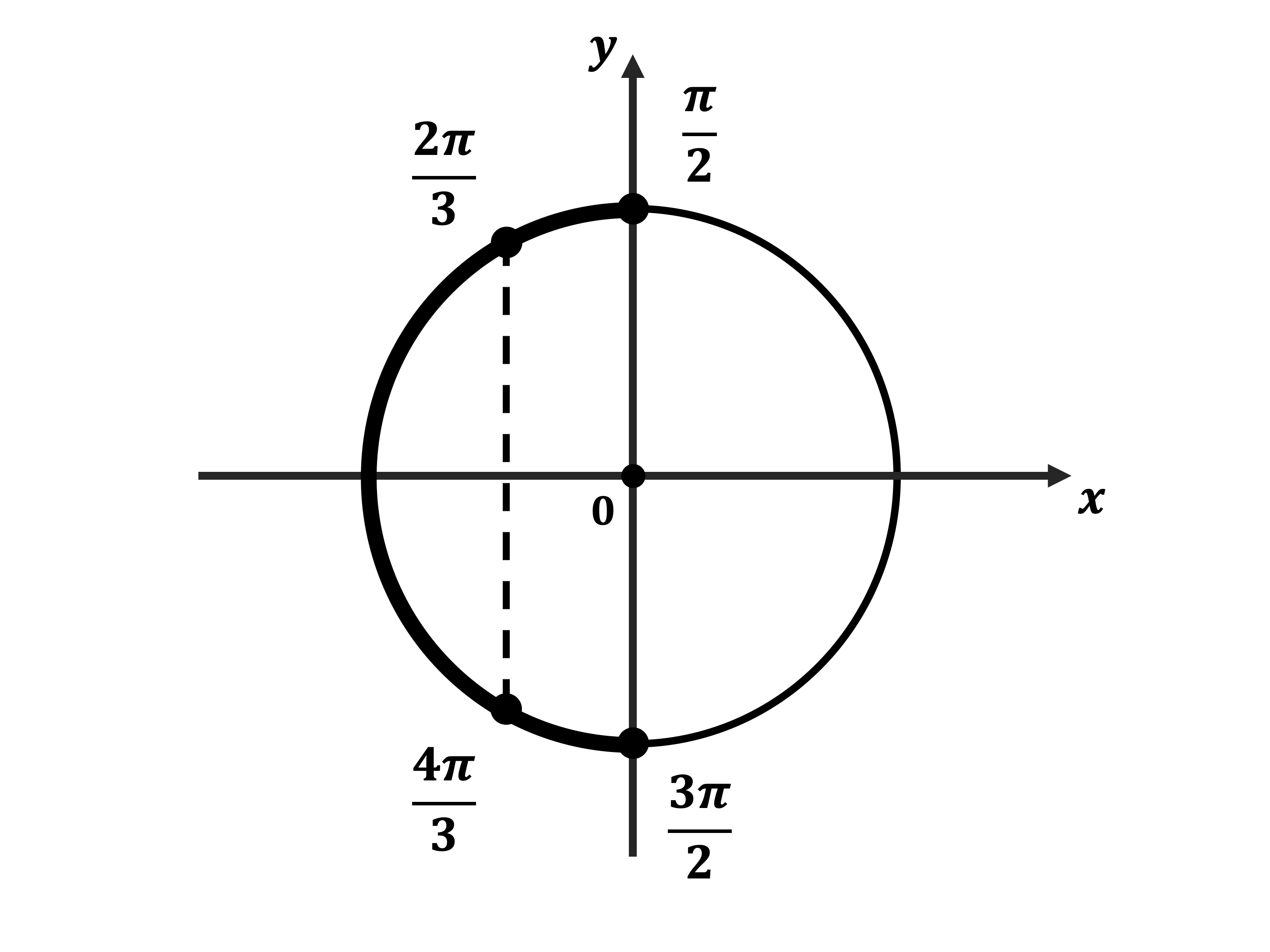
б) Корни, принадлежащие отрезку $[{π}/{2}; {3π}/{2}]$, найдём с помощью единичной окружности. Получим числа ${2π}/{3}; {4π}/{3}$.
Ответ: а)$±{2π}/{3}+2πn,n∈Z;$ б) ${2π}/{3};{4π}/{3}$
Задача 4
а) Решите уравнение $cos(x — {3π}/{2})= sin 2x$.
б) Найдите все корни этого уравнения, принадлежащие промежутку $[-{3π}/{2};0]$.
Решение
а) Преобразуем уравнение:
$−sin x = sin 2x,$
$sinx + 2 sin x cos x = 0,$
$sinx(1 + 2 cos x) = 0,$
$sin x = 0;x = πn, n ∈ Z,$
$cosx = -{1}/{2}; x = ±{2π}/{3} + 2πk, k ∈ Z .,$
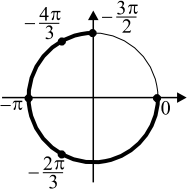
б) Корни, принадлежащие отрезку $[-{3π}/{2};0]$, найдём с помощью единичной окружности. Получим числа $−{4π}/{3}; −π; −{2π}/{3}; 0$.
Ответ: а) $x=±{2π}/{3}+2πk;x=πn,k,n∈Z$ б) $-{4π}/{3};-π;-{2π}/{3};0$.
Задача 5
а) Решите уравнение $sin({π}/{2}+ x)= sin (-2x)$.
б) Найдите все корни этого уравнения, принадлежащие промежутку $[0; π]$.
Решение
а) Преобразуем уравнение:
$cos x = − sin 2x,$
$cos x + 2 sin x cos x = 0,$
$cos x(1 + 2 sin x) = 0,$
$cos x = 0;$
$x = {π}/{2} + πn, n ∈ Z$
$sin x = −{1}/{2},$
$x = (−1)^{k+1}·{π}/{6} + πk, k ∈ Z$
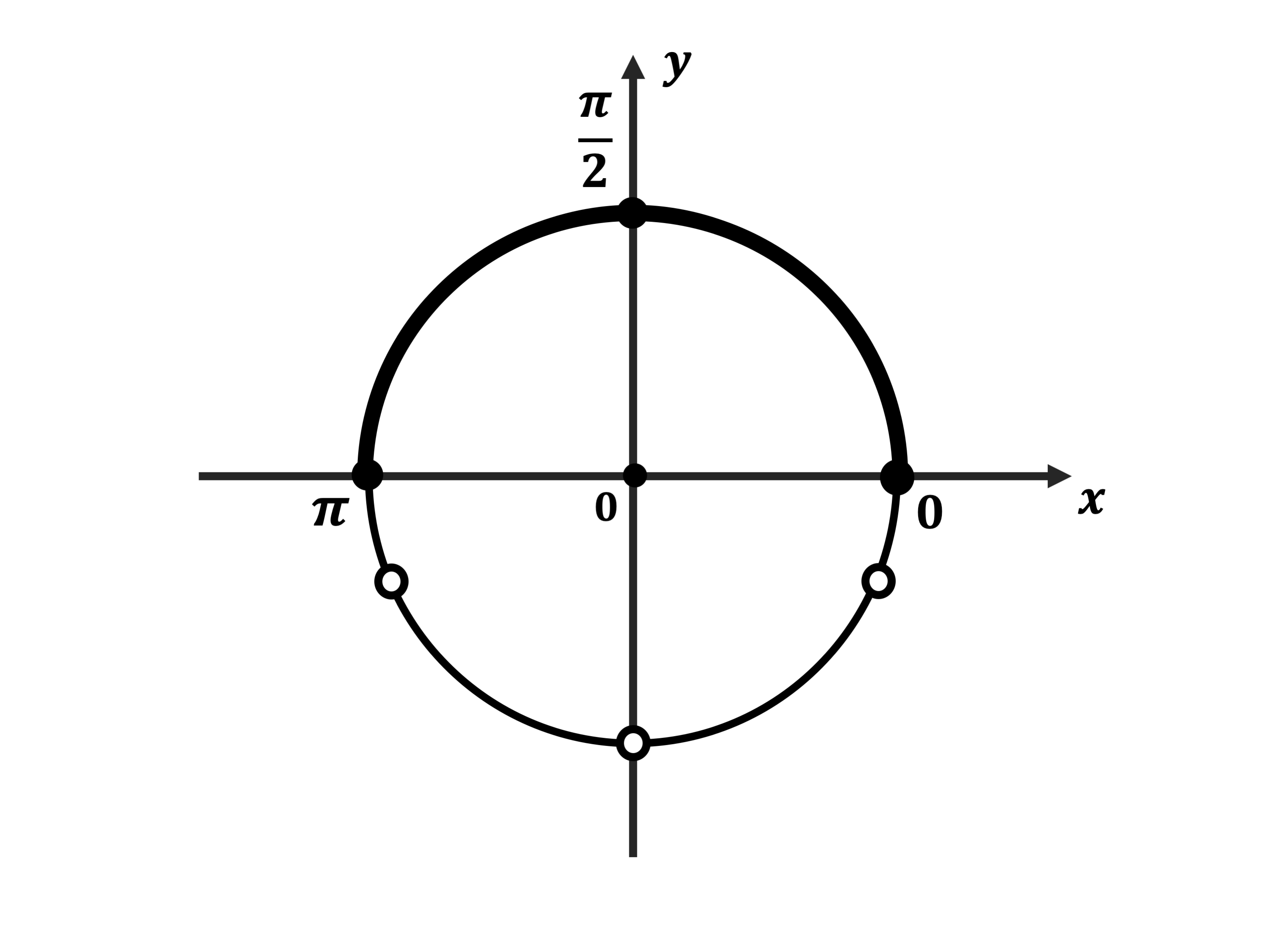
б) Корни, принадлежащие отрезку $[0; π]$, найдём с помощью единичной окружности.
Указанному промежутку принадлежит единственное число ${π}/{2}$.
Ответ: а) ${π}/{2}+πn,n∈Z;(-1)^{k+1}{π}/{6}+πk,k∈Z$; б) ${π}/{2}$
Задача 6
а) Решите уравнение $sin x(2 sin x — 1) + √3 sin x + sin {4π}/{3}= 0$.
б) Найдите все корни этого уравнения, принадлежащие промежутку $[-{π}/{2};π]$.
Решение
а) Решим уравнение $sinx(2sinx-1) +√3sinx + sin{4π}/{3} = 0$.
Так как $sin{4π}/{3} = sin(π +{π}/{3}) = − sin{π}/{3} = −{√3}/{2}$, то уравнение примет вид $sin x(2 sin x-1) +√3 sin x-{√3}/{2} = 0$. Отсюда $2 sin x(sin x-{1}/{2})+ √3(sin x-{1}/{2}) = 0; (2sinx+√3)(sin x-{1}/{2}) = 0$.
Тогда $sin x = {1}/{2}; x = (−1)^n{π}/{6} + πn$ или $sin x = −{√3}/{2}; x = (−1)^{n+1}{π}/{3} + πn$, где $n ∈ Z.$
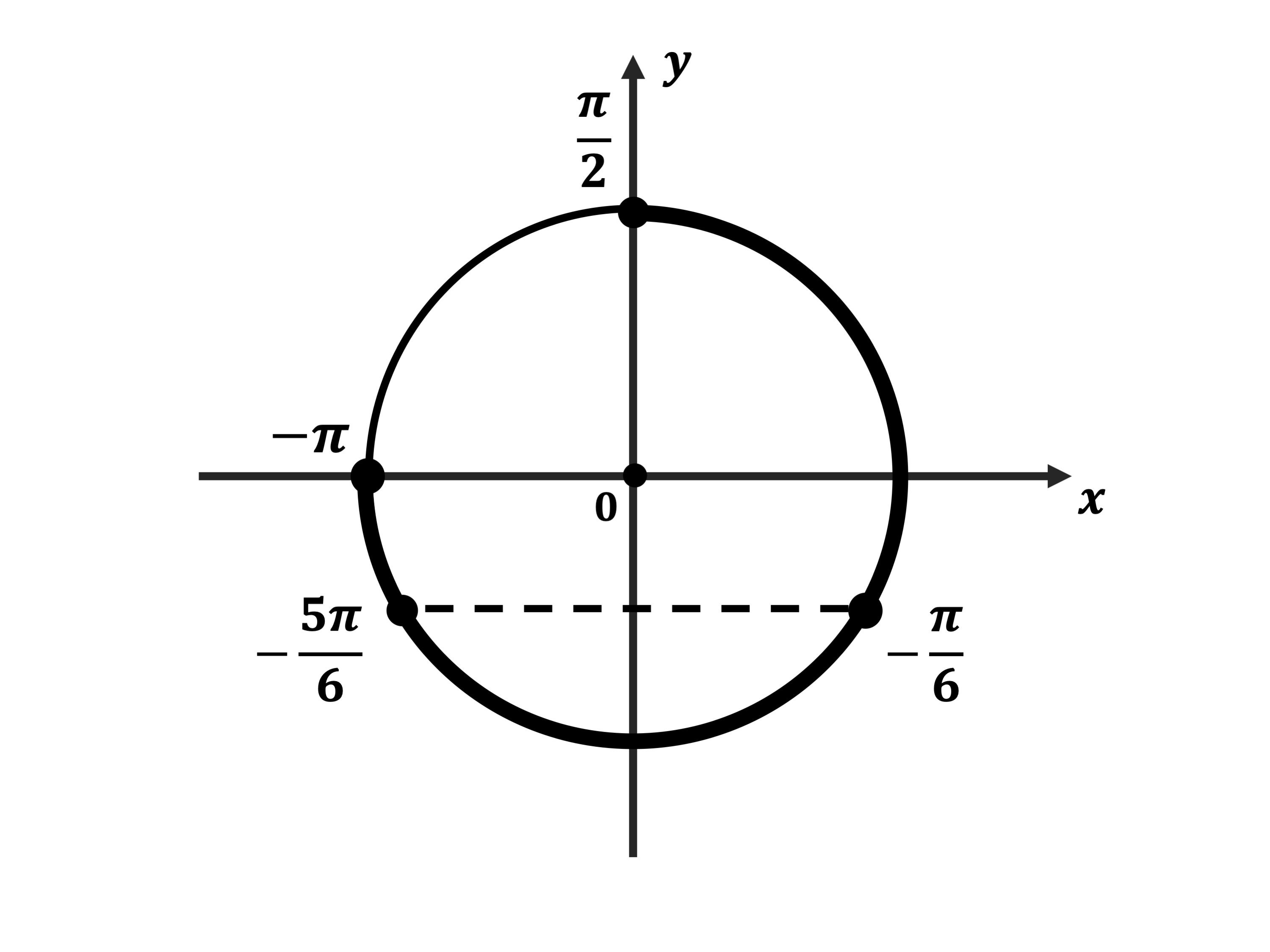
б) Корни, принадлежащие промежутку $[−{π}/{2}; π]$, найдём с помощью числовой окружности: $−{π}/{3}; {π}/{6}; {5π}/{6}$.
Ответ: а)$(-1)^{n}{π}/{6}+πn;(-1)^{n+1}{π}/{3}+πn,n∈Z$; б) $-{π}/{3};{π}/{6};{5π}/{6}$
Задача 7
а) Решите уравнение $4cos^{2}x = 3cos2x + 1$.
б) Найдите корни уравнения, принадлежащие отрезку $[-4π;-{5π}/{4})$.
Решение
a) $4cos^{2}x = 3cos2x+1$,
$4cos^{2}x = 3(2cos^{2}x-1)+1$,
$4cos^{2}x=6cos^{2}x-3+1$,
$cos^{2}x=1, [tablecosx=1; cosx=-1;$ $[tablex=2πn, n ∈ Z; x=π+2πk, k ∈ Z;$ $x=πk, k ∈ Z$
б) Корни, принадлежащие промежутку $[-4π;-{5π}/{4})$, найдем из неравенства $-4π ≤ πk < -{5π}/{4}; k=-4, -3, -2$
$x_1=-4π, x_2=-3π, x_3=-2π$.
Ответ: а)$πn,n∈Z$;б)$-4π;-3π;-π$
Задача 8
а) Решите уравнение $cos (2x) + 3 sin x — 2 = 0$.
б) Найдите корни уравнения, принадлежащие отрезку $[-3π;-π]$.
Решение
a) $cos(2x) + 3sinx-2=0$,
$1 — 2sin^{2}x + 3 sin x -2 = 0$,
$2 sin^{2}x — 3sin x +1 = 0$,
Пусть $sin x = y, |sinx| ≤ 1$, уравнение примет вид
$2y^2 — 3y + 1 = 0$,
$y_{1,2} = {3±√{9-8}}/{4} = {3±1}/{4};$
$ y_1=1, y_2={1}/{2}$.
$sin x = 1, x = {π}/{2}+2πn, n ∈ Z; sinx={1}/{2}, x=(-1)^{k}{π}/{6} + πk, k ∈ Z$.
б) Найдём корни уравнения на отрезке $[-3π;-π]$.
С помощью числовой окружности отберём корни уравнения, принадлежащие $[-3π;-π]$.
Это числа $-{11π}/{6}, -{3π}/{2}, -{7π}/{6}$.
Ответ: а)${π}/{2}+2πn,n∈Z;(-1)^{k}{π}/{6}+πk,k∈Z$;б)$-{11π}/{6};-{3π}/{2};-{7π}/{6}$
Задача 9
а) Решите уравнение $2 cos^2 x + 19 sin x + 8 = 0$.
б) Найдите корни уравнения, принадлежащие отрезку $[-π;{π}/{2}]$.
Решение
a) $2 cos^{2}x + 19sinx+8=0$,
$2(1 — sin^{2}x) + 19 sin x +8 = 0$,
$-2 sin^{2}x + 19 sin x +10 = 0$,
$2 sin^{2}x — 19 sin x -10 = 0$.
Пусть $sin x = y, |y| ≤ 1$, уравнение примет вид $2y^2 — 19y -10 = 0$, решим его: $y_{1,2} = {19±√{361 + 80}}/{4} = {19±21}/{4}$.
$y_1 = 10$ или $y_2 = -{1}/{2}$. $y_1=10$ не удовлетворяет условию $|y| ≤ 1$. $sin x = -{1}/{2}, x = (-1)^{n+1}{π}/{6} + πn, n ∈ Z$.
б) Найдём корни уравнения на отрезке $[-π;{π}/{2}]$.
Это числа $-{5π}/{6}$ и $-{π}/{6}$.
Ответ: а)$(-1)^{n+1}{π}/{6}+πn,n∈Z$; б) $-{5π}/{6},-{π}/{6}$
Задача 10
а) Решите уравнение $8sin x + 4 cos^2 x = 7$.
б) Найдите корни уравнения, принадлежащие отрезку $[-{3π}/{2};-{π}/{2}]$.
Решение
a) $8 sin x + 4 cos^{2} x = 7$,
$4(1 — sin^{2}x) + 8 sin x — 7 = 0$,
$-4 sin^{2}x + 8 sin x — 3 = 0$,
$4 sin^{2}x — 8 sin x + 3 = 0$.
Пусть $sin x = t, |t| ≤ 1$, уравнение примет вид $4t^2 — 8t + 3 = 0$, решим его: $t_{1,2} = {8±√{64 — 48}}/{8} = {8±√{16}}/{8} = {8±4}/{8} = 1±{1}/{2}$.
$t_1 = {1}/{2}$ или $t_2 = {3}/{2}$. $t_2$ не удовлетворяет условию $|t| ≤ 1$. $sin x = {1}/{2}, x = (-1)^{n}{π}/{6} + πn, n ∈ Z$.
б) Найдём корни уравнения на отрезке $[-{3π}/{2};-{π}/{2}]$.
Это число ${5π}/{6} — 2π = -{7π}/{6}$.
Ответ: а)$(-1)^{n}{π}/{6}+πn,n∈Z$;б)$-{7π}/{6}$
Задача 11
а) Решите уравнение ${sin 2x}/{sin({3π}/{2}+ x)}= 1$.
б) Укажите корни этого уравнения, принадлежащие промежутку $(3π;{9π}/{2})$.
Решение
а) ${{sin2x}/{sin({3π}/{2} + x)} = 1$.
Зная, что $sin2x = 2sinxcosx$ и $sin({3π}/{2}+ x)= −cosx$, получим: ${2sinxcosx}/{−cosx}= 1$, где $cosx≠0, x≠{π}/{2}+ πm, m ∈ Z$.
$−2sinx = 1, sinx =−{1}/{2}$.
$x=−{π}/{6}+2πn, n ∈ Z;$
$x=-{5π}/{6}+ 2πk, k ∈ Z$.
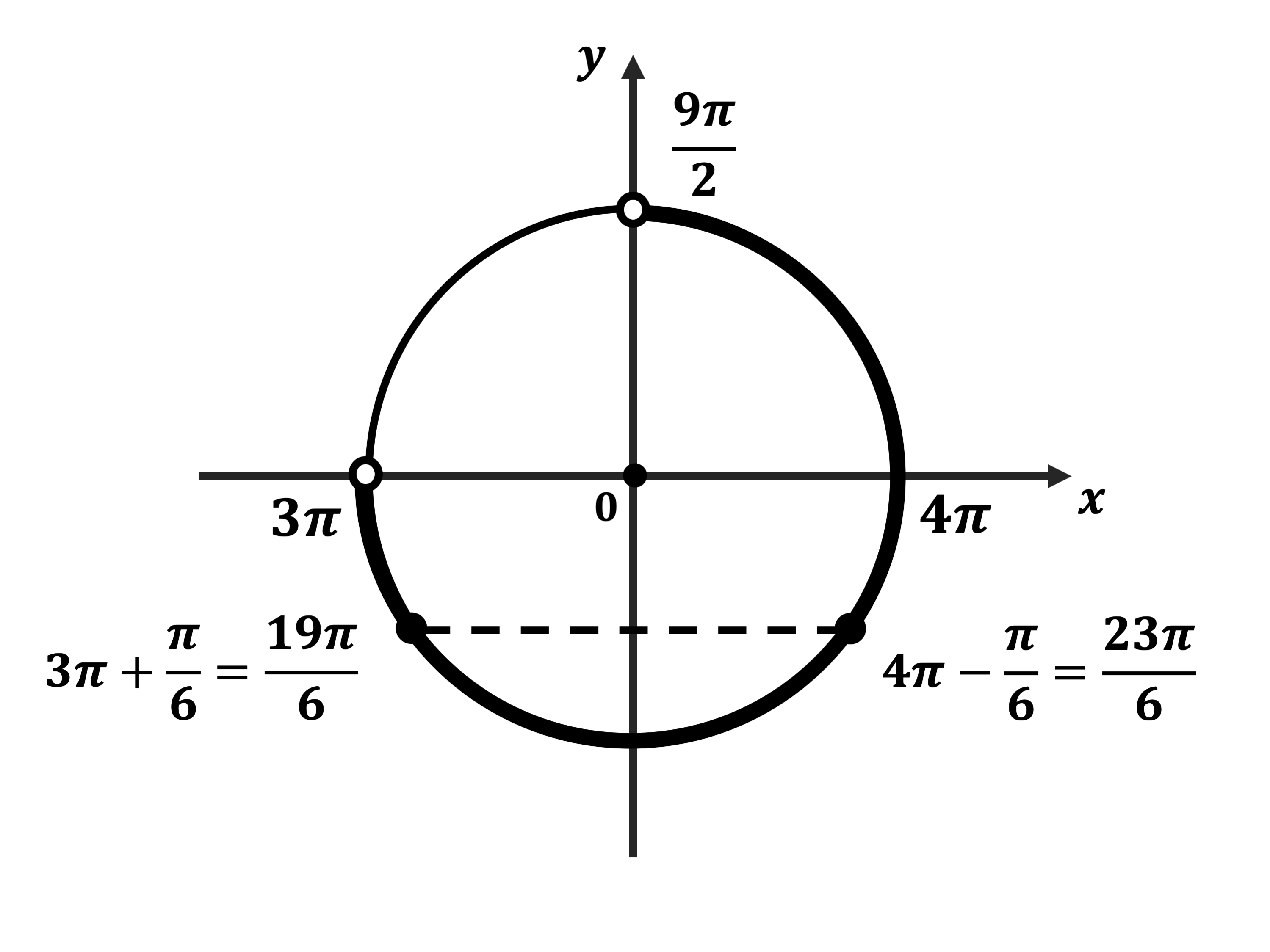
б) Отберём корни уравнения, принадлежащие промежутку $(3π; {9π}/{2})$,с помощью числовой окружности.
$x_1=3π+{π}/{6}={19π}/{6}$,
$x_2=4π−{π}/{6}={23π}/{6}$.
Ответ: а)$-{π}/{6}+2πn,-{5π}/{6}+2πk,n,k∈Z$;б)${19π}/{6};{23π}/{6}$
Задача 12
а) Решите уравнение ${sin 2x}/{sin(π — x)}= √2$.
б) Укажите корни этого уравнения, принадлежащие промежутку $[-{5π}/{2};-π)$.
Решение
а)${sin2x}/{sin(π — x)}=√2$.
а) Применим формулу синуса двойного аргумента $sin2x = 2sinxcosx$ и формулу приведения $sin(π — x) = sin x$.
Уравнение примет вид: ${2sinxcosx}/{sinx} = √2$.
Учитывая, что $sinx≠0, x≠πn, n∈Z$, получим:
$2cosx=√2$,
$cosx = {√2}/{2}$,
$x = ±{π}/{4} + 2πk, k∈Z$;
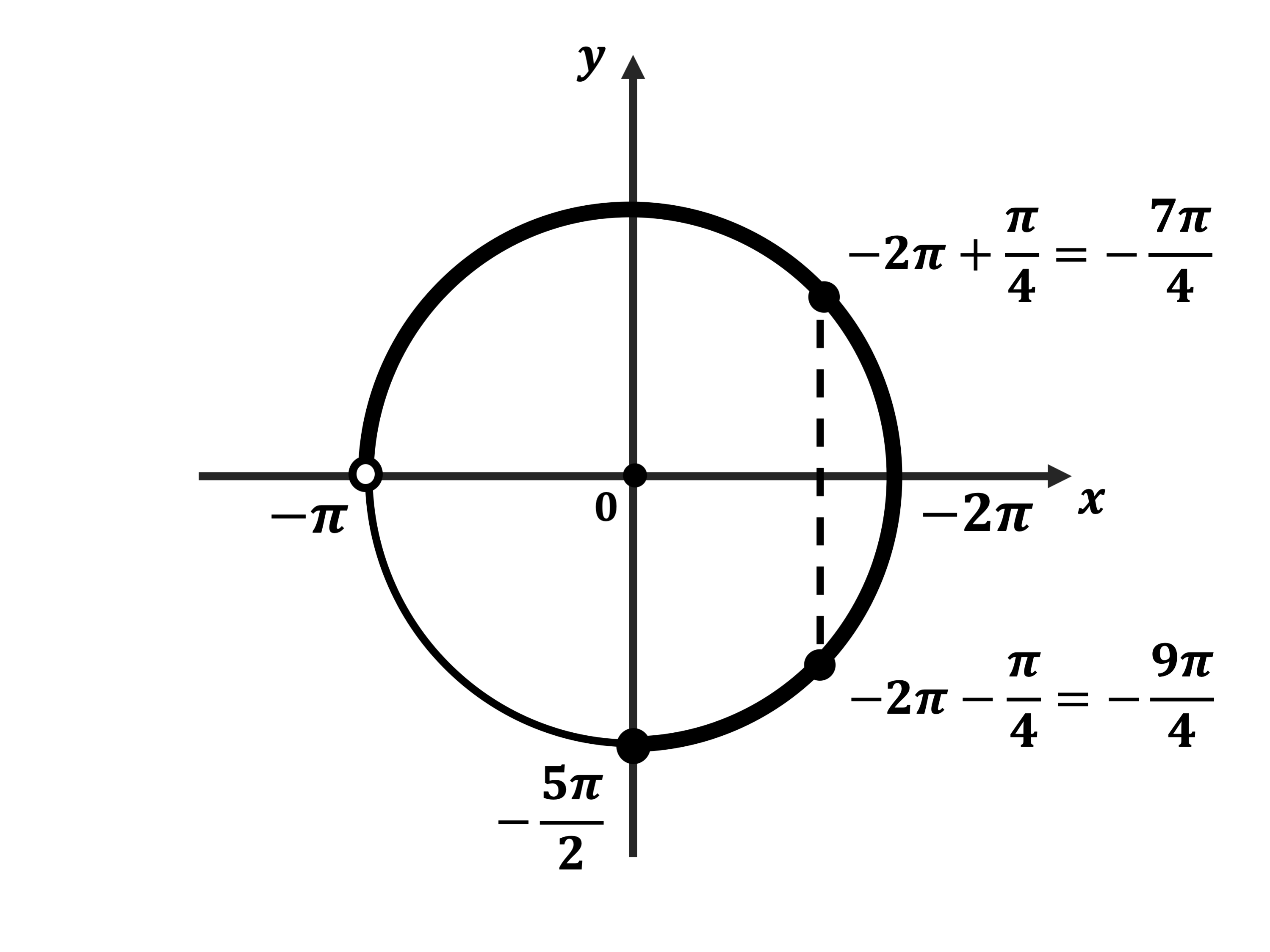
б) Отберём корни уравнения, принадлежащие промежутку $[-{5π}/{2};-π)$, с помощью окружности.
$x_1=-2π+{π}/{4}=-{7π}/{4}$
$x_2=-2π-{π}/{4}=-{9π}/{4}$
Ответ: а)$±{π}/{4}+2πk,k∈Z$;б)$-{9π}/{4};-{7π}/{4}$
Задача 13
а) Решите уравнение ${sin 2x}/{cos(π + x)}= -√2$.
б) Укажите корни этого уравнения, принадлежащие промежутку $(-2π;-{π}/{2})$.
Решение
а)${sin2x}/{cos(π + x)}=-√2$.
Зная, что $sin2x = 2sinxcosx, cos(π + x)=-cosx$, получим: ${2sinxcosx}/{-cosx}=-√2$.
Учитывая, что $cosx≠0, x≠{π}/{2} + πm, m∈Z$, имеем:
$2sinx=√2$,
$sinx = {√2}/{2}$,
$x = {π}/{4} + 2πn, n∈Z$;
$x = {3π}/{4} + 2πk, k∈Z$.
б) Отберём корни уравнения, принадлежащие промежутку $(-2π;-{π}/{2})$.
1. $x = {π}/{4} + 2πn, n∈Z$.
$-2π < {π}/{4} + 2πn < -{π}/{2},$
$-2 < {1}/{4} + 2n < -{1}/{2},$
$-2-{1}/{4} < 2n < -{1}/{2}-{1}/{4},$
$-{9}/{4} < 2n < -{3}/{4},$
$-{9}/{8} < n < -{3}/{8},$
$n = -1$.
При $n =-1$
$x = {π}/{4}-2π=-{7π}/{4}$.
2. $x = {3π}/{4} + 2πk, k∈Z$.
$-2π < {3π}/{4} + 2πk < -{π}/{2}$,
$-2 < {3}/{4} + 2k < -{1}/{2}$,
$-2-{3}/{4} < 2k < -{1}/{2}-{3}/{4}$,
$-{11}/{4} < 2k < -{5}/{4}$,
$-{11}/{8} < k < -{5}/{8}$,
$k = -1$.
При $k = -1$
$x = {3π}/{4}-2π = -{5π}/{4}$.
Ответ: а)${π}/{4}+2πn,{3π}/{4}+2πk,n,k∈Z$;б)$-{7π}/{4};-{5π}/{4}$
Задача 14
а) Решите уравнение $9·3^{2 cos x} — 10√3·3^{cos x} + 3 = 0$.
б) Укажите корни этого уравнения, принадлежащие отрезку $[{3π}/{2};4π]$.
Решение
а) После замены $t = 3^{cosx}$ исходное уравнение примет вид $9t^2 — 10√3t + 3 = 0$. Корни этого уравнения $t = √3; t = {√3}/{9}$. Возвращаясь к переменной $x$, получим
$[table3^{cosx}=√3; 3^{cosx}={√3}/{9};$ $[table3^{cosx}=3^{{1}/{2}}; 3^{cosx}=3^{-{3}/{2}};$ $[tablecosx={1}/{2}; cosx=-{3}/{2};$
Второе уравнение совокупности не имеет корней. Решая первое уравнение, получим $x =±{π}/{3} + 2πn; n ∈ Z$.
б) Запишем решение уравнения в виде $x =-{π}/{3} + 2πn; n ∈ Z$ или $x ={π}/{3} + 2πk; k ∈ Z$ и выясним, для каких целых значений $n$ и $k$ справедливы неравенства ${3π}/{2}≤-{π}/{3}+2πn≤4π$ и ${3π}/{2}≤{π}/{3}+2πk≤4π$.
Получим ${11}/{12} ≤ n ≤ {26}/{12}$ и ${7}/{12} ≤ k ≤{22}/{12}$.
Откуда следует, что два целых значения $n = 1$ и $n = 2$ удовлетворяют неравенству ${11}/{12} ≤ n ≤ {26}/{12}; k = 1$ — единственное целое $k$, удовлетворяющее неравенству ${7}/{12} ≤ k ≤{22}/{12}$.
При $n = 1$ $x = -{π}/{3} + 2π·1 = {5π}/{3}$.
При $n = 2$ $x = -{π}/{3} + 2π·2 = {11π}/{3}$.
При $k = 1$ $x = {π}/{3} + 2π·1 = {7π}/{3}$. Итак, ${5π}/{3}; {7π}/{3}; {11π}/{3}$ — корни уравнения, принадлежащие промежутку $[{3π}/{2};4π]$.
Ответ: а)$x=±{π}/{3}+2πn,n∈Z$;б)${5π}/{3};{7π}/{3};{11π}/{3}$
Задача 15
а) Решите уравнение $log_2^2(2 sin x + 1) — 17 log_2(2 sin x + 1) + 16 = 0$.
б) Укажите корни этого уравнения, принадлежащие отрезку $[{π}/{4};2π]$.
Решение
а) После замены $t = log_2(2 sin x+1)$ исходное уравнение примет вид $t^2-17t+16 = 0$. Корни этого уравнения $t = 1, t = 16$. Возвращаясь к переменной $x$, получим:
$[tablelog_2(2 sin x + 1) = 1; log_2(2 sin x + 1) = 16;$ $[table2 sin x + 1 = 2;; 2sin x + 1 = 2^{16};$
Второе уравнение совокупности не имеет корней. Решая первое уравнение, получим: $sin x = {1}/{2}; x = (-1)^n{π}/{6} + πn; n ∈ Z$.
б) Запишем решение уравнения в виде $x = {π}/{6} + 2πn; n ∈ Z$ или $x = {5π}/{6} + 2πk; k ∈ Z$ и выясним, для каких целых значений $n$ и $k$ справедливы неравенства ${π}/{4}≤{π}/{6}+2πn≤2π$ и ${π}/{4}≤{5π}/{6}+2πk≤2π$.
Получим: ${1}/{24}≤n≤{11}/{12}$ и $-{7}/{24}≤k≤{7}/{12}$, откуда следует, что нет целых значений $n$, удовлетворяющих неравенству ${1}/{24}≤n≤{11}/{12}; k = 0$ — единственное целое $k$, удовлетворяющее неравенству $-{7}/{24}≤k≤{7}/{12}$.
При $k = 0$ $x = {5π}/{6} + 2π·0 = {5π}/{6}$. Итак, ${5π}/{6}$ — корень уравнения, принадлежащий отрезку $[{π}/{4};2π]$.
Ответ: а)$(-1)^{n}{π}/{6}+πn,n∈Z$;б)${5π}/{6}$
Задача 16
а) Решите уравнение $6 log_2^2(2 cos x) — 9 log_2(2 cos x) + 3 = 0$.
б) Найдите все корни этого уравнения, принадлежащие отрезку $[-{π}/{2};π]$.
Решение
а) Решим уравнение $6log_2^2(2 cos x)-9 log_2(2 cos x)+3 = 0$. Обозначим $log_2(2 cos x) = t$ и решим получившееся квадратное уравнение.
$6t^2 — 9t + 3 = 0, t = {9±3}/{12}; t_1 = {1}/{2}; t_2 = 1$.
$[tablelog_2(2 cos x) ={1}/{2}; log_2(2 cos x) = 1;$ $[table2 cos x = √2; 2 cos x = 2;$
$[tablecos x = {√2}/{2}; cos x= 1;$ $[tablex = ±{π}/{4}+ 2π n; n ∊ Z; x = 2πk; k ∊ Z;$
б) Корни, принадлежащие отрезку $[-{π}/{2};π]$, найдём с помощью числовой окружности:
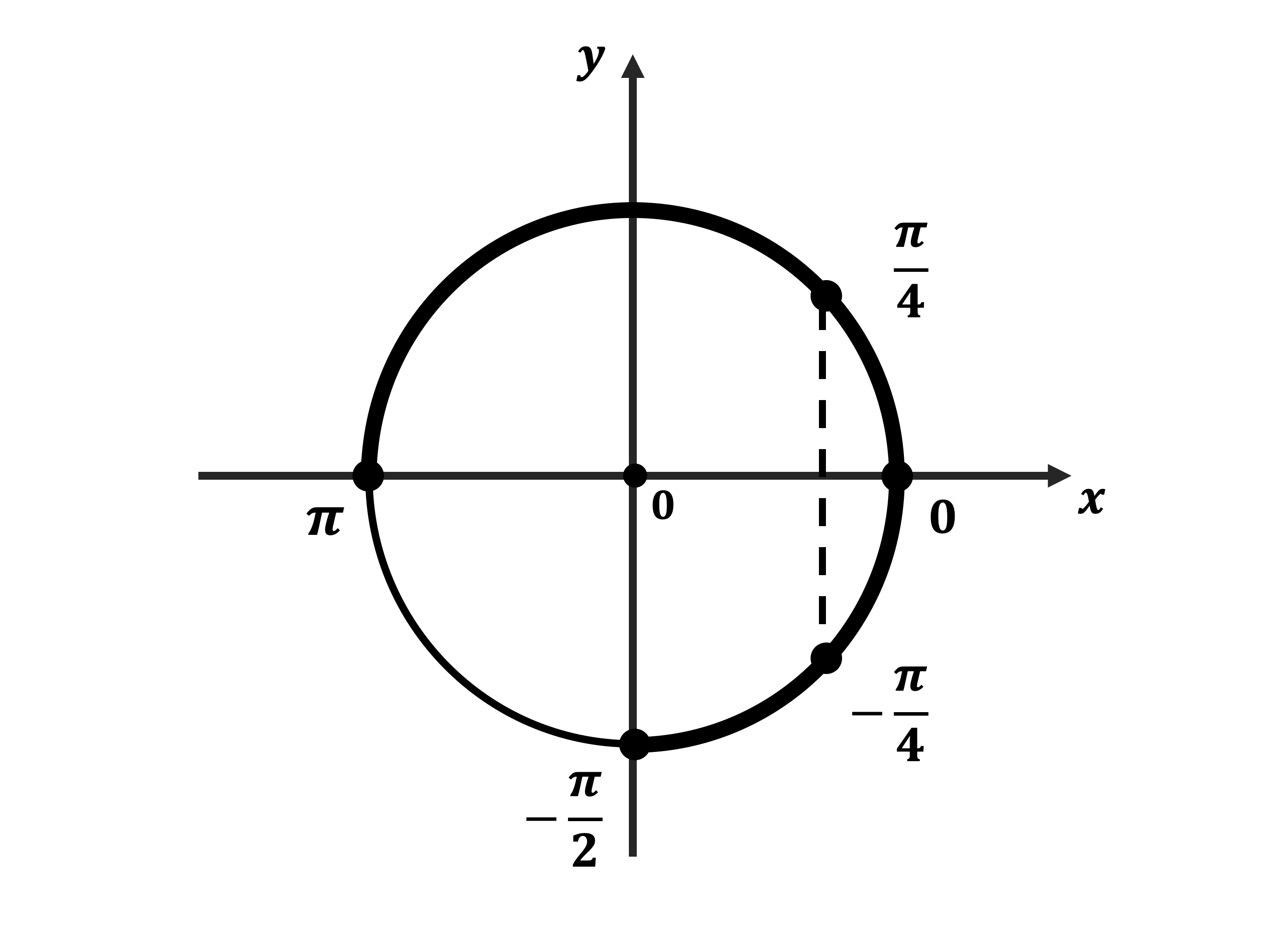
$x_1 = -{π}/{4}; x_2 = 0; x_3 ={π}/{4}$.
Ответ: а)$±{π}/{4}+2πn,n∈Z;2πk,k∈Z$;б)$-{π}/{4};0;{π}/{4}$
Задача 17
а) Решите уравнение $2log_2^2(2 sin x) — 3 log_2(2 sin x) + 1 = 0$.
б) Найдите все корни этого уравнения, принадлежащие отрезку $[{3π}/{2}; 3π]$.
Решение
а) Решим уравнение $2log_2^2(2 sin x) — 3 log_2(2 sin x) + 1 = 0$. Обозначим $log_2(2 sin x) = t$ и решим получившееся уравнение. $2t^2 — 3t + 1 = 0, t = {3±1}/{4}; t_1 = 1; t_2 ={1}/{2}$
$[tablelog_2(2 sin x) = 1; log_2(2 sin x) ={1}/{2};$ $[table2 sin x = 2; 2 sin x=√2;$
$[tablesin x = 1; sin x = {√2}/{2};$ $[tablex={π}/{2}+2πn; x=(-1)^k{π}/{4}+πk;$ $n,k∈Z$
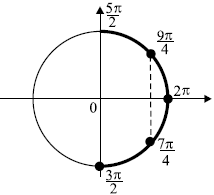
б) Корни, принадлежащие отрезку $[{3π}/{2}; 3π]$, найдём с помощью числовой окружности:
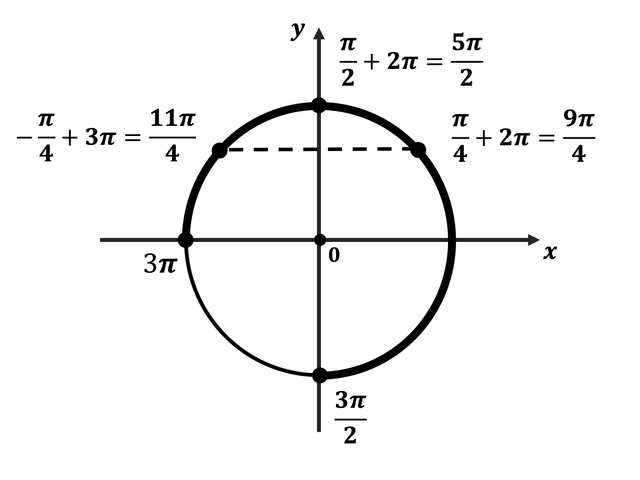
$x_1 = 2π + {π}/{4} = {9π}/{4}; x_2 = 2π + {π}/{2} ={5π}/{2}; x_3 = 3π -{π}/{4} = {11π}/{4}$.
Ответ: а)${π}/{2}+2πn,n∈Z;(-1)^k{π}/{4}+πk,k∈Z$;б)${9π}/{4};{5π}/{2};{11π}/{4}$
Задача 18
а) Решите уравнение $27^{x} — 5·9^{x} — 3^{x+4} + 405 = 0$.
б) Укажите все корни этого уравнения, принадлежащие отрезку $[log_{3}6; log_{3}10]$.
Решение
а) Преобразуем исходное уравнение и разложим на множители его левую часть.
$3^{3x} — 5·3^{2x} — 81·3^x + 405 = 0$,
$3^{2x}(3^x — 5) — 81(3^x — 5) = 0$,
$(3^{2x} — 81)(3^x — 5) = 0$.
Получаем: $3^{2x} -81 = 0$ или $3^x -5 = 0$. Значит, $3^{2x} = 81$, откуда $x = 2$ или $3^x = 5$, откуда $x = log_{3}5$.
б) Нам нужно выбрать те корни уравнения, которые принадлежат отрезку $[log_{3}6; log_{3}10]$. Заметим, что $2 = log_{3}9$. Тогда $log_{3}5 < log_{3}6 < 2 < log_{3}10$. Значит, указанному отрезку принадлежит корень $x = 2$.
Ответ: а)$2;log_{3}5$; б)$2$
Задача 19
а) Решите уравнение $3√{2}sin({π}/{2}+x)-2=2cos^{2}x$.
б) Укажите корни этого уравнения, принадлежащие отрезку $[{3π}/{2};{5π}/{2}]$.
Решение
а) Запишем исходное уравнение в виде $2 cos^2 x — 3√2 cos x + 2 = 0$.
Решая это уравнение как квадратное относительно $cos x$, получим $(cos x)_{1,2} ={3√2±√{18 — 16}}/{4}={3√2± √2}/{4}$.
Значит, $(cos x)_1 = {√2}/{2}$, откуда $x =π/4 + 2πn, n ∈ Z$ или $x =-π/4 + 2πn, n ∈ Z$.
Уравнение $(cosx)_2 = √2$ корней не имеет.
б) Отберём корни, принадлежащие отрезку $[{3π}/{2};{5π}/{2}]$ с помощью числовой окружности.
Получим числа
$2π -{π}/{4} ={7π}/{4}$;
$2π + {π}/{4} = {9π}/{4}$.
Ответ: а)$±{π}/{4}+2πn,n∈Z$;б)${7π}/{4},{9π}/{4}$
Задача 20
а) Решите уравнение $3√{3}cos({3π}/{2}+x)-3=2sin^{2}x$.
б) Укажите корни этого уравнения, принадлежащие отрезку $[2π; 3π]$.
Решение
а) Запишем исходное уравнение в виде $2sin^2 x — 3√3 sin x + 3 = 0$.
Решая это уравнение как квадратное относительно $sin x$, получим $(sin x)_{1,2} = {3√3±√{27-24}}/{4}= {3√3±√3}/{4}$.
Значит,$(sin x)_1 ={√3}/{2}$, откуда $x ={π}/{3} +2πn, n ∈ Z$ или $x ={2π}/{3}+2πm, m ∈ Z$.
Уравнение $(sin x)_2 = √3$ корней не имеет.
б) С помощью числовой окружности отберём корни, принадлежащие отрезку: $[2π; 3π]$
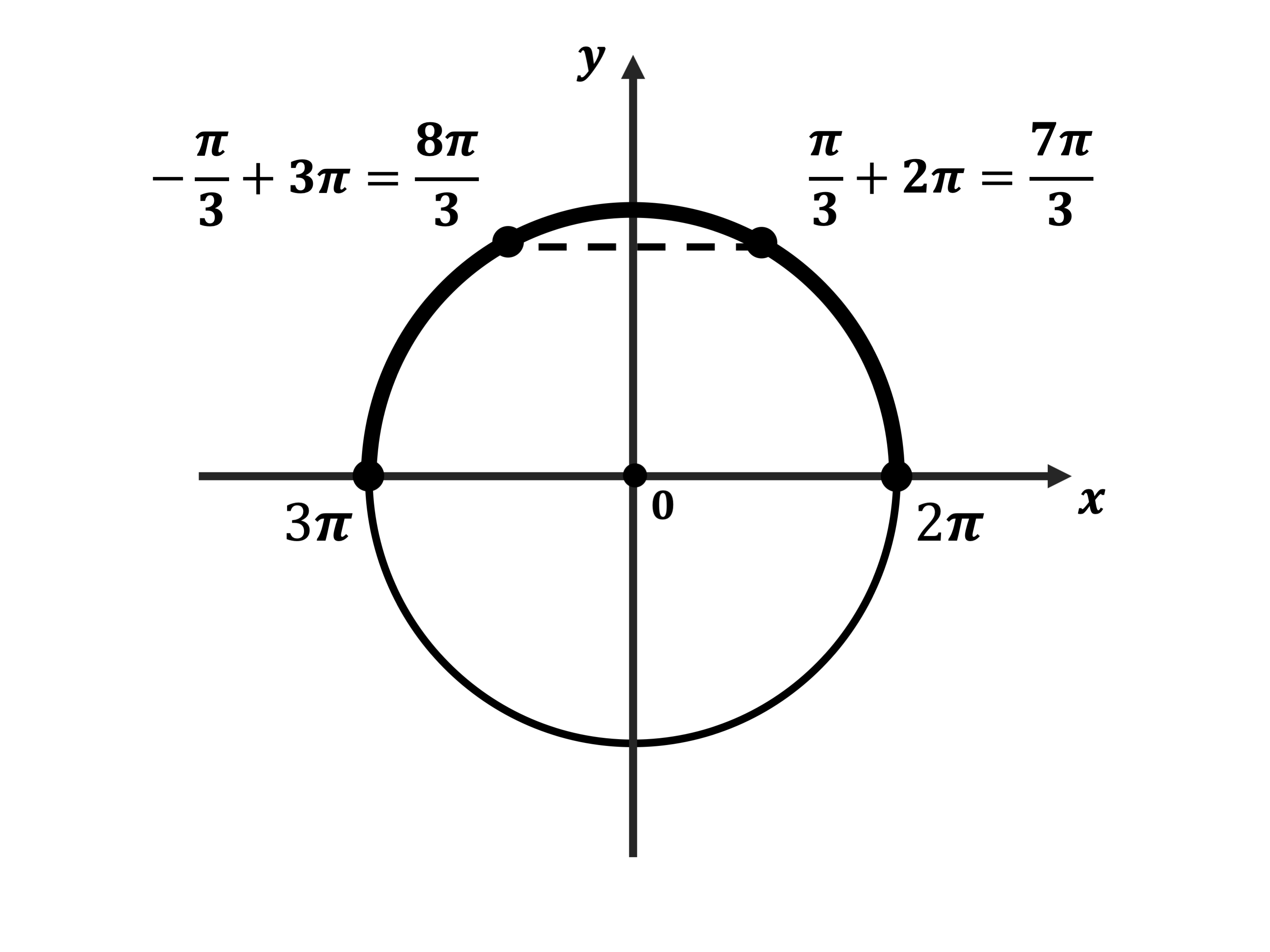
Получим числа:
$2π +{π}/{3}={7π}/{3}$;
$3π -{π}/{3}={8π}/{3}$.
Ответ: а)${π}/{3}+2πn,n∈Z;{2π}/{3}+2πm,m∈Z$;б)${7π}/{3},{8π}/{3}$