а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие промежутку
Спрятать решение
Решение.
а) Заметим, что преобразуем исходное уравнение:
Пусть тогда уравнение запишется в виде
откуда
или
При получим:
откуда
При получим:
откуда
б) Корень не принадлежит промежутку
Поскольку
и
корень
принадлежит промежутку
Ответ: а) б)
Спрятать критерии
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получены верные ответы в обоих пунктах. | 2 |
| Обоснованно получен верный ответ в пункте а),
ИЛИ получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения пункта а) и пункта б). |
1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 2 |
Источник: ЕГЭ по математике 19.06.2013. Основная волна, резервная волна. Центр. Вариант 502, Задания 13 (С1) ЕГЭ 2013
Meet the Instructors
Course content
loading…
Price:
Free
Share this course
https://stepik.org/course/161885/promo
Price:
Free
За это задание ты можешь получить 3 балла. На решение дается около 20 минут. Уровень сложности: повышенный.
Средний процент выполнения: 5.6%
Ответом к заданию 13 по математике (профильной) может быть развернутый ответ (полная запись решения с обоснованием выполненных действий).
Что нужно знать, чтобы решить задание 13:
В задании требуется решить уравнение одного из видов: тригонометрическое, рациональное, показательное, логарифмическое, уравнение с радикалом или смешанное уравнение, которое может содержать в себе несколько видов, например, логарифмы и тригонометрию. После решения уравнения, часто необходимо отобрать корни, которые принадлежат определенному промежутку.
Разбор сложных заданий в тг-канале
Задачи для практики
Задача 1
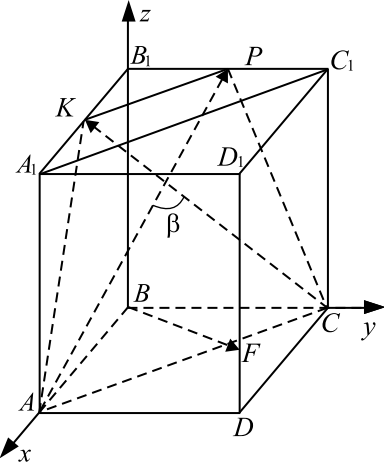
Дан куб $ABCDA_1B_1C_1D_1$. На ребре $AA_1$ отмечена точка $M$, причём $AM:MA_1=1:1$, на ребре $BB_1$ отмечена точка $N$,
причём $BN:NB_1=1:2$, на ребре $CC_1$ отмечена точка $K$, причём $CK:KC_1=1:3$.
а) В каком отношении, считая от точки $D$, плоскость $MNK$ делит ребро $DD_1$?
б) Найдите величину угла между плоскостями $MNK$ и $ABC$.
Решение
а) Пусть ребро куба равно $1$. Противоположные грани куба параллельны, поэтому плоскость $MNK$ пересекает их по параллельным отрезкам. Сечением куба плоскостью $MNK$ является параллелограмм $MNKF$, где $F$ — точка пересечения ребра $DD_1$ с плоскостью $MNK$. Рассмотрим проекцию куба на грань $CC_1D_1D$. $DM_1=AM$, $CN_1=BN$. Отрезки $M_1N_1$ и $FK$ параллельны, поэтому $N_1K={1} / {3}-{1} / {4}={1} / {12}$, и $FD=M_1D-M_1F={1} / {2}-{1} / {12}={5} / {12}$, значит, $DF:FD_1=5:7$. б) Прямая $FK$ пересекает плоскость основания куба в точке $L$, прямая $NK$ пересекает плоскость основания куба в точке $T$, поэтому плоскость $MNK$ пересекает плоскость $ABC$ по прямой $TL$. В прямоугольном треугольнике $CLT$ отрезок $CH$ — высота, по теореме о трёх перпендикулярах $KH⊥ TL$, поэтому линейный угол $CHK$ является углом между плоскостями $MNK$ и $ABC$. Треугольники $CLK$ и $DLF$ подобны, $CK={1} / {4}$, $FD={5} / {12}$, $DL=1+CL$, тогда из пропорции ${1} / {4}:{5} / {12}=CL:(1+CL)$, получим $CL={3} / {2}$. Аналогично из подобия треугольников $CTK$ и $BTN$ найдём $CT=3$. В прямоугольном треугольнике $CLT$ гипотенуза $LT$ вычисляется по теореме Пифагора:$LT={3√ 5} / {2}$, а высота $CH={CL⋅ CT} / {LT}={3} / {√ 5}$. В прямоугольном треугольнике $CHK$ вычисляем
$tg∠ CHK={CK} / {CH}={1} / {4}:{3} / {√ 5}={√ 5} / {12}$, значит, $∠ CHK=arctg{√ 5} / {12}$.
Ответ: begin{tabular}{c}а)$5:7$\б)$arctgfsm{sqrt5}{12}$end{tabular
Задача 2
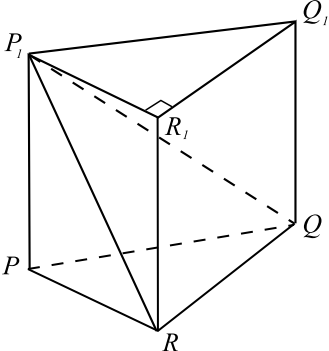
Основанием прямой треугольной призмы $PQRP_1Q_1R_1$ является прямоугольный треугольник $PQR$ с прямым углом $R$. Диагонали боковых граней $PP_1Q_1Q$ и $PP_1R_1R$ равны $17$ и $15$ соответственно, $PQ = 10$.
а) Докажите, что треугольник $P_1QR$ прямоугольный.
б) Найдите объём пирамиды $P_1QRR_1$.
Решение
По условию задачи сделаем чертёж.
а) Прямая $QR$ перпендикулярна плоскости $PP_1R_1R$, поскольку она перпендикулярна прямым $PR$ и $RR_1$. Значит, прямые $QR$ и $RP_1$ перпендикулярны, следовательно, в $△P_1QR$
$∠P_1RQ = 90°$.
б) Пусть $V$ — объём призмы $PQRP_1Q_1R_1$. Тогда объём треугольной пирамиды $PP_1QR$ равен ${V}/{3}$, поскольку её высота $PP_1$ и основание $PQR$ совпадают с высотой и основанием призмы соответственно. Аналогично, объём треугольной пирамиды $P_1Q_1R_1Q$ равен ${V}/{3}$. Призма $PQRP_1Q_1R_1$ составлена из трёх пирамид: $PP_1QR, P_1Q_1R_1Q$ и $P_1QRR_1$. Значит, объём пирамиды $P_1QRR_1$ равен ${V}/{3}$.
В призме $PQRP_1Q_1R_1 : QQ_1 = √{P_1Q^2 — P_1Q_1^2} = 3√21, QR = √{P_1Q^2 — P_1R^2} = 8, PR = √{PQ^2 — QR^2} = 6, V = PP_1 · {PR · QR}/{2} = 72√21$.
Таким образом, объём пирамиды $P_1QRR_1$ равен $24√21$.
Ответ: 24sqrt{21}
Задача 3
В правильной четырёхугольной пирамиде $SABCD$ боковое ребро $SA=12$, а высота равна $4$. На рёбрах $AB$, $CD$ и $AS$ отмечены точки $E$, $F$ и $K$ соответственно, причём $BE=CF=12$, $AK=3$.
а) Докажите, что плоскости $SBC$ и $KEF$ параллельны.
б) Найдите объём пирамиды $KSBC$.
Решение
а) Докажем, что плоскости $SBC$ и $KEF$ параллельны.
Введём прямоугольную систему координат, учитывая, что в основании правильной пирамиды квадрат $ABCD$ и угол между диагоналями квадрата прямой .
1. Найдём координаты точек $S, B, C , K , E, F$. В прямоугольном треугольнике $SOA$ по теореме Пифагора $OA^2 = SA^2 — SO^2, OA = √{12^2 — 4^2} = 8√2. OC = OB = OD = OA = 8√2$, тогда сторона квадрата $AB = {OA}/{sin 45°} = {8√2}/{{1}/{√2}} = 16, AE = AB — BE = 16 — 12 = 4$.
Проведём $KN ‖ SO, SO ⊥ (ABC)$, тогда $KN ⊥ (ABC)$ и $KN ⊥ OA, △SAO ∼ △KAN$ по первому признаку подобия $(∠SOA = ∠KNA = 90°, ∠A$ — общий) ${AS}/{AK} = {SO}/{KN}, {12}/{3} = {4}/{KN}, KN = 1$.
В прямоугольном треугольнике $ANK$ по теореме Пифагора $AN^2 = AK^2 — KN^2, AN = √{3^2 — 1^2} = 2√2$, тогда $ON = OA — AN = 8√2 — 2√2 = 6√2. EN$ — проекция $KE$ на плоскость $ABC$, значит $△ANE$ прямоугольный и равнобедренный $EN = AN = 2√2$.
Получим $S(0; 0; 4), B(0; -8√2; 0), C (-8√2; 0; 0), K (6√2; 0; 1), E(6√2; -2√2; 0), F (-2√2; 6√2; 0)$.
2. Докажем, что векторы нормали к плоскостям $SBC$ и $KEF$ коллинеарны. Для плоскости $SBC$, вектор нормали ${n_1}↖{→}(a_1; b_1; c_1)$ перпендикулярен к обеим прямым $SB$ и $SC$, поэтому он должен быть перпендикулярен к векторам ${SB}↖{→}(0; -8√2; -4)$ и ${SC}↖{→}(-8√2; 0; -4)$.
Получим систему ${table {n_1}↖{→} · {SB}↖{→} = 0; {n_1}↖{→} ·{SC}↖{→} = 0;$ ${table · a_1 — 8√2 · b_1 — 4c_1 = 0; -8√2a_1 + 0 · b_1 — 4 · c_1 = 0;$ ${table-2√2b_1 — c_1 = 0; -2√2a_1 — c_1 = 0;$
Пусть $c_1 = -1$, тогда система примет вид ${table-2√2b_1 + 1 = 0; -2√2a_1 + 1 = 0;$
Её решение $a_1 = {√2}/{4}; b_1 = {√2}/{4}$.
${n_1}↖{→}({√2}/{4}; {√2}/{4}; -1)$ — вектор нормали плоскости $SBC$ .
Для плоскости $KEF$, вектор нормали ${n_2}↖{→}(a_2; b_2; c_2)$ перпендикулярен к обеим прямым $KE$ и $KF$, поэтому он должен быть перпендикулярен к векторам ${KE}↖{→}(0; -2√2; -1)$ и ${KF}↖{→}(-8√2; 6√2; -1)$.
Получим систему ${table {n_2}↖{→} · {KE}↖{→} = 0; {n_2}↖{→} · {KF}↖{→} = 0;$ ${table · a_2 — 2√2 · b_2 — 1 · c_2 = 0; -8√2a_2 + 6√2 · b_2 — 1 · c_2 = 0;$ ${table-2√2b_2 — c_2 = 0; -8√2a_2 + 6√2b_2 — c_2 = 0$.
Пусть $c_2 = -1$, тогда система примет вид ${table-2√2b_2 + 1 = 0; 8√2a_2 + 6√2b_2 + 1 = 0;$
Её решение $a_2 = {√2}/{4}; b_2 = {√2}/{4}$.${n_2}↖{→}({√2}/{4}; {√2}/{4}; -1)$ — вектор нормали плоскости $KEF$.
Векторы ${n_1}↖{→}$ и ${n_2}↖{→}$ равны, значит коллинеарны, следовательно плоскости $SBC$ и $KEF$ параллельны.
б) Искомый объём $V = {1}/{3}S · h$, где $S$ — площадь треугольника $SBC$, а высота пирамиды $h$ — это расстояние от точки $K$ до плоскости $SBC$.
1. $S = {1}/{2}SB · SC · sin α$, где $α$ — угол между прямыми $SB$ и $SC$. $cos α ={{SB}↖{→} · {SC}↖{→}}/{|{SB}↖{→}| · |{SC}↖{→}|} = {0 · (-8√2) + (-8√2) · 0 + (-4)(-4)}/{12 · 12} = {16}/{144} = {1}/{9}$.
$sin α = √{1 — cos^2α} = √{1 — {1}/{81}} = {4√5}/{9} · S = {1}/{2} · 12 · 12 · {4√5}/{9} = 32√5$.
2. Чтобы найти $h$ необходимо найти уравнение плоскости $SBC$. Оно имеет вид $ax + by + cz + d = 0$, где ${n}↖{→}(a; b; c)$ — вектор нормали этой плоскости. Согласно пункту а), один из векторов нормали ${n_1}↖{→}({√2}/{4}; {√2}/{4}; -1)$. Значит, уравнение имеет вид ${√2}/{4}x + {√2}/{4}y — z + d = 0$. Чтобы найти значение $d$ подставим координаты точки $S(0; 0; 4)$ в это уравнение, получим $-4 + d = 0, d = 4$, тогда ${√2}/{4}x + {√2}/{4}y — z + 4 = 0$ — уравнение плоскости $SBC$. Расстояние от точки $K(6√2; 0; 1)$ до плоскости $SBC$
$h = {|ax_0+ by_0 + z_0 + d|}/{√{a_2 + b_2 + z_2}} ={|{√2}/{4} · 6√2 + {√2}/{4} · 0 + (-1) · 1 + 4|}/{√{({√2}/{4})^2 + ({√2}/{4})^2 + (-1)^2}} = {12√5}/{5}$, где $x_0, y_0, z_0$ — координаты точки $K$.
3. $V = {1}/{3} · 32√5 · {12√5}/{5} = 128$.
Ответ: 128
Задача 4
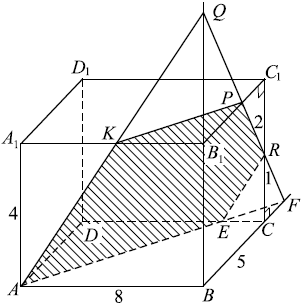
В правильной четырёхугольной призме $ABCDA_1B_1C_1D_1$ сторона основания $AB=8√ {2}$, а боковое ребро $AA_1=16$. Точка $K$ — середина ребра $A_1B_1$. На ребре $DD_1$ отмечена точка $F$ так, что $DF=4$. Плоскость $α$ параллельна прямой $A_1C_1$ и содержит точки $K$ и $A$.
а) Докажите, что прямая $BF$ перпендикулярна плоскости $α$.
б) Найдите объём пирамиды, вершина которой точка $B$, а основание — сечение данной призмы плоскостью $α$.
Решение
1. Построим сечение призмы плоскостью $α$.
Грани $ABCD$ и $A_1 B_1 C_1 D_1$ параллельны, значит плоскость α пересекает их по параллельным прямым.
По условию плоскость α параллельна прямой $A_1 C_1$, то есть содержит прямую, параллельную $A_1 C_1$. Поэтому, проведя через точку $K$ прямую $KP (P ∈ B_1 C_1)$, параллельную прямой $A_1 C_1$, и через точку $A$ — прямую $AC$, параллельную прямой $A_1 C_1$ (прямая $AC$ содержит диагональ нижнего основания) получим трапецию $AKPC$ — искомое сечение.
2. Выберем прямоугольную систему координат, как показано на рисунке. Найдём координаты нужных точек: $B(0; 0; 0), F (8√2; 8√2; 4), A(8√2; 0; 0), C (0; 8√2; 0), K (4√2; 0; 16), P (0; 4√2; 16)$.
3. Рассмотрим векторы ${BF}↖{→} (8√2; 8√2; 4), {AP}↖{→} (-8√2; 4√2; 16)$ и ${CK}↖{→} (4√2; -8√2; 16)$.
Так как ${BF}↖{→}· {AP}↖{→} = 8√2(-8√2) + 8√2 · 4√2 + 16 · 4 = 0$, то ${BF}↖{→} ⊥ {AP}↖{→}$.
Так как ${BF}↖{→} · {CK}↖{→} = 8√2 · 4√2 + 8√2 · (-8√2) + 4 · 16 = 0$, то ${BF}↖{→} ⊥ {CK}↖{→}$.
Отсюда следует, что $BF ⊥ α$ по признаку перпендикулярности прямой и плоскости ($BF$ перпендикулярна двум пересекающимся прямым плоскости).
б) Искомый объём $V = {1}/{3}S · h$, где $S$ — площадь четырёхугольника $AKPC$, а высота $h$ — расстояние от точки $B$ до плоскости $α$.
1. $S_{AKPC} = {1}/{2}AP · CK sin β$, где $β$ — угол между диагоналями $AP$ и $CK$ четырёхугольника $AKPC$.
$cos β = {{AP}↖{→} · {CK}↖{→}}/{|{AP}↖{→}| · |{CK}↖{→}|} = {-8√2 · 4√2 + 4√2(-8√2) + 16 · 16}/{√{(-8√2)^2 + (4√2)^2 + 16^2} · √{(4√2)^2 + (-8√2)^2 + 16^2}} = {-64 — 64 + 256}/{416} = {128}/{416} = {4}/{13}; |{AP}↖{→}| = |{CK}↖{→}| = √{416}$.
$sin β = √{1 — cos^2β} = √{1 — {16}/{169}} = {3√17}/{13}$.
Таким образом $S = {1}/{2} · √{416} · √{416} · {3√17}/{13} = 48√{17}$.
2. Чтобы найти $h$ необходимо найти уравнение плоскости $α$. Оно имеет вид $ax + by + cz + d = 0$, где ${n}↖{→}(a; b; c)$ — вектор нормали этой плоскости.
Согласно пункту а) одним из векторов нормали является вектор ${BF}↖{→}(8√2; 8√2; 4)$.
Значит, уравнение плоскости имеет вид $8√2x + 8√2y + 4z + d = 0 (1)$.
Чтобы найти значение $d$ подставим координаты точки $A(8√2; 0; 0)$ в уравнение (1) и получим $8√2 · 8√2 + d = 0, d = -128$.
Уравнение плоскости $α$ примет вид $8√2x + 8√2y + 4z — 128 = 0$.
Найдём расстояние $h$ от точки $B(0; 0; 0)$ до плоскости сечения.
$h = {|ax_0+ by_0 + cz_0 + d|}/{√{a^2 + b^2 + c^2}} = {|8√2 · 0 + 8√2 · 0 + 4 · 0 — 128|}/{√{(8√2)^2 + (8√2)^2 + 16}} = {32}/{√17}$, где ($x_0 ; y_0 ; z_0$ ) — координаты точки $B$.
$V = {1}/{3} · S · h = {1}/{3} · 48√{17} · {32}/{√17} = 512$.
Ответ: 512
Задача 5
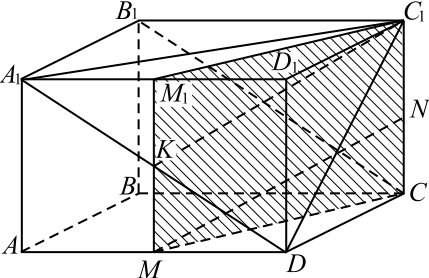
В прямоугольном параллелепипеде $ABCDA_{1}B_{1}C_{1}D_{1}$ сторона $AB=AA_{1}=3$, $AD=6$. На рёбрах $AD$ и $CC_{1}$ взяты соответственно точки $M$ и $N$ — середины этих рёбер.
а) Постройте сечение параллелепипеда плоскостью, проходящей через вершину $D$, параллельно $MN$ и $B_{1}C$.
б) Найдите объём пирамиды, основание которой — построенное сечение, а вершина — точка $D_{1}$.
Решение
а) Искомое сечение проходит через вершину $D$ параллельно $B_1 C$, следовательно, пересекает грань $AA_1 D_1 D$ по диагонали $A_1 D$
Действительно, $A_1 D||B_1 C$ (плоскость пересекает две параллельные плоскости по параллельным прямым)
Рассмотрим прямоугольник $C C_1 M_1M$, где $M_1$ середина $A_1 D_1$
Проведём $C_1 K ||M N$. $K$ — середина отрезка $M M_1$ и середина отрезка $A_1 D$, значит, принадлежит искомому сечению, поэтому $C_1 K$ лежит в плоскости сечения
Таким образом, $A_1 C_1 D$ — искомое сечение.
б) Рассмотрим пирамиду $D_1A_1C_1D$ как пирамиду с основанием $D_1DC_1$ и высотой $A_1D_1 (A_1D_1 ⊥ D_1DC_1)$.
$V_{D_1A_1C_1D} = {1}/{3}S_{D_1DC_1} ·A_1D_1 = {1}/{3} · {1}/{2}D_1C_1 ·D_1D ·A_1D_1 = {1}/{6} ·3·3·6 = 9$.
Ответ: 9
Задача 6
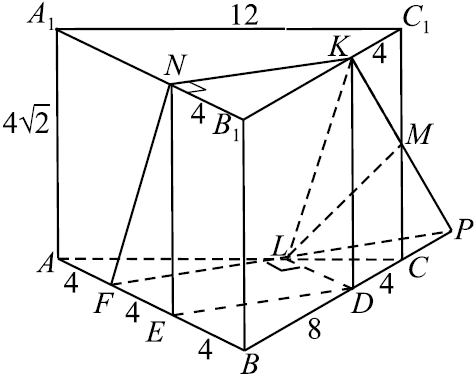
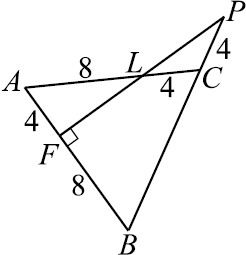
В правильной треугольной призме $ABCA_1 B_1 C_1$ сторона основания равна $12$, а боковое ребро равно $4√ {2}$. На рёбрах $AB$, $A_1 B_1$ и $B_1 C_1$ отмечены точки $F$, $N$ и $K$ соответственно, причём $AF=B_1 N=C_1 K =4$.
а) Пусть $L$ — точка пересечения плоскости $FNK$ с ребром $AC$. Докажите, что $FNKL$ — ромб.
б) Найдите площадь сечения призмы плоскостью $FNK$.
Решение
а) Докажем, что $FNKL$ — ромб.
1) Так как точка $L$ — точка пересечения плоскости $FNK$ с ребром $AC$, то (по свойству параллельных плоскостей) линии пересечения плоскости $FNK$ с основанием призмы параллельны, т.е $FL ‖ N K$.
2) В основаниях правильной треугольной призмы лежат правильные треугольники со стороной $12$.
В треугольнике $NB_1K$ $∠B1 = 60°, NB_1 = 4$ по условию, а $B_1 K = 12 — 4 = 8$. По теореме косинусов $N K = 4√3$, поэтому $N K^2 + NB_1^2 = KB_1^2$. Отсюда следует, что $∠N = 90°, ∠K = 30°$.
Значит, $N K ⊥ A_1B_1$ и $F L ⊥ AB$, т.к. $N K ‖ F L$, а $A_1B_1 ‖ AB$.
3) В $△AFL$ $∠A = 60°, ∠F = 90°, AF = 4$;
$AF$ в прямоугольном $△AFL$ лежит против $∠L = 30°$, следовательно, $AF = {1}/{2}AL, AL = AF · 2 = 4 · 2 = 8$;
$FL^2 = AL^2 — AF^2 = 8^2 — 4^2 = 64 — 16 = 48, F L = 4√3$.
Имеем $N K ‖ F L$ и $N K = F L$, следовательно $F N K L$ — параллелограмм.
Проведём $N E ⊥ F B$.
В $△NFE$ $∠E = 90°, N E = 4√2, F E = 12 — 8 = 4$.
$FN^2 = NE^2 + FE^2 = (4√2)^2 + 4^2 = 32 + 16 = 48$,
$FN = √48 = 4√3, KL = FN$ как противоположные стороны параллелограмма.
4) Имеем: $N K = K L = F N = F L$, следовательно, $F N K L$ — ромб.
б) $K N ⊥ A_1B_1 , K N ⊥ N E ⇒ K N ⊥ (AA_1B_1)$ и $K N ⊥ F N$, значит $K N F L$ — квадрат, $S_{KNFL} = FN^2 = 48$.
Построим сечение пирамиды плоскостью $FNK$ .
Продлим $FL$ до пересечения с $BC$, получим точку $P$.
Соединим точку $P$ с точкой $K$, $KP$ пересекает $CC_1$ в точке $M$. Соединим точку $M$ с точкой $L$.
Пятиугольник $F N K M L$ — искомое сечение.
В прямоугольном $△FBP$ $∠B = 60°$, значит $BP = 2FB = 16, PC = 16 — 12 = 4$.
$KC_1 = CP, ∠KC_1M = ∠MCP = 90°$, тогда $△KC_1M = △PCM$ и $C_1M = CM = 2√2. KM = √{4^2 + (2√2)^2} = √{24}$. В $△LMC$ $LM^2 = LC^2 + MC^2, LC = AC — AL = 12 — 8 = 4, MC = {1}/{2}CC_1 = 2√2, √{4^2 + (2√2)^2} = √{24}, K L = √{48}$, следовательно, $△KLM$ прямоугольный, $S_{KLM} = {1}/{2}(√{24})^2 = 12$.
$S_{сеч} = S_{KNFL} + S_{KLM} = 48 + 12 = 60$.
Ответ: 60
Задача 7
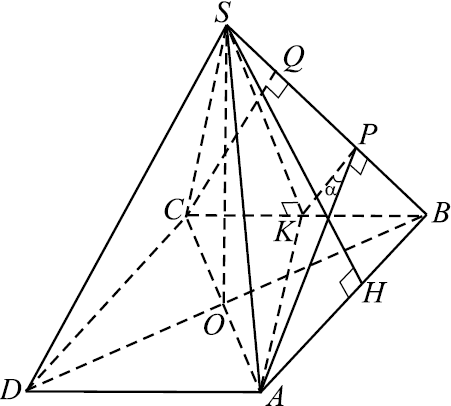
Дана четырёхугольная пирамида $SABCD$ с прямоугольником $ABCD$ в основании, $AB=6$, $BC=6√ {2}$. Высота пирамиды проектируется в точку пересечения диагоналей основания. Из вершин $A$ и $C$ на ребро $SB$ опущены перпендикуляры $AP$ и $CQ$.
а) Докажите, что точка $P$ является серединой отрезка $BQ$.
б) Найдите угол между плоскостями $SBA$ и $SBC$, если $SD=12$.
Решение
а) Пусть боковое ребро $SB$ равно $x$.
1) $△SHB∼△APB$ (прямоугольные с общим острым углом при вершине $B$). Тогда ${PB}/{BH} = {AB}/{SB}$. $H$ — середина $AB$. Тогда ${PB}/{3} = {6}/{x}; PB = {18}/{x}$.
2) $△SKB∼△CQB$ (прямоугольные с общим острым углом при вершине $B$). Тогда ${QB}/{BK} = {BC}/{SB}; {QB}/{3√2} = {6√2}/{x}; QB = {36}/{x}$.
3) Так как ${QB}/{PB} = {{36}/{x}}/{{18}/{x}} = 2$, то $PQ = PB$.
б) 1) Из пункта а) следует, что $PK$ — средняя линия $△BCQ$. Следовательно, $PK ‖ QC$. Но так как $QC ⊥ BS$, то и $PK ⊥ BS$. Значит, $∠APK$ — линейный угол двугранного угла между гранями $SBA$ и $SBC$. Пусть, $∠APK = α$.
2) $AK = √{AB^2 + BK^2} = √{6^2 + (3√2)^2} = 3√6$.
3) Так как по условию $SD = 12$ и $SB = SD$ (равным проекциям соответствуют равные наклонные), то $x = 12$, а $QB = {36}/{x} = {36}/{12}=3$.
Тогда $CQ = √{BC^2 — QB^2} = √{(6√2)^2 — 3^2} = 3√7$.
Так как $PK$ — средняя линия, то $PK = {1}/{2}CQ = {3√7}/{2}$.
4) $PB = {1}/{2}QB = {1}/{2}·3 = {3}/{2}$.
$AP = √{AB^2 — PB^2} = √{6^2 — ({3}/{2})^2} = {3}/{2}√{15}$.
5) По теореме косинусов для $△APK$:
$AK^2 = AP^2 + PK^2 — 2·AP·PK·cosα$;
$54 = {135}/{4} + {63}/{4} — 2·{3}/{2}√{15}·{3√7}/{2}·cosα$;
$cosα = — {1}/{√{105}}$;
Так как $cosα < 0$, то $α$ — тупой угол.
Значит, искомый угол между плоскостями $SBA$ и $SBC$ равен ($π-α$).
$cos(π-α) = -cosα = {1}/{√{105}}$.
Следовательно, искомый угол равен $arccos{1}/{√{105}}$.
Ответ:
Задача 8
Основанием прямой треугольной призмы $ABCA_1B_1C_1$ является прямоугольный треугольник $ABC$ с прямым углом $C$. Диагонали граней $AA_1B_1B$ и $BB_1C_1C$ равны $2√ {41}$ и $10$ соответственно, $AB=10$.
а) Докажите, что треугольник $A_1C_1B$ прямоугольный.
б) Найдите объём пирамиды $ACC_1B_1$.
Решение
а) Так как $A_1C_1 ⊥ B_1C_1$ и $A_1C_1 ⊥ CC_1$ по условию, то $A_1C_1 ⊥ BB_1C_1$ по признаку перпендикулярности прямой и плоскости.
Следовательно, $A_1C_1 ⊥ BC_1$, то есть треугольник $A_1C_1B$ прямоугольный.
б) 1) $AC = A_1C_1 = √{A_1B^2 — BC^2_1} = √{(2√{41})^2 — 10^2} = 8$.
2) $B_1C_1 = BC = √{AB^2 — AC^2} = √{10^2 — 8^2} = 6$.
3) $CC_1 = √{BC_1^2 — BC^2} = √{10^2 — 6^2} = 8$.
4) $V_{ACC_1B_1} = {1}/{3}·S_{ACC_1} ·B_1C_1 = {1}/{3} · {1}/{2} ·AC·CC_1 ·B_1C_1 = {1}/{6} ·8·8·6 = 64$.
Ответ: 64
Задача 9
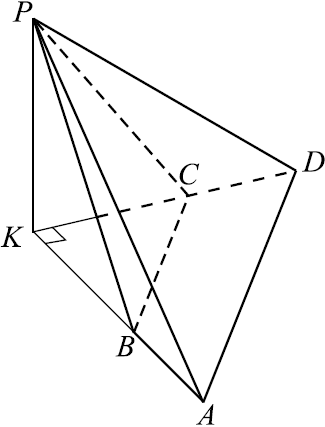
В основании четырёхугольной пирамиды $PABCD$ лежит трапеция $ABCD$ с большим основанием $AD$. Известно, что сумма углов $BAD$ и $ADC$ равна $90^°$, плоскости $PAB$ и $PCD$ перпендикулярны основанию, прямые $AB$ и $CD$ пересекаются в точке $K$.
а) Докажите, что плоскость $PAB$ перпендикулярна плоскости $PDC$.
б) Найдите объём $PKBC$, если $AB=3$, $BC=5$, $CD=4$, а высота пирамиды $PABCD$ равна $7$.
Решение
а) 1) $∠AKD = 180° — (∠A + ∠D) = 180° — 90° = 90°$.
2) Если две пересекающиеся плоскости перпендикулярны третьей, то они пересекаются по прямой, также перпендикулярной этой плоскости. Отсюда следует, что так как $PAB ⊥ ABC$ и $PCD ⊥ ABC$, то $PK ⊥ ABC$.
3) Так как $PK ⊥ ABC$, то $PK ⊥ KA$ и $PK ⊥ KD$.
Значит, $∠AKD$ — линейный угол двугранного угла между плоскостями $PAB$ и $PCD$. Следовательно, $PAB ⊥ PCD$.
б) Обозначим $BK = x, CK = y$.
1) $△BKC∼ △AKD$, так как $AD ‖ BC$.
Тогда ${AK}/{BK} = {DK}/{CK}; {AB + BK}/{BK} = {CD + CK}/{CK}; {AB}/{BK} + 1 = {CD}/{CK} + 1; {AB}/{BK} = {CD}/{CK}; {3}/{x} = {4}/{y}; x = {3}/{4}y$.
2) По теореме Пифагора $BK^2 + CK^2 = BC^2; x^2 + y^2=5^2; ({3}/{4}y)^2+y^2=25; {25}/{16}y^2=25; y=4;x={3}/{4}y=3$.
3) $S_{KBC} = {1}/{2}BK·CK = {1}/{2}·3 ·4= 6$.
4) $V_{PKBC} = {1}/{3}S_{KBC}·PK = {1}/{3}·6·7 = 14$.
Ответ: 14
Задача 10
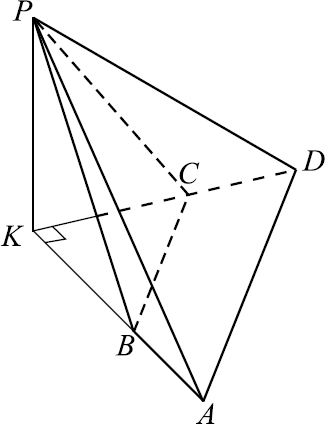
В основании четырёхугольной пирамиды $PABCD$ лежит трапеция $ABCD$ с большим основанием $AD$. Известно, что сумма углов $BAD$ и $ADC$ равна $90^°$, плоскости $PAB$ и $PCD$ перпендикулярны основанию, прямые $AB$ и $CD$ пересекаются в точке $K$.
а) Докажите, что плоскость $PAB$ перпендикулярна плоскости $PDC$.
б) Найдите объём $PKBC$, если $AB=BC=CD=4$, а высота пирамиды $PABCD$ равна $9$.
Решение
а) 1) $∠AKD = 180° — (∠A + ∠D) = 180° — 90° = 90°$.
2) Если две пересекающиеся плоскости перпендикулярны третьей, то они пересекаются по прямой, так же перпендикулярной этой плоскости. Отсюда следует, что так как $PAB ⊥ ABC$ и $PCD ⊥ ABC$, то $PK ⊥ ABC$.
3) Так как $PK ⊥ ABC$, то $PK ⊥ KA$ и $PK ⊥ KD$.
Значит, $∠AKD$ — линейный угол двугранного угла между плоскостями $PAB$ и $PCD$. Следовательно, $PAB ⊥ PCD$.
б) 1) Так как $ABCD$ — равнобедренная трапеция, то $∠A = ∠D$. Так как $BC ‖ AD$, то $∠A = ∠KBC, ∠D = ∠KCB$ как соответственные. Значит, $∠KBC = ∠KCB$, то есть $△KBC$ равнобедренный.
2) По теореме Пифагора $BK^2 + CK^2 = BC^2; 2BK^2 = BC^2; BK^2 = {BC^2}/{2} = {4^2}/{2} = 8$.
3) $S_{KBC} = {1}/{2}BK·CK = {1}/{2}BK^2 = {1}/{2}·8 = 4$.
4) $V_{PKBC} = {1}/{3}S_{KBC}·PK = {1}/{3}·4·9 = 12$.
Ответ: 12
Задача 11
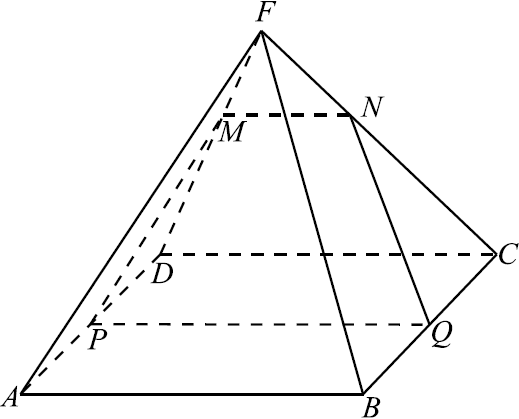
На боковом ребре $FD$ правильной четырёхугольной пирамиды ${FABCD}$ отмечена точка $M$ так, что $FM:FD=1:3$. Точки $P$и $Q$ — середины рёбер $AD$ и $BC$ соответственно.
а) Докажите, что сечение пирамиды плоскостью $MPQ$ есть равнобедренная трапеция.
б) Найдите отношение объёмов многогранников, на которые плоскость $MPQ$ разбивает пирамиду.
Решение
а) 1) Построим $MN ‖ CD$.
Так как и $PQ ‖ CD$, то $MN ‖ PQ$. Следовательно, точки $M, N, P$ и $Q$ лежат в одной плоскости. Таким образом, трапеция $MNQP$ является сечением пирамиды плоскостью $MPQ$.
2) $△FMN ∼△FDC$ (так как $MN ‖ CD$, то $∠FNM = ∠FCD$ и $∠FMN = ∠FDC$ как соответственные). Так как $△FCD$ равнобедренный, то и $△FNM$ тоже равнобедренный. Тогда $FM = FN; NC = FC — FN = FD — FM = MD$.
Кроме того, $PD = {1}/{2}AD = {1}/{2}BC = QC$. Так как $△FAD = △FBC$, то $∠MDP = ∠NCQ$. Отсюда $△PDM = △QCN$ по двум сторонам и углу между ними. Следовательно, $PM = NQ$, то есть $MNQP$ — равнобедренная трапеция.
б) 1) Пусть $MR ⊥ PQ, MS ⊥ CD, NX ⊥ PQ, NY ⊥ CD$.
Так как $MNQP$ и $MNCD$ — равнобедренные трапеции, то $V_1 = V_{PQCDMN} = V_{MRSNXY} + 2·V_{NXQCY}$ — объём первой части.
2) Пусть $a$ — сторона основания, $h$ — высота пирамиды. Тогда $QC = XY = RS = {a}/{2}; MN = {1}/{3}a; MO = {2}/{3}h(△FMN ∼△FDC$ и ${FM}/{FD} = {1}/{3}; QX = {PQ -MN}/{2} = {a -{1}/{3}a}/{2} = {1}/{3}a (MNQP$ — равнобедренная трапеция).
3) $S_{MRS} = {1}/{2}RS·MO = {1}/{2}·{a}/{2}·{2}/{3}h = {1}/{6}ah$. Объём прямой призмы $MRSNXY$ равен $V_{MRSNXY} = S_{MRS}·MN = {1}/{6}ah·{1}/{3}a = {1}/{18}a^2h$.
$V_{NXQCY} = {1}/{3}S_{XQCY}·MO = {1}/{3}·QX·QC·MO = {1}/{3}·{1}/{3}a·{a}/{2}·{2}/{3}h = {1}/{27}a^2h$.
$V_1 = V_{MRSNXY} + 2·V_{NXQCY} = {1}/{18}a^2h + 2·{1}/{27}a^2h = {7}/{54}a^2h$.
4) $V = V_{SABCD} = {1}/{3}S_{ABCD}·h = {1}/{3}a^2h$.
$V_2 = V — V_1 = ({1}/{3} — {7}/{54})a^2h = {11}/{54}a^2h$ — объём второй части.
5) ${V_1}/{V_2} ={{7}/{54}a^2h}/{{11}/{54}a^2h} = {7}/{11}$.
Ответ: 7:11
Задача 12
На боковом ребре $FD$ правильной четырёхугольной пирамиды ${FABCD}$ отмечена точка $M$ так, что $FM:FD=2:5$. Точки $P$ и $Q$ — середины рёбер $AD$ и $BC$ соответственно.
а) Докажите, что сечение пирамиды плоскостью $MPQ$ есть равнобедренная трапеция.
б) Найдите отношение объёмов многогранников, на которые плоскость $MPQ$ разбивает пирамиду.
Решение
а) 1) Построим $MN∥ CD$ (см. рис.).
Так как и $PQ∥ CD$, то $MN∥ PQ$. Следовательно, точки $M$, $N$, $P$ и $Q$ лежат в одной плоскости. Таким образом, трапеция $MNQP$ является сечением пирамиды плоскостью $MPQ$. 2) $▵ FMN∼ ▵ FDC$ (так как $MN∥ CD$, то $∠ FNM=∠ FCD$ и $∠ FMN=∠ FDC$ как соответственные). Так как $▵ FDC$ равнобедренный, то и $▵ FMN$ тоже равнобедренный. Тогда $FM=FN$; $NC=FC-FN=FD-FM=MD$. Кроме того, $PD={1} / {2}AD={1} / {2}BC=QC$. Так как $▵ FAD=▵ FBC$, то $∠ MDP=∠ NCQ$. Отсюда $▵ PDM=▵ QCN$ по двум сторонам и углу между ними. Следовательно, $PM=NQ$, то есть $MNQP$ — равнобедренная трапеция. б) 1) Пусть $MR⊥ PQ$, $MS⊥ CD$, $NX⊥ PQ$, $NY⊥ CD$ (см. рис.).
Так как $MNQP$ и $MNCD$ — равнобедренные трапеции, то $V_1=V_{PQCDMN}=V_{MRSNXY}+2⋅ V_{NXQCY}$ — объём первой части. 2) Пусть $a$ — сторона основания, $h$ — высота пирамиды. Тогда $QC=XY=RS={a} / {2}$; $MN={2} / {5}a$; $MO={3} / {5}h$ $(▵ FMN∼ ▵ FDC$ и ${FM} / {FD}={2} / {5})$; $QX={PQ-MN} / {2}={a-{2} / {5}a} / {2}={3} / {10}a$ ($MNQP$ — равнобедренная трапеция). 3) $S_{MRS}={1} / {2}RS⋅ MO={1} / {2}⋅ {a} / {2}⋅ {3} / {5}h={3} / {20}ah$. Объём прямой призмы $MRSNXY$ равен: $V_{MRSNXY}=S_{MRS}⋅ MN={3} / {20}ah⋅ {2} / {5}a={3} / {50}a^2h$. $V_{NXQCY}={1} / {3}S_{XQCY}⋅ MO={1} / {3}⋅ QX⋅ QC⋅ MO={1} / {3}⋅ {3} / {10}a⋅ {a} / {2}⋅ {3} / {5}h={3} / {100}a^2h$. $V_1=V_{MRSNXY}+2⋅ V_{NXQCY}={3} / {50}a^2h+2⋅ {3} / {100}a^2h={3} / {25}a^2h$. 4) $V=V_{SABCD}={1} / {3}S_{ABCD}⋅ h={1} / {3}a^2h$. $V_2=V-V_1=({1} / {3}-{3} / {25})a^2h={16} / {75}a^2h$ — объём второй части. 5) ${V_1} / {V_2}={{3} / {25}a^2h} / {{16} / {75}a^2h}={9} / {16}$.
Ответ: 9:16
Задача 13
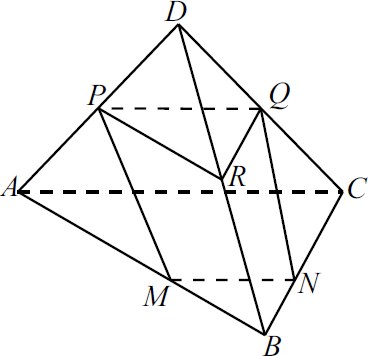
На рёбрах $AB$ и $BC$ треугольной пирамиды $DABC$ отмечены точки $M$ и $N$ так, что $AM:MB=CN:NB=2:1$. Точки $P$ и $Q$ — середины рёбер $DA$ и $DC$ соответственно.
а) Докажите, что точки $P$, $Q$, $M$ и $N$ лежат в одной плоскости.
б) Найдите отношение объёмов многогранников, на которые плоскость $PQM$ делит пирамиду.
Решение
а) 1) $△ABC ∼△MBN$ (угол $B$ общий, две пропорциональные стороны).
Значит $∠NMB = ∠CAB$. Следовательно, $MN ‖ AC$, так как равны соответствующие углы.
2) Так как $PQ$ — средняя линия $△ADC$, то $PQ ‖ AC$.
3) Так как $MN ‖ AC$ и $PQ ‖ AC$, то $MN ‖ PQ$. Следовательно, точки $P, Q, N$ и $M$ лежат в одной плоскости.
б) 1) Пусть $R$ — середина ребра $DB$. Тогда $PR$ — средняя линия $△ADB$. Следовательно, $PR ‖ AB$. Аналогично $QR ‖ BC$.
2) Обозначим через $V$ объём пирамиды $DABC, V_1 = V_{DPQR} + V_{MNBPQR}, V_2 = V — V_1, h$ — высота пирамиды $DABC, S$ — площадь $△ABC$.
Так как $△PQR∼ △ACB$ и ${PQ}/{AC} = {1}/{2}$, то $S_{PQR} ={S}/{4}$.
Так как ${DP}/{DA} = {1}/{2}$, то высота пирамиды $DPQR$ равна ${h}/{2}$.
Таким образом, $V_{DPQR} = {1}/{3}S_{PQR}· {h}/{2} = {1}/{3}· {S}/{4} ·{h}/{2} = {Sh}/{24}$.
3) Можно доказать, что $MNBPQR$ — усечёная пирамида. Её высота равна ${h}/{2}$.
Пусть $S_1 = S_{MNB}, S_2 = S_{PQR}$.
Так как $△BMN ∼ △BAC$ и ${BM}/{BA} = {1}/{3}$, то $S_1 = ({1}/{3})^2·S = {S}/{9}$.
Тогда $V_{MNBPQR} = {1}/{3}·{h}/{2}·(S_1 + √{S_1·S_2} + S_2)= {h}/{6}·({S}/{9} + √{{S}/{9}·{S}/{4}} + {S}/{4}) = {h}/{6}({S}/{9} + {S}/{6} + {S}/{4})= {19}/{216}Sh$.
4) $V_1 = V_{DPQR} + V_{MNBPQR} = {Sh}/{24} + {19}/{216}Sh = {7}/{54}Sh. V_2 = V — V_1 = {1}/{3}Sh — {7}/{54}Sh = {11}/{54}Sh$.
5) ${V_1}/{V_2} = {{7}/{54}Sh}/{{11}/{54}Sh} = {7}/{11}$.
Ответ: 7:11
Задача 14
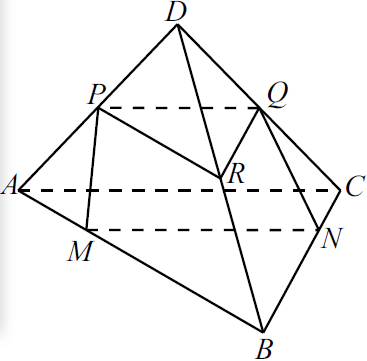
На рёбрах $AB$ и $BC$ треугольной пирамиды $DABC$ отмечены точки $M$ и $N$ так, что $AM:MB=CN:NB=1:3$. Точки $P$ и $Q$ — середины рёбер $DA$ и $DC$ соответственно.
а) Докажите, что точки $P$, $Q$, $M$ и $N$ лежат в одной плоскости.
б) Найдите отношение объёмов многогранников, на которые плоскость $PQM$ делит пирамиду.
Решение
а) 1) $△ABC ∼△MBN$ (угол $B$ общий, две пропорциональные стороны). $MB ={3}/{4}AB, BN ={3}/{4}BC$.
Следовательно, $MN ‖ AC$, так как равны соответствующие углы.
2) Так как $PQ$ — средняя линия $△ADC$, то $PQ ‖ AC$.
3) Так как $MN ‖ AC$ и $PQ ‖ AC$, то $MN ‖ PQ$. Следовательно, точки $P, Q, N$ и $M$ лежат в одной плоскости.
б) 1) Пусть $R$ — середина ребра $DB$. Тогда $PR$ — средняя линия $△ADB$. Следовательно, $PR ‖ AB, PR = {1}/{2}AB$. Аналогично $QR ‖ BC, QR = {1}/{2}BC$.
2) Обозначим через $V$ объём пирамиды $DABC, V_1 = V_{DPQR} + V_{MNBPQR}, V_2 = V — V_1, h$ — высота пирамиды $DABC, S$ — площадь $△ABC$.
Так как $△PQR∼ △ACB$ и ${PQ}/{AC} = {1}/{2}$, то $S_{PQR} ={S}/{4}$.
Так как ${DP}/{DA} = {1}/{2}$, то высота пирамиды $DPQR$ равна ${h}/{2}$.
Таким образом, $V_{DPQR} = {1}/{3}S_{PQR}· {h}/{2} = {1}/{3}· {S}/{4} ·{h}/{2} = {Sh}/{24}$.
3) Можно доказать, что $MNBPQR$ — усечёная пирамида. Её высота равна ${h}/{2}$.
Пусть $S_1 = S_{MNB}, S_2 = S_{PQR}$.
Так как $△BMN ∼ △BAC$ и ${BM}/{BA} = {3}/{4}$, то $S_1 = ({3}/{4})^2·S = {9}/{16}S$.
Тогда $V_{MNBPQR} = {1}/{3}·{h}/{2}·(S_1 + √{S_1·S_2} + S_2)= {h}/{6}·({9}/{16}S + √{{9}/{16}S·{S}/{4}} + {S}/{4}) = {h}/{6}({9}/{16}S + {3}/{8}S + {S}/{4})= {19}/{96}Sh$.
4) $V_1 = V_{DPQR} + V_{MNBPQR} = {Sh}/{24} + {19}/{96}Sh = {23}/{96}Sh. V_2 = V — V_1 = {1}/{3}Sh — {23}/{96}Sh = {3}/{32}Sh$.
5) ${V_1}/{V_2} = {{23}/{96}Sh}/{{3}/{32}Sh} = {23}/{9}$.
Ответ: 23:9
Задача 15
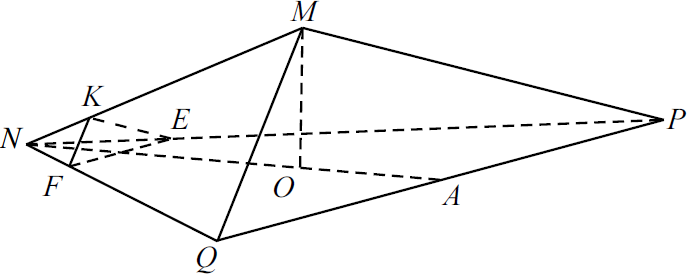
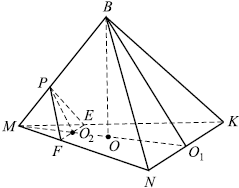
В правильной треугольной пирамиде $MNPQ$ с вершиной $M$ сторона основания равна $15$, высота равна $√ {6}$. На рёбрах $NP$, $NQ$ и $NM$ отмечены точки $E$, $F$, $K$ соответственно, причём $NE=NF=3$ и $NK={9} / {5}$. а) Докажите, что плоскости $EFK$ и $MPQ$ параллельны. б) Найдите расстояние от точки $K$ до плоскости $MPQ$.
Решение
а) Докажем, что $EFK ‖ MPQ$. Воспользуемся признаком параллельности плоскостей: если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то такие плоскости параллельны.
В плоскости $MPQ$ возьмём прямые $QP$ и $MQ$, а в плоскости $EFK$ — прямые $FE$ и $KF$. Пусть $O$ — центр основания.
В $△MNO: ∠NOM = 90°$ и по теореме Пифагора $NM = √{NO^2 +MO^2}$. Найдём $NO$: треугольник $NPQ$ — правильный, все его стороны равны, а высота $NA = {a√3}/{2}$, где $a$ — сторона треугольника $NPQ$. $NO = {2}/{3}NA = {2}/{3}·{a√3}/{2} = {a√3}/{3}$, то есть $NO = {15√3}/{3} = 5√3$. B $△NMO: ∠MON = 90°, NM = √{MO^2 + NO^2} = √{(5√3)^2 + 6} = √{75 + 6} = √{81} = 9$.
1) $△NKF∼△NMQ$, так как ${NK}/{NM} ={{9}/{5}}/{9} ={1}/{5}, {NF}/{NQ} = {3}/{15} = {1}/{5}$ и $∠MNQ$ — общий. Из подобия следует, что $∠NKF = ∠NMQ$. Это соответственные углы при прямых $KF$ и $MQ$ и секущей $NM$. Значит, $KF ‖ MQ$.
2) $△NEF∼△NPQ$, так как ${NE}/{NP} ={3}/{15} = {1}/{5}, {NF}/{NQ} ={3}/{15} = {1}/{5}$ и $∠PNQ$ — общий. Из подобия следует, что $∠NEF = ∠NPQ$. Это соответственные углы при прямых $EF$ и $PQ$ и секущей $NP$. Значит, $EF ‖ PQ$.
Итак, две пересекающейся прямые $KF$ и $FE$ плоскости $KFE$ соответственно параллельны двум пересекающимся прямым $MQ$ и $PQ$ плоскости $MPQ$, следовательно, $KFE ‖ MPQ$.
б) Найдём расстояние от точки $K$ до плоскости $MPQ$. Так как плоскость $KFE$ параллельна плоскости $MPQ$, то расстояние от точки $K$ до плоскости $MPQ$ равно расстоянию от точки $B$ до плоскости $MPQ$ и оно равно длине отрезка $BD$ ($BD$ — перпендикуляр к $AM$. Докажем это.
$NA ⊥ QP$ и $MA ⊥ QP$ (как высоты треугольников $NPQ$ и $MPQ$), значит, прямая $QP$ перпендикулярна плоскости $NMA$, и тогда прямая $PQ$ перпендикулярна любой прямой этой плоскости, в частности $BD$. С другой стороны $BD ⊥ AM$ по построению, значит, прямая $BD$ перпендикулярна двум пересекающимся прямым плоскости $MPQ$, и тогда отрезок $BD$ перпендикулярен плоскости $MPQ$ и равен расстоянию от $B$ до плоскости $MPQ$.
В $△BDA: ∠BDA = 90°; BD = BA · sin∠DAB; BA = NA — NB; NA = {15√3}/{2}; NB ={1}/{5}NA = {3√3}/{2}; BA = {15√3}/{2} — {3√3}/{2} = 6√3$.
Из $△MOA: sin∠MAO = sin∠DAB = {MO}/{MA} = {√6}/{√{MO^2 + OA^2}}={√6}/{√{6 +{75}/{4}}} = {√6·2}/{√{99}} = {2√6}/{3√{11}} ={2}/{3}√{{6}/{11}}$ (так как $AO ={1}/{3}NA = {5√3}/{2})$.
Из $△ABD:BD = AB·sin∠DAB = 6√3·{2}/{3}√{{6}/{11}} = 4√{{18}/{11}} = 12√{{2}/{11}} = {12√{22}}/{11}$.
Ответ:
Задача 16
В правильной треугольной пирамиде $DABC$ с вершиной $D$ сторона основания $AB$ равна $9$, высота равна $3$. На рёбрах $AB$, $AC$, $AD$ отмечены точки $P$, $K$, $F$ соответственно, причём $AP=AK=3$ и $AF=2$. а) Доказать, что плоскости $PKF$ и $DBC$ параллельны. б) Найти расстояние от точки $F$ до плоскости $DBC$.
Решение
Докажем, что плоскость $DBC$ параллельна плоскости $PKF$. Для этого в плоскости $PKF$ возьмём прямые $KP$ и $FP$, а в плоскости $DBC$ — прямые $CB$ и $DB$ (см. рис.). Пусть $O$ — центр основания.
В $▵ ADO$: $∠ DOA=90°$ и по теореме Пифагора $AD=√ {DO^2+AO^2}$. Найдём $AO$, треугольник $ABC$ — правильный, все его стороны равны, $AM$ — высота, $AM={a√ {3}} / {2}$, где $a$ — сторона $▵ ABC$, $AO={2} / {3} AM={2} / {3}⋅ {a√ {3}} / {2}={a√ {3}} / {3}$, то есть $AO={9√ {3}} / {3}=3√ {3}$, $AD=√ {3^2+(3√ {3})^2}=√ {9+27}=6$. $▵ APF∼ ▵ ABD$, так как ${AF} / {AD}={2} / {6}={1} / {3}$, ${AP} / {AB}={3} / {9}={1} / {3}$ и $∠ DAB$ — общий, то есть две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы между ними равны. Из подобия следует, что $∠ AFP=∠ ADB$. Это соответственные углы при прямых $FP$ и $DB$ и секущей $AD$. Значит, $FP∥ DB$. Аналогично рассуждая, получим, что $▵ AKP∼ ▵ ACB$, так как ${AK} / {AC}={3} / {9}={1} / {3}$, ${AP} / {AB}={3} / {9}={1} / {3}$ и $∠ BAC$ — общий, то есть две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы между ними равны. Из подобия следует, что $∠ APK=∠ ABC$. Это соответственные углы при прямых $KP$ и $BC$ и секущей $AB$. Значит, $KP∥ BC$. Итак, две пересекающиеся прямые $KP$ и $FP$ плоскости $PKF$ соответственно параллельны двум пересекающимся прямым $CB$ и $BD$ плоскости $DBC$. Следовательно, плоскости $DBC$ и $PKF$ параллельны по признаку параллельности плоскостей. б) Найдём расстояние от точки $F$ до плоскости $DBC$. Так как плоскость $KFP$ параллельна плоскости $DBC$, то расстояние от точки $F$ до плоскости $DBC$ равно расстоянию от точки $L$ до плоскости $DBC$ и равно длине отрезка $LN$ (см. рис.), где $LN$ — перпендикуляр к $MD$ в плоскости $AMD$.
Докажем это. $AM ⊥ BC$ и $DM⊥ BC$ (как высоты треугольников $ABC$ и $DBC$), значит, $BC⊥ MDA$ и тогда $BC$ перпендикулярен любой прямой этой плоскости, в частности, $LN$. С другой стороны, $LN ⊥ MD$ по построению, значит, $LN$ перпендикулярен двум пересекающимся прямым плоскости $DBC$, и тогда отрезок $LN$ перпендикулярен плоскости $DBC$ и равен расстоянию от точки $L$ до плоскости $DBC$. В $▵ LNM$: $∠ LNM=90°$, $LN=LM⋅ sin ∠ NML$. $ML=AM-LA$; $AM={9√ {3}} / {2}$;
$LA={1} / {3}⋅ AM={9√ {3}} / {6}={3√ {3}} / {2}$. $ML={9√ {3}} / {2}-{3√ {3}} / {2}=3√ {3}$. $sin ∠ NML={DO} / {DM}$; $DO=3$ (по условию). Из $▵ MDB$ найдём $DM$: $∠ DMB=90°$,
$MD=√ {BD^2-MB^2}=√ {36-({9} / {2})^2}={3√ {7}} / {2}$. $sin ∠ NML={2} / {√ {7}}$. $LN=LM⋅ sin ∠ NML=3√ {3}⋅{2} / {√ {7}}=6√ {{3} / {7}}$.
Ответ: 6sqrt{fsm{3}{7}}
Задача 17
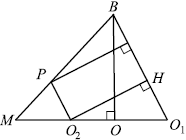
В правильной треугольной пирамиде $BMNK$ с основанием $MNK$ сторона основания равна $6$, а высота пирамиды равна $3$. На рёбрах $MN, MK$ и $MB$ соответственно отмечены точки $F, E$ и $P$, такие, что $MF = ME ={√{21}}/{2}$ и $MP ={7}/{4}$.
а) Докажите, что плоскости $FEP$ и $NBK$ параллельны.
б) Найдите расстояние от точки $P$ до плоскости $NBK$.
Решение
а) Пусть $BO -$ высота пирамиды. Чтобы доказать, что плоскости $FEP$ и $NKB$ параллельны, достаточно показать, что две пересекающиеся прямые $PF$ и $FE$ плоскости $FEP$ соответственно параллельны двум пересекающимся прямым $BN$ и $NK$ плоскости $BNK$. Покажем это.
Найдём боковое ребро $MB$ из треугольника $MBO$:
В $∆MKN:$ $MO_1 -$ высота, $MO_1 = {a√3}/{2}$, где $a -$ сторона $∆MNK$. $MO_1 = {6√3}/{2} = 3√3$.
$MO ={2}/{3} MO_1 = 2√3$,
$MB = √{OB^2 + OM^2} = √{3^2 + (2√3)^2} = √{21}$.
1. ${MP}/{MB} ={7}/{4·√{21}}={√{21}}/{12},{MF}/{MN} ={√{21}}/{2·6} = {√{21}}/{12}$. Отношения сторон равны. Используя условие, что $∠BMN$ общий, получим: $∆MPF∼∆MBN$. Из подобия треугольников следует, что $∠MPF = ∠MBN$. Эти углы — соответственные, образованные при пересечении двух прямых $PF$ и $BN$ прямой $MB$. Значит, $PF ‖ BN$.
2. Рассматривая треугольники $MEF$ и $MKN$, можно аналогично доказать, что $FE ‖ NK$.
Так как две пересекающиеся прямые $PF$ и $FE$ плоскости $PFE$ соответственно параллельны двум пересекающимся прямым $BN$ и $NK$ плоскости $NBK$, то эти плоскости параллельны.
б) Пусть $O_2$ — точка пересечения $MO_1$ и $FE$. Поскольку плоскость $PFE$ параллельна плоскости $BNK$, то расстояние от точки $P$ до плоскости $BNK$ равно расстоянию от точки $O_2$ до плоскости $BNK$, и оно равно длине отрезка $O_2H$, где точка $H$ лежит на $BO_1$ и $O_2H ⊥ BO_1$. Докажем, что $O_2H$ — расстояние от $O_2$ до плоскости $BNK$.
$NK ⊥ MO_1$ и $NK ⊥ BO_1$ ($MO_1$ и $BO_1$ — высоты $∆MNK$ и $∆NBK$), значит, $NK$ перпендикулярна плоскости $MBO_1$, и тогда $NK$ перпендикулярна любой прямой этой плоскости, в том числе $NK ⊥ O_2H$. По построению $O_2H ⊥ BO_1$. Прямая $O_2H$ перпендикулярна двум пересекающимся прямым плоскости $BNK$, значит, она перпендикулярна $BNK$, и отрезок $O_2H$ равен расстоянию от $O_2$ до плоскости $BNK$.
В треугольнике $O_2HO_1: O_2H = O_2O_1 sin∠HO_1O_2$.
$O_2O_1 = MO_1-MO_2$.
Из $∆MEO_2: ∠MO_2E = 90°, ∠EMO_2 = 30°$;
$MO_2 = MEcos30° = {√{21}}/{2}·{√3}/{2} = {3√7}/{4}$.
$O_2O_1 = 3√3 — {3√7}/{4} = {3(4√3 — √7)}/{4}$;
$sin ∠HO_1O_2 = {BO}/{BO_1} = {BO}/{√{BO^2 + OO_1^2}} = {3}/{√{3^2 + (√3)^2}} = {√3}/{2}$.
$O_2H = {3(4√3 — √7)}/{4}·{√3}/{2} = {3(12 — √{21})}/{8}$.
Ответ: ${3(12-√{21})}/{8}$
Задача 18
В прямоугольном параллелепипеде $ABCDA_{1}B_{1}C_{1}D_{1}$ стороны оснований $AB$ и $BC$ равны соответственно $8$ и $5$, а боковое ребро $AA_1$ равно $4$. На ребре $A_{1}B_1$ отмечена точка $K$, а на луче $BC$ — точка $F$, причём $A_{1}K = KB_1$ и $BF = AB$. Плоскость $AKF$ пересекает ребро $B_{1}C_1$ в точке $P$.
а) Докажите, что $B_{1}P : PC_1 = 4 : 1$.
б) Найдите площадь сечения параллелепипеда плоскостью $AKF$.
Решение
а) Построим сечение параллелепипеда плоскостью $AKF$.
$E$ — точка пересечения ребра $DC$ и отрезка $AF$.
$В$ плоскости $ABB_1$ проведём лучи $AK$ и $BB_1, AK$ пересекает $BB_1$ в точке $Q$. В плоскости $BCC_1$ проведём отрезок $FQ, FQ$ пересекает $B_1C_1$ в точке $P$, а $CC_1$ — в точке $R$. Пятиугольник $AKPRE$ — искомое сечение.
$KB_1 ‖ AB, KB_1 ={1}/{2}A_1B_1$, значит, $KB_1$ — средняя линия $△ABQ$, отсюда $BB_1 = QB_1$, а так как $BF ‖ B_1P$, то $B_1P$ — средняя линия $△FBQ, BF = 8, B_1P ={1}/{2}BF = 4. C_1P = B_1C_1 — B_1P = 5 — 4 = 1$, следовательно, $B_1P : PC_1 = 4 : 1$.
б) Прямоугольные треугольники $ABQ, FBQ$ и $ABF$ равны по двум катетам $AB = BF = BQ = 8$, отсюда $AQ = AF = QF = 8√2$. $S_{AQF} ={a^2√3}/{4}$ как площадь равностороннего треугольника со стороной $a$. $S_{AQF} = {(8√2)^2·√3}/{4} = 32√3, S_{KQP} ={1}/{4}S_{AQF}={32√3}/{4} = 8√3$.
$S_{AKPF} = S_{AQF} — S_{KQP} = 32√3 — 8√3 = 24√3$.
$△RCF~△RC_1P$ по первому признаку подобия $(∠C = ∠C_1 = 90°, ∠1 = ∠2$ как вертикальные). Из подобия следует ${CF}/{PC_1} ={FR}/{PR}$. По доказанному в а) $PC_1 = 1, BF = AB = 8$, тогда $CF = 8 — 5 = 3$ и ${FR}/{PR} ={3}/{1}$. Так как $KP$ средняя линия $△AQF$, то $PF ={1}/{2}QF = 4√2, FR = {3PF}/{4} = {4√2·3}/{4} = 3√2$.
В равнобедренном прямоугольном треугольнике $FCE$ $FC = EC = 3$, тогда $EF = 3√2$.
В $△REF$ $FR = EF = 3√2, ∠RFE = 60°$, отсюда $△REF$ — равносторонний. $S_{REF} ={(3√2)^2√3}/{4} = {9√3}/{2}$.
$S_{AKPRE} = S_{AKPF} — S_{REF} = 24√3 — {9√3}/{2} = {39√3}/{2}$.
Ответ: ${39√3}/{2}$
Рекомендуемые курсы подготовки
Новые тренировочные варианты ЕГЭ 2023 по математике базовый и профильный уровень с ответами и решением для 10 и 11 класса, больше 100 вариантов в формате реального экзамена ФИПИ вы можете решать онлайн или скачать.
Тренировочные варианты ЕГЭ 2023 по математике база и профиль
13.09.2022 Тренировочный вариант №1 ЕГЭ 2023 по математике профиль с ответами
20.09.2022 Тренировочный вариант №2 ЕГЭ 2023 по математике профиль с ответами
20.09.2022 Тренировочный вариант №2 ЕГЭ 2023 база по математике с ответами
27.09.2022 Математика 11 класс профиль входная мониторинговая работа 3 варианта с ответами
28.09.2022 Тренировочный вариант №3 ЕГЭ 2023 база по математике с ответами
28 сентября 2022 Статград математика 11 класс ЕГЭ 2023 база и профиль варианты и ответы
29 сентября 2022 Тренировочный вариант №3 ЕГЭ 2023 по математике профиль с ответами
1 октября 2022 Ларин вариант 399 ЕГЭ 2023 по математике профиль решение с ответами
6 октября Тренировочный вариант №4 ЕГЭ 2023 база по математике с ответами
6 октября Тренировочный вариант №4 ЕГЭ 2023 по математике профиль с ответами
8 октября Ларин вариант 400 ЕГЭ 2023 по математике профиль решение с ответами
12 октября Тренировочный вариант №5 ЕГЭ 2023 база по математике с ответами
12 октября Тренировочный вариант №5 ЕГЭ 2023 по математике профиль с ответами
14 октября Вариант 1 Ященко ЕГЭ 2023 математика профиль с ответами и решением
14 октября Вариант 2 Ященко ЕГЭ 2023 математика профиль с ответами и решением
15 октября Ларин вариант 401 ЕГЭ 2023 по математике профиль решение с ответами
15 октября Ларин вариант 402 ЕГЭ 2023 по математике профиль решение с ответами
16 октября Вариант 3 Ященко ЕГЭ 2023 математика профиль с ответами и решением
16 октября Вариант 4 Ященко ЕГЭ 2023 математика профиль с ответами и решением
23 октября Тренировочный вариант №6 ЕГЭ 2023 база по математике с ответами
24 октября Тренировочный вариант №6 ЕГЭ 2023 по математике профиль с ответами
25 октября Тренировочный вариант №7 ЕГЭ 2023 база по математике с ответами
26 октября Тренировочный вариант №7 ЕГЭ 2023 по математике профиль с ответами
28 октября Ларин вариант 403 ЕГЭ 2023 по математике профиль решение с ответами
29 октября Ларин вариант 404 ЕГЭ 2023 по математике профиль решение с ответами
1 ноября 2022 Тренировочный вариант №8 решу ЕГЭ 2023 база по математике с ответами
1 ноября 2022 Тренировочный вариант №8 решу ЕГЭ 2023 по математике профиль с ответами
5 ноября 2022 Вариант 1-2 распечатай и реши ЕГЭ 2023 база по математике 11 класс с ответами
6 ноября 2022 Ларин вариант 405 ЕГЭ 2023 профиль по математике решение с ответами
9 ноября 2022 Тренировочный вариант №9 решу ЕГЭ 2023 база по математике с ответами
12 ноября 2022 Тренировочный вариант №9 решу ЕГЭ 2023 по математике профиль с ответами
13 ноября 2022 Ларин вариант 406 ЕГЭ 2023 профиль по математике решение с ответами
15 ноября 2022 Тренировочный вариант №10 решу ЕГЭ 2023 база по математике 11 класс с ответами
15 ноября 2022 Тренировочный вариант №10 решу ЕГЭ 2023 по математике профиль с ответами
21 ноября 2022 Ларин вариант 407 ЕГЭ 2023 профиль по математике решение с ответами
23 ноября 2022 Тренировочный вариант №11 решу ЕГЭ 2023 база по математике 11 класс с ответами
23 ноября 2022 Тренировочный вариант №11 решу ЕГЭ 2023 по математике профиль с ответами
27 ноября 2022 Ларин вариант 408 ЕГЭ 2023 профиль по математике решение с ответами
28 ноября 2022 Вариант 3-4 распечатай и реши ЕГЭ 2023 база по математике 11 класс с ответами
30 ноября 2022 Мониторинговая работа по математике 11 класс ЕГЭ 2023 профиль 1 полугодие
3 декабря 2022 Тренировочный вариант №12 решу ЕГЭ 2023 база по математике 11 класс с ответами
3 декабря 2022 Тренировочный вариант №12 решу ЕГЭ 2023 по математике профиль с ответами
3 декабря 2022 Пробник ЕГЭ 2023 Москва по математике профиль задания и ответы
5 декабря 2022 Ларин вариант 409 ЕГЭ 2023 профиль по математике решение с ответами
9 декабря 2022 Тренировочный вариант №13 решу ЕГЭ 2023 база по математике 11 класс с ответами
10 декабря 2022 Тренировочный вариант №13 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
12 декабря 2022 Ларин вариант 410 ЕГЭ 2023 профиль по математике решение с ответами
13 декабря 2022 Статград математика 11 класс профиль ЕГЭ 2023 варианты МА2210209-МА2210212 и ответы
13 декабря 2022 Математика 11 класс база ЕГЭ 2023 статград варианты и ответы
15 декабря 2022 Тренировочный вариант №14 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
15 декабря 2022 Тренировочный вариант №14 решу ЕГЭ 2023 база по математике 11 класс с ответами
20 декабря 2022 Вариант 5-6 распечатай и реши ЕГЭ 2023 база по математике 11 класс с ответами
20 декабря 2022 Ларин вариант 411 ЕГЭ 2023 профиль по математике решение с ответами
3 января 2023 Ларин вариант 412 ЕГЭ 2023 профиль по математике решение с ответами
6 января 2023 Тренировочный вариант 1-2 ЕГЭ 2023 профиль математика задания и ответы
8 января 2023 Вариант 3-4 ЕГЭ 2023 профиль математика задания и ответы
9 января 2023 Вариант 7-8 распечатай и реши ЕГЭ 2023 база по математике 11 класс с ответами
10 января 2023 Тренировочный вариант №15 и №16 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
11 января 2023 ЕГЭ 2023 математика тренировочные задания и ответы Ященко, Семенов
11 января 2023 Тренировочный вариант №15 и №16 база ЕГЭ 2023 по математике 11 класс с ответами
19 января 2023 Тренировочные варианты №17 и №18 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
22 января 2023 Ларин вариант 413 и 414 ЕГЭ 2023 профиль по математике решение и ответы
22 января 2023 Тренировочный 19 вариант решу ЕГЭ 2023 профиль по математике 11 класс с ответами
22 января 2023 База ЕГЭ 2023 математика 11 класс тренировочный вариант 19 с ответами
25 января 2023 База ЕГЭ 2023 математика 11 класс тренировочный вариант 20 с ответами
27 января 2023 Тренировочный вариант №20 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
28 января 2023 Вариант 415 Ларина ЕГЭ 2023 по математике 11 класс задания и ответы
2 февраля 2023 Вариант 21 база ЕГЭ 2023 математика 11 класс тренировочный вариант с ответами
2 февраля 2023 Тренировочный вариант №21 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
8 февраля 2023 Математика 10-11 класс ЕГЭ 2023 статград варианты база и профиль МА2200101-МА2200110 и ответы
11 февраля 2023 Тренировочный вариант №22 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
11 февраля 2023 Тренировочный вариант №22 решу ЕГЭ 2023 база по математике 11 класс с ответами
12 февраля 2023 Вариант 416 Ларина ЕГЭ 2023 по математике 11 класс задания и ответы
12 февраля 2023 Вариант 417 Ларина ЕГЭ 2023 по математике 11 класс задания и ответы
13 февраля 2023 Вариант 9 и вариант 10 ЕГЭ 2023 база математика распечатай и реши задания
13 февраля 2023 Вариант 11 и вариант 12 ЕГЭ 2023 база математика распечатай и реши
16 февраля 2023 Тренировочный вариант №23 решу ЕГЭ 2023 база по математике 11 класс с ответами
16 февраля 2023 Тренировочный вариант №23 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
18 февраля 2023 Вариант 418 Ларина ЕГЭ 2023 по математике 11 класс задания и ответы
22 февраля 2023 Пробный ЕГЭ 2023 вариант 24 база по математике 11 класс с ответами
22 февраля 2023 Пробный ЕГЭ 2023 вариант 24 профиль по математике 11 класс с ответами
25 февраля 2023 Вариант 419 Ларина ЕГЭ 2023 по математике 11 класс задания и ответы
28 февраля 2023 Статград математика 11 класс ЕГЭ 2023 база и профиль и ответы
4 марта 2023 Пробник ЕГЭ 2023 вариант 25 база по математике 11 класс с ответами
4 марта 2023 Вариант 420 Ларин ЕГЭ 2023 по математике 11 класс задания и ответы
5 марта 2023 Пробник ЕГЭ 2023 вариант 25 профиль по математике 11 класс с ответами
8 марта 2023 Пробник ЕГЭ 2023 вариант 26 профиль по математике 11 класс с ответами
8 марта 2023 Пробник ЕГЭ 2023 вариант 26 база по математике 11 класс 100 баллов с ответами
Смотрите также на нашем сайте:
Сборник Ященко ЕГЭ 2023 математика профильный уровень 36 вариантов
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
ЕГЭ по математике — Профиль 2022. Открытый банк заданий с ответами.
- ЗАДАЧИ ЕГЭ С ОТВЕТАМИ
- АНГЛИЙСКИЙ без ГРАНИЦ
2012-07-23

НЕ ОТКЛАДЫВАЙ! Заговори на английском!
ДОЛОЙ обидные ошибки на ЕГЭ!!
Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!
Конструктор упражнений для позвоночника!
Добавить комментарий
*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.





- РубрикиРубрики
- Задачи по номерам!
№1 №2 №3 №4 №5 №6 №7 №8 №9 №10 №11 №12 №13 №14 №15 №16
- МЕТКИ
БЕЗ калькулятора Выбор варианта Как запомнить Личное Логарифмы Объём Окружность Круг Площадь Производная Треугольник Тригонометрия Трапеция Углы Уравнения Формулы Конкурсы Параллелограмм Поздравления Рекомендации Саморазвитие
- ОСТЕОХОНДРОЗУ-НЕТ!
Программа экзамена, как и в прошлые годы, составлена из материалов основных математических дисциплин. В билетах будут присутствовать и математические, и геометрические, и алгебраические задачи.
Изменений в КИМ ЕГЭ 2020 по математике профильного уровня нет.
Особенности заданий ЕГЭ по математике-2020
- Осуществляя подготовку к ЕГЭ по математике (профильной), обратите внимание на основные требования экзаменационной программы. Она призвана проверить знания углубленной программы: векторные и математические модели, функции и логарифмы, алгебраические уравнения и неравенства.
- Отдельно потренируйтесь решать задания по .
- Важно проявить нестандартность мышления.
Структура экзамена
Задания ЕГЭ профильной математики
разделены на два блока.
- Часть — краткие ответы
, включает 8 задач, проверяющих базовую математическую подготовку и умение применять знания по математике в повседневности. - Часть —
краткие и развернутые ответы
. Состоит из 11 задач, 4 из которых требуют короткого ответа, и 7 – развернутого с аргументацией выполненных действий.
- Повышенной сложности
— задания 9-17 второй части КИМа. - Высокого уровня сложности
— задачи 18-19 –. Эта часть экзаменационных заданий проверяет не только уровень математических знаний, но и наличие или отсутствие творческого подхода к решению сухих «циферных» заданий, а также эффективность умения использовать знания и навыки в качестве профессионального инструмента.
Важно!
Поэтому при подготовке к ЕГЭ теорию по математике всегда подкрепляйте решением практических задач.
Как будут распределять баллы
Задания части первой КИМов поматематике близки к тестам ЕГЭ базового уровня, поэтому высокого балла на них набрать невозможно.
Баллы за каждое задание по математике профильного уровня распределились так:
- за правильные ответы на задачи №1-12 – по 1 баллу;
- №13-15 – по 2;
- №16-17 – по 3;
- №18-19 – по 4.
Длительность экзамена и правила поведения на ЕГЭ
Для выполнения экзаменационной работы-2020
ученику отведено 3 часа 55 минут
(235 минут).
В это время ученик не должен:
- вести себя шумно;
- использовать гаджеты и другие технические средства;
- списывать;
- пытаться помогать другим, или просить помощи для себя.
За подобные действия экзаменующегося могут выдворить из аудитории.
На государственный экзамен по математике разрешено приносить
с собой только линейку, остальные материалы вам выдадут непосредственно перед ЕГЭ. выдаются на месте.
Эффективная подготовка — это решение онлайн тестов по математике 2020. Выбирай и получай максимальный балл!
ЕГЭ по математике – одно из основных испытаний для выпускников школ, прежде чем, получить аттестат и поступить в высшее учебное заведение. Такой вариант контроля знаний применяется с целью оценки знаний по дисциплинам, полученным в процессе школьного обучения. Единый государственный экзамен проходит в форме тестирования, подготовка заданий для финального испытания осуществляется Рособрнадзором и другими уполномоченными органами в сфере образования. Проходной балл по математике зависит от индивидуальных требований ВУЗа, в который поступает
выпускник. Успешная сдача экзамена на высокую оценку – важный фактор успеха при поступлении.
Математика профильного уровня необходима для поступления в ВУЗы технической, экономической направленности. Основой экзаменационных заданий является базовый уровень, к нему добавлены более сложные задачи и примеры. Предполагаются краткие и развернутые ответы:
- Первые задания не требуют углубленных знаний – это проверка знаний базового уровня;
- Следующие 5 – сложнее, требуется средний и высокий уровень овладения предметом. Эти задания проверяются при помощи компьютера, поскольку ответ на них краткий.
Развернутые ответы требуются для последних семи заданий. Для проверки собирают группу экспертов. Главное, что, не смотря на сложность заданий, которые входят в профильный уровень, они полностью соответствуют школьной программе. Почему они могут вызвать сложность? Для успешного решения данных примеров и задач, требуются не только сухие знания, но и умение креативно подойти к решению, применить знания в нестандартной ситуации. Именно формулировка вызывает трудность.
Если ученик выбирает данный уровень, это подразумевает его желание в дальнейшем продолжить изучение точных наук в высшем учебном заведении. Выбор в пользу профильного экзамена говорит еще и о том, что уровень знаний ученика довольно высокий, другими словами – фундаментальная подготовка не нужна.
Процесс подготовки включает повторение основных разделов, решение задач повышенной сложности, которые требуют нестандартного, творческого подхода.
Способы подготовки
- Базовая подготовка осуществляется в школе, где ученик осваивает основы, иногда учитель проводит дополнительные факультативы для выпускников. Главная рекомендация – внимательно и тщательно осваивать все темы, особенно в выпускном классе.
- Самостоятельная работа: для этого требуется особая самодисциплина, воля и самоконтроль. Необходимо тщательно ознакомиться с
. Проблема в направлении – только специалист может грамотно направить будущего абитуриента в те темы, которым необходимо уделить внимание.
- Репетиторство: профессиональный специалист поможет эффективно и быстро решать сложные задания.
- Курсы и онлайн-обучение: современный и проверенный способ, который позволяет экономить время и деньги. Важное преимущество: можно проходить тестовые испытания в режиме онлайн, быстро получать ответы, тренироваться на разных заданиях.
«Решу ЕГЭ по математике профильного уровня» — это возможность подготовиться к экзамену и успешно сдать его.
Оценивание
двух частей
, включающих в себя 19 заданий
. Часть 1
Часть 2
3 часа 55 минут
(235 минут).
Ответы
Но можно сделать циркуль
Калькуляторы
на экзамене не используются
.
паспорт
), пропуск
и капиллярную или ! Разрешают брать
с собой воду
(в прозрачной бутылке) и еду
Экзаменационная работа состоит из двух частей
, включающих в себя 19 заданий
. Часть 1
содержит 8 заданий базового уровня сложности с кратким ответом. Часть 2
cодержит 4 задания повышенного уровня сложности с кратким ответом и 7 заданий высокого уровня сложности с развёрнутым ответом.
На выполнение экзаменационной работы по математике отводится 3 часа 55 минут
(235 минут).
Ответы
к заданиям 1–12 записываются в виде целого числа или конечной десятичной дроби
. Числа запишите в поля ответов в тексте работы, а затем перенесите в бланк ответов № 1, выданный на экзамене!
При выполнении работы Вы можете воспользоваться , выдаваемыми вместе с работой.
Разрешается использовать только линейку
, но можно сделать циркуль
своими руками. Запрещается использовать инструменты с нанесёнными на них справочными материалами. Калькуляторы
на экзамене не используются
.
На экзамене при себе надо иметь документ удостоверяющий личность (паспорт
), пропуск
и капиллярную или гелевую ручку с черными чернилами
! Разрешают брать
с собой воду
(в прозрачной бутылке) и еду
(фрукты, шоколадку, булочки, бутерброды), но могут попросить оставить в коридоре.
Не обольщайтесь, само собой я не решу за вас ЕГЭ, не пойду за вас на экзамен, не принесу вам волшебный эликсир «Всезнания» или «Ответы на ЕГЭ по математике». Нет, всего этого не будет. Но я могу решить для вас задачи из открытого банка заданий (далее — ОБЗ) — то есть провести вас по дорожке из того, что вы с большой вероятностью увидите на экзамене. Всё зависит от вас. В данном разделе моего сайта всегда можно будет увидеть видеоуроки, разборы задач из ОБЗ, рекомендации по решению разных задач, полезную литературу для самоподготовки.
Решу ли я за Вас ЕГЭ базового уровня и Решу ли я за Вас ЕГЭ профильного уровня
Тут совсем всё просто — наш экзамен разделён на два уровня. За базовый — вы получаете в итоге оценку и аттестат. То есть, для большинства, на этом «проблемы» с математикой заканчиваются. Если же, вы собираетесь идти в техническую сферу, либо подстраховаться «на всякий случай сдать математику профиль» — то Добро пожаловать в задачи повышенной и высокой сложности, охватывающие все области математики с 5 по 11 класс плюс смежные науки и примеры из жизни.
При этом, разделение материалов всегда происходит. Вы можете увидеть пометку «профиль» или «база», поэтому не запутаетесь в большом объёме информации.
Этот раздел — для обучающихся?
Во многом — да. Но бывает и полезно почитать материалы или посмотреть видеоуроки тем, кто интересуется математикой, молодым коллегам. Всегда будет интересно получить замечания, отзывы, критику на все предлагаемые материалы. Это позволит более точно и рационально распределить усилия в работе над данным проектом.
Как ориентироваться в разделе по ЕГЭ
Решу ЕГЭ — планируется, как большой раздел. Для легкого доступа к задачам пользуйтесь поиском по сайту. Можно ориентироваться в разделе «Категории», который находится в правой колонке сайта, там выбрать необходимую категорию задач. Плюс внизу этой страницы можно видеть актуальные материалы, которые добавлены недавно. Это позволит оставаться всегда в курсе обновлений материалов.