СДАМ ГИА:
РЕШУ ЕГЭ
Образовательный портал для подготовки к экзаменам
Математика профильного уровня
Математика профильного уровня
≡ Математика
Базовый уровень
Профильный уровень
Информатика
Русский язык
Английский язык
Немецкий язык
Французский язык
Испанский язык
Физика
Химия
Биология
География
Обществознание
Литература
История
Сайты, меню, вход, новости
СДАМ ГИАРЕШУ ЕГЭРЕШУ ОГЭРЕШУ ВПРРЕШУ ЦТ
Об экзамене
Каталог заданий
Варианты
Ученику
Учителю
Школа
Эксперту
Справочник
Карточки
Теория
Сказать спасибо
Вопрос — ответ
Чужой компьютер
Зарегистрироваться
Восстановить пароль
Войти через ВКонтакте
Играть в ЕГЭ-игрушку
Новости
10 марта
Как подготовиться к ЕГЭ и ОГЭ за 45 дней
6 марта
Изменения ВПР 2023
3 марта
Разместили утвержденное расписание ЕГЭ
27 января
Вариант экзамена блокадного Ленинграда
23 января
ДДОС-атака на Решу ЕГЭ. Шантаж.
6 января
Открываем новый сервис: «папки в избранном»
22 декабря
Открыли новый портал Решу Олимп. Для подготовки к перечневым олимпиадам!
4 ноября
Материалы для подготовки к итоговому сочинению 2022–2023
31 октября
Сертификаты для учителей о работе на Решу ЕГЭ, ОГЭ, ВПР
21 марта
Новый сервис: рисование
31 января
Внедрили тёмную тему!
НАШИ БОТЫ
Все новости
ЧУЖОЕ НЕ БРАТЬ!
Экзамер из Таганрога
10 апреля
Предприниматель Щеголихин скопировал сайт Решу ЕГЭ
Наша группа
Задания
Версия для печати и копирования в MS Word
Задания Д6 № 505378
Четырёхугольник ABCD вписан в окружность. Угол ABC равен 104°, угол CAD равен 66°. Найдите угол ABD. Ответ дайте в градусах.
Спрятать решение
Решение.
Вписанный угол равен половине дуги, на которую он опирается, значит
Ответ: 38.
Аналоги к заданию № 505378: 505399 Все
Спрятать решение
·
·
Сообщить об ошибке · Помощь
О проекте · Редакция · Правовая информация · О рекламе
© Гущин Д. Д., 2011—2023
- вход
- регистрация
- Главная
- Форум
- Треды
- Тред №505378
Дискуссия
22 декабря 2012, 03:20:33
80
+ 1,14 / 5
Слушатель
Карма: +432.32
Регистрация: 04.11.2010
Сообщений: 4,179
Читатели: 5
Компания Apple сделала заказ на дисплеи для своих продуктов у крупной российской компании «Монокристалл». ЗАО «Монокристалл» располагается в Ставрополе. Компания, которой принадлежит производство, является одним из лидеров мирового рынка электронных материалов, применяемых в высокотехнологичных решениях. Деятельность компании сосредоточена вокруг синтетического сапфира и паст для фотовольтаики.В перечень выпускаемой компанией продукции входят сапфировые пластины диаметром от 2 до 10 дюймов, основной областью применения которых является производство светоизлучающих диодов. Применяться эта технология может в любых устройствах с дисплеями.ЗАО «Монокристалл» принадлежит 24 % мирового рынка сапфировых пластин. Оценочная стоимость компании — один миллиард долларов. http://www.sdelanoun…/#comments
-
+1.14 / 5
- Главная
- Форум
- Треды
- Тред №505378
Шестнадцатеричный код цвета #505378 является средне темный оттенком синий. В модели цвета RGB #505378 составляет 31.37% красного, 32.55% зеленого и 47.06% синего. В цветовом пространстве HSL #505378 имеет оттенок 236° (градусов), 20% насыщенность и 39% светлости. Этот цвет имеет приблизительную длину волны в 467.03 nm.
Цветовые вариации
- Вывернутый
#afac87 - Насыщенный на 25%
#4b4f7d - Оттенки Серого
#646464 - Светлее на 25%
#646896 - Оригинал
#505378 - Темнее на 25%
#404260 - Web-цвет: blue
#0000ff / #00f - Оттенки Серого 25%
#545674 - HTML: darkslateblue
#483d8b
Именованные цвета
-
Близко Связаны
- Тёмно-лазурный
#08457e - Лазурно-синий
#2a52be - Джинсовый синий
#1560bd - Кобальт синий
#0047ab - Глубокий фиолетовый цвет
#423189
- Тёмно-лазурный
-
Косвенно Связаны
- Зелёное море
#2e8b57 - Голубой цвет
#00bfff - Тёмный жёлто-коричневый
#918151 - Медный
#b87333 - Шоколадный
#d2691e
- Зелёное море
-
Отдаленно Связаны
- Кремовый
#fffdd0 - Лайм
#ccff00 / #cf0 - Лимонно-кремовый
#fffacd - Кукурузный
#fbec5d - Жёлто-зелёный
#adff2f
- Кремовый
Цветовые схемы
Скачать:
-
Дополнение
- #797f49
-
Аналоги
- #3a678e
- #705276
-
Разделение
- #537850
- #886d40
-
Триада
- #3b8d75
- #855743
-
Квадрат
- #7e4a4b
- #797f49
- #17abb1
-
Троичная
- #7c4c61
- #797f49
- #3b8d75
#505378 линейный градиент до дополнительного #797f49
- #505378
- #595a71
- #61616a
- #686862
- #6e705a
- #747752
- #797f49
Монохроматические Цвета
- #414468
- #46496d
- #4b4e73
- #505378
- #55587d
- #5a5d83
- #606288
Тоны
- #505378
- #545675
- #585971
- #5b5b6e
- #5e5e6b
- #616167
- #646464
Оттенки
#505378 в Белый
- #505378
- #6c6d8d
- #8888a3
- #a5a5ba
- #c2c2d0
- #e0e0e7
- #ffffff / #fff
#505378 в Черный
- #505378
- #434563
- #37384f
- #2a2b3c
- #1f1f2a
- #131318
- #000000 / #000
Краски
Связанные краски
-
Behr
- ★ Deep Orchid 630D-7
#515276 ΔE = 0.638 / LRV ≈ 9.1% - Aurora Splendor PPU16-01
#585683 ΔE = 3.445 / LRV ≈ 10.4%
- ★ Deep Orchid 630D-7
-
Pantone / PMS
- ★ P 104-16 U
#4d547a ΔE = 1.017 / LRV ≈ 9.3% - 3581 U
#555877 ΔE = 2.658 / LRV ≈ 10.2%
- ★ P 104-16 U
-
General Paint
- ★ Graoupie / CLV 1170N
#53557b ΔE = 1.034 / LRV ≈ 9.8% - Chauffeur / CL 2447N
#5b557b ΔE = 2.909 / LRV ≈ 10.2%
- ★ Graoupie / CLV 1170N
-
Valspar Paint
- ★ Deep Ocean Floor R157A
#4b527b ΔE = 1.552 / LRV ≈ 9.0% - Puttin’ on the Ritz R169A
#4b5271 ΔE = 2.486 / LRV ≈ 8.7%
- ★ Deep Ocean Floor R157A
-
ISOMAT
- ★ IST 200-06
#545175 ΔE = 1.636 / LRV ≈ 9.1% - IST 198-06
#5f5178 ΔE = 4.702 / LRV ≈ 9.7%
- ★ IST 200-06
-
Earthpaint
- ★ 3-40-6 Purple Passion
#53537d ΔE = 1.853 / LRV ≈ 9.5% - 4-40-6 Phoenician Purple
#575775 ΔE = 2.770 / LRV ≈ 10.1%
- ★ 3-40-6 Purple Passion
-
ICI Paints
- ★ 4267 Xanadu 10RB 11/250
#545179 ΔE = 1.935 / LRV ≈ 9.1% - 4242 Marble Swirl 90BB 14/242
#555e85 ΔE = 4.446 / LRV ≈ 11.6%
- ★ 4267 Xanadu 10RB 11/250
-
CHROMATIC
- ★ 0580-Violet Grue — Dorval-CH2
#4b567e ΔE = 2.145 / LRV ≈ 9.7% - 0570-Violet Irene — Dorval-CH2
#5d537e ΔE = 4.181 / LRV ≈ 10.0%
- ★ 0580-Violet Grue — Dorval-CH2
-
Dutch Boy
- ★ Medieval Blue
#4d5575 ΔE = 2.253 / LRV ≈ 9.4% - Splendiforous
#505384 ΔE = 3.705 / LRV ≈ 9.6%
- ★ Medieval Blue
-
Matthews Paint
- Labatt Blue / 2750
#465178 ΔE = 2.367 / LRV ≈ 8.5% - Cenere Blue Met. / 22031
#4b516c ΔE = 3.631 / LRV ≈ 8.5%
- Labatt Blue / 2750
-
Olympic
- Imperial Purple B44-6
#4f4e77 ΔE = 2.400 / LRV ≈ 8.4% - Roman Violet B45-6
#49567e ΔE = 2.508 / LRV ≈ 9.6%
- Imperial Purple B44-6
-
Kelly-Moore
- Rare Orchid / KM3064-5
#524e72 ΔE = 2.434 / LRV ≈ 8.5% - Dark Triumph / KM3040-5
#564d78 ΔE = 4.018 / LRV ≈ 8.6%
- Rare Orchid / KM3064-5
-
Caparol
- Bolero 2
#585474 ΔE = 2.455 / LRV ≈ 9.7% - 38S 1 / Oxidschwarz 38S 1
#485470 ΔE = 4.134 / LRV ≈ 8.9%
- Bolero 2
-
Levis
- Kleur Van Het Jaar Ultiem Blauw
#465075 ΔE = 2.491 / LRV ≈ 8.3% - Full Lavender
#4f5571 ΔE = 3.072 / LRV ≈ 9.4%
- Kleur Van Het Jaar Ultiem Blauw
-
Cloverdale Paint
- Georgian Court / 7213
#4c517e ΔE = 2.547 / LRV ≈ 8.9% - Evening Magic / 7245
#405381 ΔE = 4.118 / LRV ≈ 8.9%
- Georgian Court / 7213
-
Nippon Paint
- Magnetism / NP AC 2091 A
#57527b ΔE = 2.559 / LRV ≈ 9.5% - Crown Jewel / NP PB 1484 A
#415185 ΔE = 5.077 / LRV ≈ 8.7%
- Magnetism / NP AC 2091 A
-
Tollens
- UC031 Violet Times Square
#50516e ΔE = 2.611 / LRV ≈ 8.7% - T2009-5
#545c7b ΔE = 4.052 / LRV ≈ 11.0%
- UC031 Violet Times Square
-
Dulux
- 90BB 09/186
#4f5471 ΔE = 2.631 / LRV ≈ 9.2% - 15RB 07/237
#4c4769 ΔE = 5.053 / LRV ≈ 7.1%
- 90BB 09/186
-
Crown Diamond
- 7352-73 Wild Blueberries
#4b4d76 ΔE = 2.673 / LRV ≈ 8.1% - 7351-73 Majestic Purple
#4b4e6b ΔE = 3.410 / LRV ≈ 8.0%
- 7352-73 Wild Blueberries
-
Opaltone / OMS
- 6421
#49527f ΔE = 2.682 / LRV ≈ 9.0% - 6420
#445983 ΔE = 4.363 / LRV ≈ 10.0%
- 6421
-
Taubmans
- Starry Night Blue / T12 40.G10
#47557e ΔE = 2.684 / LRV ≈ 9.3% - Inner Depth / T58-8
#5a5a77 ΔE = 3.822 / LRV ≈ 10.8%
- Starry Night Blue / T12 40.G10
-
Bristol
- Starry Night Blue / P108-C6
#47557e ΔE = 2.684 / LRV ≈ 9.3% - Midnight Navy / P108-C7
#4b4e6c ΔE = 3.169 / LRV ≈ 8.0%
- Starry Night Blue / P108-C6
-
Glidden
- Roman Violet / PPG1170-7
#4d517f ΔE = 2.823 / LRV ≈ 9.0% - Fresh Grape Juice / 10RB 10/219
#5e537a ΔE = 4.027 / LRV ≈ 10.0%
- Roman Violet / PPG1170-7
-
PPG Pittsburgh Paints
- Roman Violet / PPG1170-7
#4d517f ΔE = 2.823 / LRV ≈ 9.0% - Royal Hyacinth / PPG1169-7
#464b6a ΔE = 4.226 / LRV ≈ 7.4%
- Roman Violet / PPG1170-7
-
Porter Paints
- Roman Violet / 345-7
#4c517f ΔE = 2.830 / LRV ≈ 9.0% - Imperial Purple / 344-7
#534b77 ΔE = 4.377 / LRV ≈ 8.2%
- Roman Violet / 345-7
-
Asian Paints
- Nautical Mile / X142
#46517d ΔE = 2.847 / LRV ≈ 8.7% - Rare Orchid / 7197
#564d70 ΔE = 3.642 / LRV ≈ 8.5%
- Nautical Mile / X142
-
Auro
- Grape Hyacinth
#545a7c ΔE = 2.920 / LRV ≈ 10.7%
- Grape Hyacinth
-
Plascon
- Ocean Frigot B6-E1-4
#505884 ΔE = 2.967 / LRV ≈ 10.4% - Rocky Ridge B5-E1-4
#4c5c88 ΔE = 4.523 / LRV ≈ 11.0%
- Ocean Frigot B6-E1-4
-
Albany Paint
- Little Boy
#4a5880 ΔE = 2.994 / LRV ≈ 10.0% - Tollard Royal
#565585 ΔE = 3.918 / LRV ≈ 10.2%
- Little Boy
-
California Paints
- DE 5902 — Blue Review
#4e5878 ΔE = 3.007 / LRV ≈ 10.0% - DE 5951 — Exotic Evening
#58516e ΔE = 3.572 / LRV ≈ 9.1%
- DE 5902 — Blue Review
-
Craig & Rose
- Don Adriano
#47567a ΔE = 3.109 / LRV ≈ 9.4%
- Don Adriano
-
New Look
- Rock your Work / G38-08
#5a5881 ΔE = 3.199 / LRV ≈ 10.7% - Topsy Turvy / G38-03
#4d5c83 ΔE = 4.129 / LRV ≈ 10.9%
- Rock your Work / G38-08
-
1829
- Smalt
#46567b ΔE = 3.230 / LRV ≈ 9.4%
- Smalt
-
Evonik-Degussa
- 316
#464c72 ΔE = 3.231 / LRV ≈ 7.7% - 194A Soaring Blue
#464b6e ΔE = 3.688 / LRV ≈ 7.5%
- 316
-
Devoe Paint
- Inspired Violet / 90BB 09/186
#52536d ΔE = 3.355 / LRV ≈ 9.1% - Huckleberry / 70BB 10/275
#44567d ΔE = 3.533 / LRV ≈ 9.4%
- Inspired Violet / 90BB 09/186
-
Dunn-Edwards
- Intergalactic / 166
#4d516c ΔE = 3.384 / LRV ≈ 8.5% - Exotic Evening / 242
#58516e ΔE = 3.572 / LRV ≈ 9.1%
- Intergalactic / 166
-
GM / General Motors
- Baffin Bay Blue
#434d76 ΔE = 3.468 / LRV ≈ 7.8% - Bluestone
#40506e ΔE = 5.044 / LRV ≈ 8.0%
- Baffin Bay Blue
-
Ford
- Blue
#42517d ΔE = 3.472 / LRV ≈ 8.5% - Shadow Blue
#464c6a ΔE = 4.187 / LRV ≈ 7.5%
- Blue
-
Resene
- Night Moves B45-048-275
#444c73 ΔE = 3.493 / LRV ≈ 7.6% - East Bay B45-040-272
#47526e ΔE = 4.105 / LRV ≈ 8.5%
- Night Moves B45-048-275
-
Brillux
- 51.09.27
#51516b ΔE = 3.499 / LRV ≈ 8.7% - 57.09.27
#4e5770 ΔE = 4.487 / LRV ≈ 9.6%
- 51.09.27
-
Dulux Australia
- Majestic Magic / A404
#555670 ΔE = 3.517 / LRV ≈ 9.8% - Intense Purple / A415
#4c4a6f ΔE = 3.651 / LRV ≈ 7.6%
- Majestic Magic / A404
-
Colortrend
- 1250
#574e70 ΔE = 3.549 / LRV ≈ 8.6% - 1264
#555183 ΔE = 4.543 / LRV ≈ 9.5%
- 1250
-
Benjamin Moore
- Darkest Grape / 2069-30
#5c5a7c ΔE = 3.559 / LRV ≈ 11.0% - Bistro Blue / 1421
#53588a ΔE = 4.549 / LRV ≈ 10.7%
- Darkest Grape / 2069-30
-
Nerolac
- Greek God — 4275
#434f7c ΔE = 3.574 / LRV ≈ 8.2% - Blue Planet — 4239
#3d4e70 ΔE = 4.951 / LRV ≈ 7.6%
- Greek God — 4275
-
ProMarker
- Midnight Blue
#4f5a7a ΔE = 3.607 / LRV ≈ 10.4%
- Midnight Blue
-
Beckers
- Midnatt 772 / S 6615-R93B
#4d4a6e ΔE = 3.708 / LRV ≈ 7.6% - Petroleum 790 / S 6511-B10G
#4f5268 ΔE = 4.724 / LRV ≈ 8.7%
- Midnatt 772 / S 6615-R93B
-
Crown Paint
- Ballgown
#454d6c ΔE = 3.963 / LRV ≈ 7.7% - Prom Night
#4c4767 ΔE = 5.236 / LRV ≈ 7.0%
- Ballgown
-
Abet Laminati
- Bleu Esperia 496
#415381 ΔE = 3.966 / LRV ≈ 8.9%
- Bleu Esperia 496
-
KILZ
- Deep Velvet / B711
#4f5873 ΔE = 4.038 / LRV ≈ 9.9%
- Deep Velvet / B711
-
Ralph Lauren
- Beach Purple / RLIB225
#504c7a ΔE = 4.079 / LRV ≈ 8.3%
- Beach Purple / RLIB225
-
Clark+Kensington
- Good Night / 40B-7
#4b4d68 ΔE = 4.117 / LRV ≈ 7.8% - Eggplant / 41C-7
#524869 ΔE = 5.226 / LRV ≈ 7.4%
- Good Night / 40B-7
-
Wattyl
- Night Goddess / D83W
#4d5c83 ΔE = 4.129 / LRV ≈ 10.9% - Syrah / D73W
#4d4b65 ΔE = 4.820 / LRV ≈ 7.5%
- Night Goddess / D83W
-
Sto
- 34200
#5a526d ΔE = 4.222 / LRV ≈ 9.3% - 34440
#4a5b7d ΔE = 4.488 / LRV ≈ 10.4%
- 34200
-
Brighto Paints
- 4-40-6 Phoenician Purple
#5a5d7d ΔE = 4.290 / LRV ≈ 11.5% - 4-41-6 Tempest
#5f5c7b ΔE = 4.653 / LRV ≈ 11.5%
- 4-40-6 Phoenician Purple
-
Peintures MF
- CD339-5
#444c7b ΔE = 4.327 / LRV ≈ 7.8% - Indigo
#5c5484 ΔE = 4.849 / LRV ≈ 10.3%
- CD339-5
-
Sigma
- Mistic Purple / S 6020-R60B
#555870 ΔE = 4.352 / LRV ≈ 10.1% - Mistic Purple / S 5040-R70B
#3d4c7b ΔE = 5.044 / LRV ≈ 7.6%
- Mistic Purple / S 6020-R60B
-
Diamond Vogel
- Voldemort / 1257
#584c71 ΔE = 4.407 / LRV ≈ 8.4% - Quiet Peace / 0592
#49536b ΔE = 4.970 / LRV ≈ 8.7%
- Voldemort / 1257
-
ECOS Paints
- Voldemort (1257)
#584c71 ΔE = 4.407 / LRV ≈ 8.4% - Quiet Peace (0592)
#49536b ΔE = 4.970 / LRV ≈ 8.7%
- Voldemort (1257)
-
Graham & Brown
- Water Street
#4e5d84 ΔE = 4.435 / LRV ≈ 11.1%
- Water Street
-
Toyo Ink
- CF10950
#46496a ΔE = 4.519 / LRV ≈ 7.1%
- CF10950
-
Sikkens
- U6.31.25
#3f557a ΔE = 4.569 / LRV ≈ 9.0% - U6.27.18
#48546d ΔE = 4.995 / LRV ≈ 8.8%
- U6.31.25
-
Vallejo Game Color
- Sombre Grey (048)
#4e5067 ΔE = 4.584 / LRV ≈ 8.3% - Heavy Violet (142)
#4f566c ΔE = 5.046 / LRV ≈ 9.4%
- Sombre Grey (048)
-
Vallejo Model Color
- Oxford Blue (807)
#4e5067 ΔE = 4.584 / LRV ≈ 8.3% - Violet (960)
#4f566c ΔE = 5.046 / LRV ≈ 9.4%
- Oxford Blue (807)
-
Reaper Master
- Twilight Blue (9020)
#4e5067 ΔE = 4.584 / LRV ≈ 8.3% - Nightshade Purple (9022)
#4f566c ΔE = 5.046 / LRV ≈ 9.4%
- Twilight Blue (9020)
-
Old Citadel
- Shadow Grey
#4e5067 ΔE = 4.584 / LRV ≈ 8.3% - Hormagaunt Purple
#4f566c ΔE = 5.046 / LRV ≈ 9.4%
- Shadow Grey
-
TRUMATCH
- 37-a7
#3d5281 ΔE = 4.639 / LRV ≈ 8.6% - 36-c6
#455488 ΔE = 4.843 / LRV ≈ 9.4%
- 37-a7
-
Pratt & Lambert
- Noblesse 29-15
#4a4e81 ΔE = 4.643 / LRV ≈ 8.5% - Oriental Night 29-14
#5c5687 ΔE = 5.058 / LRV ≈ 10.7%
- Noblesse 29-15
-
JPMA
- E 77-40L
#535e88 ΔE = 4.693 / LRV ≈ 11.6%
- E 77-40L
-
Coronado Paint
- 7197 — Rare Orchid
#4b4967 ΔE = 4.700 / LRV ≈ 7.2% - 7165 — Dark Triumph
#4c4769 ΔE = 5.053 / LRV ≈ 7.1%
- 7197 — Rare Orchid
-
Chrysler
- Rhapsody Blue
#425473 ΔE = 4.744 / LRV ≈ 8.7% - Erie Blue
#455876 ΔE = 5.203 / LRV ≈ 9.6%
- Rhapsody Blue
-
Nature Paint
- Beast
#43597e ΔE = 4.744 / LRV ≈ 9.8%
- Beast
-
Natural Color System / NCS
- S 5020-R60B
#5b506c ΔE = 4.749 / LRV ≈ 9.0% - S 4030-R80B
#4c5e89 ΔE = 5.178 / LRV ≈ 11.3%
- S 5020-R60B
-
Farrow & Ball
- Pitch Blue / 220
#535e7e ΔE = 4.791 / LRV ≈ 11.4%
- Pitch Blue / 220
-
Disney
- 3B-10 Warp Speed Blue
#475589 ΔE = 4.804 / LRV ≈ 9.6%
- 3B-10 Warp Speed Blue
-
Vallejo
- Vallejo 70.962 #56
#3b4d77 ΔE = 4.835 / LRV ≈ 7.6%
- Vallejo 70.962 #56
-
Sico
- 6048-73 Easter Choir
#625a79 ΔE = 4.998 / LRV ≈ 11.3%
- 6048-73 Easter Choir
-
CIL
- Victorian Violet
#4f588c ΔE = 5.002 / LRV ≈ 10.5% - Fashion Passion
#625475 ΔE = 5.145 / LRV ≈ 10.2%
- Victorian Violet
-
Sherwin-Williams
- Fully Purple — 6983
#514c7e ΔE = 5.066 / LRV ≈ 8.4%
- Fully Purple — 6983
-
RAL
- RAL 280 40 25
#4c5e87 ΔE = 5.078 / LRV ≈ 11.3% - RAL 280 40 20
#4f5e7e ΔE = 5.206 / LRV ≈ 11.2%
- RAL 280 40 25
-
Focoltone
- 5037
#63577f ΔE = 5.124 / LRV ≈ 11.0%
- 5037
-
Model Master
- Model Master 2950
#635578 ΔE = 5.187 / LRV ≈ 10.5%
- Model Master 2950
-
Volkswagen
- Titan Gray
#52576c ΔE = 5.199 / LRV ≈ 9.7%
- Titan Gray
-
Magnolia Home
- Silos District / JG-92
#42526e ΔE = 5.212 / LRV ≈ 8.3%
- Silos District / JG-92
-
British Standard
- BS381 110 — Roundel blue
#3d4971 ΔE = 5.235 / LRV ≈ 6.9%
- BS381 110 — Roundel blue
Дальтонизм
Monochromacy
- Ахроматопсия
#565656 - Achromatomaly
#535566
Дихроматическое зрение
- Протанопия
#51516f - дейтеранопия
#51516d - Тританопия
#506866
Trichromacy
- Protanomaly
#555273 - Deuteranomaly
#515273 - Tritanomaly
#505d71
#505378 HTML и CSS Примеры
#505378 передний план
В каждой шутке есть доля правды.
<p style="color: #505378">…</p>#505378 фон
Вы́ше головы́ не пры́гнешь.
<p style="background-color: #505378">…</p>#505378 тень текста
Своя́ руба́шка бли́же к те́лу.
<p style="text-shadow: 0.1em 0.1em 0.15em #505378">…</p>Чарт Композиций
-
RGB
-
CMYK
-
RYB
Цветовые пространства
- Десятичный
- 5264248
- Двоичный
- 01010000, 01010011, 01111000
- Шестнадцатеричный
- #505378
- LRV
- ≈ 9.2%
- Ближайший короткий шестигранник
- #557 ΔE = 1.530
- RGB
- rgb(80, 83, 120)
- RGBA
- rgba(80, 83, 120, 1.0)
- Цветность rg
- r: 0.283, g: 0.293, b: 0.424
- RYB
- красный: 31.373%, желтый: 32.467%, синий: 47.059%
- Android / android.graphics.Color
- -11512968 / 0xff505378
- HSL
- hsl(236, 20%, 39%)
- HSLA
- hsla(236, 20%, 39%, 1.0)
- HSV / HSB
- оттенок: 236° (235.500), насыщение: 33% (0.333), стоимость: 47% (0.471)
- HSP
- оттенок: 235.500, насыщение: 33.333%, воспринимаемая яркость: 34.185%
- HSLuv (HUSL)
- H: 263.385, S: 25.029, L: 36.457
- Cubehelix
- H: -126.757, S: 0.303, L: 0.338
- TSL
- T: -2.768, S: 0.087, L: 0.339
- CMYK
- голубой: 33% (0.333), пурпурный: 31% (0.308), желтый: 0% (0.000), чёрный: 53% (0.529)
- CMY
- голубой: 69% (0.686), пурпурный: 67% (0.675), желтый: 53% (0.529)
- XYZ
- X: 9.791, Y: 9.248, Z: 19.035
- xyY
- x: 0.257, y: 0.243, Y: 9.248
- CIELab
- L: 36.457, a: 8.277, b: -21.387
- CIELuv
- L: 36.457, u: -3.492, v: -30.116
- CIELCH / LCHab
- L: 36.457, C: 22.933, H: 291.157
- CIELUV / LCHuv
- L: 36.457, C: 30.318, H: 263.385
- Hunter-Lab
- L: 30.410, a: 4.252, b: -15.825
- CIECAM02
- J: 26.965, C: 27.125, h: 272.516, Q: 102.308, M: 23.720, s: 48.151, H: 317.811
- OSA-UCS
- расторопность: -10.262, желтый: -3.796, зеленый: -0.162
- LMS
- L: 8.056, M: 8.925, S: 18.874
- YCbCr
- Y: 90.152, Cb: 144.687, Cr: 124.056
- YCoCg
- Y: 91.500, Cg: -8.500, Co: 10.000
- YDbDr
- Y: 86.321, Db: 50.671, Dr: 12.028
- YPbPr
- Y: 85.025, Pb: 18.845, Pr: -3.202
- xvYCC
- Y: 89.021, Cb: 144.554, Cr: 125.187
- YIQ
- Y: 86.321, I: -13.674, Q: 10.878
- YUV
- Y: 86.321, U: 16.574, V: -5.545
- Цветовая Система Манселл
- 7.5PB 3/6 ΔE = 4.075
- Цвет бренда
- Facebook ΔE = 6.619
Случайные цвета
- #092688
- #159ab6
- #fba44e
- #01813e
- #4c7c2a
Красный
- #a15532
- #6a1711
- #c4907c
- #d15c35
- #ac4e4c
Зеленый
- #42591b
- #597036
- #2a531c
- #25651e
- #5d9b1b
Синий
- #7c90bc
- #6b8ad5
- #2f4475
- #b0b8e4
- #99a5c6
За это задание ты можешь получить 3 балла. На решение дается около 20 минут. Уровень сложности: повышенный.
Средний процент выполнения: 5.6%
Ответом к заданию 13 по математике (профильной) может быть развернутый ответ (полная запись решения с обоснованием выполненных действий).
Что нужно знать, чтобы решить задание 13:
В задании требуется решить уравнение одного из видов: тригонометрическое, рациональное, показательное, логарифмическое, уравнение с радикалом или смешанное уравнение, которое может содержать в себе несколько видов, например, логарифмы и тригонометрию. После решения уравнения, часто необходимо отобрать корни, которые принадлежат определенному промежутку.
Разбор сложных заданий в тг-канале
Задачи для практики
Задача 1
Дан куб $ABCDA_1B_1C_1D_1$. На ребре $AA_1$ отмечена точка $M$, причём $AM:MA_1=1:1$, на ребре $BB_1$ отмечена точка $N$,
причём $BN:NB_1=1:2$, на ребре $CC_1$ отмечена точка $K$, причём $CK:KC_1=1:3$.
а) В каком отношении, считая от точки $D$, плоскость $MNK$ делит ребро $DD_1$?
б) Найдите величину угла между плоскостями $MNK$ и $ABC$.
Решение
а) Пусть ребро куба равно $1$. Противоположные грани куба параллельны, поэтому плоскость $MNK$ пересекает их по параллельным отрезкам. Сечением куба плоскостью $MNK$ является параллелограмм $MNKF$, где $F$ — точка пересечения ребра $DD_1$ с плоскостью $MNK$. Рассмотрим проекцию куба на грань $CC_1D_1D$. $DM_1=AM$, $CN_1=BN$. Отрезки $M_1N_1$ и $FK$ параллельны, поэтому $N_1K={1} / {3}-{1} / {4}={1} / {12}$, и $FD=M_1D-M_1F={1} / {2}-{1} / {12}={5} / {12}$, значит, $DF:FD_1=5:7$. б) Прямая $FK$ пересекает плоскость основания куба в точке $L$, прямая $NK$ пересекает плоскость основания куба в точке $T$, поэтому плоскость $MNK$ пересекает плоскость $ABC$ по прямой $TL$. В прямоугольном треугольнике $CLT$ отрезок $CH$ — высота, по теореме о трёх перпендикулярах $KH⊥ TL$, поэтому линейный угол $CHK$ является углом между плоскостями $MNK$ и $ABC$. Треугольники $CLK$ и $DLF$ подобны, $CK={1} / {4}$, $FD={5} / {12}$, $DL=1+CL$, тогда из пропорции ${1} / {4}:{5} / {12}=CL:(1+CL)$, получим $CL={3} / {2}$. Аналогично из подобия треугольников $CTK$ и $BTN$ найдём $CT=3$. В прямоугольном треугольнике $CLT$ гипотенуза $LT$ вычисляется по теореме Пифагора:$LT={3√ 5} / {2}$, а высота $CH={CL⋅ CT} / {LT}={3} / {√ 5}$. В прямоугольном треугольнике $CHK$ вычисляем
$tg∠ CHK={CK} / {CH}={1} / {4}:{3} / {√ 5}={√ 5} / {12}$, значит, $∠ CHK=arctg{√ 5} / {12}$.
Ответ: begin{tabular}{c}а)$5:7$\б)$arctgfsm{sqrt5}{12}$end{tabular
Задача 2
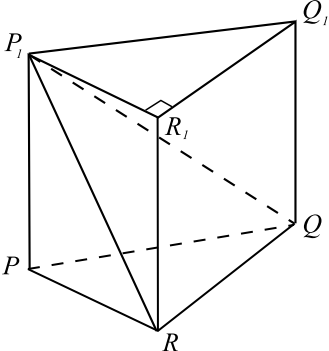
Основанием прямой треугольной призмы $PQRP_1Q_1R_1$ является прямоугольный треугольник $PQR$ с прямым углом $R$. Диагонали боковых граней $PP_1Q_1Q$ и $PP_1R_1R$ равны $17$ и $15$ соответственно, $PQ = 10$.
а) Докажите, что треугольник $P_1QR$ прямоугольный.
б) Найдите объём пирамиды $P_1QRR_1$.
Решение
По условию задачи сделаем чертёж.
а) Прямая $QR$ перпендикулярна плоскости $PP_1R_1R$, поскольку она перпендикулярна прямым $PR$ и $RR_1$. Значит, прямые $QR$ и $RP_1$ перпендикулярны, следовательно, в $△P_1QR$
$∠P_1RQ = 90°$.
б) Пусть $V$ — объём призмы $PQRP_1Q_1R_1$. Тогда объём треугольной пирамиды $PP_1QR$ равен ${V}/{3}$, поскольку её высота $PP_1$ и основание $PQR$ совпадают с высотой и основанием призмы соответственно. Аналогично, объём треугольной пирамиды $P_1Q_1R_1Q$ равен ${V}/{3}$. Призма $PQRP_1Q_1R_1$ составлена из трёх пирамид: $PP_1QR, P_1Q_1R_1Q$ и $P_1QRR_1$. Значит, объём пирамиды $P_1QRR_1$ равен ${V}/{3}$.
В призме $PQRP_1Q_1R_1 : QQ_1 = √{P_1Q^2 — P_1Q_1^2} = 3√21, QR = √{P_1Q^2 — P_1R^2} = 8, PR = √{PQ^2 — QR^2} = 6, V = PP_1 · {PR · QR}/{2} = 72√21$.
Таким образом, объём пирамиды $P_1QRR_1$ равен $24√21$.
Ответ: 24sqrt{21}
Задача 3
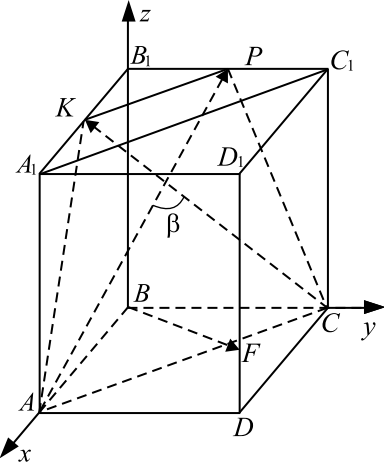
В правильной четырёхугольной пирамиде $SABCD$ боковое ребро $SA=12$, а высота равна $4$. На рёбрах $AB$, $CD$ и $AS$ отмечены точки $E$, $F$ и $K$ соответственно, причём $BE=CF=12$, $AK=3$.
а) Докажите, что плоскости $SBC$ и $KEF$ параллельны.
б) Найдите объём пирамиды $KSBC$.
Решение
а) Докажем, что плоскости $SBC$ и $KEF$ параллельны.
Введём прямоугольную систему координат, учитывая, что в основании правильной пирамиды квадрат $ABCD$ и угол между диагоналями квадрата прямой .
1. Найдём координаты точек $S, B, C , K , E, F$. В прямоугольном треугольнике $SOA$ по теореме Пифагора $OA^2 = SA^2 — SO^2, OA = √{12^2 — 4^2} = 8√2. OC = OB = OD = OA = 8√2$, тогда сторона квадрата $AB = {OA}/{sin 45°} = {8√2}/{{1}/{√2}} = 16, AE = AB — BE = 16 — 12 = 4$.
Проведём $KN ‖ SO, SO ⊥ (ABC)$, тогда $KN ⊥ (ABC)$ и $KN ⊥ OA, △SAO ∼ △KAN$ по первому признаку подобия $(∠SOA = ∠KNA = 90°, ∠A$ — общий) ${AS}/{AK} = {SO}/{KN}, {12}/{3} = {4}/{KN}, KN = 1$.
В прямоугольном треугольнике $ANK$ по теореме Пифагора $AN^2 = AK^2 — KN^2, AN = √{3^2 — 1^2} = 2√2$, тогда $ON = OA — AN = 8√2 — 2√2 = 6√2. EN$ — проекция $KE$ на плоскость $ABC$, значит $△ANE$ прямоугольный и равнобедренный $EN = AN = 2√2$.
Получим $S(0; 0; 4), B(0; -8√2; 0), C (-8√2; 0; 0), K (6√2; 0; 1), E(6√2; -2√2; 0), F (-2√2; 6√2; 0)$.
2. Докажем, что векторы нормали к плоскостям $SBC$ и $KEF$ коллинеарны. Для плоскости $SBC$, вектор нормали ${n_1}↖{→}(a_1; b_1; c_1)$ перпендикулярен к обеим прямым $SB$ и $SC$, поэтому он должен быть перпендикулярен к векторам ${SB}↖{→}(0; -8√2; -4)$ и ${SC}↖{→}(-8√2; 0; -4)$.
Получим систему ${table {n_1}↖{→} · {SB}↖{→} = 0; {n_1}↖{→} ·{SC}↖{→} = 0;$ ${table · a_1 — 8√2 · b_1 — 4c_1 = 0; -8√2a_1 + 0 · b_1 — 4 · c_1 = 0;$ ${table-2√2b_1 — c_1 = 0; -2√2a_1 — c_1 = 0;$
Пусть $c_1 = -1$, тогда система примет вид ${table-2√2b_1 + 1 = 0; -2√2a_1 + 1 = 0;$
Её решение $a_1 = {√2}/{4}; b_1 = {√2}/{4}$.
${n_1}↖{→}({√2}/{4}; {√2}/{4}; -1)$ — вектор нормали плоскости $SBC$ .
Для плоскости $KEF$, вектор нормали ${n_2}↖{→}(a_2; b_2; c_2)$ перпендикулярен к обеим прямым $KE$ и $KF$, поэтому он должен быть перпендикулярен к векторам ${KE}↖{→}(0; -2√2; -1)$ и ${KF}↖{→}(-8√2; 6√2; -1)$.
Получим систему ${table {n_2}↖{→} · {KE}↖{→} = 0; {n_2}↖{→} · {KF}↖{→} = 0;$ ${table · a_2 — 2√2 · b_2 — 1 · c_2 = 0; -8√2a_2 + 6√2 · b_2 — 1 · c_2 = 0;$ ${table-2√2b_2 — c_2 = 0; -8√2a_2 + 6√2b_2 — c_2 = 0$.
Пусть $c_2 = -1$, тогда система примет вид ${table-2√2b_2 + 1 = 0; 8√2a_2 + 6√2b_2 + 1 = 0;$
Её решение $a_2 = {√2}/{4}; b_2 = {√2}/{4}$.${n_2}↖{→}({√2}/{4}; {√2}/{4}; -1)$ — вектор нормали плоскости $KEF$.
Векторы ${n_1}↖{→}$ и ${n_2}↖{→}$ равны, значит коллинеарны, следовательно плоскости $SBC$ и $KEF$ параллельны.
б) Искомый объём $V = {1}/{3}S · h$, где $S$ — площадь треугольника $SBC$, а высота пирамиды $h$ — это расстояние от точки $K$ до плоскости $SBC$.
1. $S = {1}/{2}SB · SC · sin α$, где $α$ — угол между прямыми $SB$ и $SC$. $cos α ={{SB}↖{→} · {SC}↖{→}}/{|{SB}↖{→}| · |{SC}↖{→}|} = {0 · (-8√2) + (-8√2) · 0 + (-4)(-4)}/{12 · 12} = {16}/{144} = {1}/{9}$.
$sin α = √{1 — cos^2α} = √{1 — {1}/{81}} = {4√5}/{9} · S = {1}/{2} · 12 · 12 · {4√5}/{9} = 32√5$.
2. Чтобы найти $h$ необходимо найти уравнение плоскости $SBC$. Оно имеет вид $ax + by + cz + d = 0$, где ${n}↖{→}(a; b; c)$ — вектор нормали этой плоскости. Согласно пункту а), один из векторов нормали ${n_1}↖{→}({√2}/{4}; {√2}/{4}; -1)$. Значит, уравнение имеет вид ${√2}/{4}x + {√2}/{4}y — z + d = 0$. Чтобы найти значение $d$ подставим координаты точки $S(0; 0; 4)$ в это уравнение, получим $-4 + d = 0, d = 4$, тогда ${√2}/{4}x + {√2}/{4}y — z + 4 = 0$ — уравнение плоскости $SBC$. Расстояние от точки $K(6√2; 0; 1)$ до плоскости $SBC$
$h = {|ax_0+ by_0 + z_0 + d|}/{√{a_2 + b_2 + z_2}} ={|{√2}/{4} · 6√2 + {√2}/{4} · 0 + (-1) · 1 + 4|}/{√{({√2}/{4})^2 + ({√2}/{4})^2 + (-1)^2}} = {12√5}/{5}$, где $x_0, y_0, z_0$ — координаты точки $K$.
3. $V = {1}/{3} · 32√5 · {12√5}/{5} = 128$.
Ответ: 128
Задача 4
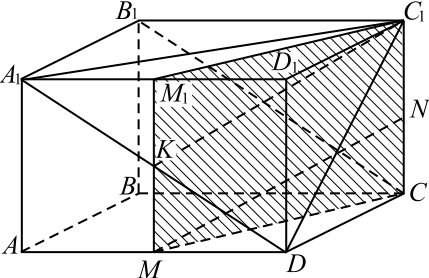
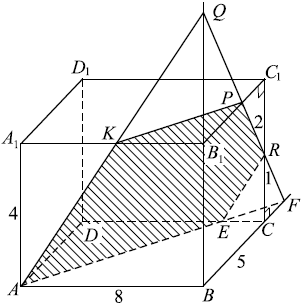
В правильной четырёхугольной призме $ABCDA_1B_1C_1D_1$ сторона основания $AB=8√ {2}$, а боковое ребро $AA_1=16$. Точка $K$ — середина ребра $A_1B_1$. На ребре $DD_1$ отмечена точка $F$ так, что $DF=4$. Плоскость $α$ параллельна прямой $A_1C_1$ и содержит точки $K$ и $A$.
а) Докажите, что прямая $BF$ перпендикулярна плоскости $α$.
б) Найдите объём пирамиды, вершина которой точка $B$, а основание — сечение данной призмы плоскостью $α$.
Решение
1. Построим сечение призмы плоскостью $α$.
Грани $ABCD$ и $A_1 B_1 C_1 D_1$ параллельны, значит плоскость α пересекает их по параллельным прямым.
По условию плоскость α параллельна прямой $A_1 C_1$, то есть содержит прямую, параллельную $A_1 C_1$. Поэтому, проведя через точку $K$ прямую $KP (P ∈ B_1 C_1)$, параллельную прямой $A_1 C_1$, и через точку $A$ — прямую $AC$, параллельную прямой $A_1 C_1$ (прямая $AC$ содержит диагональ нижнего основания) получим трапецию $AKPC$ — искомое сечение.
2. Выберем прямоугольную систему координат, как показано на рисунке. Найдём координаты нужных точек: $B(0; 0; 0), F (8√2; 8√2; 4), A(8√2; 0; 0), C (0; 8√2; 0), K (4√2; 0; 16), P (0; 4√2; 16)$.
3. Рассмотрим векторы ${BF}↖{→} (8√2; 8√2; 4), {AP}↖{→} (-8√2; 4√2; 16)$ и ${CK}↖{→} (4√2; -8√2; 16)$.
Так как ${BF}↖{→}· {AP}↖{→} = 8√2(-8√2) + 8√2 · 4√2 + 16 · 4 = 0$, то ${BF}↖{→} ⊥ {AP}↖{→}$.
Так как ${BF}↖{→} · {CK}↖{→} = 8√2 · 4√2 + 8√2 · (-8√2) + 4 · 16 = 0$, то ${BF}↖{→} ⊥ {CK}↖{→}$.
Отсюда следует, что $BF ⊥ α$ по признаку перпендикулярности прямой и плоскости ($BF$ перпендикулярна двум пересекающимся прямым плоскости).
б) Искомый объём $V = {1}/{3}S · h$, где $S$ — площадь четырёхугольника $AKPC$, а высота $h$ — расстояние от точки $B$ до плоскости $α$.
1. $S_{AKPC} = {1}/{2}AP · CK sin β$, где $β$ — угол между диагоналями $AP$ и $CK$ четырёхугольника $AKPC$.
$cos β = {{AP}↖{→} · {CK}↖{→}}/{|{AP}↖{→}| · |{CK}↖{→}|} = {-8√2 · 4√2 + 4√2(-8√2) + 16 · 16}/{√{(-8√2)^2 + (4√2)^2 + 16^2} · √{(4√2)^2 + (-8√2)^2 + 16^2}} = {-64 — 64 + 256}/{416} = {128}/{416} = {4}/{13}; |{AP}↖{→}| = |{CK}↖{→}| = √{416}$.
$sin β = √{1 — cos^2β} = √{1 — {16}/{169}} = {3√17}/{13}$.
Таким образом $S = {1}/{2} · √{416} · √{416} · {3√17}/{13} = 48√{17}$.
2. Чтобы найти $h$ необходимо найти уравнение плоскости $α$. Оно имеет вид $ax + by + cz + d = 0$, где ${n}↖{→}(a; b; c)$ — вектор нормали этой плоскости.
Согласно пункту а) одним из векторов нормали является вектор ${BF}↖{→}(8√2; 8√2; 4)$.
Значит, уравнение плоскости имеет вид $8√2x + 8√2y + 4z + d = 0 (1)$.
Чтобы найти значение $d$ подставим координаты точки $A(8√2; 0; 0)$ в уравнение (1) и получим $8√2 · 8√2 + d = 0, d = -128$.
Уравнение плоскости $α$ примет вид $8√2x + 8√2y + 4z — 128 = 0$.
Найдём расстояние $h$ от точки $B(0; 0; 0)$ до плоскости сечения.
$h = {|ax_0+ by_0 + cz_0 + d|}/{√{a^2 + b^2 + c^2}} = {|8√2 · 0 + 8√2 · 0 + 4 · 0 — 128|}/{√{(8√2)^2 + (8√2)^2 + 16}} = {32}/{√17}$, где ($x_0 ; y_0 ; z_0$ ) — координаты точки $B$.
$V = {1}/{3} · S · h = {1}/{3} · 48√{17} · {32}/{√17} = 512$.
Ответ: 512
Задача 5
В прямоугольном параллелепипеде $ABCDA_{1}B_{1}C_{1}D_{1}$ сторона $AB=AA_{1}=3$, $AD=6$. На рёбрах $AD$ и $CC_{1}$ взяты соответственно точки $M$ и $N$ — середины этих рёбер.
а) Постройте сечение параллелепипеда плоскостью, проходящей через вершину $D$, параллельно $MN$ и $B_{1}C$.
б) Найдите объём пирамиды, основание которой — построенное сечение, а вершина — точка $D_{1}$.
Решение
а) Искомое сечение проходит через вершину $D$ параллельно $B_1 C$, следовательно, пересекает грань $AA_1 D_1 D$ по диагонали $A_1 D$
Действительно, $A_1 D||B_1 C$ (плоскость пересекает две параллельные плоскости по параллельным прямым)
Рассмотрим прямоугольник $C C_1 M_1M$, где $M_1$ середина $A_1 D_1$
Проведём $C_1 K ||M N$. $K$ — середина отрезка $M M_1$ и середина отрезка $A_1 D$, значит, принадлежит искомому сечению, поэтому $C_1 K$ лежит в плоскости сечения
Таким образом, $A_1 C_1 D$ — искомое сечение.
б) Рассмотрим пирамиду $D_1A_1C_1D$ как пирамиду с основанием $D_1DC_1$ и высотой $A_1D_1 (A_1D_1 ⊥ D_1DC_1)$.
$V_{D_1A_1C_1D} = {1}/{3}S_{D_1DC_1} ·A_1D_1 = {1}/{3} · {1}/{2}D_1C_1 ·D_1D ·A_1D_1 = {1}/{6} ·3·3·6 = 9$.
Ответ: 9
Задача 6
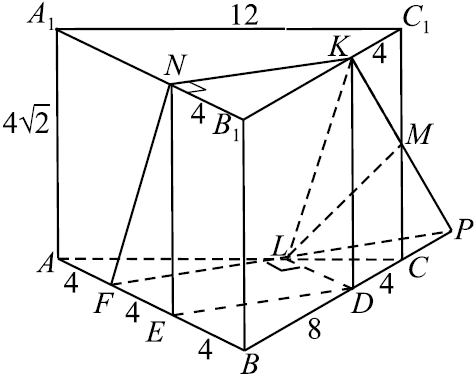
В правильной треугольной призме $ABCA_1 B_1 C_1$ сторона основания равна $12$, а боковое ребро равно $4√ {2}$. На рёбрах $AB$, $A_1 B_1$ и $B_1 C_1$ отмечены точки $F$, $N$ и $K$ соответственно, причём $AF=B_1 N=C_1 K =4$.
а) Пусть $L$ — точка пересечения плоскости $FNK$ с ребром $AC$. Докажите, что $FNKL$ — ромб.
б) Найдите площадь сечения призмы плоскостью $FNK$.
Решение
а) Докажем, что $FNKL$ — ромб.
1) Так как точка $L$ — точка пересечения плоскости $FNK$ с ребром $AC$, то (по свойству параллельных плоскостей) линии пересечения плоскости $FNK$ с основанием призмы параллельны, т.е $FL ‖ N K$.
2) В основаниях правильной треугольной призмы лежат правильные треугольники со стороной $12$.
В треугольнике $NB_1K$ $∠B1 = 60°, NB_1 = 4$ по условию, а $B_1 K = 12 — 4 = 8$. По теореме косинусов $N K = 4√3$, поэтому $N K^2 + NB_1^2 = KB_1^2$. Отсюда следует, что $∠N = 90°, ∠K = 30°$.
Значит, $N K ⊥ A_1B_1$ и $F L ⊥ AB$, т.к. $N K ‖ F L$, а $A_1B_1 ‖ AB$.
3) В $△AFL$ $∠A = 60°, ∠F = 90°, AF = 4$;
$AF$ в прямоугольном $△AFL$ лежит против $∠L = 30°$, следовательно, $AF = {1}/{2}AL, AL = AF · 2 = 4 · 2 = 8$;
$FL^2 = AL^2 — AF^2 = 8^2 — 4^2 = 64 — 16 = 48, F L = 4√3$.
Имеем $N K ‖ F L$ и $N K = F L$, следовательно $F N K L$ — параллелограмм.
Проведём $N E ⊥ F B$.
В $△NFE$ $∠E = 90°, N E = 4√2, F E = 12 — 8 = 4$.
$FN^2 = NE^2 + FE^2 = (4√2)^2 + 4^2 = 32 + 16 = 48$,
$FN = √48 = 4√3, KL = FN$ как противоположные стороны параллелограмма.
4) Имеем: $N K = K L = F N = F L$, следовательно, $F N K L$ — ромб.
б) $K N ⊥ A_1B_1 , K N ⊥ N E ⇒ K N ⊥ (AA_1B_1)$ и $K N ⊥ F N$, значит $K N F L$ — квадрат, $S_{KNFL} = FN^2 = 48$.
Построим сечение пирамиды плоскостью $FNK$ .
Продлим $FL$ до пересечения с $BC$, получим точку $P$.
Соединим точку $P$ с точкой $K$, $KP$ пересекает $CC_1$ в точке $M$. Соединим точку $M$ с точкой $L$.
Пятиугольник $F N K M L$ — искомое сечение.
В прямоугольном $△FBP$ $∠B = 60°$, значит $BP = 2FB = 16, PC = 16 — 12 = 4$.
$KC_1 = CP, ∠KC_1M = ∠MCP = 90°$, тогда $△KC_1M = △PCM$ и $C_1M = CM = 2√2. KM = √{4^2 + (2√2)^2} = √{24}$. В $△LMC$ $LM^2 = LC^2 + MC^2, LC = AC — AL = 12 — 8 = 4, MC = {1}/{2}CC_1 = 2√2, √{4^2 + (2√2)^2} = √{24}, K L = √{48}$, следовательно, $△KLM$ прямоугольный, $S_{KLM} = {1}/{2}(√{24})^2 = 12$.
$S_{сеч} = S_{KNFL} + S_{KLM} = 48 + 12 = 60$.
Ответ: 60
Задача 7
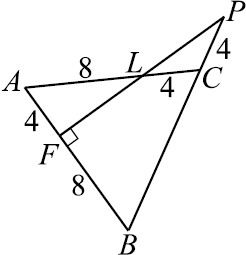
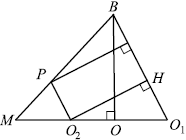
Дана четырёхугольная пирамида $SABCD$ с прямоугольником $ABCD$ в основании, $AB=6$, $BC=6√ {2}$. Высота пирамиды проектируется в точку пересечения диагоналей основания. Из вершин $A$ и $C$ на ребро $SB$ опущены перпендикуляры $AP$ и $CQ$.
а) Докажите, что точка $P$ является серединой отрезка $BQ$.
б) Найдите угол между плоскостями $SBA$ и $SBC$, если $SD=12$.
Решение
а) Пусть боковое ребро $SB$ равно $x$.
1) $△SHB∼△APB$ (прямоугольные с общим острым углом при вершине $B$). Тогда ${PB}/{BH} = {AB}/{SB}$. $H$ — середина $AB$. Тогда ${PB}/{3} = {6}/{x}; PB = {18}/{x}$.
2) $△SKB∼△CQB$ (прямоугольные с общим острым углом при вершине $B$). Тогда ${QB}/{BK} = {BC}/{SB}; {QB}/{3√2} = {6√2}/{x}; QB = {36}/{x}$.
3) Так как ${QB}/{PB} = {{36}/{x}}/{{18}/{x}} = 2$, то $PQ = PB$.
б) 1) Из пункта а) следует, что $PK$ — средняя линия $△BCQ$. Следовательно, $PK ‖ QC$. Но так как $QC ⊥ BS$, то и $PK ⊥ BS$. Значит, $∠APK$ — линейный угол двугранного угла между гранями $SBA$ и $SBC$. Пусть, $∠APK = α$.
2) $AK = √{AB^2 + BK^2} = √{6^2 + (3√2)^2} = 3√6$.
3) Так как по условию $SD = 12$ и $SB = SD$ (равным проекциям соответствуют равные наклонные), то $x = 12$, а $QB = {36}/{x} = {36}/{12}=3$.
Тогда $CQ = √{BC^2 — QB^2} = √{(6√2)^2 — 3^2} = 3√7$.
Так как $PK$ — средняя линия, то $PK = {1}/{2}CQ = {3√7}/{2}$.
4) $PB = {1}/{2}QB = {1}/{2}·3 = {3}/{2}$.
$AP = √{AB^2 — PB^2} = √{6^2 — ({3}/{2})^2} = {3}/{2}√{15}$.
5) По теореме косинусов для $△APK$:
$AK^2 = AP^2 + PK^2 — 2·AP·PK·cosα$;
$54 = {135}/{4} + {63}/{4} — 2·{3}/{2}√{15}·{3√7}/{2}·cosα$;
$cosα = — {1}/{√{105}}$;
Так как $cosα < 0$, то $α$ — тупой угол.
Значит, искомый угол между плоскостями $SBA$ и $SBC$ равен ($π-α$).
$cos(π-α) = -cosα = {1}/{√{105}}$.
Следовательно, искомый угол равен $arccos{1}/{√{105}}$.
Ответ:
Задача 8
Основанием прямой треугольной призмы $ABCA_1B_1C_1$ является прямоугольный треугольник $ABC$ с прямым углом $C$. Диагонали граней $AA_1B_1B$ и $BB_1C_1C$ равны $2√ {41}$ и $10$ соответственно, $AB=10$.
а) Докажите, что треугольник $A_1C_1B$ прямоугольный.
б) Найдите объём пирамиды $ACC_1B_1$.
Решение
а) Так как $A_1C_1 ⊥ B_1C_1$ и $A_1C_1 ⊥ CC_1$ по условию, то $A_1C_1 ⊥ BB_1C_1$ по признаку перпендикулярности прямой и плоскости.
Следовательно, $A_1C_1 ⊥ BC_1$, то есть треугольник $A_1C_1B$ прямоугольный.
б) 1) $AC = A_1C_1 = √{A_1B^2 — BC^2_1} = √{(2√{41})^2 — 10^2} = 8$.
2) $B_1C_1 = BC = √{AB^2 — AC^2} = √{10^2 — 8^2} = 6$.
3) $CC_1 = √{BC_1^2 — BC^2} = √{10^2 — 6^2} = 8$.
4) $V_{ACC_1B_1} = {1}/{3}·S_{ACC_1} ·B_1C_1 = {1}/{3} · {1}/{2} ·AC·CC_1 ·B_1C_1 = {1}/{6} ·8·8·6 = 64$.
Ответ: 64
Задача 9
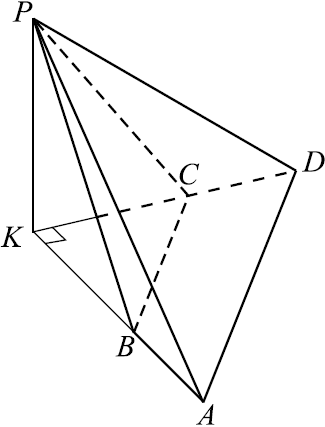
В основании четырёхугольной пирамиды $PABCD$ лежит трапеция $ABCD$ с большим основанием $AD$. Известно, что сумма углов $BAD$ и $ADC$ равна $90^°$, плоскости $PAB$ и $PCD$ перпендикулярны основанию, прямые $AB$ и $CD$ пересекаются в точке $K$.
а) Докажите, что плоскость $PAB$ перпендикулярна плоскости $PDC$.
б) Найдите объём $PKBC$, если $AB=3$, $BC=5$, $CD=4$, а высота пирамиды $PABCD$ равна $7$.
Решение
а) 1) $∠AKD = 180° — (∠A + ∠D) = 180° — 90° = 90°$.
2) Если две пересекающиеся плоскости перпендикулярны третьей, то они пересекаются по прямой, также перпендикулярной этой плоскости. Отсюда следует, что так как $PAB ⊥ ABC$ и $PCD ⊥ ABC$, то $PK ⊥ ABC$.
3) Так как $PK ⊥ ABC$, то $PK ⊥ KA$ и $PK ⊥ KD$.
Значит, $∠AKD$ — линейный угол двугранного угла между плоскостями $PAB$ и $PCD$. Следовательно, $PAB ⊥ PCD$.
б) Обозначим $BK = x, CK = y$.
1) $△BKC∼ △AKD$, так как $AD ‖ BC$.
Тогда ${AK}/{BK} = {DK}/{CK}; {AB + BK}/{BK} = {CD + CK}/{CK}; {AB}/{BK} + 1 = {CD}/{CK} + 1; {AB}/{BK} = {CD}/{CK}; {3}/{x} = {4}/{y}; x = {3}/{4}y$.
2) По теореме Пифагора $BK^2 + CK^2 = BC^2; x^2 + y^2=5^2; ({3}/{4}y)^2+y^2=25; {25}/{16}y^2=25; y=4;x={3}/{4}y=3$.
3) $S_{KBC} = {1}/{2}BK·CK = {1}/{2}·3 ·4= 6$.
4) $V_{PKBC} = {1}/{3}S_{KBC}·PK = {1}/{3}·6·7 = 14$.
Ответ: 14
Задача 10
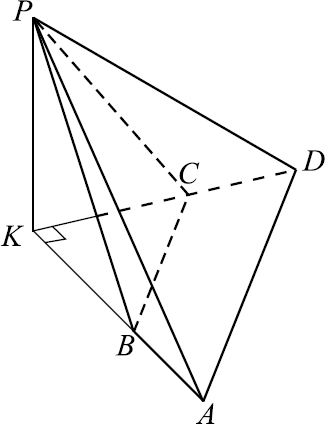
В основании четырёхугольной пирамиды $PABCD$ лежит трапеция $ABCD$ с большим основанием $AD$. Известно, что сумма углов $BAD$ и $ADC$ равна $90^°$, плоскости $PAB$ и $PCD$ перпендикулярны основанию, прямые $AB$ и $CD$ пересекаются в точке $K$.
а) Докажите, что плоскость $PAB$ перпендикулярна плоскости $PDC$.
б) Найдите объём $PKBC$, если $AB=BC=CD=4$, а высота пирамиды $PABCD$ равна $9$.
Решение
а) 1) $∠AKD = 180° — (∠A + ∠D) = 180° — 90° = 90°$.
2) Если две пересекающиеся плоскости перпендикулярны третьей, то они пересекаются по прямой, так же перпендикулярной этой плоскости. Отсюда следует, что так как $PAB ⊥ ABC$ и $PCD ⊥ ABC$, то $PK ⊥ ABC$.
3) Так как $PK ⊥ ABC$, то $PK ⊥ KA$ и $PK ⊥ KD$.
Значит, $∠AKD$ — линейный угол двугранного угла между плоскостями $PAB$ и $PCD$. Следовательно, $PAB ⊥ PCD$.
б) 1) Так как $ABCD$ — равнобедренная трапеция, то $∠A = ∠D$. Так как $BC ‖ AD$, то $∠A = ∠KBC, ∠D = ∠KCB$ как соответственные. Значит, $∠KBC = ∠KCB$, то есть $△KBC$ равнобедренный.
2) По теореме Пифагора $BK^2 + CK^2 = BC^2; 2BK^2 = BC^2; BK^2 = {BC^2}/{2} = {4^2}/{2} = 8$.
3) $S_{KBC} = {1}/{2}BK·CK = {1}/{2}BK^2 = {1}/{2}·8 = 4$.
4) $V_{PKBC} = {1}/{3}S_{KBC}·PK = {1}/{3}·4·9 = 12$.
Ответ: 12
Задача 11
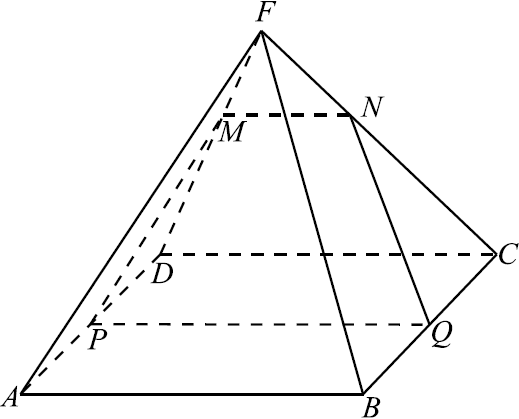
На боковом ребре $FD$ правильной четырёхугольной пирамиды ${FABCD}$ отмечена точка $M$ так, что $FM:FD=1:3$. Точки $P$и $Q$ — середины рёбер $AD$ и $BC$ соответственно.
а) Докажите, что сечение пирамиды плоскостью $MPQ$ есть равнобедренная трапеция.
б) Найдите отношение объёмов многогранников, на которые плоскость $MPQ$ разбивает пирамиду.
Решение
а) 1) Построим $MN ‖ CD$.
Так как и $PQ ‖ CD$, то $MN ‖ PQ$. Следовательно, точки $M, N, P$ и $Q$ лежат в одной плоскости. Таким образом, трапеция $MNQP$ является сечением пирамиды плоскостью $MPQ$.
2) $△FMN ∼△FDC$ (так как $MN ‖ CD$, то $∠FNM = ∠FCD$ и $∠FMN = ∠FDC$ как соответственные). Так как $△FCD$ равнобедренный, то и $△FNM$ тоже равнобедренный. Тогда $FM = FN; NC = FC — FN = FD — FM = MD$.
Кроме того, $PD = {1}/{2}AD = {1}/{2}BC = QC$. Так как $△FAD = △FBC$, то $∠MDP = ∠NCQ$. Отсюда $△PDM = △QCN$ по двум сторонам и углу между ними. Следовательно, $PM = NQ$, то есть $MNQP$ — равнобедренная трапеция.
б) 1) Пусть $MR ⊥ PQ, MS ⊥ CD, NX ⊥ PQ, NY ⊥ CD$.
Так как $MNQP$ и $MNCD$ — равнобедренные трапеции, то $V_1 = V_{PQCDMN} = V_{MRSNXY} + 2·V_{NXQCY}$ — объём первой части.
2) Пусть $a$ — сторона основания, $h$ — высота пирамиды. Тогда $QC = XY = RS = {a}/{2}; MN = {1}/{3}a; MO = {2}/{3}h(△FMN ∼△FDC$ и ${FM}/{FD} = {1}/{3}; QX = {PQ -MN}/{2} = {a -{1}/{3}a}/{2} = {1}/{3}a (MNQP$ — равнобедренная трапеция).
3) $S_{MRS} = {1}/{2}RS·MO = {1}/{2}·{a}/{2}·{2}/{3}h = {1}/{6}ah$. Объём прямой призмы $MRSNXY$ равен $V_{MRSNXY} = S_{MRS}·MN = {1}/{6}ah·{1}/{3}a = {1}/{18}a^2h$.
$V_{NXQCY} = {1}/{3}S_{XQCY}·MO = {1}/{3}·QX·QC·MO = {1}/{3}·{1}/{3}a·{a}/{2}·{2}/{3}h = {1}/{27}a^2h$.
$V_1 = V_{MRSNXY} + 2·V_{NXQCY} = {1}/{18}a^2h + 2·{1}/{27}a^2h = {7}/{54}a^2h$.
4) $V = V_{SABCD} = {1}/{3}S_{ABCD}·h = {1}/{3}a^2h$.
$V_2 = V — V_1 = ({1}/{3} — {7}/{54})a^2h = {11}/{54}a^2h$ — объём второй части.
5) ${V_1}/{V_2} ={{7}/{54}a^2h}/{{11}/{54}a^2h} = {7}/{11}$.
Ответ: 7:11
Задача 12
На боковом ребре $FD$ правильной четырёхугольной пирамиды ${FABCD}$ отмечена точка $M$ так, что $FM:FD=2:5$. Точки $P$ и $Q$ — середины рёбер $AD$ и $BC$ соответственно.
а) Докажите, что сечение пирамиды плоскостью $MPQ$ есть равнобедренная трапеция.
б) Найдите отношение объёмов многогранников, на которые плоскость $MPQ$ разбивает пирамиду.
Решение
а) 1) Построим $MN∥ CD$ (см. рис.).
Так как и $PQ∥ CD$, то $MN∥ PQ$. Следовательно, точки $M$, $N$, $P$ и $Q$ лежат в одной плоскости. Таким образом, трапеция $MNQP$ является сечением пирамиды плоскостью $MPQ$. 2) $▵ FMN∼ ▵ FDC$ (так как $MN∥ CD$, то $∠ FNM=∠ FCD$ и $∠ FMN=∠ FDC$ как соответственные). Так как $▵ FDC$ равнобедренный, то и $▵ FMN$ тоже равнобедренный. Тогда $FM=FN$; $NC=FC-FN=FD-FM=MD$. Кроме того, $PD={1} / {2}AD={1} / {2}BC=QC$. Так как $▵ FAD=▵ FBC$, то $∠ MDP=∠ NCQ$. Отсюда $▵ PDM=▵ QCN$ по двум сторонам и углу между ними. Следовательно, $PM=NQ$, то есть $MNQP$ — равнобедренная трапеция. б) 1) Пусть $MR⊥ PQ$, $MS⊥ CD$, $NX⊥ PQ$, $NY⊥ CD$ (см. рис.).
Так как $MNQP$ и $MNCD$ — равнобедренные трапеции, то $V_1=V_{PQCDMN}=V_{MRSNXY}+2⋅ V_{NXQCY}$ — объём первой части. 2) Пусть $a$ — сторона основания, $h$ — высота пирамиды. Тогда $QC=XY=RS={a} / {2}$; $MN={2} / {5}a$; $MO={3} / {5}h$ $(▵ FMN∼ ▵ FDC$ и ${FM} / {FD}={2} / {5})$; $QX={PQ-MN} / {2}={a-{2} / {5}a} / {2}={3} / {10}a$ ($MNQP$ — равнобедренная трапеция). 3) $S_{MRS}={1} / {2}RS⋅ MO={1} / {2}⋅ {a} / {2}⋅ {3} / {5}h={3} / {20}ah$. Объём прямой призмы $MRSNXY$ равен: $V_{MRSNXY}=S_{MRS}⋅ MN={3} / {20}ah⋅ {2} / {5}a={3} / {50}a^2h$. $V_{NXQCY}={1} / {3}S_{XQCY}⋅ MO={1} / {3}⋅ QX⋅ QC⋅ MO={1} / {3}⋅ {3} / {10}a⋅ {a} / {2}⋅ {3} / {5}h={3} / {100}a^2h$. $V_1=V_{MRSNXY}+2⋅ V_{NXQCY}={3} / {50}a^2h+2⋅ {3} / {100}a^2h={3} / {25}a^2h$. 4) $V=V_{SABCD}={1} / {3}S_{ABCD}⋅ h={1} / {3}a^2h$. $V_2=V-V_1=({1} / {3}-{3} / {25})a^2h={16} / {75}a^2h$ — объём второй части. 5) ${V_1} / {V_2}={{3} / {25}a^2h} / {{16} / {75}a^2h}={9} / {16}$.
Ответ: 9:16
Задача 13
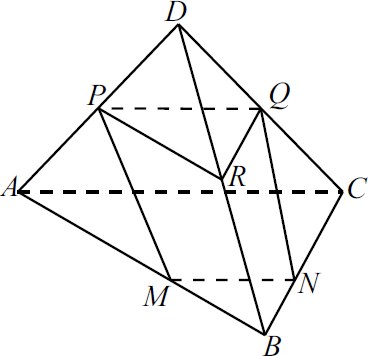
На рёбрах $AB$ и $BC$ треугольной пирамиды $DABC$ отмечены точки $M$ и $N$ так, что $AM:MB=CN:NB=2:1$. Точки $P$ и $Q$ — середины рёбер $DA$ и $DC$ соответственно.
а) Докажите, что точки $P$, $Q$, $M$ и $N$ лежат в одной плоскости.
б) Найдите отношение объёмов многогранников, на которые плоскость $PQM$ делит пирамиду.
Решение
а) 1) $△ABC ∼△MBN$ (угол $B$ общий, две пропорциональные стороны).
Значит $∠NMB = ∠CAB$. Следовательно, $MN ‖ AC$, так как равны соответствующие углы.
2) Так как $PQ$ — средняя линия $△ADC$, то $PQ ‖ AC$.
3) Так как $MN ‖ AC$ и $PQ ‖ AC$, то $MN ‖ PQ$. Следовательно, точки $P, Q, N$ и $M$ лежат в одной плоскости.
б) 1) Пусть $R$ — середина ребра $DB$. Тогда $PR$ — средняя линия $△ADB$. Следовательно, $PR ‖ AB$. Аналогично $QR ‖ BC$.
2) Обозначим через $V$ объём пирамиды $DABC, V_1 = V_{DPQR} + V_{MNBPQR}, V_2 = V — V_1, h$ — высота пирамиды $DABC, S$ — площадь $△ABC$.
Так как $△PQR∼ △ACB$ и ${PQ}/{AC} = {1}/{2}$, то $S_{PQR} ={S}/{4}$.
Так как ${DP}/{DA} = {1}/{2}$, то высота пирамиды $DPQR$ равна ${h}/{2}$.
Таким образом, $V_{DPQR} = {1}/{3}S_{PQR}· {h}/{2} = {1}/{3}· {S}/{4} ·{h}/{2} = {Sh}/{24}$.
3) Можно доказать, что $MNBPQR$ — усечёная пирамида. Её высота равна ${h}/{2}$.
Пусть $S_1 = S_{MNB}, S_2 = S_{PQR}$.
Так как $△BMN ∼ △BAC$ и ${BM}/{BA} = {1}/{3}$, то $S_1 = ({1}/{3})^2·S = {S}/{9}$.
Тогда $V_{MNBPQR} = {1}/{3}·{h}/{2}·(S_1 + √{S_1·S_2} + S_2)= {h}/{6}·({S}/{9} + √{{S}/{9}·{S}/{4}} + {S}/{4}) = {h}/{6}({S}/{9} + {S}/{6} + {S}/{4})= {19}/{216}Sh$.
4) $V_1 = V_{DPQR} + V_{MNBPQR} = {Sh}/{24} + {19}/{216}Sh = {7}/{54}Sh. V_2 = V — V_1 = {1}/{3}Sh — {7}/{54}Sh = {11}/{54}Sh$.
5) ${V_1}/{V_2} = {{7}/{54}Sh}/{{11}/{54}Sh} = {7}/{11}$.
Ответ: 7:11
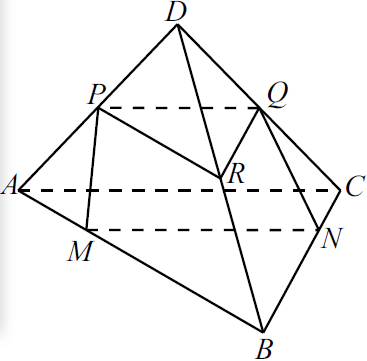
Задача 14
На рёбрах $AB$ и $BC$ треугольной пирамиды $DABC$ отмечены точки $M$ и $N$ так, что $AM:MB=CN:NB=1:3$. Точки $P$ и $Q$ — середины рёбер $DA$ и $DC$ соответственно.
а) Докажите, что точки $P$, $Q$, $M$ и $N$ лежат в одной плоскости.
б) Найдите отношение объёмов многогранников, на которые плоскость $PQM$ делит пирамиду.
Решение
а) 1) $△ABC ∼△MBN$ (угол $B$ общий, две пропорциональные стороны). $MB ={3}/{4}AB, BN ={3}/{4}BC$.
Следовательно, $MN ‖ AC$, так как равны соответствующие углы.
2) Так как $PQ$ — средняя линия $△ADC$, то $PQ ‖ AC$.
3) Так как $MN ‖ AC$ и $PQ ‖ AC$, то $MN ‖ PQ$. Следовательно, точки $P, Q, N$ и $M$ лежат в одной плоскости.
б) 1) Пусть $R$ — середина ребра $DB$. Тогда $PR$ — средняя линия $△ADB$. Следовательно, $PR ‖ AB, PR = {1}/{2}AB$. Аналогично $QR ‖ BC, QR = {1}/{2}BC$.
2) Обозначим через $V$ объём пирамиды $DABC, V_1 = V_{DPQR} + V_{MNBPQR}, V_2 = V — V_1, h$ — высота пирамиды $DABC, S$ — площадь $△ABC$.
Так как $△PQR∼ △ACB$ и ${PQ}/{AC} = {1}/{2}$, то $S_{PQR} ={S}/{4}$.
Так как ${DP}/{DA} = {1}/{2}$, то высота пирамиды $DPQR$ равна ${h}/{2}$.
Таким образом, $V_{DPQR} = {1}/{3}S_{PQR}· {h}/{2} = {1}/{3}· {S}/{4} ·{h}/{2} = {Sh}/{24}$.
3) Можно доказать, что $MNBPQR$ — усечёная пирамида. Её высота равна ${h}/{2}$.
Пусть $S_1 = S_{MNB}, S_2 = S_{PQR}$.
Так как $△BMN ∼ △BAC$ и ${BM}/{BA} = {3}/{4}$, то $S_1 = ({3}/{4})^2·S = {9}/{16}S$.
Тогда $V_{MNBPQR} = {1}/{3}·{h}/{2}·(S_1 + √{S_1·S_2} + S_2)= {h}/{6}·({9}/{16}S + √{{9}/{16}S·{S}/{4}} + {S}/{4}) = {h}/{6}({9}/{16}S + {3}/{8}S + {S}/{4})= {19}/{96}Sh$.
4) $V_1 = V_{DPQR} + V_{MNBPQR} = {Sh}/{24} + {19}/{96}Sh = {23}/{96}Sh. V_2 = V — V_1 = {1}/{3}Sh — {23}/{96}Sh = {3}/{32}Sh$.
5) ${V_1}/{V_2} = {{23}/{96}Sh}/{{3}/{32}Sh} = {23}/{9}$.
Ответ: 23:9
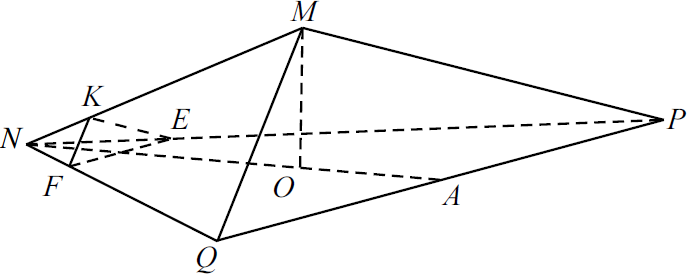
Задача 15
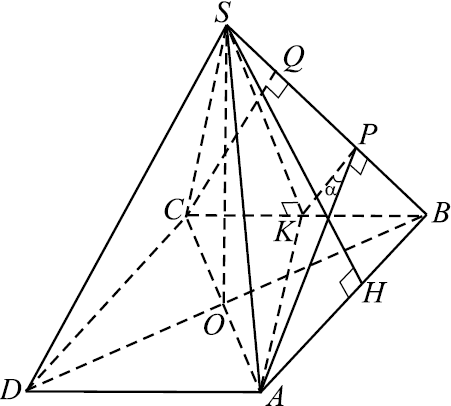
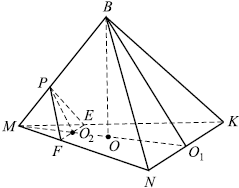
В правильной треугольной пирамиде $MNPQ$ с вершиной $M$ сторона основания равна $15$, высота равна $√ {6}$. На рёбрах $NP$, $NQ$ и $NM$ отмечены точки $E$, $F$, $K$ соответственно, причём $NE=NF=3$ и $NK={9} / {5}$. а) Докажите, что плоскости $EFK$ и $MPQ$ параллельны. б) Найдите расстояние от точки $K$ до плоскости $MPQ$.
Решение
а) Докажем, что $EFK ‖ MPQ$. Воспользуемся признаком параллельности плоскостей: если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то такие плоскости параллельны.
В плоскости $MPQ$ возьмём прямые $QP$ и $MQ$, а в плоскости $EFK$ — прямые $FE$ и $KF$. Пусть $O$ — центр основания.
В $△MNO: ∠NOM = 90°$ и по теореме Пифагора $NM = √{NO^2 +MO^2}$. Найдём $NO$: треугольник $NPQ$ — правильный, все его стороны равны, а высота $NA = {a√3}/{2}$, где $a$ — сторона треугольника $NPQ$. $NO = {2}/{3}NA = {2}/{3}·{a√3}/{2} = {a√3}/{3}$, то есть $NO = {15√3}/{3} = 5√3$. B $△NMO: ∠MON = 90°, NM = √{MO^2 + NO^2} = √{(5√3)^2 + 6} = √{75 + 6} = √{81} = 9$.
1) $△NKF∼△NMQ$, так как ${NK}/{NM} ={{9}/{5}}/{9} ={1}/{5}, {NF}/{NQ} = {3}/{15} = {1}/{5}$ и $∠MNQ$ — общий. Из подобия следует, что $∠NKF = ∠NMQ$. Это соответственные углы при прямых $KF$ и $MQ$ и секущей $NM$. Значит, $KF ‖ MQ$.
2) $△NEF∼△NPQ$, так как ${NE}/{NP} ={3}/{15} = {1}/{5}, {NF}/{NQ} ={3}/{15} = {1}/{5}$ и $∠PNQ$ — общий. Из подобия следует, что $∠NEF = ∠NPQ$. Это соответственные углы при прямых $EF$ и $PQ$ и секущей $NP$. Значит, $EF ‖ PQ$.
Итак, две пересекающейся прямые $KF$ и $FE$ плоскости $KFE$ соответственно параллельны двум пересекающимся прямым $MQ$ и $PQ$ плоскости $MPQ$, следовательно, $KFE ‖ MPQ$.
б) Найдём расстояние от точки $K$ до плоскости $MPQ$. Так как плоскость $KFE$ параллельна плоскости $MPQ$, то расстояние от точки $K$ до плоскости $MPQ$ равно расстоянию от точки $B$ до плоскости $MPQ$ и оно равно длине отрезка $BD$ ($BD$ — перпендикуляр к $AM$. Докажем это.
$NA ⊥ QP$ и $MA ⊥ QP$ (как высоты треугольников $NPQ$ и $MPQ$), значит, прямая $QP$ перпендикулярна плоскости $NMA$, и тогда прямая $PQ$ перпендикулярна любой прямой этой плоскости, в частности $BD$. С другой стороны $BD ⊥ AM$ по построению, значит, прямая $BD$ перпендикулярна двум пересекающимся прямым плоскости $MPQ$, и тогда отрезок $BD$ перпендикулярен плоскости $MPQ$ и равен расстоянию от $B$ до плоскости $MPQ$.
В $△BDA: ∠BDA = 90°; BD = BA · sin∠DAB; BA = NA — NB; NA = {15√3}/{2}; NB ={1}/{5}NA = {3√3}/{2}; BA = {15√3}/{2} — {3√3}/{2} = 6√3$.
Из $△MOA: sin∠MAO = sin∠DAB = {MO}/{MA} = {√6}/{√{MO^2 + OA^2}}={√6}/{√{6 +{75}/{4}}} = {√6·2}/{√{99}} = {2√6}/{3√{11}} ={2}/{3}√{{6}/{11}}$ (так как $AO ={1}/{3}NA = {5√3}/{2})$.
Из $△ABD:BD = AB·sin∠DAB = 6√3·{2}/{3}√{{6}/{11}} = 4√{{18}/{11}} = 12√{{2}/{11}} = {12√{22}}/{11}$.
Ответ:
Задача 16
В правильной треугольной пирамиде $DABC$ с вершиной $D$ сторона основания $AB$ равна $9$, высота равна $3$. На рёбрах $AB$, $AC$, $AD$ отмечены точки $P$, $K$, $F$ соответственно, причём $AP=AK=3$ и $AF=2$. а) Доказать, что плоскости $PKF$ и $DBC$ параллельны. б) Найти расстояние от точки $F$ до плоскости $DBC$.
Решение
Докажем, что плоскость $DBC$ параллельна плоскости $PKF$. Для этого в плоскости $PKF$ возьмём прямые $KP$ и $FP$, а в плоскости $DBC$ — прямые $CB$ и $DB$ (см. рис.). Пусть $O$ — центр основания.
В $▵ ADO$: $∠ DOA=90°$ и по теореме Пифагора $AD=√ {DO^2+AO^2}$. Найдём $AO$, треугольник $ABC$ — правильный, все его стороны равны, $AM$ — высота, $AM={a√ {3}} / {2}$, где $a$ — сторона $▵ ABC$, $AO={2} / {3} AM={2} / {3}⋅ {a√ {3}} / {2}={a√ {3}} / {3}$, то есть $AO={9√ {3}} / {3}=3√ {3}$, $AD=√ {3^2+(3√ {3})^2}=√ {9+27}=6$. $▵ APF∼ ▵ ABD$, так как ${AF} / {AD}={2} / {6}={1} / {3}$, ${AP} / {AB}={3} / {9}={1} / {3}$ и $∠ DAB$ — общий, то есть две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы между ними равны. Из подобия следует, что $∠ AFP=∠ ADB$. Это соответственные углы при прямых $FP$ и $DB$ и секущей $AD$. Значит, $FP∥ DB$. Аналогично рассуждая, получим, что $▵ AKP∼ ▵ ACB$, так как ${AK} / {AC}={3} / {9}={1} / {3}$, ${AP} / {AB}={3} / {9}={1} / {3}$ и $∠ BAC$ — общий, то есть две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы между ними равны. Из подобия следует, что $∠ APK=∠ ABC$. Это соответственные углы при прямых $KP$ и $BC$ и секущей $AB$. Значит, $KP∥ BC$. Итак, две пересекающиеся прямые $KP$ и $FP$ плоскости $PKF$ соответственно параллельны двум пересекающимся прямым $CB$ и $BD$ плоскости $DBC$. Следовательно, плоскости $DBC$ и $PKF$ параллельны по признаку параллельности плоскостей. б) Найдём расстояние от точки $F$ до плоскости $DBC$. Так как плоскость $KFP$ параллельна плоскости $DBC$, то расстояние от точки $F$ до плоскости $DBC$ равно расстоянию от точки $L$ до плоскости $DBC$ и равно длине отрезка $LN$ (см. рис.), где $LN$ — перпендикуляр к $MD$ в плоскости $AMD$.
Докажем это. $AM ⊥ BC$ и $DM⊥ BC$ (как высоты треугольников $ABC$ и $DBC$), значит, $BC⊥ MDA$ и тогда $BC$ перпендикулярен любой прямой этой плоскости, в частности, $LN$. С другой стороны, $LN ⊥ MD$ по построению, значит, $LN$ перпендикулярен двум пересекающимся прямым плоскости $DBC$, и тогда отрезок $LN$ перпендикулярен плоскости $DBC$ и равен расстоянию от точки $L$ до плоскости $DBC$. В $▵ LNM$: $∠ LNM=90°$, $LN=LM⋅ sin ∠ NML$. $ML=AM-LA$; $AM={9√ {3}} / {2}$;
$LA={1} / {3}⋅ AM={9√ {3}} / {6}={3√ {3}} / {2}$. $ML={9√ {3}} / {2}-{3√ {3}} / {2}=3√ {3}$. $sin ∠ NML={DO} / {DM}$; $DO=3$ (по условию). Из $▵ MDB$ найдём $DM$: $∠ DMB=90°$,
$MD=√ {BD^2-MB^2}=√ {36-({9} / {2})^2}={3√ {7}} / {2}$. $sin ∠ NML={2} / {√ {7}}$. $LN=LM⋅ sin ∠ NML=3√ {3}⋅{2} / {√ {7}}=6√ {{3} / {7}}$.
Ответ: 6sqrt{fsm{3}{7}}
Задача 17
В правильной треугольной пирамиде $BMNK$ с основанием $MNK$ сторона основания равна $6$, а высота пирамиды равна $3$. На рёбрах $MN, MK$ и $MB$ соответственно отмечены точки $F, E$ и $P$, такие, что $MF = ME ={√{21}}/{2}$ и $MP ={7}/{4}$.
а) Докажите, что плоскости $FEP$ и $NBK$ параллельны.
б) Найдите расстояние от точки $P$ до плоскости $NBK$.
Решение
а) Пусть $BO -$ высота пирамиды. Чтобы доказать, что плоскости $FEP$ и $NKB$ параллельны, достаточно показать, что две пересекающиеся прямые $PF$ и $FE$ плоскости $FEP$ соответственно параллельны двум пересекающимся прямым $BN$ и $NK$ плоскости $BNK$. Покажем это.
Найдём боковое ребро $MB$ из треугольника $MBO$:
В $∆MKN:$ $MO_1 -$ высота, $MO_1 = {a√3}/{2}$, где $a -$ сторона $∆MNK$. $MO_1 = {6√3}/{2} = 3√3$.
$MO ={2}/{3} MO_1 = 2√3$,
$MB = √{OB^2 + OM^2} = √{3^2 + (2√3)^2} = √{21}$.
1. ${MP}/{MB} ={7}/{4·√{21}}={√{21}}/{12},{MF}/{MN} ={√{21}}/{2·6} = {√{21}}/{12}$. Отношения сторон равны. Используя условие, что $∠BMN$ общий, получим: $∆MPF∼∆MBN$. Из подобия треугольников следует, что $∠MPF = ∠MBN$. Эти углы — соответственные, образованные при пересечении двух прямых $PF$ и $BN$ прямой $MB$. Значит, $PF ‖ BN$.
2. Рассматривая треугольники $MEF$ и $MKN$, можно аналогично доказать, что $FE ‖ NK$.
Так как две пересекающиеся прямые $PF$ и $FE$ плоскости $PFE$ соответственно параллельны двум пересекающимся прямым $BN$ и $NK$ плоскости $NBK$, то эти плоскости параллельны.
б) Пусть $O_2$ — точка пересечения $MO_1$ и $FE$. Поскольку плоскость $PFE$ параллельна плоскости $BNK$, то расстояние от точки $P$ до плоскости $BNK$ равно расстоянию от точки $O_2$ до плоскости $BNK$, и оно равно длине отрезка $O_2H$, где точка $H$ лежит на $BO_1$ и $O_2H ⊥ BO_1$. Докажем, что $O_2H$ — расстояние от $O_2$ до плоскости $BNK$.
$NK ⊥ MO_1$ и $NK ⊥ BO_1$ ($MO_1$ и $BO_1$ — высоты $∆MNK$ и $∆NBK$), значит, $NK$ перпендикулярна плоскости $MBO_1$, и тогда $NK$ перпендикулярна любой прямой этой плоскости, в том числе $NK ⊥ O_2H$. По построению $O_2H ⊥ BO_1$. Прямая $O_2H$ перпендикулярна двум пересекающимся прямым плоскости $BNK$, значит, она перпендикулярна $BNK$, и отрезок $O_2H$ равен расстоянию от $O_2$ до плоскости $BNK$.
В треугольнике $O_2HO_1: O_2H = O_2O_1 sin∠HO_1O_2$.
$O_2O_1 = MO_1-MO_2$.
Из $∆MEO_2: ∠MO_2E = 90°, ∠EMO_2 = 30°$;
$MO_2 = MEcos30° = {√{21}}/{2}·{√3}/{2} = {3√7}/{4}$.
$O_2O_1 = 3√3 — {3√7}/{4} = {3(4√3 — √7)}/{4}$;
$sin ∠HO_1O_2 = {BO}/{BO_1} = {BO}/{√{BO^2 + OO_1^2}} = {3}/{√{3^2 + (√3)^2}} = {√3}/{2}$.
$O_2H = {3(4√3 — √7)}/{4}·{√3}/{2} = {3(12 — √{21})}/{8}$.
Ответ: ${3(12-√{21})}/{8}$
Задача 18
В прямоугольном параллелепипеде $ABCDA_{1}B_{1}C_{1}D_{1}$ стороны оснований $AB$ и $BC$ равны соответственно $8$ и $5$, а боковое ребро $AA_1$ равно $4$. На ребре $A_{1}B_1$ отмечена точка $K$, а на луче $BC$ — точка $F$, причём $A_{1}K = KB_1$ и $BF = AB$. Плоскость $AKF$ пересекает ребро $B_{1}C_1$ в точке $P$.
а) Докажите, что $B_{1}P : PC_1 = 4 : 1$.
б) Найдите площадь сечения параллелепипеда плоскостью $AKF$.
Решение
а) Построим сечение параллелепипеда плоскостью $AKF$.
$E$ — точка пересечения ребра $DC$ и отрезка $AF$.
$В$ плоскости $ABB_1$ проведём лучи $AK$ и $BB_1, AK$ пересекает $BB_1$ в точке $Q$. В плоскости $BCC_1$ проведём отрезок $FQ, FQ$ пересекает $B_1C_1$ в точке $P$, а $CC_1$ — в точке $R$. Пятиугольник $AKPRE$ — искомое сечение.
$KB_1 ‖ AB, KB_1 ={1}/{2}A_1B_1$, значит, $KB_1$ — средняя линия $△ABQ$, отсюда $BB_1 = QB_1$, а так как $BF ‖ B_1P$, то $B_1P$ — средняя линия $△FBQ, BF = 8, B_1P ={1}/{2}BF = 4. C_1P = B_1C_1 — B_1P = 5 — 4 = 1$, следовательно, $B_1P : PC_1 = 4 : 1$.
б) Прямоугольные треугольники $ABQ, FBQ$ и $ABF$ равны по двум катетам $AB = BF = BQ = 8$, отсюда $AQ = AF = QF = 8√2$. $S_{AQF} ={a^2√3}/{4}$ как площадь равностороннего треугольника со стороной $a$. $S_{AQF} = {(8√2)^2·√3}/{4} = 32√3, S_{KQP} ={1}/{4}S_{AQF}={32√3}/{4} = 8√3$.
$S_{AKPF} = S_{AQF} — S_{KQP} = 32√3 — 8√3 = 24√3$.
$△RCF~△RC_1P$ по первому признаку подобия $(∠C = ∠C_1 = 90°, ∠1 = ∠2$ как вертикальные). Из подобия следует ${CF}/{PC_1} ={FR}/{PR}$. По доказанному в а) $PC_1 = 1, BF = AB = 8$, тогда $CF = 8 — 5 = 3$ и ${FR}/{PR} ={3}/{1}$. Так как $KP$ средняя линия $△AQF$, то $PF ={1}/{2}QF = 4√2, FR = {3PF}/{4} = {4√2·3}/{4} = 3√2$.
В равнобедренном прямоугольном треугольнике $FCE$ $FC = EC = 3$, тогда $EF = 3√2$.
В $△REF$ $FR = EF = 3√2, ∠RFE = 60°$, отсюда $△REF$ — равносторонний. $S_{REF} ={(3√2)^2√3}/{4} = {9√3}/{2}$.
$S_{AKPRE} = S_{AKPF} — S_{REF} = 24√3 — {9√3}/{2} = {39√3}/{2}$.
Ответ: ${39√3}/{2}$
Рекомендуемые курсы подготовки
- Главная
- Новости
- ЕГЭ
- ЕГЭ Профиль 2023
- ЕГЭ Профиль 2022
- ЕГЭ Профиль 2016-2021
- Варианты профильного ЕГЭ
- ЕГЭ База 2023
- ЕГЭ База 2022
- ЕГЭ База 2016-2021
- ОГЭ
- ОГЭ 2019
- ОГЭ 2023
- ГВЭ
- ГВЭ 11 класс
- ВПР
- ВПР 4 класс
- ВПР 5 класс
- ВПР 6 класс
- ВПР 7 класс
- ВПР 8 класс
- Алгебра
- Алгебра 7-9
- Алгебра 10-11
- Геометрия
- Геометрия 7-9
- Геометрия 10-11
- YouTube
- Прочее
- Class100
- Разработки
- Обо мне
- Репетитор
ЕГЭ по математике — Профиль 2022. Открытый банк заданий с ответами.
- ЗАДАЧИ ЕГЭ С ОТВЕТАМИ
- АНГЛИЙСКИЙ без ГРАНИЦ
2012-07-21

НЕ ОТКЛАДЫВАЙ! Заговори на английском!
ДОЛОЙ обидные ошибки на ЕГЭ!!
Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!
Конструктор упражнений для позвоночника!
Добавить комментарий
*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.





- РубрикиРубрики
- Задачи по номерам!
№1 №2 №3 №4 №5 №6 №7 №8 №9 №10 №11 №12 №13 №14 №15 №16
- МЕТКИ
БЕЗ калькулятора Выбор варианта Как запомнить Личное Логарифмы Объём Окружность Круг Площадь Производная Треугольник Тригонометрия Трапеция Углы Уравнения Формулы Конкурсы Параллелограмм Поздравления Рекомендации Саморазвитие
- ОСТЕОХОНДРОЗУ-НЕТ!
Свойства числа 505378
| Множители | 2 * 71 * 3559 | |
| Делители | 1, 2, 71, 142, 3559, 7118, 252689, 505378 | |
| Количество делителей | 8 | |
| Сумма делителей | 768960 | |
| Предыдущее целое | 505377 | |
| Следующее целое | 505379 | |
| Простое число? | NO | |
| Предыдущее простое | 505369 | |
| Следующее простое | 505399 | |
| 505378th простое число | 7453709 | |
| Является числом Фибоначчи? | NO | |
| Число Белла? | NO | |
| Число Каталана? | NO | |
| Факториал? | NO | |
| Регулярное число? | NO | |
| Совершенное число? | NO | |
| Полигональное число (s < 11)? | NO | |
| Двоичное | 1111011011000100010 | |
| Восьмеричная | 1733042 | |
| Двенадцатеричный | 20456a | |
| Шестнадцатиричная | 7b622 | |
| Квадрат | 255406922884 | |
| Квадратный корень | 710.89943029939 | |
| Натуральный логарифм | 13.133061943111 | |
| Десятичный логарифм | 5.7036163323869 | |
| Синус | 0.55253701482381 | |
| Косинус | -0.83348836059635 | |
| Тангенс | -0.66292109277744 |
Deutsch
English
Español
Français
Italiano
Nederlands
Polski
Português
Русский
中文
日本語
한국어
Используя этот сайт, вы подтверждаете свое согласие с Условиями и соглашениями и Политикой приватности.
© 2023
numberempire.com
Все права защищены