СДАМ ГИА:
РЕШУ ЕГЭ
Образовательный портал для подготовки к экзаменам
Математика базового уровня
Математика базового уровня
≡ Математика
Базовый уровень
Профильный уровень
Информатика
Русский язык
Английский язык
Немецкий язык
Французский язык
Испанский язык
Физика
Химия
Биология
География
Обществознание
Литература
История
Сайты, меню, вход, новости
СДАМ ГИАРЕШУ ЕГЭРЕШУ ОГЭРЕШУ ВПРРЕШУ ЦТ
Об экзамене
Каталог заданий
Варианты
Ученику
Учителю
Школа
Справочник
Сказать спасибо
Вопрос — ответ
Чужой компьютер
Зарегистрироваться
Восстановить пароль
Войти через ВКонтакте
Играть в ЕГЭ-игрушку
Новости
10 марта
Как подготовиться к ЕГЭ и ОГЭ за 45 дней
6 марта
Изменения ВПР 2023
3 марта
Разместили утвержденное расписание ЕГЭ
27 января
Вариант экзамена блокадного Ленинграда
23 января
ДДОС-атака на Решу ЕГЭ. Шантаж.
6 января
Открываем новый сервис: «папки в избранном»
22 декабря
Открыли новый портал Решу Олимп. Для подготовки к перечневым олимпиадам!
4 ноября
Материалы для подготовки к итоговому сочинению 2022–2023
31 октября
Сертификаты для учителей о работе на Решу ЕГЭ, ОГЭ, ВПР
21 марта
Новый сервис: рисование
31 января
Внедрили тёмную тему!
НАШИ БОТЫ
 |
|
Все новости
ЧУЖОЕ НЕ БРАТЬ!
Экзамер из Таганрога
10 апреля
Предприниматель Щеголихин скопировал сайт Решу ЕГЭ
Наша группа
Задания
Версия для печати и копирования в MS Word
Тип 12 № 506418 
В параллелограмме ABCD АВ = 8, АС = ВD =17. Найдите площадь параллелограмма.
Спрятать решение
Решение.
Данный параллелограмм является прямоугольником, поскольку его диагонали равны.
Найдём сторону AD:
Найдём площадь прямоугольника:
Ответ: 120.
Источник: Апробация базового ЕГЭ по математике, 13—17 октября: вариант 166082.
Раздел кодификатора ФИПИ: Четырёхугольники и их элементы
Спрятать решение
·
·
Сообщить об ошибке · Помощь
О проекте · Редакция · Правовая информация · О рекламе
© Гущин Д. Д., 2011—2023
Каталог заданий
Версия для печати и копирования в MS Word
1
Тип 12 № 506418
В параллелограмме ABCD АВ = 8, АС = ВD =17. Найдите площадь параллелограмма.
Источник: Апробация базового ЕГЭ по математике, 13—17 октября: вариант 166082.
Раздел кодификатора ФИПИ: Четырёхугольники и их элементы
Решение
·
·
Сообщить об ошибке · Помощь
Вариант № 8349415
1. Задание 1 № 506993
Найдите значение выражения 
2. Задание 2 № 508383
Найдите значение выражения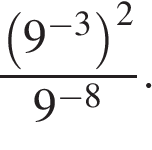 
3. Задание 3 № 509768
Пятая часть всех отдыхающих в пансионате — дети. Какой процент от всех отдыхающих составляют дети?
4. Задание 4 № 506298
Площадь треугольника 
можно вычислить по формуле 
, где 
— сторона треугольника, 
— высота, проведенная к этой стороне (в метрах). Пользуясь этой формулой, найдите сторону 
, если площадь треугольника равна 
, а высота равна 14 м.
5. Задание 5 № 26855
Найдите значение выражения 
.
6. Задание 6 № 77336
Поезд Новосибирск-Красноярск отправляется в 15:20, а прибывает в 4:20 на следующий день (время московское). Сколько часов поезд находится в пути?
7. Задание 7 № 26651
Найдите корень уравнения 
.
8. Задание 8 № 510684
Диагональ прямоугольного телевизионного экрана равна 100 см, а высота экрана — 60 см. Найдите ширину экрана. Ответ дайте в сантиметрах.
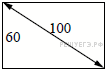
9. Задание 9 № 510915
Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент второго столбца.
|
ВЕЛИЧИНЫ |
ВОЗМОЖНЫЕ ЗНАЧЕНИЯ |
|
|
А) Объём воды в озере Байкал Б) Объём пакета кефира В) Объём бассейна Г) Объём ящика для фруктов |
1) 1 л 2) 23 615,39 км3 3) 72 л 4) 600 м3 |
В таблице под каждой буквой укажите соответствующий номер.
|
A |
Б |
В |
Г |
10. Задание 10 № 282857
Фабрика выпускает сумки. В среднем на 100 качественных сумок приходится восемь сумок со скрытыми дефектами. Найдите вероятность того, что купленная сумка окажется качественной. Результат округлите до сотых.
11. Задание 11 № 27518
На диаграмме показана среднемесячная температура воздуха в Екатеринбурге (Свердловске) за каждый месяц 1973 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме наибольшую среднемесячную температуру во второй половине 1973 года. Ответ дайте в градусах Цельсия.
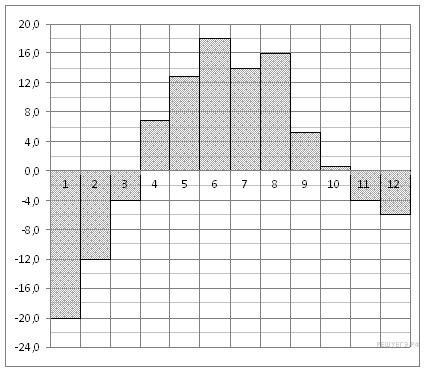
12. Задание 12 № 26688
Своему постоянному клиенту компания сотовой связи решила предоставить на выбор одну из скидок. Либо скидку 25% на звонки абонентам других сотовых компаний в своем регионе, либо скидку 5% на звонки в другие регионы, либо 15% на услуги мобильного интернета. Клиент посмотрел распечатку своих звонков и выяснил, что за месяц он потратил 300 рублей на звонки абонентам других компаний в своем регионе, 200 рублей на звонки в другие регионы и 400 рублей на мобильный интернет. Клиент предполагает, что в следующем месяце затраты будут такими же, и, исходя из этого, выбирает наиболее выгодную для себя скидку. Какую скидку выбрал клиент? В ответ запишите, сколько рублей составит эта скидка.
13. Задание 13 № 25561
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
14. Задание 14 № 514621
Установите соответствие между функциями и характеристиками этих функций на отрезке [1; 7].
|
ТОЧКИ |
ХАРАКТЕРИСТИКИ ФУНКЦИИ ИЛИ ПРОИЗВОДНОЙ |
|
|
А) Б) В) Г) |
1) Функция имеет точку максимума на отрезке [1; 7] 2) Функция убывает на отрезке [1; 7] 3) Функция имеет точку минимума на отрезке [1; 7] 4) Функция возрастает на отрезке [1; 7] |
В таблице под каждой буквой укажите соответствующий номер.
|
А |
Б |
В |
Г |
15. Задание 15 № 506418
В параллелограмме ABCD АВ = 8, АС = ВD =17. Найдите площадь параллелограмма.
16. Задание 16 № 509781
Радиус основания цилиндра равен 26, а его образующая равна 9. Сечение, параллельное оси цилиндра, удалено от неё на расстояние, равное 24. Найдите площадь этого сечения.
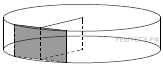
17. Задание 17 № 510033
На координатной прямой отмечены точки A, B, C, и D. Про число m известно, что оно равно 
.
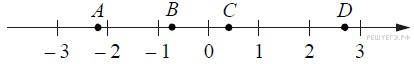
Установите соответствие между указанными точками и числами из правого столбца, которые им соответствуют.
|
ТОЧКИ |
ЧИСЛА |
|
|
А) A Б) B В) C Г) D |
1) 2) 3) 4) |
В таблице под каждой буквой укажите соответствующий номер.
|
А |
Б |
В |
Г |
18. Задание 18 № 507070
Отец обещал сыну-студенту подарить ноутбук, если он сдаст сессию без троек. Отец всегда выполняет свои обещания. Выберите утверждения, которые следуют из приведённых фактов.
1) Если сессия сдана на отлично, то ноутбук будет подарен
2) Если сын получит тройку, то отец не подарит ему ноутбук
3) Если ноутбук не был подарен, то сессия не сдана успешно (без троек)
4) Если ноутбук был подарен, то сессия сдана без троек
В ответе укажите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
19. Задание 19 № 510715
Найдите натуральное число, большее 1340, но меньшее 1640, которое делится на каждую свою цифру и все цифры которого различны и не равны нулю. В ответе укажите какое-нибудь одно такое число.
20. Задание 20 № 512428
Про натуральные числа A, B и С известно, что каждое из них больше 6, но меньше 10. Загадали натуральное число, затем его умножили на A, потом прибавили к полученному произведению B и вычли С. Получилось 186. Какое число было загадано?
Новые тренировочные варианты в формате решу ЕГЭ 2022 по математике профильный уровень 11 класс для подготовки к экзамену, каждый вариант составлен по новой демоверсии ФИПИ ЕГЭ 2022 года, к тренировочным заданиям прилагаются правильные ответы и пояснения.
-
Тренировочный вариант №41054170 с ответами
-
Тренировочный вариант №41054171 с ответами
-
Тренировочный вариант №41054172 с ответами
-
Тренировочный вариант №41054173 с ответами
-
Тренировочный вариант №41054174 с ответами
-
Тренировочный вариант №41054175 с ответами
-
Тренировочный вариант №41054176 с ответами
-
Тренировочный вариант №41054177 с ответами
-
Тренировочный вариант №41054178 с ответами
-
Тренировочный вариант №41054179 с ответами
-
Тренировочный вариант №41054180 с ответами
-
Тренировочный вариант №41054181 с ответами
-
Тренировочный вариант №41054182 с ответами
-
Тренировочный вариант №41054183 с ответами
-
Тренировочный вариант №41054184 с ответами
Другие тренировочные варианты ЕГЭ 2022 по математике:
Тренировочные варианты ЕГЭ по математике 11 класс задания с ответами
Пробный вариант ЕГЭ 2022 №211004 по математике 11 класс с ответами
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
ЕГЭ по математике — Профиль 2022. Открытый банк заданий с ответами.
Решение и ответы заданий варианта МА2210309 СтатГрад 28 февраля ЕГЭ 2023 по математике (профильный уровень). Тренировочная работа №3. ГДЗ профиль для 11 класса.
+Задания №1, №4, №6, №10 из варианта МА2210311.
Все материалы получены из открытых источников и публикуются после окончания тренировочного экзамена в ознакомительных целях.
Задания №13,16,17,18 долго оформлять, решу их позже, если будет время и желание. Решены те задания, у которых кнопка «Смотреть решение» зелёная.
Задание 1.
В треугольнике ABC угол C равен 90°, CH – высота, BC = 5, cosA=frac{2sqrt{6}}{5}. Найдите длину отрезка AH.
Задание 1 из варианта 2210311.
Найдите периметр прямоугольника, если его площадь равна 12, а отношение соседних сторон равно 1:3.
Задание 2.
Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 2. Объём параллелепипеда равен 3,2. Найдите высоту цилиндра.
Задание 3.
В группе 16 человек, среди них – Анна и Татьяна. Группу случайным образом делят на 4 одинаковые по численности подгруппы. Найдите вероятность того, что Анна и Татьяна окажутся в одной подгруппе.
Задание 4.
Агрофирма закупает куриные яйца только в двух домашних хозяйствах. Известно, что 40 % яиц из первого хозяйства – яйца высшей категории, а из второго хозяйства – 60 % яиц высшей категории. В этой агрофирме 50 % яиц высшей категории. Найдите вероятность того, что яйцо, купленное у этой агрофирмы, окажется из первого хозяйства.
Задание 4 из варианта 2210311.
Игральный кубик бросают дважды. Известно, что в сумме выпало 11 очков. Найдите вероятность того, что во второй раз выпало 5 очков.
Задание 5.
Решите уравнение frac{x–1}{5x+11}=frac{x–1}{3x-7}. Если уравнение имеет больше одного корня, в ответе запишите больший из корней.
Задание 6.
Найдите значение выражения frac{(4^{frac{3}{5} }cdot7^{frac{2}{3}})^{15}}{28^{9}} .
Задание 6 из варианта 2210311.
Найдите 98cos2α, если cosα = frac{4}{7}.
Задание 7.
На рисунке изображён график y = f’(x) – производной функции f(x), определённой на интервале (−5; 5). В какой точке отрезка [−4; −1] функция f(x) принимает наибольшее значение?
Задание 8.
На верфи инженеры проектируют новый аппарат для погружения на небольшие глубины. Конструкция имеет кубическую форму, а значит, действующая на аппарат выталкивающая (архимедова) сила, выражаемая в ньютонах, будет определяться по формуле FA = ρgl3, где l – длина ребра куба в метрах, ρ = 1000 кг/м3 – плотность воды, а g – ускорение свободного падения (считайте, что g = 9,8 Н/кг). Какой может быть максимальная длина ребра куба, чтобы обеспечить его эксплуатацию в условиях, когда выталкивающая сила при погружении будет не больше чем 2116800 Н? Ответ дайте в метрах.
Задание 9.
Пристани A и B расположены на озере, расстояние между ними равно 280 км. Баржа отправилась с постоянной скоростью из A в B. На следующий день после прибытия она отправилась обратно со скоростью на 4 км/ч больше прежней, сделав по пути остановку на 8 часов. В результате она затратила на обратный путь столько же времени, сколько на путь из A в B. Найдите скорость баржи на пути из A в B. Ответ дайте в км/ч.
Задание 10.
На рисунке изображён график функции f(x) = ax2 + bx + c. Найдите значение f(−1).
Задание 10 из варианта 2210311.
На рисунке изображены графики функций f(x) = frac{k}{x} и g(x) = ax + b, которые пересекаются в точках A и B. Найдите абсциссу точки B.
Задание 11.
Найдите точку минимума функции y = x3 − 27x2 + 13.
Задание 12.
а) Решите уравнение 2cos3x = –sin(frac{3pi}{2} + x)
б) Найдите все корни этого уравнения, принадлежащие отрезку [3π; 4π]
Задание 13.
Основанием правильной пирамиды PABCD является квадрат ABCD. Сечение пирамиды проходит через вершину В и середину ребра PD перпендикулярно этому ребру.
а) Докажите, что угол наклона бокового ребра пирамиды к её основанию равен 60°.
б) Найдите площадь сечения пирамиды, если AB = 30.
Задание 14.
Решите неравенство frac{9^{x}–13cdot 3^{x}+30}{3^{x+2}–3^{2x+1}}ge frac{1}{3^{x}}.
Задание 15.
По вкладу «А» банк в конце каждого года планирует увеличивать на 13 % сумму, имеющуюся на вкладе в начале года, а по вкладу «Б» – увеличивать эту сумму на 7 % в первый год и на целое число n процентов за второй год. Найдите наименьшее значение n, при котором за два года хранения вклад «Б» окажется выгоднее вклада «А» при одинаковых суммах первоначальных взносов.
Задание 16.
В треугольнике ABC медианы AA1, BB1 и CC1 пересекаются в точке M. Известно, что AC = 3MB.
а) Докажите, что треугольник ABC прямоугольный.
б) Найдите сумму квадратов медиан AA1 и CC1, если известно, что AC = 22.
Задание 17.
Найдите все значения a, при каждом из которых система уравнений
begin{cases} (x-5a+1)^{2}+(y-2a-1)^{2}=a-2 \ 3x-4y=2a+3 end{cases}
не имеет решений.
Задание 18.
У Ани есть 800 рублей. Ей нужно купить конверты (большие и маленькие). Большой конверт стоит 32 рубля, а маленький – 25 рублей. При этом число маленьких конвертов не должно отличаться от числа больших конвертов больше чем на пять.
а) Может ли Аня купить 24 конверта?
б) Может ли Аня купить 29 конвертов?
в) Какое наибольшее число конвертов может купить Аня?
Источник варианта: СтатГрад/statgrad.org.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 5 / 5. Количество оценок: 2
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
ОГЭ 2023. Экзаменационная работа состоит из двух частей, включающие в себя 25 заданий. Часть 1 содержит 19 заданий, часть 2 содержит 6 заданий с развернутым ответом. На выполнение экзаменационной работы по математике отводится 3 часа 55 минут (235 минут).
В конце варианта приведены правильные ответы ко всем заданиям. Вы можете свериться с ними и найти у себя ошибки.
Скачать тренировочный вариант ОГЭ: Скачать
Интересные задания:
На плане изображено домохозяйство по адресу с. Иволгино, 5-й Заречный пер, д. 3 (сторона каждой клетки на плане равна 1 м). Участок имеет прямоугольную форму. Выезд и въезд осуществляются через единственные ворота. При входе на участок слева от ворот находится сарай, а справа – гараж. Площадь, занятая гаражом, равна 48 кв. м. Жилой дом находится в глубине территории. Помимо гаража, жилого дома и сарая, на участке имеется теплица, расположенная на территории огорода (огород отмечен на плане цифрой 5). Перед гаражом имеется площадка, вымощенная тротуарной плиткой размером 0,2 м × 0,1 м и отмеченная на плане цифрой 6.
1. Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, а в бланк перенесите последовательность четырёх цифр.
Ответ: 2143
2. Тротуарная плитка продаётся в упаковках по 40 штук. Сколько упаковок плитки понадобилось, чтобы выложить площадку перед гаражом?
Ответ: 68
3. Найдите расстояние между противоположными углами гаража (длину диагонали) в метрах.
Ответ: 10
4. Найдите площадь, которую занимает жилой дом. Ответ дайте в квадратных метрах.
Ответ: 108
5. Хозяин участка хочет сделать пристройку к дому. Для этого он планирует купить 15 тонн силикатного кирпича. Один кирпич весит 3 кг. Цена кирпича и условия доставки всей покупки приведены в таблице. Во сколько рублей обойдётся наиболее дешёвый вариант?
Ответ: 66300
7. На координатной прямой отмечены точки 𝐴, 𝐵, 𝐶, 𝐷. Одна из них соответствует числу √95. Какая это точка?
Ответ: 2
10. В среднем из 150 карманных фонариков, поступивших в продажу, три неисправных. Найдите вероятность того, что выбранный наудачу в магазине фонарик окажется исправен.
Ответ: 0,98
12. Мощность постоянного тока (в ваттах) вычисляется по формуле 𝑃 = 𝐼 2𝑅, где 𝐼 − сила тока (в амперах), 𝑅 − сопротивление (в омах). Пользуясь этой формулой, найдите сопротивление 𝑅, если мощность составляет 29,25 Вт, а сила тока равна 1,5 А. Ответ дайте в омах.
Ответ: 13
14. Известно, что на высоте 2205 м над уровнем моря атмосферное давление составляет 550 мм рт. ст. Считая, что при подъёме на каждые 10,5 м давление уменьшается примерно на 1 мм рт. ст., определите атмосферное давление на высоте 1890 м над уровнем моря.
Ответ: 580
15. Диагональ 𝐴𝐶 параллелограмма 𝐴𝐵𝐶𝐷 образует с его сторонами углы, равные 30° и 45°. Найдите больший угол этого параллелограмма. Ответ дайте в градусах.
Ответ: 105
16. Угол 𝐴 трапеции 𝐴𝐵𝐶𝐷 с основаниями 𝐴𝐷 и 𝐵𝐶, вписанной в окружность, равен 81°. Найдите угол 𝐶 этой трапеции. Ответ дайте в градусах.
Ответ: 99
17. В треугольнике 𝐴𝐵𝐶 известно, что 𝐴𝐵 = 6, 𝐵𝐶 = 10, sin ∠𝐴𝐵𝐶 = 1 3 . Найдите площадь треугольника 𝐴𝐵𝐶.
Ответ: 10
18. На клетчатой бумаге с размером клетки 1 × 1 отмечены три точки: 𝐴, 𝐵 и 𝐶. Найдите расстояние от точки 𝐴 до середины отрезка 𝐵𝐶.
Ответ: 3
19. Какое из следующих утверждений верно?
1) Через точку, не лежащую на данной прямой, можно провести прямую, перпендикулярную этой прямой.
2) В любой прямоугольник можно вписать окружность.
3) Каждая из биссектрис равнобедренного треугольника является его медианой.
Ответ: 1
21. Первый рабочий за час делает на 10 деталей больше, чем второй, и выполняет заказ, состоящий из 60 деталей, на 3 часа быстрее, чем второй рабочий, выполняющий такой же заказ. Сколько деталей в час делает второй рабочий?
Ответ: 10
23. Окружность пересекает стороны 𝐴𝐵 и 𝐴𝐶 треугольника 𝐴𝐵𝐶 в точках 𝐾 и 𝑃 соответственно и проходит через вершины 𝐵 и 𝐶. Найдите длину отрезка 𝐾𝑃, если 𝐴𝑃 = 36, а сторона 𝐵𝐶 в 1,8 раза меньше стороны 𝐴𝐵.
Ответ: 20
24. Биссектрисы углов 𝐴 и 𝐷 параллелограмма 𝐴𝐵𝐶𝐷 пересекаются в точке 𝐾, лежащей на стороне 𝐵𝐶. Докажите, что 𝐾 − середина 𝐵𝐶.
25. В треугольнике 𝐴𝐵𝐶 известны длины сторон 𝐴𝐵 = 84, 𝐴𝐶 = 98, точка 𝑂 − центр окружности, описанной около треугольника 𝐴𝐵𝐶. Прямая 𝐵𝐷, перпендикулярная прямой 𝐴𝑂, пересекает сторону 𝐴𝐶 в точке 𝐷. Найдите 𝐶𝐷.
Ответ: 26
Вам будет интересно:
ОГЭ по Математике 9 класс 2023. Новый типовой тренировочный вариант №3 — №221003 (задания и ответы)
* Олимпиады и конкурсы
* Готовые контрольные работы
* Работы СтатГрад
* Официальные ВПР
Поделиться: