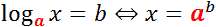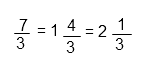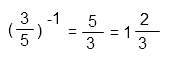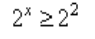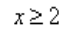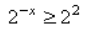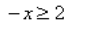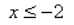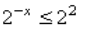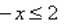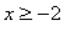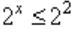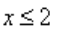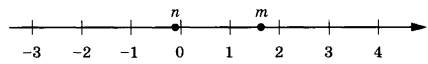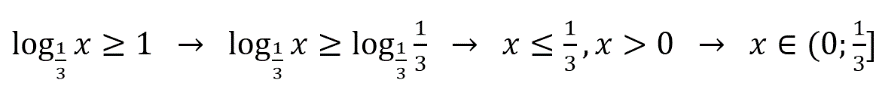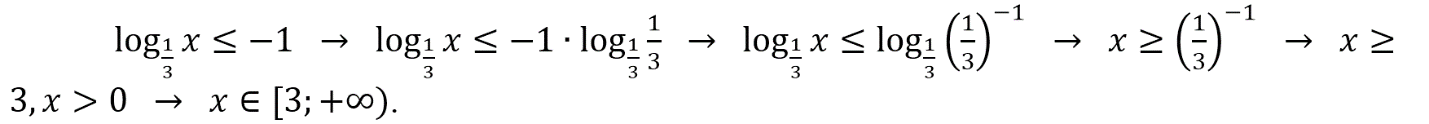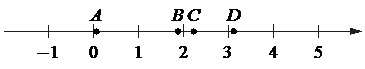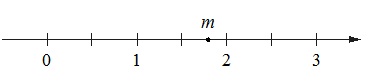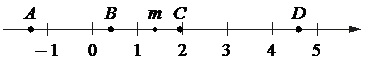При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
Версия для печати и копирования в MS Word
1
Только 57% из 23 000 выпускников города правильно решили задачу B9. Сколько человек правильно решили задачу B9?
Ответ:
2
Городской бюджет составляет 27 млн рублей, а расходы на одну из его статей составили 10%. Сколько рублей потрачено на эту статью бюджета?
Номер в банке ФИПИ: CA1206
Ответ:
3
В начале года число абонентов телефонной компании «Восток» составляло 800 тыс. человек, а в конце года их стало 880 тыс. человек. На сколько процентов увеличилось за год число абонентов этой компании?
Номер в банке ФИПИ: 28D0FF
Ответ:
4
Клиент взял в банке кредит 60 000 рублей на год под 17% годовых. Он должен погашать кредит, внося в банк ежемесячно одинаковую сумму денег, с тем чтобы через год выплатить всю сумму, взятую в кредит, вместе с процентами. Сколько рублей он должен вносить в банк ежемесячно?
Ответ:
5
14 выпускников школы собираются учиться в технических вузах. Они составляют 28% от числа всех выпускников. Сколько в школе выпускников?
Ответ:
6
Магазин делает пенсионерам скидку на определённое количество процентов от стоимости покупки. Батон хлеба стоит в магазине 15 рублей, а пенсионер заплатил за него 13 рублей 80 копеек. Сколько процентов составляет скидка для пенсионера?
Ответ:
7
Держатели дисконтной карты книжного магазина получают при покупке скидку 3%. Книга стоит 300 рублей. Сколько рублей заплатит держатель дисконтной карты за эту книгу?
Ответ:
8
Магазин делает пенсионерам скидку на определенное количество процентов от цены покупки. Пакет кефира стоит в магазине 40 рублей. Пенсионер заплатил за пакет кефира 38 рублей. Сколько процентов составляет скидка для пенсионеров?
Ответ:
9
Клиент взял в банке кредит 12 000 рублей на год под 16%. Он должен погашать кредит, внося в банк ежемесячно одинаковую сумму денег, с тем чтобы через год выплатить всю сумму, взятую в кредит, вместе с процентами. Сколько рублей он должен вносить в банк ежемесячно?
Ответ:
10
Налог на доходы физических лиц (НДФЛ) в РФ составляет 13% от начисленной заработной платы. Сколько рублей получает работник после уплаты НДФЛ, если начисленная заработная плата составляет 20 000 рублей?
Ответ:
11
Футболка стоила 360 рублей. После повышения цены она стала стоить 378 рублей. На сколько процентов была повышена цена на футболку?
Ответ:
12
Железнодорожный билет для взрослого стоит 720 рублей. Стоимость билета для школьника составляет 50% от стоимости билета для взрослого. Группа состоит из 15 школьников и 2 взрослых. Сколько рублей стоят билеты на всю группу?
Ответ:
13
Флакон шампуня стоит 160 рублей. Какое наибольшее число флаконов можно купить на 1000 рублей во время распродажи, когда скидка составляет 25% ?
Ответ:
14
Магазин делает пенсионерам скидку на определенное количество процентов от цены покупки. Упаковка пельменей стоит в магазине 75 рублей. Пенсионер заплатил за упаковку пельменей 72 рубля. Сколько процентов составляет скидка для пенсионеров?
Ответ:
15
В сентябре 1 кг огурцов стоил 50 рублей, в октябре огурцы подорожали на 20%, а в ноябре еще на 20%. Сколько рублей стоил 1 кг огурцов после подорожания в ноябре?
Ответ:
16
В начале года число абонентов телефонной компании «Восток» составляло 400 тыс. человек, а в конце года их стало 480 тыс. человек. На сколько процентов увеличилось за год число абонентов этой компании?
Ответ:
17
Рост Джона 6 футов 1 дюйм. Выразите рост Джона в сантиметрах, если в 1 футе 12 дюймов, а в 1 дюйме 2,54 см. Результат округлите до целого числа сантиметров.
Ответ:
18
Налог на доходы составляет 13% от заработной платы. После удержания налога на доходы Мария Константиновна получила 10 005 рублей. Сколько рублей составляет заработная плата Марии Константиновны?
Ответ:
19
Цена на электрический чайник была повышена на 16% и составила 3480 рублей. Сколько рублей стоил чайник до повышения цены?
Ответ:
20
Цена на электрический чайник была повышена на 17% и составила 1755 рублей. Сколько рублей стоил чайник до повышения цены?
Ответ:
Завершить тестирование, свериться с ответами, увидеть решения.
Неравенства и сравнения
В семнадцатом задании нам необходимо сравнить данные числа с положением на координатной прямой или решить и сопоставить решения неравенств с областью на прямой. В данном задании можно пользоваться правилом исключения, поэтому достаточно правильно определить три решения из четырех, выбирая в первую очередь простые. Итак, приступим к разбору 17 задания базового варианта ЕГЭ по математике.
Разбор типовых вариантов заданий №17 ЕГЭ по математике базового уровня
Вариант 17МБ1
На координатной прямой отмечены точки A, B, C и D.
Каждой точке соответствует одно из чисел в правом столбце. Установите соответствие между указанными точками и числами.
| ТОЧКИА
В С D |
ЧИСЛА1) log2 10
2) 7/3 3) √26 4) (3/5)-1 |
Алгоритм выполнения:
- Проанализировать рядом с каким из целых чисел стоит данная точка.
- Проанализировать на каком интервале лежат числа из правого столбца.
- Сравнить полученные интервалы и поставить в соответствие.
Решение:
- Рассмотрим точку А. Ее значение больше 1 и меньше 2.
- Рассмотрим точку B. Ее значение больше 2 и меньше 3.
- Рассмотрим точку С. Ее значение больше 3 и меньше 4.
- Рассмотрим точку D. Ее значение больше 5 и меньше 6.
- Вспомним что такое логарифм.
Логарифм по основанию a от аргумента x — это степень, в которую надо возвести число a, чтобы получить число x.
Обозначение: loga x = b, где a — основание, x — аргумент, b — собственно, чему равен логарифм.
В нашем случае а = 2, x = 10.
То есть нас интересует число 2b = 10. 23 = 8 и 24 = 16, следовательно, b лежит в промежутке от 3 до 4.
Следовательно, 7/3 больше 2 и меньше 3.
Рассмотрим √26. √25 = 5, √36 = 6. Значит, √26 больше 5 и меньше 6.
То есть (3/5)-1 больше 1 и меньше 2.
Поставим в соответствие полученные интервалы.
А — (3/5)-1 — 4
В — 7/3 – 2
С — log2 10 – 1
D — √26 – 3
Ответ: 4213.
Вариант 17МБ2
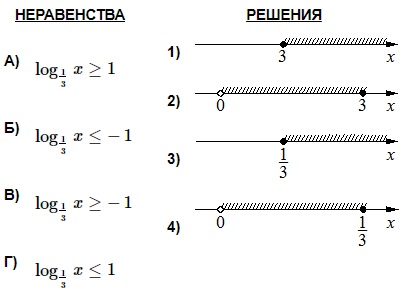
Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
Алгоритм выполнения:
- Представить правые и левые части неравенств в виде степени одного и того же числа.
- Сравнить степени, так как основания равны.
- Поставить в соответствие предложенные интервалы.
Решение:
А)
Представим 4 в виде степени с основанием 2. 22 = 4.
Неравенство примет вид:
Основания степеней одинаковы, следовательно, степени соотносятся так же.
то есть, 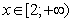
Б)
Число 0,5 можно представить как 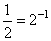
Неравенство примет вид:
Основания степеней одинаковы, следовательно, степени соотносятся так же.
Если умножить и правую и левую часть неравенства на -1, то знак изменится на противоположный.
то есть, 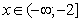
В)
Аналогично с вариантом Б.
Число 0,5 можно представить как 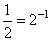
Неравенство примет вид:
Основания степеней одинаковы, следовательно, степени соотносятся так же.
Если умножить и правую и левую часть неравенства на -1, то знак изменится на противоположный.
то есть, 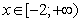
Г)
Представим 4 в виде степени с основанием 2. 22 = 4.
Неравенство примет вид:
Основания степеней одинаковы, следовательно, степени соотносятся так же.
и 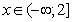
Ответ: 2143.
Вариант 17МБ3
На прямой отмечены числа m и n.
Каждому из четырёх чисел в левом столбце соответствует отрезок, которому оно принадлежит. Установите соответствие между числами и отрезками из правого столбца.
Алгоритм выполнения:
- Найти промежутки в которых лежат числа m и n.
- Оценить интервалы, в которых лежат выражения в левом столбце.
- Поставить им в соответствие интервалы из правого столбца.
Решение:
Из рисунка видно, что число n немного меньше 0, а число m много больше отстоит от 1. Следовательно, их сумма m+n даст число в пределах [1; 2] – вариант ответа под номером 3.
Число m>1, следовательно, при делении на 1 получим положительное число меньше 1. Добавляя небольшое отрицательное значение n останемся в диапазоне [0; 1]. Вариант ответа 2.
Произведение mn положительного и отрицательного чисел дают отрицательное число. Подходит только один вариант [-1; 0] под номером 1.
Г) Квадрат числа m много больше квадрата числа n, поэтому их разница будет положительной и принадлежать диапазону [2; 3] – вариант под номером 4.
Ответ: 3214.
Вариант 17МБ4
Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
Рассмотрим первое неравенство:
2x≥4
представим 4 как 22, тогда:
2x ≥ 22
x ≥ 2
Остальные неравенства решаются аналогичным образом, достаточно вспомнить, что 0,5 = ½ = 2-1:
2-x ≥ 4
2-x ≥ 22
-x ≥ 2
x≤-2
Ответ: А-4, Б-3, В-2, А-1.
Вариант 17МБ5
Каждому из четырех неравенств в левом столбце соответствует одно из решений в правом столбце. Установить соответствие между неравенствами и их решениями.
Алгоритм выполнения
- Решаем по очереди каждое из неравенств (А–Г). При необходимости (для наглядности) отображаем полученное решение на координатной прямой.
- Записываем результаты в форме, которая предложена в столбце «Решения». Находим соответствующие пары «буква–число».
Решение:
А. 2–х+1 < 0,5 → 2–x+1 < 2–1 → –x+1 < –1 → –x < –2 → x > 2. Ответ: х ϵ (2; +∞). Получаем: А–3.
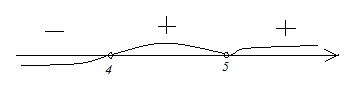
Б.
Неравенство преобразований не требует, поэтому сразу применяем метод интервалов, отобразив корни неравенства на координатной прямой.
Корни в данном случае – это х=4 и х=5. Имеем в виду, что неравенство строгое, т.е. значения корней в промежуток для ответа не включаем. В точке х=5 перехода знака не происходит, т.к. по условию (х–5) дано в квадрате. Поскольку нам нужен промежуток, где х<0, то ответ в данном случае: х ϵ (–∞; 4).
Соответственно, имеем: Б–4.
В. log4x > 1 → log4x > log44 → x > 4. Т.е.: х ϵ (4; +∞). Ответ: В–1.
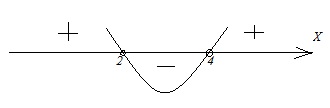
Г. (х–4)(х–2) < 0. Здесь так же, как и в неравенстве Б, нужно сразу отобразить решение на координатной прямой.
Неравенство дано квадратное, его корни – х=2 и х=4. Для получения промежутков с положительными и отрицательными значениями схематически изображаем параболу, пересекающую координатную прямую в точках корней. Промежуток «внутри» параболы отрицательный, промежутки «вне» ее положительны. Т.к. в неравенстве дано «<0», то для ответа следует взять промежуток отрицательных значений. Учитываем, что неравенство строгое. Получаем: х ϵ (2; 4).
Ответ: Г–2.
Вариант 17МБ6
На координатной прямой отмечены точки А, В, С и D.
Число m равно √2.
Каждой точке соответствует одно из чисел в правом столбце. Установите соответствие между указанными точками и числами.
Алгоритм выполнения
Для каждого из выражений правого столбца делаем следующее:
- Подставляем вместо m его числовое значение (√2). Вычисляем приблизительное значение.
- Ориентируясь на целую часть полученного числа, находим соответствующее значение на координатной прямой.
- Фиксируем пару «буква–число».
Решение:
Это значение на прямой находится между значениями –3 и –2 и соответствует точке А. Получили: А–1.
Число находится между значениями 2 и 3 и соответствует точке D. Имеем: D–2.
Число находится на прямой между 0 и 1. Это – точка С. Имеем: С–3.
Число размещается на прямой между значениями –1 и 0, что отображает т.В. Получаем: В–4.
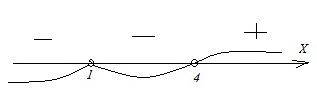
Вариант 17МБ7
Каждому из четырех неравенств в левом столбце соответствует одно из решений в правом столбце. Установить соответствие между неравенствами и их решениями.
Алгоритм выполнения
- Последовательно решаем каждое неравенство (А–Г), получая в ответе промежуток значений. Находим соответствующее ему графическое отображение в правой колонке (Решения).
- При решении неравенств учитываем, что: 1) при снятии знаков логарифма с основанием, меньшим 1, знак неравенства меняется на противоположный; 2) выражение под знаком логарифма всегда больше 0.
Решение:
А.
Полученный промежуток-ответ отображен на 4-й координатной прямой. Поэтому имеем: А–4.
Б.
Полученный промежуток представлен на 1-й прямой. Отсюда имеем: Б–1.
В. Это неравенство аналогично предыдущему (Б) с разницей исключительно в знаке. Поэтому и ответ будет подобен с той только разницей, что в конечном неравенстве будет противоположный знак. Т.е. получим: х ≤ 3, х > 0 → x ϵ (0; 3]. Соответственно, получаем пару: В–2.
Г. Это неравенство аналогично 1-му (А), но с противоположным знаком. Поэтому ответ здесь будет таким: х ≥ 1/3, х > 0 → х ϵ [1/3; +∞). Т.о., ответ: Г–3.
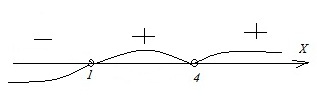
Вариант 17МБ8
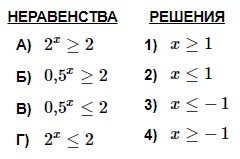
Каждому из четырех неравенств в левом столбце соответствует одно из решений в правом столбце. Установить соответствие между неравенствами и их решениями.
Алгоритм выполнения
- Решаем неравенство А. Находим номер соответствующего ответу решения из правой колонки.
- Рассматриваем неравенство Г как подобное неравенству А. Определяем для него номер решения из правого столбца.
- Решаем неравенство Б, перейдя к основанию 2. Определяем соответствующий для него номер варианта решения.
- По аналогии с неравенством Б решаем неравенство В.
Решение:
А. 2х ≥ 2 → 2х ≥ 21 → х ≥ 1. Имеем: А–1.
Г. По аналогии с неравенством А получаем в ответе: х ≤ 1. Имеем: Г–2.
Б. 0,5х ≥ 2 → (1/2)х ≥ 2 →2–х ≥ 21 х ≤ –1. Имеем: Б–3.
В. По аналогии с неравенством Б получаем в ответе: х ≥ –1. Имеем: В–4.
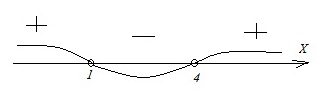
Вариант 17МБ9
Каждому из четырех неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
Алгоритм выполнения
- Подобные неравенства решаются методом интервалов. На координатной прямой отмечаются точки, являющиеся корнями соответствующего кв.ур-ния; промежутки между этими точками имеют определенные знаки, причем 1-й из них справа (от +∞ до самого большого корня) всегда имеет знак «+». Далее, продвигаясь справа налево, знаки чередуем, т.е. 2-й справа промежуток будет иметь знак «–», 3-й – «+» и т.д.
- Если в неравенстве имеется выражение вида (х–а)2, то знак промежутка при прохождении точки а не меняется.
- Поскольку все неравенства строгие, то точки-корни в промежутки для ответов не включаются, что в результате фиксируется посредством круглых скобок.
- Знак «ᴗ» является объединяющим и должен прочитываться как «или».
Решение:
Корнями в этих неравенствах являются х=1 и х=4.
Для неравенства А на прямой имеем:
Результатом здесь будут промежутки с отрицательным знаком, т.е. х < 1 или 1 < x < 4. Ответ: А–3.
Для неравенств Б и В получаем на прямой:
Для ответа в неравенстве Б следует взять промежутки со знаком «+». Получим: х < 1 или x > 4. Ответ: Б–1.
В неравенстве В нужно взять промежуток с отрицательным знаком. Тогда имеем: 1 < x < 4. Ответ: В–4.
Б. Отмечаем на прямой корни и промежутки с соответствующими знаками:
Для неравенства Г на прямой получили:
Результат – промежутки с положительным знаком. Тогда имеем: 1 < x < 4 или x > 4. Ответ: Г–2.
Вариант 17МБ10
На координатной прямой отмечены точки А, В, С и D.
Каждой точке соответствует одно из чисел в правом столбце. Установите соответствие между указанными точками и числами.
Алгоритм выполнения
- Определяем приблизительное значение чисел, приведенных в правом столбце, или их целую часть, что позволит выяснить, между какими двумя целыми числами на координатной прямой они располагаются.
- Фиксируем пары «буква–число» для заполнения итоговой таблицы ответов.
Решение:
Число 1. log55=1, log525=log552=2log55=2·1=2. Т.к. 5<20<25, то 1<log520<2. Значит, на координатной прямой число log520 отображено точкой В. Ответ: В–1.
Число 2. . Это означает, что число отображено на прямой точкой С. Ответ: С–2.
Число 3. √10 совсем немного больше, чем √9=3. Это число точно меньше 4, поскольку 4=√16. Соответственно, √10 на прямой расположен между 3 и 4 и отображен точкой D. Ответ: D–3.
Число 4. 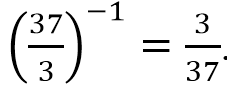
Вариант 17МБ11
Каждому из четырех неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
Алгоритм выполнения
- Решаем последовательно неравенства А–Г, учитывая ОДЗ.
- По результату (полученному простейшему неравенству) находим соответствующее графическое решение из правого столбца.
Решение:
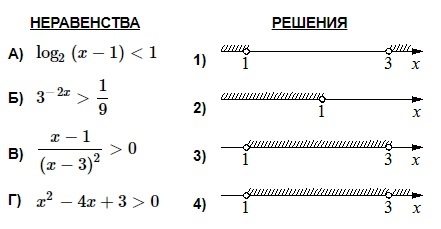
- log2 (x–1) < 1 → log2 (x–1) < log2 2 → x–1 < 2 → x < 3. ОДЗ: х–1 > 0 → x > 1.
Объединяем полученный промежуток с ОДЗ, получаем: x ϵ (1; 3). Это соответствует решению №3. Ответ: А–3.
- . ОДЗ не дает ограничений
Тогда в результате имеем: х ϵ (1; +∞). Ответ: Б–2.
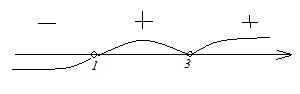
- Здесь не требуются преобразования. Решается неравенство методом интервалов. Точки пересечения с координатной прямой: х=1, х=3. Тогда имеем:
Для решения требуется взять промежутки с положительным знаком. ОДЗ: х≠3. Получаем: х ϵ (1; 3)ᴗ(3; +∞). Ответ: В–4.
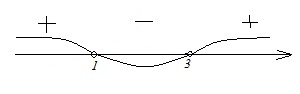
- х2 – 4х + 3 > 0 → (x–1)(x–3) > 0. Применив метод интервалов, получим:
ОДЗ не дает ограничений. Значит, х ϵ (–∞; 1)ᴗ(3; +∞). Ответ: Г–1.
Вариант 17МБ12
На координатной прямой отмечено число m.
Каждому из четырех чисел в левом столбце соответствует отрезок, которому оно принадлежит. Установите соответствие между числами и отрезками из правого столбца.
Алгоритм выполнения
- Определяем приблизительное значение для m.
- Подставляем найденное значение для m последовательно в каждое из выражений (А–Г), вычисляем их числовые значения.
- Сопоставляем полученные числа с отрезками, предложенными в правом столбце, находим пары «буква–число» для ответа.
Решение:
Число m располагается на прямой между 1,5 и 2 и немного смещено от середины этого отрезка к двойке. Следовательно, наиболее точным для него является 1,8.
Число А. Имеем: √1,8. Известно, что √1=1, √2≈1,4. Т.е. √1,8 наверняка располагается на отрезке между 1 и 2. Ответ: А–1.
Число Б. Оно равно: 1,83=5,832, т.е. это число принадлежит промежутку [5; 6]. Ответ: Б–4.
Число В. Это число равно: 1,8+1=2,8, что соответствует отрезку [2; 3]. Ответ: В–2.
Число Г. Тут получаем: 6/1,8≈3,33. Этому значению соответствует отрезок [3; 4]. Ответ: Г–3.
Вариант 17МБ13
Число m равно √0,15.
Каждому из четырех чисел в левом столбце соответствует отрезок, которому оно принадлежит. Установите соответствие между числами и отрезками из правого столбца.
Алгоритм выполнения
- Преобразуем число m так, чтобы вынести значение из-под корня.
- Подставляем последовательно полученную величину для m в каждое из выражений в левом столбце. Получаемые результаты соотносим с подходящим отрезком из правого.
Решение:
Число √0,15 очень немногим отличается от √0,16, а из 0,16 можно точно извлечь корень. Делая подобное приближение – всего на 0,01 – мы не выходим за пределы приемлемой абсолютной погрешности. Поэтому имеем право принять, что √0,15≈√0,16=0,4.
Находим значения выражений А–Г и определяем их соответствия отрезкам:
А. –1/0,4=–2,5. Результат соответствует отрезку [–3; –2]. Ответ: А–1.
Б. 0,42=0,16. Число входит в промежуток [0; 1]. Ответ: Б–3.
В. 4·0,4=1,6. Это число находится в интервале [1; 2]. Ответ: В–4.
Г. 0,4–1=–0,6. Результат попадает на отрезок [–1; 0]. Ответ: Г–2.
Вариант семнадцатого задания 2019 года (10)
На координатной прямой отмечено число m и точки А, В, С и D.
Каждой точке соответствует одно из чисел в правом столбце. Установите соответствие между указанными точками и числами.
Алгоритм выполнения
- Определяем приблизительное значение для m.
- Вычисляем значения выражений 1–4, находим соответствие между полученными результатами и точками А–D на координатной прямой.
Решение:
Точка m располагается почти посередине между 1 и 2, но немного ближе к 1, чем к 2. Максимально приближенным к реальному в данном случае следует считать значение m=1,4.
Определяем соответствие чисел и точек на прямой:
- 6–1,4=4,6. Это значение отображено точкой D. Ответ: D–1.
- 1,42=1,96. Такое число отображается в точке С. Ответ: С–2.
- 1,4–1=0,4. Это число соответствует точке В. Ответ: В–3.
- Здесь можно не вычислять результат, поскольку имеет место единственное отрицательное число, а на прямой обозначена единственная точка слева от 0 – т.А. Ответ: А–4.
Стереометрия на Профильном ЕГЭ по математике, 1 часть, основные типы
Стереометрия на ЕГЭ. Вычисление объемов и площадей поверхности

- Куб, параллелепипед, призма, пирамида. Объем и площадь поверхности
- Цилиндр, конус, шар. Объем и площадь поверхности
Часто в задачах ЕГЭ, посвященных стереометрии, требуется посчитать объем тела или площадь его поверхности. Или как-то использовать эти данные. Поэтому заглянем в толковый словарь русского языка и уточним понятия.
Объем — величина чего-нибудь в длину, ширину и высоту, измеряемая в кубических единицах.
Другими словами, чем больше объем, тем больше места тело занимает в трехмерном пространстве.
Площадь — величина чего-нибудь в длину и ширину, измеряемая в квадратных единицах.
Представьте себе, что вам нужно оклеить всю поверхность объемного тела. Сколько квадратных сантиметров (или метров) вы бы обклеили? Это и есть его площадь поверхности.
Объемные тела — это многогранники (куб, параллелепипед, призма, пирамида) и тела вращения (цилиндр, конус, шар).
Если в задаче по стереометрии речь идет о многограннике, вам встретятся термины «вершины», «грани» и «ребра». Вот они, на картинке.
Чтобы найти площадь поверхности многогранника, сложите площади всех его граней.
Вам могут также встретиться понятия «прямая призма», правильная призма», «правильная пирамида».
Прямой называется призма, боковые ребра которой перпендикулярны основанию.
Если призма — прямая и в ее основании лежит правильный многоугольник, призма будет называться правильной.
А правильная пирамида — такая, в основании которой лежит правильный многоугольник, а вершина проецируется в центр основания.
Перейдем к практике.
1. Одна из распространенных задач в части 1 — такая, где надо посчитать объем или площадь поверхности многогранника, из которого какая-нибудь часть вырезана. Например, такого:
Что тут нарисовано? Очевидно, это большой параллелепипед, из которого вырезан «кирпичик», так что получилась «полочка». Если вы увидели на рисунке что-то другое — обратите внимание на сплошные и штриховые линии. Сплошные линии — видимы. Штриховыми линиями показываются те ребра, которые мы не видим, потому что они находятся сзади.
Объем найти просто. Из объема большого «кирпича» вычитаем объем маленького. Получаем:
А как быть с площадью поверхности? Почему-то многие школьники пытаются посчитать ее по аналогии с объемом, как разность площадей большого и малого «кирпичей». В ответ на такое «решение» я обычно предлагаю детскую задачу — если у четырехугольного стола отпилить один угол, сколько углов у него останется? 
На самом деле нам нужно посчитать сумму площадей всех граней — верхней, нижней, передней, задней, правой, левой, а также сумму площадей трех маленьких прямоугольников, которые образуют «полочку». Можно сделать это «в лоб», напрямую. Но есть и способ попроще.
Прежде всего, если бы из большого параллелепипеда ничего не вырезали, его площадь поверхности была бы равна . А как повлияет на него вырезанная «полочка»?
Давайте посчитаем сначала площадь всех горизонтальных участков, то есть «дна», «крыши» и нижней поверхности «полочки». С дном — все понятно, оно прямоугольное, его площадь равна .
А вот сумма площадей «крыши» и горизонтальной грани «полочки» тоже равна ! Посмотрите на них сверху.
…В этот момент и наступает понимание. Кому-то проще нарисовать вид сверху. Кому-то — представить, что мы передвигаем дно и стенки полочки и получаем целый большой параллелепипед, площадь поверхности которого равна . Каким бы способом вы ни решали, результат один — площадь поверхности будет такой же, как и у целого параллелепипеда, из которого ничего не вырезали.
Ответ: .
2. Следующую задачу, попроще, вы теперь решите без труда. Здесь тоже надо найти площадь поверхности многогранника:
. Из площади поверхности «целого кирпича» вычитаем площади двух квадратиков со стороной
— на верхней и нижней гранях.
Ответ: 92.

Сначала посчитайте сумму площадей всех граней. Представьте, что вы дизайнер, а эта штучка — украшение. И вам надо оклеить эту штуку чем-то ценным, например, бриллиантами Сваровски. И вы их покупаете на свои деньги. (Я не знаю почему, но эта фраза мгновенно повышает вероятность правильного ответа!) Оклеивайте все грани плитки. Но только из площадей передней и задней граней вычтите площадь «окошка». А затем — само «окошко». Оклеивайте всю его «раму».
Ответ: .
Следующий тип задач — когда одно объемное тело вписано в другое.
4. Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны . Найдите объем параллелепипеда.
Прежде всего, заметим, что высота цилиндра равна высоте параллелепипеда. Нарисуйте вид сверху, то есть круг, вписанный в прямоугольник. Тут сразу и увидите, что этот прямоугольник — на самом деле квадрат, а сторона его в два раза больше, чем радиус вписанной в него окружности. Итак, площадь основания параллелепипеда равна , высота равна
, объем равен
.
Ответ: 4.

и
. Боковые ребра равны
. Найдите объем цилиндра, описанного около этой призмы. В ответ запишите
.
Очевидно, высота цилиндра равна боковому ребру призмы, то есть . Осталось найти радиус его основания.
Рисуем вид сверху. Прямоугольный треугольник вписан в окружность. Где будет находиться радиус этой окружности? Правильно, посередине гипотенузы. Гипотенузу находим по теореме Пифагора, она равна . Тогда радиус основания цилиндра равен пяти. Находим объем цилиндра по формуле и записываем ответ:
.
Ответ: 100.
6. В прямоугольный параллелепипед вписан шар радиуса . Найдите объем параллелепипеда.
Эта задача тоже проста. Нарисуйте вид сверху. Или сбоку. Или спереди. В любом случае вы увидите одно и то же — круг, вписанный в прямоугольник. Очевидно, этот прямоугольник будет квадратом. Можно даже ничего не рисовать, а просто представить себе шарик, который положили в коробочку так, что он касается всех стенок, дна и крышки. Ясно, что такая коробочка будет кубической формы. Длина, ширина и высота этого куба в два раза больше, чем радиус шара.
Ответ: .
Следующий тип задач — такие, в которых увеличили или уменьшили какой-либо линейный размер (или размеры) объемного тела. А узнать нужно, как изменится объем или площадь поверхности.

см. На какой высоте будет находиться уровень воды, если ее перелить в другой такой же сосуд, у которого сторона основания в
раза больше, чем у первого? Ответ выразите в сантиметрах.
Слова «другой такой же сосуд» означают, что другой сосуд тоже имеет форму правильной треугольной призмы. То есть в его основании — правильный треугольник, у которого все стороны в два раза больше, чем у первого. Мы уже говорили о том, что площадь этого треугольника будет больше в раза. Объем воды остался неизменным. Следовательно, в
раза уменьшится высота.
Ответ: .

Давайте вспомним, как мы решали стандартные задачи, на движение и работу. Мы рисовали таблицу, верно? И здесь тоже нарисуем таблицу. Мы помним, что объем цилиндра равен .
| Высота | Радиус | Объем | |
| Первая кружка | |||
| Вторая кружка |
Считаем объем второй кружки. Он равен . Получается, что он в два раза больше, чем объем первой.

9. Через среднюю линию основания треугольной призмы, объем которой равен , проведена плоскость, параллельная боковому ребру. Найдите объем отсеченной треугольной призмы.
Высота меньшей призмы такая же, как и у большой. А какой же будет ее площадь основания? Очевидно, в раза меньше. Вспомните свойство средней линии треугольника — она равна половине основания. Значит, объем отсеченной призмы равен
.

10. Во сколько раз увеличится площадь поверхности октаэдра, если все его ребра увеличить в раза?
Только не надо обмирать от ужаса при слове «октаэдр». Тем более — он здесь нарисован и представляет собой две сложенные вместе четырехугольные пирамиды. А мы уже говорили — если все ребра многогранника увеличить в три раза, площадь поверхности увеличится в раз, поскольку
.
Ответ: .

11. Найдите объем части цилиндра, изображенной на рисунке. Радиус цилиндра равен 15, высота равна 5. В ответе укажите
.
Изображен не целый цилиндр, а его часть. Из него, как из круглого сыра, вырезали кусок. Надо найти объем оставшегося «сыра».
Какая же часть цилиндра изображена? Вырезан кусок с углом градусов, а
— это одна шестая часть полного круга. Значит, от всего объема цилиндра осталось пять шестых. Находим объем всего цилиндра, умножаем на пять шестых, делим на
, записываем ответ:
.
Продолжение: другие типы задач по стереометрии. Удачи вам в подготовке к ЕГЭ!
Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Стереометрия на Профильном ЕГЭ по математике, 1 часть, основные типы» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
08.03.2023
Новые тренировочные варианты ЕГЭ 2023 по математике базовый и профильный уровень с ответами и решением для 10 и 11 класса, больше 100 вариантов в формате реального экзамена ФИПИ вы можете решать онлайн или скачать.
Тренировочные варианты ЕГЭ 2023 по математике база и профиль
13.09.2022 Тренировочный вариант №1 ЕГЭ 2023 по математике профиль с ответами
20.09.2022 Тренировочный вариант №2 ЕГЭ 2023 по математике профиль с ответами
20.09.2022 Тренировочный вариант №2 ЕГЭ 2023 база по математике с ответами
27.09.2022 Математика 11 класс профиль входная мониторинговая работа 3 варианта с ответами
28.09.2022 Тренировочный вариант №3 ЕГЭ 2023 база по математике с ответами
28 сентября 2022 Статград математика 11 класс ЕГЭ 2023 база и профиль варианты и ответы
29 сентября 2022 Тренировочный вариант №3 ЕГЭ 2023 по математике профиль с ответами
1 октября 2022 Ларин вариант 399 ЕГЭ 2023 по математике профиль решение с ответами
6 октября Тренировочный вариант №4 ЕГЭ 2023 база по математике с ответами
6 октября Тренировочный вариант №4 ЕГЭ 2023 по математике профиль с ответами
8 октября Ларин вариант 400 ЕГЭ 2023 по математике профиль решение с ответами
12 октября Тренировочный вариант №5 ЕГЭ 2023 база по математике с ответами
12 октября Тренировочный вариант №5 ЕГЭ 2023 по математике профиль с ответами
14 октября Вариант 1 Ященко ЕГЭ 2023 математика профиль с ответами и решением
14 октября Вариант 2 Ященко ЕГЭ 2023 математика профиль с ответами и решением
15 октября Ларин вариант 401 ЕГЭ 2023 по математике профиль решение с ответами
15 октября Ларин вариант 402 ЕГЭ 2023 по математике профиль решение с ответами
16 октября Вариант 3 Ященко ЕГЭ 2023 математика профиль с ответами и решением
16 октября Вариант 4 Ященко ЕГЭ 2023 математика профиль с ответами и решением
23 октября Тренировочный вариант №6 ЕГЭ 2023 база по математике с ответами
24 октября Тренировочный вариант №6 ЕГЭ 2023 по математике профиль с ответами
25 октября Тренировочный вариант №7 ЕГЭ 2023 база по математике с ответами
26 октября Тренировочный вариант №7 ЕГЭ 2023 по математике профиль с ответами
28 октября Ларин вариант 403 ЕГЭ 2023 по математике профиль решение с ответами
29 октября Ларин вариант 404 ЕГЭ 2023 по математике профиль решение с ответами
1 ноября 2022 Тренировочный вариант №8 решу ЕГЭ 2023 база по математике с ответами
1 ноября 2022 Тренировочный вариант №8 решу ЕГЭ 2023 по математике профиль с ответами
5 ноября 2022 Вариант 1-2 распечатай и реши ЕГЭ 2023 база по математике 11 класс с ответами
6 ноября 2022 Ларин вариант 405 ЕГЭ 2023 профиль по математике решение с ответами
9 ноября 2022 Тренировочный вариант №9 решу ЕГЭ 2023 база по математике с ответами
12 ноября 2022 Тренировочный вариант №9 решу ЕГЭ 2023 по математике профиль с ответами
13 ноября 2022 Ларин вариант 406 ЕГЭ 2023 профиль по математике решение с ответами
15 ноября 2022 Тренировочный вариант №10 решу ЕГЭ 2023 база по математике 11 класс с ответами
15 ноября 2022 Тренировочный вариант №10 решу ЕГЭ 2023 по математике профиль с ответами
21 ноября 2022 Ларин вариант 407 ЕГЭ 2023 профиль по математике решение с ответами
23 ноября 2022 Тренировочный вариант №11 решу ЕГЭ 2023 база по математике 11 класс с ответами
23 ноября 2022 Тренировочный вариант №11 решу ЕГЭ 2023 по математике профиль с ответами
27 ноября 2022 Ларин вариант 408 ЕГЭ 2023 профиль по математике решение с ответами
28 ноября 2022 Вариант 3-4 распечатай и реши ЕГЭ 2023 база по математике 11 класс с ответами
30 ноября 2022 Мониторинговая работа по математике 11 класс ЕГЭ 2023 профиль 1 полугодие
3 декабря 2022 Тренировочный вариант №12 решу ЕГЭ 2023 база по математике 11 класс с ответами
3 декабря 2022 Тренировочный вариант №12 решу ЕГЭ 2023 по математике профиль с ответами
3 декабря 2022 Пробник ЕГЭ 2023 Москва по математике профиль задания и ответы
5 декабря 2022 Ларин вариант 409 ЕГЭ 2023 профиль по математике решение с ответами
9 декабря 2022 Тренировочный вариант №13 решу ЕГЭ 2023 база по математике 11 класс с ответами
10 декабря 2022 Тренировочный вариант №13 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
12 декабря 2022 Ларин вариант 410 ЕГЭ 2023 профиль по математике решение с ответами
13 декабря 2022 Статград математика 11 класс профиль ЕГЭ 2023 варианты МА2210209-МА2210212 и ответы
13 декабря 2022 Математика 11 класс база ЕГЭ 2023 статград варианты и ответы
15 декабря 2022 Тренировочный вариант №14 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
15 декабря 2022 Тренировочный вариант №14 решу ЕГЭ 2023 база по математике 11 класс с ответами
20 декабря 2022 Вариант 5-6 распечатай и реши ЕГЭ 2023 база по математике 11 класс с ответами
20 декабря 2022 Ларин вариант 411 ЕГЭ 2023 профиль по математике решение с ответами
3 января 2023 Ларин вариант 412 ЕГЭ 2023 профиль по математике решение с ответами
6 января 2023 Тренировочный вариант 1-2 ЕГЭ 2023 профиль математика задания и ответы
8 января 2023 Вариант 3-4 ЕГЭ 2023 профиль математика задания и ответы
9 января 2023 Вариант 7-8 распечатай и реши ЕГЭ 2023 база по математике 11 класс с ответами
10 января 2023 Тренировочный вариант №15 и №16 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
11 января 2023 ЕГЭ 2023 математика тренировочные задания и ответы Ященко, Семенов
11 января 2023 Тренировочный вариант №15 и №16 база ЕГЭ 2023 по математике 11 класс с ответами
19 января 2023 Тренировочные варианты №17 и №18 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
22 января 2023 Ларин вариант 413 и 414 ЕГЭ 2023 профиль по математике решение и ответы
22 января 2023 Тренировочный 19 вариант решу ЕГЭ 2023 профиль по математике 11 класс с ответами
22 января 2023 База ЕГЭ 2023 математика 11 класс тренировочный вариант 19 с ответами
25 января 2023 База ЕГЭ 2023 математика 11 класс тренировочный вариант 20 с ответами
27 января 2023 Тренировочный вариант №20 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
28 января 2023 Вариант 415 Ларина ЕГЭ 2023 по математике 11 класс задания и ответы
2 февраля 2023 Вариант 21 база ЕГЭ 2023 математика 11 класс тренировочный вариант с ответами
2 февраля 2023 Тренировочный вариант №21 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
8 февраля 2023 Математика 10-11 класс ЕГЭ 2023 статград варианты база и профиль МА2200101-МА2200110 и ответы
11 февраля 2023 Тренировочный вариант №22 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
11 февраля 2023 Тренировочный вариант №22 решу ЕГЭ 2023 база по математике 11 класс с ответами
12 февраля 2023 Вариант 416 Ларина ЕГЭ 2023 по математике 11 класс задания и ответы
12 февраля 2023 Вариант 417 Ларина ЕГЭ 2023 по математике 11 класс задания и ответы
13 февраля 2023 Вариант 9 и вариант 10 ЕГЭ 2023 база математика распечатай и реши задания
13 февраля 2023 Вариант 11 и вариант 12 ЕГЭ 2023 база математика распечатай и реши
16 февраля 2023 Тренировочный вариант №23 решу ЕГЭ 2023 база по математике 11 класс с ответами
16 февраля 2023 Тренировочный вариант №23 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
18 февраля 2023 Вариант 418 Ларина ЕГЭ 2023 по математике 11 класс задания и ответы
22 февраля 2023 Пробный ЕГЭ 2023 вариант 24 база по математике 11 класс с ответами
22 февраля 2023 Пробный ЕГЭ 2023 вариант 24 профиль по математике 11 класс с ответами
25 февраля 2023 Вариант 419 Ларина ЕГЭ 2023 по математике 11 класс задания и ответы
28 февраля 2023 Статград математика 11 класс ЕГЭ 2023 база и профиль и ответы
4 марта 2023 Пробник ЕГЭ 2023 вариант 25 база по математике 11 класс с ответами
4 марта 2023 Вариант 420 Ларин ЕГЭ 2023 по математике 11 класс задания и ответы
5 марта 2023 Пробник ЕГЭ 2023 вариант 25 профиль по математике 11 класс с ответами
8 марта 2023 Пробник ЕГЭ 2023 вариант 26 профиль по математике 11 класс с ответами
8 марта 2023 Пробник ЕГЭ 2023 вариант 26 база по математике 11 класс 100 баллов с ответами
Смотрите также на нашем сайте:
Сборник Ященко ЕГЭ 2023 математика профильный уровень 36 вариантов
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
ЕГЭ по математике — Профиль 2022. Открытый банк заданий с ответами.
Решение и ответы заданий варианта МА2210309 СтатГрад 28 февраля ЕГЭ 2023 по математике (профильный уровень). Тренировочная работа №3. ГДЗ профиль для 11 класса.
+Задания №1, №4, №6, №10 из варианта МА2210311.


Задание 1.
В треугольнике ABC угол C равен 90°, CH – высота, BC = 5, cosA=frac{2sqrt{6}}{5}. Найдите длину отрезка AH.
Задание 1 из варианта 2210311.
Найдите периметр прямоугольника, если его площадь равна 12, а отношение соседних сторон равно 1:3.
Задание 2.
Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 2. Объём параллелепипеда равен 3,2. Найдите высоту цилиндра.
Задание 3.
В группе 16 человек, среди них – Анна и Татьяна. Группу случайным образом делят на 4 одинаковые по численности подгруппы. Найдите вероятность того, что Анна и Татьяна окажутся в одной подгруппе.
Задание 4.
Агрофирма закупает куриные яйца только в двух домашних хозяйствах. Известно, что 40 % яиц из первого хозяйства – яйца высшей категории, а из второго хозяйства – 60 % яиц высшей категории. В этой агрофирме 50 % яиц высшей категории. Найдите вероятность того, что яйцо, купленное у этой агрофирмы, окажется из первого хозяйства.
Задание 4 из варианта 2210311.
Игральный кубик бросают дважды. Известно, что в сумме выпало 11 очков. Найдите вероятность того, что во второй раз выпало 5 очков.
Задание 5.
Решите уравнение frac{x–1}{5x+11}=frac{x–1}{3x-7}. Если уравнение имеет больше одного корня, в ответе запишите больший из корней.
Задание 6.
Найдите значение выражения frac{(4^{frac{3}{5} }cdot7^{frac{2}{3}})^{15}}{28^{9}} .
Задание 6 из варианта 2210311.
Найдите 98cos2α, если cosα = frac{4}{7}.
Задание 7.
На рисунке изображён график y = f’(x) – производной функции f(x), определённой на интервале (−5; 5). В какой точке отрезка [−4; −1] функция f(x) принимает наибольшее значение?
Задание 8.
На верфи инженеры проектируют новый аппарат для погружения на небольшие глубины. Конструкция имеет кубическую форму, а значит, действующая на аппарат выталкивающая (архимедова) сила, выражаемая в ньютонах, будет определяться по формуле FA = ρgl3, где l – длина ребра куба в метрах, ρ = 1000 кг/м3 – плотность воды, а g – ускорение свободного падения (считайте, что g = 9,8 Н/кг). Какой может быть максимальная длина ребра куба, чтобы обеспечить его эксплуатацию в условиях, когда выталкивающая сила при погружении будет не больше чем 2116800 Н? Ответ дайте в метрах.
Задание 9.
Пристани A и B расположены на озере, расстояние между ними равно 280 км. Баржа отправилась с постоянной скоростью из A в B. На следующий день после прибытия она отправилась обратно со скоростью на 4 км/ч больше прежней, сделав по пути остановку на 8 часов. В результате она затратила на обратный путь столько же времени, сколько на путь из A в B. Найдите скорость баржи на пути из A в B. Ответ дайте в км/ч.
Задание 10.
На рисунке изображён график функции f(x) = ax2 + bx + c. Найдите значение f(−1).
Задание 10 из варианта 2210311.
На рисунке изображены графики функций f(x) = frac{k}{x} и g(x) = ax + b, которые пересекаются в точках A и B. Найдите абсциссу точки B.
Задание 11.
Найдите точку минимума функции y = x3 − 27x2 + 13.
Задание 12.
а) Решите уравнение 2cos3x = –sin(frac{3pi}{2} + x)
б) Найдите все корни этого уравнения, принадлежащие отрезку [3π; 4π]
Задание 13.
Основанием правильной пирамиды PABCD является квадрат ABCD. Сечение пирамиды проходит через вершину В и середину ребра PD перпендикулярно этому ребру.
а) Докажите, что угол наклона бокового ребра пирамиды к её основанию равен 60°.
б) Найдите площадь сечения пирамиды, если AB = 30.
Задание 14.
Решите неравенство frac{9^{x}–13cdot 3^{x}+30}{3^{x+2}–3^{2x+1}}ge frac{1}{3^{x}}.
Задание 15.
По вкладу «А» банк в конце каждого года планирует увеличивать на 13 % сумму, имеющуюся на вкладе в начале года, а по вкладу «Б» – увеличивать эту сумму на 7 % в первый год и на целое число n процентов за второй год. Найдите наименьшее значение n, при котором за два года хранения вклад «Б» окажется выгоднее вклада «А» при одинаковых суммах первоначальных взносов.
Задание 16.
В треугольнике ABC медианы AA1, BB1 и CC1 пересекаются в точке M. Известно, что AC = 3MB.
а) Докажите, что треугольник ABC прямоугольный.
б) Найдите сумму квадратов медиан AA1 и CC1, если известно, что AC = 22.
Задание 17.
Найдите все значения a, при каждом из которых система уравнений
begin{cases} (x-5a+1)^{2}+(y-2a-1)^{2}=a-2 \ 3x-4y=2a+3 end{cases}
не имеет решений.
Задание 18.
У Ани есть 800 рублей. Ей нужно купить конверты (большие и маленькие). Большой конверт стоит 32 рубля, а маленький – 25 рублей. При этом число маленьких конвертов не должно отличаться от числа больших конвертов больше чем на пять.
а) Может ли Аня купить 24 конверта?
б) Может ли Аня купить 29 конвертов?
в) Какое наибольшее число конвертов может купить Аня?
Источник варианта: СтатГрад/statgrad.org.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 5 / 5. Количество оценок: 2
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
Решу егэ математика 512488
Задание 21 № 512488
Про натуральные числа A, B и С известно, что каждое из них больше 5, но меньше 9. Загадали натуральное число, затем его умножили на A, потом прибавили к полученному произведению B и вычли С. Получилось 249. Какое число было загадано?
Числа А, В и С могут быть равны 6, 7 или 8.
Пусть загадали натуральное число Х, тогда Х · А + В – С = 249 или Х · А = 249 + (С – В). Рассмотрим различные случаи.
1) С – В = 0 (6 – 6 = 0, 7 – 7 = 0 или 8 – 8 = 0), тогда Х · А = 249. Число 249 не делится нацело на 6, на 7 и на 8, значит, этот случай не подходит.
2) С – В = 1 (7 – 6 = 1 или 8 – 7 = 1), тогда Х · А = 250. Число 250 не делится нацело на 6, на 7 и на 8, значит, этот случай не подходит.
3) С – В = –1 (6 – 7 = –1 или 7 – 8 = –1), тогда Х · А = 248. Число 248 делится нацело на А = 8, значит, Х = 31.
4) С – В = 2 (8 – 6 = 2), тогда Х · А = 251. Число 251 не делится нацело на 6, на 7 и на 8, значит, этот случай не подходит.
5) С – В = –2 (6 – 8 = –2), тогда Х·А = 247. Число 247 не делится нацело на 6, на 7 и на 8, значит, этот случай не подходит.
Задание 21 № 512488
Какое число было загадано.
Mathb-ege. sdamgia. ru
28.02.2018 7:52:18
2018-02-28 07:52:18
Источники:
Https://mathb-ege. sdamgia. ru/problem? id=512488
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword { color: red; } Решу егэ математика 512488
Решу егэ математика 512488
Решу егэ математика 512488
Задания Д1 № 512488
Материальная точка движется от начального до конечного положения. На рисунке изображён график её движения. На оси абсцисс откладывается время в секундах, на оси ординат — расстояние от начального положения точки (в метрах). Найдите среднюю скорость движения точки. Ответ дайте в метрах в секунду.
Чтобы найти среднюю скорость движения точки, необходимо перемещение поделить на время прохождения: м/с
Некорректная задача. Так как нам представлен график ускоренного движения, в связи с тем, что изображена кривая, а если говорить о том как, вы решили эту задачу, то линия должна быть прямой.
Каким бы ни было движение (равномерным, равноускоренным, произвольным) средняя скорость вычисляется одинаково: перемещение делится на время, за которое это перемещение произошло
Задания Д1 № 512488
Решу егэ математика 512488.
Ege. sdamgia. ru
17.01.2017 2:55:13
2017-01-17 02:55:13
Источники:
Https://ege. sdamgia. ru/problem? id=512488
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword { color: red; } Решу егэ математика 512488
Решу егэ математика 512488
Решу егэ математика 512488
При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
Одного рулона обоев хватает для оклейки полосы от пола до потолка шириной 1,6 м. Сколько рулонов обоев нужно купить для оклейки прямоугольной комнаты размерами 2,3 м на 4,2 м?
Выставленные учителем баллы отобразятся в вашей статистике.
Math-ege. sdamgia. ru
07.05.2020 4:20:58
2020-05-07 04:20:58
Источники:
Https://math-ege. sdamgia. ru/test? id=38005119