507646 решу егэ математика - Помощь в подготовке к экзаменам и поступлению

Решите неравенство

Спрятать решение

Решение.

Левая часть неравенства имеет смысл при и то есть при и При этих условиях получаем:

Сделаем замену тогда

Возвращаясь к исходной переменной, получаем:

Из полученного набора нужно ещё исключить точку 2. Таким образом, множество решений исходного неравенства:

Ответ:

Спрятать критерии

Критерии проверки:

Критерии оценивания выполнения задания	Баллы
Обоснованно получен верный ответ	2
Обоснованно получен ответ, отличающийся от верного исключением точек, ИЛИ получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения	1
Решение не соответствует ни одному из критериев, перечисленных выше.	0
Максимальный балл	2

Источник

Решу егэ профиль математика 517739

Задание 12 № 517746

А) Решите уравнение

Б) Укажите корни этого уравнения, принадлежащие отрезку

А) Из уравнения получаем:

Б) Заметим, что Значит, указанному отрезку принадлежит корень −3.

Ответ: а) −3 и 27; б) −3.

Аналоги к заданию № 517739: 517746 517747 Все

Задание 12 № 517747

Задание 12 № 517746

Задание 12 № 517747

Ответ а 3 и 27; б 3.

Ege. sdamgia. ru

12.01.2020 13:48:01

2020-01-12 13:48:01

Источники:

Https://ege. sdamgia. ru/test? likes=517739

Решу егэ профиль математика 517739 — Математика и Английский » /> » /> .keyword { color: red; } Решу егэ профиль математика 517739

Решу егэ профиль математика 517739

Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!

Задание 12 № 517746

А) Решите уравнение

Б) Укажите корни этого уравнения, принадлежащие отрезку

А) Из уравнения получаем:

Б) Заметим, что Значит, указанному отрезку принадлежит корень −3.

Ответ: а) −3 и 27; б) −3.

Аналоги к заданию № 517739: 517746 517747 Все

Задание 12 № 517747

Задание 12 № 517746

Б Заметим, что Значит, указанному отрезку принадлежит корень 3.

Источники:

ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword < color: red; >Решу егэ профиль математика 517739

Решу егэ профиль математика 517739

Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!

Задание 12 № 514082

А) Решите уравнение

Б) Укажите корни этого уравнения, принадлежащие отрезку

А) Запишем исходное уравнение в виде:

Б) Поскольку отрезку принадлежит единственный корень −2.

Ответ: а) −2; 1, б) −2.

Почему такое странное ОДЗ?? Где 2-х>0, х>0, следовательно х0; тогда х (0;2)

Екатерина, в решении не находили ОДЗ.

В решении было использован равносильный переход, при котором условия достаточно для решения примера

А у Вас ОДЗ найдено с ошибкой.

Задание 12 № 517739

А) Решите уравнение

Б) Укажите корни этого уравнения, принадлежащие отрезку

А) Из уравнения получаем:

Б) Заметим, что Значит, указанному отрезку принадлежит только корень −2.

Ответ: а) −2 и 16; б) −2.

В пункте «а» ответ только 16,вы не проверили ОДЗ

В этом уравнении не нужно искать ОДЗ. Это лишнее действие

Задание 12 № 502094

А) Решите уравнение

Б) Найдите все корни этого уравнения, принадлежащие промежутку

А) Заметим, что преобразуем исходное уравнение:

Пусть тогда уравнение запишется в виде откуда или

При получим: откуда

Б) Корень не принадлежит промежутку Поскольку и корень принадлежит промежутку

Источник: ЕГЭ по математике 19.06.2013. Основная волна, резервный день. Центр. Вариант 502., Задания 13 (С1) ЕГЭ 2013

В строчке а) откуда-то взялась «3»

Путём каких преобразований мы получили ответ log(3)5 ?

1) Уравнение начинается с числе 9 в степени. Т. е. Мы раскладываем 9 как 3*3. Однако в первой строке решения мы видим 9*3. От туда и дальнейшее неверное вычисление.

2) Когда мы возвращаем замену (четвёртая строчка решения) вместо этого (если, допустим, t и правда равно 5/3) должно получиться Х-1= логорифм 5/3 по основанию 3. Верно?

Так ли это? Ибо мне свойственно ошибаться. Это правда ошибка, или я чего-то не понимаю? Если второе, то объясните, если можно.

Задание 12 № 517739

Задание 12 № 502094

Задание 12 502094.

Источники:

Решу егэ профиль математика 517739

Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!

При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.

Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.

Диагональ экрана телевизора равна 64 дюймам. Выразите диагональ экрана в сантиметрах, если в одном дюйме 2,54 см. Результат округлите до целого числа сантиметров.

Источники:

Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!

Задание 12 № 514082

А) Решите уравнение

Б) Укажите корни этого уравнения, принадлежащие отрезку

А) Запишем исходное уравнение в виде:

Б) Поскольку отрезку принадлежит единственный корень −2.

Ответ: а) −2; 1, б) −2.

Почему такое странное ОДЗ?? Где 2-х>0, х>0, следовательно х0; тогда х (0;2)

Екатерина, в решении не находили ОДЗ.

В решении было использован равносильный переход, при котором условия достаточно для решения примера

А у Вас ОДЗ найдено с ошибкой.

Задание 12 № 517739

А) Решите уравнение

Б) Укажите корни этого уравнения, принадлежащие отрезку

А) Из уравнения получаем:

Б) Заметим, что Значит, указанному отрезку принадлежит только корень −2.

Ответ: а) −2 и 16; б) −2.

В пункте «а» ответ только 16,вы не проверили ОДЗ

В этом уравнении не нужно искать ОДЗ. Это лишнее действие

Задание 12 № 502094

А) Решите уравнение

Б) Найдите все корни этого уравнения, принадлежащие промежутку

А) Заметим, что преобразуем исходное уравнение:

Пусть тогда уравнение запишется в виде откуда или

При получим: откуда

Б) Корень не принадлежит промежутку Поскольку и корень принадлежит промежутку

Источник: ЕГЭ по математике 19.06.2013. Основная волна, резервный день. Центр. Вариант 502., Задания 13 (С1) ЕГЭ 2013

В строчке а) откуда-то взялась «3»

Путём каких преобразований мы получили ответ log(3)5 ?

Задание 12 № 517739

Задание 12 № 502094

Задание 12 502094.

Уско рен ная под го тов ка к ЕГЭ с ре пе ти то ра ми Учи.

Dankonoy. com

16.06.2020 6:45:22

2020-06-16 06:45:22

Источники:

Https://dankonoy. com/ege/ege11/archives/10087

Материал для подготовки к экзамену по математике 1 курс. » /> » /> .keyword { color: red; } Решу егэ профиль математика 517739

Материал для подготовки к экзамену по математике 1 курс

Материал для подготовки к экзамену по математике 1 курс.

Материал для подготовки к экзамену по математике для 1 курса СПО.

Просмотр содержимого документа
«Материал для подготовки к экзамену по математике 1 курс.»

Логарифмические уравнения

1. Задание 5 № 26646

Найдите корень уравнения

2. Задание 5 № 26647

Найдите корень уравнения

3. Задание 5 № 26648

Найдите корень уравнения

4. Задание 5 № 26649

Найдите корень уравнения

5. Задание 5 № 26657

Найдите корень уравнения

6. Задание 5 № 26658

Найдите корень уравнения

7. Задание 5 № 26659

Найдите корень уравнения

8. Задание 5 № 77380

Решите уравнение

9. Задание 5 № 77381

Решите уравнение

10. Задание 5 № 77382

Решите уравнение Если уравнение имеет более одного корня, в ответе укажите меньший из них.

11. Задание 5 № 315120

Найдите корень уравнения

12. Задание 5 № 315535

Найдите корень уравнения

13. Задание 5 № 525399

Решите уравнение

Тригонометрические уравнения

1. Задание 5 № 26669

Найдите корни уравнения: В ответ запишите наибольший отрицательный корень.

Значениям соответствуют положительные корни.

Если, то и

Значениям соответствуют меньшие значения корней.

Следовательно, наибольшим отрицательным корнем является число

2. Задание 5 № 77376

Решите уравнение В ответе напишите наибольший отрицательный корень.

Значению соответствует Положительным значениям параметра соответствуют положительные значения корней, отрицательным значениям параметра соответствуют меньшие значения корней. Следовательно, наибольшим отрицательным корнем является число −1.

3. Задание 5 № 77377

Решите уравнение В ответе напишите наименьший положительный корень.

Значениям соответствуют отрицательные корни.

Если, то и

Значениям соответствуют большие положительные корни.

Наименьшим положительным решением является 0,5.

Преобразования числовых логарифмических выражений

1. Задание 9 № 26843

Найдите значение выражения

2. Задание 9 № 26844

Найдите значение выражения

3. Задание 9 № 26845

Найдите значение выражения

4. Задание 9 № 26846

Найдите значение выражения

5. Задание 9 № 26847

Найдите значение выражения

6. Задание 9 № 26848

Найдите значение выражения

7. Задание 9 № 26849

Найдите значение выражения

8. Задание 9 № 26850

Найдите значение выражения

9. Задание 9 № 26851

Найдите значение выражения

10. Задание 9 № 26852

Найдите значение выражения

11. Задание 9 № 26853

Найдите значение выражения

12. Задание 9 № 26854

Найдите значение выражения

13. Задание 9 № 26855

Найдите значение выражения

14. Задание 9 № 26856

Найдите значение выражения

15. Задание 9 № 26857

Найдите значение выражения

16. Задание 9 № 26858

Найдите значение выражения

17. Задание 9 № 26859

Найдите значение выражения

18. Задание 9 № 26860

Найдите значение выражения

19. Задание 9 № 26861

Найдите значение выражения

20. Задание 9 № 26862

Найдите значение выражения

21. Задание 9 № 26882

Найдите значение выражения

22. Задание 9 № 26883

Найдите значение выражения

23. Задание 9 № 26885

Найдите значение выражения

24. Задание 9 № 26889

Найдите значение выражения

25. Задание 9 № 26892

Найдите значение выражения

26. Задание 9 № 26893

Найдите значение выражения

27. Задание 9 № 26894

Найдите значение выражения

28. Задание 9 № 26896

Найдите значение выражения

29. Задание 9 № 77418

Вычислите значение выражения:

30. Задание 9 № 505097

Найдите значение выражения

31. Задание 9 № 509086

Найдите значение выражения

32. Задание 9 № 510939

Найдите значение выражения

33. Задание 9 № 525403

Найдите значение выражения

Вычисление значений тригонометрических выражений

1. Задание 9 № 26775

Найдите, если и

2. Задание 9 № 26776

Найдите, если и

3. Задание 9 № 26777

Найдите, если и

4. Задание 9 № 26778

Найдите, если и

5. Задание 9 № 26779

Найдите, если

6. Задание 9 № 26780

Найдите, если

7. Задание 9 № 26783

Найдите значение выражения, если

8. Задание 9 № 26784

Найдите, если и

9. Задание 9 № 26785

Найдите, если и

10. Задание 9 № 26786

Найдите, если

11. Задание 9 № 26787

Найдите, если

12. Задание 9 № 26788

Найдите, если

13. Задание 9 № 26789

Найдите, если

14. Задание 9 № 26790

Найдите, если

15. Задание 9 № 26791

Найдите, если

16. Задание 9 № 26792

Найдите значение выражения, если

17. Задание 9 № 26793

Найдите значение выражения, если

18. Задание 9 № 26794

Найдите, если

19. Задание 9 № 316350

Найдите, если

20. Задание 9 № 501598

Найдите значение выражения

21. Задание 9 № 502014

Найдите значение выражения

22. Задание 9 № 502045

Найдите значение выражения

23. Задание 9 № 502106

Найдите значение выражения

24. Задание 9 № 502285

Найдите значение выражения

25. Задание 9 № 502305

Найдите значение выражения если и

26. Задание 9 № 504410

Найдите значение выражения:

27. Задание 9 № 504824

Найдите значение выражения

28. Задание 9 № 508966

Найдите если

29. Задание 9 № 510424

Найдите если и

30. Задание 9 № 549336

Найдите если и

Преобразования числовых тригонометрических выражений

1. Задание 9 № 26755

Найдите значение выражения

2. Задание 9 № 26756

Найдите значение выражения

3. Задание 9 № 26757

Найдите значение выражения

4. Задание 9 № 26758

Найдите значение выражения

5. Задание 9 № 26759

Найдите значение выражения

6. Задание 9 № 26760

Найдите значение выражения

7. Задание 9 № 26761

Найдите значение выражения

8. Задание 9 № 26762

Найдите значение выражения

9. Задание 9 № 26763

Найдите значение выражения

10. Задание 9 № 26764

Найдите значение выражения

11. Задание 9 № 26765

Найдите значение выражения

12. Задание 9 № 26766

Найдите значение выражения

13. Задание 9 № 26767

Найдите значение выражения

14. Задание 9 № 26769

Найдите значение выражения

15. Задание 9 № 26770

Найдите значение выражения

16. Задание 9 № 26771

Найдите значение выражения

17. Задание 9 № 26772

Найдите значение выражения

18. Задание 9 № 26773

Найдите значение выражения

19. Задание 9 № 26774

Найдите значение выражения

20. Задание 9 № 77412

Найдите значение выражения

21. Задание 9 № 77413

Найдите значение выражения

22. Задание 9 № 77414

Найдите значение выражения:

23. Задание 9 № 245169

Найдите значение выражения

24. Задание 9 № 245170

Найдите значение выражения

25. Задание 9 № 245171

Найдите значение выражения

26. Задание 9 № 245172

Найдите значение выражения

27. Задание 9 № 501701

Найдите значение выражения

28. Задание 9 № 502994

Найдите значение выражения

29. Задание 9 № 503310

Найдите значения выражения

30. Задание 9 № 510013

Найдите если и

31. Задание 9 № 510312

Найдите значение выражения

32. Задание 9 № 510386

Найдите значение выражения

33. Задание 9 № 510405

Найдите значение выражения

34. Задание 9 № 510824

Найдите значение выражения

35. Задание 9 № 510843

Найдите значение выражения

36. Задание 9 № 525113

Найдите значение выражения

37. Задание 9 № 526009

Найдите значение выражения

Логарифмические и показательные уравнения

1. Задание 13 № 514082

А) Решите уравнение

Б) Укажите корни этого уравнения, принадлежащие отрезку

2. Задание 13 № 517739

А) Решите уравнение

Б) Укажите корни этого уравнения, принадлежащие отрезку

3. Задание 13 № 502094

А) Решите уравнение

Б) Найдите все корни этого уравнения, принадлежащие промежутку

4. Задание 13 № 516760

А) Решите уравнение:

Б) Определите, какие из его корней принадлежат отрезку

5. Задание 13 № 514623

А) Решите уравнение

Б) Найдите все корни этого уравнения, принадлежащие отрезку

6. Задание 13 № 502053

А) Решите уравнение

Б) Найдите все корни этого уравнения, принадлежащие отрезку

7. Задание 13 № 525377

А) Решите уравнение

Б) Найдите все корни этого уравнения, принадлежащие отрезку

8. Задание 13 № 513605

А) Решите уравнение

Б) Укажите корни этого уравнения, принадлежащие отрезку

9. Задание 13 № 503127

А) Решите уравнение

Б) Найдите все корни этого уравнения, принадлежащие отрезку

10. Задание 13 № 514081

А) Решите уравнение

Б) Укажите корни этого уравнения, принадлежащего отрезку

11. Задание 13 № 502999

А) Решите уравнение

Б) Найдите все корни этого уравнения, принадлежащие отрезку [−1; 2].

12. Задание 13 № 528517

А) Решите уравнение

Б) Укажите корни этого уравнения, принадлежащие отрезку

13. Задание 13 № 550261

А) Решите уравнение

Б) Укажите корни этого уравнения, принадлежащие промежутку

14. Задание 13 № 555265

А) Решите уравнение

Б) Укажите корни этого уравнения, принадлежащие отрезку

15. Задание 13 № 555583

А) Решите уравнение

Б) Укажите корни этого уравнения, принадлежащие отрезку

16. Задание 13 № 561853

А) Решите уравнение

Б) Найдите все корни этого уравнения, принадлежащие отрезку [−2,5; −1,5].

17. Задание 13 № 562032

А) Решите уравнение

Б) Найдите все корни этого уравнения, принадлежащие отрезку [−0,5; 0,5].

18. Задание 13 № 562757

А) Решите уравнение

Б) Найдите все корни этого уравнения, принадлежащие отрезку

б) Укажите корни этого уравнения, принадлежащие отрезку

Решите уравнение В ответе напишите наименьший положительный корень.

Просмотр содержимого документа «Материал для подготовки к экзамену по математике 1 курс.»

Б Укажите корни этого уравнения, принадлежащие отрезку.

Multiurok. ru

06.02.2020 18:29:01

2020-02-06 18:29:01

Источники:

Https://multiurok. ru/files/material-dlia-podgotovki-k-ekzamenu-po-matematike. html

Источник

Задание 14 Профильного ЕГЭ по математике можно считать границей между «неплохо сдал ЕГЭ» и «поступил в вуз с профильной математикой». Здесь не обойтись без отличного знания алгебры. Потому что встретиться вам может любое неравенство: показательное, логарифмическое, комбинированное (например, логарифмы и тригонометрия). И еще бывают неравенства с модулем и иррациональные неравенства. Некоторые из них мы разберем в этой статье.

Хотите получить на Профильном ЕГЭ не менее 70 баллов? Учитесь решать неравенства!

Темы для повторения:

^New

Решаем задачи из сборника И. В. Ященко, 2021

Квадратичные неравенства

Метод интервалов

Уравнения и неравенства с модулем

Иррациональные неравенства

Показательные неравенства

Логарифмические неравенства

Метод замены множителя (рационализации)

Решение неравенств: основные ошибки и полезные лайфхаки

Решаем задачи из сборника И. В. Ященко, 2020. Вариант 8, задача 15

Решаем задачи из сборника И. В. Ященко, 2020. Вариант 32, задача 15

Решаем задачи из сборника И. В. Ященко, 2020. Вариант 36, задача 15

Логарифмические неравенства повышенной сложности

Разберем неравенства разных типов из вариантов ЕГЭ по математике.

Дробно-рациональные неравенства

1. Решите неравенство:

$frac{{ 2}}{{ 0,5x}sqrt{{ 5}}{ -}{ 1}}{ +}frac{{ 0,5x}sqrt{{ 5}}{ -}{ 2}}{{ 0,5x}sqrt{{ 5}}{ -}{ 3}} geq { 2.}$

Сделаем замену

Тогда , а

Получим:

$frac{{ 2}}{{ t+1}}{ +}frac{{ t}}{{ t-1}} geq { 2};$

$frac{{ 2}{ t}{ -}{ 2+}{{ t}}^{{ 2}}{ +}{ t}}{{{ t}}^{{ 2}}{ -}{ 1}}{ -}{ 2} geq{ 0};$

$frac{{{ t}}^{{ 2}}{ +3}{ t}{ -}{ 2-2}{{ t}}^{{ 2}}{ +2}}{{{ t}}^{{ 2}}{ -}{ 1}} geq { 0};$

$frac{{ 3}{ t}{ -}{{ t}}^{{ 2}}}{{{ t}}^{{ 2}}{ -}{ 1}} geq { 0};$

$frac{{ t}left({ t}{ -}{ 3}right)}{left({ t}{ -}{ 1}right)left({ t}{ +1}right)}le { 0}.$

Решим неравенство относительно t методом интервалов:

Получим:

$left[ begin{array}{c}{ -}{ 1 textless t}le { 0} \{ 1 textless t}le { 3} end{array}right..$

Вернемся к переменной x: $left[ begin{array}{c} -1 textless 0,5xsqrt{5}-2leq0 \ 1 textless 0,5xsqrt{5}-2leq 3 end{array} right. .$

$left[ begin{array}{c} {{2}over{sqrt{5}}} textless xleq {{4}over{sqrt{5}}}\ {{6}over{sqrt{5}}} textless xleq {{10}over{sqrt{5}}} end{array} right. .$

Ответ: $xin left(frac{{ 2}}{sqrt{{ 5}}};frac{{ 4}}{sqrt{{ 5}}}right]cup left(frac{{ 6}}{sqrt{{ 5}}};{ 2}sqrt{{ 5}}right].$

Показательные неравенства

2. Решите неравенство $2^x+17cdot 2^{3-x}le 25.$

$2^x+17cdot frac{8}{2^x}le 25.$

Сделаем замену Получим:

$t+17cdot frac{8}{t}-25le 0.$ Умножим неравенство на

Дискриминант квадратного уравнения

$D={left(-25right)}^2-4cdot 136=625-544=81.$ Значит, корни этого уравнения: $left[ begin{array}{c}t_1=17 \t_2=8 end{array}.right.$

Разложим квадратный трехчлен на множители.

. Вернемся к переменной x.

Внимание. Сначала решаем неравенство относительно переменной t. Только после этого возвращаемся к переменной x. Запомнили?

$2^3le 2^xle 2^{{{log }_2 17}};$

$3le xle {{log }_2 17};$

Ответ: $xin left[3;{{log }_2 17}right].$

Следующая задача — с секретом. Да, такие тоже встречаются в вариантах ЕГЭ.

3. Решите неравенство $2^{2x-x^2-1}+frac{1}{2^{2x-x^2}-1}le 2.$

Сделаем замену $2^{2x-x^2}=t,t textgreater 0.$ Получим:

$frac{t}{2}+frac{1}{t-1}-2le 0;$

$frac{t^2-t+2-4t+4}{2left(t-1right)}le 0;$

$frac{t^2-5t+6}{t-1}le 0;$

$frac{left(t-2right)left(t-3right)}{t-1}le 0.$

$left[ begin{array}{c}t textless 1 \2le tle 3 end{array} .right.$

Вернемся к переменной $x:left[ begin{array}{c}2^{2x-x^2} textless 1 \{2le 2}^{2x-x^2}le 3 end{array}.right.$

Первое неравенство решим легко: С неравенством ${2le 2}^{2x-x^2}$ тоже все просто. Но что делать с неравенством $2^{2x-x^2}le 3$ ? Ведь $3 = 2^{{{log }_2 3}}.$ Представляете, как трудно будет выразить х?

Оценим $t=2^{2x-x^2}.$ Для этого рассмотрим функцию $tleft(xright)=2^{2x-x^2}.$

Сначала оценим показатель степени. Пусть Это парабола с ветвями вниз, и наибольшее значение этой функции достигается в вершине параболы, при х = 1. При этом

Мы получили, что

Тогда $2^{zleft(xright)}le 2$ , и это значит, что Значение не достигается ни при каких х.

Но если ${2le 2}^{2x-x^2}$ и $2^{2x-x^2}le 2$ , то $2^{2x-x^2}=2.$

Мы получили:

$left[ begin{array}{c} 2x-x^2 textless 0\ 2x-x^2=1end{array} right. Leftrightarrow left[ begin{array}{c} x(x-2) textgreater 0\ x^2-2x+1=0end{array} right. Leftrightarrow left[ begin{array}{c} x textless 0\ x textgreater 2\(x-1)^2=0end{array} right. Leftrightarrow$

$Leftrightarrow left[ begin{array}{c} x textless 0\ x textgreater 2\ x=1end{array}. right.$

Ответ:

Логарифмические неравенства

4. Решите неравенство $2{{log}_{frac{1}{2}} left(1-xright) textless {{log}_{frac{1}{2}} left(3x+1right)}}.$

Запишем решение как цепочку равносильных переходов. Лучше всего оформлять решение неравенства именно так.

$2log_{{1}over{2}}(1-x) textless log_{{1}over{2}}(3x+1)Leftrightarrow left{begin{matrix} 1-x textgreater 0\3x+1 textgreater 0 \(1-x)^2 textgreater 3x+1 end{matrix}right.Leftrightarrow left{begin{matrix} x textless 1\x textgreater -{{1}over{3}} \ 1+x^2-2x textgreater 3x+1 end{matrix}right.Leftrightarrow$

$Leftrightarrow left{begin{matrix} x textless 1\x textgreater {-{{1}over{3}}} \ x^2-5x textgreater 0 end{matrix}right.Leftrightarrow left{begin{matrix} x textless 1\ x textgreater {-{{1}over{3}}} \ x(x-5) textgreater 0 end{matrix} .right.$

Ответ: $xin left(-frac{1}{3};0right).$

Следующее неравенство — комбинированное. И логарифмы, и тригонометрия!

5. Решите неравенство $2{{{log}_2}^2 {{cos}^2 x+7{{log}_2 {cos x} geq 1}}}.$

$2{{{log }_2}^2 {{cos }^{{ 2}} x+7{{log }_2 {cos x} geq 1}}}.$

ОДЗ:

Замена ${{log }_2 {cos x}=t} Rightarrow {{log }_2 {{cos }^{{ 2}} x}}=2{{log }_2 {cos x=2t}}.$

$2cdot {left(2tright)}^2+7t-1 geq 0;$

$t_1=frac{-7-9}{16}=-1;$

$t_2=frac{-7+9}{16}=frac{1}{8}.$

$(t+1)(t-{{1}over{8}})geq 0Leftrightarrow left[ begin{array}{c} t leq -1 \ t geq {{1}over{8}} end{array} right. Leftrightarrow left[ begin{array}{c} log_2,cosx leq-1 \ log_2,cosx geq {{1}over{8}} end{array} right.$
$Leftrightarrow left{begin{matrix} left[ begin{array}{c} cosxleq{{1}over{2}} \ cosxgeqsqrt[8]{2} end{array} right. \ cosx textgreater 0 end{matrix}right.Leftrightarrow 0 textless cosxleq{{1}over{2}}.$

Ответ: $xin left(-frac{pi }{2}+2pi k;left.-frac{pi }{3}+2pi kright]right.cup left[frac{pi }{3}+2pi k;left.frac{pi }{2}+2pi kright), kright.in Z.$

А вот и метод замены множителя (рационализации). Смотрите, как он применяется. А на ЕГЭ не забудьте доказать формулы, по которым мы заменяем логарифмический множитель на алгебраический.

6. Решите неравенство: ${{log }_{{ 3-x}} frac{{ x+4}}{{left({ x-3}right)}^{{ 2}}}} geq { -2}.$

$log_{3-x}frac{x+4}{(x-3)^2}geq-2Leftrightarrow left{begin{matrix} 3-x textgreater 0\3-xneq1 \ {x+4over (x-3)^2} textgreater 0 \ log_{3-x} {{x+4}over(x-3)^2}+2geq 0 end{matrix} .right.$

Мы объединили в систему и область допустимых значений, и само неравенство. Применим формулу логарифма частного, учитывая, что ${left({ a-b}right)}^{{ 2}}{ =}{left({ b-a}right)}^{{ 2}}{ }$ . Используем также условия

$left{begin{matrix} x textless 3\xneq2 \ x+4 textgreater 0 \ log_{3-x}(x+4)-log_{3-x}(3-x)^2+2geq0 end{matrix}right. Leftrightarrow$

$Leftrightarrow left{begin{matrix} x textless 3\xneq2 \ x textgreater -4 \ log_{3-x}(x+4)geq0 end{matrix}.right.$

Обратите внимание, как мы применили формулу для логарифма степени. Строго говоря, ${{log }_{{ a}} {left({ b}left({ x}right)right)}^{{ 2}}{ =2}{{log }_{{ a}} left|{ b}left({ x}right)right|}}.$

Поскольку ${ 3-}{ x}{ textgreater 0,}{{ log}}_{{ 3-x}}{left({ 3-x}right)}^{{ 2}}{ =2}{{log }_{{ 3-x}} left|{ 3-x}right|{ =}}{ 2}{{log }_{{ 3-x}} left({ 3-x}right){ =2.}}$

Согласно методу замены множителя, выражение ${{ log}}_{{ 3-x}}left({ x+4}right)$ заменим на

Получим систему:

$left{ begin{array}{c}{ x}ne { 2} \{ -}{ 4}{ textless x textless 3} \left({ 2-x}right)left({ x+3}right) geq { 0} end{array}.right.$

Решить ее легко.

Ответ: .

Разберем какое-нибудь нестандартное неравенство. Такое, что не решается обычными способами.

7. Решите неравенство:

${{log }_2 left(x-5right)+{{log }_3 xleq 4}}.$

ОДЗ: $left{ begin{array}{c}x-5 textgreater 0 \x textgreater 0 end{array}Longleftrightarrow x textgreater 5.right.$

Привести обе части к одному основанию не получается. Ищем другой способ.

Заметим, что при x = 9 оба слагаемых равны 2 и их сумма равна 4.

${{log }_2 left(9-5right)={{log }_2 4=2}};$

${{log }_3 9=2};$

${{log }_2 left(9-5right)+{{log }_3 9=4}}.$

Функции и — монотонно возрастающие, следовательно, их сумма также является монотонно возрастающей функцией и каждое свое значение принимает только один раз.

Поскольку при x=9 значение монотонно возрастающей функции ${{{ y=}log }_2 left(x-5right)+{{log }_3 x}}$ равно 4, при значения этой функции меньше 4. Конечно, при этом , то есть x принадлежит ОДЗ.

Ответ: (5; 9].

Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Задание 14. Неравенства u0026#8212; профильный ЕГЭ по математике» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.

Публикация обновлена:
09.03.2023

Источник

Новые тренировочные варианты ЕГЭ 2023 по математике базовый и профильный уровень с ответами и решением для 10 и 11 класса, больше 100 вариантов в формате реального экзамена ФИПИ вы можете решать онлайн или скачать.

Тренировочные варианты ЕГЭ 2023 по математике база и профиль

13.09.2022 Тренировочный вариант №1 ЕГЭ 2023 по математике профиль с ответами

20.09.2022 Тренировочный вариант №2 ЕГЭ 2023 по математике профиль с ответами

20.09.2022 Тренировочный вариант №2 ЕГЭ 2023 база по математике с ответами

27.09.2022 Математика 11 класс профиль входная мониторинговая работа 3 варианта с ответами

28.09.2022 Тренировочный вариант №3 ЕГЭ 2023 база по математике с ответами

28 сентября 2022 Статград математика 11 класс ЕГЭ 2023 база и профиль варианты и ответы

29 сентября 2022 Тренировочный вариант №3 ЕГЭ 2023 по математике профиль с ответами

1 октября 2022 Ларин вариант 399 ЕГЭ 2023 по математике профиль решение с ответами

6 октября Тренировочный вариант №4 ЕГЭ 2023 база по математике с ответами

6 октября Тренировочный вариант №4 ЕГЭ 2023 по математике профиль с ответами

8 октября Ларин вариант 400 ЕГЭ 2023 по математике профиль решение с ответами

12 октября Тренировочный вариант №5 ЕГЭ 2023 база по математике с ответами

12 октября Тренировочный вариант №5 ЕГЭ 2023 по математике профиль с ответами

14 октября Вариант 1 Ященко ЕГЭ 2023 математика профиль с ответами и решением

14 октября Вариант 2 Ященко ЕГЭ 2023 математика профиль с ответами и решением

15 октября Ларин вариант 401 ЕГЭ 2023 по математике профиль решение с ответами

15 октября Ларин вариант 402 ЕГЭ 2023 по математике профиль решение с ответами

16 октября Вариант 3 Ященко ЕГЭ 2023 математика профиль с ответами и решением

16 октября Вариант 4 Ященко ЕГЭ 2023 математика профиль с ответами и решением

23 октября Тренировочный вариант №6 ЕГЭ 2023 база по математике с ответами

24 октября Тренировочный вариант №6 ЕГЭ 2023 по математике профиль с ответами

25 октября Тренировочный вариант №7 ЕГЭ 2023 база по математике с ответами

26 октября Тренировочный вариант №7 ЕГЭ 2023 по математике профиль с ответами

28 октября Ларин вариант 403 ЕГЭ 2023 по математике профиль решение с ответами

29 октября Ларин вариант 404 ЕГЭ 2023 по математике профиль решение с ответами

1 ноября 2022 Тренировочный вариант №8 решу ЕГЭ 2023 база по математике с ответами

1 ноября 2022 Тренировочный вариант №8 решу ЕГЭ 2023 по математике профиль с ответами

5 ноября 2022 Вариант 1-2 распечатай и реши ЕГЭ 2023 база по математике 11 класс с ответами

6 ноября 2022 Ларин вариант 405 ЕГЭ 2023 профиль по математике решение с ответами

9 ноября 2022 Тренировочный вариант №9 решу ЕГЭ 2023 база по математике с ответами

12 ноября 2022 Тренировочный вариант №9 решу ЕГЭ 2023 по математике профиль с ответами

13 ноября 2022 Ларин вариант 406 ЕГЭ 2023 профиль по математике решение с ответами

15 ноября 2022 Тренировочный вариант №10 решу ЕГЭ 2023 база по математике 11 класс с ответами

15 ноября 2022 Тренировочный вариант №10 решу ЕГЭ 2023 по математике профиль с ответами

21 ноября 2022 Ларин вариант 407 ЕГЭ 2023 профиль по математике решение с ответами

23 ноября 2022 Тренировочный вариант №11 решу ЕГЭ 2023 база по математике 11 класс с ответами

23 ноября 2022 Тренировочный вариант №11 решу ЕГЭ 2023 по математике профиль с ответами

27 ноября 2022 Ларин вариант 408 ЕГЭ 2023 профиль по математике решение с ответами

28 ноября 2022 Вариант 3-4 распечатай и реши ЕГЭ 2023 база по математике 11 класс с ответами

30 ноября 2022 Мониторинговая работа по математике 11 класс ЕГЭ 2023 профиль 1 полугодие

3 декабря 2022 Тренировочный вариант №12 решу ЕГЭ 2023 база по математике 11 класс с ответами

3 декабря 2022 Тренировочный вариант №12 решу ЕГЭ 2023 по математике профиль с ответами

3 декабря 2022 Пробник ЕГЭ 2023 Москва по математике профиль задания и ответы

5 декабря 2022 Ларин вариант 409 ЕГЭ 2023 профиль по математике решение с ответами

9 декабря 2022 Тренировочный вариант №13 решу ЕГЭ 2023 база по математике 11 класс с ответами

10 декабря 2022 Тренировочный вариант №13 решу ЕГЭ 2023 профиль по математике 11 класс с ответами

12 декабря 2022 Ларин вариант 410 ЕГЭ 2023 профиль по математике решение с ответами

13 декабря 2022 Статград математика 11 класс профиль ЕГЭ 2023 варианты МА2210209-МА2210212 и ответы

13 декабря 2022 Математика 11 класс база ЕГЭ 2023 статград варианты и ответы

15 декабря 2022 Тренировочный вариант №14 решу ЕГЭ 2023 профиль по математике 11 класс с ответами

15 декабря 2022 Тренировочный вариант №14 решу ЕГЭ 2023 база по математике 11 класс с ответами

20 декабря 2022 Вариант 5-6 распечатай и реши ЕГЭ 2023 база по математике 11 класс с ответами

20 декабря 2022 Ларин вариант 411 ЕГЭ 2023 профиль по математике решение с ответами

3 января 2023 Ларин вариант 412 ЕГЭ 2023 профиль по математике решение с ответами

6 января 2023 Тренировочный вариант 1-2 ЕГЭ 2023 профиль математика задания и ответы

8 января 2023 Вариант 3-4 ЕГЭ 2023 профиль математика задания и ответы

9 января 2023 Вариант 7-8 распечатай и реши ЕГЭ 2023 база по математике 11 класс с ответами

10 января 2023 Тренировочный вариант №15 и №16 решу ЕГЭ 2023 профиль по математике 11 класс с ответами

11 января 2023 ЕГЭ 2023 математика тренировочные задания и ответы Ященко, Семенов

11 января 2023 Тренировочный вариант №15 и №16 база ЕГЭ 2023 по математике 11 класс с ответами

19 января 2023 Тренировочные варианты №17 и №18 решу ЕГЭ 2023 профиль по математике 11 класс с ответами

22 января 2023 Ларин вариант 413 и 414 ЕГЭ 2023 профиль по математике решение и ответы

22 января 2023 Тренировочный 19 вариант решу ЕГЭ 2023 профиль по математике 11 класс с ответами

22 января 2023 База ЕГЭ 2023 математика 11 класс тренировочный вариант 19 с ответами

25 января 2023 База ЕГЭ 2023 математика 11 класс тренировочный вариант 20 с ответами

27 января 2023 Тренировочный вариант №20 решу ЕГЭ 2023 профиль по математике 11 класс с ответами

28 января 2023 Вариант 415 Ларина ЕГЭ 2023 по математике 11 класс задания и ответы

2 февраля 2023 Вариант 21 база ЕГЭ 2023 математика 11 класс тренировочный вариант с ответами

2 февраля 2023 Тренировочный вариант №21 решу ЕГЭ 2023 профиль по математике 11 класс с ответами

8 февраля 2023 Математика 10-11 класс ЕГЭ 2023 статград варианты база и профиль МА2200101-МА2200110 и ответы

11 февраля 2023 Тренировочный вариант №22 решу ЕГЭ 2023 профиль по математике 11 класс с ответами

11 февраля 2023 Тренировочный вариант №22 решу ЕГЭ 2023 база по математике 11 класс с ответами

12 февраля 2023 Вариант 416 Ларина ЕГЭ 2023 по математике 11 класс задания и ответы

12 февраля 2023 Вариант 417 Ларина ЕГЭ 2023 по математике 11 класс задания и ответы

13 февраля 2023 Вариант 9 и вариант 10 ЕГЭ 2023 база математика распечатай и реши задания

13 февраля 2023 Вариант 11 и вариант 12 ЕГЭ 2023 база математика распечатай и реши

16 февраля 2023 Тренировочный вариант №23 решу ЕГЭ 2023 база по математике 11 класс с ответами

16 февраля 2023 Тренировочный вариант №23 решу ЕГЭ 2023 профиль по математике 11 класс с ответами

18 февраля 2023 Вариант 418 Ларина ЕГЭ 2023 по математике 11 класс задания и ответы

22 февраля 2023 Пробный ЕГЭ 2023 вариант 24 база по математике 11 класс с ответами

22 февраля 2023 Пробный ЕГЭ 2023 вариант 24 профиль по математике 11 класс с ответами

25 февраля 2023 Вариант 419 Ларина ЕГЭ 2023 по математике 11 класс задания и ответы

28 февраля 2023 Статград математика 11 класс ЕГЭ 2023 база и профиль и ответы

4 марта 2023 Пробник ЕГЭ 2023 вариант 25 база по математике 11 класс с ответами

4 марта 2023 Вариант 420 Ларин ЕГЭ 2023 по математике 11 класс задания и ответы

5 марта 2023 Пробник ЕГЭ 2023 вариант 25 профиль по математике 11 класс с ответами

8 марта 2023 Пробник ЕГЭ 2023 вариант 26 профиль по математике 11 класс с ответами

8 марта 2023 Пробник ЕГЭ 2023 вариант 26 база по математике 11 класс 100 баллов с ответами

Смотрите также на нашем сайте:

Сборник Ященко ЕГЭ 2023 математика профильный уровень 36 вариантов

ПОДЕЛИТЬСЯ МАТЕРИАЛОМ

Источник

Шкалирование

Первичный	Тестовый	Оценка
5-6	27-34	3
7-8	40-46	4
9-10	52-58
11-12-13	64-66-68	5
14-15-16	70-72-74
17-18-19	76-78-80
20-21-22	82-84-86
23-24-25	88-90-92
26-27-28	94-96-98
29-30-31	100

Первичный балл / Тестовый балл	5/27	6/34	7/40	8/46	9/52	10/58	11/64	12/66	13/68	14/70
15/72	16/74	17/76	18/78	19/80	20/82	X / 2X+42	29+ / 100

Источник

Регистрация
Вход

Форум
Поиск
FAQ   alexlarin.net

Текущее время: 10 мар 2023, 12:33
Часовой пояс: UTC + 3 часа

Сообщения без ответов | Активные темы

Страница 1 из 2 [ Сообщений: 12 ] На страницу 1, 2 След.

Начать новую тему»>

Ответить

Тренировочный вариант №420

Для печати

Предыдущая тема | Следующая тема

Тренировочный вариант №420

Автор

Сообщение

Заголовок сообщения: Тренировочный вариант №420

Добавлено: 04 мар 2023, 10:06

Администратор

Центр пользователя

Зарегистрирован: 10 июн 2010, 15:00
Сообщений: 6118

https://alexlarin.net/ege/2023/trvar420.html

Kirill Kolokolcev

Заголовок сообщения: Re: Тренировочный вариант №420

Добавлено: 04 мар 2023, 13:42

Центр пользователя

Зарегистрирован: 08 май 2015, 03:53
Сообщений: 1610
Откуда: Москва

Спасибо за интересный вариант!
17

Подробности:

ega7001

Заголовок сообщения: Re: Тренировочный вариант №420

Добавлено: 05 мар 2023, 23:29

Центр пользователя

Зарегистрирован: 07 окт 2022, 07:38
Сообщений: 5

12.

Подробности:

13.

Подробности:

14.

Подробности:

ega7001

Заголовок сообщения: Re: Тренировочный вариант №420

Добавлено: 06 мар 2023, 10:45

Центр пользователя

Зарегистрирован: 07 окт 2022, 07:38
Сообщений: 5

15.

Подробности:

16.

Подробности:

Владимiръ

Заголовок сообщения: Re: Тренировочный вариант №420

Добавлено: Вчера, 00:00

Центр пользователя

Зарегистрирован: 08 мар 2017, 23:11
Сообщений: 545
Откуда: Пущино

Задача 18

Подробности:

Вложения:

Задача 420-18.pdf [66.3 KIB]

Скачиваний: 725

Тюрин

Заголовок сообщения: Re: Тренировочный вариант №420

Добавлено: Вчера, 00:00

Центр пользователя

Зарегистрирован: 16 май 2022, 22:37
Сообщений: 141

Задача 18

Подробности:

Вложения:

Задача №420-18.pdf [129.95 KIB]

Скачиваний: 695

Raisa

Заголовок сообщения: Re: Тренировочный вариант №420

Добавлено: Вчера, 00:07

Центр пользователя

Зарегистрирован: 23 янв 2014, 20:36
Сообщений: 1463
Откуда: г. Дубна МО

12, 14, 17

Подробности:

Вложения:

12, 14, 17 вар 420.pdf [1.44 MIB]

Скачиваний: 693

Raisa

Заголовок сообщения: Re: Тренировочный вариант №420

Добавлено: Вчера, 00:14

Центр пользователя

Зарегистрирован: 23 янв 2014, 20:36
Сообщений: 1463
Откуда: г. Дубна МО

13, 15, 16

Подробности:

Вложения:

13, 15, 16 вар 420.pdf [1.97 MIB]

Скачиваний: 684

netka

Заголовок сообщения: Re: Тренировочный вариант №420

Добавлено: Вчера, 00:46

Центр пользователя

Зарегистрирован: 20 мар 2011, 22:29
Сообщений: 2788
Откуда: Казань

Всем здравствуйте! %%- %%- %%-

Решение заданий 12 и 14.

Подробности:

Решение задания 17.

Подробности:

Вложения:

420-17.pdf [438.22 KIB]

Скачиваний: 675

420-12;14.pdf [474.44 KIB]

Скачиваний: 681

netka

Заголовок сообщения: Re: Тренировочный вариант №420

Добавлено: Вчера, 00:58

Центр пользователя

Зарегистрирован: 20 мар 2011, 22:29
Сообщений: 2788
Откуда: Казань

Решение задания 13.

Вложение:

420-13.ggb [14.19 KIB]

Скачиваний: 22

скрин решения

Подробности:

Показать сообщения за: Сортировать по:

Страница 1 из 2 [ Сообщений: 12 ] На страницу 1, 2 След.

Текущее время: 10 мар 2023, 12:33 | Часовой пояс: UTC + 3 часа

Удалить cookies форума | Наша команда | Вернуться наверх

Кто сейчас на форуме

Сейчас этот форум просматривают: нет зарегистрированных пользователей и гости: 14

Вы не можете начинать темы
Вы не можете отвечать на сообщения
Вы не можете редактировать свои сообщения
Вы не можете удалять свои сообщения
Вы не можете добавлять вложения

Найти:

Перейти:

Источник

БАЗА ЗАДАНИЙ

Задание № 2. Стереометрия.

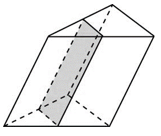
1. Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсеченной треугольной призмы равна 8. Найдите площадь боковой поверхности исходной призмы.

Ответ: 16

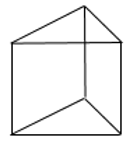
2. Через среднюю линию основания треугольной призмы, объем которой равен 32, проведена плоскость, параллельная боковому ребру. Найдите объем отсеченной треугольной призмы.

Ответ: 8

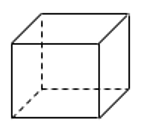
3. Во сколько раз увеличится площадь поверхности куба, если его ребро увеличить в три раза?

Ответ: 9

4. Площадь поверхности куба равна 24. Найдите его объем.

Ответ: 8

5. Если каждое ребро куба увеличить на 1, то его площадь поверхности увеличится на 30. Найдите ребро куба.

Ответ: 2

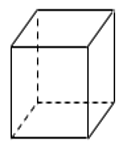
6. Площадь поверхности куба равна 8. Найдите его диагональ.

Ответ: 2

7. Объем куба равен 24√3. Найдите его диагональ.

Ответ: 6

8. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 3 и 5. Объем призмы равен 30. Найдите ее боковое ребро.

Ответ: 4

9. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 3 и 4. Площадь ее поверхности равна 132. Найдите высоту призмы.

Ответ: 10

10. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, боковое ребро равно 5. Найдите объем призмы.

Ответ: 120

11. Найдите боковое ребро правильной четырехугольной призмы, если сторона ее основания равна 20, а площадь поверхности равна 1760.

Ответ: 12

12. Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 6 и 8, и боковым ребром, равным 10.

Ответ: 248

13. В основании прямой призмы лежит ромб с диагоналями, равными 9 и 12. Площадь ее поверхности равна 468. Найдите боковое ребро этой призмы.

Ответ: 12

14. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2. Объем параллелепипеда равен 6. Найдите площадь его поверхности.

Ответ: 22

15. Три ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 4, 6, 9. Найдите ребро равновеликого ему куба.

Ответ: 6

16. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 3. Объем параллелепипеда равен 36. Найдите его диагональ.

Ответ: 7

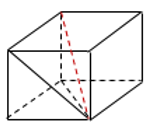
17. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 4. Диагональ параллелепипеда равна 6. Найдите объем параллелепипеда.

Ответ:32

18. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2. Площадь поверхности параллелепипеда равна 16. Найдите его диагональ.

Ответ: 3

19. Диагональ прямоугольного параллелепипеда равна √8 и образует углы 30°,30° и 45° с плоскостями граней параллелепипеда. Найдите объем параллелепипеда.

Ответ: 4

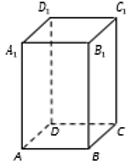
20. В прямоугольном параллелепипеде ABCDA1B1C1D1 известно, что BB1=32, AB=12, AD=9. Найдите площадь сечения проходящее через вершины A, A1, C.

Ответ: 480

21. В прямоугольном параллелепипеде ABCDA₁B₁C₁D₁ известно, что BB₁=16, А₁B₁=2, A₁D₁=8. Найдите длину диагонали AC₁.

Ответ: 18

22. Дана правильная четырёхугольная призма

ABCDA1B1C1D1, площадь основания которой равна 6, а боковое ребро равно 7. Найдите объём многогранника, вершинами которого являются точки A, B, C, B1.

Ответ: 7

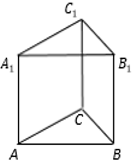
23. Найдите объём многогранника, вершинами которого являются точки C, A₁, B₁ , C₁ правильной треугольной призмы ABCA₁B₁C₁ , площадь основания которой равна 4, а боковое ребро равно 9.

Ответ: 12

24. Найдите объём многогранника, вершинами которого являются точки A, C, A1, B₁, C1 правильной треугольной призмы ABCA1B1C1. Площадь основания призмы равна 7, а боковое ребро равно 9.

Ответ: 42

25. В правильной треугольной призме ABCA₁B₁C₁ все ребра равны 3. Найдите угол между прямыми AA₁и BC₁. Ответ дайте в градусах.

26. В правильной треугольной призме ABCA₁B₁C₁ известно, что AB=√3AA₁. Найдите угол между прямыми AB₁ и CC₁. Ответ дайте в градусах.

Ответ: 60°

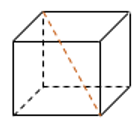
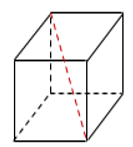
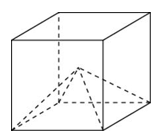
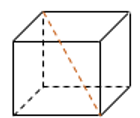
27. Объём куба равен 16. Найдите объём треугольной призмы, отсекаемой от куба плоскостью, проходящей через середины двух рёбер, выходящих из одной вершины, и параллельной третьему ребру, выходящему из этой же вершины.

Ответ: 2

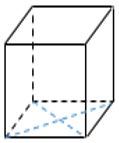
28. Объем куба равен 12. Найдите объем четырехугольной пирамиды, основанием которой является грань куба, а вершиной — центр куба.

Ответ: 2

29. Объем параллелепипеда

ABCDA1B1C1D1

равен 4,5. Найдите объем треугольной пирамиды AD1CB1.

Ответ: 1,5

30. Объем параллелепипеда

ABCDA1B1C1D1

равен 1,5. Найдите объем треугольной пирамиды ABCB1.

Ответ: 0,25

31. Найдите объем параллелепипеда

ABCDA1B1C1D1, если объем треугольной пирамиды ABDA1 равен 3.

Ответ: 18

32. Гранью параллелепипеда является ромб со стороной 1 и острым углом 60°. Одно из ребер параллелепипеда составляет с этой гранью угол 60° и равно 2. Найдите объем параллелепипеда.

Ответ: 1,5

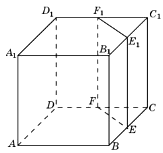
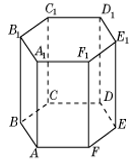
33. Найдите объём многогранника ACDFA1C1D1F1 правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1, площадь основания которой равна 9, а боковое ребро равно 11.

Ответ: 66

34. В правильной шестиугольной призме

ABCDEFA1B1C1D1E1F1, стороны основания которой равны 5, а боковые рёбра равны 11, найдите расстояние от точки A до прямой E1D1.

Ответ: 14

35. Найдите объём многогранника DA1B1C1D1E1F1

правильной шестиугольной призмы

ABCDEFA1B1C1D1E1F1, площадь основания которой равна 12, а боковое ребро равно 2.

Ответ: 8

36. Найдите объём многогранника CDEC1D1E1 правильной шестиугольной призмы

ABCDEFA1B1C1D1E1F1, площадь основания которой равна 6, а боковое ребро равно 14.

Ответ:14

37. Найдите объём многогранника A1B1F1A правильной шестиугольной призмы

ABCDEFA1B1C1D1E1F1, площадь основания которой равна 12, а боковое ребро равно 15.

Ответ: 10

38. В правильной четырёхугольной пирамиде высота равна 2, боковое ребро равно 5. Найдите её объём.

Ответ: 28

39. В правильной четырёхугольной пирамиде боковое ребро равно 7,5, а сторона основания равна 10. Найдите высоту пирамиды.

Ответ: 2,5

40. Найдите площадь поверхности правильной четырехугольной пирамиды, стороны основания которой равны 6 и высота равна 4.

Ответ: 96

41. В правильной четырехугольной пирамиде высота равна 12, объем равен 200. Найдите боковое ребро этой пирамиды.

Ответ: 13

42. В правильной треугольной пирамиде боковое ребро равно 7, а сторона основания равна 10,5. Найдите высоту пирамиды.

Ответ: 3,5

Источник

Источники:

Решу егэ профиль математика 517739

Решу егэ профиль математика 517739

Источники:

Решу егэ профиль математика 517739

Решу егэ профиль математика 517739

Источники:

Решу егэ профиль математика 517739

Решу егэ профиль математика 517739

Источники:

Источники:

Материал для подготовки к экзамену по математике 1 курс

Материал для подготовки к экзамену по математике 1 курс.

Просмотр содержимого документа «Материал для подготовки к экзамену по математике 1 курс.»

Источники:

Тренировочные варианты ЕГЭ 2023 по математике база и профиль

Смотрите также на нашем сайте:

ПОДЕЛИТЬСЯ МАТЕРИАЛОМ

Шкалирование

<img decoding="async" onError="javascript: wp_broken_images = window.wp_broken_images || function(){}; wp_broken_images(this);" src="https://alexlarin.com/egetren4.png" />

Тренировочный вариант №420

Тренировочный вариант №420

Кто сейчас на форуме

Просмотр содержимого документа
«Материал для подготовки к экзамену по математике 1 курс.»