507784 решу егэ - Помощь в подготовке к экзаменам и поступлению

Решите неравенство:

Спрятать решение

Решение.

Сделаем замену и упростим левую и правую части:

Учитывая, что получаем:

или

Первый случай:

Второй случай:

Тогда откуда

Ответ:

Спрятать критерии

Критерии проверки:

Критерии оценивания выполнения задания	Баллы
Обоснованно получен верный ответ	2
Обоснованно получен ответ, отличающийся от верного исключением точек, ИЛИ получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения	1
Решение не соответствует ни одному из критериев, перечисленных выше.	0
Максимальный балл	2

Источник

1. Прикладные задачи (задачи из повседневной жизни)

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

В данных задачах необходимо округлять ответ до целого числа, причем в зависимости от контекста задачи – в большую или меньшую сторону.

Например, если необходимо округлить число (18,8) в большую сторону до целого числа, то результатом будет (19), в меньшую сторону – (18).

Как определить, в какую сторону округлять? Обычно это понимается интуитивно, но если вы сомневаетесь в своем решении, то подставьте под условие вашей задачи результат, округленный в большую сторону, и результат, округленный в меньшую сторону. И сравните полученные данные. Исходя из условия задачи будет понятно, какой из результатов подходит, а какой – нет.

Например, на празднике нужно рассадить (17) человек за столы, причем каждый стол умещает (5) человек. Сколько нужно столов, чтобы поместились все гости?

Следовательно, ответом будет либо (3), либо (4). Из условия задачи понятно, что округлить необходимо в большую сторону (т.к. столы должны уместить как минимум (17) человек).
Можно сделать проверку: если взять (3) стола, то за ними уместятся (15) человек – а этого недостаточно.
Ответ: (4).

Задание
29

#2993

Уровень задания: Сложнее ЕГЭ

Таня живет в доме с 10 этажами и несколькими подъездами, на каждом этаже, кроме первого, по три квартиры, а на первом – одна. На каком этаже живет Таня, если она живет в квартире под номером 185?

В каждом подъезде (1+9cdot 3=28) квартир. Следовательно, разделив 185 на 28, получим количество подъездов, вмещающихся в 185 квартир: [185:28=6frac{17}{28}]

После округления в большую сторону получаем, что Таня живет в седьмом подъезде. В шести подъездах (6cdot 28=168) квартир, следовательно, в седьмом подъезде Танина квартира 17-ая по счету ((185-168=17)). Так как на первом этаже одна квартира, на остальных – по три, то [(17-1):3=5frac13] То есть если не считать первый этаж, Таня жила бы на шестом. Следовательно, учитывая первый этаж, Таня живет на седьмом.

(Так как на первых шести этажах (1+3cdot 5=16) квартир, а на седьмом этаже – 17-ая, 18-ая и 19-ая квартиры)

Ответ: 7

Задание
30

#4015

Уровень задания: Легче ЕГЭ

Больному прописано лекарство, которое нужно принимать по (0,5) г 2 раза в день в течение 15 дней. В одной упаковке 6 таблеток лекарства по (0,25) г. Какого наименьшего количества упаковок хватит на весь курс лечения?

На весь курс больному нужно (0,5cdot 2cdot 15=15) г лекарства. В одной упаковке (6cdot 0,25=1,5) г лекарства. Следовательно, найдем (15:1,5=10). Значит, больному нужно минимум 10 упаковок лекарства.

Ответ:

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ

Источник

Задание 14 Профильного ЕГЭ по математике можно считать границей между «неплохо сдал ЕГЭ» и «поступил в вуз с профильной математикой». Здесь не обойтись без отличного знания алгебры. Потому что встретиться вам может любое неравенство: показательное, логарифмическое, комбинированное (например, логарифмы и тригонометрия). И еще бывают неравенства с модулем и иррациональные неравенства. Некоторые из них мы разберем в этой статье.

Хотите получить на Профильном ЕГЭ не менее 70 баллов? Учитесь решать неравенства!

Темы для повторения:

^New

Решаем задачи из сборника И. В. Ященко, 2021

Квадратичные неравенства

Метод интервалов

Уравнения и неравенства с модулем

Иррациональные неравенства

Показательные неравенства

Логарифмические неравенства

Метод замены множителя (рационализации)

Решение неравенств: основные ошибки и полезные лайфхаки

Решаем задачи из сборника И. В. Ященко, 2020. Вариант 8, задача 15

Решаем задачи из сборника И. В. Ященко, 2020. Вариант 32, задача 15

Решаем задачи из сборника И. В. Ященко, 2020. Вариант 36, задача 15

Логарифмические неравенства повышенной сложности

Разберем неравенства разных типов из вариантов ЕГЭ по математике.

Дробно-рациональные неравенства

1. Решите неравенство:

$frac{{ 2}}{{ 0,5x}sqrt{{ 5}}{ -}{ 1}}{ +}frac{{ 0,5x}sqrt{{ 5}}{ -}{ 2}}{{ 0,5x}sqrt{{ 5}}{ -}{ 3}} geq { 2.}$

Сделаем замену

Тогда , а

Получим:

$frac{{ 2}}{{ t+1}}{ +}frac{{ t}}{{ t-1}} geq { 2};$

$frac{{ 2}{ t}{ -}{ 2+}{{ t}}^{{ 2}}{ +}{ t}}{{{ t}}^{{ 2}}{ -}{ 1}}{ -}{ 2} geq{ 0};$

$frac{{{ t}}^{{ 2}}{ +3}{ t}{ -}{ 2-2}{{ t}}^{{ 2}}{ +2}}{{{ t}}^{{ 2}}{ -}{ 1}} geq { 0};$

$frac{{ 3}{ t}{ -}{{ t}}^{{ 2}}}{{{ t}}^{{ 2}}{ -}{ 1}} geq { 0};$

$frac{{ t}left({ t}{ -}{ 3}right)}{left({ t}{ -}{ 1}right)left({ t}{ +1}right)}le { 0}.$

Решим неравенство относительно t методом интервалов:

Получим:

$left[ begin{array}{c}{ -}{ 1 textless t}le { 0} \{ 1 textless t}le { 3} end{array}right..$

Вернемся к переменной x: $left[ begin{array}{c} -1 textless 0,5xsqrt{5}-2leq0 \ 1 textless 0,5xsqrt{5}-2leq 3 end{array} right. .$

$left[ begin{array}{c} {{2}over{sqrt{5}}} textless xleq {{4}over{sqrt{5}}}\ {{6}over{sqrt{5}}} textless xleq {{10}over{sqrt{5}}} end{array} right. .$

Ответ: $xin left(frac{{ 2}}{sqrt{{ 5}}};frac{{ 4}}{sqrt{{ 5}}}right]cup left(frac{{ 6}}{sqrt{{ 5}}};{ 2}sqrt{{ 5}}right].$

Показательные неравенства

2. Решите неравенство $2^x+17cdot 2^{3-x}le 25.$

$2^x+17cdot frac{8}{2^x}le 25.$

Сделаем замену Получим:

$t+17cdot frac{8}{t}-25le 0.$ Умножим неравенство на

Дискриминант квадратного уравнения

$D={left(-25right)}^2-4cdot 136=625-544=81.$ Значит, корни этого уравнения: $left[ begin{array}{c}t_1=17 \t_2=8 end{array}.right.$

Разложим квадратный трехчлен на множители.

. Вернемся к переменной x.

Внимание. Сначала решаем неравенство относительно переменной t. Только после этого возвращаемся к переменной x. Запомнили?

$2^3le 2^xle 2^{{{log }_2 17}};$

$3le xle {{log }_2 17};$

Ответ: $xin left[3;{{log }_2 17}right].$

Следующая задача — с секретом. Да, такие тоже встречаются в вариантах ЕГЭ.

3. Решите неравенство $2^{2x-x^2-1}+frac{1}{2^{2x-x^2}-1}le 2.$

Сделаем замену $2^{2x-x^2}=t,t textgreater 0.$ Получим:

$frac{t}{2}+frac{1}{t-1}-2le 0;$

$frac{t^2-t+2-4t+4}{2left(t-1right)}le 0;$

$frac{t^2-5t+6}{t-1}le 0;$

$frac{left(t-2right)left(t-3right)}{t-1}le 0.$

$left[ begin{array}{c}t textless 1 \2le tle 3 end{array} .right.$

Вернемся к переменной $x:left[ begin{array}{c}2^{2x-x^2} textless 1 \{2le 2}^{2x-x^2}le 3 end{array}.right.$

Первое неравенство решим легко: С неравенством ${2le 2}^{2x-x^2}$ тоже все просто. Но что делать с неравенством $2^{2x-x^2}le 3$ ? Ведь $3 = 2^{{{log }_2 3}}.$ Представляете, как трудно будет выразить х?

Оценим $t=2^{2x-x^2}.$ Для этого рассмотрим функцию $tleft(xright)=2^{2x-x^2}.$

Сначала оценим показатель степени. Пусть Это парабола с ветвями вниз, и наибольшее значение этой функции достигается в вершине параболы, при х = 1. При этом

Мы получили, что

Тогда $2^{zleft(xright)}le 2$ , и это значит, что Значение не достигается ни при каких х.

Но если ${2le 2}^{2x-x^2}$ и $2^{2x-x^2}le 2$ , то $2^{2x-x^2}=2.$

Мы получили:

$left[ begin{array}{c} 2x-x^2 textless 0\ 2x-x^2=1end{array} right. Leftrightarrow left[ begin{array}{c} x(x-2) textgreater 0\ x^2-2x+1=0end{array} right. Leftrightarrow left[ begin{array}{c} x textless 0\ x textgreater 2\(x-1)^2=0end{array} right. Leftrightarrow$

$Leftrightarrow left[ begin{array}{c} x textless 0\ x textgreater 2\ x=1end{array}. right.$

Ответ:

Логарифмические неравенства

4. Решите неравенство $2{{log}_{frac{1}{2}} left(1-xright) textless {{log}_{frac{1}{2}} left(3x+1right)}}.$

Запишем решение как цепочку равносильных переходов. Лучше всего оформлять решение неравенства именно так.

$2log_{{1}over{2}}(1-x) textless log_{{1}over{2}}(3x+1)Leftrightarrow left{begin{matrix} 1-x textgreater 0\3x+1 textgreater 0 \(1-x)^2 textgreater 3x+1 end{matrix}right.Leftrightarrow left{begin{matrix} x textless 1\x textgreater -{{1}over{3}} \ 1+x^2-2x textgreater 3x+1 end{matrix}right.Leftrightarrow$

$Leftrightarrow left{begin{matrix} x textless 1\x textgreater {-{{1}over{3}}} \ x^2-5x textgreater 0 end{matrix}right.Leftrightarrow left{begin{matrix} x textless 1\ x textgreater {-{{1}over{3}}} \ x(x-5) textgreater 0 end{matrix} .right.$

Ответ: $xin left(-frac{1}{3};0right).$

Следующее неравенство — комбинированное. И логарифмы, и тригонометрия!

5. Решите неравенство $2{{{log}_2}^2 {{cos}^2 x+7{{log}_2 {cos x} geq 1}}}.$

$2{{{log }_2}^2 {{cos }^{{ 2}} x+7{{log }_2 {cos x} geq 1}}}.$

ОДЗ:

Замена ${{log }_2 {cos x}=t} Rightarrow {{log }_2 {{cos }^{{ 2}} x}}=2{{log }_2 {cos x=2t}}.$

$2cdot {left(2tright)}^2+7t-1 geq 0;$

$t_1=frac{-7-9}{16}=-1;$

$t_2=frac{-7+9}{16}=frac{1}{8}.$

$(t+1)(t-{{1}over{8}})geq 0Leftrightarrow left[ begin{array}{c} t leq -1 \ t geq {{1}over{8}} end{array} right. Leftrightarrow left[ begin{array}{c} log_2,cosx leq-1 \ log_2,cosx geq {{1}over{8}} end{array} right.$
$Leftrightarrow left{begin{matrix} left[ begin{array}{c} cosxleq{{1}over{2}} \ cosxgeqsqrt[8]{2} end{array} right. \ cosx textgreater 0 end{matrix}right.Leftrightarrow 0 textless cosxleq{{1}over{2}}.$

Ответ: $xin left(-frac{pi }{2}+2pi k;left.-frac{pi }{3}+2pi kright]right.cup left[frac{pi }{3}+2pi k;left.frac{pi }{2}+2pi kright), kright.in Z.$

А вот и метод замены множителя (рационализации). Смотрите, как он применяется. А на ЕГЭ не забудьте доказать формулы, по которым мы заменяем логарифмический множитель на алгебраический.

6. Решите неравенство: ${{log }_{{ 3-x}} frac{{ x+4}}{{left({ x-3}right)}^{{ 2}}}} geq { -2}.$

$log_{3-x}frac{x+4}{(x-3)^2}geq-2Leftrightarrow left{begin{matrix} 3-x textgreater 0\3-xneq1 \ {x+4over (x-3)^2} textgreater 0 \ log_{3-x} {{x+4}over(x-3)^2}+2geq 0 end{matrix} .right.$

Мы объединили в систему и область допустимых значений, и само неравенство. Применим формулу логарифма частного, учитывая, что ${left({ a-b}right)}^{{ 2}}{ =}{left({ b-a}right)}^{{ 2}}{ }$ . Используем также условия

$left{begin{matrix} x textless 3\xneq2 \ x+4 textgreater 0 \ log_{3-x}(x+4)-log_{3-x}(3-x)^2+2geq0 end{matrix}right. Leftrightarrow$

$Leftrightarrow left{begin{matrix} x textless 3\xneq2 \ x textgreater -4 \ log_{3-x}(x+4)geq0 end{matrix}.right.$

Обратите внимание, как мы применили формулу для логарифма степени. Строго говоря, ${{log }_{{ a}} {left({ b}left({ x}right)right)}^{{ 2}}{ =2}{{log }_{{ a}} left|{ b}left({ x}right)right|}}.$

Поскольку ${ 3-}{ x}{ textgreater 0,}{{ log}}_{{ 3-x}}{left({ 3-x}right)}^{{ 2}}{ =2}{{log }_{{ 3-x}} left|{ 3-x}right|{ =}}{ 2}{{log }_{{ 3-x}} left({ 3-x}right){ =2.}}$

Согласно методу замены множителя, выражение ${{ log}}_{{ 3-x}}left({ x+4}right)$ заменим на

Получим систему:

$left{ begin{array}{c}{ x}ne { 2} \{ -}{ 4}{ textless x textless 3} \left({ 2-x}right)left({ x+3}right) geq { 0} end{array}.right.$

Решить ее легко.

Ответ: .

Разберем какое-нибудь нестандартное неравенство. Такое, что не решается обычными способами.

7. Решите неравенство:

${{log }_2 left(x-5right)+{{log }_3 xleq 4}}.$

ОДЗ: $left{ begin{array}{c}x-5 textgreater 0 \x textgreater 0 end{array}Longleftrightarrow x textgreater 5.right.$

Привести обе части к одному основанию не получается. Ищем другой способ.

Заметим, что при x = 9 оба слагаемых равны 2 и их сумма равна 4.

${{log }_2 left(9-5right)={{log }_2 4=2}};$

${{log }_3 9=2};$

${{log }_2 left(9-5right)+{{log }_3 9=4}}.$

Функции и — монотонно возрастающие, следовательно, их сумма также является монотонно возрастающей функцией и каждое свое значение принимает только один раз.

Поскольку при x=9 значение монотонно возрастающей функции ${{{ y=}log }_2 left(x-5right)+{{log }_3 x}}$ равно 4, при значения этой функции меньше 4. Конечно, при этом , то есть x принадлежит ОДЗ.

Ответ: (5; 9].

Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Задание 14. Неравенства u0026#8212; профильный ЕГЭ по математике» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.

Публикация обновлена:
09.03.2023

Источник

Свойства числа 507784

Множители		2 * 2 * 2 * 63473
Делители	1, 2, 4, 8, 63473, 126946, 253892, 507784
Количество делителей	8
Сумма делителей	952110
Предыдущее целое	507783
Следующее целое	507785
Простое число?	NO
Предыдущее простое	507781
Следующее простое	507797
507784th простое число	7492249
Является числом Фибоначчи?	NO
Число Белла?	NO
Число Каталана?	NO
Факториал?	NO
Регулярное число?	NO
Совершенное число?	NO
Полигональное число (s < 11)?	NO
Двоичное	1111011111110001000
Восьмеричная	1737610
Двенадцатеричный	205a34
Шестнадцатиричная	7bf88
Квадрат	257844590656
Квадратный корень	712.58964348354
Натуральный логарифм	13.137811439288
Десятичный логарифм	5.7056790123684
Синус	0.8651140341043
Косинус	-0.50157522665676
Тангенс	-1.7247941846544

Математические настройки для вашего сайта Выберите язык:
Deutsch
English
Español
Français
Italiano
Nederlands
Polski
Português
Русский
中文
日本語
한국어 Империя чисел — мощные математические инструменты для каждого | Связь с веб-мастером
Используя этот сайт, вы подтверждаете свое согласие с Условиями и соглашениями и Политикой приватности.

© 2023
numberempire.com
Все права защищены

Источник

Неравенства профильного ЕГЭ (задания 15) — еще немного!

И еще немного неравенств… Обязательно помним про ОДЗ там, где есть корни, логарифмы, дроби!

Задание 1. Решить неравенство: $log_2 (4+3x-x^2)+7 log_{0,5} (4+3x-x^2)+10>0$

Обозначаем: за :

Корни по Виету:

Получили два новых неравенства:

Решаем первое:

Основание логарифма больше 1 – знак неравенства сохраняем:

Решение

Решаем второе:

Основание логарифма больше 1 – знак неравенства сохраняем:

Этот трехчлен всегда больше 0, так как дискриминант его отрицателен, а старший коэффициент – положителен. Неравенство не имеет решений.

Решение первого неравенства накладываем на ОДЗ:

Так как сумма первого и третьего коэффициентов равна второму, то первый корень – (-1), а второй – 4.

Тогда ОДЗ:

Общее решение:

Задание 2. Решить неравенство: ${log_ {1-2x} (x+1)(1-4x+4x^2)}/{ log_{x+1} (1-2x)}<=-1$

Составляем систему уравнений ОДЗ:

$delim{lbrace}{matrix{6}{1}{{x+1<>1} {1-2x>0}{x-1>0}{1-2x<>1}{(x+1)(1-4x+4x^2)>0}{ log_{x+1} (1-2x)<>0}}}{ }$

$delim{lbrace}{matrix{5}{1}{{x<>0} {2x<1}{x>1}{(x+1)(1-2x) ^2>0}{ log_{x+1} (1-2x)<>0}}}{ }$

Решение предпоследнего неравенства изображено на рисунке:

Решение последнего: $log_{x+1} (1-2x)<>0$

x<> 0

ОДЗ полностью:

Теперь решим само неравенство:

${log_ {1-2x} (x+1)(1-4x+4x^2)}/{log_{x+1} (1-2x)}<=-1$

Перетащим единицу влево и заменим ее дробью, значение которой равно 1, приводим, таким образом, к общему знаменателю:

${log_ {1-2x} (x+1)(1-4x+4x^2)}/{log_{x+1} (1-2x)}+1<=0$

${log_ {1-2x} (x+1)(1-2x) ^2}/{ log_{x+1} (1-2x)}+ {log_ {x+1} (1-2x)}/{log_ {x+1} (1-2x)}<=0$

Произведение подлогарифмических выражений заменим суммой логарифмов:

${log_ {1-2x} (x+1)+ log_ {1-2x} (1-2x) ^2+ log_ {x+1} (1-2x)}/{log_ {x+1} (1-2x)}<=0$

${log_ {1-2x} (x+1)+ 2log_ {1-2x} (1-2x)+ log_{x+1} (1-2x)}/{log_ {x+1} (1-2x)}<=0$

Вводим замену:

$log_ {1-2x} (x+1)=t$

Получаем:

– это неравенство выполняется лишь при одном условии: t+1=0 , t=-1

Наше неравенство выродилось в уравнение, делаем обратную замену:

$log_ {1-2x} (x+1)=-1$

Корень, равный нулю, посторонний – не входит в ОДЗ, остается один:

Ответ:

Задание 3. Решить неравенство: $log_ {x/{x-1}} 5<= log_{x/2} 5$

$1/{log_5 {x/{x-1}}} <=1/{log_5 {x/2}}$

$log_5 {x/{x-1}} >=log_5 {x/2}$

${3x - x^2}/{2(x-1)} >=0$

Решение неравенства:

ОДЗ данного неравенства:

Решение первого:

Второе неравенство ОДЗ выполняется всегда.

Тогда ОДЗ:

Окончательное решение неравенства с учетом ОДЗ: ( 2; 3 ]

Задание 4. Решить неравенство: ${81^x+2*25^{x*log_5 3}-5}/(4x-1)^2>=0$

ОДЗ данного неравенства – не равенство нулю знаменателя:

4x-1<>0

Так как в знаменателе – квадрат, то неравенство может быть преобразовано к виду:

$81^x+2*25^{x*log_5 3}-5>=0$

$81^x+2*5^{2x*log_5 3}-5>=0$

$81^x+2*5^{log_5 {3^{2x}}}-5>=0$

$81^x+2*3^{2x}-5>=0$

$3^{4x}+2*3^{2x}-5>=0$

Замена: $3^{2x}=a$

$a_1={-2-2sqrt{6}}/2; a_2={-2+2sqrt{6}}/2$

$a_1={-1-sqrt{6}}; a_2={-1+sqrt{6}}$

Решение неравенства:

Так как мы ввели замену $3^{2x}=a$ , то первый корень – отрицательный – посторонний. Вводим обратную замену:

$3^{2x}={-1+sqrt{6}}$

$9^x={-1+sqrt{6}}$

$x=log_9 (-1+sqrt{6})$

Тогда решение: $x in (log_9 (-1+sqrt{6}); +infty)$

Теперь, чтобы записать ответ, нужно наложить на это решение ОДЗ, а для этого нужно сравнить числа $log_9 (-1+sqrt{6})$ и {1/4} – это выколотая точка ОДЗ.

Преобразуем число $log_9 (-1+sqrt{6})$ :

$log_9 (-1+sqrt{6})= log_9 (sqrt{6}(1-1/{sqrt{6}}))= log_9 6^{1/2}+log_9 (1-1/{sqrt{6}})$

${1/2}log_9 6+log_9 (1-1/{sqrt{6}})={1/2}log_9 3+{1/2}log_9 2+log_9 (1-1/{sqrt{6}})={1/4}+{1/2}log_9 2+log_9 (1-1/{sqrt{6}})$

Так как в этой сумме два последних слагаемых, очевидно, отрицательные, то $log_9 (-1+sqrt{6})<{1/4}$

Таким образом, решение неравенства: $x in (log_9 (-1+sqrt{6});{1/4}) union({1/4}; +infty)$

Задание 5. Решить неравенство: ${sqrt{x^2-2x+1}-sqrt{x^2+x}}/{x^2+x-1}<= 0$

ОДЗ: $delim{lbrace}{matrix{3}{1}{{x^2-2x+1>=0} {x^2+x>=0}{x^2+x-1<>0}}}{ }$

$delim{lbrace}{matrix{3}{1}{{(x-1)^2>=0} {x(x+1)>=0}{x^2+x-1<>0}}}{ }$

Корнями последнего будут: $x_1= {-1+sqrt{5}}/2, x_2= {-1-sqrt{5}}/2$

На рисунке показаны решения всех неравенств и выполнено наложение решений друг на друга, записываем ОДЗ: ( ] union [)

Решаем само неравенство:

$delim{lbrace}{matrix{2}{1}{{sqrt{x^2-2x+1}-sqrt{x^2+x}>=0} {x^2+x-1< 0}}}{}$

или

$delim{lbrace}{matrix{2}{1}{{sqrt{x^2-2x+1}-sqrt{x^2+x}<=0} {x^2+x-1> 0}}}{ }$

Решаем первое неравенство первой системы:

$sqrt{x^2-2x+1}>=sqrt{x^2+x}$

Возведем в квадрат: $delim{|}{x^2-2x+1}{|}>=delim{|}{x^2+x}{|}$

Так как выражение под левым модулем всегда неотрицательно, то модули можно просто снять:

-3x>=-1

x<=1/3

Корни для решения второго неравенства уже найдены: $x_1= {-1+sqrt{5}}/2, x_2= {-1-sqrt{5}}/2$

Решение неравенства:

Решение системы: x in (]

Решение второй системы данной совокупности совершенно аналогично, только, согласно знаку неравенства, выбираем другие области:

Решение системы: x in (]

Задание 6. Решить неравенство: $log_ {x^2+x} (x^2-2x+1)<= 1$

Определим ОДЗ:

$delim{lbrace}{matrix{3}{1}{{x^2+x>0}{x^2+x<>1}{x^2-2x+1>0}}}{ }$

$delim{lbrace}{matrix{3}{1}{{x^2+x>0}{x^2+x<>1}{(x-1)^2>0}}}{ }$

Решение первого неравенства системы ОДЗ найдем по методу интервалов:

Второе неравенство системы:

D=5

$x_1={-1+sqrt{5}}/2, x_2={-1-sqrt{5}}/2$

Полученные значения – запрещенные, и будут нами выколоты из области допустимых значений.

Третье неравенство системы, кажется, выполняется всегда, однако здесь можно допустить ошибку: неравенство строгое, то есть можно записать его так:

x<>1

Окончательно ОДЗ:

Решение системы:

Теперь решаем само неравенство:

$log_ {x^2+x} (x^2-2x+1)<= 1$

$log_ {x^2+x} (x^2-2x+1)<= log_ {x^2+x} (x^2+x)$

Если основание больше 1, то переходим к сравнению подлогарифмических выражений с сохранением знака неравенства:

3x>= 1

– решение актуально при условии x^2+x>1 , то есть при

Если основание больше нуля, но меньше 1, то переходим к сравнению подлогарифмических выражений с изменением знака неравенства:

3x<= 1

– решение актуально при условии x^2+x<1 , x^2+x>0 то есть при x in ({-1-sqrt{5}}/2; -1) union (0;{-1+sqrt{5}}/2)

Изобразим это на рисунке:

Осталось на два этих решения наложить ОДЗ, и дело в шляпе! Решение:

( 0;{1/3} ]

Задание 7. Решить систему неравенств: $delim{lbrace}{matrix{2}{1}{{ log_{4-x} (x+4)*log_{x+5} (6-x)<=0} {25^(x^2-2x+10)-0,2^(2x^2-4x-80)<=0}}}{ }$

ОДЗ:

Решим сначала второе неравенство:

$5^(2x^2-4x+20) <=5^{-1}(2x^2-4x-80)$

Теперь основания одинаковые и можно перейти к сравнению показателей степеней с сохранением знака неравенства, так как основание больше 1:

Получили квадратное неравенство:

, или

По Виету легко находим корни:

Решение неравенства уже с учетом ОДЗ:

x in [ -3;3 ))

Решим теперь первое неравенство, используем метод рационализации:

$log_{4-x} (x+4)*log_{x+5} (6-x)<=0$

Преобразуем неравенство:

Решение:

Накладываем решение этого неравенства на решение предыдущего и ОДЗ:

Решение:

Источник

Задание 1

Площадь ромба равна 9. Одна из его диагоналей в 8 раз больше другой. Найдите меньшую диагональ.

Ответ: 1,5

Скрыть

Задание 2

Длина окружности основания конуса равна 6, образующая равна 4. Найдите площадь боковой поверхности конуса.

Ответ: 12

Скрыть

Задание 3

Из районного центра в деревню ежедневно ходит автобус. Вероятность того, что в понедельник в автобусе окажется меньше 18 пассажира, равна 0,9. Вероятность того, что окажется меньше 9 пассажиров, равна 0,66. Найдите вероятность того, что число пассажиров будет от 9 до 17 включительно.

Ответ: 0,24

Скрыть

Задание 4

Перед началом волейбольного матча капитаны команд тянут честный жребий, чтобы определить, какая из команд начнёт игру с мячом. Команда «Стартер» по очереди играет с командами «Ротор», «Мотор» и «Монтёр». Найдите вероятность того, что «Стартер» будет начинать только вторую игру.

Ответ: 0,125

Скрыть

Задание 5

Решите уравнение $$cos frac{pi(8x+8)}{3}=frac{1}{2}$$. В ответе запишите наибольший отрицательный корень.

Ответ: 0,375

Скрыть

Задание 6

Найдите значение выражения $$frac{125^{3,2}}{25^{3,3}}$$

Ответ: 125

Скрыть

Задание 7

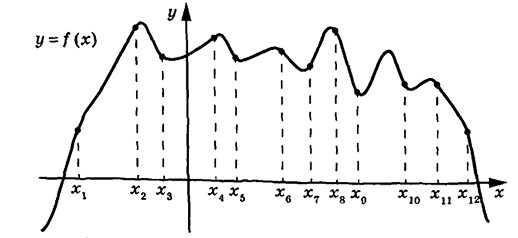
На рисунке изображён график функции $$y=f(x)$$. На оси абсцисс отмечено двенадцать точек: $$x_1$$, $$x_2$$, $$x_3$$, $$x_4$$, $$x_5$$, $$x_6$$, $$x_7$$, $$x_8$$, $$x_9$$, $$x_{10}$$, $$x_{11}$$, $$x_{12}$$. В ответе укажите количество точек (из отмеченных), в которых производная функции $$f(x)$$ отрицательна.

Ответ: 8

Скрыть

Задание 8

Наблюдатель находится на высоте $$h$$, выраженной в метрах. Расстояние от наблюдателя до наблюдаемой им линии горизонта, выраженное в километрах, вычисляется по формуле $$l=sqrt{frac{Rh}{500}}$$, где $$R=6400$$ км — радиус Земли. На какой высоте находится наблюдатель, если он видит линию горизонта на расстоянии 60 километров? Ответ дайте в метрах.

Ответ: 281,25

Скрыть

Задание 9

Заказ на изготовление 216 деталей первый рабочий выполняет на 6 часов быстрее, чем второй. Сколько деталей за час изготавливает первый рабочий, если известно, что он за час изготавливает на 6 деталей больше?

Ответ: 18

Скрыть

Задание 10

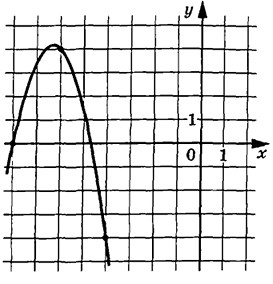
На рисунке изображён график функции $$f(x)=ax^2+bx+c$$. Найдите ординату точки пересечения графика функции $$y=f(x)$$ с осью ординат.

Ответ: -56

Скрыть

Задание 11

Найдите точку минимума функции $$y=10x-ln (x+11)+3$$.

Ответ: -10,9

Скрыть

Задание 12

а) Решите уравнение $$5^{x+sqrt{x}-1}+6cdot 5^{x-sqrt{x}+1}-5^{x+1}=0$$

б) Найдите все корни этого уравнения, принадлежащие отрезку $$[1;2,56]$$

Ответ: а)$$log^{2}_{5}10;log^{2}_{5}15$$ б)$$log^{2}_{5}10$$

Скрыть

Задание 13

В прямой пятиугольной призме $$ABCDEA_1B_1C_1D_1E_1$$ высота равна $$2sqrt{3}$$ , треугольник $$BCD$$ — правильный, со стороной 6, а четырёхугольник $$ABDE$$ — равнобедренная трапеция со сторонами $$AB=DE=2$$, $$BD=6$$ и $$AE=4$$.

а) Докажите, что плоскости $$CA_1E_1$$ и $$AED_1$$ перпендикулярны.

б) Найдите объём многогранника $$CAED_1B_1$$.

Ответ: 40

Скрыть

Задание 14

Решите неравенство $$log_{tg 0,9}(log_{frac{1}{4}}(x^2-2))leq 0$$

Ответ: $$(-sqrt{3};-1,5];[1,5;sqrt{3})$$

Скрыть

Задание 15

В июле Борис планирует взять кредит в банке на некоторую сумму. Банк предложил Борису два варианта кредитования.

1-й вариант:

— кредит предоставляется на 3 года;

— в январе каждого года действия кредита долг увеличивается на 10 % от суммы долга на конец предыдущего года;

— в период с февраля по июнь каждого года действия кредита выплачиваются равные суммы, причём последний платёж должен погасить долг по кредиту полностью,

2-й вариант:

— кредит предоставляется на 2 года; — в январе каждого года действия кредита долг увеличивается на 16 %;

— в период с февраля по июнь каждого года действия кредита выплачиваются равные суммы, причём последний платёж должен погасить долг по кредиту полностью.

Когда Борис подсчитал, то выяснил, что по 1-му варианту кредитования ему придётся выплачивать на 353 740 рублей меньше, чем по 2-му варианту. Какую сумму Борис планирует взять в кредит?

Ответ: 8937 тыс. руб.

Скрыть

Задание 16

Четырёхугольник $$ABCD$$ со сторонами $$BC=14$$ и $$AB=CD=40$$ вписан в окружность радиусом $$R=25$$.

а) Докажите, что прямые $$BC$$ и $$AD$$ параллельны.

б) Найдите $$AD$$.

Ответ: 42,16

Скрыть

Задание 17

Найдите все значения $$а$$, при каждом из которых уравнение $$frac{log_{0,2}(6x^2+13ax+7x+8a^2+2a-2)}{sqrt{4-3a-2x}}=0$$ имеет единственный корень.

Ответ: $$(-infty;-7];[2;+infty);-frac{11}{8}$$

Скрыть

Задание 18

Все члены конечной последовательности являются натуральными числами. Каждый член этой последовательности, начиная со второго, либо в 8 раз больше, либо в 7 раз меньше предыдущего. Сумма всех членов последовательности равна 4040.

а) Может ли последовательность состоять из трёх членов?

б) Может ли последовательность состоять из пяти членов?

в) Какое наибольшее количество членов может быть в последовательности?

Ответ: а)да б)нет в)897

Скрыть

Источник