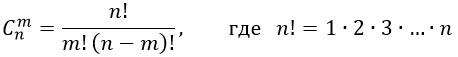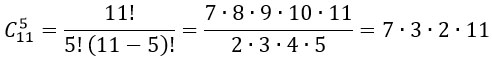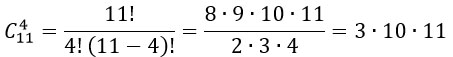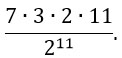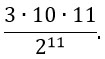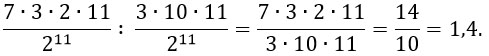508780 решу егэ математика профильный

Симметричную монету бросают 10 раз. Во сколько раз вероятность события «выпадет ровно 5 орлов» больше вероятности события «выпадет ровно 4 орла»?

Спрятать решение

Решение.

Воспользуемся формулой Бернулли. Найдем вероятность события А, состоящего в том, что при десяти бросаниях выпадет ровно 5 орлов:

P левая круглая скобка A правая круглая скобка =C в степени 5 _10 умножить на левая круглая скобка дробь: числитель: 1, знаменатель: 2 конец дроби правая круглая скобка в степени 5 умножить на левая круглая скобка дробь: числитель: 1, знаменатель: 2 конец дроби правая круглая скобка в степени 5 .

Аналогично найдем вероятность события B, состоящего в том, что при десяти бросаниях выпадет ровно 4 орла:

P левая круглая скобка B правая круглая скобка =C в степени 4 _10 умножить на левая круглая скобка дробь: числитель: 1, знаменатель: 2 конец дроби правая круглая скобка в степени 4 умножить на левая круглая скобка дробь: числитель: 1, знаменатель: 2 конец дроби правая круглая скобка в степени 6 .

Тогда

дробь: числитель: P левая круглая скобка A правая круглая скобка , знаменатель: P левая круглая скобка B правая круглая скобка конец дроби = дробь: числитель: C в степени 5 _10 умножить на левая круглая скобка дробь: числитель: 1, знаменатель: 2 конец дроби правая круглая скобка в степени левая круглая скобка 10 правая круглая скобка , знаменатель: C в степени 4 _10 умножить на левая круглая скобка дробь: числитель: 1, знаменатель: 2 конец дроби правая круглая скобка в степени левая круглая скобка 10 правая круглая скобка конец дроби = дробь: числитель: 10!, знаменатель: 5! умножить на 5! конец дроби умножить на дробь: числитель: 4! умножить на 6!, знаменатель: 10! конец дроби = дробь: числитель: 6, знаменатель: 5 конец дроби =1,2.

Ответ: 1,2

Приведем решение Ирины Шраго.

Вероятность того, что выпадет ровно 5 орлов, равна отношению количества вариантов, при которых выпадает ровно 5 орлов, к общему количеству вариантов: P левая круглая скобка A правая круглая скобка = дробь: числитель: N левая круглая скобка A правая круглая скобка , знаменатель: N конец дроби . Вероятность того, что выпадет ровно 4 орла, равна отношению количества вариантов, при которых выпадает ровно 4 орла, к общему количеству вариантов: P левая круглая скобка B правая круглая скобка = дробь: числитель: N левая круглая скобка B правая круглая скобка , знаменатель: N конец дроби . Тогда отношение этих вероятностей дробь: числитель: P левая круглая скобка A правая круглая скобка , знаменатель: P левая круглая скобка B правая круглая скобка конец дроби = дробь: числитель: N левая круглая скобка A правая круглая скобка , знаменатель: N левая круглая скобка B правая круглая скобка конец дроби .

Количество вариантов, при которых выпадет ровно 5 орлов, равно C в степени 5 _10= дробь: числитель: 10 умножить на 9 умножить на 8 умножить на 7 умножить на 6, знаменатель: 5! конец дроби .

Количество вариантов, при которых выпадет ровно 4 орла, равно C в степени 4 _10= дробь: числитель: 10 умножить на 9 умножить на 8 умножить на 7, знаменатель: 4! конец дроби .

Тогда

дробь: числитель: P левая круглая скобка A правая круглая скобка , знаменатель: P левая круглая скобка B правая круглая скобка конец дроби = дробь: числитель: 10 умножить на 9 умножить на 8 умножить на 7 умножить на 6, знаменатель: 5! конец дроби : дробь: числитель: 10 умножить на 9 умножить на 8 умножить на 7, знаменатель: 4! конец дроби = дробь: числитель: 10 умножить на 9 умножить на 8 умножить на 7 умножить на 6 умножить на 1 умножить на 2 умножить на 3 умножить на 4, знаменатель: 10 умножить на 9 умножить на 8 умножить на 7 умножить на 1 умножить на 2 умножить на 3 умножить на 4 умножить на 5 конец дроби = дробь: числитель: 6, знаменатель: 5 конец дроби =1,2.

Источник

При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.

Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.

Версия для печати и копирования в MS Word

1

Найдите 9 косинус 2 альфа , если косинус альфа = дробь: числитель: 1, знаменатель: 3 конец дроби .

Ответ:

2

Найдите значение выражения  дробь: числитель: 12, знаменатель: синус в квадрате 27 в степени левая круглая скобка circ правая круглая скобка плюс косинус в квадрате 207 в степени левая круглая скобка circ правая круглая скобка конец дроби .

Ответ:

3

4

Найдите значение выражения дробь: числитель: 5 синус 74 в степени левая круглая скобка circ правая круглая скобка , знаменатель: косинус 37 в степени левая круглая скобка circ правая круглая скобка умножить на косинус 53 в степени левая круглая скобка circ правая круглая скобка конец дроби .

Ответ:

5

Найдите 61a минус 11b плюс 50, если дробь: числитель: 2a минус 7b плюс 5, знаменатель: 7a минус 2b плюс 5 конец дроби =9.

Ответ:

6

Найдите значение выражения 5 синус левая круглая скобка альфа минус 7 Пи правая круглая скобка минус 11 косинус левая круглая скобка дробь: числитель: 3 Пи , знаменатель: 2 конец дроби плюс альфа правая круглая скобка , если синус альфа = минус 0,25.

Ответ:

7

Найдите значение выражения левая круглая скобка 2x минус 5 правая круглая скобка левая круглая скобка 2x плюс 5 правая круглая скобка минус 4x в квадрате .

Ответ:

8

Найдите значение выражения дробь: числитель: левая круглая скобка 4x минус 3y правая круглая скобка в квадрате минус левая круглая скобка 4x плюс 3y правая круглая скобка в квадрате , знаменатель: 4xy конец дроби .

Ответ:

9

Найдите значение выражения 5 в степени левая круглая скобка log правая круглая скобка _2549 .

Ответ:

10

Найдите значение выражения дробь: числитель: 9axy минус левая круглая скобка минус 7xya правая круглая скобка , знаменатель: 4yax конец дроби .

Ответ:

11

Найдите значение выражения дробь: числитель: 6 в степени левая круглая скобка корень из 3 правая круглая скобка умножить на 7 в степени левая круглая скобка корень из 3 правая круглая скобка , знаменатель: 42 в степени левая круглая скобка корень из 3 правая круглая скобка минус 1 конец дроби .

Ответ:

12

Найдите значение выражения 7 в степени левая круглая скобка 2x минус 1 правая круглая скобка :49 в степени x :x при x= дробь: числитель: 1, знаменатель: 14 конец дроби .

Ответ:

13

Найдите значение выражения корень из 3 косинус в квадрате дробь: числитель: 5 Пи , знаменатель: 12 конец дроби минус корень из 3 синус в квадрате дробь: числитель: 5 Пи , знаменатель: 12 конец дроби .

Ответ:

14

Найдите значение выражения дробь: числитель: 5 корень из x плюс 2, знаменатель: корень из x конец дроби минус дробь: числитель: 2 корень из x, знаменатель: x конец дроби  при x больше 0.

Ответ:

15

Найдите значение выражения дробь: числитель: левая круглая скобка корень 3 степени из левая круглая скобка 7a в квадрате правая круглая скобка правая круглая скобка в степени левая круглая скобка 6 правая круглая скобка , знаменатель: a в степени 4 конец дроби при a не равно 0.

Ответ:

16

Найдите дробь: числитель: 3 косинус альфа минус 4 синус альфа , знаменатель: 2 синус альфа минус 5 косинус альфа конец дроби , если тангенс альфа =3.

Ответ:

17

Найдите значение выражения дробь: числитель: корень из 81 корень 7 степени из левая круглая скобка b правая круглая скобка , знаменатель: корень 14 степени из левая круглая скобка b правая круглая скобка конец дроби при b больше 0.

Ответ:

18

Найдите значение выражения дробь: числитель: a в квадрате b в степени левая круглая скобка минус 6 правая круглая скобка , знаменатель: левая круглая скобка 4a правая круглая скобка в кубе b в степени левая круглая скобка минус 2 правая круглая скобка конец дроби умножить на дробь: числитель: 16, знаменатель: a в степени левая круглая скобка минус 1 правая круглая скобка b в степени левая круглая скобка минус 4 правая круглая скобка конец дроби .

Ответ:

19

Найдите значение выражения  левая круглая скобка 4a правая круглая скобка в кубе :a в степени 7 умножить на a в степени 4 .

Ответ:

20

Найдите значение выражения log _ дробь: числитель: 1, знаменатель: 13 конец дроби корень из 13.

Ответ:

21

Найдите значение выражения дробь: числитель: log _325, знаменатель: log _35 конец дроби .

Ответ:

22

Найдите значение выражения b в степени левая круглая скобка дробь: числитель: 1, знаменатель: 5 конец дроби правая круглая скобка умножить на левая круглая скобка b в степени левая круглая скобка дробь: числитель: 9, знаменатель: 10 конец дроби правая круглая скобка правая круглая скобка в квадрате при b=7.

Ответ:

23

Найдите значение выражения log _4log _525.

Ответ:

24

Найдите значение выражения 36 корень из 6 тангенс дробь: числитель: Пи , знаменатель: 6 конец дроби синус дробь: числитель: Пи , знаменатель: 4 конец дроби .

Ответ:

25

Найдите значение выражения дробь: числитель: 5 тангенс 163 градусов , знаменатель: тангенс 17 градусов конец дроби .

Ответ:

26

Найдите значение выражения левая круглая скобка целая часть: 2, дробная часть: числитель: 4, знаменатель: 7 минус 2,5 правая круглая скобка : дробь: числитель: 1, знаменатель: 70 конец дроби .

Ответ:

27

Найдите значение выражения b в степени 5 :b в степени 9 умножить на b в степени 6 при b=0,01.

Ответ:

28

Найдите значение выражения дробь: числитель: левая круглая скобка b в степени левая круглая скобка корень из 3 правая круглая скобка правая круглая скобка в степени левая круглая скобка 2 корень из 3 правая круглая скобка , знаменатель: b в степени 4 конец дроби при b=5.

Ответ:

29

Найдите дробь: числитель: a, знаменатель: b конец дроби , если дробь: числитель: 2a плюс 5b, знаменатель: 5a плюс 2b конец дроби =1.

Ответ:

30

Найдите значение выражения дробь: числитель: log _6 корень из 13, знаменатель: log _613 конец дроби .

Ответ:

Завершить тестирование, свериться с ответами, увидеть решения.

Источник

Решение:

Расписывать в этой задаче все варианты выпадения орлов нереально, ведь монету подкидывают 11 раз. 11 раз, Карл!

Поэтому эту задачу будем решать с помощью сочетаний.

Рекомендую про перестановки, сочетания и размещения посмотреть тут, чтобы не путаться в них в дальнейшем)

Итак, формула, которая нам потребуется выглядит так:

Найдем количество исходов для события «выпадет ровно 5 орлов»:

Найдем количество исходов для события «выпадет ровно 4 орлов»:

Чтобы найти всевозможные события надо количество сторон монетки возвести в степень, равную количеству бросков, т.е. 211. В данном случае считать это не имеет смысла.

Вероятность находится делением благоприятных событий на всевозможные, т.е.

вероятность события «выпадет ровно 5 орлов» равна 

Специально ничего не умножаю)

А вероятность события «выпадет ровно 4 орла» равна 

А теперь найдем во сколько раз вероятность события «выпадет ровно 5 орлов» больше вероятности события «выпадет ровно 4 орла»:

Ответ: 1,4

#922

Источник

11 октября 2021

В закладки

Обсудить

Жалоба

Пять вероятностных задач

Решение непростых задач по теории вероятностей.

1) Симметричную монету бросают 16 раз. Во сколько раз вероятность события «выпадет ровно 8 орлов» больше вероятности события «выпадет ровно 7 орлов»?

2) Стрелок стреляет по пяти одинаковым мишеням. На каждую мишень даётся не более двух выстрелов, и известно, что вероятность поразить мишень каждым отдельным выстрелом равна 0,8. Во сколько раз вероятность события «стрелок поразит ровно пять мишеней» больше вероятности события «стрелок поразит ровно четыре мишени»?

3) В викторине участвуют 5 команд. Все команды разной силы, и в каждой встрече выигрывает та команда, которая сильнее. В первом раунде встречаются две случайно выбранные команды. Ничья невозможна. Проигравшая команда выбывает из викторины, а победившая команда играет со следующим случайно выбранным соперником. Известно, что в первых двух играх победила команда А. Какова вероятность того, что эта команда выиграет третий раунд?

4) Турнир по настольному теннису проводится по олимпийской системе в несколько туров: если в туре участвует чётное число игроков, то они разбиваются на случайные игровые пары. Если число игроков нечётно, то с помощью жребия выбираются случайные игровые пары, а один игрок остаётся без пары и не участвует в туре. Проигравший в каждой паре (ничья невозможна) выбывает из турнира, а победители и игрок без пары, если он есть, выходят в следующий тур, который проводится по таким же правилам. Так продолжается до тех пор, пока не останутся двое, которые играют между собой финальный тур, то есть последнюю партию, которая выявляет победителя турнира. Всего в турнире участвует 10 игроков, все они играют одинаково хорошо, поэтому в каждой встрече вероятность выигрыша и поражения у каждого игрока равна 0,5. Среди игроков два друга — Иван и Алексей. Какова вероятность того, что этим двоим в каком-то туре придётся сыграть друг с другом?

5) Первый член последовательности целых чисел равен 0. Каждый следующий член последовательности с вероятностью р = 20/23 на единицу больше предыдущего и с вероятностью 1 — р на единицу меньше предыдущего. Какова вероятность того, что какой-то член этой последовательности окажется равен —1?

Источник: vk.com/egeatom

Источник
Skip to content

ЕГЭ по математике — Профиль 2022. Открытый банк заданий с ответами.

ЕГЭ по математике — Профиль 2022. Открытый банк заданий с ответами.admin2022-08-27T23:17:48+03:00

Источник

Решу егэ математика профиль 508780

—>

Задание 10 № 508781

Симметричную монету бросают 11 раз. Во сколько раз вероятность события «выпадет ровно 5 орлов» больше вероятности события «выпадет ровно 4~орла»?

Задание 10 № 508782

Симметричную монету бросают 12 раз. Во сколько раз вероятность события «выпадет ровно 4 орла» меньше вероятности события «выпадет ровно 5~орлов»?

Задание 10 № 508783

Симметричную монету бросают 8 раз. Во сколько раз вероятность события «выпало ровно 4 орла» больше вероятности события «выпадет ровно 3~орла»?

Задание 10 № 508784

Симметричную монету бросают 9 раз. Во сколько раз вероятность события «выпадет ровно 4 орла» больше вероятности события «выпадет ровно 3~орла»?

Задание 10 № 508785

Симметричную монету бросают 10 раз. Во сколько раз вероятность события «выпадет ровно 4 орла» больше вероятности события «выпадет ровно 3~орла»?

Задание 10 № 508786

Симметричную монету бросают 16 раз. Во сколько раз вероятность события «выпадет ровно 8 орлов» больше вероятности события «выпадет ровно 7~орлов»?

Задание 10 № 508787

Симметричную монету бросают 17 раз. Во сколько раз вероятность события «выпадет ровно 8 орлов» больше вероятности события «выпадет ровно 7~орлов»?

Задание 10 № 508788

Симметричную монету бросают 20 раз. Во сколько раз вероятность события «выпадет ровно 10 орлов» больше вероятности события «выпадет ровно 9~орлов»?

Задание 10 № 508789

Симметричную монету бросают 21 раз. Во сколько раз вероятность события «выпадет ровно 10 орлов» больше вероятности события «выпадет ровно 9~орлов»?

Задание 10 № 508790

Симметричную монету бросают 22 раза. Во сколько раз вероятность события «выпадет ровно 10 орлов» больше вероятности события «выпадет ровно 9~орлов»?

Задание 10 № 508785

Задание 10 № 508787

Задание 10 508785.

Ege. sdamgia. ru

11.06.2017 5:54:40

2018-11-10 15:26:08

Источники:

Https://ege. sdamgia. ru/test? likes=508780

ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword { color: red; } Решу егэ математика профиль 508780

Решу егэ математика профиль 508780

Решу егэ математика профиль 508780

Задание 10 № 508780

Симметричную монету бросают 10 раз. Во сколько раз вероятность события «выпадет ровно 5 орлов» больше вероятности события «выпадет ровно 4 орла»?

Воспользуемся формулой Бернулли. Найдем вероятность события А, состоящего в том, что при десяти бросаниях выпадет ровно 5 орлов:

Аналогично найдем вероятность события B, состоящего в том, что при десяти бросаниях выпадет ровно 4 орла:

Приведем решение Ирины Шраго.

Вероятность того, что выпадет ровно 5 орлов, равна отношению количества вариантов, при которых выпадает ровно 5 орлов, к общему количеству вариантов: Вероятность того, что выпадет ровно 4 орла, равна отношению количества вариантов, при которых выпадает ровно 4 орла, к общему количеству вариантов: Тогда отношение этих вероятностей

Задание 10 № 508780

Во сколько раз вероятность события выпадет ровно 5 орлов больше вероятности события выпадет ровно 4 орла.

Ege. sdamgia. ru

19.08.2019 2:23:20

2019-08-19 02:23:20

Источники:

Https://ege. sdamgia. ru/problem? id=508780

Решу егэ математика профиль 508780 — Математика и Английский » /> » /> .keyword { color: red; } Решу егэ математика профиль 508780

Решу егэ математика профиль 508780

Решу егэ математика профиль 508780

Уско­рен­ная под­го­тов­ка к ЕГЭ с ре­пе­ти­то­ра­ми Учи. До­ма. За­пи­сы­вай­тесь на бес­плат­ное за­ня­тие!

Задание 10 № 508781

Симметричную монету бросают 11 раз. Во сколько раз вероятность события «выпадет ровно 5 орлов» больше вероятности события «выпадет ровно 4~орла»?

Задание 10 № 508782

Симметричную монету бросают 12 раз. Во сколько раз вероятность события «выпадет ровно 4 орла» меньше вероятности события «выпадет ровно 5~орлов»?

Задание 10 № 508783

Симметричную монету бросают 8 раз. Во сколько раз вероятность события «выпало ровно 4 орла» больше вероятности события «выпадет ровно 3~орла»?

Задание 10 № 508784

Симметричную монету бросают 9 раз. Во сколько раз вероятность события «выпадет ровно 4 орла» больше вероятности события «выпадет ровно 3~орла»?

Задание 10 № 508785

Симметричную монету бросают 10 раз. Во сколько раз вероятность события «выпадет ровно 4 орла» больше вероятности события «выпадет ровно 3~орла»?

Задание 10 № 508786

Симметричную монету бросают 16 раз. Во сколько раз вероятность события «выпадет ровно 8 орлов» больше вероятности события «выпадет ровно 7~орлов»?

Задание 10 № 508787

Симметричную монету бросают 17 раз. Во сколько раз вероятность события «выпадет ровно 8 орлов» больше вероятности события «выпадет ровно 7~орлов»?

Задание 10 № 508788

Симметричную монету бросают 20 раз. Во сколько раз вероятность события «выпадет ровно 10 орлов» больше вероятности события «выпадет ровно 9~орлов»?

Задание 10 № 508789

Симметричную монету бросают 21 раз. Во сколько раз вероятность события «выпадет ровно 10 орлов» больше вероятности события «выпадет ровно 9~орлов»?

Задание 10 № 508790

Симметричную монету бросают 22 раза. Во сколько раз вероятность события «выпадет ровно 10 орлов» больше вероятности события «выпадет ровно 9~орлов»?

Задание 10 № 508789

Задание 10 № 508781

Задание 10 508789.

Источники:

ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword < color: red; >Решу егэ математика профиль 508780

Решу егэ математика профиль 508780

Решу егэ математика профиль 508780

Уско­рен­ная под­го­тов­ка к ЕГЭ с ре­пе­ти­то­ра­ми Учи. До­ма. За­пи­сы­вай­тесь на бес­плат­ное за­ня­тие!

Задание 10 № 508780

Симметричную монету бросают 10 раз. Во сколько раз вероятность события «выпадет ровно 5 орлов» больше вероятности события «выпадет ровно 4 орла»?

Воспользуемся формулой Бернулли. Найдем вероятность события А, состоящего в том, что при десяти бросаниях выпадет ровно 5 орлов:

Аналогично найдем вероятность события B, состоящего в том, что при десяти бросаниях выпадет ровно 4 орла:

Приведем решение Ирины Шраго.

Вероятность того, что выпадет ровно 5 орлов, равна отношению количества вариантов, при которых выпадает ровно 5 орлов, к общему количеству вариантов: Вероятность того, что выпадет ровно 4 орла, равна отношению количества вариантов, при которых выпадает ровно 4 орла, к общему количеству вариантов: Тогда отношение этих вероятностей

Задание 10 № 508780

Аналогично найдем вероятность события B, состоящего в том, что при десяти бросаниях выпадет ровно 4 орла.

Источники:

ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword < color: red; >Решу егэ математика профиль 508780

Решу егэ математика профиль 508780

Решу егэ математика профиль 508780

Уско­рен­ная под­го­тов­ка к ЕГЭ с ре­пе­ти­то­ра­ми Учи. До­ма. За­пи­сы­вай­тесь на бес­плат­ное за­ня­тие!

Задание 10 № 508780

Симметричную монету бросают 10 раз. Во сколько раз вероятность события «выпадет ровно 5 орлов» больше вероятности события «выпадет ровно 4 орла»?

Воспользуемся формулой Бернулли. Найдем вероятность события А, состоящего в том, что при десяти бросаниях выпадет ровно 5 орлов:

Аналогично найдем вероятность события B, состоящего в том, что при десяти бросаниях выпадет ровно 4 орла:

Приведем решение Ирины Шраго.

Вероятность того, что выпадет ровно 5 орлов, равна отношению количества вариантов, при которых выпадает ровно 5 орлов, к общему количеству вариантов: Вероятность того, что выпадет ровно 4 орла, равна отношению количества вариантов, при которых выпадает ровно 4 орла, к общему количеству вариантов: Тогда отношение этих вероятностей

Количество вариантов, при которых выпадет ровно 5 орлов, равно

Количество вариантов, при которых выпадет ровно 4 орла, равно

Задание 10 № 508791

В одном ресторане в г. Тамбове администратор предлагает гостям сыграть в «Шеш-беш»: гость бросает одновременно две игральные кости. Если он выбросит комбинацию 5 и 6 очков хотя бы один раз из двух попыток, то получит комплимент от ресторана: чашку кофе или десерт бесплатно. Какова вероятность получить комплимент? Результат округлите до сотых.

Сначала найдём вероятность того, что при двух бросках игральных костей комбинация 5 и 6 очков не выпадет ни разу. Заметим, что вероятность выбросить комбинацию 5 и 6 очков складывается из двух несовместных событий: на первом кубике выпало 5 очков, а на втором кубике выпало 6 очков или на первом кубике выпало 6 очков, а на втором кубике выпало 5 очков. Тогда вероятность того, что при броске двух игральных костей выпадет комбинация 5 и 6 очков, равна

Вероятность противоположного события, состоящего в том, что при одном броске костей комбинация 5 и 6 очков не выпадет, равна

Каждое бросание костей не зависит от предыдущего. Вероятность произведения независимых событий равна произведению вероятностей этих событий. Поэтому вероятность того, что при двух бросках игральных костей комбинация 5 и 6 очков не выпадет ни разу, равна Следовательно, вероятность противоположного события, состоящего в том, что при двух бросаниях игральных костей комбинация 5 и 6 очков выпадет хотя бы один раз, равна

Округляя до сотых, получаем ответ.

Приведем другое решение.

Пусть событие A состоит в том, что при первом бросании выпала комбинация 5 и 6 очков, а событие B состоит в том, что при втором бросании выпала комбинация 5 и 6 очков. Событие, состоящее в том, что комбинация 5 и 6 очков выпадет хотя бы один раз из двух попыток, является суммой этих событий. События A и B являются совместными и независимыми, вероятность их суммы вычисляется по формуле:

Источники:

ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword < color: red; >Решу егэ математика профиль 508780

Уско­рен­ная под­го­тов­ка к ЕГЭ с ре­пе­ти­то­ра­ми Учи. До­ма. За­пи­сы­вай­тесь на бес­плат­ное за­ня­тие!

Задание 10 № 508780

Симметричную монету бросают 10 раз. Во сколько раз вероятность события «выпадет ровно 5 орлов» больше вероятности события «выпадет ровно 4 орла»?

Воспользуемся формулой Бернулли. Найдем вероятность события А, состоящего в том, что при десяти бросаниях выпадет ровно 5 орлов:

Аналогично найдем вероятность события B, состоящего в том, что при десяти бросаниях выпадет ровно 4 орла:

Приведем решение Ирины Шраго.

Вероятность того, что выпадет ровно 5 орлов, равна отношению количества вариантов, при которых выпадает ровно 5 орлов, к общему количеству вариантов: Вероятность того, что выпадет ровно 4 орла, равна отношению количества вариантов, при которых выпадает ровно 4 орла, к общему количеству вариантов: Тогда отношение этих вероятностей

Задание 10 № 508780

Аналогично найдем вероятность события B, состоящего в том, что при десяти бросаниях выпадет ровно 4 орла.

Аналогично найдем вероятность события B, состоящего в том, что при десяти бросаниях выпадет ровно 4 орла.

Dankonoy. com

21.01.2020 19:20:41

2019-05-30 20:46:26

Источники:

Https://dankonoy. com/ege/ege12/archives/4538

Источник

Понравилась статья? Поделить с друзьями:
  • 506741 решу егэ
  • 506712 решу егэ
  • 506694 решу егэ
  • 506616 решу егэ
  • 506602 егэ математика