Образовательный портал для подготовки к экзаменам
Математика базового уровня
Математика базового уровня
Сайты, меню, вход, новости
Задания
Версия для печати и копирования в MS Word
Деталь имеет форму изображённого на рисунке многогранника (все двугранные углы прямые). Числа на рисунке обозначают длины рёбер в сантиметрах. Найдите объём этой детали. Ответ дайте в кубических сантиметрах.
Спрятать решение
Решение.
На рисунке изображен многогранник, состоящий из двух параллелепипедов: один со сторонами — 2,1,3, второй — 1,3, 1. Тогда объем двух параллелепипедов равен:
Ответ: 9.
Номер в банке ФИПИ: 9D0CDF
За это задание ты можешь получить 1 балл. На решение дается около 3 минут. Уровень сложности: повышенный.
Средний процент выполнения: 60.5%
Ответом к заданию 13 по информатике может быть цифра (число) или слово.
Разбор сложных заданий в тг-канале
Задачи для практики
Задача 1
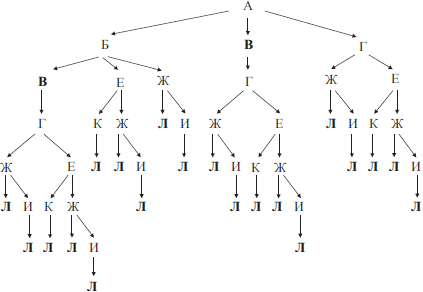
На рисунке изображена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К?
Решение
Построим таблицу. В первую строку таблицы запишем наименование всех вершин в следующем порядке. Сначала запишем вершину К. Затем те вершины, из которых в К ведёт прямой путь и из которых в вершину К можно попасть только через уже просмотренные вершины. Далее вершины, из которых в уже просмотренные вершины ведёт прямой путь и из которых можно попасть только через уже просмотренные вершины. Получим:
| К | З | И | Ж | Е | В | Б | Д | Г | А |
Вторую строку таблицы заполним числами, соответствующими количеству исходящих путей Px(K) из просматриваемой вершины x в K. Если из вершины x выходит несколько путей, например, в вершины x1, x2, и x3, то количество путей, ведущих из этой вершины в К, будет равно сумме путей, ведущих из x1, x2, и x3 в К.
То есть Px(K) = Px1 (K) + Px2 (K) + Px3 (K).
Для вершины К в таблицу заносим значение PК(K) = 1.
Следующей идёт вершина З. Из этой вершины выходит путь только в одну вершину К. PЗ(K) = PК(K) = 1.
Из вершины И выходят два пути в вершины З и К.
PИ(K) = PЗ(K) + PК(K) = 1 + 1 = 2.
Из вершины Ж выходит путь только в одну вершину К.
PЖ(K) = PК(K) = 1.
Из вершины Е выходят два пути в вершины Ж и К.
PЕ(K) = PЖ(K) + PК(K) = 1 + 1 = 2.
Из вершины В выходит путь только в одну вершину З.
PВ(K) = PЗ(K) = 1.
Из вершины Б выходят пути в вершины Е, Ж и В. Следовательно, PБ(K) = PЕ(K) + PЖ(K) + PВ(K) = 2 + 1 + 1 = 4.
Из вершины Д выходит путь только в одну вершину И.
PД(K) = PИ(K) = 2.
Из вершины Г выходят два пути в вершины И и Д.
PГ(K) = PД(K) + PИ(K) = 2 + 2 = 4.
Из вершины А выходят пути в вершины Б, В, Г и Д. Следовательно, PА(K) = PБ(K) + PВ(K) + PГ(K) + PД(K) = 4 + 1 + 4 + 2 = 11.
Получим:
| К | З | И | Ж | Е | В | Б | Д | Г | А |
| 1 | 1 | 2 | 1 | 2 | 1 | 4 | 2 | 4 | 11 |
Ответ: 11
Задача 2
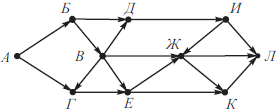
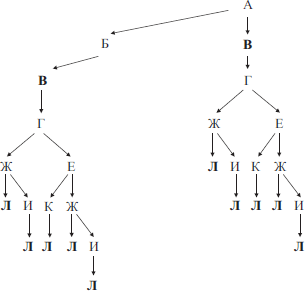
На рисунке изображена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К, Л. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город Л, не проходящих через пункт Ж?
Решение
Построим таблицу. В первую строку таблицы запишем наименование всех вершин в следующем порядке. Сначала запишем вершину Л. Затем те вершины, из которых в Л ведёт прямой путь и из которых в вершину Л можно попасть только через уже просмотренные вершины. Далее вершины, из которых в уже просмотренные вершины ведёт прямой путь и из которых можно попасть только через уже просмотренные вершины. Получим:
| Л | К | Ж | Е | И | Д | Г | В | Б | А |
Вторую строку таблицы заполним числами, соответствующими количеству исходящих путей Px(Л) из просматриваемой вершины x в Л, не проходящих через пункт Ж. Если из вершины x выходит несколько путей, например, в вершины x1, x2, и x3, то количество путей, ведущих из этой вершины в Л, не проходящих через пункт Ж, будет равно сумме путей, ведущих из x1, x2, и x3 в Л.
То есть Px(Л) = Px1(Л) + Px2 (Л) + Px3(Л).
Для вершины Л в таблицу заносим значение PЛ(Л) = 1.
Следующей идёт вершина К. Из этой вершины выходит путь только в одну вершину Л. PК(Л) = PЛ(Л) = 1.
Следующей в таблице идёт вершина Ж. Так как мы ищем пути, не проходящие через эту вершину, то PЖ(Л) = 0.
Из вершины Е выходят два пути в вершины Ж и К.
PЕ(Л) = PК(Л) + PЖ(Л) = 1 + 0 = 1.
Из вершины И выходят два пути в вершины Л и Ж.
PИ(Л) = PЖ(Л) + PЛ(Л) = 0 + 1 = 1.
Из вершины Д выходит путь только в одну вершину И.
PД(Л) = PИ(Л) = 1.
Из вершины Г выходит путь только в вершину Е. PГ(Л) = PЕ(Л) = 1.
Из вершины В выходят пути в вершины Д, Ж, Е и Г. Следовательно, PВ(Л) = PД(Л) + PЖ(Л) + PЕ(Л) + PГ(Л) = 1 + 0 + 1 + 1 = 3.
Из вершины Б выходят два пути в вершины Д и В.
PБ(Л) = PД(Л) + PВ(Л) = 1 + 3 = 4.
Из вершины А выходят два пути в вершины Б и Г.
PА(Л) = PБ(Л) + PГ(Л) = 4 + 1 = 5.
Получим:
| Л | К | Ж | Е | И | Д | Г | В | Б | А |
| 1 | 1 | 0 | 1 | 1 | 1 | 1 | 3 | 4 | 5 |
Ответ: 5
Задача 3
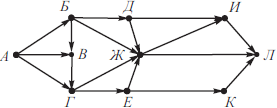
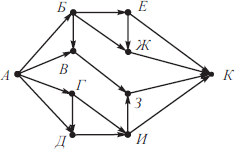
На рисунке изображена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К, Л. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город Л, проходящих через пункт В?
Решение
Построим граф, соответствующий данной схеме дорог. На графе будем для каждого города отмечать все возможные перемещения в города, связанные с ним исходящими дорогами.
Согласно условию задачи, требуется определить количество путей, проходящих через город В.
По графу определяем, что существует всего 10 различных путей, проходящих через город В.
Ответ: 10
Задача 4
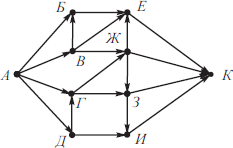
На рисунке изображена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К?
Решение
Построим таблицу. В первую строку таблицы запишем наименование всех вершин в следующем порядке. Сначала запишем вершину К. Затем те вершины, из которых в К ведёт прямой путь и из которых в вершину К можно попасть только через уже просмотренные вершины. Далее вершины, из которых в уже просмотренные вершины ведёт прямой путь и из которых можно попасть только через уже просмотренные вершины. Получим:
| К | И | Е | З | Ж | Б | В | Г | Д | А |
Вторую строку таблицы заполним числами, соответствующими количеству исходящих путей Px(K) из просматриваемой вершины x в K. Если из вершины x выходит несколько путей, например, в вершины x1, x2, и x3, то количество путей, ведущих из этой вершины в К, будет равно сумме путей, ведущих из x1, x2, и x3 в К.
То есть Px(K) = Px1(K) + Px2(K) + Px3(K).
Например, из вершины Ж выходят пути в вершины Е, З и К. Следовательно, PЖ(K) = PЕ(K) + PЗ(K) + PК(K) = 1 + 2 + 1 = 4. Получим:
| К | И | Е | З | Ж | Б | В | Г | Д | А |
| 1 | 1 | 1 | 2 | 4 | 1 | 6 | 6 | 7 | ‘20 |
Ответ: 20
Задача 5
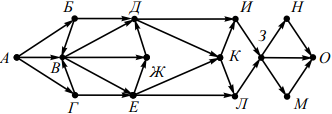
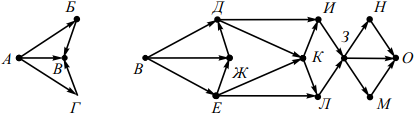
На рисунке изображена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К, Л, М, Н, О. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город О, проходящих через город В?
Решение
Заметим, что количество путей из города А в город О, проходящих через город В равно произведению количества путей из города А в город В на количество путей из города В в город О. Разобъём заданный граф на два: один из которых будет содержать только города и соответствующие дороги, ведущие из А в В, а другой — только города и соответствующие дороги из В в О.
Построим таблицу, соответствующую каждой из полученных схем. В первую строку таблицы запишем наименование всех вершин в следующем порядке.
Для первой схемы сначала запишем вершину В. Затем те вершины, из которых в В ведёт прямой путь и из которых в вершину В можно попасть только через уже просмотренные вершины. Получим:
Вторую строку таблицы заполним числами, соответствующими количеству исходящих путей Px (B) из просматриваемой вершины x в B. Если из вершины x выходит несколько путей, например, в вершины x1, x2, и x3, то количество путей, ведущих из этой вершины в К, будет равно сумме путей, ведущих из x1, x2, и x3 в К.
То есть Px (B) = Px1 (B) + Px2 (B) + Px3 (B). Получим:
Количество путей из А в В равно 3.
Для определения количества путей из города В в О аналогично построим таблицу, соответствующую второй схеме.
| О | Н | М | З | И | Л | К | Д | Ж | Е | В |
| 1 | 1 | 1 | 3 | 3 | 3 | 6 | 9 | 9 | 18 | 36 |
Количество путей из В в О равно 36.
Следовательно, количество путей из города А в город О, проходящих через город В, равно 3 · 36 = 108.
Ответ: 108
Задача 6
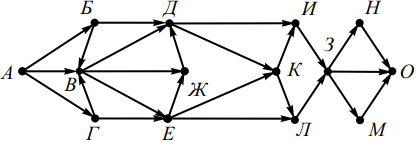
На рисунке изображена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К, Л, М, Н, О. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город О?
Решение
Построим таблицу, соответствующую заданной схеме. В первую строку таблицы запишем наименование всех вершин в следующем порядке. Сначала запишем вершину О. Затем те вершины, из которых в О ведёт прямой путь и из которых в вершину О можно попасть только через уже просмотренные вершины. Далее вершины, из которых в уже просмотренные вершины ведёт прямой путь и из которых можно попасть только через уже просмотренные вершины. Получим:
| О | Н | М | З | И | Л | К | Д | Ж | Е | В | Б | Г | А |
Вторую строку таблицы заполним числами, соответствующими количеству исходящих путей Px (O) из просматриваемой вершины x в O. Если из вершины x выходит несколько путей, например, в вершины x1, x2, и x3, то количество путей, ведущих из этой вершины в К, будет равно сумме путей, ведущих из x1, x2, и x3 в К.
То есть Px (O) = Px1 (O) + Px2 (O) + Px3 (O). Получим:
| О | Н | М | З | И | Л | К | Д | Ж | Е | В | Б | Г | А |
| 1 | 1 | 1 | 3 | 3 | 3 | 6 | 9 | 9 | 18 | 36 | 45 | 54 | 135 |
Ответ: 135
Задача 7
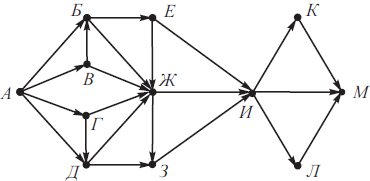
На рисунке изображена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К, Л, М. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город М?
Задача 8
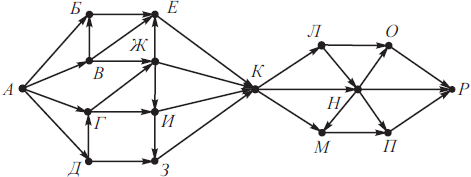
На рисунке изображена схема дорог, связывающих города А, Б, В, Г, Д, Е,Ж, З, И, К, Л, М, Н, О, П, Р. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой.
Сколько существует различных путей из города А в город Р, не проходящих через города Б и М?
Задача 9
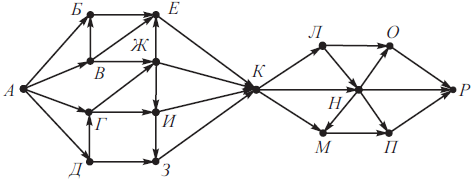
На рисунке изображена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К, Л, М, Н, О, П, Р. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой.
Сколько существует различных путей из города А в город Р, не проходящих через города Е и Н?
Задача 10
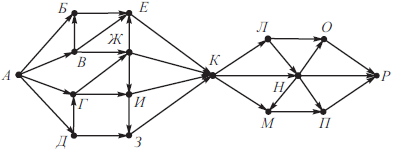
На рисунке изображена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К, Л, М, Н, О, П, Р. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город Р, проходящих через города З иМ?
Задача 11
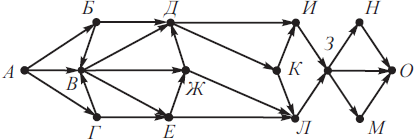
На рисунке изображена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К, Л, М, Н, О. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город О, проходящих через город Е и не проходящих через город И?
Задача 12
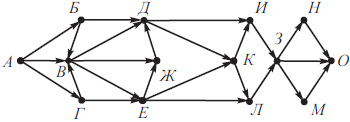
На рисунке изображена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К, Л, М, Н, О. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город О, проходящих через город Д и не проходящих через город Л?
Задача 13
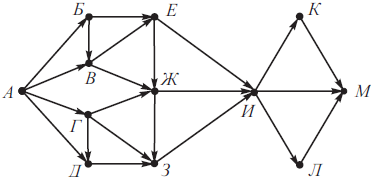
На рисунке изображена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К, Л, М. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город М, не проходящих через город В?
Задача 14
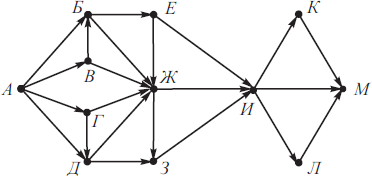
На рисунке изображена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К, Л, М. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город М, не проходящих через город Д?
Задача 15
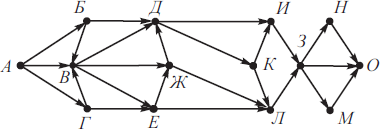
На рисунке изображена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К, Л, М, Н, О. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город О, не проходящих через город Д?
Задача 16
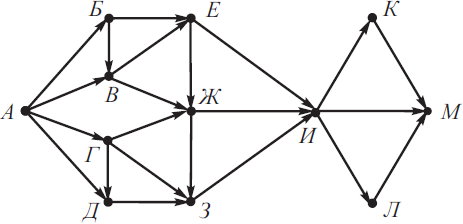
На рисунке изображена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К, Л, М. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город М, проходящих через город Е?
Задача 17
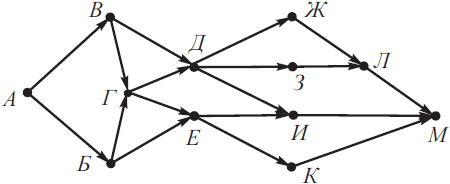
На рисунке изображена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К, Л, М. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город М, проходящих через город Б?
Задача 18
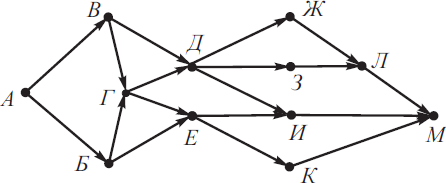
На рисунке изображена схема дорог, связывающих города А, Б, В, Г, Д, Е,Ж, З, И, К, Л, М. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город М, проходящих через город Д?
Задача 19
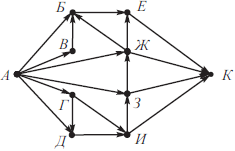
На рисунке изображена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К?
Задача 20
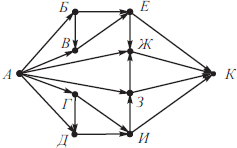
На рисунке изображена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К?
Рекомендуемые курсы подготовки
Новые тренировочные варианты ЕГЭ 2023 по математике базовый и профильный уровень с ответами и решением для 10 и 11 класса, больше 100 вариантов в формате реального экзамена ФИПИ вы можете решать онлайн или скачать.
Тренировочные варианты ЕГЭ 2023 по математике база и профиль
13.09.2022 Тренировочный вариант №1 ЕГЭ 2023 по математике профиль с ответами
20.09.2022 Тренировочный вариант №2 ЕГЭ 2023 по математике профиль с ответами
20.09.2022 Тренировочный вариант №2 ЕГЭ 2023 база по математике с ответами
27.09.2022 Математика 11 класс профиль входная мониторинговая работа 3 варианта с ответами
28.09.2022 Тренировочный вариант №3 ЕГЭ 2023 база по математике с ответами
28 сентября 2022 Статград математика 11 класс ЕГЭ 2023 база и профиль варианты и ответы
29 сентября 2022 Тренировочный вариант №3 ЕГЭ 2023 по математике профиль с ответами
1 октября 2022 Ларин вариант 399 ЕГЭ 2023 по математике профиль решение с ответами
6 октября Тренировочный вариант №4 ЕГЭ 2023 база по математике с ответами
6 октября Тренировочный вариант №4 ЕГЭ 2023 по математике профиль с ответами
8 октября Ларин вариант 400 ЕГЭ 2023 по математике профиль решение с ответами
12 октября Тренировочный вариант №5 ЕГЭ 2023 база по математике с ответами
12 октября Тренировочный вариант №5 ЕГЭ 2023 по математике профиль с ответами
14 октября Вариант 1 Ященко ЕГЭ 2023 математика профиль с ответами и решением
14 октября Вариант 2 Ященко ЕГЭ 2023 математика профиль с ответами и решением
15 октября Ларин вариант 401 ЕГЭ 2023 по математике профиль решение с ответами
15 октября Ларин вариант 402 ЕГЭ 2023 по математике профиль решение с ответами
16 октября Вариант 3 Ященко ЕГЭ 2023 математика профиль с ответами и решением
16 октября Вариант 4 Ященко ЕГЭ 2023 математика профиль с ответами и решением
23 октября Тренировочный вариант №6 ЕГЭ 2023 база по математике с ответами
24 октября Тренировочный вариант №6 ЕГЭ 2023 по математике профиль с ответами
25 октября Тренировочный вариант №7 ЕГЭ 2023 база по математике с ответами
26 октября Тренировочный вариант №7 ЕГЭ 2023 по математике профиль с ответами
28 октября Ларин вариант 403 ЕГЭ 2023 по математике профиль решение с ответами
29 октября Ларин вариант 404 ЕГЭ 2023 по математике профиль решение с ответами
1 ноября 2022 Тренировочный вариант №8 решу ЕГЭ 2023 база по математике с ответами
1 ноября 2022 Тренировочный вариант №8 решу ЕГЭ 2023 по математике профиль с ответами
5 ноября 2022 Вариант 1-2 распечатай и реши ЕГЭ 2023 база по математике 11 класс с ответами
6 ноября 2022 Ларин вариант 405 ЕГЭ 2023 профиль по математике решение с ответами
9 ноября 2022 Тренировочный вариант №9 решу ЕГЭ 2023 база по математике с ответами
12 ноября 2022 Тренировочный вариант №9 решу ЕГЭ 2023 по математике профиль с ответами
13 ноября 2022 Ларин вариант 406 ЕГЭ 2023 профиль по математике решение с ответами
15 ноября 2022 Тренировочный вариант №10 решу ЕГЭ 2023 база по математике 11 класс с ответами
15 ноября 2022 Тренировочный вариант №10 решу ЕГЭ 2023 по математике профиль с ответами
21 ноября 2022 Ларин вариант 407 ЕГЭ 2023 профиль по математике решение с ответами
23 ноября 2022 Тренировочный вариант №11 решу ЕГЭ 2023 база по математике 11 класс с ответами
23 ноября 2022 Тренировочный вариант №11 решу ЕГЭ 2023 по математике профиль с ответами
27 ноября 2022 Ларин вариант 408 ЕГЭ 2023 профиль по математике решение с ответами
28 ноября 2022 Вариант 3-4 распечатай и реши ЕГЭ 2023 база по математике 11 класс с ответами
30 ноября 2022 Мониторинговая работа по математике 11 класс ЕГЭ 2023 профиль 1 полугодие
3 декабря 2022 Тренировочный вариант №12 решу ЕГЭ 2023 база по математике 11 класс с ответами
3 декабря 2022 Тренировочный вариант №12 решу ЕГЭ 2023 по математике профиль с ответами
3 декабря 2022 Пробник ЕГЭ 2023 Москва по математике профиль задания и ответы
5 декабря 2022 Ларин вариант 409 ЕГЭ 2023 профиль по математике решение с ответами
9 декабря 2022 Тренировочный вариант №13 решу ЕГЭ 2023 база по математике 11 класс с ответами
10 декабря 2022 Тренировочный вариант №13 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
12 декабря 2022 Ларин вариант 410 ЕГЭ 2023 профиль по математике решение с ответами
13 декабря 2022 Статград математика 11 класс профиль ЕГЭ 2023 варианты МА2210209-МА2210212 и ответы
13 декабря 2022 Математика 11 класс база ЕГЭ 2023 статград варианты и ответы
15 декабря 2022 Тренировочный вариант №14 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
15 декабря 2022 Тренировочный вариант №14 решу ЕГЭ 2023 база по математике 11 класс с ответами
20 декабря 2022 Вариант 5-6 распечатай и реши ЕГЭ 2023 база по математике 11 класс с ответами
20 декабря 2022 Ларин вариант 411 ЕГЭ 2023 профиль по математике решение с ответами
3 января 2023 Ларин вариант 412 ЕГЭ 2023 профиль по математике решение с ответами
6 января 2023 Тренировочный вариант 1-2 ЕГЭ 2023 профиль математика задания и ответы
8 января 2023 Вариант 3-4 ЕГЭ 2023 профиль математика задания и ответы
9 января 2023 Вариант 7-8 распечатай и реши ЕГЭ 2023 база по математике 11 класс с ответами
10 января 2023 Тренировочный вариант №15 и №16 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
11 января 2023 ЕГЭ 2023 математика тренировочные задания и ответы Ященко, Семенов
11 января 2023 Тренировочный вариант №15 и №16 база ЕГЭ 2023 по математике 11 класс с ответами
19 января 2023 Тренировочные варианты №17 и №18 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
22 января 2023 Ларин вариант 413 и 414 ЕГЭ 2023 профиль по математике решение и ответы
22 января 2023 Тренировочный 19 вариант решу ЕГЭ 2023 профиль по математике 11 класс с ответами
22 января 2023 База ЕГЭ 2023 математика 11 класс тренировочный вариант 19 с ответами
25 января 2023 База ЕГЭ 2023 математика 11 класс тренировочный вариант 20 с ответами
27 января 2023 Тренировочный вариант №20 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
28 января 2023 Вариант 415 Ларина ЕГЭ 2023 по математике 11 класс задания и ответы
2 февраля 2023 Вариант 21 база ЕГЭ 2023 математика 11 класс тренировочный вариант с ответами
2 февраля 2023 Тренировочный вариант №21 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
8 февраля 2023 Математика 10-11 класс ЕГЭ 2023 статград варианты база и профиль МА2200101-МА2200110 и ответы
11 февраля 2023 Тренировочный вариант №22 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
11 февраля 2023 Тренировочный вариант №22 решу ЕГЭ 2023 база по математике 11 класс с ответами
12 февраля 2023 Вариант 416 Ларина ЕГЭ 2023 по математике 11 класс задания и ответы
12 февраля 2023 Вариант 417 Ларина ЕГЭ 2023 по математике 11 класс задания и ответы
13 февраля 2023 Вариант 9 и вариант 10 ЕГЭ 2023 база математика распечатай и реши задания
13 февраля 2023 Вариант 11 и вариант 12 ЕГЭ 2023 база математика распечатай и реши
16 февраля 2023 Тренировочный вариант №23 решу ЕГЭ 2023 база по математике 11 класс с ответами
16 февраля 2023 Тренировочный вариант №23 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
18 февраля 2023 Вариант 418 Ларина ЕГЭ 2023 по математике 11 класс задания и ответы
22 февраля 2023 Пробный ЕГЭ 2023 вариант 24 база по математике 11 класс с ответами
22 февраля 2023 Пробный ЕГЭ 2023 вариант 24 профиль по математике 11 класс с ответами
25 февраля 2023 Вариант 419 Ларина ЕГЭ 2023 по математике 11 класс задания и ответы
28 февраля 2023 Статград математика 11 класс ЕГЭ 2023 база и профиль и ответы
4 марта 2023 Пробник ЕГЭ 2023 вариант 25 база по математике 11 класс с ответами
4 марта 2023 Вариант 420 Ларин ЕГЭ 2023 по математике 11 класс задания и ответы
5 марта 2023 Пробник ЕГЭ 2023 вариант 25 профиль по математике 11 класс с ответами
8 марта 2023 Пробник ЕГЭ 2023 вариант 26 профиль по математике 11 класс с ответами
8 марта 2023 Пробник ЕГЭ 2023 вариант 26 база по математике 11 класс 100 баллов с ответами
Смотрите также на нашем сайте:
Сборник Ященко ЕГЭ 2023 математика профильный уровень 36 вариантов
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
ЕГЭ по математике — Профиль 2022. Открытый банк заданий с ответами.
ОГЭ
Освоение образовательных программ основного общего образования завершается обязательной государственной итоговой аттестацией (далее – ГИА 9) по русскому языку и математике.
Нормативно-правовые документы
Приказы и методические документы
Демоверсии, спецификации, кодификаторы
В данном разделе представлены документы, определяющие структуру и содержание контрольных измерительных материалов основного государственного экзамена.
Для предметных комиссий субъектов РФ
Открытый банк заданий ОГЭ
Новая версия открытого банка заданий