На какие числа делится число онлайн калькулятор. Посчитать делители числа.
Какие числа делятся на 511782?
На число 511782 без остатка (нацело) делятся следующие числа: 511782, 1023564, 1535346, 2047128, 2558910, 3070692, 3582474, 4094256, 4606038, 5117820, 5629602, 6141384 и многие другие.
Какие четные числа делятся на 511782?
На число 511782 делятся следующие четные числа: 511782, 1023564, 1535346, 2047128, 2558910, 3070692, 3582474, 4094256, 4606038, 5117820, 5629602, 6141384 и многие други.
Какие нечетные числа делятся на 511782?
Таких чисел нет
На какое наибольшее число делится число 511782 без остатка?
Наибольшее число на которое делится число 511782 есть само число 511782. т.е делиться на само себя без остатка.
На какое наибольшее число делится число 511782 без остатка, не считая числа 511782 и 1?
Наибольшим делителем числа 511782 не считая самого числа 511782 является число 255891.
Какое наименьшее натуральное число делится на 511782?
Наименьшее натуральное число которое делиться на число 511782 является само число 511782.
На какое наименьшее натуральное число делится число 511782?
Наименьшее натуральное число на которое можно разделить число 511782 — это число 1.
Делители числа 511782.
(что бы не забыть запишите все делители числа 511782 в блокнот.)На какие целые и(или) натуральные числа делится число 511782?
Число 511782 делится на следующие целые, натуральные числа (все делители числа 511782): 1, 2, 3, 6, 85297, 170594, 255891, 511782
На какие четные числа делится число 511782?
Число 511782 делится на следующие четные числа (четные делители числа): 2, 6, 170594, 511782
На какие нечетные числа делится число 511782?
Число 511782 делится на следующие нечетные числа (нечетные делители числа): 1, 3, 85297, 255891
Сколько делителей имеет число 511782?
Число 511782 имеет 8 делителей
Сколько четных делителей имеет число 511782?
Число 511782 имеет 4 четных делителя
Сколько нечетных делителей имеет число 511782?
Число 511782 имеет 4 нечетных делителя
Число 511782 прописью, словами.
— пятьсот одиннадцать тысяч семьсот восемьдесят два
(что бы не забыть запишите число 511782 прописью в блокнот.)
Числа кратные 511782.
— кратные числа, числу 511782 : 1023564, 1535346, 2047128, 2558910, 3070692, 3582474, 4094256, 4606038, 5117820, 5629602, 6141384 и многие другие.
Простые множители числа 511782.
У числа 511782 нет простых множителей кроме 1.
Сумма цифр числа 511782.
Сумма цифр числа 511782 равна 24
Произведение цифр числа 511782.
Произведение цифр числа 511782 равна 560
Квадрат числа 511782.
Квадрат числа 511782 равен 261920815524
Куб числа 511782.
Куб числа 511782 равен 134046358810503768
Квадратный корень числа 511782.
Квадратный корень числа 511782 равен 715.3894.
Число 511782 в двоичной системе счисления.
Запись числа 511782 в двоичной системе счисления выглядит так: 1111100111100100110
Количество значащих нулей в двоичной записи числа 511782 = 7
Количество едениц в двоичной записи числа 511782 = 12
(что бы не забыть запишите число 511782 в двоичной системе счисления в блокнот.)Число 511782 в шестнадцатеричной системе счисления.
Запись числа 511782 в шестнадцатеричной системе счисления выглядит так: 7cf26
(что бы не забыть запишите число 511782 в шестнадцатеричной системе счисления в блокнот.)Число 511782 в восьмеричной системе счисления.
Запись числа 511782 в восьмеричной системе счисления выглядит так: 1747446
(что бы не забыть запишите число 511782 в восьмеричной системе счисления в блокнот.)Число 511782 не является простым!
Корни числа 511782.
Корень 3 степени из 511782.
Корень 3 (третьей) степени из 511782 равен 79.988644221488
Корень 4 степени из 511782.
Корень 4 (четвертой) степени из 511782 равен 26.74676437348
Корень 5 степени из 511782.
Корень 5 (пятой) степени из 511782 равен 13.861716149685
Корень 6 степени из 511782.
Корень 6 (шестой) степени из 511782 равен 8.943637080153
Корень 7 степени из 511782.
Корень 7 (седьмой) степени из 511782 равен 6.5400877055546
Корень 8 степени из 511782.
Корень 8 (восьмой) степени из 511782 равен 5.1717274071127
Корень 9 степени из 511782.
Корень 9 (девятой) степени из 511782 равен 4.3086654930567
Корень 10 степени из 511782.
Корень 10 (десятой) степени из 511782 равен 3.7231325721339
Корень 11 степени из 511782.
Корень 11 (одиннадцатой) степени из 511782 равен 3.3037541975075
Корень 12 степени из 511782.
Корень 12 (двенадцатой) степени из 511782 равен 2.9905914264829
Корень 13 степени из 511782.
Корень 13 (тринадцатой) степени из 511782 равен 2.7489091391685
Корень 14 степени из 511782.
Корень 14 (четырнадцатой) степени из 511782 равен 2.5573595182443
Корень 15 степени из 511782.
Корень 15 (пятнадцатой) степени из 511782 равен 2.4021806655751
Степени числа 511782.
511782 в 3 степени.
511782 в 3 степени равно 134046358810503768.
511782 в 4 степени.
511782 в 4 степени равно 6.8602513604757E+22.
511782 в 5 степени.
511782 в 5 степени равно 3.510953161767E+28.
511782 в 6 степени.
511782 в 6 степени равно 1.7968426310354E+34.
511782 в 7 степени.
511782 в 7 степени равно 9.1959171539658E+39.
511782 в 8 степени.
511782 в 8 степени равно 4.7063048728909E+45.
511782 в 9 степени.
511782 в 9 степени равно 2.4086021204579E+51.
511782 в 10 степени.
511782 в 10 степени равно 1.2326792104122E+57.
511782 в 11 степени.
511782 в 11 степени равно 6.3086303166316E+62.
511782 в 12 степени.
511782 в 12 степени равно 3.2286434407063E+68.
511782 в 13 степени.
511782 в 13 степени равно 1.6523615973716E+74.
511782 в 14 степени.
511782 в 14 степени равно 8.4564892302602E+79.
511782 в 15 степени.
511782 в 15 степени равно 4.327878971241E+85.
Какое число имеет такую же сумму цифр как и число 511782?Математика. Найти сумму цифр числа 511782.
Число 511782 состоит из следующих цифр — 5, 1, 1, 7, 8, 2.
Определить сумму цифр числа 511782 не так уж и сложно.
Сумма цифр шестизначного числа 511782 равна 5 + 1 + 1 + 7 + 8 + 2 = 24.
Числа сумма цифр которых равна 24.
Следующие числа имеют такую же сумму цифр как и число 511782 — 699, 789, 798, 879, 888, 897, 969, 978, 987, 996, 1599, 1689, 1698, 1779, 1788, 1797, 1869, 1878, 1887, 1896.
Трехзначные числа сумма цифр которых равна 24 — 699, 789, 798, 879, 888, 897, 969, 978, 987, 996.
Четырехзначные числа сумма цифр которых равна 24 — 1599, 1689, 1698, 1779, 1788, 1797, 1869, 1878, 1887, 1896.
Пятизначные числа сумма цифр которых равна 24 — 10599, 10689, 10698, 10779, 10788, 10797, 10869, 10878, 10887, 10896.
Шестизначные числа сумма цифр которых равна 24 — 100599, 100689, 100698, 100779, 100788, 100797, 100869, 100878, 100887, 100896.
Квадрат суммы цифр числа 511782.
Квадрат суммы цифр шестизначного числа 511782 равен 5 + 1 + 1 + 7 + 8 + 2 = 24² = 576.
Сумма квадратов цифр шестизначного числа 511782.
Сумма квадратов цифр числа 511782 равна 5² + 1² + 1² + 7² + 8² + 2² = 25 + 1 + 1 + 49 + 64 + 4 = 144.
Сумма четных цифр числа 511782.
Сумма четных цифр шестизначного числа 511782 равна 8 + 2 = 10.
Квадрат суммы четных цифр шестизначного числа 511782.
Квадрат суммы четных цифр числа 511782 равна 8 + 2 = 10² = 100.
Сумма квадратов четных цифр шестизначного числа 511782.
Сумма квадратов четных цифр числа 511782 равна 8² + 2² = 64 + 4 = 68.
Сумма нечетных цифр числа 511782.
Сумма нечетных цифр шестизначного числа 511782 равна 5 + 1 + 1 + 7 = 14.
Квадрат суммы нечетных цифр шестизначного числа 511782.
Квадрат суммы нечетных цифр числа 511782 равна 5 + 1 + 1 + 7 = 14² = 196.
Сумма квадратов нечетных цифр шестизначного числа 511782.
Сумма квадратов нечетных цифр числа 511782 равна 5² + 1² + 1² + 7² = 25 + 1 + 1 + 49 = 76.
Произведение цифр числа 511782.
Какое число имеет такое же произведение цифр как и число 511782?Математика. Найти произведение цифр числа 511782.
Число 511782 состоит из следующих цифр — 5, 1, 1, 7, 8, 2.
Найти сумму цифр числа 511782 просто.
Решение:
Произведение цифр числа 511782 равно 5 * 1 * 1 * 7 * 8 * 2 = 560.
Числа произведение цифр которых равно 560.
Следующие числа имеют такое же произведение цифр как и число 511782 — 2578, 2587, 2758, 2785, 2857, 2875, 4457, 4475, 4547, 4574, 4745, 4754, 5278, 5287, 5447, 5474, 5728, 5744, 5782, 5827.
Четырехзначные числа произведение цифр которых равно 560 — 2578, 2587, 2758, 2785, 2857, 2875, 4457, 4475, 4547, 4574.
Пятизначные числа произведение цифр которых равно 560 — 12578, 12587, 12758, 12785, 12857, 12875, 14457, 14475, 14547, 14574.
Шестизначные числа произведение цифр которых равно 560 — 112578, 112587, 112758, 112785, 112857, 112875, 114457, 114475, 114547, 114574.
Квадрат произведения цифр числа 511782.
Квадрат произведения цифр шестизначного числа 511782 равен 5 * 1 * 1 * 7 * 8 * 2 = 560² = 313600.
Произведение квадратов цифр шестизначного числа 511782.
Произведение квадратов цифр числа 511782 равна 5² * 1² * 1² * 7² * 8² * 2² = 25 * 1 * 1 * 49 * 64 * 4 = 313600.
Произведение четных цифр числа 511782.
Произведение четных цифр шестизначного числа 511782 равно 8 * 2 = 16.
Квадрат произведения четных цифр шестизначного числа 511782.
Квадрат произведения четных цифр числа 511782 равен 8 * 2 = 16² = 256.
Произведение квадратов четных цифр шестизначного числа 511782.
Произведение квадратов четных цифр числа 511782 равно 8² * 2² = 64 * 4 = 256.
Запишите числа которые в сумме дают число 511782.
Задача: Данно число 511782.Какие 2(два) числа дают в сумме число 511782?Решение:
1) 77995 + 433787 = 511782
2) 12549 + 499233 = 511782
3) 160939 + 350843 = 511782
4) 743 + 511039 = 511782
5) 183538 + 328244 = 511782
Какие 3(три) числа дают в сумме число 511782?Решение:
1) 2472 + 69353 + 439957 = 511782
2) 50922 + 2040 + 458820 = 511782
3) 89672 + 120918 + 301192 = 511782
4) 12634 + 220259 + 278889 = 511782
5) 45121 + 136859 + 329802 = 511782
Какие 4(четыре) числа дают в сумме число 511782?Решение:
1) 55358 + 73298 + 46592 + 336534 = 511782
2) 77521 + 11119 + 207575 + 215567 = 511782
3) 56476 + 125288 + 114061 + 215957 = 511782
4) 9091 + 130350 + 38932 + 333409 = 511782
5) 82975 + 40525 + 154175 + 234107 = 511782
Какие 5(пять) чисел дают в сумме число 511782?Решение:
1) 39747 + 1710 + 80241 + 190534 + 199550 = 511782
2) 78443 + 3828 + 79187 + 163065 + 187259 = 511782
3) 15873 + 11620 + 9771 + 236563 + 237955 = 511782
4) 4546 + 28730 + 68138 + 89906 + 320462 = 511782
5) 4192 + 10156 + 53619 + 136375 + 307440 = 511782
Новые тренировочные варианты ЕГЭ 2023 по математике базовый и профильный уровень с ответами и решением для 10 и 11 класса, больше 100 вариантов в формате реального экзамена ФИПИ вы можете решать онлайн или скачать.
Тренировочные варианты ЕГЭ 2023 по математике база и профиль
13.09.2022 Тренировочный вариант №1 ЕГЭ 2023 по математике профиль с ответами
20.09.2022 Тренировочный вариант №2 ЕГЭ 2023 по математике профиль с ответами
20.09.2022 Тренировочный вариант №2 ЕГЭ 2023 база по математике с ответами
27.09.2022 Математика 11 класс профиль входная мониторинговая работа 3 варианта с ответами
28.09.2022 Тренировочный вариант №3 ЕГЭ 2023 база по математике с ответами
28 сентября 2022 Статград математика 11 класс ЕГЭ 2023 база и профиль варианты и ответы
29 сентября 2022 Тренировочный вариант №3 ЕГЭ 2023 по математике профиль с ответами
1 октября 2022 Ларин вариант 399 ЕГЭ 2023 по математике профиль решение с ответами
6 октября Тренировочный вариант №4 ЕГЭ 2023 база по математике с ответами
6 октября Тренировочный вариант №4 ЕГЭ 2023 по математике профиль с ответами
8 октября Ларин вариант 400 ЕГЭ 2023 по математике профиль решение с ответами
12 октября Тренировочный вариант №5 ЕГЭ 2023 база по математике с ответами
12 октября Тренировочный вариант №5 ЕГЭ 2023 по математике профиль с ответами
14 октября Вариант 1 Ященко ЕГЭ 2023 математика профиль с ответами и решением
14 октября Вариант 2 Ященко ЕГЭ 2023 математика профиль с ответами и решением
15 октября Ларин вариант 401 ЕГЭ 2023 по математике профиль решение с ответами
15 октября Ларин вариант 402 ЕГЭ 2023 по математике профиль решение с ответами
16 октября Вариант 3 Ященко ЕГЭ 2023 математика профиль с ответами и решением
16 октября Вариант 4 Ященко ЕГЭ 2023 математика профиль с ответами и решением
23 октября Тренировочный вариант №6 ЕГЭ 2023 база по математике с ответами
24 октября Тренировочный вариант №6 ЕГЭ 2023 по математике профиль с ответами
25 октября Тренировочный вариант №7 ЕГЭ 2023 база по математике с ответами
26 октября Тренировочный вариант №7 ЕГЭ 2023 по математике профиль с ответами
28 октября Ларин вариант 403 ЕГЭ 2023 по математике профиль решение с ответами
29 октября Ларин вариант 404 ЕГЭ 2023 по математике профиль решение с ответами
1 ноября 2022 Тренировочный вариант №8 решу ЕГЭ 2023 база по математике с ответами
1 ноября 2022 Тренировочный вариант №8 решу ЕГЭ 2023 по математике профиль с ответами
5 ноября 2022 Вариант 1-2 распечатай и реши ЕГЭ 2023 база по математике 11 класс с ответами
6 ноября 2022 Ларин вариант 405 ЕГЭ 2023 профиль по математике решение с ответами
9 ноября 2022 Тренировочный вариант №9 решу ЕГЭ 2023 база по математике с ответами
12 ноября 2022 Тренировочный вариант №9 решу ЕГЭ 2023 по математике профиль с ответами
13 ноября 2022 Ларин вариант 406 ЕГЭ 2023 профиль по математике решение с ответами
15 ноября 2022 Тренировочный вариант №10 решу ЕГЭ 2023 база по математике 11 класс с ответами
15 ноября 2022 Тренировочный вариант №10 решу ЕГЭ 2023 по математике профиль с ответами
21 ноября 2022 Ларин вариант 407 ЕГЭ 2023 профиль по математике решение с ответами
23 ноября 2022 Тренировочный вариант №11 решу ЕГЭ 2023 база по математике 11 класс с ответами
23 ноября 2022 Тренировочный вариант №11 решу ЕГЭ 2023 по математике профиль с ответами
27 ноября 2022 Ларин вариант 408 ЕГЭ 2023 профиль по математике решение с ответами
28 ноября 2022 Вариант 3-4 распечатай и реши ЕГЭ 2023 база по математике 11 класс с ответами
30 ноября 2022 Мониторинговая работа по математике 11 класс ЕГЭ 2023 профиль 1 полугодие
3 декабря 2022 Тренировочный вариант №12 решу ЕГЭ 2023 база по математике 11 класс с ответами
3 декабря 2022 Тренировочный вариант №12 решу ЕГЭ 2023 по математике профиль с ответами
3 декабря 2022 Пробник ЕГЭ 2023 Москва по математике профиль задания и ответы
5 декабря 2022 Ларин вариант 409 ЕГЭ 2023 профиль по математике решение с ответами
9 декабря 2022 Тренировочный вариант №13 решу ЕГЭ 2023 база по математике 11 класс с ответами
10 декабря 2022 Тренировочный вариант №13 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
12 декабря 2022 Ларин вариант 410 ЕГЭ 2023 профиль по математике решение с ответами
13 декабря 2022 Статград математика 11 класс профиль ЕГЭ 2023 варианты МА2210209-МА2210212 и ответы
13 декабря 2022 Математика 11 класс база ЕГЭ 2023 статград варианты и ответы
15 декабря 2022 Тренировочный вариант №14 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
15 декабря 2022 Тренировочный вариант №14 решу ЕГЭ 2023 база по математике 11 класс с ответами
20 декабря 2022 Вариант 5-6 распечатай и реши ЕГЭ 2023 база по математике 11 класс с ответами
20 декабря 2022 Ларин вариант 411 ЕГЭ 2023 профиль по математике решение с ответами
3 января 2023 Ларин вариант 412 ЕГЭ 2023 профиль по математике решение с ответами
6 января 2023 Тренировочный вариант 1-2 ЕГЭ 2023 профиль математика задания и ответы
8 января 2023 Вариант 3-4 ЕГЭ 2023 профиль математика задания и ответы
9 января 2023 Вариант 7-8 распечатай и реши ЕГЭ 2023 база по математике 11 класс с ответами
10 января 2023 Тренировочный вариант №15 и №16 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
11 января 2023 ЕГЭ 2023 математика тренировочные задания и ответы Ященко, Семенов
11 января 2023 Тренировочный вариант №15 и №16 база ЕГЭ 2023 по математике 11 класс с ответами
19 января 2023 Тренировочные варианты №17 и №18 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
22 января 2023 Ларин вариант 413 и 414 ЕГЭ 2023 профиль по математике решение и ответы
22 января 2023 Тренировочный 19 вариант решу ЕГЭ 2023 профиль по математике 11 класс с ответами
22 января 2023 База ЕГЭ 2023 математика 11 класс тренировочный вариант 19 с ответами
25 января 2023 База ЕГЭ 2023 математика 11 класс тренировочный вариант 20 с ответами
27 января 2023 Тренировочный вариант №20 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
28 января 2023 Вариант 415 Ларина ЕГЭ 2023 по математике 11 класс задания и ответы
2 февраля 2023 Вариант 21 база ЕГЭ 2023 математика 11 класс тренировочный вариант с ответами
2 февраля 2023 Тренировочный вариант №21 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
8 февраля 2023 Математика 10-11 класс ЕГЭ 2023 статград варианты база и профиль МА2200101-МА2200110 и ответы
11 февраля 2023 Тренировочный вариант №22 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
11 февраля 2023 Тренировочный вариант №22 решу ЕГЭ 2023 база по математике 11 класс с ответами
12 февраля 2023 Вариант 416 Ларина ЕГЭ 2023 по математике 11 класс задания и ответы
12 февраля 2023 Вариант 417 Ларина ЕГЭ 2023 по математике 11 класс задания и ответы
13 февраля 2023 Вариант 9 и вариант 10 ЕГЭ 2023 база математика распечатай и реши задания
13 февраля 2023 Вариант 11 и вариант 12 ЕГЭ 2023 база математика распечатай и реши
16 февраля 2023 Тренировочный вариант №23 решу ЕГЭ 2023 база по математике 11 класс с ответами
16 февраля 2023 Тренировочный вариант №23 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
18 февраля 2023 Вариант 418 Ларина ЕГЭ 2023 по математике 11 класс задания и ответы
22 февраля 2023 Пробный ЕГЭ 2023 вариант 24 база по математике 11 класс с ответами
22 февраля 2023 Пробный ЕГЭ 2023 вариант 24 профиль по математике 11 класс с ответами
25 февраля 2023 Вариант 419 Ларина ЕГЭ 2023 по математике 11 класс задания и ответы
28 февраля 2023 Статград математика 11 класс ЕГЭ 2023 база и профиль и ответы
4 марта 2023 Пробник ЕГЭ 2023 вариант 25 база по математике 11 класс с ответами
4 марта 2023 Вариант 420 Ларин ЕГЭ 2023 по математике 11 класс задания и ответы
5 марта 2023 Пробник ЕГЭ 2023 вариант 25 профиль по математике 11 класс с ответами
8 марта 2023 Пробник ЕГЭ 2023 вариант 26 профиль по математике 11 класс с ответами
8 марта 2023 Пробник ЕГЭ 2023 вариант 26 база по математике 11 класс 100 баллов с ответами
Смотрите также на нашем сайте:
Сборник Ященко ЕГЭ 2023 математика профильный уровень 36 вариантов
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
Решение и ответы заданий варианта МА2210309 СтатГрад 28 февраля ЕГЭ 2023 по математике (профильный уровень). Тренировочная работа №3. ГДЗ профиль для 11 класса.
+Задания №1, №4, №6, №10 из варианта МА2210311.


Задание 1.
В треугольнике ABC угол C равен 90°, CH – высота, BC = 5, cosA=frac{2sqrt{6}}{5}. Найдите длину отрезка AH.
Задание 1 из варианта 2210311.
Найдите периметр прямоугольника, если его площадь равна 12, а отношение соседних сторон равно 1:3.
Задание 2.
Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 2. Объём параллелепипеда равен 3,2. Найдите высоту цилиндра.
Задание 3.
В группе 16 человек, среди них – Анна и Татьяна. Группу случайным образом делят на 4 одинаковые по численности подгруппы. Найдите вероятность того, что Анна и Татьяна окажутся в одной подгруппе.
Задание 4.
Агрофирма закупает куриные яйца только в двух домашних хозяйствах. Известно, что 40 % яиц из первого хозяйства – яйца высшей категории, а из второго хозяйства – 60 % яиц высшей категории. В этой агрофирме 50 % яиц высшей категории. Найдите вероятность того, что яйцо, купленное у этой агрофирмы, окажется из первого хозяйства.
Задание 4 из варианта 2210311.
Игральный кубик бросают дважды. Известно, что в сумме выпало 11 очков. Найдите вероятность того, что во второй раз выпало 5 очков.
Задание 5.
Решите уравнение frac{x–1}{5x+11}=frac{x–1}{3x-7}. Если уравнение имеет больше одного корня, в ответе запишите больший из корней.
Задание 6.
Найдите значение выражения frac{(4^{frac{3}{5} }cdot7^{frac{2}{3}})^{15}}{28^{9}} .
Задание 6 из варианта 2210311.
Найдите 98cos2α, если cosα = frac{4}{7}.
Задание 7.
На рисунке изображён график y = f’(x) – производной функции f(x), определённой на интервале (−5; 5). В какой точке отрезка [−4; −1] функция f(x) принимает наибольшее значение?
Задание 8.
На верфи инженеры проектируют новый аппарат для погружения на небольшие глубины. Конструкция имеет кубическую форму, а значит, действующая на аппарат выталкивающая (архимедова) сила, выражаемая в ньютонах, будет определяться по формуле FA = ρgl3, где l – длина ребра куба в метрах, ρ = 1000 кг/м3 – плотность воды, а g – ускорение свободного падения (считайте, что g = 9,8 Н/кг). Какой может быть максимальная длина ребра куба, чтобы обеспечить его эксплуатацию в условиях, когда выталкивающая сила при погружении будет не больше чем 2116800 Н? Ответ дайте в метрах.
Задание 9.
Пристани A и B расположены на озере, расстояние между ними равно 280 км. Баржа отправилась с постоянной скоростью из A в B. На следующий день после прибытия она отправилась обратно со скоростью на 4 км/ч больше прежней, сделав по пути остановку на 8 часов. В результате она затратила на обратный путь столько же времени, сколько на путь из A в B. Найдите скорость баржи на пути из A в B. Ответ дайте в км/ч.
Задание 10.
На рисунке изображён график функции f(x) = ax2 + bx + c. Найдите значение f(−1).
Задание 10 из варианта 2210311.
На рисунке изображены графики функций f(x) = frac{k}{x} и g(x) = ax + b, которые пересекаются в точках A и B. Найдите абсциссу точки B.
Задание 11.
Найдите точку минимума функции y = x3 − 27x2 + 13.
Задание 12.
а) Решите уравнение 2cos3x = –sin(frac{3pi}{2} + x)
б) Найдите все корни этого уравнения, принадлежащие отрезку [3π; 4π]
Задание 13.
Основанием правильной пирамиды PABCD является квадрат ABCD. Сечение пирамиды проходит через вершину В и середину ребра PD перпендикулярно этому ребру.
а) Докажите, что угол наклона бокового ребра пирамиды к её основанию равен 60°.
б) Найдите площадь сечения пирамиды, если AB = 30.
Задание 14.
Решите неравенство frac{9^{x}–13cdot 3^{x}+30}{3^{x+2}–3^{2x+1}}ge frac{1}{3^{x}}.
Задание 15.
По вкладу «А» банк в конце каждого года планирует увеличивать на 13 % сумму, имеющуюся на вкладе в начале года, а по вкладу «Б» – увеличивать эту сумму на 7 % в первый год и на целое число n процентов за второй год. Найдите наименьшее значение n, при котором за два года хранения вклад «Б» окажется выгоднее вклада «А» при одинаковых суммах первоначальных взносов.
Задание 16.
В треугольнике ABC медианы AA1, BB1 и CC1 пересекаются в точке M. Известно, что AC = 3MB.
а) Докажите, что треугольник ABC прямоугольный.
б) Найдите сумму квадратов медиан AA1 и CC1, если известно, что AC = 22.
Задание 17.
Найдите все значения a, при каждом из которых система уравнений
begin{cases} (x-5a+1)^{2}+(y-2a-1)^{2}=a-2 \ 3x-4y=2a+3 end{cases}
не имеет решений.
Задание 18.
У Ани есть 800 рублей. Ей нужно купить конверты (большие и маленькие). Большой конверт стоит 32 рубля, а маленький – 25 рублей. При этом число маленьких конвертов не должно отличаться от числа больших конвертов больше чем на пять.
а) Может ли Аня купить 24 конверта?
б) Может ли Аня купить 29 конвертов?
в) Какое наибольшее число конвертов может купить Аня?
Источник варианта: СтатГрад/statgrad.org.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 5 / 5. Количество оценок: 2
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
В США тоже есть ЕГЭ — причём он был задолго до нас. Вот одна задачка оттуда. Мы перевели её на русский и заменили центы на привычные рубли. Сама задача звучит так:
Эту задачку можно решить на листочке за несколько минут. Попробуйте сами, а если не получится — кат в помощь ↓
Это звучит удивительно, но для решения нам не нужно считать точное количество монет обоих видов у каждого (хотя никто не мешает вам попробовать это сделать). Вместо этого мы применим хитрость и смекалку.
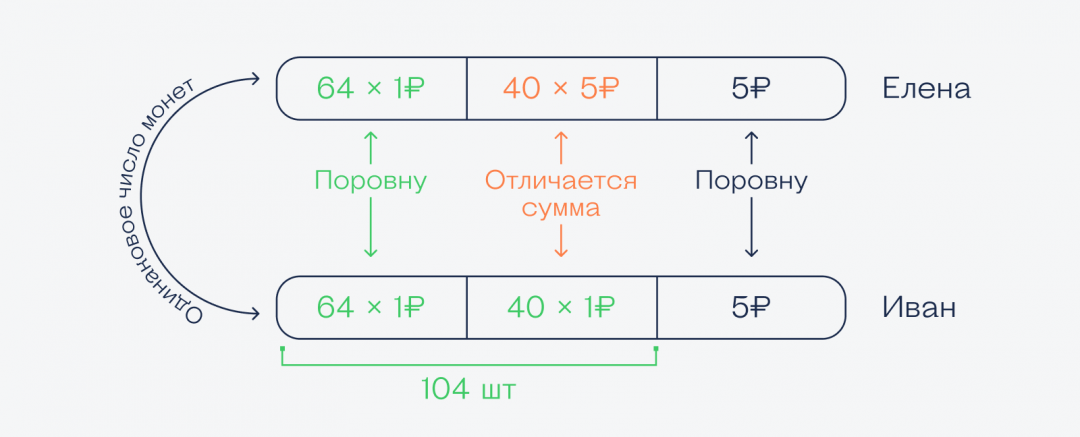
Нам неважно, сколько у кого монет, главное, что их одинаковое количество и у Елены, и у Ивана, а вот количество рублёвых монет разное. Зная это, достаточно нарисовать простую картинку, по которой легко найти ответ на этот вопрос:
Глядя на неё становится понятно, что общую часть из 64 рублёвых монет можно выкинуть у обоих, потому что и там и там одинаковая сумма. А то, что осталось, и даст нужную разницу.
👉 Так как количество монет у каждого одинаковое, то у Ивана вместо 40 пятирублёвок лежит 40 рублёвых монет, а остальные пятирублёвки снова у обоих в одинаковом количестве, и их тоже можно отбросить. Получается, разница в деньгах такая:
- у Елены — 40 × 5 ₽ = 200 ₽
- у Ивана — 40 × 1 ₽ = 40 ₽
Значит, у Елены на 200 − 40 = 160 ₽ больше.
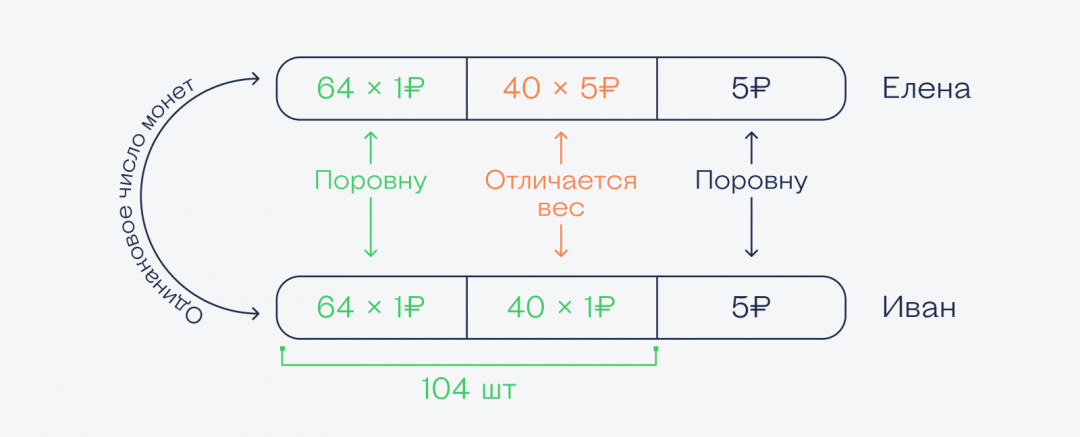
На этом этапе спотыкается большинство решающих, потому что они пытаются найти точное количество монет Ивана. Но мы-то с вами уже знаем, что это необязательно — достаточно найти разницу в весе и по ней посчитать вес монет.
Используем тот же рисунок, но уже в разрезе веса монет:
Получается, что разница в весе зависит от тех же монет, что мы считали в первой части.
Так как одна рублёвая монета легче одной пятирублёвой на 2,7 грамма, то у 40 монет разница в весе будет 40 × 2,7 = 108 грамм. А раз у Ивана пятирублёвок меньше, чем у Елены, то и монеты будут весить как раз на эти 108 грамм легче: 1,134 − 0,108 = 1,026 килограмма.
Решение 22 варианта ЕГЭ профильного уровня из сборника 36 вариантов Ященко 2023
Скачать сборник в pdf
В треугольнике АВС высота СН равна 6, АВ=ВС, АС=8. Найдите синус угла АСВ.
В правильной треугольной призме (ABCA_1B_1C_1) все рёбра которой равны 2, найдите угол между прямыми (BB_1) и (AC_1). Ответ дайте в градусах.
Всего в группе туристов 21 человек, в том числе Лёня и Ваня. Группу случайным образом делят на три подгруппы по 7 человек для посадки в три микроавтобуса. Какова вероятность того, что Лёня и Ваня случайно окажутся в одном микроавтобусе?
Помещение освещается фонарем с двумя лампами. Вероятность перегорания одной лампы в течение года равна 0,16. Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит.
Найдите корень уравнения (dfrac1{5x-14}=dfrac1{4x-3})
Найдите значение выражения (dfrac{{{log }_9 32 }}{{{log }_{27} 0{,}5 }})
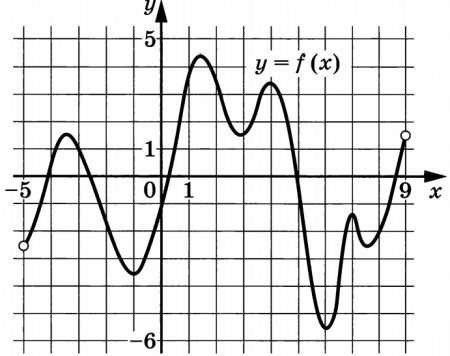
На рисунке изображён график функции (y= f(x)), определённой на интервале ((-5; 9)). Найдите количество решений уравнения (f ‘ (x)=0) на отрезке ([-2; 8]).
Автомобиль разгоняется на прямолинейном участке шоссе с постоянным ускорением (a = 6500 ,км/ч^2). Скорость (v) (в км/ч) вычисляется по формуле (v=sqrt{2la}), где (l) — пройденный автомобилем путь (в км). Найдите, сколько километров проедет автомобиль к моменту, когда он разгонится до скорости 130 км/ч.
Теплоход проходит по течению реки до пункта назначения 416 км и после стоянки возвращается в пункт отправления. Найдите скорость течения, если скорость теплохода в неподвижной воде равна 21 км/ч, стоянка длится 8 часов, а в пункт отправления теплоход возвращается через 50 часов. Ответ дайте в км/ч.
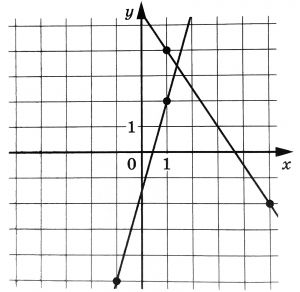
На рисунке изображены графики двух линейных функций. Найдите ординату точки пересечения графиков.
Найдите точку максимума функции (y=left(5x-6right)cos x-5sin x -8), принадлежащую промежутку (left(0;dfrac{pi }{2}right))
а) Решите уравнение (cos 2x — sqrt{2}cos Big(dfrac{3pi}{2} + xBig) – 1 = 0).
б) Укажите корни этого уравнения, принадлежащие отрезку (Big[dfrac{3pi}{2}; 3piBig]).
Выберите все верные ответы на пункты а) и б). Запишите их номера по возрастанию, через запятую, без пробелов.
a)
| 1. 2πn, n∈Z | 2. π/6+2πn, n∈Z | 3. π/4+2πn, n∈Z | 4. π/3+2πn, n∈Z |
| 5. π/2+2πn, n∈Z | 6. 2π/3+2πn, n∈Z | 7. 3π/4+2πn, n∈Z | 8. 5π/6+2πn, n∈Z |
| 9. π+2πn, n∈Z | 10. -π/6+2πn, n∈Z | 11. -π/4+2πn, n∈Z | 12. -π/3+2πn, n∈Z |
| 13. -π/2+2πn, n∈Z | 14. -2π/3+2πn, n∈Z | 15. -3π/4+2πn, n∈Z | 16. -5π/6+2πn, n∈Z |
б)
| 17. 3π/2 | 18. 5π/3 | 19. 7π/4 | 20. 11π/6 |
| 21. 2π | 22. 13π/6 | 23. 9π/4 | 24. 7π/3 |
| 25. 5π/2 | 26. 8π/3 | 27. 11π/4 | 28. 17π/6 |
| 29. 3π |
В основании четырехугольной пирамиды (SABCD) лежит прямоугольник (ABCD) со сторонами (AB=8) и (BC=6). Длины боковых ребер пирамиды (SA=sqrt{21}), (SB=sqrt{85}), (SD=sqrt{57}).
а) Докажите, что (SA) – высота пирамиды.
б) Найдите угол между прямыми (SC) и (BD).
Решите неравенство (x^2log_{243} (-x-3)geqslant log_3 (x^2+6x+9))
В июле 2022 года планируется взять кредит на пять лет в размере 220 тыс. рублей. Условия его возврата таковы:
– каждый январь долг возрастает на r% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;
– в июле 2023, 2024 и 2025 годов долг остаётся равным 220 тыс. рублей;
– выплаты в 2026 и 2027 годах равны;
– к июлю 2027 года долг будет выплачен полностью.
Найдите r, если известно, что долг будет выплачен полностью и общий размер выплат составит 420 тыс. рублей.
Две окружности разных радиусов касаются внешним образом в точке С. Вершины А и В равнобедренного прямоугольного треугольника АВС с прямым углом С лежат на меньшей и большей окружностях соответственно. Прямая АС вторично пересекает большую окружность в точке Е, а прямая ВС вторично пересекает меньшую окружность в точке D.
а) Докажите, что прямые AD и BE параллельны.
б) Найдите ВС, если радиусы окружностей равны √15 и 15.
Найдите все значения (a), при каждом из которых система уравнений (begin{cases} sqrt{a-y^2}=sqrt{a-x^2} \ x^2+y^2=2x+4y end{cases}) имеет ровно два различных решения.
На доске было написано несколько различных натуральных чисел. Эти числа разбили на три группы, в каждой из которых оказалось хотя бы одно число. К каждому числу из первой группы приписали справа цифру 1, к каждому числу из второй группы — цифру 8, а числа из третьей группы оставили без изменений.
а) Могла ли сумма всех этих чисел увеличиться в 4 раза?
б) Могла ли сумма всех этих чисел увеличиться в 18 раз?
в) Сумма всех этих чисел увеличилась в 11 раз. Какое наибольшее количество чисел могло быть написано на доске?
Введите ответ в форме строки «да;да;1234». Где ответы на пункты разделены «;», и первые два ответа с маленькой буквы.
ЕГЭ по математике — Профиль 2022. Открытый банк заданий с ответами.