Рациональное целое
шестизначное
число 513337
– составное число.
Произведение и сумма цифр числа: 945, 22.
8 — количество делителей у числа 513337.
Сумма делителей: 584640.
513337 и 0.000001948038033494566 — обратные числа.
Факторизация этого числа: 11 * 23 * 2029.
Другие представления числа:
двоичный вид числа: 1111101010100111001, троичный вид числа: 222002011111, восьмеричный вид числа: 1752471, шестнадцатеричный вид числа: 7D539.
Количество информации в числе байт 513337 это 501 килобайт 313 байтов .
Кодирование азбукой Морзе: ….. .—- …— …— …— —…
Число — не число Фибоначчи.
Синус: 0.6892, косинус: 0.7246, тангенс: 0.9512.
Натуральный логарифм: 13.1487.
Логарифм десятичный числа: 5.7104.
716.4754 — корень квадратный из числа 513337, 80.0696 — кубический.
Возведение числа 513337 в квадрат: 2.6351e+11.
Число 513337 в секундах это 5 дней 22 часа 35 минут 37 секунд .
Нумерологическое значение числа 513337 – цифра 4.
Задание 1
В треугольнике $$ABC$$ известно, что $$AC=BC$$, высота $$AH$$ равна $$6sqrt{6}$$, $$BH=3$$ Найдите $$cos BAC$$.
Ответ: 0,2
Скрыть
Задание 2
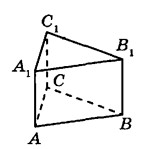
Найдите объём многогранника, вершинами которого являются точки $$B$$, $$C$$, $$A_1$$, $$C_1$$ правильной треугольной призмы $$ABCA_1B_1C_1$$ площадь основания которой равна 5, а боковое ребро равно 6.
Ответ: 10
Скрыть
Задание 3
В группе туристов 25 человек. Их вертолётом доставляют в труднодоступный район, перевозя по 5 человек за рейс. Порядок, в котором вертолёт перевозит туристов, случаен. Найдите вероятность того, что турист 3. полетит третьим рейсом вертолёта.
Ответ: 0,2
Скрыть
Номер рейса в этой задаче не имеет значения. Важно, что за один рейс перевозятся 5 человек. То есть, вероятность попасть туристу З. на какой-либо рейс (в том числе и 3-й), равна:
$$P=frac{m}{n}=frac{5}{25}=frac{1}{5}=0,2$$
Задание 4
Игральную кость бросали до тех пор, пока сумма всех выпавших очков не превысила число 5. Какова вероятность того, что для этого потребовалось два броска? Ответ округлите до сотых.
Ответ: 0,56
Скрыть
Задание 5
Найдите корень уравнения $$(frac{1}{4})^{x+2}=256^{x}$$
Ответ: -0,4
Скрыть
Задание 6
Найдите значение выражения $$log_{2,5}6cdot log_{6} 0,4$$
Ответ: -1
Скрыть
Задание 7
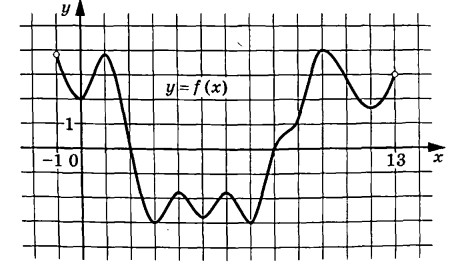
На рисунке изображён график функции $$y=f(x)$$, определённой на интервале $$(-1; 13)$$. Найдите количество точек, в которых касательная к графику функции $$y=f(x)$$ параллельна прямой $$y=-2$$.
Ответ: 9
Скрыть
Задание 8
Высота над землёй подброшенного вверх мяча меняется по закону $$y=1,4+11t-5t^2$$, где $$h$$ — высота в метрах, $$t$$ — время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее 7 метров?
Ответ: 0,6
Скрыть
Задание 9
Смешав 8-процентный и 26-процентный растворы кислоты и добавив 10 кг чистой воды, получили 16-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 20-процентный раствор кислоты. Сколько килограммов 8-процентного раствора использовали для получения смеси? Сколько секунд мяч будет находиться на высоте не менее 7 метров?
Ответ: 55
Скрыть
Задание 10
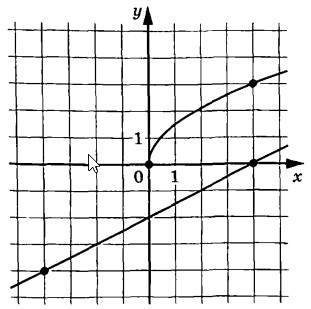
На рисунке изображены графики функций $$f(x)=asqrt{x}$$ и $$g(x)=kx+b$$, которые пересекаются в точке $$A(x_0; y_0)$$. Найдите $$y_0$$.
Ответ: 6
Скрыть
Задание 11
Найдите точку максимума функции промежутку $$y=(2x-1)cos x-2sin x+9$$, принадлежащую промежутку $$(0;frac{pi}{2})$$
Ответ: 0,5
Скрыть
Задание 12
а) Решите уравнение $$log^{2}_{2}(4x^{2})+3log_{0,5}(8x)=1$$
б) Найдите все корни этого уравнения, принадлежащие отрезку $$[0,15;1,5]$$
Ответ: а)$$0,25;sqrt[4]{8}$$ б)$$0,25$$
Скрыть
Задание 13
Сторона основания правильной четырёхугольной пирамиды $$SABCD$$ относится к боковому ребру как $$1:sqrt{2}$$. Через вершину $$D$$ проведена плоскость $$alpha$$, перпендикулярная боковому ребру $$SB$$ и пересекающая его в точке $$M$$.
а) Докажите, что $$M$$ — середина $$SB$$.
б) Найдите расстояние между прямыми $$AC$$ и $$DM$$, если высота пирамиды равна $$6sqrt{3}$$.
Ответ: 3
Скрыть
Задание 14
Решите неравенство $$frac{sqrt{x+4}(8-3^{2+x^{2}})}{4^{x-1}-3}leq 0$$
Ответ: $$-4;(log_{4}12;+infty)$$
Скрыть
Задание 15
15 июня 2025 года Сергей Данилович планирует взять кредит в банке на 4 года в размере целого числа миллионов рублей. Условия его возврата таковы:
— в январе каждого года действия кредита долг увеличивается на 15 % от суммы долга на конец предыдущего года;
— в период с февраля по июнь в каждый из 2026 и 2027 годов необходимо выплатить только начисленные в январе проценты по кредиту;
— в период с февраля по июнь в каждый из 2028 и 2029 годов выплачиваются равные суммы, причём последний платёж должен погасить долг по кредиту полностью.
Найдите наименьший размер кредита, при котором общая сумма выплат по кредиту превысит 12 млн рублей.
Ответ: 8 млн. руб.
Скрыть
Задание 16
Окружность с центром в точке $$C$$ касается гипотенузы $$AB$$ прямоугольного треугольника $$ABC$$ и пересекает его катеты $$AC$$ и $$BC$$ в точках $$E$$ и $$F$$. Точка $$D$$ — основание высоты, опущенной из вершины $$C$$. $$I$$ и $$J$$ — центры окружностей, вписанных в треугольники $$BCD$$ и $$ACD$$.
а) Докажите, что $$I$$ и $$J$$ лежат на отрезке $$EF$$.
б) Найдите расстояние от точки $$C$$ до прямой $$IJ$$, если $$AC=15$$, $$BC = 20$$.
Ответ: $$6sqrt{2}$$
Скрыть
Задание 17
Найдите все значения $$a$$, при каждом из которых оба уравнения $$a+frac{x}{2}=|x|$$ и $$asqrt{2}+x=sqrt{2asqrt{2}-x^{2}+12}$$ имеют ровно по 2 различных корня, и строго между корнями каждого из уравнений лежит корень другого уравнения.
Ответ: $$[sqrt{2};frac{3sqrt{6}}{sqrt{13}})$$
Скрыть
Задание 18
Трёхзначное число, меньшее 910, поделили на сумму его цифр и получили натуральное число $$n$$.
а) Может ли $$n$$ равняться 68?
б) Может ли $$n$$ равняться 86?
в) Какое наибольшее значение может принимать $$n$$, если все цифры ненулевые?
Ответ: а)да б)нет в)79
Скрыть
ОГЭ
Освоение образовательных программ основного общего образования завершается обязательной государственной итоговой аттестацией (далее – ГИА 9) по русскому языку и математике.
Нормативно-правовые документы
Приказы и методические документы
Демоверсии, спецификации, кодификаторы
В данном разделе представлены документы, определяющие структуру и содержание контрольных измерительных материалов основного государственного экзамена.
Для предметных комиссий субъектов РФ
Открытый банк заданий ОГЭ
Новая версия открытого банка заданий