Вклад планируется открыть на четыре года. Первоначальный вклад составляет целое число миллионов рублей. В конце каждого года вклад увеличивается на 10% по сравнению с его размером в начале года, а, кроме этого, в начале третьего и четвёртого годов вклад ежегодно пополняется на 3 млн рублей. Найдите наибольший размер первоначального вклада, при котором через четыре года вклад будет меньше 25 млн рублей.
Спрятать решение
Решение.
Пусть первоначальный вклад равен S млн рублей. Тогда в конце первого года вклад составит 1,1S, а в конце второго — 1,21S. В начале третьего года вклад составит 1,21S + 3, а в конце — 1,331S + 3,3. В начале четвёртого года вклад составит 1,331S + 6,3, а в конце — 1,4641S + 6,93.
По условию, нужно найти наибольшее целое S, для которого выполнено неравенство
откуда Наибольшее целое решение этого неравенства — число 12. Значит, размер первоначального вклада составляет 12 млн рублей.
Ответ: 12 млн рублей.
Спрятать критерии
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получен верный ответ | 2 |
| Верно построена математическая модель | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 2 |
Источник: Задания 17 (С5) ЕГЭ 2016, ЕГЭ по математике 28.03.2016. Досрочная волна, вариант 2 (только часть С)
Тренировочный вариант и ответы с решением пробник ЕГЭ 2023 по информатике 11 класс ФИПИ состоит из 27 заданий с кратким ответом, выполняемых с помощью компьютера. На выполнение экзаменационной работы по информатике и ИКТ отводится 3 часа 55 минут (235 минут).
Скачать тренировочный вариант с ответами
Скачать файлы для варианта
Другие тренировочные варианты
ege_2023_informatika_23_02
Разбор варианта. ЕГЭ по Информатике 2023
1. На рисунке справа схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведения о длинах этих дорог (в километрах). Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. В таблице в левом столбце указаны номера пунктов, откуда совершается движение, в первой строке – куда. Определите минимально возможную длину пути BDE. Передвигаться можно только по указанным дорогам.
2. Логическая функция F задаётся выражением w ∨ (y → z) ∧ x. На рисунке приведён частично заполненный фрагмент таблицы истинности функции F, содержащий неповторяющиеся строки. Определите, какой столбец в таблице каждой переменной в выражении. В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы. Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
3. В файле приведён фрагмент базы данных «Продукты» о поставках товаров в магазины районов города. База данных состоит из трёх таблиц. Таблица «Движение товаров» содержит записи о поставках товаров в магазины в течение первой декады августа 2021 г., а также информацию о проданных товарах. Поле Тип операции содержит значение Поступление или Продажа, а в соответствующее поле Количество упаковок внесена информация о том, сколько упаковок товара поступило в магазин или было продано в течение дня. Заголовок таблицы имеет следующий вид.
4. Все заглавные буквы русского алфавита закодированы неравномерным двоичным кодом, в котором никакое кодовое слово не является началом другого кодового слова. Это условие обеспечивает возможность однозначной расшифровки закодированных сообщений. Известно, что слово СПОРТЛОТО кодируется как 10010100110011110000100. Какой код соответствует букве Л, если известно, что коды подбирались под минимальную длину заданного слова.
5. На вход алгоритма подаётся натуральное число N большее 4. Алгоритм строит по нему новое число R следующим образом. 1. Строится двоичная запись числа N. 2. Далее эта запись обрабатывается по следующему правилу: а) если количество цифр в двоичной записи числа нечётное, то центральный бит двоичного представления инвертируется; б) если количество цифр в двоичной записи числа чётное, то два центральных бита двоичного представления инвертируется; Например, для исходного числа 610 = 1102 результатом является число 1002 = 410, а для исходного числа 910 = 10012 результатом является число 11112 = 1510. Укажите минимальное число N, после обработки которого с помощью этого алгоритма получается число R, большее 100 и меньшее N. В ответе запишите это число в десятичной системе счисления.
6. Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует 5 команд: Поднять хвост, означающая переход к перемещению без рисования; Опустить хвост, означающая переход в режим рисования; Вперёд n (где n – целое число), вызывающая передвижение Черепахи на n единиц в том направлении, куда указывает её голова; Назад n (где n – целое число), вызывающая передвижение в противоположном голове направлении; Направо m (где m – целое число), вызывающая изменение направления движения на m градусов по часовой стрелке, Налево m (где m – целое число), вызывающая изменение направления движения на m градусов против часовой стрелки. Запись Повтори k [Команда1 Команда2 … КомандаS] означает, что последовательность из S команд повторится k раз.
7. Спутник каждую секунду делает снимок 20 на 7.6 километра. Размер пикселя на местности 0.65х0.65 метра. Цвет пикселя выбирается из палитры в 256 цветов. Оцените объем памяти (в МБ) для хранения одного изображения. Сжатие не производится. Ответ округлите до большего целого числа.
8. Определите количество десятизначных чисел, записанных в восьмеричной системе счисления, в записи которых ровно пять цифры 7 и при этом никакая нечетная цифра не стоит рядом с цифрой 7.
9. Откройте файл электронной таблицы, содержащей в каждой строке шесть натуральных чисел. Определите количество строк таблицы, содержащих числа, для которых выполнено строго одно из условий: – в строке есть повторяющиеся числа; – в строке есть ровно три нечетных числа. В ответе запишите только число.
10. Текст произведения Ника Горькавого «Теория Катастроф» представлен в виде текстового файла. Откройте файл и определите, сколько бифуркационных технологий содержал итоговый список. В ответе запишите только число.
11. Вася решил закодировать персональные данные всех 1347 учеников всей школы. Для каждого ученика был сформирован ID из нескольких полей: номер класса, буква (а,б,в,г,д), пол, день и месяц рождения, номер имени по таблице имен (всего 103), номер фамилии по таблице фамилий (всего 733). Сперва Вася для каждого поля выделил минимальное количество байт. Затем попробовал закодировать все поля непрерывной битовой строкой и для каждого ID выделил минимальное количество байт. Сколько байт сэкономил Вася во втором случае для кодирования всех учеников школы?
12. Исполнитель Редактор получает на вход строку цифр и преобразовывает её. Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки цифр) А) заменить(v, w). Эта команда заменяет в строке первое слева вхождение цепочки v на цепочку w. Например, выполнение команды заменить(111, 27) преобразует строку 05111150 в строку 0512750. Если в строке нет вхождений цепочки v, то выполнение команды заменить(v, w) не меняет эту строку. Б) нашлось(v). Эта команда проверяет, встречается ли цепочка v в строке исполнителя Редактор. Если она встречается, то команда возвращает логическое значение «истина», в противном случае возвращает значение «ложь». Строка исполнителя при этом не изменяется. Цикл выполняется, пока условие истинно.
13. На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К, Л. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Определите количество различных путей ненулевой длины, которые начинаются и заканчиваются в городе Е, не содержат этот город в качестве промежуточного пункта и проходят через промежуточные города не более одного раза.
14. Дано выражение 12×4536 + 1×12345 В записи чисел переменной x обозначена неизвестная цифра из допустимого алфавита для указанных систем счисления. Определите наибольшее значение x, при котором значение данного арифметического выражения кратно 13. Для найденного значения x вычислите частное от деления значения арифметического выражения на 13 и укажите его в ответе в десятичной системе счисления.
15. На числовой прямой даны два отрезка: B = [23;37] и C = [41;73]. Укажите наименьшую длину такого отрезка А, для которого логическое выражение ¬((¬(x ∈ B) → (x ∈ C)) → (x ∈ A)) ложно (т.е. принимает значение 0) при любом значении переменной x.
16. Обозначим частное от деления натурального числа a на натуральное число b как a//b, а остаток как a%b. Например, 17//3 = 5, 17%3 = 2. Алгоритм вычисления значения функции F(n), где n – целое неотрицательное число, задан следующими соотношениями: F(n) = n при n < 10; F(n) = F(n//10) + F(n%10) , если 10 ⩽ n < 1000; F(n) = F(n//1000) — F(n%1000) , если n ⩾ 1000. Определите количество значений n, не превышающих 106 , для которых F(n) = 0?
17. В файле содержится последовательность целых чисел по модулю менее 10000. а) рассматриваются только пары в которых строго одно число оканчивается на 7. б) квадрат разности элементов пары меньше модуля разности квадратов хотя бы одной пары (отвечающей условию а). В ответе запишите два числа: сначала количество найденных пар, затем минимальный квадрат разности. В данной задаче под парой подразумевается два идущих подряд элемента последовательности.
18. Квадрат разлинован на N×N клеток (1 < N < 30). Роботу нужно перейти через поле с севера (верхняя строка) на юг (нижняя строка). Он может начать переход с любой клетки первой строки и закончить на любой клетке нижней строки. С каждым шагом Робот переходит в следующую строку и может за одно перемещение попасть в одну из трех клеток следующей строки (на клетку прямо вниз или на одну из клеток слева/справа от неё). Ходы только влево или вправо (без смены строки), назад (в предыдущую строку) и за границы поля запрещены. В каждой клетке поля лежит монета достоинством от 1 до 100. Робот собирает все монеты по пройденному маршруту. Определите максимальную возможную денежную сумму и количество монет с чётным значением, которую может собрать Робот, пройдя с северной границы поля (сверху) до южной границы поля (снизу). В ответе укажите два числа: сначала максимальную сумму, затем количество монет с четным значением по маршруту с максимальной суммой.
19. Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в меньшую кучу один или три камня. Изменять количество камней в большей куче не разрешается. Игра завершается, когда количество камней в кучах становится равным. Победителем считается игрок, сделавший последний ход, то есть первым сравнявшим количество камней в двух кучах. Игроки играют рационально, т.е. без ошибок. В начальный момент в первой куче было 13 камней, а во второй – S камней, 1 ≤ S ≤ 23? Укажите такое минимальное значение S, при котором Петя не может выиграть за один ход, но при любом ходе Пети Ваня может выиграть своим первым ходом.
20. Для игры, описанной в задании 19, найдите два наименьших значения S, при которых у Пети есть выигрышная стратегия, причём одновременно выполняются два условия: – Петя не может выиграть за один ход; – Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня. Найденные значения запишите в ответ в порядке возрастания
21. Для игры, описанной в задании 19, найдите два значения S, при котором одновременно выполняются три условия: – у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети; – у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом; – Петя может выбирать, каким ходом выиграет Ваня;
22. В файле содержится информация о совокупности N вычислительных процессов, которые могут выполняться параллельно или последовательно. Будем говорить, что процесс B зависит от процесса A, если для выполнения процесса B необходимы результаты выполнения процесса A. В этом случае процессы могут выполняться только последовательно. Информация о процессах представлена в файле в виде таблицы. В первом столбце таблицы указан идентификатор процесса (ID), во втором столбце таблицы – время его выполнения в миллисекундах, в третьем столбце перечислены с разделителем «;» ID процессов, от которых зависит данный процесс. Если процесс является независимым, то в таблице указано значение 0. Определите максимальное количество процессов, которые завершатся за 73 мс, при условии, что все независимые друг от друга процессы могут выполняться параллельно.
23. У исполнителя Кузнечик есть 4 команды: 1. Прибавить 1 2. Прибавить 3 3. Вычесть 1 4. Вычесть 3 Сколько существует программ, для которых при исходном числе 42 результатом будет являться число 42, при этом траектория вычисления содержит только числа от 40 до 49, притом не более 1 раза, т.е. без повторов.
24. Текстовый файл содержит строку из десятичных цифр и букв латинского алфавита. Найдите минимальную длину подстроки включающей все шестнадцатеричные цифры. Строка может включать повторяющиеся цифры и другие символы. В ответе укажите найденную длину..
25. Назовём маской числа последовательность цифр, в которой также могут встречаться следующие символы: символ «?» означает ровно одну произвольную цифру; символ «*» означает любую последовательность цифр произвольной длины; в том числе «*» может задавать и пустую последовательность. Например, маске 123*4?5 соответствуют числа 123405 и 12300405. Найдите все натуральные числа, не превышающие 1010, которые соответствуют маске 1?1?1?1*1 и при этом без остатка делятся на 2023, а сумма цифр числа равна 22. В ответе запишите все найденные числа в порядке возрастания. Количество строк в таблице для ответа избыточно.
26. В сетевом приложении реализован кэш размером V МБ для файлов размером от 1 до 999 МБ. Пользователи запрашивают файлы в порядке, заданном в исходном файле. Алгоритм кэширования сперва заполняет весь кэш. Для размещение следующего файла кэш нужно освободить. Для этого из кэша удаляется один подходящий файл, так чтобы свободное место было минимальным и достаточным для размещения нового файла. Если удаление даже самого большого файла не освобождает необходимого места, то удаляется самый большой файл и алгоритм рекурсивно повторяется, пока не будет достаточного места для нового файла.
27. Дана последовательность натуральных чисел. Расстояние между элементами последовательности – это разность их порядковых номеров. Например, если два элемента стоят в последовательности рядом, расстояние между ними равно 1, если два элемента стоят через один – расстояние равно 2 и т. д. Назовём тройкой любые три числа из последовательности, расстояние между которыми не меньше 17. Необходимо определить количество троек, в которых сумма чисел в тройке делится без остатка на 7717.
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
Положительное вещественное
шестизначное
число 513628
является составным числом.
Произведение цифр: 1440.
12 — количество делителей у числа.
Обратным числом является 0.000001946934357161214.
Это число представляется произведением: 2 * 2 * 73 * 1759.
Число в других системах счисления:
двоичный вид: 1111101011001011100, троичный вид: 222002120021, восьмеричный вид: 1753134, шестнадцатеричный вид: 7D65C.
В числе байт 513628 содержится 501 килобайт 604 байта .
Число 513628 в виде кода азбуки Морзе: ….. .—- …— -…. ..— —..
Косинус числа: -0.9180, синус числа: 0.3965, тангенс числа: -0.4319.
Логарифм натуральный числа 513628 равен 13.1493.
Десятичный логарифм: 5.7106.
716.6784 — корень квадратный, 80.0847 — кубический.
Квадрат числа: 2.6381e+11.
Если представить это число как секунды, то это 5 дней 22 часа 40 минут 28 секунд .
Цифра 7 — это нумерологическое значение этого числа.
ЕГЭ по математике — Профиль 2023. Открытый банк заданий с ответами.
Решение и ответы заданий варианта МА2210309 СтатГрад 28 февраля ЕГЭ 2023 по математике (профильный уровень). Тренировочная работа №3. ГДЗ профиль для 11 класса.
+Задания №1, №4, №6, №10 из варианта МА2210311.


Задание 1.
В треугольнике ABC угол C равен 90°, CH – высота, BC = 5, cosA=frac{2sqrt{6}}{5}. Найдите длину отрезка AH.
Задание 1 из варианта 2210311.
Найдите периметр прямоугольника, если его площадь равна 12, а отношение соседних сторон равно 1:3.
Задание 2.
Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 2. Объём параллелепипеда равен 3,2. Найдите высоту цилиндра.
Задание 3.
В группе 16 человек, среди них – Анна и Татьяна. Группу случайным образом делят на 4 одинаковые по численности подгруппы. Найдите вероятность того, что Анна и Татьяна окажутся в одной подгруппе.
Задание 4.
Агрофирма закупает куриные яйца только в двух домашних хозяйствах. Известно, что 40 % яиц из первого хозяйства – яйца высшей категории, а из второго хозяйства – 60 % яиц высшей категории. В этой агрофирме 50 % яиц высшей категории. Найдите вероятность того, что яйцо, купленное у этой агрофирмы, окажется из первого хозяйства.
Задание 4 из варианта 2210311.
Игральный кубик бросают дважды. Известно, что в сумме выпало 11 очков. Найдите вероятность того, что во второй раз выпало 5 очков.
Задание 5.
Решите уравнение frac{x–1}{5x+11}=frac{x–1}{3x-7}. Если уравнение имеет больше одного корня, в ответе запишите больший из корней.
Задание 6.
Найдите значение выражения frac{(4^{frac{3}{5} }cdot7^{frac{2}{3}})^{15}}{28^{9}} .
Задание 6 из варианта 2210311.
Найдите 98cos2α, если cosα = frac{4}{7}.
Задание 7.
На рисунке изображён график y = f’(x) – производной функции f(x), определённой на интервале (−5; 5). В какой точке отрезка [−4; −1] функция f(x) принимает наибольшее значение?
Задание 8.
На верфи инженеры проектируют новый аппарат для погружения на небольшие глубины. Конструкция имеет кубическую форму, а значит, действующая на аппарат выталкивающая (архимедова) сила, выражаемая в ньютонах, будет определяться по формуле FA = ρgl3, где l – длина ребра куба в метрах, ρ = 1000 кг/м3 – плотность воды, а g – ускорение свободного падения (считайте, что g = 9,8 Н/кг). Какой может быть максимальная длина ребра куба, чтобы обеспечить его эксплуатацию в условиях, когда выталкивающая сила при погружении будет не больше чем 2116800 Н? Ответ дайте в метрах.
Задание 9.
Пристани A и B расположены на озере, расстояние между ними равно 280 км. Баржа отправилась с постоянной скоростью из A в B. На следующий день после прибытия она отправилась обратно со скоростью на 4 км/ч больше прежней, сделав по пути остановку на 8 часов. В результате она затратила на обратный путь столько же времени, сколько на путь из A в B. Найдите скорость баржи на пути из A в B. Ответ дайте в км/ч.
Задание 10.
На рисунке изображён график функции f(x) = ax2 + bx + c. Найдите значение f(−1).
Задание 10 из варианта 2210311.
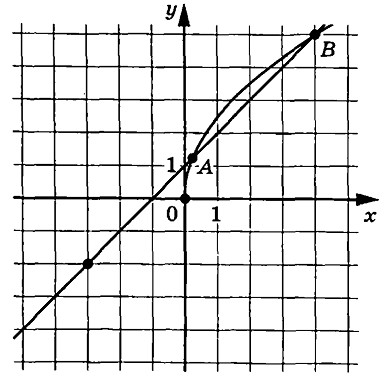
На рисунке изображены графики функций f(x) = frac{k}{x} и g(x) = ax + b, которые пересекаются в точках A и B. Найдите абсциссу точки B.
Задание 11.
Найдите точку минимума функции y = x3 − 27x2 + 13.
Задание 12.
а) Решите уравнение 2cos3x = –sin(frac{3pi}{2} + x)
б) Найдите все корни этого уравнения, принадлежащие отрезку [3π; 4π]
Задание 13.
Основанием правильной пирамиды PABCD является квадрат ABCD. Сечение пирамиды проходит через вершину В и середину ребра PD перпендикулярно этому ребру.
а) Докажите, что угол наклона бокового ребра пирамиды к её основанию равен 60°.
б) Найдите площадь сечения пирамиды, если AB = 30.
Задание 14.
Решите неравенство frac{9^{x}–13cdot 3^{x}+30}{3^{x+2}–3^{2x+1}}ge frac{1}{3^{x}}.
Задание 15.
По вкладу «А» банк в конце каждого года планирует увеличивать на 13 % сумму, имеющуюся на вкладе в начале года, а по вкладу «Б» – увеличивать эту сумму на 7 % в первый год и на целое число n процентов за второй год. Найдите наименьшее значение n, при котором за два года хранения вклад «Б» окажется выгоднее вклада «А» при одинаковых суммах первоначальных взносов.
Задание 16.
В треугольнике ABC медианы AA1, BB1 и CC1 пересекаются в точке M. Известно, что AC = 3MB.
а) Докажите, что треугольник ABC прямоугольный.
б) Найдите сумму квадратов медиан AA1 и CC1, если известно, что AC = 22.
Задание 17.
Найдите все значения a, при каждом из которых система уравнений
begin{cases} (x-5a+1)^{2}+(y-2a-1)^{2}=a-2 \ 3x-4y=2a+3 end{cases}
не имеет решений.
Задание 18.
У Ани есть 800 рублей. Ей нужно купить конверты (большие и маленькие). Большой конверт стоит 32 рубля, а маленький – 25 рублей. При этом число маленьких конвертов не должно отличаться от числа больших конвертов больше чем на пять.
а) Может ли Аня купить 24 конверта?
б) Может ли Аня купить 29 конвертов?
в) Какое наибольшее число конвертов может купить Аня?
Источник варианта: СтатГрад/statgrad.org.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 5 / 5. Количество оценок: 3
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
8 226
Купить задания с ответами на математику ОГЭ 27.05.2023 и 28 мая
ОГЭ по математике будет проходить в 2 дня, данная система сдачи была перенята с ЕГЭ 2023, где русский язык проходил аналогичным образом. На нашем сайте Вы сможете приобрести конфиденциальные материалы на ОГЭ по математике на 27 и 28 мая. Варианты на 2 дня будут совершенно уникальные по отношению
1 302
Варианты с ответами на ОГЭ по русскому языку 08.09.2022 – на Ваш регион
Впервые сентябрьская пересдача экзаменов ОГЭ будет значимой в такой степени, в которой мы получили неутешительные результаты. По большей части проблемы возникли с математикой, но русский язык также оказал сильное влияние на % сдающих, т.е. подвел учащихся к сентябрьской пересдаче без возможности
5 916
Купить ответы на русский язык для 24 мая и 25 мая на ОГЭ 2023
В данной статье мы подробнее расскажем, как получить ответы на ОГЭ по русскому языку и благополучно списать в 2023 году. Если Вы находитесь на временном пороге, когда в ближайшие дни предстоит сдавать русский язык ОГЭ, то наш проект готов оказать поддержку в данном дела полностью.
1 735
Варианты на 5 сентября по математике ОГЭ 2022 для пересдачи
Здравствуйте! В 2022 году многих постигла двойная неудача на экзаменах, которая моментально отправила на сентябрьскую пересдачу. Мы предвидели данное развитие событий, т.к. отмена ОГЭ 2021 сказалась негативно на общем понимании, “что такое ОГЭ и как его сдавать”, а также постоянное ожидание, что
8 833
Слив КИМов и ответов по математике: ОГЭ 2022 — 24.05.2022
Здравствуйте! Вы сейчас находитесь на сайте, который предоставляет конфиденциальные материалы для государственных экзаменов ЕГЭ/ОГЭ. В данной статье расскажем, как получить ответы на ОГЭ по математике. В 2022 году ожидать слив материалов в открытую сеть дело максимально сомнительное, т.к. последние
8 147
Как получить ответы на русский язык ОГЭ 7 и 8 июня 2022
Здравствуйте! Приветствуем всех пользователей в 2022 году, которые желают списать русский язык ОГЭ, в данной статьей расскажем, как проходит получение конфиденциальных материалов для ОГЭ в рамках нашего проекта. Если Вы задумались о том, что необходимо списать экзамены в 9 классе, то наш проект
7 377
Здравствуйте! Наш проект занимается предоставлением конфиденциальных материалов на государственные экзамены ОГЭ/ЕГЭ. Сейчас мы подробнее расскажем о экзамене ОГЭ по географии, который состоится 7 июня в 10:00 по местному времени в каждом регионе нашей страны. Если Вы выбрали географию, то не
Задание 1
В треугольнике $$ABC$$ известно, что $$AC=BC$$, высота $$AH$$ равна 8, $$BH=20$$. Найдите $$tg BAC$$.
Ответ: 0,4
Скрыть
Задание 2
Найдите объём многогранника, вершинами которого являются точки $$A_1$$, $$B_1$$, $$F_1$$, $$E$$ правильной шестиугольной призмы $$ABCDEFA_1B_1C_1D_1E_1F_1$$, площадь основания которой равна 10, а боковое ребро равно 9.
Ответ: 5
Скрыть
Задание 3
В группе туристов 32 человека. Их вертолётом доставляют в труднодоступный район, перевозя по 4 человека за рейс. Порядок, в котором вертолёт перевозит туристов, случаен. Найдите вероятность того, что турист Г. полетит четвёртым рейсом вертолёта.
Ответ: 0,125
Скрыть
Задание 4
Игральную кость бросали до тех пор, пока сумма всех выпавших очков не превысила число 9. Какова вероятность того, что для этого потребовалось три броска? Ответ округлите до сотых.
Ответ: 0,46
Скрыть
Задание 5
Найдите корень уравнения $$(frac{1}{9})^{x+4}=729$$
Ответ: -7
Скрыть
Задание 6
Найдите значение выражения $$log_{6}1,25cdot log_{0,8}6$$
Ответ: -1
Скрыть
Задание 7
На рисунке изображён график функции $$y=f(x)$$, определённой на интервале (-11; 2). Найдите количество точек, в которых касательная к графику функции $$y=f(x)$$ параллельна прямой $$y=-4$$.
Ответ: 7
Скрыть
Задание 8
Высота над землёй подброшенного вверх мяча меняется по закону $$h(t)=1+11t-5t^{2}$$, где $$h$$ — высота в метрах, $$t$$ — время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее 3 метров?
Ответ: 1,8
Скрыть
Задание 9
Имеется два сосуда. Первый содержит 25 кг, а второй — 20 кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 52 % кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 53 % кислоты. Сколько килограммов кислоты содержится в первом сосуде?
Ответ: 11
Скрыть
Задание 10
На рисунке изображены графики функций $$f(x)=asqrt{x}$$ и $$g(x)=kx+b$$, которые пересекаются в точках $$A$$ и $$B$$. Найдите абсциссу точки $$A$$.
Ответ: 0,25
Скрыть
Задание 11
Найдите наименьшее значение функции $$y=6x-sin x+17$$ на отрезке $$[0;frac{pi}{2}]$$
Ответ: 17
Скрыть
Задание 12
а) Решите уравнение $$log^{2}_{2}(8x^{2})-log_{4}(2x)-1=0$$
б) Найдите все корни этого уравнения, принадлежащие отрезку [0,4; 0,8].
Ответ: а)$$0,5;frac{sqrt[8]{2}}{4}$$; б)$$0,5$$
Скрыть
Задание 13
Сторона основания правильной четырёхугольной пирамиды $$SABCD$$ относится к боковому ребру как $$1:sqrt{2}$$ . Через вершину $$D$$ проведена плоскость $$alpha$$, перпендикулярная боковому ребру $$SB$$ и пересекающая его в точке $$M$$.
а) Докажите, что сечение пирамиды $$SABCD$$ плоскостью $$alpha$$ — это четырёхугольник, диагонали которого перпендикулярны.
б) Найдите площадь этого сечения, если боковое ребро пирамиды равно 6.
Ответ: $$6sqrt{3}$$
Скрыть
Задание 14
Решите неравенство $$frac{sqrt{x-2}(4-3^{x-1})}{2^{1-x^{2}}-3}geq 0$$
Ответ: $$2;[log_{3}12;+infty)$$
Скрыть
Задание 15
15 июня 2025 года Данила Сергеевич планирует взять кредит в банке на 4 года в размере целого числа миллионов рублей. Условия его возврата таковы:
— в январе каждого года действия кредита долг увеличивается на 15 % от суммы долга на конец предыдущего года;
— в период с февраля по июнь в каждый из 2026 и 2027 годов необходимо выплатить только начисленные в январе проценты по кредиту;
— в период с февраля по июнь в каждый из 2028 и 2029 годов выплачиваются равные суммы, причём последний платёж должен погасить долг по кредиту полностью.
Найдите наибольший размер кредита, при котором общая сумма выплат по кредиту не превысит 20 млн рублей.
Ответ: 13 млн. руб.
Скрыть
Задание 16
Окружность с центром в точке $$C$$ касается гипотенузы $$AB$$ прямоугольного треугольника $$ABC$$ и пересекает его катеты $$AC$$ и $$BC$$ в точках $$E$$ и $$F$$. Точка $$D$$ — основание высоты, опущенной на $$AB$$. $$I$$ и $$J$$ — центры окружностей, вписанных в треугольники $$BCD$$ и $$ACD$$.
а) Докажите, что точки $$E$$ и $$F$$ лежат на прямой $$IJ$$.
б) Найдите расстояние от точки $$C$$ до прямой $$IJ$$, если $$AC=2sqrt{3}$$, $$BC=2$$.
Ответ: $$frac{sqrt{6}}{2}$$
Скрыть
Задание 17
Найдите все значения $$a$$, при каждом из которых оба уравнения $$a+frac{x}{3}=|x|$$ и $$2a+x=sqrt{2a^{2}+4ax-x^{2}+12}$$ имеют ровно по 2 различных корня, и строго между корнями каждого из уравнений лежит корень другого уравнения.
Ответ: $$(frac{2sqrt{6}}{sqrt{13}};frac{4sqrt{6}}{5})$$
Скрыть
Задание 18
Трёхзначное число, меньшее 700, поделили на сумму его цифр и получили натуральное число $$n$$.
а) Может ли $$n$$ равняться 64?
б) Может ли $$n$$ равняться 78?
в) Какое наибольшее значение может принимать $$n$$, если все цифры ненулевые?
Ответ: а)да б)нет в)73
Скрыть