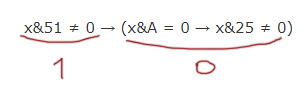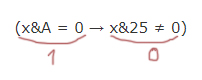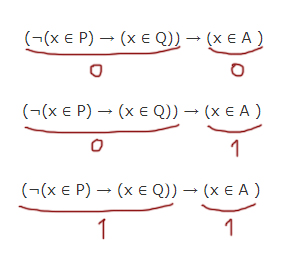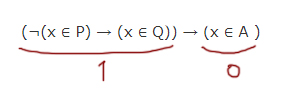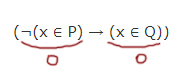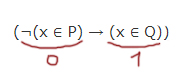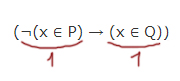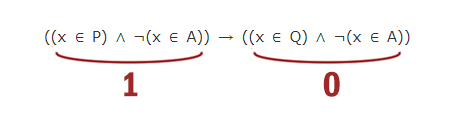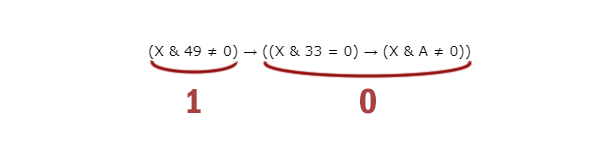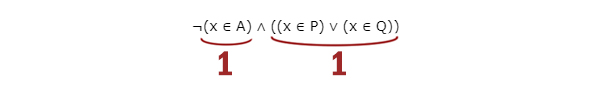514765 решу егэ - Помощь в подготовке к экзаменам и поступлению

В городском парке работает 5 аттракционов: карусель, колесо обозрения, автодром, «Ромашка» и «Весёлый тир». В кассах продаётся 6 видов билетов, каждый из которых на один или два аттракциона. Сведения о стоимости билетов представлены в таблице.

Номер билета	Набор аттракционов	Стоимость (руб.)
1	Карусель	200
2	Автодром, «Весёлый тир»	350
3	Колесо обозрения, «Весёлый тир»	450
4	«Ромашка», колесо обозрения	300
5	Автодром, карусель	400
6	Карусель, «Ромашка»	300

Какие билеты должен купить Андрей, чтобы посетить все пять аттракционов и затратить не более 900 рублей? В ответе укажите какой-нибудь один набор номеров билетов без пробелов, запятых и других дополнительных символов.

Источник

Новые тренировочные варианты ЕГЭ 2023 по математике базовый и профильный уровень с ответами и решением для 10 и 11 класса, больше 100 вариантов в формате реального экзамена ФИПИ вы можете решать онлайн или скачать.

Тренировочные варианты ЕГЭ 2023 по математике база и профиль

13.09.2022 Тренировочный вариант №1 ЕГЭ 2023 по математике профиль с ответами

20.09.2022 Тренировочный вариант №2 ЕГЭ 2023 по математике профиль с ответами

20.09.2022 Тренировочный вариант №2 ЕГЭ 2023 база по математике с ответами

27.09.2022 Математика 11 класс профиль входная мониторинговая работа 3 варианта с ответами

28.09.2022 Тренировочный вариант №3 ЕГЭ 2023 база по математике с ответами

28 сентября 2022 Статград математика 11 класс ЕГЭ 2023 база и профиль варианты и ответы

29 сентября 2022 Тренировочный вариант №3 ЕГЭ 2023 по математике профиль с ответами

1 октября 2022 Ларин вариант 399 ЕГЭ 2023 по математике профиль решение с ответами

6 октября Тренировочный вариант №4 ЕГЭ 2023 база по математике с ответами

6 октября Тренировочный вариант №4 ЕГЭ 2023 по математике профиль с ответами

8 октября Ларин вариант 400 ЕГЭ 2023 по математике профиль решение с ответами

12 октября Тренировочный вариант №5 ЕГЭ 2023 база по математике с ответами

12 октября Тренировочный вариант №5 ЕГЭ 2023 по математике профиль с ответами

14 октября Вариант 1 Ященко ЕГЭ 2023 математика профиль с ответами и решением

14 октября Вариант 2 Ященко ЕГЭ 2023 математика профиль с ответами и решением

15 октября Ларин вариант 401 ЕГЭ 2023 по математике профиль решение с ответами

15 октября Ларин вариант 402 ЕГЭ 2023 по математике профиль решение с ответами

16 октября Вариант 3 Ященко ЕГЭ 2023 математика профиль с ответами и решением

16 октября Вариант 4 Ященко ЕГЭ 2023 математика профиль с ответами и решением

23 октября Тренировочный вариант №6 ЕГЭ 2023 база по математике с ответами

24 октября Тренировочный вариант №6 ЕГЭ 2023 по математике профиль с ответами

25 октября Тренировочный вариант №7 ЕГЭ 2023 база по математике с ответами

26 октября Тренировочный вариант №7 ЕГЭ 2023 по математике профиль с ответами

28 октября Ларин вариант 403 ЕГЭ 2023 по математике профиль решение с ответами

29 октября Ларин вариант 404 ЕГЭ 2023 по математике профиль решение с ответами

1 ноября 2022 Тренировочный вариант №8 решу ЕГЭ 2023 база по математике с ответами

1 ноября 2022 Тренировочный вариант №8 решу ЕГЭ 2023 по математике профиль с ответами

5 ноября 2022 Вариант 1-2 распечатай и реши ЕГЭ 2023 база по математике 11 класс с ответами

6 ноября 2022 Ларин вариант 405 ЕГЭ 2023 профиль по математике решение с ответами

9 ноября 2022 Тренировочный вариант №9 решу ЕГЭ 2023 база по математике с ответами

12 ноября 2022 Тренировочный вариант №9 решу ЕГЭ 2023 по математике профиль с ответами

13 ноября 2022 Ларин вариант 406 ЕГЭ 2023 профиль по математике решение с ответами

15 ноября 2022 Тренировочный вариант №10 решу ЕГЭ 2023 база по математике 11 класс с ответами

15 ноября 2022 Тренировочный вариант №10 решу ЕГЭ 2023 по математике профиль с ответами

21 ноября 2022 Ларин вариант 407 ЕГЭ 2023 профиль по математике решение с ответами

23 ноября 2022 Тренировочный вариант №11 решу ЕГЭ 2023 база по математике 11 класс с ответами

23 ноября 2022 Тренировочный вариант №11 решу ЕГЭ 2023 по математике профиль с ответами

27 ноября 2022 Ларин вариант 408 ЕГЭ 2023 профиль по математике решение с ответами

28 ноября 2022 Вариант 3-4 распечатай и реши ЕГЭ 2023 база по математике 11 класс с ответами

30 ноября 2022 Мониторинговая работа по математике 11 класс ЕГЭ 2023 профиль 1 полугодие

3 декабря 2022 Тренировочный вариант №12 решу ЕГЭ 2023 база по математике 11 класс с ответами

3 декабря 2022 Тренировочный вариант №12 решу ЕГЭ 2023 по математике профиль с ответами

3 декабря 2022 Пробник ЕГЭ 2023 Москва по математике профиль задания и ответы

5 декабря 2022 Ларин вариант 409 ЕГЭ 2023 профиль по математике решение с ответами

9 декабря 2022 Тренировочный вариант №13 решу ЕГЭ 2023 база по математике 11 класс с ответами

10 декабря 2022 Тренировочный вариант №13 решу ЕГЭ 2023 профиль по математике 11 класс с ответами

12 декабря 2022 Ларин вариант 410 ЕГЭ 2023 профиль по математике решение с ответами

13 декабря 2022 Статград математика 11 класс профиль ЕГЭ 2023 варианты МА2210209-МА2210212 и ответы

13 декабря 2022 Математика 11 класс база ЕГЭ 2023 статград варианты и ответы

15 декабря 2022 Тренировочный вариант №14 решу ЕГЭ 2023 профиль по математике 11 класс с ответами

15 декабря 2022 Тренировочный вариант №14 решу ЕГЭ 2023 база по математике 11 класс с ответами

20 декабря 2022 Вариант 5-6 распечатай и реши ЕГЭ 2023 база по математике 11 класс с ответами

20 декабря 2022 Ларин вариант 411 ЕГЭ 2023 профиль по математике решение с ответами

3 января 2023 Ларин вариант 412 ЕГЭ 2023 профиль по математике решение с ответами

6 января 2023 Тренировочный вариант 1-2 ЕГЭ 2023 профиль математика задания и ответы

8 января 2023 Вариант 3-4 ЕГЭ 2023 профиль математика задания и ответы

9 января 2023 Вариант 7-8 распечатай и реши ЕГЭ 2023 база по математике 11 класс с ответами

10 января 2023 Тренировочный вариант №15 и №16 решу ЕГЭ 2023 профиль по математике 11 класс с ответами

11 января 2023 ЕГЭ 2023 математика тренировочные задания и ответы Ященко, Семенов

11 января 2023 Тренировочный вариант №15 и №16 база ЕГЭ 2023 по математике 11 класс с ответами

19 января 2023 Тренировочные варианты №17 и №18 решу ЕГЭ 2023 профиль по математике 11 класс с ответами

22 января 2023 Ларин вариант 413 и 414 ЕГЭ 2023 профиль по математике решение и ответы

22 января 2023 Тренировочный 19 вариант решу ЕГЭ 2023 профиль по математике 11 класс с ответами

22 января 2023 База ЕГЭ 2023 математика 11 класс тренировочный вариант 19 с ответами

25 января 2023 База ЕГЭ 2023 математика 11 класс тренировочный вариант 20 с ответами

27 января 2023 Тренировочный вариант №20 решу ЕГЭ 2023 профиль по математике 11 класс с ответами

28 января 2023 Вариант 415 Ларина ЕГЭ 2023 по математике 11 класс задания и ответы

2 февраля 2023 Вариант 21 база ЕГЭ 2023 математика 11 класс тренировочный вариант с ответами

2 февраля 2023 Тренировочный вариант №21 решу ЕГЭ 2023 профиль по математике 11 класс с ответами

8 февраля 2023 Математика 10-11 класс ЕГЭ 2023 статград варианты база и профиль МА2200101-МА2200110 и ответы

11 февраля 2023 Тренировочный вариант №22 решу ЕГЭ 2023 профиль по математике 11 класс с ответами

11 февраля 2023 Тренировочный вариант №22 решу ЕГЭ 2023 база по математике 11 класс с ответами

12 февраля 2023 Вариант 416 Ларина ЕГЭ 2023 по математике 11 класс задания и ответы

12 февраля 2023 Вариант 417 Ларина ЕГЭ 2023 по математике 11 класс задания и ответы

13 февраля 2023 Вариант 9 и вариант 10 ЕГЭ 2023 база математика распечатай и реши задания

13 февраля 2023 Вариант 11 и вариант 12 ЕГЭ 2023 база математика распечатай и реши

16 февраля 2023 Тренировочный вариант №23 решу ЕГЭ 2023 база по математике 11 класс с ответами

16 февраля 2023 Тренировочный вариант №23 решу ЕГЭ 2023 профиль по математике 11 класс с ответами

18 февраля 2023 Вариант 418 Ларина ЕГЭ 2023 по математике 11 класс задания и ответы

22 февраля 2023 Пробный ЕГЭ 2023 вариант 24 база по математике 11 класс с ответами

22 февраля 2023 Пробный ЕГЭ 2023 вариант 24 профиль по математике 11 класс с ответами

25 февраля 2023 Вариант 419 Ларина ЕГЭ 2023 по математике 11 класс задания и ответы

28 февраля 2023 Статград математика 11 класс ЕГЭ 2023 база и профиль и ответы

4 марта 2023 Пробник ЕГЭ 2023 вариант 25 база по математике 11 класс с ответами

4 марта 2023 Вариант 420 Ларин ЕГЭ 2023 по математике 11 класс задания и ответы

5 марта 2023 Пробник ЕГЭ 2023 вариант 25 профиль по математике 11 класс с ответами

8 марта 2023 Пробник ЕГЭ 2023 вариант 26 профиль по математике 11 класс с ответами

8 марта 2023 Пробник ЕГЭ 2023 вариант 26 база по математике 11 класс 100 баллов с ответами

Смотрите также на нашем сайте:

Сборник Ященко ЕГЭ 2023 математика профильный уровень 36 вариантов

ПОДЕЛИТЬСЯ МАТЕРИАЛОМ

Источник

Главная
Новости
ЕГЭ
- ЕГЭ Профиль 2023
- ЕГЭ Профиль 2022
- ЕГЭ Профиль 2016-2021
- Варианты профильного ЕГЭ
- ЕГЭ База 2023
- ЕГЭ База 2022
- ЕГЭ База 2016-2021
ОГЭ
- ОГЭ 2019
- ОГЭ 2023
ГВЭ
- ГВЭ 11 класс
ВПР
- ВПР 4 класс
- ВПР 5 класс
- ВПР 6 класс
- ВПР 7 класс
- ВПР 8 класс
Алгебра
- Алгебра 7-9
- Алгебра 10-11
Геометрия
- Геометрия 7-9
- Геометрия 10-11
YouTube
Прочее
- Class100
- Разработки
- Обо мне
- Репетитор

ЕГЭ по математике — Профиль 2022. Открытый банк заданий с ответами.

ЕГЭ по математике — Профиль 2022. Открытый банк заданий с ответами.admin2022-08-27T23:17:48+03:00

Источник

На уроке рассмотрено решение 25 задания ЕГЭ по информатике: дается подробное объяснение и разбор заданий демонстрационных вариантов и досрочных экзаменов

Содержание:

Объяснение задания 25 ЕГЭ по информатике
- Алгоритмизация и программирование
Решение 25 заданий ЕГЭ по информатике
- Делители числа
- Простые числа
Задания прошлых лет для тренировки (до 2021)
- Задачи с поэлементной обработкой массива
- Задачи на обработку элементов массива с последующей заменой
- Задачи на обработку пар элементов массива (два подряд идущих)
- Задачи на обработку трёх подряд идущих элементов массива (тройки элементов массива)
- Задачи на поиск максимума, минимума элементов массива и другие
Решение 25 заданий ЕГЭ по информатике: более сложные задания

25-е задание: «Программная обработка целочисленной информации»

Уровень сложности

— высокий,

Требуется использование специализированного программного обеспечения

— да,

Максимальный балл

— 2,

Примерное время выполнения

— 20 минут.

Проверяемые элементы содержания: Умение создавать собственные программы (10–20 строк) для обработки целочисленной информации

Рекомендации по выполнению:

«В этом задании требуется написать фрагмент программы, реализующий простую обработку целочисленного массива. У экзаменуемых, хорошо освоивших технику программирования, это задание обычно не вызывает серьёзных затруднений, поскольку алгоритм обработки массива не относится к сложным»

Типичные ошибки и рекомендации по их предотвращению:

«в цикле происходит выход за границу массива;

не инициализируется или неверно инициализируется искомое значение;

исходный массив не изменяется;

изменяются не все требуемые элементы (например, только первый или последний из них);

отсутствует вывод ответа, или ответ выводится не полностью (например, только один элемент массива ввиду пропущенного цикла вывода элементов или операторных скобок);

используется переменная, не объявленная в разделе описания переменных;

не указано или неверно указано условие завершения цикла»

«Часто бывает, что увлекшись написанием решения, экзаменуемый совершает ошибки в простых ситуациях: организация ввода-вывода, описание и инициализация переменных, обработка массива (выход за границу) и т.д. Эти ошибки могут стоить Вам нескольких баллов, старайтесь их не допускать»

ФГБНУ «Федеральный институт педагогических измерений»

Алгоритмизация и программирование

Для решения задания требуется вспомнить темы:

Одномерные массивы.
Двумерные массивы.

Решение 25 заданий ЕГЭ по информатике

Плейлист видеоразборов задания на YouTube:
Задание демонстрационного варианта 2022 года ФИПИ

Делители числа

25_7:

Напишите программу, которая ищет среди целых чисел, принадлежащих числовому отрезку [126849; 126871], числа, имеющие ровно 4 различных делителя.
Выведите эти четыре делителя для каждого найденного числа в порядке возрастания.

✍ Решение:

PascalABC.net:

begin
  var divCount := 4;
  for var n := 126849 to 126871 do
  begin
    var divs := new List<integer>; 
    for var d := 1 to n do
      if n mod d = 0 then begin
        divs.Add(d);      
        if divs.Count > divCount then break;
      end;
    if divs.Count = divCount then
    begin
      divs.Sort();
      Println(divs);
    end;
  end;
end.

Python:

for n in range(126849,126871+1):
      divs = [] # чистим список делителей
      for d in range(1,n+1): #
        if n % d == 0:
          divs = divs + [d] # добавляем делитель в список
          if len(divs) > 4: break
      if len(divs) == 4:
        print(*divs)

С++:

✎ Решение (оптимизированный вариант):

Будем использовать оптимизированный вариант программы, подходящий для «медленных» компьютеров. Для этого перебор делителей для числа n будем выполнять от 2 до √n, округлив его до ближайшего целого числа (не включая точный квадратный корень, если он существует):

вместо диапазона делителей [1; число]
использовать диапазон [1; округл(√n)]

При переборе делителей будем определять: если делитель – это точный квадратный корень(n), то в список делителей добавлять будем только сам делитель, если нет – то добавляем пару делителей (делитель и n // делитель):

Пример:
число 8 = 2 * 4
Достаточно рассмотреть цикл от 2 до округл(√8) (=2)
если 8 делится на 2 и 8/2 не равно 2, то делители: 2 и 4 (8/2)

PascalABC.net:

begin
  var divCount := 4;
  for var n := 126849 to 126871 do
  begin
    var divs := new List<integer>;
    var d := 1;
    while d * d <= n do  // можно цикл for var d := 1 to round(sqrt(n)) do
    begin
      if n mod d = 0 then begin
        divs.Add(d);      
        if d * d <> n then 
          divs.Add(n div d);
        if divs.Count > divCount then break;
      end;
      d := d+1;
    end;
    if divs.Count = divCount then
    begin
      divs.Sort();
      Println(divs);
    end;
  end;
end.

Python:

# import math # для квадратного корня числа (sqrt)
divCount = 4  # нужное количество делителей
for n in range(126849,126871 + 1):
  divs = [] # чистим список делителей
  d = 1
  #  вместо while можно цикл for d in range(1,round(math.sqrt(n))):
  while d*d <= n: # перебор делителей
    if n % d == 0:
      divs.append(d) # добавляем делитель в список
      if d != n//d: # если делитель - не точный квадратный корень n
        divs.append(n//d)
      if len(divs) > divCount: break
    d+=1
  if len(divs) == divCount:
    divs.sort()
    print(divs)

С++:

✎ Решение: Генерация списка делителей.
Общая идея:

Для каждого числа указанного диапазона генерируем список делителей.
Если длина списка равна четырем, выводим его.

PascalABC.net:	Python: for n in range(126849, 126871+1): divs = [d for d in range(1, n+1) if n % d == 0] if len(divs) == 4: print( *divs )
С++:

Ответ:

1 3 42283 126849
1 47 2699 126853
1 5 25373 126865
1 293 433 126869

25_8:

Напишите программу, которая ищет среди целых чисел, принадлежащих числовому отрезку [164700; 164752], числа, имеющие ровно 6 различных делителей.
Выведите эти делители для каждого найденного числа в порядке возрастания.

✍ Решение:

PascalABC.net:

begin
  var divCount := 6;
  for var n := 164700 to 164752 do
  begin
    var divs := new List<integer>; 
    for var d := 1 to round(sqrt(n)) do
      if n mod d = 0 then begin
        divs.Add(d);      
        if d * d <> n then 
          divs.Add(n div d);
        if divs.Count > divCount then break;
      end;
    if divs.Count = divCount then
    begin
      divs.Sort();
      Println(divs);
    end;
  end;
end.

Python:

import math # для квадратного корня sqrt
divCount = 6  # нужное количество делителей
for n in range(164700, 164752 + 1):
  divs = [] # чистим список делителей
  for d in range(1,round(math.sqrt(n))): # перебор делителей
    if n % d == 0:
      divs.append(d) # добавляем делитель в список
      if d != n//d:
        divs.append(n//d)
      if len(divs) > divCount: break
  if len(divs) == divCount:
    divs.sort()
    print(divs)

С++:

✎ Решение: Генерация списка делителей.
Общая идея:

Для каждого числа указанного диапазона генерируем список делителей.
Если длина списка равна четырем, выводим его.

PascalABC.net:	Python: for n in range(164700, 164752+1): divs = [d for d in range(1, n+1) if n % d == 0] if len(divs) == 6: print( *divs )
С++:

Ответ:

1 2 4 41177 82354 164708
1 3 9 18301 54903 164709
1 2 4 41179 82358 164716
1 2 4 41183 82366 164732

25_9:

Напишите программу, которая ищет среди целых чисел, принадлежащих числовому отрезку [190201; 190230], числа, имеющие ровно 4 различных делителя.
Выведите эти четыре делителя для каждого найденного числа в порядке убывания.

✍ Решение:

PascalABC.net:

begin
  var divs := new integer[4];
  for var n := 190201 to 190230 do
  begin
    var i := 0; // для индекса массива
    for var d := 1 to n do
    begin
      if n mod d = 0 then 
      begin
        if i < 4 then
          divs[i] := d;
        inc(i);
      end;
      if i > 4 then 
        break; 
    end;
    if i = 4 then begin
      println(divs.Reverse())
    end;
  end;
end.

Python:

for n in range(190201,190230+1):
      divs = [] # чистим список делителей
      for d in range(1,n+1): #
        if n % d == 0:
          divs = divs + [d] # добавляем делитель в список
          if len(divs) > 4: break
      if len(divs) == 4:
        divs.reverse()
        print(*divs)

С++:

✎ Решение (оптимизированный вариант):

PascalABC.net:

begin
  var divCount := 4;
  for var n := 190201 to 190230 do
  begin
    var divs := new List<integer>; 
    for var d := 1 to round(sqrt(n)) do
      if n mod d = 0 then begin
        divs.Add(d);      
        if d * d <> n then 
          divs.Add(n div d);
        if divs.Count > divCount then break;
      end;
    if divs.Count = divCount then
    begin
      divs.Sort();
      divs.Reverse();
      Println(divs);
    end;
  end;
end.

Python:

import math # для квадратного корня sqrt
divCount = 4  # нужное количество делителей
for n in range(190201, 190230 + 1):
  divs = [] # чистим список делителей
  for d in range(1,round(math.sqrt(n))): # перебор делителей
    if n % d == 0:
      divs.append(d) # добавляем делитель в список
      if d != n//d:
        divs.append(n//d)
      if len(divs) > divCount: break
  if len(divs) == divCount:
    divs.sort()
    divs.reverse()
    print(divs)

С++:

✎ Решение: Генерация списка делителей.
Общая идея:

Для каждого числа указанного диапазона генерируем список делителей.
Если длина списка равна четырем, выводим его.

PascalABC.net:	Python: for n in range(190201, 190230+1): divs = [d for d in range(1, n+1) if n % d == 0] if len(divs) == 4: divs.reverse() # реверсируем (по убыванию) print( *divs )
С++:

Ответ:

190201 17291 11 1
190202 95101 2 1
190214 95107 2 1
190219 853 223 1
190222 95111 2 1
190223 17293 11 1
190227 63409 3 1
190229 14633 13 1

Видеоразбор задания:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

25_10:

Напишите программу, которая ищет среди целых чисел, принадлежащих числовому отрезку [190201; 190280], числа, имеющие ровно 4 различных ЧЁТНЫХ делителя.
Выведите эти четыре делителя для каждого найденного числа в порядке убывания.

✍ Решение:

PascalABC.net:

begin
  var divs := new integer[4];
  for var n := 190201 to 190280 do
  begin
    var i := 0; // для индекса массива
    for var d := 1 to n do
    begin
      if (n mod d = 0) and (d mod 2 = 0) then 
      begin
        if i < 4 then
          divs[i] := d;
        inc(i);
      end;
      if i > 4 then 
        break; 
    end;
    if i = 4 then begin
      println(divs.Reverse())
    end;
  end;
end.

Python:

for n in range(190201,190280+1):
      divs = [] # чистим список делителей
      for d in range(1,n+1): #
        if n % d == 0 and d%2==0:
          divs = divs + [d] # добавляем делитель в список
          if len(divs) > 4: break
      if len(divs) == 4:
        divs.reverse()
        print(*divs)

С++:

✎ Решение: Генерация списка делителей.

Общая идея:

Для каждого числа указанного диапазона генерируем список делителей.
Если длина списка равна четырем, выводим его.

PascalABC.net:	Python: for n in range(190201, 190280+1): divs = [d for d in range(1, n+1) if n % d == 0 and d % 2 == 0] if len(divs) == 4: divs.reverse() print( *divs )
С++:

Ответ:

190226 838 454 2
190234 17294 22 2
190238 2606 146 2
190252 95126 4 2
190258 758 502 2
190274 27182 14 2
190276 95138 4 2

25_11:

Напишите программу, которая ищет среди целых чисел, принадлежащих числовому отрезку [394441; 394505], числа, имеющие максимальное количество различных делителей. Если таких чисел несколько, то найдите минимальное из них.
Выведите количество делителей найденного числа и два наибольших делителя в порядке убывания.

✍ Решение:

PascalABC.net:

begin
  var max := 0;
  var divsMax := new List<integer>; 
  for var n := 394441 to 394505 do
  begin
    var divs := new List<integer>; 
    for var d := 1 to n do
      if n mod d = 0 then 
        divs.Add(d);      
    if divs.Count > max then 
    begin
      max := divs.Count;
      divsMax := divs;
    end;
  end;
  divsMax.Reverse();
  print(max, divsMax[0], divsMax[1])
end.

Python:

maxim = 0  # нужное количество делителей
divsMax = []
for n in range(394441, 394505 + 1):
  divs = [] # чистим список делителей
  for d in range(1,n+1): # перебор делителей
    if n % d == 0:
      divs.append(d) # добавляем делитель в список
  if len(divs) > maxim: 
    maxim = len(divs)
    divsMax = divs
divsMax.reverse()
print(maxim,divsMax[0],divsMax[1])

С++:

✎ Решение (Генерация списка делителей):

PascalABC.net:

Python:

maxim=0
divsmax=[]
for n in range(394441, 394505+1):
    divs = [d for d in range(1, n+1) if n % d == 0] 
    if len(divs) > maxim:
        maxim = len(divs)
        divsmax = divs # сохраняем делители для числа с макс кол-вом дел-ей
divsmax.reverse()
print(maxim, divsmax[0], divsmax[1])

С++:

Ответ: 48 394450 197225

Видео

Простые числа

25_12:

Напишите программу, которая ищет среди целых чисел, принадлежащих числовому отрезку [3532000; 3532160], простые числа.
Выведите все найденные простые числа в порядке убывания, слева от каждого числа выведите его номер по порядку.

✍ Решение:

PascalABC.net:

begin
  var count := 0;
  for var n := 3532160 downto 3532000 do // цикл с конца 
  begin
    var flag := true; 
    for var d := 2 to n - 1 do // перебор делителей, начиная с двух до n-1
    begin
      if n mod d = 0 then begin // есть делитель помимо единицы и самого n
        flag := false; // число не простое     
        break;
      end;
    end;
    if flag = true then // если число простое
    begin
      inc(count);
      Println(count, n);
    end;
  end;
end.

Python:

count = 0
for n in range(3532160, 3532000-1, -1): # цикл с конца и с шагом (-1) 
  flag = True
  for d in range(2, n): # перебор делителей, начиная с двух
    if n % d == 0: # есть делитель помимо единицы и самого n
      flag = False # число не простое
      break
  if flag == True: # число простое
    count+=1
    print(count , n)

С++:

✎ Решение (оптимизированный вариант):

PascalABC.net:

begin
  var count := 0;
  for var n := 3532160 downto 3532000 do // цикл с конца 
  begin
    var flag := true; 
    var d := 2;
    while d * d <= n - 1 do // перебор делителей, начиная с двух
    begin
      if n mod d = 0 then begin // есть делитель помимо единицы и самого n
        flag := false;  // число не простое    
        break;
      end;
      d := d + 1;
    end;
    if flag = true then // если число простое
    begin
      inc(count);
      Println(count, n);
    end;
  end;
end.

Python:

count = 0
for n in range(3532160, 3532000-1, -1): # цикл с конца и с шагом (-1) 
      flag = True
      d = 2
      while d*d <= n-1: # перебор делителей, начиная с двух
            if n % d == 0: # есть делитель помимо единицы и самого n
                  flag = False # число не простое
                  break
            d+=1
      if flag == True: # число простое
            count+=1
            print(count , n)

С++:

Ответ:

Задания прошлых лет для тренировки (до 2021)

Задачи с поэлементной обработкой массива

25_1: ЕГЭ по информатике 2017 года (один из вариантов со слов выпускника):

Дан целочисленный массив из 20 элементов. Элементы массива могут принимать целые значения от 0 до 10 000 включительно. Опишите на естественном языке или на одном из языков программирования алгоритм, позволяющий найти и вывести количество элементов массива НЕ кратных 3.

Исходные данные объявлены так, как показано ниже. Запрещается использовать переменные, не описанные ниже, но использовать все описанные переменные не обязательно.

const N = 20;
var i,j,k:integer;
a:array [1..N] of integer; 
begin
for i:=1 to N do 
  readln(a[i]); 
…
end.

✍ Решение:

Рассмотрим заданный фрагмент решения:

в цикле со счетчиком i запрашиваются значения элементов массива, т.е. формируется массив;
из постановки задания видим, что необходимо найти количество чего-то, это значит, что нужно использовать переменную счетчик;
объявлены три целочисленных переменных: i, j, k; переменная i использована в первом цикле, значит для счетчика можно взять переменную k;
счетчик всегда нужно обнулять, поэтому следующим оператором будет:
определим, количество чего нам необходимо считать: количество элементов массива не кратных 3. Кратность можно определить через остаток от деления: если значение элемента массива при делении на 3 в остатке не возвращает 0, значит элемент не кратен трем;
остаток при делении в паскале — оператор mod. Поскольку необходимо просмотреть каждый элемент массива, то это нужно делать в цикле for;
переменная i уже использована в первом цикле for, значит, для очередного цикла возьмем неиспользованную переменную j:

for j:=1 to N do
  if a[j] mod 3 <> 0 then

если условие истинно (т.е. нашелся элемент массива, не кратный трем), то увеличиваем счетчик:
после цикла остается вывести значение счетчика, т.е. вывести количество элементов массива не кратных 3:

Результат:

k:=0;
for j:=1 to N do
  if a[j] mod 3 <> 0 then
    inc(k);
writeln(k);

Смотрите видео с подробным объяснением и разбором данного 25 задания:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

Задачи на обработку элементов массива с последующей заменой

25_3: Решение 25 задания ЕГЭ по информатике Демоверсия 2018:

Дан целочисленный массив из 30 элементов. Элементы массива могут принимать целые значения от 0 до 10000 включительно. Опишите на одном из языков программирования алгоритм, который находит количество элементов массива, больших 100 и при этом кратных 5, а затем заменяет каждый такой элемент на число, равное найденному количеству. Гарантируется, что хотя бы один такой элемент в массиве есть. В качестве результата необходимо вывести измененный массив, каждый элемент массива выводится с новой строчки.

Например, для массива из шести элементов: 4 115 7 195 25 106
программа должна вывести числа 4 2 7 2 25 106

Исходные данные объявлены так, как показано ниже на примерах для некоторых языков программирования. Запрещается использовать переменные, не описанные ниже, но разрешается не использовать некоторые из описанных переменных.

Паскаль:

const
N = 30;
var
a: array [1..N] of longint;
i, j, k: longint;
begin
	for i := 1 to N do
		readln(a[i]);
	...
end.

В качестве ответа Вам необходимо привести фрагмент программы, который должен находиться на месте многоточия. Вы можете записать решение также на другом языке программирования (укажите название и используемую версию языка программирования, например Free Pascal 2.6). В этом случае Вы должны использовать те же самые исходные данные и переменные, какие были предложены в условии.

Похожие задания для тренировки

✍ Решение:

k := 0;
for i := 1 to N do
	if (a[i] > 100) and (a[i] mod 5 = 0) then
		k:=k+1;
for i := 1 to N do begin
	if (a[i] > 100) and (a[i] mod 5 = 0) then
		a[i] := k;
writeln(a[i])
end

25_6:

Дан массив, содержащий неотрицательные целые числа. Необходимо вывести:

максимальный чётный элемент, если количество чётных элементов не меньше, чем нечётных;

максимальный нечётный элемент, если количество нечётных эле-ментов больше, чем чётных.

Например, для массива из шести элементов: 4 6 12 17 3 8
ответом будет 12 — наибольшее чётное число, поскольку чётных чисел в этом массиве больше

Исходные данные объявлены так, как показано ниже. Запрещается использовать переменные, не описанные ниже, но разрешается не использовать некоторые из описанных переменных.

Python:

# допускается также использовать
# целочисленные переменные j, k, m
a = []
n = 2000 // менять значение n нельзя
for i in range(0, n):
  a.append(int(input()))

✍ Решение:

a = []
n = 2000 // менять значение n нельзя
for i in range(0, n):
    a.append(int(input()))
j = 0 
k = 0 
m = 0 
for i in range(0, n):
	if a[i]%2 == 0:
		j+=1
	else:
		k+=1
if k>j:
	j = 0
	for i in range(0, n):
		if a[i]>j and a[i] % 2 != 0:
			j = a[i]
	print(j)
else:
	for i in range(0, n):
		if a[i]>m and a[i] % 2 == 0:
			m = a[i]
	print(m)

Задачи на обработку пар элементов массива (два подряд идущих)

25_4:

Дан целочисленный массив из 40 элементов. Элементы массива могут принимать целые значения от 0 до 10 000 включительно. Опишите на естественном языке или на одном из языков программирования алгоритм, позволяющий найти и вывести количество пар элементов массива, в которых одно из чисел двузначное. В данной задаче под парой подразумевается два подряд идущих элемента массива.

Например, для массива из семи элементов: 13; 323; 12; 33; 117 — ответ: 4.

const
  N = 40;
var
  a: array [1..N] of integer;
  i, j, k: integer;
begin
  for i := 1 to N do 
    readln(a[i]);
  ...
end.

✍ Решение:

k := 0;
for i := 1 to N - 1 do
 if ((a[i] < 100) and (a[i] > 9)) or ((a[i + l] < 100) and (a[i + 1] > 9)) then 
      inc(k);
writeln(k);

25_5:

Дан целочисленный массив из 20 элементов. Элементы массива могут принимать целые значения от -10 000 до 10 000 включительно. Опишите алгоритм, позволяющий найти и вывести количество пар элементов массива, в которых сумма элементов делится на 2, но не делится на 4. В данной задаче под парой подразумевается два подряд идущих элемента массива.

Python:

#  допускается также использовать
#  две целочисленные переменные
#  j и k
a = []
n = 20
for i in range(0, n):
  a.append(int(input()))

✍ Решение:

В первой строчке кода объявляется список а. Дальше, идет объявление переменной n = 20, она отвечает за размер массива.

При решении такого рода задач, необходимо помнить, что массив в Python — это список и это динамический тип данных. Кроме того, нумерация элементов массива начинается с 0.

Ниже мы видим инициализацию списка а. Мы должны дописать код дальнейшей программы, который последует после заполнения списка пользователем.
Итак, по условию мы должны находить пары элементов, сумма которых делится на 2, но не делится на 4, причем парами считаются соседние элементы, например: a[0] и a[1], a[1] и a[2].
Мы можем узнать, делится ли данный элемент на число, если остаток от деления на него равен 0, и не делится — в противном случае. Тогда сумма соседних элементов при делении на 2 должна давать остаток 0, а при делении на 4 наоборот — отличный от 0.
Введем цикл, который будет перебирать все элементы массива, считать сумму соседей и проверять истинность условия.

for i in range(0, n-1):
    j = a[i] + a[i+1]
    if j%2 == 0 and j%4 != 0:

Так как мы рассматриваем элемент a[i + 1], значит, цикл должен работать до n — 1, чтобы не выйти за границы диапазона массива.

Когда мы определились с условием, за счетчик возьмем переменную k, которую допустимо брать исходя из комментариев к программе.

...
 if j%2 == 0 and j%4 != 0:
        k+=1

Мы добавили допустимую переменную j, чтобы условный оператор выглядел компактнее.
Однако задача еще не решена. Во-первых, мы должны до цикла инициализировать счетчик k = 0. Так как иначе Python выдаст ошибку.

Дело в том, что мы пытаемся присвоить переменной k его же значение, но на 1 больше, но интерпретатор «не встречал» раньше переменной k, из-за чего возникает ошибка.

Кроме того, добавим вывод результата после цикла.
Таким образом, правильный вариант с учетом доработок:

a = []
n = 20
for i in range(0, n):
  a.append(int(input()))
k = 0
for i in range(0, n - 1):
    j = a[i] + a[i + 1]
    if j%2 == 0 and j%4 != 0:
        k += 1
print(k)

Задачи на обработку трёх подряд идущих элементов массива (тройки элементов массива)

25_2:

Дан целочисленный массив из 40 элементов. Элементы массива могут принимать целые значения от 0 до 10 000 включительно. Опишите на естественном языке или на одном из языков программирования алгоритм, позволяющий найти и вывести количество троек элементов массива, состоящих из равных между собой чисел. В данной задаче под тройкой подразумевается три подряд идущих элемента массива.

Например, для массива из семи элементов: 2; 2; 2; 4; 4; 4; 4 — ответ: 3.

const
  N=40;
var
  a: array[1..N] of integer;
  i, j, k:integer;
begin
  for i:=1 to N do
    readln(a[i]);
  ...
end.

✍ Решение:

из постановки задания видим, что необходимо искать количество чего-то, это значит, что нужно использовать переменную счетчик; возьмем для нее объявленную переменную k;
счетчик всегда нужно сначала обнулять, поэтому следующим оператором будет:
определим, количество чего нам необходимо считать: количество троек элементов массива, состоящих из равных между собой чисел. Т.е. необходимо сравнивать между собой каждые три подряд идущих элемента массива, например так:

if (a[i]=a[i+1]) and (a[i]=a[i+2]) then
    inc(k);

inc(k) — оператор, увеличивающий счетчик k на единицу;
условие необходимо выполнять в цикле, так как нужно проверить все элементы массива; цикл со счетчиком необходимо организовать от 1 до N-2, в противном случае индексы элементов a[i+2] выйдут за границы диапазона массива (например, при i = 40, получим … a[40+2], а 42-го элемента массива не существует, поэтому цикл надо делать до i = 38, т.е. N-2).

Результат:

for i:=1 to N-2 do
    if (a[i]=a[i+1]) and (a[i]=a[i+2]) then
      inc(k);
writeln(k);

Более подробное объяснение предлагаем посмотреть на видео:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

Задачи на поиск максимума, минимума элементов массива и другие

Источник

Сегодняшний урок посвящён 15 заданию из ЕГЭ по информатике 2022.

Темой этого урока связана с преобразованием логических выражений.

Теорию для преобразования логических выражений Вы можете посмотреть в этой статье. Как можно работать с логическими выражениями на питоне, можно прочитать в этой статье.

Перейдём к практике решения задач 15 задания из ЕГЭ по информатике 2022.

Задача (Неравенство, одна переменная)

Какое количество натуральных чисел удовлетворяет логическому условию:

¬(X² ≥ 9) ∨ ¬((X < 7) ∨ (X ≥ 10)) ?

Решение:

Первый способ (с помощью питона).

k=0
for x in range(1, 1000):
    if not(x**2 >= 9) or not((x < 7) or (x>=10)):
        k = k + 1
        
print(k)

Здесь перебираем с помощью цикла for натуральные числа от 1 до 1000.

Если логическое выражение выдаёт истину, то мы подсчитываем такой вариант.

Программа напечатает число 5.

Второй способ (с помощью рассуждений).

Натуральные числа — это целые, положительные числа. Например: 1, 2, 3, 4, и т. д.

Преобразуем первое выражение ¬(X² ≥ 9) = (X² < 9). Отрицание внесли в скобки. В этом случае знак, который находится в скобках, нужно поменять на противоположный.

Важно: Если было строгое неравенство, то оно станет нестрогим, и наоборот, если было неравенство нестрогим, то оно станет строгим.

Получается, что выражение (X² < 9) будет истинно только при двух значениях: X = 1, X = 2.

Во втором выражении ¬((X < 7) ∨ (X ≥ 10)) удобно применить формулу Де Моргана.

Формула де Моргана:

¬(A ∨ B) = ¬A ∧ ¬B

¬(A ∧ B) = ¬A ∨ ¬B

Преобразуем выражение по формуле де Моргана и внесём отрицание в скобки:

¬((X < 7) ∨ (X ≥ 10)) = ¬(X < 7) ∧ ¬(X ≥ 10) = (X ≥ 7) ∧ (X < 10)

Получилось выражение (X ≥ 7) ∧ (X < 10). Между двумя выражениями стоит логическое умножение. Значит, одновременно должны выполняться и первое неравенство, и второе. Таким образом, получается, что подходят три значение для выражения (X ≥ 7) ∧ (X < 10). Это X = 7, X = 8, X = 9.

Обратимся к самому начальному логическому условию. Там два выражения соединятся логическим сложением. Значит, мы должны объединить те случаи, когда у нас первое выражение становится истинным (X=1, X=2), и те случаи, когда второе выражение становится истинным (X = 7, X = 8, X = 9).

Получается всего 5 натуральных чисел удовлетворяют изначальному логическому условию.

Ответ: 5

Разберём ещё одну разминочную задачу для подготовки к ЕГЭ по информатике 2022.

Задача (Неравенство, две переменные)

Для какого наибольшего целого неотрицательного числа A выражение

(x ≥ A) ∨ (y ≥ A) ∨ (x * y ≤ 205)

тождественно истинно, т.е. принимает значение 1 при любых целых положительных x и y ?

Решение:

Первый способ (с помощью питона).

for A in range(0, 300):
    k=0
    for x in range(1, 301):
        for y in range(1, 301):
            if (x >= A) or (y >= A) or (x * y <= 205):
                k=k+1
    if k==90000:
        print(A)

В первом цикле перебираем значения для A. Здесь мы пытаемся подобрать ответ в диапазоне от 0 до 300. Этот диапазон меньше, чем в прошлой задаче. Потому что здесь три вложенных цикла, и если перебирать числа от 0 до 1000, то программа может работать очень долго. При необходимости можно указать другой диапазон.

Для каждого A устанавливаем счётчик k в ноль.

Затем перебираем все числа в диапазоне от 1 до 300 (включительно) для переменных x и y, тем самым имитируем фразу «для любых x и y».

Если логическое выражение сработает при каждом значении x и y, то считается, что значение A нам подходит, и в счётчике по окончанию вложенных циклов будет значение 90000 (300 * 300 = 90000).

Наибольшее число, которое напечатает программа равно 15.

Второй способ (с помощью рассуждений).

Здесь есть три выражения в скобках, которые соединены логическим сложением. При логическом сложении достаточно хотя бы одного выражения, где будет истина, чтобы всё общее выражение было истинно.

Если мы сделаем A слишком большим, к примеру A = 250, то найдутся такие x = 16, y = 16, при которых все три условия в скобках не будут выполняться, и, значит, всё общее выражение будет ложным.

Следовательно, нам нужно выбрать таким A, чтобы не было возможности подобрать x, y, при которых все три выражения ложны.

Сделаем так: пока x и y меньше A, должно «работать» третье выражение в скобках. Как только x или y сравняются с A — начинают «работать» первое или второе выражение.

До какого же максимального значения могут дойти x и y, чтобы перемножение этих двух чисел было меньше или равно 205 (x * y <= 205) ?

15 * 15 = 225
14 * 14 = 196

Получается, пока числа x и y меньше 15, «выручает» третье выражение (x * y ≤ 205), как только станут x ≥ 15 и y ≥ 15, будут «работать» первое и второе выражение.

Отсюда получаем, что максимальное число A = 15

Ответ: 15

Задача (Функция ДЕЛ)

Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m». Для какого наибольшего натурального числа А формула

¬ДЕЛ(x, А) → (ДЕЛ(x, 6) → ¬ДЕЛ(x, 9))

тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной x)?

Решение:

Первый способ (с помощью питона).

def D(n, m):
    if n%m==0:
        return True
    else:
        return False

for A in range(1, 1000):
    k=0
    for x in range(1, 1001):
        if D(x, A) or (not(D(x, 6)) or not(D(x, 9))):
            k=k+1
    if k==1000:
        print(A)

Здесь мы формируем функцию ДЕЛ (функцию D). Если n делится на m, то функция возвращает Истину, в противном случае функция возвращает Ложь.

Далее решаем примерно так же, как и в прошлых задачах: для каждого числа A перебираем все значения x. Следование расписываем по формуле A ⟶ B = ¬A ∨ B.

Наибольшее число здесь получается равно 18.

Второй способ (с помощью рассуждений).

Рассмотрим случай, когда в левой части логического выражения будет 1, а в правой 0. В остальных случаях беспокоится не за что, потому что вся формула будет выдавать истину.

Посмотрим, когда в правой части получается ноль. Функция ДЕЛ(x, 6) должна выдавать истину. Т.е. x должен делится на 6. А функция ¬ДЕЛ(x, 9) должна выдавать ноль. Т.е. без отрицания ДЕЛ(x, 9) должна выдавать истину. Значит, x так же делится на 9.

x делится на 6 => x = 2*3*n, n ∈ N
x делится на 9 => x = 3*3*n, n ∈ N

Чтобы выполнялся случай, когда в правой части получается ноль, икс должен быть равен x = 3*3*2*n (n ∈ N). Т.е. получается, что икс должен быть кратен 18.

Т.е. получается, что когда x делится на 18, в правой части логического выражения будет получатся ноль. Чтобы спасти ситуацию, мы должны в левой части логического выражения не получать 1. Следовательно, ¬ДЕЛ(x, А) должно выдавать ноль. Значит, ДЕЛ(x, А) должно выдавать 1. Таким образом, приходим к выводу, что A должно равняться 18.

Если получится опасная ситуация, когда x кратен 18, то она будет нейтрализована, ведь в левой части будет получатся ноль.

Ответ: 18

Ещё один важный тип задач 15 задания ЕГЭ по информатике 2022

Задача (Поразрядная конъюнкция)

Обозначим через m&n поразрядную конъюнкцию неотрицательных целых чисел m и n. Так, например, 14&5 = 1110₂ & 0101₂ = 4

Для какого наименьшего неотрицательного целого числа A формула

x&51 ≠ 0 → (x&A = 0 → x&25 ≠ 0)

тождественно истинна (то есть принимает значение 1 при любом неотрицательном целом значении переменной x)?

Решение:

Первый способ (с помощью питона).

for A in range(0, 1000):
    k=0
    for x in range(0, 1000):
        if x&51==0 or (x&A!=0 or x&25!=0):
            k=k+1

    if k==1000:
        print(A)

Здесь следование преобразовываем по формуле: A ⟶ B = ¬A ∨ B. Так же и A, и x неотрицательные числа. Поэтому мы перебираем их диапазон, начиная с нуля. Из-за этого в цикле, который перебирает переменную x, мы устанавливаем верхнюю границы равной 1000, а не 1001. Тогда тоже будет 1000 повторений в этом цикле.

Наименьшее число равно 34.

Второй способ (с помощью рассуждений).

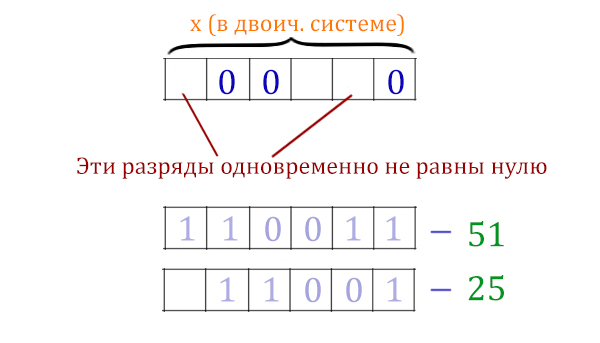
Переведём числа 51 и 25 в двоичную систему.

51 = 110011₂
25 = 11001₂

Формула будет тождественно ложна, когда

Этого допустить нельзя!

При каком x получается в левой выражении формулы истина ? Если у икса в двоичном представлении в тех разрядах, где у числа 51 стоят 1, будет хотя бы в одном месте 1.

Рассмотрим правое выражение формулы. Ноль получается в единственном случае:

Рассмотрим выражение x&25 ≠ 0. Чтобы в этом логическом выражении получился ноль, нужно x&25 = 0. Посмотрим на двоичное представление числа 25. В тех разрядах, где стоят единицы, у икс должны быть нули (для x&25 = 0).

Сформулируем окончательное условие для x, при котором возникает опасность превращение общей формулы в ложь.

Нам нужно «поломать эту песенку» с помощью x&A = 0. Т.е. нельзя допускать, чтобы это выражение было истинно.

Получается, что A = 100010₂. Это наименьшее из возможных число, при котором мы точно себя обезопасим от того, что вся формула будет ложна.

A = 100010₂ в десятичной системе будет 34.

Ответ: 34

Ещё один тип задач 15 задания ЕГЭ по информатике

Задача (числовая прямая)

На числовой прямой даны отрезки P=[5, 13] и Q=[8, 19]. Укажите наименьшую возможную длину такого отрезка A, что формула (¬(x ∈ P) → (x ∈ Q)) → (x ∈ A ) верна при любых значениях x.

Решение:

Первый способ (с помощью питона).

def F(a, b, x):
    if a <= x <= b:
        return True
    else:
        return False

mn=10**9

for a in  range(0, 200):
    for b in  range(a, 200):
        k=0
        for i in  range(-200, 200):
            x = i / 2
            if not((F(5, 13, x) or F(8, 19, x))) or F(a, b, x):
                k=k+1

        if k==400:
            mn= min(mn, b-a)

 print(mn)

Получается ответ 14. Более подробно, как решать задачи на ОТРЕЗКИ из 15 задания ЕГЭ по информатике на Python, можете посмотреть в этой статье.

Второй способ (с помощью рассуждений).

Если будут такие варианты:

То нам беспокоится не о чём. Потому что формула всегда будет истинна! (см. таблицу истинности для следования →)

Нас же будет интересовать этот случай.

При таком раскладе вся формула будет ложна! Нам нужно этого не допустить при любом значении x!

Единица получается в первом подвыражении в трёх случаях:

1) Случай

Выражение ¬(x ∈ P) получается ложно, когда (x ∈ P) будет истинно! Получается при x ∈ [5, 13] выражение ¬(x ∈ P) — ложно!

Выражение (x ∈ Q) ложно, когда x ∉ [8, 19]

Какой же минимальной длины должен быть отрезок A, чтобы этот случай не проходил при любом x ? При этом случае отрезок A должен быть равен [5, 8). Тогда левое выражение пусть и может стать единицей при x ∈ [5, 8), но выражение (x ∈ A) будет также равно 1 при x ∈ [5, 8)! И схема 1 → 0 не пройдёт. Будет 1 → 1.

Для 1 случая A=[5, .

2) Случай

При каких x выражение ¬(x ∈ P) обращается в ноль, мы уже рассматривали: x ∈ [5, 13].

Второе выражение «выдаёт» 1 при x ∈ [8, 19].

Получается, что при при x ∈ [8; 13] первое выражение в скобках в главной формуле будет тождественно истинно!

С помощью отрезка A нужно это нейтрализовать путём превращения второго выражения в скобках в главной формуле в 1, пока x ∈ [8; 13]. Значит, для этого случая A = [8; 13]

3) Случай

В выражении ¬(x ∈ P) единица получается, когда в выражении (x ∈ P) получается ноль. Тогда x ∉ [5, 13]!

Чтобы во втором выражении (x ∈ Q) была единица, нужно, чтобы x ∈ [8, 19].

Получается, что 3 случай выполняется, если x ∈ (13, 19].

С помощью отрезка A нужно этому противодействовать! Нужно чтобы выражение (x ∈ A) было всегда 1 при x ∈ (13, 19]. Тогда A должно быть (13, 19].

Следовательно, для третьего случая A=(13, 19].

Нам нельзя допустить ни одного случая! Поэтому, объединив все случаи, получаем, что A=[5, 19].

Длина отрезка равна 14.

Ответ: 14

Ещё одна задача про числовую прямую из банка тренировочных заданий ЕГЭ по информатике 2021.

Задача (Числовая прямая, закрепление)

На числовой прямой даны отрезки P=[5, 13] и Q=[8, 19]. Укажите наименьшую возможную длину такого отрезка A, что формула ((x ∈ P) ∧ ¬(x ∈ A)) → ((x ∈ Q) ∧ ¬(x ∈ A)) верна при любых значениях x.

Решение:

Первый способ (с помощью питона).

def F(a, b, x):
    if a <= x <= b:
        return True
    else:
        return False

mn=10**9

for a in range(0, 200):
    for b in range(a, 200):
        k=0
        for i in range(-200, 200):
            x = i / 2
            if not((F(5, 13, x) and not(F(a, b, x)))) or (F(8, 19, x) and not(F(a, b, x))):
                k=k+1

        if k==400:
            mn=min(mn, b-a)

print(mn)

Второй способ (с помощью рассуждений).

Формула может быть ложна, когда

Во всех остальных случаях, формула всегда верна.

Чтобы выражение ((x ∈ P) ∧ ¬(x ∈ A)) было тождественно 1, выражение (x ∈ P) обязательно должно быть тождественно 1. А, значит, x ∈ [5, 13] — это опасная зона, при которой появляется возможность обратить всю формулу в ноль!

Мы можем сразу пресечь эту опасность с помощью отрезка A. Выбрать такой отрезок, чтобы он всегда «выдавал» ложь при x ∈ [5, 13]. Для этого достаточно выбрать A=[5, 13]! Но вдруг его можно сделать ещё более маленьким за счёт правой части формулы ?

Предположим, что отрезок A сделали ещё меньшим. Тогда при каком-то x (x ∈ [5, 13]) выражение ¬(x ∈ A) будет «выдавать» 1! Причём такое же выражение стоит и в правой части формулы! Там тоже будет 1 для выражения ¬(x ∈ A).

Нас же в этом случае должно выручить выражение (x ∈ Q). Если оно «выдаст» 1 в этот «сложный» момент, то мы спасены! Ведь тогда получается, что правая часть всей формулы будет «выдавать» не 0, а 1. Посмотрим при каких x из отрезка [5, 13] приходит это спасение.

Видим, что в интервале x ∈ [8, 13] нас спасает выражение (x ∈ Q).

Значит, отрезок A можно сократить до A=[5, 8).

Длина отрезка будет равна 3!

Ответ: 3

Задачи для закрепления

Задача (Неравенство, две переменные, закрепление)

Для какого наибольшего целого неотрицательного числа A выражение

(x < A) ∧ (y < A) ∧ (x * y > 603)

тождественно ложно, т.е. принимает значение 0 при любых целых положительных x и y ?

Решение:

Первый способ (с помощью питона).

for A in range(0, 300):
    k=0
    for x in range(1, 301):
        for y in range(1, 301):
            if not( (x < A) and (y < A) and (x * y > 603) ):
                k=k+1
    if k==90000:
        print(A)

Т.к. выражение должно быть ЛОЖНО, то обернём логическое выражение в функцию not(). Видим, что программа не сильно отличается от прошлой задачи. Данный шаблон подходит для большинства задач подобного типа.

Наибольшее число получается равно 25.

Второй способ (с помощью рассуждений).

В этой задаче нужно, чтобы общее выражение было ложно!

Если мы поставим отрицание над всем выражением, то можно искать такое максимальное A, при котором всё выражение тождественно истинно, а не ложно!

¬((x < A) ∧ (y < A) ∧ (x * y > 603)) = ¬(x < A) ∨ ¬(y < A) ∨ ¬(x * y > 603)

Здесь применили формулу де Моргана! Т.е. каждое подвыражение получило отрицание + соединительная логическая операция (логическое умножение) сменилась на противоположную операцию (логическое сложение).

Внесём отрицание в скобки. Получается:

(x ≥ A) ∨ (y ≥ A) ∨ (x * y ≤ 603)

Получили ситуацию, как в прошлой задаче! Напомню, что теперь нужно, чтобы общее выражение было истинно.

Найдём максимальное число, до которого могут «подняться» x и y, чтобы ещё работало третье выражение!

Обратите внимание, что x и y — симметричны. Значит, что верхняя планка для x и y будет одно и тоже число.

Поэтому вспоминаем таблицу квадратов.

25 * 25 = 625
24 * 24 = 576

Получается, что максимальное число до которого могут «дойти» x и y, чтобы «работало» третье выражение, равно 24.

Тогда, начиная с 25 для x и y, должны работать первое и второе выражение.

Получается, что максимальное число для A равно 25.

Ответ: 25

Ещё одна задачка подобного типа из тренировочных упражнений 15 задания ЕГЭ по информатике.

Задача (Неравенство, две переменные, закрепление)

Для какого наименьшего целого числа A формула

(3 * x + y < A) ∨ (x < y) ∨ (16 ≤ x)

тождественно истинна, т.е. принимает значение 1 при любых целых неотрицательных x и y ?

Решение:

Первый способ (с помощью питона).

for A in range(-300, 300):
    k=0
    for x in range(1, 301):
        for y in range(1, 301):
            if (3*x + y < A) or (x < y) or (16 <= x):
                k=k+1
    if k==90000:
        print(A)

Наименьшее число равно 61. Здесь не сказали, что A принимает неотрицательные значения, поэтому мы включили в диапазон для A числа, которые меньше нуля. Из-за этого увеличилось время выполнения программы, но ответ получим за приемлемое время.

Второй способ (с помощью рассуждений).

Чтобы вся формула была тождественно истинна, нужно, чтобы хотя бы одно выражение «выдавало» истину, т.к. выражения в формуле соединяются с помощью логического сложения!

Взглянем на третье выражение. Пока x ≥ 16, всё идёт как надо. Третье выражение будет истинно, и, значит, вся формула будет истинна.

Но если x ≤ 15, то нужно, чтобы нас «спасало» первое или второе выражение.

Рассмотрим второе выражение. Пока y > x (x ≤ 15) => y > 15, у нас всё нормально, второе выражение будет истинно, и вся формула будет истинна.

Теперь обратим внимание на первое выражение. Оно должно нас «спасать», когда третье и второе выражение «не спасло»! Это возможно, если x ≤ 15 (иначе «спасло» бы третье выражение), а так же y ≤ 15 (иначе «спасало» бы второе выражение).

Но, чтобы первое выражение было всегда истинно при x ≤ 15 и y ≤ 15, мы должны подобрать число A при максимальных x и y (x=15, y=15)! Ведь для более маленьких значений выражение (3 * x + y < A) точно будет истинно.

Получается:

3 * 15 + 15 < A
60 < A

Нужно найти наименьшее число для A, при котором A > 60. Тогда там, где не «спасли» третье и второе выражение, точно «спасёт» первое выражение. Получается A = 61.

Ответ: 61

Задача (ЕГЭ по информатике, Москва, 2020)

Для какого наибольшего целого неотрицательного числа A выражение

(x > A) ∨ (y > x) ∨ (2 * y + x < 110)

тождественно истинно, то есть принимает значение 1 при любых целых неотрицательных x и y ?

Решение:

Первый способ (с помощью питона).

for A in range(0, 300):
    k=0
    for x in range(1, 301):
        for y in range(1, 301):
            if (x > A) or (y > x) or (2 * y + x < 110):
                k=k+1
    if k==90000:
        print(A)

Максимальное число получается равно 36.

Второй способ (с помощью рассуждений).

Пока y > x, второе подвыражение всегда истинно, значит, и всё выражение истинно.

Теперь будем рассматривать случай y ≤ x.

Рассмотрим третье подвыражение. Найдём максимальные значения для x и для y, которые они одновременно могут принимать, и при которых ещё выполняется третье условие.

Т.к. мы рассматриваем случай y ≤ x, то максимальное число для y будет x_max т.е. y_max = x_max.

Тогда

2 * x_max + x_max < 110

3 * x_max < 110

36 * 3 = 108
37 * 3 = 111

x_max = y_max = 36

Если x «перевалит» за 36, и при этом y ≤ x (иначе «спасает» второе подвыражение), то должно «спасать» первое выражение.

Получается, что наибольшее значение A будет равно 36.

Ответ: 36

Следующий тип задач часто можно встретить в тренировочных вариантах ЕГЭ по информатике 2022.

Задача (С функцией ДЕЛ, закрепление)

Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m». Для какого наибольшего натурального числа A формула

ДЕЛ(120, A) ∧ ((ДЕЛ(x, 70) ∧ ДЕЛ(x, 30)) → ДЕЛ(x, A))

тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной х)?

Решение:

Первый способ (с помощью питона).

def D(n, m):
    if n%m==0:
        return True
    else:
        return False

for A in range(1, 1000):
    k=0
    for x in range(1, 1001):
        if D(120, A) and (not(D(x, 70) and D(x, 30)) or D(x, A)):
            k=k+1
    if k==1000:
        print(A)

Наибольшее число получается равно 30.

Второй способ (с помощью рассуждений).

Рассмотрим левую часть логического выражения. Мы видим, что число 120 должно делится на A. Значит, для A уже есть некоторое ограничение (A <= 120).

Рассмотрим правую часть выражения. Изучим, когда она превращается в ноль. Тогда

Т.е. x должен делится на 70 и одновременно x должен делится на 30.

x = 70*n = 2*5*7*n (n ∈ N)

x = 30*n = 2*5*3*n (n ∈ N)

Чтобы одновременно выполнялись два условия, икс должен быть равен x = 2*5*7*3*n (n ∈ N).

Для того, чтобы правое выражение не превращалось в ноль, x как раз должен делится на число 2*5*7*3. Тогда будет 1->1. Т.е. число A должно равняться 2*5*7*3. Но мы сказали, что A <= 120, плюс, должно являться делителем числа 120. Значит, должны снизить значение для A.

Рассмотрим значение 2*5*7 для числа A (Предыдущее число, но без тройки). Для правой части оно подходит, т.к. «при малейшей» возможности превращения правого выражения в ноль (т.е. ДЕЛ(x, 70) = True), у нас будет спасаться ситуация, т.к. ДЕЛ(x, A) так же
будет равно 1. И снова получаем 1->1. Но это значение не подходит для левой части, ведь тогда A не является делителем числа 120.

Приходится брать число 2*5*3 (без семёрки). Здесь ситуация аналогично предыдущему случаю, только теперь это число является делителем числа 120.

В ответе напишем 30.

Ответ: 30

Задача (Поразрядная конъюнкция, закрепление)

Введём выражение M & K, обозначающее поразрядную конъюнкцию M и K (логическое «И» между соответствующими битами двоичной записи). Определите наименьшее натуральное число A, такое что выражение

(X & 49 ≠ 0) → ((X & 33 = 0) → (X & A ≠ 0))

тождественно истинно (то есть принимает значение 1 при любом натуральном значении переменной X)?

Решение:

Первый способ (с помощью питона).

for A in range(1, 1000):
    k=0
    for x in range(1, 1001):
        if (x&49==0) or ((x&33!=0) or (x&A!=0)):
            k=k+1

    if k==1000:
        print(A)

Наименьшее число равно 16.

Второй способ (с помощью рассуждений).

Переведём числа 49 и 33 в двоичную систему.

49₁₀ = 110001₂

33₁₀ = 100001₂

Рассмотрим случай, когда функция стремится превратится в ноль.

Чтобы левое выражение выдавало истину, икс должен иметь 1 (единицу) в первом разряде или во второй разряде, или в последнем разряде (в 6-ти битном числе).

Рассмотрим правое выражение. Посмотрим, когда выражение (X & 33 = 0) выдаёт истину. Первый бит и последний бит должен быть равен нулю. Т.е получается, что в 6-ти битном числе нас интересует второй бит. Если он будет равен 1 и при этом первый бит и последний будут равны 0, то возникает опасная ситуация, которую нужно спасть.

При выше описанных условиях выражение (X & A ≠ 0) должно выдавать истину. Тогда наименьшее A равно 10000₂ = 16₂.

Ответ: 16

Задача (числовая прямая, закрепление 2)

На числовой прямой даны два отрезка: P = [20, 30] и Q = [35, 60]. Найдите наименьшую возможную длину отрезка A, при котором формула

¬(x ∈ A) ∧ ((x ∈ P) ∨ (x ∈ Q))

тождественно ложна, то есть принимает значение 0 при любых x.

Решение:

Первый способ (с помощью питона).

def F(a, b, x):
    if a <= x <= b:
        return True
    else:
        return False

mn=10**9

for a in range(0, 200):
    for b in range(a, 200):
        k=0
        for i in range(-200, 200):
            x = i / 2
            if not(not(F(a, b, x)) and (F(20, 30, x) or F(35, 60, x))):
                k=k+1

        if k==400:
            mn=min(mn, b-a)

print(mn)

Ответ будет 40.

Второй способ (с помощью рассуждений).

Рассмотрим наоборот, когда логическое выражение выдаёт истину.

В правой части получается 1, когда x ∈ P или x ∈ Q. Именно в эти моменты выражение ¬(x ∈ A) должно спасать ситуацию и выдавать 0. Тогда без отрицания (x ∈ A) должно выдавать 1. Чтобы покрыть два отрезка, берём A=[20; 60].

Минимальная длина получается 60-20=40.

Ответ: 40

На этом всё! Увидимся в новых уроках по подготовке к ЕГЭ по информатике!

Добрый день! А как в 5 задаче (про числовую прямую) получился ответ 14?
В конце же получается, что A принадлежит [5, 19], то есть длина отрезка 15.

5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 — 15 штук
Или я что-то неправильно понял?

Считается количество единиц, а не сколько целых чисел в этом отрезке.

И в самой последней задаче на закрепление, у вас, видимо, та же ошибка. Не 40, а 41 должно быть?

Как решать 15 задание с «~» тильдой на питоне?
Как например это задание:
На числовой прямой даны два отрезка: P = [7, 14] и Q = [9, 11]. Укажите наибольшую возможную длину промежутка A, для которого формула
((x ∈ P) ~ (x ∈ Q)) → ¬(x ∈ A)

Грамотное объяснение. Безумно здорово, что есть объяснения как на питон (перебором) так и чисто в математической форме, потому что в информатике оба подхода, мне кажется, равносильны. Спасибо

Источник

Что это такое?

Здесь представлены материалы для подготовки к ЕГЭ по информатике.
В отличие от известной литературы, для большинства задач из демо-вариантов ЕГЭ
сравниваются несколько способов решения,
анализируются их достоинства и недостатки, возможные проблемы и
«ловушки». Приведены рекомендации, позволяющие выбрать
эффективные методы решения каждой конкретной задачи.

Автор признателен
О.А. Тузовой (г. Санкт-Петербург) за обсуждение
этих материалов и конструктивную критику. Спасибо всем, кто присылал и
присылает мне замечания, предложения, сообщения об опечатках и неточностях.

Особая благодарность Н.Н. Паньгиной (г. Сосновый Бор) за
взаимовыгодное сотрудничество и разностороннюю поддержку проекта.

Автор будет благодарен за новые отзывы по поводу представленных
здесь материалов для подготовки к ЕГЭ по информатике.
Если вы заметили ошибку или у вас просто есть что
сказать по существу вопроса, пишите.

Тренажёр компьютерного ЕГЭ

ЕГЭ по информатике в 2023 году будет проводиться в компьютерной форме.
На этом сайте вы можете попробовать, как это будет выглядеть в
тренажёре. Он является копией официального тренажёра,
но позволяет загружать любой вариант из генератора. Кроме того, после завершения
пробного экзамена вы узнаете, сколько баллов вы набрали бы на ЕГЭ, если бы
отправили такие ответы. Попробуйте:

Авторские семинары

Если вы хотите пригласить авторов учебника в свой город
для проведения выездного семинара,
пишите.

Робот-Blockly

Робот-Blockly — это версия исполнителей Робот и Водолей,
программы для которых составляются из готовых блоков, как в Scratch. Это избавляет учеников от
синтаксических ошибок, которые неминуемо возникают при ручном наборе текстовой программы.
Программа подходит для вводного курса алгоритмизации в 5-6 (и даже более старших) классах.
У программы есть оффлайн-версия, которую можно использовать
без доступа к Интернету. Вы можете создавать свои наборы задач, а
не только использовать готовые.

Коллеги тащат то, что не приколочено…

Мартынов Антон Иванович, председатель предметной комиссии по информатике Ульяновской области,
опубликовал представленные здесь рекомендации по решению задач части C под своим именем в
официальном аналитическом отчете (Ульяновск, 2009).

Актуальные публикации

В.С. Попов.

Новая задача ЕГЭ по информатике № 22: решение с помощью графа
// Потенциал: Математика, Физика, Информатика, № 8, 2022.
К.Ю. Поляков.

Особенности решения задач 25 и 26 в компьютерном
ЕГЭ по информатике. Материалы вебинара для учителей г. Сочи, 24.03.2021.
К.Ю. Поляков.

Динамическое программирование в задачах обработки последовательностей ЕГЭ по информатике.
К.Ю. Поляков.

Задачи на анализ логических выражений в ЕГЭ по информатике. //
Информатика в школе, № 9, 2019, с. 29–35.
А.Н. Сидоров

Задача 18 ЕГЭ по информатике: логическое выражение с делимостью.
Н.Л. Конина

Задачи 18 с делимостью.
Н.И. Герасименко

Задачи 18 с делителями в КИМ ЕГЭ по информатике.
К.Ю. Поляков

Линейное (и нелинейное) программирование в задаче 18 ЕГЭ по информатике (презентация).
К.Ю. Поляков,

Битовые операции в задаче 18 КИМ ЕГЭ по информатике. Часть 2.
К.Ю. Поляков,

Множества и логика в задачах ЕГЭ //
Информатика, № 10, 2015, с. 38-42.
Е.А. Мирончик.

Алгебра предикатов и построение геометрических моделей на ЕГЭ по информатике //
Информатика, № 3, 2019, с. 40-47.

См. также полный список статей.

Что еще посмотреть?

Тренажёр для подготовки к компьютерному ЕГЭ
Тесты для подготовки к ЕГЭ (для системы NetTest)
Онлайн-тесты для подготовки к ЕГЭ
Генератор тренировочных вариантов ЕГЭ
Программное обеспечение
Статьи, презентации
Видеоматериалы
Дополнительные материалы
Материалы прошлых лет (демо-варианты, анализ, разбор задач)
Вопросы и ответы
Отзывы

Новости теперь и в
Telegram-канале

9 марта 2023 г.
Исправлено условие задаче 8.330.
Исправлен ответ к задаче 14.403.

5 марта 2023 г.
Новые задачи для тренировки 8, 9.

4 марта 2023 г.
    Новые задачи для тренировки 14.
    Новые задачи для тренировки 1-3, 7-9, 12-16, 19-25, 27 (А. Богданов).
    Новая задача для тренировки 8 (А. Малышев).
    Новая задача для тренировки 17 (Д. Статный).

3 марта 2023 г.
Новые задачи для тренировки 26.
Новые задачи для тренировки 23 (Д. Муфаззалов).

2 марта 2023 г.
Новые задачи для тренировки 27.

28 февраля 2023 г.
Новая задача для тренировки 27 (А. Бойко).

25 февраля 2023 г.
    Новые задачи для тренировки 17 (И. Митин).
    Новые задачи для тренировки 23, 24, 25.
    Новые задачи для тренировки 23 (М. Шагитов).
    Новая задача для тренировки 27 (А. Рогов).

24 февраля 2023 г.
Новые задачи для тренировки 25, 26 (А. Рогов).

23 февраля 2023 г.
Изменено условие и ответ к задаче 26.94.

Приложение для ОС Android

Багрепорты, замечания, предложения можно присылать на
форум.

Официальные материалы

Тренажёры для подготовки к компьютерному ЕГЭ (КЕГЭ)

Лицензионное соглашение

Все опубликованные ниже материалы для
подготовки к ЕГЭ по информатике могут быть свободно использованы
в некоммерческих целях при условии сохранения авторства.

Без письменного согласия автора ЗАПРЕЩАЕТСЯ:

1) публикация материалов в любой форме, в том числе размещение материалов на других Web-сайтах;
2) распространение неполных или измененных материалов;
3) включение материалов в сборники на любых носителях информации;
4) получение коммерческой выгоды от продажи или другого использования материалов.

Использование и скачивание материалов означает, что вы приняли условия этого лицензионного соглашения.

Скачать все сразу

Пароль к архиву — kpolyakov.spb.ru

Информация

Системы счисления

Логика

Пользовательский курс

Алгоритмизация и основы программирования

Ответы и решения

Источник

11:29 10.03.2023
(обновлено: 12:21 10.03.2023)

https://ria.ru/20230310/ekzameny-1856951080.html

Вице-спикер Госдумы призвал обсудить отмену ЕГЭ

Вице-спикер Госдумы призвал обсудить отмену ЕГЭ — РИА Новости, 10.03.2023

Вице-спикер Госдумы призвал обсудить отмену ЕГЭ

Тема отмены ЕГЭ нуждается во всестороннем обсуждении, и чем скорее оно начнется, тем лучше, заявил вице-спикер Госдумы Петр Толстой («Единая Россия»). РИА Новости, 10.03.2023

2023-03-10T11:29

2023-03-10T12:21

общество

россия

петр толстой

анзор музаев

единая россия

госдума рф

федеральная служба по надзору в сфере образования и науки (рособрнадзор)

единый государственный экзамен (егэ)

/html/head/meta[@name=’og:title’]/@content

/html/head/meta[@name=’og:description’]/@content

https://cdnn21.img.ria.ru/images/07e6/06/08/1794077403_0:97:3072:1825_1920x0_80_0_0_8fb2880b77c924e87b1e22d2dbd1a31e.jpg

МОСКВА, 10 мар — РИА Новости. Тема отмены ЕГЭ нуждается во всестороннем обсуждении, и чем скорее оно начнется, тем лучше, заявил вице-спикер Госдумы Петр Толстой («Единая Россия»). Ранее глава Рособрнадзора Анзор Музаев заявил журналистам, что отмена ЕГЭ в России в связи с выходом из Болонской системы не обсуждается. Толстой, комментируя сообщение, тогда отметил, что тема отмены ЕГЭ обсуждается, систему будут «демонтировать» постепенно. «Тема отмены ЕГЭ нуждается во всестороннем обсуждении. И чем раньше оно начнется, тем лучше», — написал он в телеграм-канале. По словам политика, у системы на практике оказалось больше недостатков, чем достоинств. При этом он назвал попыткой «чиновников ничего не менять» отрицание того, что ЕГЭ появилось в результате «так называемых реформ образования». «А менять эту систему надо, такова воля большинства наших избирателей», — резюмировал он.

https://ria.ru/20230307/ege-1856449728.html

https://ria.ru/20230304/ege-1855788901.html

россия

РИА Новости

internet-group@rian.ru

7 495 645-6601

ФГУП МИА «Россия сегодня»

https://xn--c1acbl2abdlkab1og.xn--p1ai/awards/

2023

Новости

ru-RU

https://ria.ru/docs/about/copyright.html

https://xn--c1acbl2abdlkab1og.xn--p1ai/

РИА Новости

internet-group@rian.ru

7 495 645-6601

ФГУП МИА «Россия сегодня»

https://xn--c1acbl2abdlkab1og.xn--p1ai/awards/

https://cdnn21.img.ria.ru/images/07e6/06/08/1794077403_0:0:2732:2048_1920x0_80_0_0_40dd2897d8e6452d54553e41bdd5df84.jpg

РИА Новости

internet-group@rian.ru

7 495 645-6601

ФГУП МИА «Россия сегодня»

https://xn--c1acbl2abdlkab1og.xn--p1ai/awards/

общество, россия, петр толстой, анзор музаев, единая россия, госдума рф, федеральная служба по надзору в сфере образования и науки (рособрнадзор), единый государственный экзамен (егэ)

Общество, Россия, Петр Толстой, Анзор Музаев, Единая Россия, Госдума РФ, Федеральная служба по надзору в сфере образования и науки (Рособрнадзор), Единый государственный экзамен (ЕГЭ)

Вице-спикер Госдумы призвал обсудить отмену ЕГЭ

Вице-спикер Госдумы Толстой призвал не медлить с обсуждением отмены ЕГЭ

МОСКВА, 10 мар — РИА Новости. Тема отмены ЕГЭ нуждается во всестороннем обсуждении, и чем скорее оно начнется, тем лучше, заявил вице-спикер Госдумы Петр Толстой («Единая Россия»).

Ранее глава Рособрнадзора Анзор Музаев заявил журналистам, что отмена ЕГЭ в России в связи с выходом из Болонской системы не обсуждается. Толстой, комментируя сообщение, тогда отметил, что тема отмены ЕГЭ обсуждается, систему будут «демонтировать» постепенно.

Рособрнадзор заявил, что не обсуждает отмену ЕГЭ

«Тема отмены ЕГЭ нуждается во всестороннем обсуждении. И чем раньше оно начнется, тем лучше», — написал он в телеграм-канале.

По словам политика, у системы на практике оказалось больше недостатков, чем достоинств. При этом он назвал попыткой «чиновников ничего не менять» отрицание того, что ЕГЭ появилось в результате «так называемых реформ образования».

«А менять эту систему надо, такова воля большинства наших избирателей», — резюмировал он.

В Госдуме попросили Голикову рассмотреть возможность отмены ЕГЭ

Источник