По вкладу «А» банк в конце каждого года планирует увеличивать на 10% сумму, имеющуюся на вкладе в начале года, а по вкладу «Б» — увеличивать эту сумму на 9% в первый год и на одинаковое целое число n процентов и за второй, и за третий годы. Найдите наименьшее значение n, при котором за три года хранения вклад «Б» окажется выгоднее вклада «А» при одинаковых суммах первоначальных взносов.
Спрятать решение
Решение.
Пусть на каждый тип вклада была внесена одинаковая сумма S . На вкладе «А» каждый год сумма увеличивается на 10%, то есть увеличивается в 1,1 раза. Поэтому через три года сумма на вкладе «А» будет равна:
Аналогично сумма на вкладе «Б» будет равна:
где n — некоторое натуральное число процентов.
По условию требуется найти наименьшее натуральное решение неравенства:
При неравенство
верно, а при неравенство
неверно, как и при всех меньших n.
Ответ: 11.
Спрятать критерии
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получен верный ответ | 2 |
| Верно построена математическая модель | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 2 |
Свойства числа 516404
| Множители | 2 * 2 * 7 * 18443 | |
| Делители | 1, 2, 4, 7, 14, 28, 18443, 36886, 73772, 129101, 258202, 516404 | |
| Количество делителей | 12 | |
| Сумма делителей | 1032864 | |
| Предыдущее целое | 516403 | |
| Следующее целое | 516405 | |
| Простое число? | NO | |
| Предыдущее простое | 516391 | |
| Следующее простое | 516407 | |
| 516404th простое число | 7628627 | |
| Является числом Фибоначчи? | NO | |
| Число Белла? | NO | |
| Число Каталана? | NO | |
| Факториал? | NO | |
| Регулярное число? | NO | |
| Совершенное число? | NO | |
| Полигональное число (s < 11)? | NO | |
| Двоичное | 1111110000100110100 | |
| Восьмеричная | 1760464 | |
| Двенадцатеричный | 20aa18 | |
| Шестнадцатиричная | 7e134 | |
| Квадрат | 266673091216 | |
| Квадратный корень | 718.61255207518 | |
| Натуральный логарифм | 13.154644683858 | |
| Десятичный логарифм | 5.7129895975975 | |
| Синус | 0.99998837030985 | |
| Косинус | 0.0048227839523475 | |
| Тангенс | 207.34670683788 |
Deutsch
English
Español
Français
Italiano
Nederlands
Polski
Português
Русский
中文
日本語
한국어
Используя этот сайт, вы подтверждаете свое согласие с Условиями и соглашениями и Политикой приватности.
© 2023
numberempire.com
Все права защищены
ЕГЭ по математике — Профиль 2022. Открытый банк заданий с ответами.
Тренировочный вариант заданий 31926141 решу ЕГЭ 2023 по русскому языку 11 класс с ответами, проблема текста и пример сочинения.
Решу вариант ЕГЭ 2023 по русскому языку онлайн на сайте
вариант31926141-решу-егэ2023-русский-ответы
Задания и ответы для варианта
Задание 1. Самостоятельно подберите притяжательное местоимение, которое должно стоять на месте пропуска во втором предложении текста. Запишите это местоимение. Целесообразное и незатрудненное применение языка в целях общения обеспечивают качество «хорошей» речи: точность, чистота, логичность, выразительность, богатство, уместность. Точность — соответствие смыслового содержания речи и информации, которая лежит в […] основе. Точность речи связывается с точностью словоупотребления, с правильным использованием многозначных слов, синонимов, антонимов, омонимов.
Важнейшее условие точности речи — это соблюдение лексических норм. Речь является точной, если говорящий отбирает те слова и конструкции, которые точнее других передают оттенки смысла, существенные именно для данного высказывания. Чистота означает отсутствие в речи чуждых литературному языку элементов (диалектных, профессиональных, жаргонных и др.) Логичность — это выражение в смысловых связях компонентов речи связей и отношений между частями компонентами мысли. Выразительностью речи называется качество, возникающее в результате реализации заложенных в языке выразительных возможностей. Выразительность может создаваться языковыми единицами всех уровней.
Кроме того, существуют специфические изобразительные свойства языка (тропы, стилистические фигуры), делающие высказывание ярким, образным, эмоциональным. Речевой опыт каждого из нас говорит о том, что по степени воздействия на наше сознание речь не одинакова. Две лекции, прочтенные на одну и ту же тему, оказывают на человека совершенно разный эффект. Эффект зависит от степени выразительности речи. Человек — существо социальное, а ведущим коммуникативным средством является речь. Неслучайно Декарт писал: «Я мыслю, следовательно, я существую».
Задание №2 № 45134 В тексте выделено пять слов. Укажите варианты ответов, в которых лексическое значение выделенного слова соответствует его значению в данном тексте. Запишите номера ответов.
- 1 ) КАЧЕСТВО. То или иное свойство, достоинство, степень пригодности кого-чего-нибудь. Качество работы.
- 2) БОГАТСТВО. Обилие материальных ценностей. Накопил несметные богатства.
- 3 ) ЭЛЕМЕНТ. Составная часть какого-либо целого. Элементом композиции художественного произведения является экспозиция.
- 4) СВЯЗЬ. Отрасль экономики, предоставляющей коммуникационные услуги. Телефонная связь.
- 5) ВОЗМОЖНОСТЬ. Средство, условие, необходимое для осуществления чего-нибудь, возможное обстоятельство. Большие возможности. Возможность упущена.
Ответ: 135
Задание 3 № 38849 Укажите варианты ответов, в которых даны верные характеристики фрагмента текста. Запишите номера этих ответов.
- 1) В тексте частотны существительные с определенным типом лексического значения и морфологическими характеристиками. Например, существительные, выражающие понятие признака, состояния, изменения на -ние, -ость, -ство, -ие, -ция (выразительность, точность, применение, богатство, информация). Это признак научного стиля.
- 2) Сферой применения данного текста является сфера законодательства, делопроизводства, административно правовой деятельности.
- 3) В тексте представлены в равной степени повествование и рассуждение.
- 4) Типичным для данного текста научного стиля является употребление именного сказуемого, что способствует созданию именного характера текста. Примеры таких предложений: «Точность — соответствие смыслового содержания речи и информации, которая лежит в … основе», «Логичность — это выражение в смысловых связях компонентов речи связей и отношений между частями компонентами мысли».
- 5) Отвлеченный, обобщенный характер текста проявляется на лексическом уровне в том, что в нем широко употребляются слова с абстрактным значением: реализация, применение. Слова бытового характера также приобретают в научном тексте обобщенное, часто терминологическое значение, например, слова: речь, язык, фигура — являются в контексте содержания терминами.
Ответ: 145
Задание 4 № 45332 Укажите варианты ответов, в которых верно выделена буква, обозначающая ударный гласный звук. Запишите номера ответов.
- манЯщий
- каталОг
- добелА
- избАлованный
- пЕрчить
Ответ: 1235
Задание 5 № 3807 В одном из приведённых ниже предложений НЕВЕРНО употреблено выделенное слово. Исправьте лексическую ошибку, подобрав к выделенному слову пароним. Запишите подобранное слово. Это комнатное растение отличается ЭФФЕКТНОЙ окраской листьев. ПРОИЗВОДСТВЕННЫЕ помещения соответствуют нормативам по освещённости. ПОКУПАТЕЛЬНАЯ способность населения зависит от многих факторов. На ДИПЛОМАТИЧНУЮ встречу приглашены политики дружественных стран. Истоки современного ГУМАНИЗМА восходят к эпохе Возрождения.
Ответ: дипломатический
Задание 6 № 16738 Отредактируйте предложение: исправьте лексическую ошибку, заменив неверно употреблённое слово. Запишите подобранное слово, соблюдая нормы современного русского литературного языка. Хороший руководитель, без всякого сомнения, заботится о своих подчинённых и стремится показывать им образец во всём.
Ответ: пример
Задание 7 № 4666 В одном из выделенных ниже слов допущена ошибка в образовании формы слова. Исправьте ошибку и запишите слово правильно.
- капает со СВЕЧЕЙ
- НАИБОЛЕЕ удачно
- СЕМЬЮДЕСЯТЬЮ помощниками
- ЕХАЙ прямо
- новых ПОЛОТЕНЕЦ
Ответ: поезжай
Задание 9 № 45786 Укажите варианты ответов, в которых во всех словах одного ряда пропущена одна и та же буква. Запишите номера ответов.
- 1) заж..мать, оп..раться, прим..рение (сторон)
- 2) к..сательная, оз..рение, отв..рить (овощи)
- 3) г..ревать, зар..сли, прик..снуться
- 4) изл..жить, несг..раемый, к..сички
- 5) п..рила, зам..реть, ст..листический
Ответ: 1234
Задание 10. Укажите варианты ответов, в которых во всех словах одного ряда пропущена одна и та же буква. Запишите номера ответов.
- 1) не..держанный, бе..шумный, чере..страничный
- 2) с..митировать, сверх..дея, супер..нтеллектуальный
- 3) пр..сыщенный, беспр..кословно, пр..одолеть
- 4) раз..гнавшись, под..брать, пр..говорить (два часа)
- 5) от..явленный, с..ёжиться, нав..ючивать
Ответ: 134
Задание 11. № 16716 Укажите варианты ответов, в которых в обоих словах одного ряда пропущена одна и та же буква. Запишите номера ответов.
- 1) вкрадч..вый, отапл..вать
- 2) продл..вать, син..ва
- 3) леденц..вый, ухаж..р
- 4) экзотич..ский, увес..стый
- 5) свидетельн..ца, задабр..ваемый
Ответ: 125
Задание 12 № 16744 Укажите варианты ответов, в которых в обоих словах одного ряда пропущена одна и та же буква. Запишите номера ответов.
- 1) дремл..щий, (они) гон..тся (друг за другом)
- 2) установл..нный, неуправля..мый
- 3) (они) шепч..тся, маш..щий (крыльями)
- 4) (вы) остан..тесь, встрет..вшись
- 5) насто..нный, леле..мый
Ответ: 23
Задание 13. № 14871 Определите предложение, в котором НЕ со словом пишется СЛИТНО. Раскройте скобки и выпишите это слово. Эта комната только кажется большой, а так она ничуть (НЕ)ПРОСТОРНЕЕ нашей. (НЕ)СУМЕВШИЙ справиться с эмоциями гость вёл себя грубо. Оля что-то всё время (НЕ)ДОГОВАРИВАЛА нам, скрывала. Он пытался меня убедить, что моя попытка уйти от разговора — это (НЕ)ЧТО иное, как боязнь смотреть правде в глаза. Всё это я рассказал просто, спокойно, (НЕ)СПЕША.
Ответ: недоговаривала
Задание 14. № 9333 Определите предложение, в котором оба выделенных слова пишутся СЛИТНО. Раскройте скобки и выпишите эти два слова. Пока дорога шла близ болот, (В)ВИДУ соснового леса, всё время отклоняясь (В)БОК, мы то и дело вспугивали целые выводки уток, приютившихся здесь. (В)ТЕЧЕНИЕ целого дня наш отряд с трудом шёл вперёд, двигаясь (НА)ОЩУПЬ. В лесу (ПО)ОСЕННЕМУ пахло сыростью, было холодно и промозгло, и мы, ЧТО(БЫ) согреться, развели костёр. (ПО)СРЕДИ комнаты стоял огромный дубовый стол, а ТАК(ЖЕ) крепкие, под стать столу, тяжёлые стулья. Маруся долго не могла понять, (ПО)ЧЕМУ никто вот так прямо, (С)ХОДУ не может дать ответ на мучивший её вопрос.
Ответ: посреди также
Задание 15. № 9253 Укажите все цифры, на месте которых пишется одна буква Н. Ю(1)ая красавица смущё(2)о улыбнулась и выронила золочё(3)ую пудре(4)ицу из рук.
Ответ: 134
Задание 16 № 250 Расставьте знаки препинания. Укажите предложения, в которых нужно поставить ОДНУ запятую. Запишите номера этих предложений.
- 1) Работа шла быстро и весело и была вовремя закончена.
- 2) Причастия способны как образно описать предмет или явление так и представить его признак в динамике.
- 3) Алогичность соединения слов создаёт особый психологический эффект и приковывает внимание читателя и усиливает образность.
- 4) Три раза зимовал он в Мирном и каждый раз возвращение домой казалось ему пределом человеческого счастья.
- 5) Довольно скоро он обжился в этом районе да подружился с соседями.
Ответ: 24
Задание 17. № 4411 Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых) в предложении должна(-ы) стоять запятая(-ые). Не растерявшийся и в этой ситуации Остап (1) уклонился вправо (2) отыскивая глазами лодку (3) с сидящим в ней (4) верным Ипполитом Матвеевичем.
Ответ: 2
Задание 18. № 17011 Расставьте знаки препинания: укажите цифру(-ы), на месте которой(-ых) в предложениях должна(- ы) стоять запятая(-ые). Такая (1) жизненная полоса (2) А (3) может быть (4) предначертанье свыше. Других я различаю (5) голоса, А собственного голоса не слышу. И (6) всё же (7) он, как близкая родня, Единственный, кто согревает в стужу. До смерти будет он внутри меня. Да и (8) потом (9) не вырвется наружу. (Р. Рождественский)
Ответ: 24
Задание 19. № 18954 Расставьте знаки препинания: укажите цифру(-ы), на месте которой(-ых) в предложении должна(-ы) стоять запятая(-ые). Неподалёку находилось поместье (1) владельцы (2) которого (3) мало что заслужили, кроме худой о себе славы по округе (4) где их не любили (5) несмотря на то что (6) никто уже даже не мог сказать (7) из-за чего (8) именно появилась такая ненависть.
Ответ: 1457
Задание 20. № 13771 Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых) в предложении должна(-ы) стоять запятая(-ые). Он только чувствовал (1) что поза у него была неестественная, напряжённая (2) и (3) что (4) поэтому офицеры (5) которые умеют держаться в седле (6) должны нравиться Манюне больше, чем он.
Ответ: 156
Задание 21. № 17042 Найдите предложения, в которых тире ставится в соответствии с одним и тем же правилом пунктуации. Запишите номера этих предложений. (1)Севернее города Одинцово раскинулся Подушкинский лесопарк — живописная лесная территория. (2)Этот лес получил своё название благодаря селу Подушкино и лично Ивану Владимировичу Подушке — помещику, которому принадлежали эти земли в XV веке. (3)Село Подушкино и прилегающие к нему леса не раз меняли хозяев: так, одно время этими угодьями владел Илья Данилович Милославский, дед царевны Софьи и двух царей — Фёдора III и Ивана V. (4)А в XIX веке в Подушкино провели железную дорогу — здесь появились дачники. (5)Сейчас, прогуливаясь по парку, можно увидеть двухсотлетние дубы, однако бóльшая часть сохранившихся на сегодня деревьев появилась 50−80 лет назад. (6)По оценкам биологов, в Подушкинском лесу обитает 73 вида животных, причём помимо привычных белок и зайцев в лесной глуши можно увидеть норы барсука и встретить орешниковую соню — небольшого грызуна, занесённого в Красную книгу. (7)Зелёные дятлы, глухари, рябчики, чёрные коршуны и сапсаны — эти редкие птицы также обитают на территории Подушкинского лесопарка. (По материалам интернета)
Ответ: 1236
Задание 22 № 750 Какие из высказываний соответствуют содержанию текста? Укажите номера ответов. Цифры укажите в порядке возрастания.
- 1) Чем больше дерево, тем труднее его сломать.
- 2) Вся прожитая жизнь сохраняется в памяти человека.
- 3) Жизнь рассказчика далека от ясности.
- 4) Дерево не может делать ошибок.
- 5) Человек может достигнуть совершенства даже после совершения многочисленных ошибок.
Ответ: 234
Задание 26. № 760 Прочитайте фрагмент рецензии. В нём рассматриваются языковые особенности текста. Некоторые термины, использованные в рецензии, пропущены. Вставьте на места пропусков цифры, соответствующие номеру термина из списка. «(А) (предложения 17—20) помогает автору передать основную мысль текста. Сравнивая человеческую жизнь с жизнью дерева, автор в 15-м предложении использует (Б) («шагал по свету, мечтал, воевал, ссорился, кому-то завидовал, ревновал, искал славы, отчаивался, ленился, писал…»). Жизнь дерева отличается от жизни человека. Такой троп, как (В) («срез, словно картину» в предложении 19), наводит автора на вопрос: «Как же прожить жизнь, чтобы не жалеть о сделанных ошибках, чтобы сохранить себя, выстоять в невзгодах и испытаниях?» Отвечая н а этот вопрос, Д. Гранин использует (Г) .
Ответ: 5416
Задание 27. № 2356 Напишите сочинение по прочитанному тексту. Сформулируйте одну из проблем, поставленных автором текста. Прокомментируйте сформулированную проблему. Включите в комментарий два примера-иллюстрации из прочитанного текста, которые важны для понимания проблемы исходного текста (избегайте чрезмерного цитирования). Дайте пояснение к каждому примеру-иллюстрации. Проанализируйте смысловую связь между примерами-иллюстрациями.
Варианты по русскому языку в формате ЕГЭ 2023
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
Задание 1
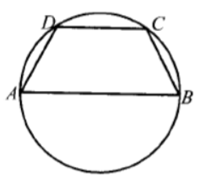
Боковая сторона равнобедренной трапеции равна её меньшему основанию, угол при основании трапеции равен 60°, большее основание равно 18. Найдите радиус описанной окружности этой трапеции
Ответ: 9
Скрыть
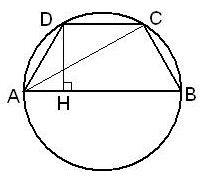
Рассмотрим треугольник ADC, в котором AD=DC по условию задания, а угол D равен:
$$angle D=frac{360^{circ}-angle A-angle B}{2}=frac{360^{circ}-60^{circ}-60^{circ}}{2}=120^{circ}.$$
Найдем сторону AD=DC из треугольника ADH:
$$AD=frac{AH}{cos60^{circ}}=frac{(AB-DC):2}{0,5}=AB-DC$$
$$2AD=AB=18$$
$$AD=frac{18}{2}=9$$
Радиус описанной окружности можно найти по теореме синусов для треугольника ADC, имеем:
$$R=frac{AD}{2sinangle DCA}=frac{9}{2cdotsin30^{circ}}=9.$$
Задание 2
Цилиндр вписан в правильную шестиугольную призму. Радиус основания цилиндра равен $$sqrt{3},$$ а высота равна 2. Найдите площадь боковой поверхности призмы.
Ответ: 24
Скрыть
В основании правильной четырёхугольной призмы лежит правильный шестиугольник:
Найдем сторону этого шестиугольника из треугольника, у которого известен угол 120 градусов между сторонами и противолежащая сторона $$D = 2sqrt{3}.$$ По теореме косинусов можно записать:
$$D^2=a^2+a^2-2cdot acdot acdotcos120$$
$$(2sqrt{3})^2=2a^2-2a^2cdot(-frac{1}{2})$$
$$12=3a^2$$
$$a=2$$
Площадь боковой поверхности правильной шестиугольной призмы со стороной a = 2 и высотой h = 3, равна:
Площадь боковой поверхности правильной призмы со стороной a = 6 и высотой h = 2, равна:
$$S=6cdot acdot h=6cdot2cdot2=24$$
Задание 3
Какова вероятность того, что последние три цифры номера случайно выбранного паспорта одинаковы?
Ответ: 0,01
Скрыть
Цифры меняются от 0 до 9, значит, совпадение трех последних цифр – это одно из $$m = 10$$ событий:
$$000, 111, 222, …, 999.$$
Всего возможных комбинаций из трех цифр $$n=10^3=1000.$$ Получаем значение искомой вероятности:
$$P=frac{m}{n}=frac{10}{1000}=0,01$$
Задание 4
Игральную кость бросали до тех пор, пока сумма всех выпавших очков не превысила число 9. Какова вероятность того, что для этого потребовалось три броска? Ответ округлите до сотых.
Ответ: 0,46
Скрыть
Пусть первое число — результат первого броска, второе — второго, третье — третьего. Тогда возможные варианты превысить число 9 в сумме за три броска:
1 3…6 6 — четыре исхода: $$frac{1}{6}cdotfrac{1}{6}cdotfrac{1}{6}cdot4=frac{4}{216}$$
1 4…6 5 — три исхода: $$frac{1}{6}cdotfrac{1}{6}cdotfrac{1}{6}cdot3=frac{3}{216}$$
1 5…6 4 — два исхода: $$frac{1}{6}cdotfrac{1}{6}cdotfrac{1}{6}cdot2=frac{2}{216}$$
1 6 3 — один исход: $$frac{1}{6}cdotfrac{1}{6}cdotfrac{1}{6}=frac{1}{216}$$
Аналогично рассматривается с первой двойкой (15 исходов всего $$frac{15}{216}$$), тройкой — 21 исход $$frac{21}{216}$$
4 1…5 6 — 5 исходов: $$frac{5}{216}$$
4 1…5 5 — 5 исходов: $$frac{5}{216}$$
4 2…5 4 — 4 исхода: $$frac{4}{216}$$
4 3…5 3 — 3 исхода: $$frac{3}{216}$$
4 4…5 2 — 2 исхода: $$frac{2}{216}$$
4 5 1 — 1 исход: $$frac{1}{216}$$
Заметьте, что 4 6 не рассматриваем уже, т.к. тогда на втором броске уже будет больше 9.
Аналогично с пятеркой: 18 исходов: $$frac{18}{216}$$ и шестеркой: 15 исходов: $$frac{15}{216}$$
В итоге получили: $$10+15+21+20+18+15=99$$ исходов с вероятность $$frac{1}{216}$$
$$P(A)=frac{99}{216}=0,458(3)approx0,46$$
Задание 5
Решите уравнение $$sqrt{2log_8(-x)}-log_8sqrt{x^2}=0.$$ Если уравнение имеет несколько корней, в ответе укажите их сумму.
Ответ: -65
Скрыть
Учтём, что $$log_8sqrt{x^2}=log_8|x|.$$ Так как есть $$log_8(-x),$$ то $$-x>0Rightarrow x<0.$$ Тогда $$log_8|x|=log_8(-x)$$
Пусть $$log_8(-x)=y.$$ Получим: $$sqrt{2y}=yRightarrowleft{begin{matrix} 2y=y^2\ ygeq0 end{matrix}right.Leftrightarrowleft[begin{matrix} y=0\ y=2 end{matrix}right.$$
Обратная замена:
$$left[begin{matrix} log_8(-x)=0\ log_8(-x)=2 end{matrix}right.Leftrightarrowleft[begin{matrix} -x=1\ -x=64 end{matrix}right.Leftrightarrowleft[begin{matrix} x=-1\ x=-64 end{matrix}right.$$
Сумма корней $$(-1)+(-64)=-65.$$
Задание 6
Найдите значение выражения $$frac{p(b)}{p(frac{1}{b})},$$ если $$p(b)=(b+frac{3}{b})(3b+frac{1}{b})$$ при $$bneq0$$
Ответ: 1
Скрыть
$$frac{p(b)}{p(frac{1}{b})}=frac{(b+frac{3}{b})(3b+frac{1}{b})}{(frac{1}{b}+3b)(frac{3}{b}+b)}=1$$
Задание 7
Прямая $$y=x+7$$ является касательной к графику функции $$y=ax^2-15x+15.$$ Найдите $$a.$$
Ответ: 8
Скрыть
Приравниваем производные и функции:
$$left{begin{matrix} (x+7)’=(ax^2-15x+15)’\ x+7=ax^2-15x+15 end{matrix}right.Leftrightarrowleft{begin{matrix} 1=2ax-15\ ax^2-16x+8 end{matrix}right.Leftrightarrowleft{begin{matrix} x=frac{8}{a}\ acdotfrac{64}{a^2}-frac{16cdot8}{a}+8=0 end{matrix}right.$$
$$frac{64}{a}-frac{128}{a}=-8Rightarrow -frac{64}{a}=-8Rightarrow a=8$$
Задание 8
Если достаточно быстро вращать ведёрко с водой на верёвке в вертикальной плоскости, то вода не будет выливаться. При вращении ведёрка сила давления воды на дно не остаётся постоянной: она максимальна в нижней точке и минимальна в верхней. Вода не будет выливаться, если сила её давления на дно будет положительной во всех точках траектории, кроме верхней, где она может быть равной нулю. В верхней точке сила давления, выраженная в ньютонах, равна $$P=m(frac{v^2}{L}-g),$$ где $$m$$ — масса воды в килограммах, $$v$$ — скорость движения ведёрка в м/с, $$L$$ — длина верёвки в метрах, $$g$$ — ускорение свободного падения (считайте, что $$g = 10$$ м/с2). С какой минимальной скоростью надо вращать ведёрко, чтобы вода не выливалась, если длина верёвки равна 0,625 м? Ответ выразите в м/с.
Ответ: 2,5
Скрыть
Чем выше скорость вращения, тем больше давление воды ⇒ нужно найти минимальную скорость, давление должно быть равно 0.
$$m(frac{v_2}{0,625}-10)=0$$
Произведение равно 0, когда один из множителей равен 0. m ≠ 0
$$frac{v_2}{0,625}-10=0$$
$$frac{v_2}{0,625}=10$$
$$v_2 = 10cdot0,625$$
$$v_2 = 6,25$$
$$v = 2,5$$
Задание 9
Трем рабочим поручили изготовить одинаковые партии деталей. Производительность первого рабочего была на 10% меньше, чем у второго, и на 20% больше, чем у третьего. Первым приступил к работе третий рабочий, спустя 6 минут начал свою работу первый рабочий и они закончили свои задания одновременно. На сколько минут позже третьего рабочего начал работать второй, если он свое задание выполнил на 2 минуты раньше, чем первый и третий рабочий?
Ответ: 7
Скрыть
Пусть производительность третьего рабочего $$x$$ раб/мин, тогда производительность первого рабочего — $$(x+0,2x)=1,2x$$ раб/мин, а производительность третьего считаем по пропорции
1,2x — 90%
пр.тр. — 100%
пр.тр. $$=frac{1,2xcdot100}{90}=frac{4x}{3}$$ — производительность третьего рабочего.
Всю работу примем за 1. Тогда время на выполнение работы первым рабочим $$frac{1}{1,2x}$$ минут, третьим — $$frac{1}{x}$$ минут. Первый рабочий выполнил работу на 6 минут быстрее третьего. Составим и решим уравнение:
$$frac{1}{x}-frac{1}{1,2x}=6$$
$$frac{6-5}{6x}=6$$
$$frac{1}{6x}=6$$
$$36x=1$$
$$x=frac{1}{36}$$ раб/мин — производительность третьего рабочего, значит, всю работу он выполнит за 36 минут.
$$frac{4}{3}cdotfrac{1}{36}=frac{1}{27}$$ раб/мин — производительность второго рабочего, значит, всю работу он выполнит за 27 минут.
$$36-27=9$$ минут — на столько дольше работу выполняет третий рабочий, чем второй.
Если второй выполнил работу на 2 минуты раньше третьего, то
$$9-2=7$$ минут — на столько позже третьего второй начал работу.
Задание 10
На рисунке изображен график функции $$f(x)=b+log_a(-frac{1}{x}),$$ где $$a, b$$ — целые числа. Найдите значение $$x,$$ при котором $$f(x)=5.$$
Ответ: -0,25
Скрыть
График проходит через (-4;1) и (-1;3). Получим:
$$left{begin{matrix} 1=b+log_afrac{1}{4}\ 3=b+log_a 1 end{matrix}right.Leftrightarrowleft{begin{matrix} log_afrac{1}{4}=-2\ b=3 end{matrix}right.Leftrightarrowleft{begin{matrix} a=2\ b=3 end{matrix}right.$$
Получили $$f(x)=3+log_2(-frac{1}{x})=5Rightarrow log_2(-frac{1}{x})=2Rightarrow -frac{1}{x}=4Rightarrow x=-0,25$$
Задание 11
Найдите наименьшее значение функции $$f(x)=3x^4+4x^3-12x^2-12$$ на отрезке $$[-0,5;2].$$
Ответ: -17
Скрыть
Найдем производную и приравняем ее к нулю
$$12x^3+12x^2−24x=0$$
$$x(12x^2+12x−24)=0$$
$$x=0$$
$$x=1$$
$$x=−2$$ – не попадет в промежуток
Проверяем методом интервалов точка 1 – точка минимума
$$f(1)=−17$$
Задание 12
А) Решите уравнение $$(-2cos^2x+sin x+1)cdotlog_{0,5}(-0,8cos x)=0$$
Б) Найдите все корни уравнения, принадлежащие отрезку $$[-6pi;-4pi]$$
Ответ: А)$$frac{5pi}{6}+2pi n,nin Z$$ Б)$$-frac{31pi}{6}$$
Задание 13
Конус и полусфера имеют общее основание, радиус которого относится к высоте конуса как 1:3.
А) Докажите, что поверхность полусферы делит образующую конуса в отношении 4:1, считая от вершины конуса.
Б) Найдите площадь поверхности полусферы, находящейся внутри конуса, если радиус их общего основания равен 5.
Ответ: $$20pi$$
Задание 14
Решите неравенство: $$sqrt{2-log_{frac{1}{2}}x}cdotfrac{(x-1)(x+7)}{x+2}geq0$$
Ответ: $$left{frac{1}{4}right},[1;infty)$$
Задание 15
Строительство нового цеха по производству роботов-пылесосов стоит 300 млн рублей. Затраты на производство $$x$$ тыс. единиц продукции на такой линии равны $$0,1x^2+3x+100$$ млн рублей в год. Если продукцию продавать по цене $$р$$ тыс. рублей за единицу, то прибыль фирмы (в млн рублей) за один год составит $$px-(0,1x^2+3x+100).$$ Когда цех будет построен, каждый год фирма будет выпускать продукцию в таком количестве, чтобы прибыль была наибольшей. В первый год после постройки цеха цена продукции $$p = 12$$ тыс. руб. за единицу, каждый следующий год цена продукции увеличивается на 1 тыс. руб. за единицу. За сколько лет окупится строительство цеха?
Ответ: 3
Задание 16
Дана равнобедренная трапеция ABCD. На боковой стороне АВ и большем основании AD взяты соответственно точки К и L так, что KL||CD и CK=DL.
А) Докажите, что $$angle BCK = angle AKL$$
Б) Найдите площадь трапеции ABCD, если $$KL = 12,DL = 2,5BK, S_{CDLK} = 26sqrt{6}$$
Ответ: $$frac{196sqrt{6}}{5}$$
Задание 17
Найдите все положительные значения параметра $$a,$$ при каждом из которых любое значение $$x$$ из отрезка $$[-1;1]$$ будет являться решением неравенства
$$3a^{2x}-16^x+2cdot(4a)^xgeq0$$
Ответ: $$[frac{4}{3};12]$$
Задание 18
В натуральном числе $$n$$ между всеми парами соседних цифр вставили одну и ту же цифру $$c.$$ Получилось число $$m,$$ которое делится на $$n.$$ Их частное равно $$k.$$
А) Может ли быть $$k = 10$$?
Б) Может ли быть $$k = 2$$?
В) Чему может быть равно наименьшее значение числа $$k$$?
Ответ: А) да, Б) нет, В) 6
11:29 10.03.2023
(обновлено: 12:21 10.03.2023)
https://ria.ru/20230310/ekzameny-1856951080.html
Вице-спикер Госдумы призвал обсудить отмену ЕГЭ
Вице-спикер Госдумы призвал обсудить отмену ЕГЭ — РИА Новости, 10.03.2023
Вице-спикер Госдумы призвал обсудить отмену ЕГЭ
Тема отмены ЕГЭ нуждается во всестороннем обсуждении, и чем скорее оно начнется, тем лучше, заявил вице-спикер Госдумы Петр Толстой («Единая Россия»). РИА Новости, 10.03.2023
2023-03-10T11:29
2023-03-10T11:29
2023-03-10T12:21
общество
россия
петр толстой
анзор музаев
единая россия
госдума рф
федеральная служба по надзору в сфере образования и науки (рособрнадзор)
единый государственный экзамен (егэ)
/html/head/meta[@name=’og:title’]/@content
/html/head/meta[@name=’og:description’]/@content
https://cdnn21.img.ria.ru/images/07e6/06/08/1794077403_0:97:3072:1825_1920x0_80_0_0_8fb2880b77c924e87b1e22d2dbd1a31e.jpg
МОСКВА, 10 мар — РИА Новости. Тема отмены ЕГЭ нуждается во всестороннем обсуждении, и чем скорее оно начнется, тем лучше, заявил вице-спикер Госдумы Петр Толстой («Единая Россия»). Ранее глава Рособрнадзора Анзор Музаев заявил журналистам, что отмена ЕГЭ в России в связи с выходом из Болонской системы не обсуждается. Толстой, комментируя сообщение, тогда отметил, что тема отмены ЕГЭ обсуждается, систему будут «демонтировать» постепенно. «Тема отмены ЕГЭ нуждается во всестороннем обсуждении. И чем раньше оно начнется, тем лучше», — написал он в телеграм-канале. По словам политика, у системы на практике оказалось больше недостатков, чем достоинств. При этом он назвал попыткой «чиновников ничего не менять» отрицание того, что ЕГЭ появилось в результате «так называемых реформ образования». «А менять эту систему надо, такова воля большинства наших избирателей», — резюмировал он.
https://ria.ru/20230307/ege-1856449728.html
https://ria.ru/20230304/ege-1855788901.html
россия
РИА Новости
internet-group@rian.ru
7 495 645-6601
ФГУП МИА «Россия сегодня»
https://xn--c1acbl2abdlkab1og.xn--p1ai/awards/
2023
Новости
ru-RU
https://ria.ru/docs/about/copyright.html
https://xn--c1acbl2abdlkab1og.xn--p1ai/
РИА Новости
internet-group@rian.ru
7 495 645-6601
ФГУП МИА «Россия сегодня»
https://xn--c1acbl2abdlkab1og.xn--p1ai/awards/
https://cdnn21.img.ria.ru/images/07e6/06/08/1794077403_0:0:2732:2048_1920x0_80_0_0_40dd2897d8e6452d54553e41bdd5df84.jpg
РИА Новости
internet-group@rian.ru
7 495 645-6601
ФГУП МИА «Россия сегодня»
https://xn--c1acbl2abdlkab1og.xn--p1ai/awards/
общество, россия, петр толстой, анзор музаев, единая россия, госдума рф, федеральная служба по надзору в сфере образования и науки (рособрнадзор), единый государственный экзамен (егэ)
Общество, Россия, Петр Толстой, Анзор Музаев, Единая Россия, Госдума РФ, Федеральная служба по надзору в сфере образования и науки (Рособрнадзор), Единый государственный экзамен (ЕГЭ)
Вице-спикер Госдумы призвал обсудить отмену ЕГЭ
Вице-спикер Госдумы Толстой призвал не медлить с обсуждением отмены ЕГЭ
МОСКВА, 10 мар — РИА Новости. Тема отмены ЕГЭ нуждается во всестороннем обсуждении, и чем скорее оно начнется, тем лучше, заявил вице-спикер Госдумы Петр Толстой («Единая Россия»).
Ранее глава Рособрнадзора Анзор Музаев заявил журналистам, что отмена ЕГЭ в России в связи с выходом из Болонской системы не обсуждается. Толстой, комментируя сообщение, тогда отметил, что тема отмены ЕГЭ обсуждается, систему будут «демонтировать» постепенно.
Рособрнадзор заявил, что не обсуждает отмену ЕГЭ
«Тема отмены ЕГЭ нуждается во всестороннем обсуждении. И чем раньше оно начнется, тем лучше», — написал он в телеграм-канале.
По словам политика, у системы на практике оказалось больше недостатков, чем достоинств. При этом он назвал попыткой «чиновников ничего не менять» отрицание того, что ЕГЭ появилось в результате «так называемых реформ образования».
«А менять эту систему надо, такова воля большинства наших избирателей», — резюмировал он.
В Госдуме попросили Голикову рассмотреть возможность отмены ЕГЭ
В историческом здании в Рахмановском переулке, где в настоящее время располагается Министерство здравоохранения Российской Федерации, расширят офисные площади за счет реставрации и приспособления под современное использование чердачного пространства. Главгосэкспертиза России выдала положительное заключение по итогам рассмотрения проектно-сметной документации на проведение работ.
Здание Главной Московской сберегательной кассы, или Московских Государственных сберегательных касс, построенное в 1902-1907 годах по проекту архитектора Иллариона Иванова-Шица, имеет статус объекта культурного наследия регионального значения. Отмечается, что в структуре его фасадов отслеживается стремление к ордерной упорядоченности, а в деталях – прежняя приверженность архитектора, являющегося сторонником сдержанного, объемно и декоративно уравновешенного модерна, к классицизированному «венскому» варианту этого архитектурного стиля.
Строение украшало изрядное количество нарисованных декоративных деталей и элементов отделки, многие из которых были утрачены. После Октябрьской революции здесь размещалась Московская биржа труда, позже Министерство здравоохранения СССР и, наконец, Минздрав России. Чтобы разместить в здании больше сотрудников ведомства, было решено приспособить под дополнительные офисные помещения его чердачное пространство, в том числе выполнив его реставрацию.
«Приспособление помещений Московской сберегательной кассы выполнят с учетом передового опыта применения инновационных технологий и материалов. При усилении перекрытий предметы охраны затронуты не будут. Согласно архивным фотографиям 1907 года, эта часть чердака, как и затрагиваемые надстроенные стены, относится к более поздним конструкциям», – уточнил главный эксперт проекта Службы ГЭП по объектам культурного наследия и инженерно-технической инфраструктуры Главгосэкспертизы России Кирилл Кунаков.
Помимо прочего, проектными решениями запланированы утепление наружных ограждающих конструкций, устройство мансардных окон, увеличение существующей лестничной клетки в объеме чердачного пространства и так далее. Покрытие и ограждение кровли, решетки, открытия слуховых окон, парапет отреставрируют с применением аналогичного историческому по типу и цвету материала – оцинкованного металла, а обрешетки и контробрешетки крыши, балки, стропила, столбы крыши – с применением дерева – для их сохранения и усиления.
Застройщик объекта – Министерство здравоохранения Российской Федерации. Генпроектировщик – ООО «БС 98 Констракшн».
Фото: ООО «БС 98 Констракшн»