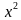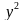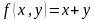Вадим является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары при использовании одинаковых технологий. Если рабочие на одном из заводов трудятся суммарно часов в неделю, то за эту неделю они производят t единиц товара.
За каждый час работы на заводе, расположенном в первом городе, Вадим платит рабочему 200 рублей, а на заводе, расположенном во втором городе, — 300 рублей.
Вадим готов выделять 1 200 000 рублей в неделю на оплату труда рабочих. Какое наибольшее количество единиц товара можно произвести за неделю на этих двух заводах?
Спрятать решение
Решение.
Допустим, что на заводе, расположенном в первом городе, рабочие трудятся часов, а на заводе, расположенном во втором городе,
часов. Тогда в неделю будет произведено
единиц товара, а затраты на оплату труда составят
Выразим y через x:
Значит, нам нужно найти наибольшее значение функции при
Для этого найдем производную функции
Найдем критические точки:
то есть — единственная критическая точка, удовлетворяющая условию
Найдем значения функции в найденной точке и на концах отрезка:
Наибольшее значение функции равно 100, значит, наибольшее количество единиц товара равно 100.
Ответ: 100.
Приведем другое решение
Пусть на первом заводе работают суммарно а на втором —
часов в неделю. Требуется найти максимум суммы
при условии
Выразим y из первого соотношения: подставим в (*), получим уравнение:
Полученное уравнение имеет решения, если неотрицателен его дискриминант, а значит, и четверть дискриминанта:
Тем самым, наибольшее возможное значение равно 100. Покажем, что оно достигается при натуральных значениях переменных: действительно, из (**) находим, что значению
соответствует
а тогда
Ответ: 100.
Спрятать критерии
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получен верный ответ | 2 |
| Верно построена математическая модель | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 2 |
Источник: ЕГЭ по математике 28.06.2017. Резервный день. Вариант 501 (C часть), Задания 17 (С5) ЕГЭ 2017
Задание 17 ЕГЭ по математике (профиль). Задачи на оптимальный выбор. Владельцы заводов. Объем производства
Задача 1. (№ 517742)
Вадим является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары при использовании одинаковых технологий. Если рабочие на одном из заводов трудятся суммарно t2 часов в неделю, то за эту неделю они производят t единиц товара.
За каждый час работы на заводе, расположенном в первом городе, Вадим платит рабочему 200 рублей, а на заводе, расположенном во втором городе, — 300 рублей.
Вадим готов выделять 1 200 000 рублей в неделю на оплату труда рабочих. Какое наибольшее количество единиц товара можно произвести за неделю на этих двух заводах?
Решение:
Составим таблицу:
|
Завод |
Количество часов в неделю |
Количество единиц товара |
Оплата труда, руб. |
|
I |
|
х |
200 |
|
II |
|
y |
300 |
|
Сумма |
|
1200000 |
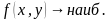
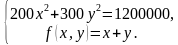
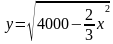
Из первого уравнения выразим y через x:
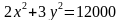
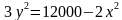
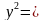
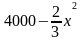
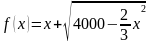
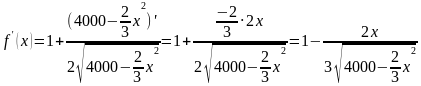
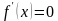
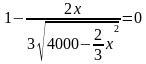
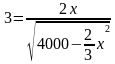
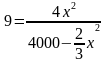
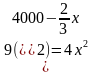
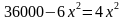
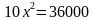
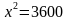
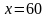
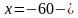
f
’(x) +
f
60
(x)
Значит, точка максимума функции и в ней функция принимает наибольшее значение:
Следовательно, наибольшее количество единиц товара равно 100.
Ответ: 100 единиц товара.
Задания для самостоятельного решения:
1. (№ 517753)
Вадим является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары при использовании одинаковых технологий. Если рабочие на одном из заводов трудятся суммарно t2 часов в неделю, то за эту неделю они производят t единиц товара.
За каждый час работы на заводе, расположенном в первом городе, Вадим платит рабочему 500 рублей, а на заводе, расположенном во втором городе, — 300 рублей.
Вадим готов выделять 1 200 000 рублей в неделю на оплату труда рабочих. Какое наибольшее количество единиц товара можно произвести за неделю на этих двух заводах?
Ответ: 80 единиц товара.
2. (№ 509824)
Антон является владельцем двух заводов в разных городах. На заводах производится абсолютно одинаковые товары при использовании одинаковых технологий. Если рабочие на одном из заводов трудятся суммарно t2 часов в неделю, то за эту неделю они производят t единиц товара.
За каждый час работы на заводе, расположенном в первом городе, Антон платит рабочему 250 рублей, а на заводе, расположенном во втором городе, — 200 рублей.
Антон готов выделять 900 000 рублей в неделю на оплату труда рабочих. Какое наибольшее количество единиц товара можно произвести за неделю на этих двух заводах?
Ответ: 90 единиц товара.
Решу егэ профиль математика 517739
Задание 12 № 517746
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
А) Из уравнения получаем:
Б) Заметим, что Значит, указанному отрезку принадлежит корень −3.
Ответ: а) −3 и 27; б) −3.
Аналоги к заданию № 517739: 517746 517747 Все
Задание 12 № 517747
Задание 12 № 517746
Задание 12 № 517747
Ответ а 3 и 27; б 3.
Ege. sdamgia. ru
12.01.2020 13:48:01
2020-01-12 13:48:01
Источники:
Https://ege. sdamgia. ru/test? likes=517739
Решу егэ профиль математика 517739 — Математика и Английский » /> » /> .keyword { color: red; } Решу егэ профиль математика 517739
Решу егэ профиль математика 517739
Решу егэ профиль математика 517739
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
Задание 12 № 517746
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
А) Из уравнения получаем:
Б) Заметим, что Значит, указанному отрезку принадлежит корень −3.
Ответ: а) −3 и 27; б) −3.
Аналоги к заданию № 517739: 517746 517747 Все
Задание 12 № 517747
Задание 12 № 517746
Б Заметим, что Значит, указанному отрезку принадлежит корень 3.
Источники:
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword < color: red; >Решу егэ профиль математика 517739
Решу егэ профиль математика 517739
Решу егэ профиль математика 517739
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
Задание 12 № 514082
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
А) Запишем исходное уравнение в виде:
Б) Поскольку отрезку принадлежит единственный корень −2.
Ответ: а) −2; 1, б) −2.
Почему такое странное ОДЗ?? Где 2-х>0, х>0, следовательно х0; тогда х (0;2)
Екатерина, в решении не находили ОДЗ.
В решении было использован равносильный переход, при котором условия достаточно для решения примера
А у Вас ОДЗ найдено с ошибкой.
Задание 12 № 517739
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
А) Из уравнения получаем:
Б) Заметим, что Значит, указанному отрезку принадлежит только корень −2.
Ответ: а) −2 и 16; б) −2.
В пункте «а» ответ только 16,вы не проверили ОДЗ
В этом уравнении не нужно искать ОДЗ. Это лишнее действие
Задание 12 № 502094
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие промежутку
А) Заметим, что преобразуем исходное уравнение:
Пусть тогда уравнение запишется в виде откуда или
При получим: откуда
При получим: откуда
Б) Корень не принадлежит промежутку Поскольку и корень принадлежит промежутку
Источник: ЕГЭ по математике 19.06.2013. Основная волна, резервный день. Центр. Вариант 502., Задания 13 (С1) ЕГЭ 2013
В строчке а) откуда-то взялась «3»
Путём каких преобразований мы получили ответ log(3)5 ?
1) Уравнение начинается с числе 9 в степени. Т. е. Мы раскладываем 9 как 3*3. Однако в первой строке решения мы видим 9*3. От туда и дальнейшее неверное вычисление.
2) Когда мы возвращаем замену (четвёртая строчка решения) вместо этого (если, допустим, t и правда равно 5/3) должно получиться Х-1= логорифм 5/3 по основанию 3. Верно?
Так ли это? Ибо мне свойственно ошибаться. Это правда ошибка, или я чего-то не понимаю? Если второе, то объясните, если можно.
Задание 12 № 517739
Задание 12 № 502094
Задание 12 502094.
Источники:
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword < color: red; >Решу егэ профиль математика 517739
Решу егэ профиль математика 517739
Решу егэ профиль математика 517739
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
Диагональ экрана телевизора равна 64 дюймам. Выразите диагональ экрана в сантиметрах, если в одном дюйме 2,54 см. Результат округлите до целого числа сантиметров.
Источники:
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword < color: red; >Решу егэ профиль математика 517739
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
Задание 12 № 514082
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
А) Запишем исходное уравнение в виде:
Б) Поскольку отрезку принадлежит единственный корень −2.
Ответ: а) −2; 1, б) −2.
Почему такое странное ОДЗ?? Где 2-х>0, х>0, следовательно х0; тогда х (0;2)
Екатерина, в решении не находили ОДЗ.
В решении было использован равносильный переход, при котором условия достаточно для решения примера
А у Вас ОДЗ найдено с ошибкой.
Задание 12 № 517739
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
А) Из уравнения получаем:
Б) Заметим, что Значит, указанному отрезку принадлежит только корень −2.
Ответ: а) −2 и 16; б) −2.
В пункте «а» ответ только 16,вы не проверили ОДЗ
В этом уравнении не нужно искать ОДЗ. Это лишнее действие
Задание 12 № 502094
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие промежутку
А) Заметим, что преобразуем исходное уравнение:
Пусть тогда уравнение запишется в виде откуда или
При получим: откуда
При получим: откуда
Б) Корень не принадлежит промежутку Поскольку и корень принадлежит промежутку
Источник: ЕГЭ по математике 19.06.2013. Основная волна, резервный день. Центр. Вариант 502., Задания 13 (С1) ЕГЭ 2013
В строчке а) откуда-то взялась «3»
Путём каких преобразований мы получили ответ log(3)5 ?
1) Уравнение начинается с числе 9 в степени. Т. е. Мы раскладываем 9 как 3*3. Однако в первой строке решения мы видим 9*3. От туда и дальнейшее неверное вычисление.
2) Когда мы возвращаем замену (четвёртая строчка решения) вместо этого (если, допустим, t и правда равно 5/3) должно получиться Х-1= логорифм 5/3 по основанию 3. Верно?
Так ли это? Ибо мне свойственно ошибаться. Это правда ошибка, или я чего-то не понимаю? Если второе, то объясните, если можно.
Задание 12 № 517739
Задание 12 № 502094
Задание 12 502094.
Уско рен ная под го тов ка к ЕГЭ с ре пе ти то ра ми Учи.
Dankonoy. com
16.06.2020 6:45:22
2020-06-16 06:45:22
Источники:
Https://dankonoy. com/ege/ege11/archives/10087
Материал для подготовки к экзамену по математике 1 курс. » /> » /> .keyword { color: red; } Решу егэ профиль математика 517739
Материал для подготовки к экзамену по математике 1 курс
Материал для подготовки к экзамену по математике 1 курс.
Материал для подготовки к экзамену по математике для 1 курса СПО.
Просмотр содержимого документа
«Материал для подготовки к экзамену по математике 1 курс.»
Логарифмические уравнения
1. Задание 5 № 26646
Найдите корень уравнения
2. Задание 5 № 26647
Найдите корень уравнения
3. Задание 5 № 26648
Найдите корень уравнения
4. Задание 5 № 26649
Найдите корень уравнения
5. Задание 5 № 26657
Найдите корень уравнения
6. Задание 5 № 26658
Найдите корень уравнения
7. Задание 5 № 26659
Найдите корень уравнения
8. Задание 5 № 77380
Решите уравнение
9. Задание 5 № 77381
Решите уравнение
10. Задание 5 № 77382
Решите уравнение Если уравнение имеет более одного корня, в ответе укажите меньший из них.
11. Задание 5 № 315120
Найдите корень уравнения
12. Задание 5 № 315535
Найдите корень уравнения
13. Задание 5 № 525399
Решите уравнение
Тригонометрические уравнения
1. Задание 5 № 26669
Найдите корни уравнения: В ответ запишите наибольший отрицательный корень.

Значениям соответствуют положительные корни.
Если, то и
Если, то и
Значениям соответствуют меньшие значения корней.
Следовательно, наибольшим отрицательным корнем является число
2. Задание 5 № 77376
Решите уравнение В ответе напишите наибольший отрицательный корень.
Значению соответствует Положительным значениям параметра соответствуют положительные значения корней, отрицательным значениям параметра соответствуют меньшие значения корней. Следовательно, наибольшим отрицательным корнем является число −1.
3. Задание 5 № 77377
Решите уравнение В ответе напишите наименьший положительный корень.
Значениям соответствуют отрицательные корни.
Если, то и
Если, то и
Значениям соответствуют большие положительные корни.
Наименьшим положительным решением является 0,5.
Преобразования числовых логарифмических выражений
1. Задание 9 № 26843
Найдите значение выражения
2. Задание 9 № 26844
Найдите значение выражения
3. Задание 9 № 26845
Найдите значение выражения
4. Задание 9 № 26846
Найдите значение выражения
5. Задание 9 № 26847
Найдите значение выражения
6. Задание 9 № 26848
Найдите значение выражения
7. Задание 9 № 26849
Найдите значение выражения
8. Задание 9 № 26850
Найдите значение выражения
9. Задание 9 № 26851
Найдите значение выражения
10. Задание 9 № 26852
Найдите значение выражения
11. Задание 9 № 26853
Найдите значение выражения
12. Задание 9 № 26854
Найдите значение выражения
13. Задание 9 № 26855
Найдите значение выражения
14. Задание 9 № 26856
Найдите значение выражения
15. Задание 9 № 26857
Найдите значение выражения
16. Задание 9 № 26858
Найдите значение выражения
17. Задание 9 № 26859
Найдите значение выражения
18. Задание 9 № 26860
Найдите значение выражения
19. Задание 9 № 26861
Найдите значение выражения
20. Задание 9 № 26862
Найдите значение выражения
21. Задание 9 № 26882
Найдите значение выражения
22. Задание 9 № 26883
Найдите значение выражения
23. Задание 9 № 26885
Найдите значение выражения
24. Задание 9 № 26889
Найдите значение выражения
25. Задание 9 № 26892
Найдите значение выражения
26. Задание 9 № 26893
Найдите значение выражения
27. Задание 9 № 26894
Найдите значение выражения
28. Задание 9 № 26896
Найдите значение выражения
29. Задание 9 № 77418
Вычислите значение выражения:
30. Задание 9 № 505097
Найдите значение выражения
31. Задание 9 № 509086
Найдите значение выражения
32. Задание 9 № 510939
Найдите значение выражения
33. Задание 9 № 525403
Найдите значение выражения
Вычисление значений тригонометрических выражений
1. Задание 9 № 26775
Найдите, если и
2. Задание 9 № 26776
Найдите, если и
3. Задание 9 № 26777
Найдите, если и
4. Задание 9 № 26778
Найдите, если и
5. Задание 9 № 26779
Найдите, если
6. Задание 9 № 26780
Найдите, если
7. Задание 9 № 26783
Найдите значение выражения, если
8. Задание 9 № 26784
Найдите, если и
9. Задание 9 № 26785
Найдите, если и
10. Задание 9 № 26786
Найдите, если
11. Задание 9 № 26787
Найдите, если
12. Задание 9 № 26788
Найдите, если
13. Задание 9 № 26789
Найдите, если
14. Задание 9 № 26790
Найдите, если
15. Задание 9 № 26791
Найдите, если
16. Задание 9 № 26792
Найдите значение выражения, если
17. Задание 9 № 26793
Найдите значение выражения, если
18. Задание 9 № 26794
Найдите, если
19. Задание 9 № 316350
Найдите, если
20. Задание 9 № 501598
Найдите значение выражения
21. Задание 9 № 502014
Найдите значение выражения
22. Задание 9 № 502045
Найдите значение выражения
23. Задание 9 № 502106
Найдите значение выражения
24. Задание 9 № 502285
Найдите значение выражения
25. Задание 9 № 502305
Найдите значение выражения если и
26. Задание 9 № 504410
Найдите значение выражения:
27. Задание 9 № 504824
Найдите значение выражения
28. Задание 9 № 508966
Найдите если
29. Задание 9 № 510424
Найдите если и
30. Задание 9 № 549336
Найдите если и
Преобразования числовых тригонометрических выражений
1. Задание 9 № 26755
Найдите значение выражения
2. Задание 9 № 26756
Найдите значение выражения
3. Задание 9 № 26757
Найдите значение выражения
4. Задание 9 № 26758
Найдите значение выражения
5. Задание 9 № 26759
Найдите значение выражения
6. Задание 9 № 26760
Найдите значение выражения
7. Задание 9 № 26761
Найдите значение выражения
8. Задание 9 № 26762
Найдите значение выражения
9. Задание 9 № 26763
Найдите значение выражения
10. Задание 9 № 26764
Найдите значение выражения
11. Задание 9 № 26765
Найдите значение выражения
12. Задание 9 № 26766
Найдите значение выражения
13. Задание 9 № 26767
Найдите значение выражения
14. Задание 9 № 26769
Найдите значение выражения
15. Задание 9 № 26770
Найдите значение выражения
16. Задание 9 № 26771
Найдите значение выражения
17. Задание 9 № 26772
Найдите значение выражения
18. Задание 9 № 26773
Найдите значение выражения
19. Задание 9 № 26774
Найдите значение выражения
20. Задание 9 № 77412
Найдите значение выражения
21. Задание 9 № 77413
Найдите значение выражения
22. Задание 9 № 77414
Найдите значение выражения:
23. Задание 9 № 245169
Найдите значение выражения
24. Задание 9 № 245170
Найдите значение выражения
25. Задание 9 № 245171
Найдите значение выражения
26. Задание 9 № 245172
Найдите значение выражения
27. Задание 9 № 501701
Найдите значение выражения
28. Задание 9 № 502994
Найдите значение выражения
29. Задание 9 № 503310
Найдите значения выражения
30. Задание 9 № 510013
Найдите если и
31. Задание 9 № 510312
Найдите значение выражения
32. Задание 9 № 510386
Найдите значение выражения
33. Задание 9 № 510405
Найдите значение выражения
34. Задание 9 № 510824
Найдите значение выражения
35. Задание 9 № 510843
Найдите значение выражения
36. Задание 9 № 525113
Найдите значение выражения
37. Задание 9 № 526009
Найдите значение выражения
Логарифмические и показательные уравнения
1. Задание 13 № 514082
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
2. Задание 13 № 517739
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
3. Задание 13 № 502094
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие промежутку
4. Задание 13 № 516760
А) Решите уравнение:
Б) Определите, какие из его корней принадлежат отрезку
5. Задание 13 № 514623
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие отрезку
6. Задание 13 № 502053
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие отрезку
7. Задание 13 № 525377
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие отрезку
8. Задание 13 № 513605
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
9. Задание 13 № 503127
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие отрезку
10. Задание 13 № 514081
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащего отрезку
11. Задание 13 № 502999
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие отрезку [−1; 2].
12. Задание 13 № 528517
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
13. Задание 13 № 550261
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие промежутку
14. Задание 13 № 555265
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
15. Задание 13 № 555583
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
16. Задание 13 № 561853
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие отрезку [−2,5; −1,5].
17. Задание 13 № 562032
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие отрезку [−0,5; 0,5].
18. Задание 13 № 562757
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие отрезку
б) Укажите корни этого уравнения, принадлежащие отрезку
Решите уравнение В ответе напишите наименьший положительный корень.
Просмотр содержимого документа «Материал для подготовки к экзамену по математике 1 курс.»
Б Укажите корни этого уравнения, принадлежащие отрезку.
Multiurok. ru
06.02.2020 18:29:01
2020-02-06 18:29:01
Источники:
Https://multiurok. ru/files/material-dlia-podgotovki-k-ekzamenu-po-matematike. html
Новые тренировочные варианты ЕГЭ 2023 по математике базовый и профильный уровень с ответами и решением для 10 и 11 класса, больше 100 вариантов в формате реального экзамена ФИПИ вы можете решать онлайн или скачать.
Тренировочные варианты ЕГЭ 2023 по математике база и профиль
13.09.2022 Тренировочный вариант №1 ЕГЭ 2023 по математике профиль с ответами
20.09.2022 Тренировочный вариант №2 ЕГЭ 2023 по математике профиль с ответами
20.09.2022 Тренировочный вариант №2 ЕГЭ 2023 база по математике с ответами
27.09.2022 Математика 11 класс профиль входная мониторинговая работа 3 варианта с ответами
28.09.2022 Тренировочный вариант №3 ЕГЭ 2023 база по математике с ответами
28 сентября 2022 Статград математика 11 класс ЕГЭ 2023 база и профиль варианты и ответы
29 сентября 2022 Тренировочный вариант №3 ЕГЭ 2023 по математике профиль с ответами
1 октября 2022 Ларин вариант 399 ЕГЭ 2023 по математике профиль решение с ответами
6 октября Тренировочный вариант №4 ЕГЭ 2023 база по математике с ответами
6 октября Тренировочный вариант №4 ЕГЭ 2023 по математике профиль с ответами
8 октября Ларин вариант 400 ЕГЭ 2023 по математике профиль решение с ответами
12 октября Тренировочный вариант №5 ЕГЭ 2023 база по математике с ответами
12 октября Тренировочный вариант №5 ЕГЭ 2023 по математике профиль с ответами
14 октября Вариант 1 Ященко ЕГЭ 2023 математика профиль с ответами и решением
14 октября Вариант 2 Ященко ЕГЭ 2023 математика профиль с ответами и решением
15 октября Ларин вариант 401 ЕГЭ 2023 по математике профиль решение с ответами
15 октября Ларин вариант 402 ЕГЭ 2023 по математике профиль решение с ответами
16 октября Вариант 3 Ященко ЕГЭ 2023 математика профиль с ответами и решением
16 октября Вариант 4 Ященко ЕГЭ 2023 математика профиль с ответами и решением
23 октября Тренировочный вариант №6 ЕГЭ 2023 база по математике с ответами
24 октября Тренировочный вариант №6 ЕГЭ 2023 по математике профиль с ответами
25 октября Тренировочный вариант №7 ЕГЭ 2023 база по математике с ответами
26 октября Тренировочный вариант №7 ЕГЭ 2023 по математике профиль с ответами
28 октября Ларин вариант 403 ЕГЭ 2023 по математике профиль решение с ответами
29 октября Ларин вариант 404 ЕГЭ 2023 по математике профиль решение с ответами
1 ноября 2022 Тренировочный вариант №8 решу ЕГЭ 2023 база по математике с ответами
1 ноября 2022 Тренировочный вариант №8 решу ЕГЭ 2023 по математике профиль с ответами
5 ноября 2022 Вариант 1-2 распечатай и реши ЕГЭ 2023 база по математике 11 класс с ответами
6 ноября 2022 Ларин вариант 405 ЕГЭ 2023 профиль по математике решение с ответами
9 ноября 2022 Тренировочный вариант №9 решу ЕГЭ 2023 база по математике с ответами
12 ноября 2022 Тренировочный вариант №9 решу ЕГЭ 2023 по математике профиль с ответами
13 ноября 2022 Ларин вариант 406 ЕГЭ 2023 профиль по математике решение с ответами
15 ноября 2022 Тренировочный вариант №10 решу ЕГЭ 2023 база по математике 11 класс с ответами
15 ноября 2022 Тренировочный вариант №10 решу ЕГЭ 2023 по математике профиль с ответами
21 ноября 2022 Ларин вариант 407 ЕГЭ 2023 профиль по математике решение с ответами
23 ноября 2022 Тренировочный вариант №11 решу ЕГЭ 2023 база по математике 11 класс с ответами
23 ноября 2022 Тренировочный вариант №11 решу ЕГЭ 2023 по математике профиль с ответами
27 ноября 2022 Ларин вариант 408 ЕГЭ 2023 профиль по математике решение с ответами
28 ноября 2022 Вариант 3-4 распечатай и реши ЕГЭ 2023 база по математике 11 класс с ответами
30 ноября 2022 Мониторинговая работа по математике 11 класс ЕГЭ 2023 профиль 1 полугодие
3 декабря 2022 Тренировочный вариант №12 решу ЕГЭ 2023 база по математике 11 класс с ответами
3 декабря 2022 Тренировочный вариант №12 решу ЕГЭ 2023 по математике профиль с ответами
3 декабря 2022 Пробник ЕГЭ 2023 Москва по математике профиль задания и ответы
5 декабря 2022 Ларин вариант 409 ЕГЭ 2023 профиль по математике решение с ответами
9 декабря 2022 Тренировочный вариант №13 решу ЕГЭ 2023 база по математике 11 класс с ответами
10 декабря 2022 Тренировочный вариант №13 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
12 декабря 2022 Ларин вариант 410 ЕГЭ 2023 профиль по математике решение с ответами
13 декабря 2022 Статград математика 11 класс профиль ЕГЭ 2023 варианты МА2210209-МА2210212 и ответы
13 декабря 2022 Математика 11 класс база ЕГЭ 2023 статград варианты и ответы
15 декабря 2022 Тренировочный вариант №14 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
15 декабря 2022 Тренировочный вариант №14 решу ЕГЭ 2023 база по математике 11 класс с ответами
20 декабря 2022 Вариант 5-6 распечатай и реши ЕГЭ 2023 база по математике 11 класс с ответами
20 декабря 2022 Ларин вариант 411 ЕГЭ 2023 профиль по математике решение с ответами
3 января 2023 Ларин вариант 412 ЕГЭ 2023 профиль по математике решение с ответами
6 января 2023 Тренировочный вариант 1-2 ЕГЭ 2023 профиль математика задания и ответы
8 января 2023 Вариант 3-4 ЕГЭ 2023 профиль математика задания и ответы
9 января 2023 Вариант 7-8 распечатай и реши ЕГЭ 2023 база по математике 11 класс с ответами
10 января 2023 Тренировочный вариант №15 и №16 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
11 января 2023 ЕГЭ 2023 математика тренировочные задания и ответы Ященко, Семенов
11 января 2023 Тренировочный вариант №15 и №16 база ЕГЭ 2023 по математике 11 класс с ответами
19 января 2023 Тренировочные варианты №17 и №18 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
22 января 2023 Ларин вариант 413 и 414 ЕГЭ 2023 профиль по математике решение и ответы
22 января 2023 Тренировочный 19 вариант решу ЕГЭ 2023 профиль по математике 11 класс с ответами
22 января 2023 База ЕГЭ 2023 математика 11 класс тренировочный вариант 19 с ответами
25 января 2023 База ЕГЭ 2023 математика 11 класс тренировочный вариант 20 с ответами
27 января 2023 Тренировочный вариант №20 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
28 января 2023 Вариант 415 Ларина ЕГЭ 2023 по математике 11 класс задания и ответы
2 февраля 2023 Вариант 21 база ЕГЭ 2023 математика 11 класс тренировочный вариант с ответами
2 февраля 2023 Тренировочный вариант №21 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
8 февраля 2023 Математика 10-11 класс ЕГЭ 2023 статград варианты база и профиль МА2200101-МА2200110 и ответы
11 февраля 2023 Тренировочный вариант №22 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
11 февраля 2023 Тренировочный вариант №22 решу ЕГЭ 2023 база по математике 11 класс с ответами
12 февраля 2023 Вариант 416 Ларина ЕГЭ 2023 по математике 11 класс задания и ответы
12 февраля 2023 Вариант 417 Ларина ЕГЭ 2023 по математике 11 класс задания и ответы
13 февраля 2023 Вариант 9 и вариант 10 ЕГЭ 2023 база математика распечатай и реши задания
13 февраля 2023 Вариант 11 и вариант 12 ЕГЭ 2023 база математика распечатай и реши
16 февраля 2023 Тренировочный вариант №23 решу ЕГЭ 2023 база по математике 11 класс с ответами
16 февраля 2023 Тренировочный вариант №23 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
18 февраля 2023 Вариант 418 Ларина ЕГЭ 2023 по математике 11 класс задания и ответы
22 февраля 2023 Пробный ЕГЭ 2023 вариант 24 база по математике 11 класс с ответами
22 февраля 2023 Пробный ЕГЭ 2023 вариант 24 профиль по математике 11 класс с ответами
25 февраля 2023 Вариант 419 Ларина ЕГЭ 2023 по математике 11 класс задания и ответы
28 февраля 2023 Статград математика 11 класс ЕГЭ 2023 база и профиль и ответы
4 марта 2023 Пробник ЕГЭ 2023 вариант 25 база по математике 11 класс с ответами
4 марта 2023 Вариант 420 Ларин ЕГЭ 2023 по математике 11 класс задания и ответы
5 марта 2023 Пробник ЕГЭ 2023 вариант 25 профиль по математике 11 класс с ответами
8 марта 2023 Пробник ЕГЭ 2023 вариант 26 профиль по математике 11 класс с ответами
8 марта 2023 Пробник ЕГЭ 2023 вариант 26 база по математике 11 класс 100 баллов с ответами
Смотрите также на нашем сайте:
Сборник Ященко ЕГЭ 2023 математика профильный уровень 36 вариантов
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
ЕГЭ по математике — Профиль 2022. Открытый банк заданий с ответами.
В США тоже есть ЕГЭ — причём он был задолго до нас. Вот одна задачка оттуда. Мы перевели её на русский и заменили центы на привычные рубли. Сама задача звучит так:
Эту задачку можно решить на листочке за несколько минут. Попробуйте сами, а если не получится — кат в помощь ↓
Это звучит удивительно, но для решения нам не нужно считать точное количество монет обоих видов у каждого (хотя никто не мешает вам попробовать это сделать). Вместо этого мы применим хитрость и смекалку.
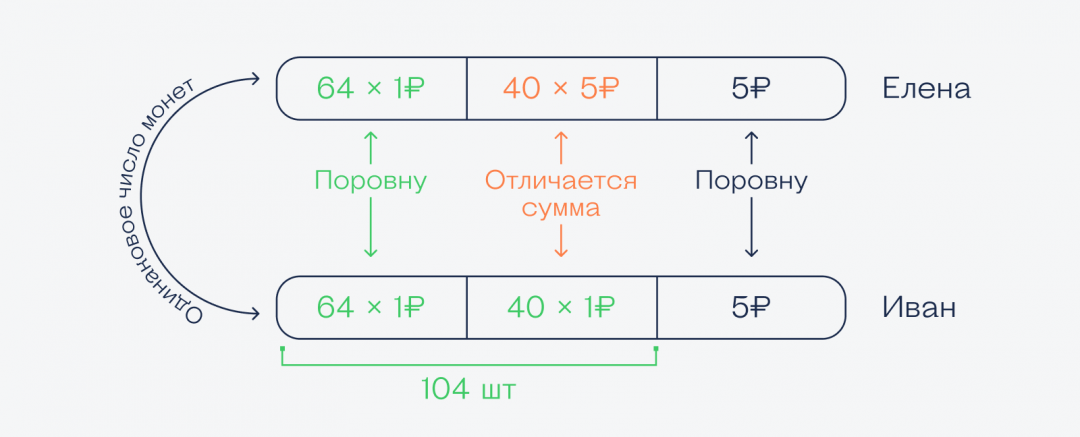
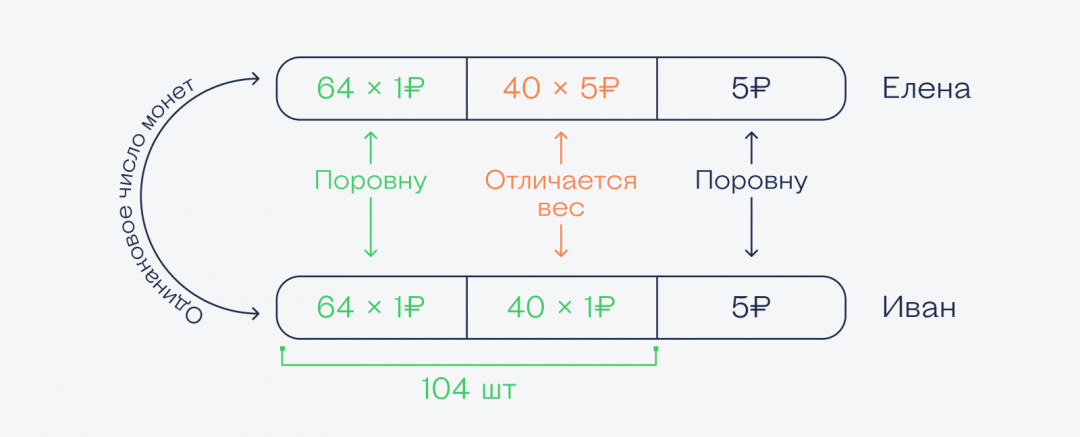
Нам неважно, сколько у кого монет, главное, что их одинаковое количество и у Елены, и у Ивана, а вот количество рублёвых монет разное. Зная это, достаточно нарисовать простую картинку, по которой легко найти ответ на этот вопрос:
Глядя на неё становится понятно, что общую часть из 64 рублёвых монет можно выкинуть у обоих, потому что и там и там одинаковая сумма. А то, что осталось, и даст нужную разницу.
👉 Так как количество монет у каждого одинаковое, то у Ивана вместо 40 пятирублёвок лежит 40 рублёвых монет, а остальные пятирублёвки снова у обоих в одинаковом количестве, и их тоже можно отбросить. Получается, разница в деньгах такая:
- у Елены — 40 × 5 ₽ = 200 ₽
- у Ивана — 40 × 1 ₽ = 40 ₽
Значит, у Елены на 200 − 40 = 160 ₽ больше.
На этом этапе спотыкается большинство решающих, потому что они пытаются найти точное количество монет Ивана. Но мы-то с вами уже знаем, что это необязательно — достаточно найти разницу в весе и по ней посчитать вес монет.
Используем тот же рисунок, но уже в разрезе веса монет:
Получается, что разница в весе зависит от тех же монет, что мы считали в первой части.
Так как одна рублёвая монета легче одной пятирублёвой на 2,7 грамма, то у 40 монет разница в весе будет 40 × 2,7 = 108 грамм. А раз у Ивана пятирублёвок меньше, чем у Елены, то и монеты будут весить как раз на эти 108 грамм легче: 1,134 − 0,108 = 1,026 килограмма.
Мы подошли к 14 заданию из ЕГЭ по информатике 2022. Оно связано с различными системами счисления. Что такое различные системы счисления, мы рассматривали в этой статье. Так же будет полезно посмотреть эту статью.
Переходим к первому тренировочному 14-ому заданию из ЕГЭ по информатике. Раньше это задание было под номером 16.
Задача (ЕГЭ по информатике, 2019, Москва)
Значение выражения 536 + 524 — 25 записали в системе счисления с основанием 5. Сколько цифр «4» содержится в этой записи?
Решение:
Первый способ. (С помощью Питона)
f = 5**36 + 5**24 - 25 s='' while f>0: s = s + str(f%5) f = f // 5 print(s.count('4'))
В переменную f записываем функцию. Две звёздочки подряд обозначают возведение в степень. Заводим строчку s, где и будет сформировано число в пятеричной системе.
Сам перевод числа f в пятеричную систему происходит в цикле WHILE.
Записываем остатки от деления на 5 в строку s. Делаем так же, как если бы переводили в ручную. И так же производим само целочисленное деление. Это мы тоже делаем, когда переводим на листке бумаги.
В строке s получается число в пятеричной системе, но в цифры в этой записи стоят в обратном порядке. Ведь, когда мы переводим в ручную, остатки должны записать задом наперёд.
Здесь и не важен порядок цифр, важно количество четвёрок!
С помощью функции count находим количество четвёрок в строке s.
В ответе напишем 22.
Второй способ. (Классический)
Сформулируем главное правило, на которое будем опираться при решении подобного типа задач.
Примеры:
54 (в десятичной системе) — это 100005 (в пятеричной системе)
72 (в десятичной системе) — это 1007 (в семеричной системе)
29 (в десятичной системе) — это 10000000002 (в двоичной системе)
Перепишем наше выражение, чтобы все числа были в виде степени представлены.
536 + 524 — 52
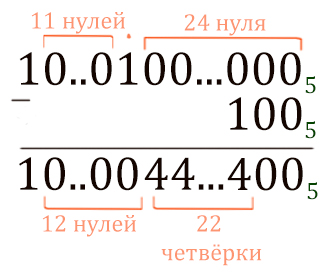
Посчитаем 536 + 524 в пятеричной системе столбиком, используя основное правило.
Здесь всё просто: ноль прибавить ноль, будет ноль. Единица плюс ноль, будет один.
Теперь от получившегося числа нужно отнять 52 (1005).
Первые два разряда посчитать легко. Ноль минус ноль, будет ноль.
Третий разряд: из нуля отнять единицу мы не можем, поэтому занимаем у более старших разрядов.
В более старших разрядах тоже нули, поэтому идём до единицы, у которой можно занять. Получается 22 четвёрки.
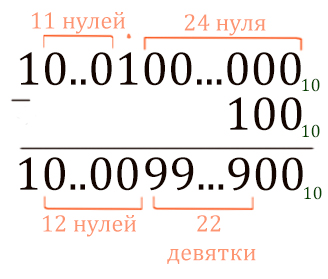
Вот как было бы, если бы считали в нашей родной десятичной системе счисления в аналогичной ситуации.
Здесь мы считаем в десятичной системе, поэтому получаются девятки. В нашей задаче считали в пятеричной системе, поэтому получаются четвёрки.
В ответе напишем 22 четвёрки.
Ответ: 22
Задача (ЕГЭ по информатике, 2020, Москва)
Значение выражения 168 × 420 — 45 — 64 записали в системе счисления с основанием 4. Сколько цифр «3» содержится в этой записи?
Решение:
Первый способ. (С помощью Питона)
f = 16**8 * 4**20 - 4**5 - 64 s='' while f>0: s = s + str(f%4) f = f // 4 print(s.count('3'))
Второй способ. (Классический)
Преобразуем наше выражение. Приведём всё к 4-ам.
168 × 420 — 45 — 64 =
= (42)8 × 420 — 45 — 43 =
= 416 × 420 — 45 — 43 =
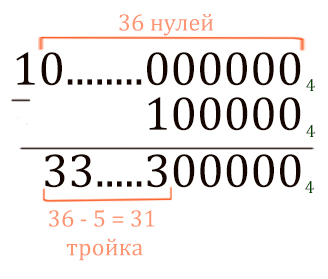
= 436 — 45 — 43
Здесь не можем применить технику устного счёта, потому что стоят два минуса. Значит, будем решать с помощью столбиков.
Сначала посчитаем 436 — 45.
Теперь от этого числа нужно отнять 43 (10004)
Получается 32 тройки.
В последнем вычислении нет ничего сложно. В десятичной системе вы бы легко вычислили в аналогичной ситуации.
Ответ: 32
Задача (Тренировочная)
Укажите через запятую в порядке возрастания все десятичные натуральные числа, не превосходящие 17, запись которых в троичной системе счисления оканчивается на две одинаковые цифры.
Решение:
1) Переведём число 17 в троичную систему.
Получилось 1223.
2) Теперь выпишем все числа, которые не превосходят 1223 (Т.е. 1223 тоже подходит!), запись которых в троичной системе счисления оканчивается на две одинаковые цифры. В троичной системе могут применяться цифры 0, 1, 2.
1223
1223
1113
1003
223
113
Теперь переведём эти числа в десятичную систему.
1223 = 2 × 30 + 2 × 31 + 1 × 32 = 1710
1113 = 1 × 30 + 1 × 31 + 1 × 32 = 1310
1003 = 0 × 30 + 0 × 31 + 1 × 32 = 910
223 = 2 × 30 + 2 × 31 = 810
113 = 1 × 30 + 1 × 31 = 410
Ответ: 4, 8, 9, 13, 17
Ещё один интересный тип задания номер 14, который вполне может быть на реальном ЕГЭ по информатике 2022.
Задача (Уравнение)
Чему равно наименьшее основание позиционной системы счисления x, при котором 225x = 405y?
Ответ записать в виде целого числа.
Решение:
Переведём каждое из чисел 225x и 405y в десятичную систему счисления и приравняем, т.к. эти числа равны.
5 × x0 + 2 × x1 + 2 × x2 = 5 × y0 + 0 × y1 + 4 × y2
Любое число в нулевой степени — это 1. Значит, 5 × x0 = 5 × y0 = 5. Эти два выражения равны одному и тому же значению, следовательно, их можно убрать и слева, и справа.
2x + 2x2 = 4y2
x + x2 = 2y2
x(1 + x) = 2y2
Получили уравнение в целых числах. Слева умножение двух последовательных чисел. Нужно начать подбирать целые числа.
При y = 6 :
x (1 + x) = 2 × 62 = 72 ; Произведение двух последовательных чисел 8 * 9 = 72. Значит, x = 8.
Мы начали проверку с числа 6, потому что у нас в уравнении присутствуют цифра 5. Значит, система счисления может быть минимум с основанием 6.
Получается, что наименьшее значение x равно 8.
В подобных задач нужно знать, что числа обязательно найдутся, нужно их просто хорошо поискать.
Для качественной проработки 14 задания из ЕГЭ по информатике 2022 разберём ещё некоторые задачи.
Задача (Основание системы)
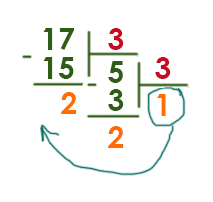
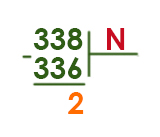
Запись числа 338 в системе счисления с основанием N содержит 3 цифры и оканчивается на 2. Чему равно максимально возможное основание системы счисления?
Решение:
В этой задаче применим формулу:
Примером для данной формулы можно взять два разряда в двоичной системе. Максимальное число в двоичной системе равно 112. А в десятичной системе это число равно 310. Т.е. 22 — 1.
338 число будет точно больше, чем двухзначное число с основанием N.
Получается неравенство:
338 > N2 — 1
N2 < 339
N — положительное целое число. Тогда:
N < √339 ≈ 18
N ≤ 18
Сказано, что число в системе с основанием N оканчивается на 2. Поэтому первый остаток должен быть равен 2!
Будем идти вниз от числа 18 и проверять, на что делится 336.
Число 336 должно делится на N.
Подошло число 16 (16 * 21 = 336!)
Ответ: 16
Продолжаем подготовку к 14 заданию из ЕГЭ по информатике 2022
Задача (На понимание)
Запись числа в девятеричной системе счисления заканчивается цифрой 4. Какой будет последняя цифра в записи этого числа в троичной системе счисления?
Решение:
Подберём такие числа в десятичной системе, которые в остатке при первом делении на 9 дадут 4!
Посмотрим, какой остаток будет при делении этого же числа на 3 при первом делении. Получается 1. Это и будет ответ.
Ответ: 1
Задача (Закрепление материала)
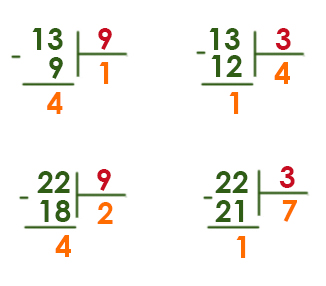
Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 23 оканчивается на 2.
Решение:
Нужно перебрать все числа от 3 до 23 и определить, какие из них при делении числа 23 дадут остаток 2.
23 : 3 = 7 (ост. 2) +
23 : 4 = 5 (ост. 3) —
23 : 5 = 4 (ост. 3) —
23 : 6 = 3 (ост. 5) —
23 : 7 = 3 (ост. 2) +
23 : 8 = 2 (ост. 7) —
23 : 9 = 2 (ост. 5) —
23 : 10 = 2 (ост. 3) —
23 : 11 = 2 (ост. 1) —
23 : 12 = 1 (ост. 11) —
23 : 13 = 1 (ост. 10) —
23 : 14 = 1 (ост. 9) —
23 : 15 = 1 (ост. 
23 : 16 = 1 (ост. 7) —
23 : 17 = 1 (ост. 6) —
23 : 18 = 1 (ост. 5) —
23 : 19 = 1 (ост. 4) —
23 : 20 = 1 (ост. 3) —
23 : 21 = 1 (ост. 2) +
23 : 22 = 1 (ост. 1) —
23 : 23 = 1 (ост. 0) —
Подходят числа 3, 7, 21.
Здесь можно и написать программу:
for i in range(3, 24): if 23%i==2: print(i)
Ответ: 3, 7, 21
Задача (Добьём 14 задание из ЕГЭ по информатике 2022)
В некоторой системе счисления записи десятичных чисел 66 и 40 заканчиваются на 1. Определите основание системы счисления.
Решение:
Нужно найти такое число, чтобы числа 66 и 40 при делении на это число давали остаток 1.
Т.е. искомое число должно быть делителем чисел 65 (66-1) и 39 (40-1). У числа 39 не так много делителей: 1, 3, 13, 39
Видим, что число 65 делится на 13 (65 : 13 = 5). Поэтому искомое число равно 13.
Ответ: 13
Задача (Для чемпионов!)
В какой системе счисления выполняется равенство 12 · 13 = 222?
В ответе укажите число – основание системы счисления.
Решение:
Если бы мы находились в десятичной системе, то последней цифрой была бы 6 (2 * 3). Но у нас 2! Т.е. Система счисления меньше или равна 6, т.к. если бы система счисления была больше 6, то у нас была бы 6 последняя цифра.
Шестёрка не «поместилась» в младший разряд, от неё осталось только 2. Остальные 4 единицы ушли в более старший разряд. Если 4 единицы составляют единицу более старшего разряда, то значит, мы находимся в четверичной системе.
Ответ: 4
Задача (Новый тип, Статград окт 2022)
В выражении 1xBAD16 + 2CxFE16 x обозначает некоторую цифру из алфавита шестнадцатеричной системы счисления. Определите наименьшее значение x, при котором значение данного выражения кратно 15. Для найденного x вычислите частное от деления данного выражения на 15 и запишите его в ответе в десятичной системе счисления.
Решение:
Здесь дана сумма чисел, которые написаны в шестнадцатеричной системе счисления.
Мы будем перебирать каждую цифру из шестнадцатеричной системы (0-15) с помощью цикла. Нас будут интересовать те значения x, при котором сумма этих чисел будет делится на 15.
for x in range(0, 16): a=13*16**0 + 10*16**1 + 11*16**2 + x*16**3 + 1*16**4 b=14*16**0 + 15*16**1 + x*16**2 + 12*16**3 + 2*16**4 if (a+b)%15==0: print(x, (a+b)//15)
Чтобы проверить, делится ли данное выражение на 15, переводим оба слагаемых в нашу родную десятичную систему. Переводим стандартным образом, об этом можно прочитать здесь.
В задаче нужно написать для наименьшего найденного значения x результат от деления данной суммы на 15.
Получается 18341
Ответ: 18341
Задача(Новый тип, закрепление)
(Богданов) Операнды арифметического выражения записаны в системе счисления с основанием 17:
9759x17 + 3×10817
В записи чисел переменной x обозначена неизвестная цифра из алфавита 17-ричной системы счисления. Определите наименьшее значение x, при котором значение данного арифметического выражения кратного 11. Для найденного значения x вычислите частное от деления значения арифметического выражения на 11 и укажите его в ответе в десятичной системе счисления. Основание системы счисления в ответе указывать не нужно.
Решение:
Решим задание с помощью предыдущего шаблона на языке Python.
for x in range(0, 17): a=x*17**0 + 9*17**1 + 5*17**2 + 7*17**3 + 9*17**4 b=8*17**0 + 0*17**1 + 1*17**2 + x*17**3 + 3*17**4 if (a+b)%11==0: print(x, (a+b)//11)
Ответ: 95306
Задача (Новый тип, две переменные)
(В. Шубинкин) Числа M и N записаны в системах счисления с основаниями 15 и 13 соответственно.
M = 2y23x515, N = 67x9y13
В записи чисел переменными x и y обозначены допустимые в данных системах счисления неизвестные цифры. Определите наименьшее значение натурального числа A, при котором существуют такие x, y, что M + A кратно N.
Решение:
Принцип решения данной задачи похож на решение 15 задания из ЕГЭ по информатике.
for A in range(1, 5000): for x in range(0, 13): for y in range(0, 13): M=5*15**0 + x*15**1 + 3*15**2 + 2*15**3 + y*15**4 + 2*15**5 N=y*13**0 + 9*13**1 + x*13**2 + 7*13**3 + 6*13**4 if (M+A)%N==0: print(A)
Нужно найти A, значит, начинаем перебирать A. Идём от 1, т.к. речь идёт о натуральных числах. Перебираем x и y. Они могут принимать значения из алфавита в 13-ой системе. Берём меньшую, т.к. эти переменные и в первом числе, и во втором одинаковые.
Если выполняется условие задачи, то нам интересно такое A при котором это произошло.
В этой задаче A получается достаточно большим, поэтому перебираем эту переменную до 5000.
Ответ: 1535
На этом всё! Вы прошли чемпионскую тренировку по подготовке 14 задания из ЕГЭ по информатике 2022. Успехов на экзамене!
«В переменную f записываем функцию». В переменную f мы записываем не функцию, а выражение
Господа, вот это я понимаю, по-настоящему чемпионская подготовка. Тут же и язык свой придумали, и решение на нём сделали. Скажите, зачем над змеёй то издеваться? Очень уж режет слух неправильное произношение. «Пайтон» — вот как должно быть. Я бы промолчал, увидев это раз, но видя подобное насилие над словом постоянно — молчать более не могу
Для ласт задачи модно сделать код куда проще и короче
for a in range(1, 10000):
for x in ‘0123456789ABC’:
for y in ‘0123456789ABC’:
M = int(f’2{y}23{x}5′, 15)
N = int(f’67{x}9{y}’, 13)
if (M + a) % N == 0:
print(a)
break
Первое задание, первое решение, очепятка: «В ответе напишем 4»,
вместо: «В ответе напишем 22».
И спасибо Вам за этот сайт!)