Образовательный портал для подготовки к экзаменам
Математика профильного уровня
Математика профильного уровня
Сайты, меню, вход, новости
Задания
Версия для печати и копирования в MS Word
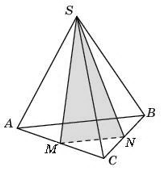
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку
Спрятать решение
Решение.
а) Имеем:
б) При помощи числовой оси отберем корни, принадлежащие отрезку
получим число
Ответ: а) б)
Спрятать критерии
Критерии проверки:
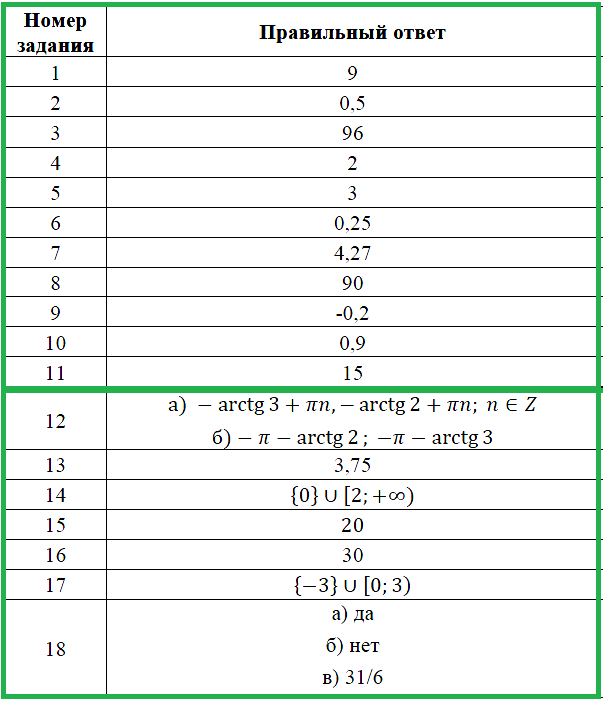
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получены верные ответы в обоих пунктах. | 2 |
| Обоснованно получен верный ответ в пункте а),
ИЛИ получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения пункта а) и пункта б). |
1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 2 |
Источник: ЕГЭ по математике 28.06.2017. Резервная волна. Восток (C часть)
Спрятать решение
·
·
Курс Д. Д. Гущина
·
Владимир Кулинич 04.01.2019 16:28
Произведение равно ноль, когда один из множителей равен нулю, а второй существует.При х=4 множитель 2cosx-1 не будет существовать. Число 4 не будет входить в общий ответ. Или я ошибаюсь?
Александр Иванов
Первое предложение верно, а в остальном Вы ошибаетесь.
517829 математика егэ
Задание 12 № 517829
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
Б) При помощи числовой оси отберем корни, принадлежащие отрезку получим число
Произведение равно ноль, когда один из множителей равен нулю, а второй существует. При х=4 множитель 2cosx-1 не будет существовать. Число 4 не будет входить в общий ответ. Или я ошибаюсь?
Задание 12 № 517829
Б При помощи числовой оси отберем корни, принадлежащие отрезку получим число.
Ege. sdamgia. ru
29.01.2019 17:24:01
2019-01-29 17:24:01
Источники:
Https://ege. sdamgia. ru/problem? id=517829
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword { color: red; } 517829 математика егэ
517829 математика егэ
517829 математика егэ
Задание 12 № 517829
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
Б) При помощи числовой оси отберем корни, принадлежащие отрезку получим число
Произведение равно ноль, когда один из множителей равен нулю, а второй существует. При х=4 множитель 2cosx-1 не будет существовать. Число 4 не будет входить в общий ответ. Или я ошибаюсь?
Задание 12 № 517829
А Решите уравнение.
Math-ege. sdamgia. ru
07.06.2018 18:49:46
2018-06-07 18:49:46
Источники:
Https://math-ege. sdamgia. ru/test? pid=517829
ЕГЭ по математике 2022 » /> » /> .keyword { color: red; } 517829 математика егэ
517829 математика егэ
517829 математика егэ
Сжатый конспект. Задание №6 профильного ЕГЭ по математике.
Алгоритм построения сечения многогранника
Статья на тему «Использование алгоритмов на уроках математики на примере алгоритма построения сечений многогранника».
Нестандартные способы решения логарифмических уравнений и неравенств
Финансово-экономическая задача
12 примеров заданий с решениями.
Задачи по стереометрии для подготовки к олимпиадам и ЕГЭ
Учебно-методическое пособие рекомендовано для учащихся старших классов в классах с углубленным изучением математики.
Рекомендации по подготовке к выполнению задания №17
Задачи с параметром. Профильный уровень.
Рекомендации по подготовке к выполнению задания №16
Планиметрическая задача на нахождение геометрических величин (длин, углов, площадей).
Рекомендации ФИПИ по организации индивидуальной подготовки к ЕГЭ по математике
Решение иррациональных неравенств
Цель пособия — повторить понятия: иррациональных чисел и их свойств, методов решения иррациональных неравенств и подготовится к занятию по теме «Решение иррациональных и тригонометрических неравенств».
Рекомендации по подготовке к выполнению задания №18
Задача, связанная со свойствами делимости целых чисел, логическим перебором.
Задачи с параметром. Профильный уровень.
Планиметрическая задача на нахождение геометрических величин (длин, углов, площадей).
Цель пособия — повторить понятия: иррациональных чисел и их свойств, методов решения иррациональных неравенств и подготовится к занятию по теме «Решение иррациональных и тригонометрических неравенств».
Рекомендации по подготовке к выполнению задания 17.
4ege. ru
16.03.2019 5:46:58
2019-03-16 05:46:58
Источники:
Https://4ege. ru/matematika/
Структура профильного уровня ЕГЭ по математике
Экзаменационная работа состоит из двух частей, которые различаются по содержанию, сложности и числу заданий:
- 8 заданий первой части (задания 1–8) с кратким ответом в виде целого числа или конечной десятичной дроби
- 4 задания второй части (задания 9–12) с кратким ответом в виде целого числа или конечной десятичной дроби
- 7 заданий второй части (задания 13–19) с развернутым ответом (полная запись решения с обоснованием выполненных действий)
Задания первой части направлены на проверку освоения базовых умений и практических навыков применения математических знаний в повседневных ситуациях.
Посредством заданий второй части осуществляется проверка освоения математики на профильном уровне, необходимом для применения математики в профессиональной деятельности и на творческом уровне.
По уровню сложности задания распределяются следующим образом:
- задания 1–8 имеют базовый уровень
- задания 9–17 – повышенный уровень
- задания 18 и 19 относятся к высокому уровню сложности
При выполнении заданий с развернутым ответом части 2 экзаменационной работы в бланке ответов № 2 должны быть записаны полное обоснованное решение и ответ для каждой задачи.
Распределение заданий по частям экзаменационной работы
| Части работы | Количество заданий | Максимальный первичный бал | Тип заданий |
| 1 часть | 8 | 8 | Краткий ответ |
| 2 часть | 11 | 24 | Развернутый ответ |
| Итого | 19 | 32 |
Разбор заданий ЕГЭ по математике (профиль)
Пробные и тренировочные варианты по математике профильного уровня в формате ЕГЭ 2023 из различных источников.
Варианты составлены в соответствии с демоверсией 2023 года
Тренировочные варианты ЕГЭ 2023 по математике (профиль)
| vk.com/pezhirovschool | |
| Вариант 1 | решения |
| Вариант 2 | решения |
| Вариант 3 | решения |
| Вариант 4 | решения |
| Вариант 5 (с ответами) | |
| Вариант 6 (с ответами) | |
| Вариант 7 (с ответами) | |
| Вариант 8 (с ответами) | |
| egemath.ru | |
| вариант 1 | скачать |
| вариант 2 | скачать |
| вариант 3 | скачать |
| вариант 4 | скачать |
| вариант 5 | скачать |
| вариант 6 | скачать |
| вариант 7 | скачать |
| вариант 8 | скачать |
| вариант 9 | скачать |
| вариант 10 | скачать |
| вариант 11 | скачать |
| вариант 12 | скачать |
| вариант 13 | скачать |
| вариант 14 | скачать |
| вариант 15 | скачать |
| вариант 16 | скачать |
| вариант 17 | скачать |
| вариант 18 | скачать |
| вариант 19 | скачать |
| вариант 20 | скачать |
| time4math.ru | |
| вариант 1-2 | ответы |
| вариант 3-4 | ответы |
| вариант 5-6 | ответы |
| вариант 7-8 | |
| yagubov.ru | |
| вариант 33 (сентябрь) | ege2023-yagubov-prof-var33 |
| вариант 34 (октябрь) | ege2023-yagubov-prof-var34 |
| вариант 35 (ноябрь) | ege2023-yagubov-prof-var35 |
| вариант 36 (декабрь) | ege2023-yagubov-prof-var36 |
| вариант 37 (январь) | ege2023-yagubov-prof-var37 |
| вариант 38 (февраль) | ege2023-yagubov-prof-var38 |
| math100.ru (с ответами) | |
| variant 179 | скачать |
| variant 180 | скачать |
| variant 181 | скачать |
| variant 182 | скачать |
| variant 183 | скачать |
| variant 184 | скачать |
| variant 185 | скачать |
| variant 186 | скачать |
| variant 187 | скачать |
| variant 188 | скачать |
| variant 189 | скачать |
| variant 190 | скачать |
| variant 191 | скачать |
| variant 192 | скачать |
| variant 193 | скачать |
| variant 194 | скачать |
| variant 195 | скачать |
| variant 196 | скачать |
| variant 197 | скачать |
| variant 198 | скачать |
| variant 199 | скачать |
| variant 200 | скачать |
| variant 201 | скачать |
| variant 202 | скачать |
| variant 203 | скачать |
| variant 204 | скачать |
| variant 205 | скачать |
| alexlarin.net | |
| Вариант 397 | проверить ответы |
| Вариант 398 | проверить ответы |
| Вариант 399 | проверить ответы |
| Вариант 400 | проверить ответы |
| Вариант 401 | проверить ответы |
| Вариант 402 | проверить ответы |
| Вариант 403 | проверить ответы |
| Вариант 404 | проверить ответы |
| Вариант 405 | проверить ответы |
| Вариант 406 | проверить ответы |
| Вариант 407 | проверить ответы |
| Вариант 408 | проверить ответы |
| Вариант 409 | проверить ответы |
| Вариант 410 | проверить ответы |
| Вариант 411 | проверить ответы |
| Вариант 412 | проверить ответы |
| Вариант 413 | проверить ответы |
| vk.com/ege100ballov | |
| вариант 1 | скачать |
| вариант 2 | скачать |
| вариант 3 | скачать |
| вариант 4 | скачать |
| вариант 5 | скачать |
| вариант 6 | скачать |
| вариант 7 | скачать |
| вариант 8 | скачать |
| вариант 9 | скачать |
| вариант 10 | скачать |
| вариант 11 | скачать |
| vk.com/math.studying | |
| Вариант 1 | ответы |
| vk.com/marsel_tutor | |
| Вариант 1 | разбор |
| Вариант 2 | конспект / разбор |
| Вариант 3 | конспект / разбор |
| Вариант 4 | конспект / разбор |
| Вариант 5 | конспект / разбор |
| Вариант 6 | разбор |
| vk.com/shkolkovo_easy_math | |
| Вариант 1 | решение |
| Вариант 2 | решение |
| Вариант 3 | решение |
| Вариант 5 | решение |
| Вариант 6 | решение |
| vk.com/mathlearn_ru | |
| вариант 1 | разбор |
| vk.com/ekaterina_chekmareva | |
| Вариант 1 | ответы |
| Вариант 2 | ответы |
| Вариант 3 | ответы |
| Вариант 4 | ответы |
| Вариант 5 | ответы |
| Вариант 6 | ответы |
| Вариант 7 | ответы |
| Вариант 8 | ответы |
Структура варианта КИМ ЕГЭ 2023 по математике профильного уровня
Экзаменационная работа состоит из двух частей и включает в себя 18 заданий, которые различаются по содержанию, сложности и количеству заданий:
– часть 1 содержит 11 заданий (задания 1–11) с кратким ответом в виде целого числа или конечной десятичной дроби;
– часть 2 содержит 7 заданий (задания 12–18) с развёрнутым ответом (полная запись решения с обоснованием выполненных действий).
Задания части 1 направлены на проверку освоения базовых умений и практических навыков применения математических знаний в повседневных ситуациях. Посредством заданий части 2 осуществляется проверка освоения математики на профильном уровне, необходимом для применения математики в профессиональной деятельности и на творческом уровне.
Задания части 1 предназначены для определения математических компетентностей выпускников образовательных организаций, реализующих программы среднего (полного) общего образования на базовом уровне. Задание с кратким ответом (1–11) считается выполненным, если в бланке ответов № 1 зафиксирован верный ответ в виде целого числа или конечной десятичной дроби.
Задания 12–18 с развёрнутым ответом, в числе которых 5 заданий повышенного уровня и 2 задания высокого уровня сложности, предназначены для более точной дифференциации абитуриентов вузов.
Примеры заданий:
1. Перед началом первого тура чемпионата по бадминтону участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 76 бадминтонистов, среди которых 22 спортсмена из России, в том числе Игорь Чаев. Найдите вероятность того, что в первом туре Игорь Чаев будет играть с каким-либо бадминтонистом из России.
2. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орёл не выпадет ни разу
3. На доске написали несколько не обязательно различных двузначных натуральных чисел без нулей в десятичной записи. Сумма этих чисел оказалась равной 363. Затем в каждом числе поменяли местами первую и вторую цифры (например, число 17 заменили на число 71).
а) Приведите пример исходных чисел, для которых сумма получившихся чисел ровно в 4 раза больше, чем сумма исходных чисел.
б) Могла ли сумма получившихся чисел быть ровно в 2 раза больше, чем сумма исходных чисел?
в) Найдите наибольшее возможное значение суммы получившихся чисел.
Смотрите также:
БАЗА ЗАДАНИЙ
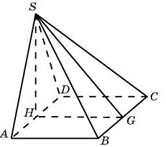
Задание № 2. Стереометрия.
81. Около шара описан цилиндр, площадь поверхности которого равна 18. Найдите площадь поверхности шара.
82. Шар вписан в цилиндр. Площадь поверхности шара равна 48. Найдите площадь полной поверхности цилиндра.
83. Шар вписан в цилиндр. Объем шара равен 6. Найдите объем цилиндра.
84. В куб с ребром 3 вписан шар. Найдите объем этого шара, деленный на π.
85. Объем прямоугольного параллелепипеда, описанного около сферы, равен 216. Найдите радиус сферы.
86. Прямоугольный параллелепипед описан около единичной сферы. Найдите его площадь поверхности.
Ответ: 24
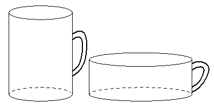
87. Первая цилиндрическая кружка вдвое выше второй, зато вторая в три раза шире. Найдите отношение объёма второй кружки к объёму первой.
88. Объем первой цилиндрической кружки равен 12. У второй кружки высота в два раза меньше, а радиус основания в три раза больше. Найдите объём второй кружки.
89. Во сколько раз увеличится объем шара, если его радиус увеличить в три раза?
90. Площадь большого круга шара равна 3. Найдите площадь поверхности шара.
91. Объем шара равен 288 π. Найдите площадь его поверхности, деленную на π.
92. Радиусы двух шаров равны 6, 8. Найдите радиус шара, площадь поверхности которого равна сумме площадей их поверхностей.
93. Объем первого шара в 27 раз больше объема второго. Во сколько раз площадь поверхности первого шара больше площади поверхности второго.
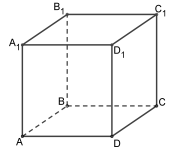
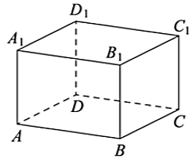
94. В кубе ABCDA1B1C1D1 найдите угол между прямыми AD1 и B1D1. Ответ дайте в градусах.
Ответ: 60
95. В кубе ABCDA1B1C1D1 точка K – середина ребра AA1, точка L — середина ребра A1B1, точка M — середина ребра A1D1. Найдите угол MLK. Ответ дайте в градусах.
Ответ: 60°
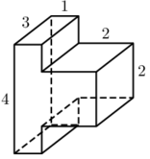
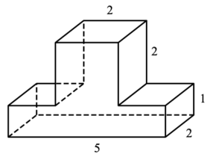
96. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
97. Найдите площадь поверхности многогранника, изображенного на рисунке.
Ответ: 50
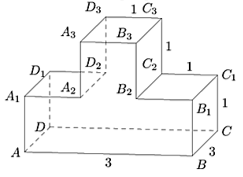
98. На рисунке изображен многогранник, все двугранные углы прямые. Найдите квадрат расстояния между вершинами A и
C3.
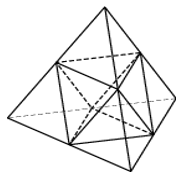
99. Объем тетраэдра равен 19. Найдите объем многогранника, вершинами которого являются середины сторон данного тетраэдра.
100. Площадь поверхности тетраэдра равен 12. Найдите площадь поверхности многогранника, вершинами которого являются середины сторон данного тетраэдра.
101. Во сколько раз увеличится площадь поверхности октаэдра, если все его ребра увеличить в 3 раза?
102. Найдите объем пространственного креста, изображенного на рисунке и составленного из единичных кубов.
103. Найдите площадь поверхности пространственного креста, изображенного на рисунке и составленного из единичных кубов.
104. Ребра тетраэдра равны 1. Найдите площадь сечения, проходящего через середины четырех его ребер.
105. Объем треугольной пирамиды SABC равен 15. Плоскость проходит через сторону AB основания этой пирамиды и пересекает противоположное боковое ребро в точке D, делящей ребро SC в отношении 1: 2, считая от вершины S. Найдите объем пирамиды DABC.
106. От треугольной пирамиды, объем которой равен 12, отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания. Найдите объем отсеченной треугольной пирамиды.
107. От призмы ABCA1B1C1, объем которой равен 6, отсечена треугольная пирамида C1ABC. Найдите объем оставшейся части.
108. Площадь осевого сечения цилиндра равна 4. Найдите площадь боковой поверхности цилиндра, деленную на π.
109. Найдите объем цилиндра, площадь основания которого равен 1, а образующая равна 6 и наклонена к плоскости основания под углом 30.
110. Конус описан около правильной четырехугольной пирамиды со стороной основания 4 и высотой 6. Найдите его объем, деленный на π.
111. Во сколько раз объем конуса, описанного около правильной четырехугольной пирамиды, больше объема конуса, вписанного в эту пирамиду?
112. В основании прямой призмы лежит квадрат со стороной 2. Боковые ребра равны 2/ π. Найдите объем цилиндра, описанного около этой призмы.
113. Найдите площадь боковой поверхности правильной треугольной призмы, вписанной в цилиндр, радиус основания которого равен 2√3, а высота равна 2.
114. Найдите площадь боковой поверхности правильной треугольной призмы, описанной около цилиндра, радиус основания которого равен √3, а высота равна 2.
115. Найдите площадь боковой поверхности правильной шестиугольной призмы, описанной около цилиндра, радиус основания которого равен √3, а высота равна 2.
116. Около куба с ребром √3 описан шар. Найдите объем этого шара, деленный на π.
117. Боковые ребра треугольной пирамиды взаимно перпендикулярны, каждое из них равно 3. Найдите объем пирамиды.
118. Основанием пирамиды служит прямоугольник, одна боковая грань перпендикулярна плоскости основания, а три другие боковые грани наклонены к плоскости основания под углом 60°. Высота пирамиды равна 6. Найдите объем пирамиды.
119. Найдите объем призмы, в основаниях которой лежат правильные шестиугольники со сторонами 2, а боковые ребра равны 2√3 и наклонены к плоскости основания под углом 30°.
120. Из единичного куба вырезана правильная четырехугольная призма со стороной основания 0,5 и боковым ребром 1. Найдите площадь поверхности оставшейся части куба.
121. В треугольной призме две боковые грани перпендикулярны. Их общее ребро равно 10 и отстоит от других боковых ребер на 6 и 8. Найдите площадь боковой поверхности этой призмы.
122. В правильной четырёхугольной призме ABCDA1B1C1D1 известно, что BD1 =2AD. Найдите угол между диагоналями DB1 и CA1. Ответ дайте в градусах.
123. В прямоугольном параллелепипеде ABCDA1B1C1D1 ребро АВ=2, ребро AD=√5, ребро AA1=2. Точка К – середина ребра BB1. Найдите площадь сечения,проходящего через точки A1, D1 и K.
124. В прямоугольном параллелепипеде
ABCDA1B1C1D1 ребро АВ=8, ребро AD=6, ребро AA1=21. Найдите синус угла между прямыми CD и A1C1.
Ответ: 0,6
125. Найдите объем правильной
треугольной пирамиды, стороны основания которой равны 1, а высота равна √3.
126. Одна из граней прямоугольного
параллелепипеда – квадрат. Диагональ параллелепипеда равна
√8 и образует с плоскостью
этой грани угол 45°. Найдите
объем параллелепипеда.
Ответ: 4
127. Найдите угол ABD1 прямоугольного параллелепипеда, для которого AB =5, AD =4, AA1 =3. Ответ дайте в градусах.
128. Найдите угол DBD1 прямоугольного параллелепипеда, для которого AB=4, AD=3, AA1=5. Ответ дайте в градусах.
Ответ: 45
Ответ: 45
ЕГЭ 2022 Математика Профильный уровень: ВАРИАНТЫ с ответами и решениями. Тренировочный вариант № 11 от 23.11.2021 г. (КИМ № 210901) от Всероссийского проекта «ЕГЭ 100 БАЛЛОВ». Составитель: Евгений Пифагор.
Инструкция по выполнению работы.
Экзаменационная работа состоит из двух частей, включающих в себя 18 заданий. Часть 1 содержит 11 заданий с кратким ответом базового и повышенного уровней сложности. Часть 2 содержит 7 заданий с развёрнутым ответом повышенного и высокого уровней сложности.
На выполнение экзаменационной работы по математике отводится 3 часа 55 минут (235 минут).
Ответы к заданиям 1–11 записываются по приведённому ниже образцу в виде целого числа или конечной десятичной дроби. Числа запишите в поля ответов в тексте работы, а затем перенесите их в бланк ответов № 1.
При выполнении заданий 12–18 требуется записать полное решение и ответ в бланке ответов № 2.
Все бланки ЕГЭ заполняются яркими чёрными чернилами. Допускается использование гелевой или капиллярной ручки.
При выполнении заданий можно пользоваться черновиком. Записи в черновике, а также в тексте контрольных измерительных материалов не учитываются при оценивании работы.
Баллы, полученные Вами за выполненные задания, суммируются. Постарайтесь выполнить как можно больше заданий и набрать наибольшее количество баллов.
После завершения работы проверьте, что ответ на каждое задание в бланках ответов №1 и №2 записан под правильным номером.
ЕГЭ Математика П 2022.
Тренировочный вариант № 11
ЧАСТЬ 1: задания 1-11
Ответом к заданиям 1–11 является целое число или конечная десятичная дробь. Запишите число в поле ответа в тексте работы, затем перенесите его в БЛАНК ОТВЕТОВ № 1 справа от номера соответствующего задания, начиная с первой клеточки. Каждую цифру, знак «минус» и запятую пишите в отдельной клеточке в соответствии с приведёнными в бланке образцами. Единицы измерений писать не нужно.
№ 1. Найдите корень уравнения (х + 9)2 = 36х.
№ 2. Механические часы с двенадцатичасовым циферблатом в какой-то момент сломались и перестали идти. Найдите вероятность того, что часовая стрелка остановилась, достигнув отметки 7, но не дойдя до отметки 1.
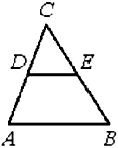
№ 3. В треугольнике ABC DE – средняя линия. Площадь треугольника CDE равна 24. Найдите площадь треугольника АВС.
№ 4. Найдите значение выражения (√1,2 • √1,4) : √0,42.
№ 5. Площадь поверхности шара равна 12. Найдите площадь большого круга шара.
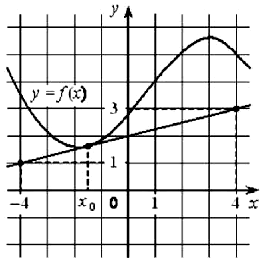
№ 6. На рисунке изображены график функции у = f(x) и касательная к нему в точке с абсциссой х0. Найдите значение производной функции f(x) в точке х0.
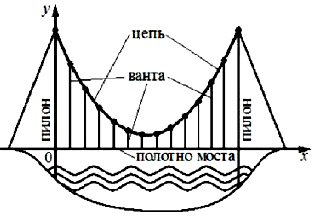
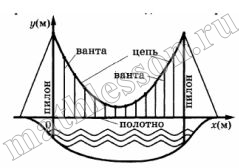
№ 7. На рисунке изображена схема моста. Вертикальные пилоны связаны провисающей цепью. Тросы, которые свисают с цепи и поддерживают полотно моста, называются вантами.
Введём систему координат: ось Оу направим вертикально вверх вдоль одного из пилонов, а ось Ох направим вдоль полотна моста, как показано на рисунке. В этой системе координат линия, по которой провисает цепь моста, задаётся формулой у = 0,0043х2 – 0,74х + 35, где х и у измеряются в метрах. Найдите длину ванты, расположенной в 70 метрах от пилона. Ответ дайте в метрах.
№ 8. Первые 120 км автомобиль ехал со скоростью 60 км/ч, следующие 200 км –со скоростью 100 км/ч, а затем 160 км – со скоростью 120 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.
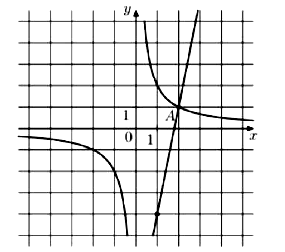
№ 9. На рисунке изображены графики функций f(x) = k/x и g(х) = ах + b, которые пересекаются в точках А и В. Найдите абсциссу точки В.
№ 10. На фабрике керамической посуды 20% произведённых тарелок имеют дефект. При контроле качества продукции выявляется 55% дефектных тарелок. Остальные тарелки поступают в продажу. Найдите вероятность того, что случайно выбранная при покупке тарелка не имеет дефектов. Ответ округлите до сотых.
№ 11. Найдите наибольшее значение функции у = ln(x + 6)3 – 3х на отрезке [–5,5; 0].
Не забудьте перенести все ответы в бланк ответов № 1 в соответствии с инструкцией по выполнению работы. Проверьте, чтобы каждый ответ был записан в строке с номером соответствующего задания.
ЧАСТЬ 2: задания 12-18
Для записи решений и ответов на задания 12–18 используйте БЛАНК ОТВЕТОВ № 2. Запишите сначала номер выполняемого задания (12, 13 и т. д.), а затем полное обоснованное решение и ответ. Ответы записывайте чётко и разборчиво.
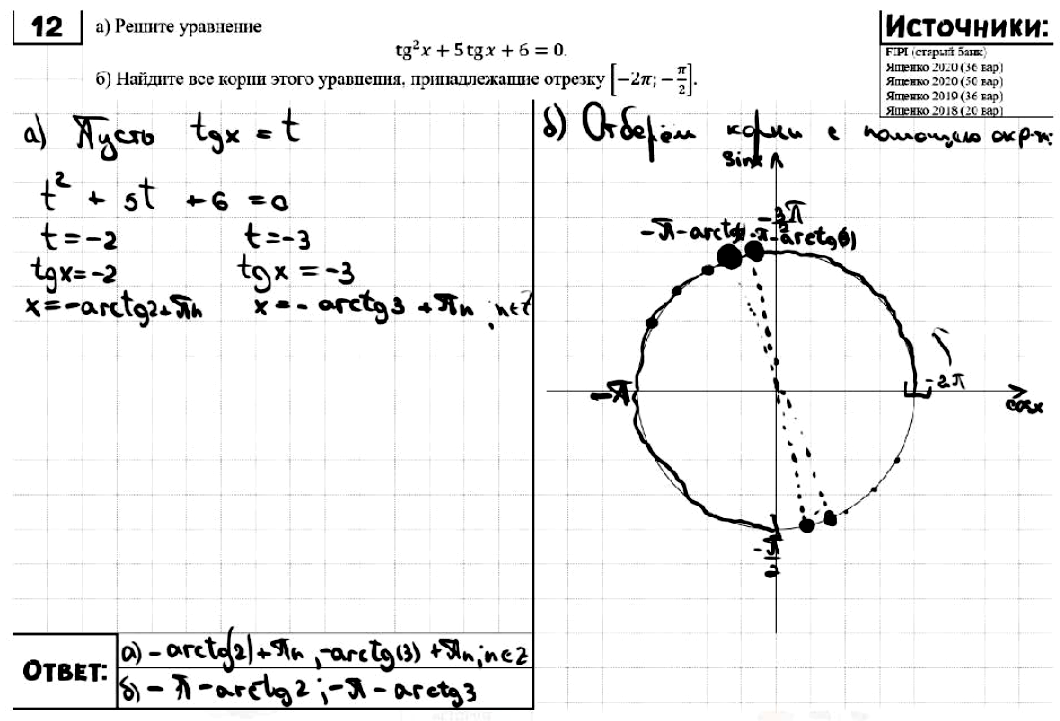
№ 12. а) Решите уравнение tg2 x + 5 tg x + 6 = 0.
б) Найдите все корни этого уравнения, принадлежащие отрезку [–2π; – π/2].
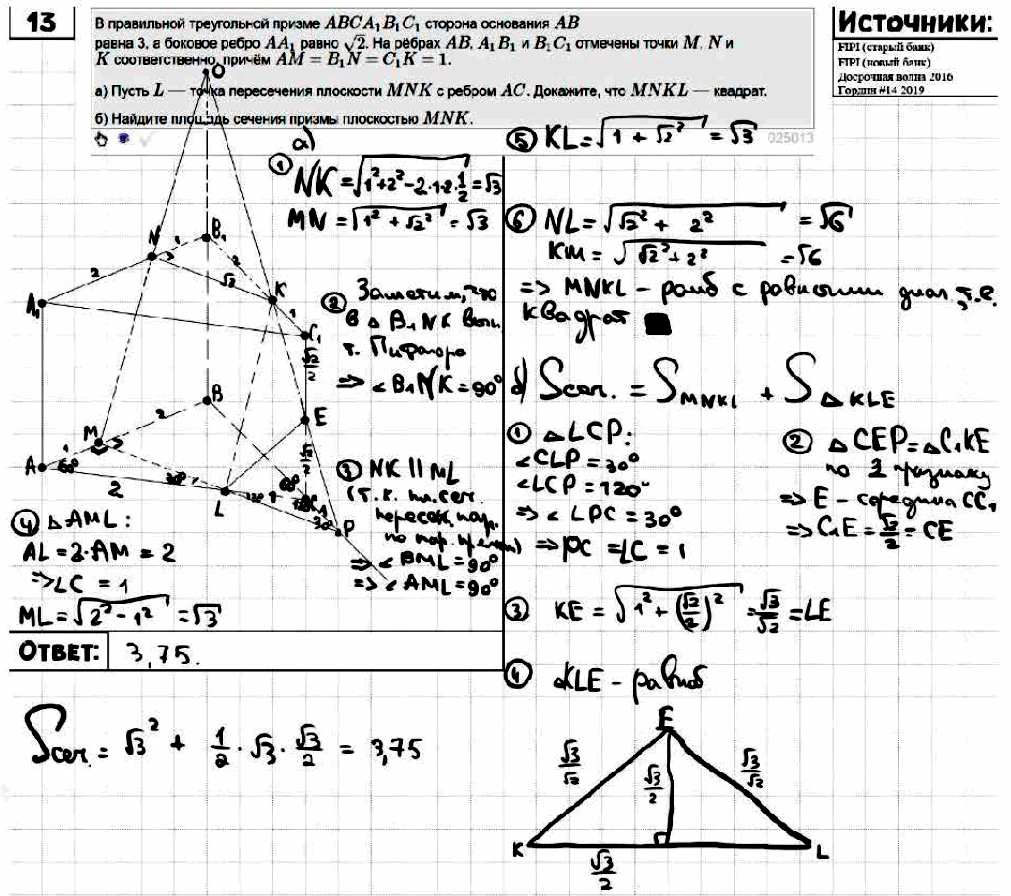
№ 13. В правильной треугольной призме АВСА1В1С1 сторона основания АВ равна 3, а боковое ребро АА1 равно √2. На рёбрах АВ, А1В1 и В1С1 отмечены точки М, N и К соответственно, причём AM = B1N = С1К = 1.
а) Пусть L – точка пересечения плоскости MNK с ребром АС. Докажите, что MNKL – квадрат.
б) Найдите площадь сечения призмы плоскостью MNK.
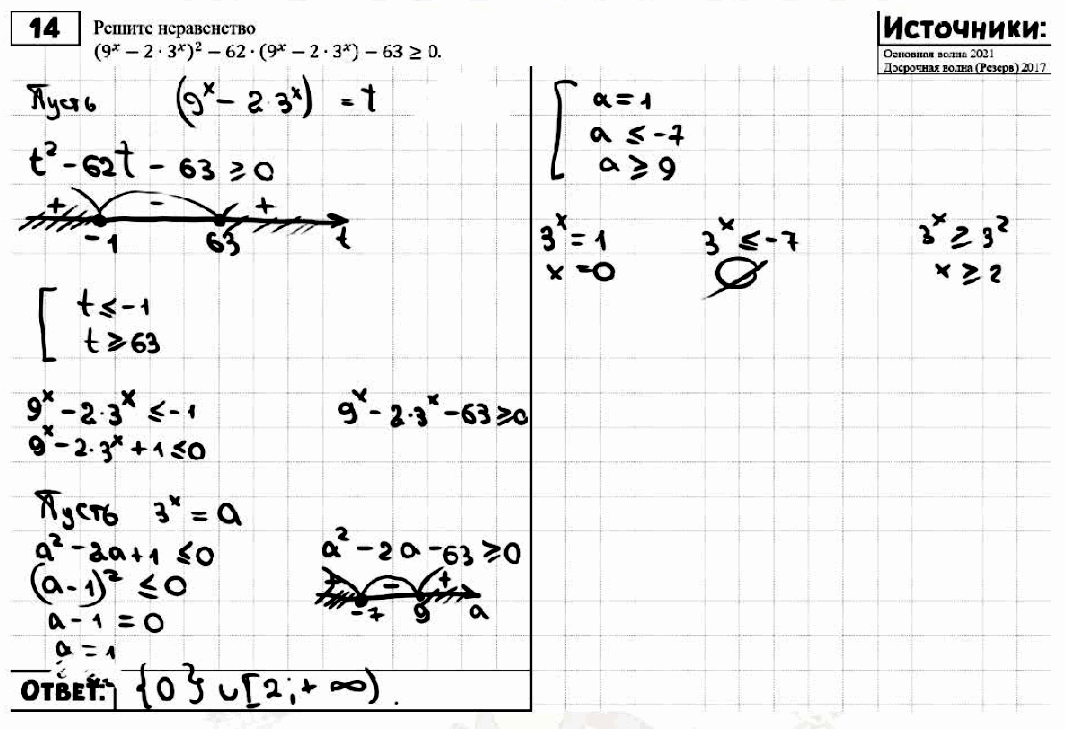
№ 14. Решите неравенство (9х –2 • 3х)2 – 62 • (9х – 2 • 3х) – 63 ≥ 0.
№ 15. В июле 2020 года планируется взять кредит в банке на сумму 300 000 рублей. Условия его возврата таковы:
– каждый январь долг увеличивается на r % по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить одним платежом часть долга.
Найдите r, если известно, что кредит будет полностью погашен за два года, причём в первый год будет выплачено 160 000 рублей, а во второй год –240 000 рублей.
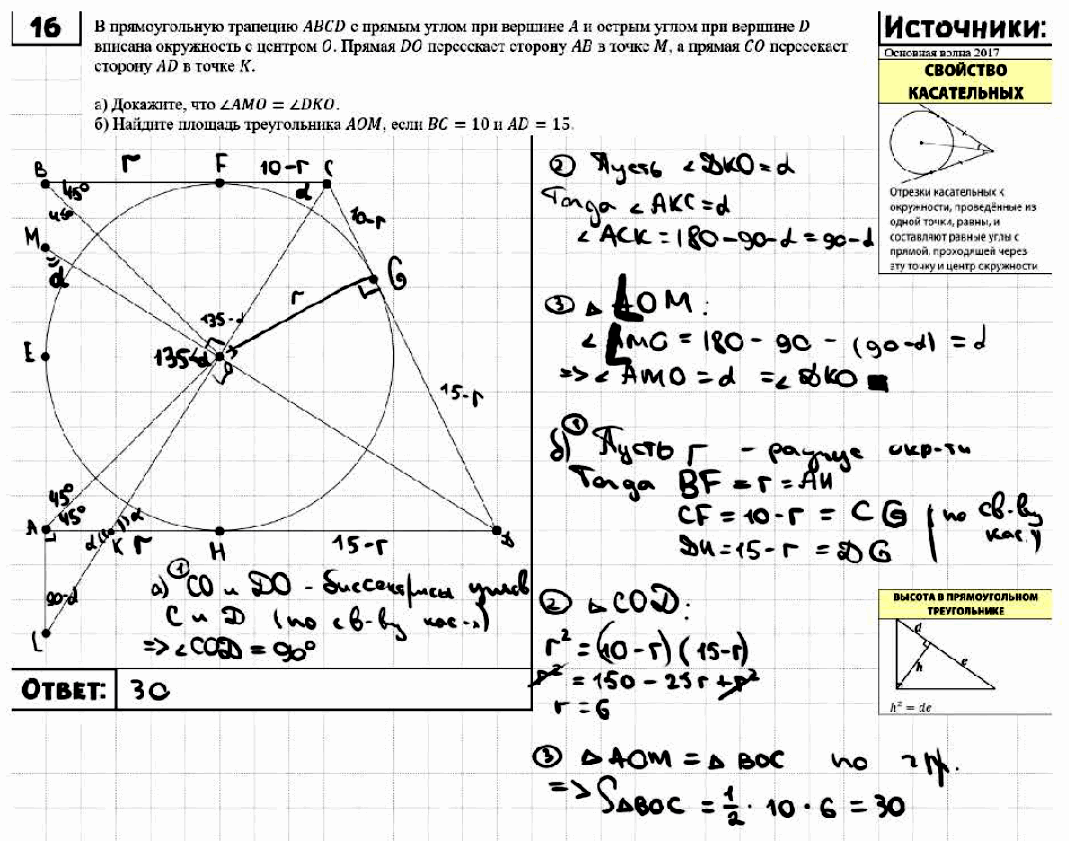
№ 16. В прямоугольную трапецию ABCD с прямым углом при вершине А и острым углом при вершине D вписана окружность с центром О. Прямая DO пересекает сторону АВ в точке М, а прямая СО пересекает сторону AD в точке К.
а) Докажите, что ∠АМО = ∠DKO.
б) Найдите площадь треугольника АОМ, если ВС = 10 и AD = 15.
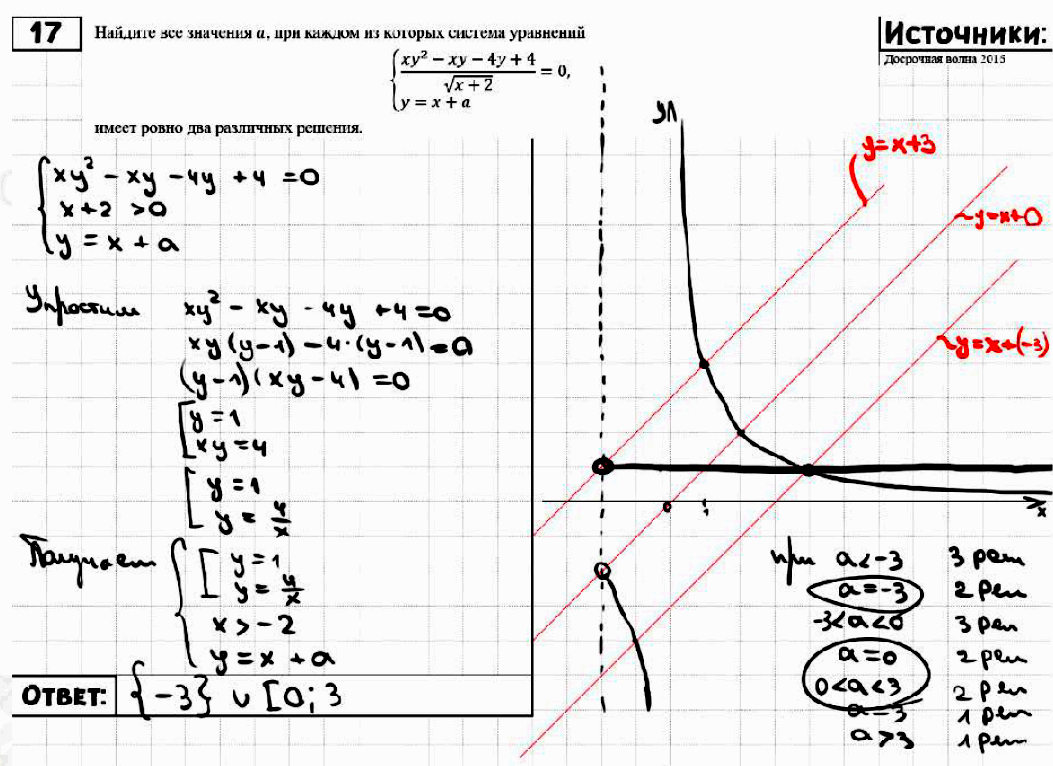
№ 17. Найдите все значения а, при каждом из которых система уравнений 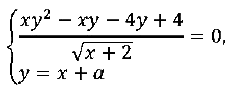
№ 18. В каждой клетке квадратной таблицы 6×6 стоит натуральное число, меньшее 7. Вася в каждом столбце находит наименьшее число и складывает шесть найденных чисел. Петя в каждой строке находит наименьшее число и складывает шесть найденных чисел.
а) Может ли сумма у Пети получиться в два раза больше, чем сумма у Васи?
б) Может ли сумма у Пети получиться в шесть раз больше, чем сумма у Васи?
в) В какое наибольшее число раз сумма у Пети может быть больше, чем сумма у Васи?
Проверьте, чтобы каждый ответ был записан рядом с номером соответствующего задания.
СКАЧАТЬ задания в формате ЕГЭ
(файл PDF)
СКАЧАТЬ Пробный вариант № 11
ОТВЕТЫ на тренировочный вариант № 11
Каждое из заданий 1–11 считается выполненными верно, если экзаменуемый дал верный ответ в виде целого числа или конечной десятичной дроби. Верный ответ на каждое задание оценивается 1 баллом.
Количество баллов, выставленных за выполнение заданий 12–18, зависит от полноты решения и правильности ответа. Общие требования к выполнению заданий с развёрнутым ответом: решение должно быть математически грамотным, полным, все возможные случаи должны быть рассмотрены. Методы решения, формы его записи и формы записи ответа могут быть разными. За решение, в котором обоснованно получен правильный ответ, выставляется максимальное количество баллов. Правильный ответ при отсутствии текста решения оценивается в 0 баллов.
РЕШЕНИЯ заданий с развернутым ответом
При выполнении заданий 12-18 могут использоваться без доказательства и ссылок любые математические факты, содержащиеся в учебниках и учебных пособиях, входящих в Федеральный перечень учебников, рекомендуемых к использованию при реализации имеющих государственную аккредитацию образовательных программ среднего общего образования.
Задание № 12. а) Решите уравнение tg2 x + 5 tg x + 6 = 0.
б) Найдите все корни этого уравнения, принадлежащие отрезку [–2π; – π/2].
ОТВЕТ: а) – arctg 3 + πn, – arctg 2 + πn; π ∈ Z;
б) –π – arctg 2; –π – arctg 3.
РЕШЕНИЕ:
Нажмите на спойлер, чтобы увидеть РЕШЕНИЕ
Задание № 13. В правильной треугольной призме АВСА1В1С1 сторона основания АВ равна 3, а боковое ребро АА1 равно √2. На рёбрах АВ, А1В1 и В1С1 отмечены точки М, N и К соответственно, причём AM = B1N = С1К = 1.
а) Пусть L – точка пересечения плоскости MNK с ребром АС. Докажите, что MNKL – квадрат.
б) Найдите площадь сечения призмы плоскостью MNK.
ОТВЕТ: б) 3,75.
РЕШЕНИЕ:
Нажмите на спойлер, чтобы увидеть РЕШЕНИЕ
Задание № 14. Решите неравенство (9х –2 • 3х)2 – 62 • (9х – 2 • 3х) – 63 ≥ 0.
ОТВЕТ: {0} ∪ [2; +oo).
РЕШЕНИЕ:
Нажмите на спойлер, чтобы увидеть РЕШЕНИЕ
Задание № 15. В июле 2020 года планируется взять кредит в банке на сумму 300 000 рублей. Условия его возврата таковы:
– каждый январь долг увеличивается на r % по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить одним платежом часть долга.
Найдите r, если известно, что кредит будет полностью погашен за два года, причём в первый год будет выплачено 160 000 рублей, а во второй год –240 000 рублей.
ОТВЕТ: r = 20.
РЕШЕНИЕ:
Нажмите на спойлер, чтобы увидеть РЕШЕНИЕ

Задание № 16. В прямоугольную трапецию ABCD с прямым углом при вершине А и острым углом при вершине D вписана окружность с центром О. Прямая DO пересекает сторону АВ в точке М, а прямая СО пересекает сторону AD в точке К.
а) Докажите, что ∠АМО = ∠DKO.
б) Найдите площадь треугольника АОМ, если ВС = 10 и AD = 15.
ОТВЕТ: б) 30.
РЕШЕНИЕ:
Нажмите на спойлер, чтобы увидеть РЕШЕНИЕ
Задание № 17. Найдите все значения а, при каждом из которых система уравнений 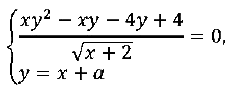
ОТВЕТ: {–3} ∪ [0; 3).
РЕШЕНИЕ:
Нажмите на спойлер, чтобы увидеть РЕШЕНИЕ
№ 18. В каждой клетке квадратной таблицы 6×6 стоит натуральное число, меньшее 7. Вася в каждом столбце находит наименьшее число и складывает шесть найденных чисел. Петя в каждой строке находит наименьшее число и складывает шесть найденных чисел.
а) Может ли сумма у Пети получиться в два раза больше, чем сумма у Васи?
б) Может ли сумма у Пети получиться в шесть раз больше, чем сумма у Васи?
в) В какое наибольшее число раз сумма у Пети может быть больше, чем сумма у Васи?
ОТВЕТ: а) да; б) нет; в) 31/6.
РЕШЕНИЕ:
Нажмите на спойлер, чтобы увидеть РЕШЕНИЕ

Вы смотрели: ЕГЭ 2022 Математика Профильный уровень: ВАРИАНТЫ с ответами и решениями. Тренировочный вариант № 11 от 23.11.2022 г. (КИМ № 210901) от Всероссийского проекта «ЕГЭ 100 БАЛЛОВ».
Просмотров:
15 233
Задание 1
В треугольнике $$АВС$$ известно, что $$АС=ВС=9,$$ $$tg A=frac{sqrt{5}}{2}.$$ Найдите $$АВ.$$
Ответ: 12
Скрыть
Пусть $$CH$$ — высота. Так как треугольник $$ABC$$ — равнобедренный, то $$AH=HB.$$
Из треугольника ACH:
$$tg A=frac{CH}{AH}=frac{sqrt{5}}{2}$$
Пусть $$CH=sqrt{5}x,$$ а $$AH=2x.$$ По теореме Пифагора:
$$(sqrt{5}x)^2+(2x)^2=9^2Leftrightarrow 9x^2=9^2Rightarrow x=3$$
Тогда $$AB=4x=12$$
Задание 2
Объем параллелепипеда $$ABCDA_1B_1C_1D_1$$ равен 3. Найдите объем треугольной пирамиды $$AD_1CB_1.$$
Ответ: 1
Скрыть
$$V_1=ABcdot BCcdot BB_1$$
$$V_{ABCB_1}=frac{1}{3}S_{осн}cdot BB_1=frac{1}{3}cdotfrac{1}{2}cdot ABcdot BCcdot BB_1=frac{1}{6}V_1$$
$$V_{AD_1CB_1}=V_1-frac{4}{6}V_1=frac{2}{6}V_1=frac{1}{3}V_1=frac{1}{3}cdot3=1$$
Задание 3
Автоматическая линия изготавливает батарейки. Вероятность того, что готовая батарейка неисправна, равна 0,03. Перед упаковкой каждая батарейка проходит систему контроля качества. Вероятность того, что неисправная батарейка будет забракована, равна 0,97. Вероятность того, что система по ошибке забракует исправную батарейку, равна 0,02. Найдите вероятность того, что случайно выбранная батарейка будет забракована системой контроля.
Ответ: 0,0485
Скрыть
Выделим два несовместных исхода, при которых система контроля бракует батарейку:
— батарейка неисправна и она бракуется системой;
— батарейка исправна и она бракуется системой.
Вероятность первого исхода равна $$P_1=0,03cdot0,97,$$ вероятность второго исхода равна $$P_2=(1-0,03)cdot0,02.$$ В результате, искомая вероятность, равна:
$$P=P_1+P_2=0,03cdot0,97+0,97cdot0,02$$
$$P=0,0291+0,0194=0,0485$$
Задание 4
Игральную кость бросали до тех пор, пока сумма всех выпавших очков не превысила число 6. Какова вероятность того, что для этого потребовалось два броска? Ответ округлите до сотых.
Ответ: 0,58
Скрыть
Найдём исходы, когда за 2 броска НЕ набралось более 6 очков:
$$11;12;13;14;15;21;22;23;24;31;32;33;41;42;51$$ — всего 15 исходов.
При $$2^x$$ бросках всего $$6cdot6=36$$ исходов. Тогда в $$36-15=21$$ исходах получили более 6 за 2 броска:
$$P(A)=frac{21}{36}=0,58(3)approx0,58$$
Задание 5
Решите уравнение $$sqrt{-x}=x+6.$$ Если уравнение имеет несколько корней, в ответе укажите их сумму.
Ответ: -4
Скрыть
$$sqrt{-x}=x+6Leftrightarrowleft{begin{matrix} -x=(x+6)^2\ x+6geq0 end{matrix}right.Leftrightarrowleft{begin{matrix} x^2+12x+36+x=0\ xgeq-6 end{matrix}right.Leftrightarrow$$
$$Leftrightarrowleft{begin{matrix} x^2+13+36=0\ xgeq-6 end{matrix}right.Leftrightarrowleft{begin{matrix} x=-4; -9\ xgeq-6 end{matrix}right.Leftrightarrow x=-4$$
Так как -9 не является корнем уравнения, то сумму не находим, тогда ответом будет -4.
Задание 6
Найдите значение выражения $$((sqrt[4]{3}-sqrt[4]{27})^2+7)cdot((sqrt[4]{3}+sqrt[4]{27})^2-7)$$
Ответ: 47
Скрыть
$$(sqrt[4]{3}-sqrt[4]{27})^2=(sqrt[4]{3}^)2−2sqrt[4]{3}cdotsqrt[4]{27}+(sqrt[4]{27})^2=$$
$$sqrt{3}-2sqrt[4]{3cdot27}+sqrt{27}=sqrt{3}-2sqrt[4]{81}+3sqrt{3}=4sqrt{3}+2cdot3=4sqrt{3}-6$$
и
$$(sqrt[4]{3}+sqrt[4]{27})^2=(sqrt[4]{3}^)2+2sqrt[4]{3}cdotsqrt[4]{27}+(sqrt[4]{27})^2=$$
$$sqrt{3}+2sqrt[4]{3cdot27}+sqrt{27}=sqrt{3}+2sqrt[4]{81}+3sqrt{3}=4sqrt{3}-2cdot3=4sqrt{3}+6$$
то
$$((sqrt[4]{3}-sqrt[4]{27})^2+7)cdot((sqrt[4]{3}+sqrt[4]{27})^2-7)=(4sqrt{3}-6+7)cdot(4sqrt{3}+6-7)=$$
$$(4sqrt{3}+1)cdot((4sqrt{3}-1)=(4sqrt{3})^2-1^2=48-1=47$$
Задание 7
На рисунке изображены график функции $$y=f(x)$$ и касательная к нему в точке с абсциссой $$x_0.$$ Найдите значение производной функции $$f(x)$$ в точке $$x_0.$$
Ответ: -2
Скрыть
Значение производной в точке равно значению тангенса между касательной к графику в эту точку и осью $$Ox.$$ Достроим прямоугольный треугольник $$A(0;2); B(0;8); C(3;2)$$
$$tg ACB=frac{AB}{AC}=frac{8-2}{3-0}=2$$
Так как функция убывает, то $$f'(x)=-2$$
Задание 8
На рисунке изображена схема вантового моста. Вертикальные пилоны связаны провисающей цепью. Тросы, которые свисают с цепи и поддерживают полотно моста, называются вантами. Введем систему координат: ось Оу направим вертикально вдоль одного из пилонов, а ось Ох направим вдоль полотна моста, как показано на рисунке. В этой системе координат линия, по которой провисает цепь моста, имеет уравнение $$y=0,0041x^{2}-0,71x+34$$, где x и y измеряются в метрах. Найдите длину ванты, расположенной в 60 метрах от пилона. Ответ дайте в метрах.
Ответ: 6,16
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$y(60)=0,0041*60^{2}-0,71*60+34=$$$$0,41*36-7,1+34=$$$$14,76-42,6+34=6,16$$
Задание 9
Имеются два сплава, состоящие из цинка, меди и олова. Известно, что первый сплав содержит 40% олова, а второй ‐ 25% меди. Процентное содержание цинка в первом и втором сплавах одинаково. Соединив 150 кг первого сплава и 250 кг второго, получили новый сплав, в котором оказалось 30% цинка. Сколько килограммов олова содержится в получившемся сплаве?
Ответ: 172,5
Скрыть
Пусть $$х$$ кг – количество олова в новом сплаве. Так как новый сплав весит 400 кг и в нём находится 30 % цинка, то он содержит $$400cdotfrac{30}{100}=120$$ кг, а во втором сплаве $$(120-y)$$ кг цинка. По условию задачи процентное содержание цинка в двух сплавах равно, следовательно, можно составить уравнение:
$$frac{100y}{150}=frac{100(120-y)}{250}$$
$$frac{y}{150}=frac{120-y}{250}$$
$$5y=3(120-y)$$
$$5y=360-3y$$
$$y=45$$
Из этого уравнения находим, что $$у = 45.$$ Поскольку первый сплав содержит 40% олова, то в 150 кг первого сплава олова будет $$150cdotfrac{40}{100}=60$$ кг, а во втором сплаве олова будет $$(х-60)$$ кг. Поскольку второй сплав содержит 26% меди, то во втором сплаве меди будет $$250cdotfrac{25}{100}=62,5$$ кг.
Во втором сплаве олова содержится $$(х-60)$$ кг, цинка $$120-45 = 75$$ (кг), меди $$62,5$$ кг и, так как весь сплав весит $$250$$ кг, то имеем:
$$x-60+75+62,5=250,$$ откуда $$x=172,5$$ кг
Задание 10
На рисунке изображен график функции $$f(x)=ax^2+bx+c,$$ где $$a,b,c$$ ‐ целые. Найдите $$f(-1).$$
Ответ: 34
Скрыть
Пусть $$f(x)=a(x-m)^2+n.$$ Вершина смещена относительно $$(0;0)$$ на 5 вправо $$Rightarrow m=5$$ и на 2 вниз $$Rightarrow n=-2.$$ Наклон параболы стандартный (соответствует $$y=x^2$$), значит $$a=1.$$ Получим $$f(x)=(x-5)^2-2.$$
Тогда $$f(-1)=(-1-5)^2-2=36-2=34$$
Задание 11
Найдите наибольшее значение функции $$y=sqrt{2lg x-1}-lg x$$
Ответ: 0
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$${y}’=frac{1}{2sqrt{2lg x-1}}*frac{2}{xln 10}-frac{1}{xln10}=0$$
$$frac{1}{xln 10}(frac{1}{2sqrt{2lg x-1}})=0$$
$$left{begin{matrix}xneq 0 \sqrt{2lg x-1}=1(1)end{matrix}right.$$
$$(1): sqrt{2lg x-1}=1Leftrightarrow$$ $$2lg x-1leq 1Leftrightarrow$$ $$2lg x=2Leftrightarrow$$ $$lg x=1Leftrightarrow x=10$$
$$y(10)=y=sqrt{2lg 10-1}-lg 10=1-1=0$$
Задание 12
А) Решите уравнение $$sqrt{2sin x+sqrt{2}}cdotlog_4(2cos x)=0$$
Б) Найдите все корни уравнения, принадлежащие отрезку $$[-frac{5pi}{2};-pi]$$
Ответ: А)$$-frac{pi}{4}+2pi n;frac{pi}{3}+2pi n,nin Z$$ б)$$-frac{9pi}{4},-frac{5pi}{3}$$
Задание 13
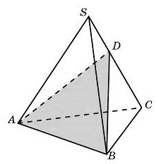
SMNK – правильный тетраэдр. На ребре SK отмечена точка Р такая, что КР:PS=1:3, точка L – середина ребра MN.
А) Доказать, что плоскости SLK и MPN перпендикулярны
Б) Найдите длину отрезка PL, если длина ребра MN равна 4.
Ответ: 3
Задание 14
Решите неравенство: $$2^{frac{x}{x+1}}-2^{frac{5x+3}{x+1}}+8leq2^{frac{2x}{x+1}}$$
Ответ: $$(-infty;-1),[0;infty)$$
Задание 15
15 января планируется взять кредит в банке на 18 месяцев. Условия его возврата таковы:
— 1‐го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца;
— со 2‐го по 14‐е число каждого месяца необходимо выплатить часть долга;
— 15‐го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15‐е число предыдущего месяца.
Сколько процентов от суммы кредита составляет общая сумма денег, которую нужно выплатить банку за весь срок кредитования?
Ответ: 119
Скрыть
Пусть кредит составляет А рублей, 2 % – процентная ставка, 18 месяцев–срок, на который взят кредит.
Ежемесячно нужно выплачивать одинаковую сумму долга $$frac{A}{n},$$
Выплаты процентов составят:
за первый месяц $$0,02cdot А$$ (сумма выплаты идет со всей взятой суммы)
за второй месяц $$0,02cdot(А–(frac{A}{18}))=0,02cdotfrac{17A}{18}$$ (сумма выплат уже уменьшилась на $$frac{1}{18}A$$)
за третий месяц $$0,02cdot(А–(frac{2A}{18}))=0,02cdotfrac{16A}{18}$$ (сумма выплат уже уменьшилась на $$frac{2}{18}A$$)
…
за 18–й месяц $$0,02cdotfrac{A}{18}$$ (сумма выплат уменьшилась на $$frac{17A}{18}$$)
Тогда за 18 месяцев придется вернуть всю взятую сумму
$$18cdotfrac{A}{18}=A$$
и проценты, т.е.
$$0,02cdot А+0,02cdotfrac{17A}{18}+…+0,02cdotfrac{A}{18}=0,02cdot А(1+frac{17A}{18}+frac{16A}{18}+cdots+frac{A}{18})$$
В скобках приводим к общему знаменателю и в числителе находим сумму 18 слагаемых от 18 до 1 по формуле суммы арифметической прогрессии.
$$А+0,02cdotfrac{А(18+17+cdots+1)}{18}=А+0,19А=1,19А$$ руб.– общая сумма выплат
А руб составляют 100%
1,19А руб. составляют х%
$$х=1,19Аcdotfrac{100}{A}=119$$%
Ответ. общая сумма денег, которую нужно выплатить банку за весь срок кредитования 119 % от суммы кредита.
Задание 16
В трапеции АВСD боковая сторона CD перпендикулярна основаниям AD и ВС. В эту трапецию вписали окружность с центром О. Прямая АО пересекает продолжение отрезка ВС в точке Е
А) Докажите, что AD=CE+CD
Б) Найдите площадь трапеции ABCD, если АЕ=10, $$angle BAD=60^{circ}$$
Ответ: $$frac{25(2+sqrt{3})}{2sqrt{3}}$$
Задание 17
Найдите все значения параметра $$a,$$ при каждом из которых уравнение
$$(x^2-4ax+a(4a-1))^2-3(x^2-4ax+a(4a-1))-|a|(|a|-3)=0$$
имеет более двух корней.
Ответ: $$(-frac{3}{2};frac{3}{2}),(frac{3}{2};infty)$$
Задание 18
А) В арифметической прогрессии $${a_n}$$ первый член $$a_1=5$$ и разность прогрессии $$d=9.$$ Какие члены прогрессии имеют четное количество делителей?
Б) В последовательности $${x_n},$$ состоящей из целых чисел, известны первые два члена: $$x_1=1, x_2=2,$$ а следующие члены последовательности находятся по формуле $$x_{n+2}=5x_{n+1}-6x_n$$ для всех $$ngeq1.$$ Какой самый большой простой делитель имеет число $$x_{2023}?$$
В) Может ли натуральное число иметь 100 делителей, если сумма его делителей является простым числом?
Ответ: А) все, Б) 2, В) нет