На рисунке изображен график производной функции f(x), определенной на интервале (−10; 2). Найдите количество точек, в которых касательная к графику функции f(x) параллельна прямой y = 3x или совпадает с ней.
Спрятать решение
Решение.
Значение производной в точке касания равно угловому коэффициенту касательной. Поскольку касательная параллельна прямой y = 3x или совпадает с ней, их угловые коэффициенты равны 3. Найдем количество точек, в которых это соответствует количеству точек пересечения графика производной с прямой y = 3. Таких точек две.
Ответ: 2.
Источник: Пробный ЕГЭ по математике, Санкт-Петербург, 04.03.2018. Вариант 1.
Новые тренировочные варианты ЕГЭ 2023 по математике базовый и профильный уровень с ответами и решением для 10 и 11 класса, больше 100 вариантов в формате реального экзамена ФИПИ вы можете решать онлайн или скачать.
Тренировочные варианты ЕГЭ 2023 по математике база и профиль
13.09.2022 Тренировочный вариант №1 ЕГЭ 2023 по математике профиль с ответами
20.09.2022 Тренировочный вариант №2 ЕГЭ 2023 по математике профиль с ответами
20.09.2022 Тренировочный вариант №2 ЕГЭ 2023 база по математике с ответами
27.09.2022 Математика 11 класс профиль входная мониторинговая работа 3 варианта с ответами
28.09.2022 Тренировочный вариант №3 ЕГЭ 2023 база по математике с ответами
28 сентября 2022 Статград математика 11 класс ЕГЭ 2023 база и профиль варианты и ответы
29 сентября 2022 Тренировочный вариант №3 ЕГЭ 2023 по математике профиль с ответами
1 октября 2022 Ларин вариант 399 ЕГЭ 2023 по математике профиль решение с ответами
6 октября Тренировочный вариант №4 ЕГЭ 2023 база по математике с ответами
6 октября Тренировочный вариант №4 ЕГЭ 2023 по математике профиль с ответами
8 октября Ларин вариант 400 ЕГЭ 2023 по математике профиль решение с ответами
12 октября Тренировочный вариант №5 ЕГЭ 2023 база по математике с ответами
12 октября Тренировочный вариант №5 ЕГЭ 2023 по математике профиль с ответами
14 октября Вариант 1 Ященко ЕГЭ 2023 математика профиль с ответами и решением
14 октября Вариант 2 Ященко ЕГЭ 2023 математика профиль с ответами и решением
15 октября Ларин вариант 401 ЕГЭ 2023 по математике профиль решение с ответами
15 октября Ларин вариант 402 ЕГЭ 2023 по математике профиль решение с ответами
16 октября Вариант 3 Ященко ЕГЭ 2023 математика профиль с ответами и решением
16 октября Вариант 4 Ященко ЕГЭ 2023 математика профиль с ответами и решением
23 октября Тренировочный вариант №6 ЕГЭ 2023 база по математике с ответами
24 октября Тренировочный вариант №6 ЕГЭ 2023 по математике профиль с ответами
25 октября Тренировочный вариант №7 ЕГЭ 2023 база по математике с ответами
26 октября Тренировочный вариант №7 ЕГЭ 2023 по математике профиль с ответами
28 октября Ларин вариант 403 ЕГЭ 2023 по математике профиль решение с ответами
29 октября Ларин вариант 404 ЕГЭ 2023 по математике профиль решение с ответами
1 ноября 2022 Тренировочный вариант №8 решу ЕГЭ 2023 база по математике с ответами
1 ноября 2022 Тренировочный вариант №8 решу ЕГЭ 2023 по математике профиль с ответами
5 ноября 2022 Вариант 1-2 распечатай и реши ЕГЭ 2023 база по математике 11 класс с ответами
6 ноября 2022 Ларин вариант 405 ЕГЭ 2023 профиль по математике решение с ответами
9 ноября 2022 Тренировочный вариант №9 решу ЕГЭ 2023 база по математике с ответами
12 ноября 2022 Тренировочный вариант №9 решу ЕГЭ 2023 по математике профиль с ответами
13 ноября 2022 Ларин вариант 406 ЕГЭ 2023 профиль по математике решение с ответами
15 ноября 2022 Тренировочный вариант №10 решу ЕГЭ 2023 база по математике 11 класс с ответами
15 ноября 2022 Тренировочный вариант №10 решу ЕГЭ 2023 по математике профиль с ответами
21 ноября 2022 Ларин вариант 407 ЕГЭ 2023 профиль по математике решение с ответами
23 ноября 2022 Тренировочный вариант №11 решу ЕГЭ 2023 база по математике 11 класс с ответами
23 ноября 2022 Тренировочный вариант №11 решу ЕГЭ 2023 по математике профиль с ответами
27 ноября 2022 Ларин вариант 408 ЕГЭ 2023 профиль по математике решение с ответами
28 ноября 2022 Вариант 3-4 распечатай и реши ЕГЭ 2023 база по математике 11 класс с ответами
30 ноября 2022 Мониторинговая работа по математике 11 класс ЕГЭ 2023 профиль 1 полугодие
3 декабря 2022 Тренировочный вариант №12 решу ЕГЭ 2023 база по математике 11 класс с ответами
3 декабря 2022 Тренировочный вариант №12 решу ЕГЭ 2023 по математике профиль с ответами
3 декабря 2022 Пробник ЕГЭ 2023 Москва по математике профиль задания и ответы
5 декабря 2022 Ларин вариант 409 ЕГЭ 2023 профиль по математике решение с ответами
9 декабря 2022 Тренировочный вариант №13 решу ЕГЭ 2023 база по математике 11 класс с ответами
10 декабря 2022 Тренировочный вариант №13 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
12 декабря 2022 Ларин вариант 410 ЕГЭ 2023 профиль по математике решение с ответами
13 декабря 2022 Статград математика 11 класс профиль ЕГЭ 2023 варианты МА2210209-МА2210212 и ответы
13 декабря 2022 Математика 11 класс база ЕГЭ 2023 статград варианты и ответы
15 декабря 2022 Тренировочный вариант №14 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
15 декабря 2022 Тренировочный вариант №14 решу ЕГЭ 2023 база по математике 11 класс с ответами
20 декабря 2022 Вариант 5-6 распечатай и реши ЕГЭ 2023 база по математике 11 класс с ответами
20 декабря 2022 Ларин вариант 411 ЕГЭ 2023 профиль по математике решение с ответами
3 января 2023 Ларин вариант 412 ЕГЭ 2023 профиль по математике решение с ответами
6 января 2023 Тренировочный вариант 1-2 ЕГЭ 2023 профиль математика задания и ответы
8 января 2023 Вариант 3-4 ЕГЭ 2023 профиль математика задания и ответы
9 января 2023 Вариант 7-8 распечатай и реши ЕГЭ 2023 база по математике 11 класс с ответами
10 января 2023 Тренировочный вариант №15 и №16 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
11 января 2023 ЕГЭ 2023 математика тренировочные задания и ответы Ященко, Семенов
11 января 2023 Тренировочный вариант №15 и №16 база ЕГЭ 2023 по математике 11 класс с ответами
19 января 2023 Тренировочные варианты №17 и №18 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
22 января 2023 Ларин вариант 413 и 414 ЕГЭ 2023 профиль по математике решение и ответы
22 января 2023 Тренировочный 19 вариант решу ЕГЭ 2023 профиль по математике 11 класс с ответами
22 января 2023 База ЕГЭ 2023 математика 11 класс тренировочный вариант 19 с ответами
25 января 2023 База ЕГЭ 2023 математика 11 класс тренировочный вариант 20 с ответами
27 января 2023 Тренировочный вариант №20 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
28 января 2023 Вариант 415 Ларина ЕГЭ 2023 по математике 11 класс задания и ответы
2 февраля 2023 Вариант 21 база ЕГЭ 2023 математика 11 класс тренировочный вариант с ответами
2 февраля 2023 Тренировочный вариант №21 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
8 февраля 2023 Математика 10-11 класс ЕГЭ 2023 статград варианты база и профиль МА2200101-МА2200110 и ответы
11 февраля 2023 Тренировочный вариант №22 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
11 февраля 2023 Тренировочный вариант №22 решу ЕГЭ 2023 база по математике 11 класс с ответами
12 февраля 2023 Вариант 416 Ларина ЕГЭ 2023 по математике 11 класс задания и ответы
12 февраля 2023 Вариант 417 Ларина ЕГЭ 2023 по математике 11 класс задания и ответы
13 февраля 2023 Вариант 9 и вариант 10 ЕГЭ 2023 база математика распечатай и реши задания
13 февраля 2023 Вариант 11 и вариант 12 ЕГЭ 2023 база математика распечатай и реши
16 февраля 2023 Тренировочный вариант №23 решу ЕГЭ 2023 база по математике 11 класс с ответами
16 февраля 2023 Тренировочный вариант №23 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
18 февраля 2023 Вариант 418 Ларина ЕГЭ 2023 по математике 11 класс задания и ответы
22 февраля 2023 Пробный ЕГЭ 2023 вариант 24 база по математике 11 класс с ответами
22 февраля 2023 Пробный ЕГЭ 2023 вариант 24 профиль по математике 11 класс с ответами
25 февраля 2023 Вариант 419 Ларина ЕГЭ 2023 по математике 11 класс задания и ответы
28 февраля 2023 Статград математика 11 класс ЕГЭ 2023 база и профиль и ответы
4 марта 2023 Пробник ЕГЭ 2023 вариант 25 база по математике 11 класс с ответами
4 марта 2023 Вариант 420 Ларин ЕГЭ 2023 по математике 11 класс задания и ответы
5 марта 2023 Пробник ЕГЭ 2023 вариант 25 профиль по математике 11 класс с ответами
8 марта 2023 Пробник ЕГЭ 2023 вариант 26 профиль по математике 11 класс с ответами
8 марта 2023 Пробник ЕГЭ 2023 вариант 26 база по математике 11 класс 100 баллов с ответами
Смотрите также на нашем сайте:
Сборник Ященко ЕГЭ 2023 математика профильный уровень 36 вариантов
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
Решу егэ математика профиль 519508
Задание 6 № 519508
На рисунке изображен график производной функции F(x), определенной на интервале (−10; 2). Найдите количество точек, в которых касательная к графику функции F(x) параллельна прямой Y = 3X или совпадает с ней.
Значение производной в точке касания равно угловому коэффициенту касательной. Поскольку касательная параллельна прямой Y = 3X или совпадает с ней, их угловые коэффициенты равны 3. Найдем количество точек, в которых это соответствует количеству точек пересечения графика производной с прямой Y = 3. Таких точек две.
Задание 6 № 519508
Поскольку касательная параллельна прямой y 3 x или совпадает с ней, их угловые коэффициенты равны 3.
Ege. sdamgia. ru
25.07.2019 13:24:27
2019-07-25 13:24:27
Источники:
Https://ege. sdamgia. ru/problem? id=519508
Решу егэ математика профиль 519508 — Математика и Английский » /> » /> .keyword { color: red; } Решу егэ математика профиль 519508
Решу егэ математика профиль 519508
Решу егэ математика профиль 519508
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
Задание 6 № 8579
На рисунке изображен график производной функции
Определенной на интервале
Найдите количество точек, в которых касательная к графику функции
Параллельна прямой или совпадает с ней.
Это задание ещё не решено, приводим решение прототипа.
На рисунке изображен график производной функции F(x), определенной на интервале (−10; 2). Найдите количество точек, в которых касательная к графику функции F(x) параллельна прямой Y = −2X − 11 или совпадает с ней.
Значение производной в точке касания равно угловому коэффициенту касательной. Поскольку касательная параллельна прямой Y = −2X − 11 или совпадает с ней, их угловые коэффициенты равны –2. Найдем количество точек, в которых это соответствует количеству точек пересечения графика производной с прямой Y = −2. На данном интервале таких точек 5.
Задание 6 № 8579
Найдите количество точек, в которых касательная к графику функции f x параллельна прямой y 2 x 11 или совпадает с ней.
Источники:
Решу егэ математика 8799 — Математика и Английский » /> » /> .keyword < color: red; >Решу егэ математика профиль 519508
Решу егэ математика 8799
Решу егэ математика 8799
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
Задание 6 № 8799
На рисунке изображен график производной функции F(x), определенной на интервале (−9; 3). Найдите количество точек, в которых касательная к графику функции F(x) параллельна прямой Y = 2X − 19 или совпадает с ней.
Значение производной в точке касания равно угловому коэффициенту касательной. Поскольку касательная параллельна прямой Y = 2X − 19 или совпадает с ней, их угловые коэффициенты равны 2. Найдем количество точек, в которых производная равна 2: геометрически это соответствует количеству точек пересечения графика производной с прямой Y = 2. На данном интервале таких точек 3.
Задание 6 № 8799
За пи сы вай тесь на бес плат ное за ня тие.
Источники:
ЕГЭ–2022, математика базовый уровень: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword Решу егэ математика 8799
Решу егэ математика 8799
Решу егэ математика 8799
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
Задания Д2 № 8799
На рисунке изображен график производной функции F(x), определенной на интервале (−9; 3). Найдите количество точек, в которых касательная к графику функции F(x) параллельна прямой Y = 2X − 19 или совпадает с ней.
Значение производной в точке касания равно угловому коэффициенту касательной. Поскольку касательная параллельна прямой Y = 2X − 19 или совпадает с ней, их угловые коэффициенты равны 2. Найдем количество точек, в которых производная равна 2: геометрически это соответствует количеству точек пересечения графика производной с прямой Y = 2. На данном интервале таких точек 3.
Задания Д2 № 8799
Уско рен ная под го тов ка к ЕГЭ с ре пе ти то ра ми Учи.
Источники:
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword Решу егэ математика 8799
Решу егэ математика 8799
Решу егэ математика 8799
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
Задание 6 № 519508
На рисунке изображен график производной функции F(x), определенной на интервале (−10; 2). Найдите количество точек, в которых касательная к графику функции F(x) параллельна прямой Y = 3X или совпадает с ней.
Значение производной в точке касания равно угловому коэффициенту касательной. Поскольку касательная параллельна прямой Y = 3X или совпадает с ней, их угловые коэффициенты равны 3. Найдем количество точек, в которых это соответствует количеству точек пересечения графика производной с прямой Y = 3. Таких точек две.
Источники:
ЕГЭ–2022, математика базовый уровень: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword Решу егэ математика 8799
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
Задания Д2 № 8799
На рисунке изображен график производной функции F(x), определенной на интервале (−9; 3). Найдите количество точек, в которых касательная к графику функции F(x) параллельна прямой Y = 2X − 19 или совпадает с ней.
Значение производной в точке касания равно угловому коэффициенту касательной. Поскольку касательная параллельна прямой Y = 2X − 19 или совпадает с ней, их угловые коэффициенты равны 2. Найдем количество точек, в которых производная равна 2: геометрически это соответствует количеству точек пересечения графика производной с прямой Y = 2. На данном интервале таких точек 3.
Задания Д2 № 8799
Уско рен ная под го тов ка к ЕГЭ с ре пе ти то ра ми Учи.
За пи сы вай тесь на бес плат ное за ня тие.
Источники:
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword < color: red; >Решу егэ математика профиль 519508
Решу егэ математика профиль 519508
Решу егэ математика профиль 519508
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
Задание 6 № 519508
На рисунке изображен график производной функции F(x), определенной на интервале (−10; 2). Найдите количество точек, в которых касательная к графику функции F(x) параллельна прямой Y = 3X или совпадает с ней.
Значение производной в точке касания равно угловому коэффициенту касательной. Поскольку касательная параллельна прямой Y = 3X или совпадает с ней, их угловые коэффициенты равны 3. Найдем количество точек, в которых это соответствует количеству точек пересечения графика производной с прямой Y = 3. Таких точек две.
Источники:
Решу егэ математика 8799 — Математика и Английский » /> » /> .keyword < color: red; >Решу егэ математика профиль 519508
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
Задание 6 № 8799
На рисунке изображен график производной функции F(x), определенной на интервале (−9; 3). Найдите количество точек, в которых касательная к графику функции F(x) параллельна прямой Y = 2X − 19 или совпадает с ней.
Значение производной в точке касания равно угловому коэффициенту касательной. Поскольку касательная параллельна прямой Y = 2X − 19 или совпадает с ней, их угловые коэффициенты равны 2. Найдем количество точек, в которых производная равна 2: геометрически это соответствует количеству точек пересечения графика производной с прямой Y = 2. На данном интервале таких точек 3.
Задание 6 № 8799
За пи сы вай тесь на бес плат ное за ня тие.
Решу егэ математика 8799.
Dankonoy. com
28.07.2018 20:50:20
2018-07-28 20:50:20
Источники:
Https://dankonoy. com/ege/ege12/archives/4576
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword { color: red; } Решу егэ математика профиль 519508
Решу егэ математика профиль 519508
Решу егэ математика профиль 519508
Задание 6 № 8585
На рисунке изображен график производной функции
Определенной на интервале
Найдите количество точек, в которых касательная к графику функции
Параллельна прямой или совпадает с ней.
Это задание ещё не решено, приводим решение прототипа.
На рисунке изображен график производной функции F(x), определенной на интервале (−10; 2). Найдите количество точек, в которых касательная к графику функции F(x) параллельна прямой Y = −2X − 11 или совпадает с ней.
Значение производной в точке касания равно угловому коэффициенту касательной. Поскольку касательная параллельна прямой Y = −2X − 11 или совпадает с ней, их угловые коэффициенты равны −2. Найдем количество точек, в которых это соответствует количеству точек пересечения графика производной с прямой Y = −2. На данном интервале таких точек 5.
Задание 6 № 8585
Параллельна прямой или совпадает с ней.
Reshuege. ru
31.12.2018 13:47:40
2018-12-31 13:47:40
Источники:
Https://reshuege. ru/test? pid=8585
Решение и ответы заданий варианта МА2210309 СтатГрад 28 февраля ЕГЭ 2023 по математике (профильный уровень). Тренировочная работа №3. ГДЗ профиль для 11 класса.
+Задания №1, №4, №6, №10 из варианта МА2210311.


Задание 1.
В треугольнике ABC угол C равен 90°, CH – высота, BC = 5, cosA=frac{2sqrt{6}}{5}. Найдите длину отрезка AH.
Задание 1 из варианта 2210311.
Найдите периметр прямоугольника, если его площадь равна 12, а отношение соседних сторон равно 1:3.
Задание 2.
Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 2. Объём параллелепипеда равен 3,2. Найдите высоту цилиндра.
Задание 3.
В группе 16 человек, среди них – Анна и Татьяна. Группу случайным образом делят на 4 одинаковые по численности подгруппы. Найдите вероятность того, что Анна и Татьяна окажутся в одной подгруппе.
Задание 4.
Агрофирма закупает куриные яйца только в двух домашних хозяйствах. Известно, что 40 % яиц из первого хозяйства – яйца высшей категории, а из второго хозяйства – 60 % яиц высшей категории. В этой агрофирме 50 % яиц высшей категории. Найдите вероятность того, что яйцо, купленное у этой агрофирмы, окажется из первого хозяйства.
Задание 4 из варианта 2210311.
Игральный кубик бросают дважды. Известно, что в сумме выпало 11 очков. Найдите вероятность того, что во второй раз выпало 5 очков.
Задание 5.
Решите уравнение frac{x–1}{5x+11}=frac{x–1}{3x-7}. Если уравнение имеет больше одного корня, в ответе запишите больший из корней.
Задание 6.
Найдите значение выражения frac{(4^{frac{3}{5} }cdot7^{frac{2}{3}})^{15}}{28^{9}} .
Задание 6 из варианта 2210311.
Найдите 98cos2α, если cosα = frac{4}{7}.
Задание 7.
На рисунке изображён график y = f’(x) – производной функции f(x), определённой на интервале (−5; 5). В какой точке отрезка [−4; −1] функция f(x) принимает наибольшее значение?
Задание 8.
На верфи инженеры проектируют новый аппарат для погружения на небольшие глубины. Конструкция имеет кубическую форму, а значит, действующая на аппарат выталкивающая (архимедова) сила, выражаемая в ньютонах, будет определяться по формуле FA = ρgl3, где l – длина ребра куба в метрах, ρ = 1000 кг/м3 – плотность воды, а g – ускорение свободного падения (считайте, что g = 9,8 Н/кг). Какой может быть максимальная длина ребра куба, чтобы обеспечить его эксплуатацию в условиях, когда выталкивающая сила при погружении будет не больше чем 2116800 Н? Ответ дайте в метрах.
Задание 9.
Пристани A и B расположены на озере, расстояние между ними равно 280 км. Баржа отправилась с постоянной скоростью из A в B. На следующий день после прибытия она отправилась обратно со скоростью на 4 км/ч больше прежней, сделав по пути остановку на 8 часов. В результате она затратила на обратный путь столько же времени, сколько на путь из A в B. Найдите скорость баржи на пути из A в B. Ответ дайте в км/ч.
Задание 10.
На рисунке изображён график функции f(x) = ax2 + bx + c. Найдите значение f(−1).
Задание 10 из варианта 2210311.
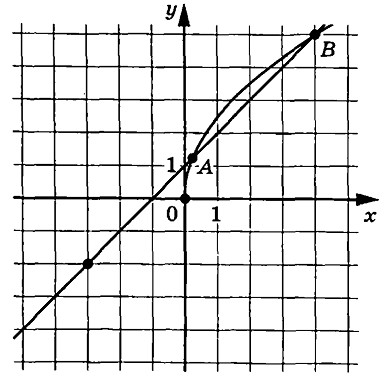
На рисунке изображены графики функций f(x) = frac{k}{x} и g(x) = ax + b, которые пересекаются в точках A и B. Найдите абсциссу точки B.
Задание 11.
Найдите точку минимума функции y = x3 − 27x2 + 13.
Задание 12.
а) Решите уравнение 2cos3x = –sin(frac{3pi}{2} + x)
б) Найдите все корни этого уравнения, принадлежащие отрезку [3π; 4π]
Задание 13.
Основанием правильной пирамиды PABCD является квадрат ABCD. Сечение пирамиды проходит через вершину В и середину ребра PD перпендикулярно этому ребру.
а) Докажите, что угол наклона бокового ребра пирамиды к её основанию равен 60°.
б) Найдите площадь сечения пирамиды, если AB = 30.
Задание 14.
Решите неравенство frac{9^{x}–13cdot 3^{x}+30}{3^{x+2}–3^{2x+1}}ge frac{1}{3^{x}}.
Задание 15.
По вкладу «А» банк в конце каждого года планирует увеличивать на 13 % сумму, имеющуюся на вкладе в начале года, а по вкладу «Б» – увеличивать эту сумму на 7 % в первый год и на целое число n процентов за второй год. Найдите наименьшее значение n, при котором за два года хранения вклад «Б» окажется выгоднее вклада «А» при одинаковых суммах первоначальных взносов.
Задание 16.
В треугольнике ABC медианы AA1, BB1 и CC1 пересекаются в точке M. Известно, что AC = 3MB.
а) Докажите, что треугольник ABC прямоугольный.
б) Найдите сумму квадратов медиан AA1 и CC1, если известно, что AC = 22.
Задание 17.
Найдите все значения a, при каждом из которых система уравнений
begin{cases} (x-5a+1)^{2}+(y-2a-1)^{2}=a-2 \ 3x-4y=2a+3 end{cases}
не имеет решений.
Задание 18.
У Ани есть 800 рублей. Ей нужно купить конверты (большие и маленькие). Большой конверт стоит 32 рубля, а маленький – 25 рублей. При этом число маленьких конвертов не должно отличаться от числа больших конвертов больше чем на пять.
а) Может ли Аня купить 24 конверта?
б) Может ли Аня купить 29 конвертов?
в) Какое наибольшее число конвертов может купить Аня?
Источник варианта: СтатГрад/statgrad.org.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 5 / 5. Количество оценок: 2
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
ЕГЭ по математике — Профиль 2022. Открытый банк заданий с ответами.
С пятым сезоном возвращается сериал «Бумажный дом». Картина рассказывает о попытке команды грабителей взять Монетный Двор в Испании. В центре внимания сюжета оказывается множество интереснейших событий, разворачивающихся во время и вокруг этого ограбления. Во главе команды стоит гениальный профессор, который разработал схему ограбления. Он считает, что его идея идеальна и очень хороша, поэтому персонаж ни капли не удивлён тому, что его ожидает, скорее всего, успех. Главный персонаж привлёк под свои знамена восемь самых мастеровитых профи своего дела. Конечно же, если им удастся провернуть дело, то персонажи получат огромные деньги. Порядка двух с половиной миллионов евро можно унести с собой. Скрыться от преследователей — самая трудная задача. Главные действующие лица начинают свою криминальную операцию. Они попадают в здание, где, как оказалось, всё далеко не так, как было в плане. Преступники оказываются в ловушке. Выходы и входы перекрыты, поэтому персонажам предстоит импровизировать, а к этому они, как оказалось, готовы не были. Теперь вместе с многочисленными заложниками главные действующие лица окажутся в течение одиннадцати дней заперты в стенах этого финансового заведения. Что же будет дальше? Удастся ли пленникам выжить?
- Название: La Casa de Papel
- Год выхода: 2017-05-02
- Страна: Испания
- Режиссер: Хесус Кольменар, Алекс Родриго, Кольдо Серра
- Статус сериала: Завершен
- Перевод: LostFilm
- Качество: FHD (1080p) (50 мин)
- Возраст: Сериал для зрителей старше 16+ лет
-
8.0
8.2
- В главных ролях: Урсула Корберо, Альваро Морте, Ициар Итуньо, Педро Алонсо, Мигель Эрран, Хайме Лорэнте, Эстер Асебо, Энрике Арсе, Дарко Перич, Альба Флорес
- Подборки: С наградами, Про ограбления, аферы и мошенников
- Жанры: Триллер, Зарубежный
5 сезон 10 серия
Бумажный дом смотреть онлайн в хорошем качестве бесплатно
Смотреть онлайн
Плеер 2
Плеер 3
Свет
Задание 1
В треугольнике $$ABC$$ известно, что $$AC=BC$$, высота $$AH$$ равна 8, $$BH=20$$. Найдите $$tg BAC$$.
Ответ: 0,4
Скрыть
Задание 2
Найдите объём многогранника, вершинами которого являются точки $$A_1$$, $$B_1$$, $$F_1$$, $$E$$ правильной шестиугольной призмы $$ABCDEFA_1B_1C_1D_1E_1F_1$$, площадь основания которой равна 10, а боковое ребро равно 9.
Ответ: 5
Скрыть
Задание 3
В группе туристов 32 человека. Их вертолётом доставляют в труднодоступный район, перевозя по 4 человека за рейс. Порядок, в котором вертолёт перевозит туристов, случаен. Найдите вероятность того, что турист Г. полетит четвёртым рейсом вертолёта.
Ответ: 0,125
Скрыть
Задание 4
Игральную кость бросали до тех пор, пока сумма всех выпавших очков не превысила число 9. Какова вероятность того, что для этого потребовалось три броска? Ответ округлите до сотых.
Ответ: 0,46
Скрыть
Задание 5
Найдите корень уравнения $$(frac{1}{9})^{x+4}=729$$
Ответ: -7
Скрыть
Задание 6
Найдите значение выражения $$log_{6}1,25cdot log_{0,8}6$$
Ответ: -1
Скрыть
Задание 7
На рисунке изображён график функции $$y=f(x)$$, определённой на интервале (-11; 2). Найдите количество точек, в которых касательная к графику функции $$y=f(x)$$ параллельна прямой $$y=-4$$.
Ответ: 7
Скрыть
Задание 8
Высота над землёй подброшенного вверх мяча меняется по закону $$h(t)=1+11t-5t^{2}$$, где $$h$$ — высота в метрах, $$t$$ — время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее 3 метров?
Ответ: 1,8
Скрыть
Задание 9
Имеется два сосуда. Первый содержит 25 кг, а второй — 20 кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 52 % кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 53 % кислоты. Сколько килограммов кислоты содержится в первом сосуде?
Ответ: 11
Скрыть
Задание 10
На рисунке изображены графики функций $$f(x)=asqrt{x}$$ и $$g(x)=kx+b$$, которые пересекаются в точках $$A$$ и $$B$$. Найдите абсциссу точки $$A$$.
Ответ: 0,25
Скрыть
Задание 11
Найдите наименьшее значение функции $$y=6x-sin x+17$$ на отрезке $$[0;frac{pi}{2}]$$
Ответ: 17
Скрыть
Задание 12
а) Решите уравнение $$log^{2}_{2}(8x^{2})-log_{4}(2x)-1=0$$
б) Найдите все корни этого уравнения, принадлежащие отрезку [0,4; 0,8].
Ответ: а)$$0,5;frac{sqrt[8]{2}}{4}$$; б)$$0,5$$
Скрыть
Задание 13
Сторона основания правильной четырёхугольной пирамиды $$SABCD$$ относится к боковому ребру как $$1:sqrt{2}$$ . Через вершину $$D$$ проведена плоскость $$alpha$$, перпендикулярная боковому ребру $$SB$$ и пересекающая его в точке $$M$$.
а) Докажите, что сечение пирамиды $$SABCD$$ плоскостью $$alpha$$ — это четырёхугольник, диагонали которого перпендикулярны.
б) Найдите площадь этого сечения, если боковое ребро пирамиды равно 6.
Ответ: $$6sqrt{3}$$
Скрыть
Задание 14
Решите неравенство $$frac{sqrt{x-2}(4-3^{x-1})}{2^{1-x^{2}}-3}geq 0$$
Ответ: $$2;[log_{3}12;+infty)$$
Скрыть
Задание 15
15 июня 2025 года Данила Сергеевич планирует взять кредит в банке на 4 года в размере целого числа миллионов рублей. Условия его возврата таковы:
— в январе каждого года действия кредита долг увеличивается на 15 % от суммы долга на конец предыдущего года;
— в период с февраля по июнь в каждый из 2026 и 2027 годов необходимо выплатить только начисленные в январе проценты по кредиту;
— в период с февраля по июнь в каждый из 2028 и 2029 годов выплачиваются равные суммы, причём последний платёж должен погасить долг по кредиту полностью.
Найдите наибольший размер кредита, при котором общая сумма выплат по кредиту не превысит 20 млн рублей.
Ответ: 13 млн. руб.
Скрыть
Задание 16
Окружность с центром в точке $$C$$ касается гипотенузы $$AB$$ прямоугольного треугольника $$ABC$$ и пересекает его катеты $$AC$$ и $$BC$$ в точках $$E$$ и $$F$$. Точка $$D$$ — основание высоты, опущенной на $$AB$$. $$I$$ и $$J$$ — центры окружностей, вписанных в треугольники $$BCD$$ и $$ACD$$.
а) Докажите, что точки $$E$$ и $$F$$ лежат на прямой $$IJ$$.
б) Найдите расстояние от точки $$C$$ до прямой $$IJ$$, если $$AC=2sqrt{3}$$, $$BC=2$$.
Ответ: $$frac{sqrt{6}}{2}$$
Скрыть
Задание 17
Найдите все значения $$a$$, при каждом из которых оба уравнения $$a+frac{x}{3}=|x|$$ и $$2a+x=sqrt{2a^{2}+4ax-x^{2}+12}$$ имеют ровно по 2 различных корня, и строго между корнями каждого из уравнений лежит корень другого уравнения.
Ответ: $$(frac{2sqrt{6}}{sqrt{13}};frac{4sqrt{6}}{5})$$
Скрыть
Задание 18
Трёхзначное число, меньшее 700, поделили на сумму его цифр и получили натуральное число $$n$$.
а) Может ли $$n$$ равняться 64?
б) Может ли $$n$$ равняться 78?
в) Какое наибольшее значение может принимать $$n$$, если все цифры ненулевые?
Ответ: а)да б)нет в)73
Скрыть