Вокруг куба ABCDA1B1C1D1 с ребром 3 описана сфера. На ребре CC1 взята точка M так, что плоскость, проходящая через точки A, B и M, образует угол 15° с плоскостью ABC.
a) Постройте линию пересечения сферы и плоскости, проходящей через точки A, B и M.
б) Найдите длину линии пересечения плоскости сечения и сферы
Спрятать решение
Решение.
а) Сечение сферы плоскостью является окружностью. Пусть прямая BM пересекает сферу в точке K. Искомая линия пересечения сферы и плоскости — окружность, описанная около треугольника ABK.
б) Точка K — точка пересечения прямой BM c описанной окружностью квадрата
так как BC1 — диаметр окружности, поэтому
Так как то
откуда
Так как треугольник ABK прямоугольный, то длина описанной около него окружности равна произведению ее диаметра на число Вычисляя
получаем ответ
Ответ:
Спрятать критерии
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Имеется верное доказательство утверждения пункта a) и обоснованно получен верный ответ в пункте б) | 3 |
| Получен обоснованный ответ в пункте б)
ИЛИ имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки |
2 |
| Имеется верное доказательство утверждения пункта а)
ИЛИ при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, ИЛИ обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен |
1 |
| Решение не соответствует ни одному из критериев, приведённых выше | 0 |
| Максимальный балл | 3 |
Источник: Типовые тестовые задания по математике под редакцией И.В. Ященко, 2018.
Решу егэ профиль математика 517739
Задание 12 № 517746
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
А) Из уравнения получаем:
Б) Заметим, что Значит, указанному отрезку принадлежит корень −3.
Ответ: а) −3 и 27; б) −3.
Аналоги к заданию № 517739: 517746 517747 Все
Задание 12 № 517747
Задание 12 № 517746
Задание 12 № 517747
Ответ а 3 и 27; б 3.
Ege. sdamgia. ru
12.01.2020 13:48:01
2020-01-12 13:48:01
Источники:
Https://ege. sdamgia. ru/test? likes=517739
Решу егэ профиль математика 517739 — Математика и Английский » /> » /> .keyword { color: red; } Решу егэ профиль математика 517739
Решу егэ профиль математика 517739
Решу егэ профиль математика 517739
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
Задание 12 № 517746
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
А) Из уравнения получаем:
Б) Заметим, что Значит, указанному отрезку принадлежит корень −3.
Ответ: а) −3 и 27; б) −3.
Аналоги к заданию № 517739: 517746 517747 Все
Задание 12 № 517747
Задание 12 № 517746
Б Заметим, что Значит, указанному отрезку принадлежит корень 3.
Источники:
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword < color: red; >Решу егэ профиль математика 517739
Решу егэ профиль математика 517739
Решу егэ профиль математика 517739
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
Задание 12 № 514082
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
А) Запишем исходное уравнение в виде:
Б) Поскольку отрезку принадлежит единственный корень −2.
Ответ: а) −2; 1, б) −2.
Почему такое странное ОДЗ?? Где 2-х>0, х>0, следовательно х0; тогда х (0;2)
Екатерина, в решении не находили ОДЗ.
В решении было использован равносильный переход, при котором условия достаточно для решения примера
А у Вас ОДЗ найдено с ошибкой.
Задание 12 № 517739
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
А) Из уравнения получаем:
Б) Заметим, что Значит, указанному отрезку принадлежит только корень −2.
Ответ: а) −2 и 16; б) −2.
В пункте «а» ответ только 16,вы не проверили ОДЗ
В этом уравнении не нужно искать ОДЗ. Это лишнее действие
Задание 12 № 502094
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие промежутку
А) Заметим, что преобразуем исходное уравнение:
Пусть тогда уравнение запишется в виде откуда или
При получим: откуда
При получим: откуда
Б) Корень не принадлежит промежутку Поскольку и корень принадлежит промежутку
Источник: ЕГЭ по математике 19.06.2013. Основная волна, резервный день. Центр. Вариант 502., Задания 13 (С1) ЕГЭ 2013
В строчке а) откуда-то взялась «3»
Путём каких преобразований мы получили ответ log(3)5 ?
1) Уравнение начинается с числе 9 в степени. Т. е. Мы раскладываем 9 как 3*3. Однако в первой строке решения мы видим 9*3. От туда и дальнейшее неверное вычисление.
2) Когда мы возвращаем замену (четвёртая строчка решения) вместо этого (если, допустим, t и правда равно 5/3) должно получиться Х-1= логорифм 5/3 по основанию 3. Верно?
Так ли это? Ибо мне свойственно ошибаться. Это правда ошибка, или я чего-то не понимаю? Если второе, то объясните, если можно.
Задание 12 № 517739
Задание 12 № 502094
Задание 12 502094.
Источники:
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword < color: red; >Решу егэ профиль математика 517739
Решу егэ профиль математика 517739
Решу егэ профиль математика 517739
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
Диагональ экрана телевизора равна 64 дюймам. Выразите диагональ экрана в сантиметрах, если в одном дюйме 2,54 см. Результат округлите до целого числа сантиметров.
Источники:
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword < color: red; >Решу егэ профиль математика 517739
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
Задание 12 № 514082
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
А) Запишем исходное уравнение в виде:
Б) Поскольку отрезку принадлежит единственный корень −2.
Ответ: а) −2; 1, б) −2.
Почему такое странное ОДЗ?? Где 2-х>0, х>0, следовательно х0; тогда х (0;2)
Екатерина, в решении не находили ОДЗ.
В решении было использован равносильный переход, при котором условия достаточно для решения примера
А у Вас ОДЗ найдено с ошибкой.
Задание 12 № 517739
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
А) Из уравнения получаем:
Б) Заметим, что Значит, указанному отрезку принадлежит только корень −2.
Ответ: а) −2 и 16; б) −2.
В пункте «а» ответ только 16,вы не проверили ОДЗ
В этом уравнении не нужно искать ОДЗ. Это лишнее действие
Задание 12 № 502094
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие промежутку
А) Заметим, что преобразуем исходное уравнение:
Пусть тогда уравнение запишется в виде откуда или
При получим: откуда
При получим: откуда
Б) Корень не принадлежит промежутку Поскольку и корень принадлежит промежутку
Источник: ЕГЭ по математике 19.06.2013. Основная волна, резервный день. Центр. Вариант 502., Задания 13 (С1) ЕГЭ 2013
В строчке а) откуда-то взялась «3»
Путём каких преобразований мы получили ответ log(3)5 ?
1) Уравнение начинается с числе 9 в степени. Т. е. Мы раскладываем 9 как 3*3. Однако в первой строке решения мы видим 9*3. От туда и дальнейшее неверное вычисление.
2) Когда мы возвращаем замену (четвёртая строчка решения) вместо этого (если, допустим, t и правда равно 5/3) должно получиться Х-1= логорифм 5/3 по основанию 3. Верно?
Так ли это? Ибо мне свойственно ошибаться. Это правда ошибка, или я чего-то не понимаю? Если второе, то объясните, если можно.
Задание 12 № 517739
Задание 12 № 502094
Задание 12 502094.
Уско рен ная под го тов ка к ЕГЭ с ре пе ти то ра ми Учи.
Dankonoy. com
16.06.2020 6:45:22
2020-06-16 06:45:22
Источники:
Https://dankonoy. com/ege/ege11/archives/10087
Материал для подготовки к экзамену по математике 1 курс. » /> » /> .keyword { color: red; } Решу егэ профиль математика 517739
Материал для подготовки к экзамену по математике 1 курс
Материал для подготовки к экзамену по математике 1 курс.
Материал для подготовки к экзамену по математике для 1 курса СПО.
Просмотр содержимого документа
«Материал для подготовки к экзамену по математике 1 курс.»
Логарифмические уравнения
1. Задание 5 № 26646
Найдите корень уравнения
2. Задание 5 № 26647
Найдите корень уравнения
3. Задание 5 № 26648
Найдите корень уравнения
4. Задание 5 № 26649
Найдите корень уравнения
5. Задание 5 № 26657
Найдите корень уравнения
6. Задание 5 № 26658
Найдите корень уравнения
7. Задание 5 № 26659
Найдите корень уравнения
8. Задание 5 № 77380
Решите уравнение
9. Задание 5 № 77381
Решите уравнение
10. Задание 5 № 77382
Решите уравнение Если уравнение имеет более одного корня, в ответе укажите меньший из них.
11. Задание 5 № 315120
Найдите корень уравнения
12. Задание 5 № 315535
Найдите корень уравнения
13. Задание 5 № 525399
Решите уравнение
Тригонометрические уравнения
1. Задание 5 № 26669
Найдите корни уравнения: В ответ запишите наибольший отрицательный корень.

Значениям соответствуют положительные корни.
Если, то и
Если, то и
Значениям соответствуют меньшие значения корней.
Следовательно, наибольшим отрицательным корнем является число
2. Задание 5 № 77376
Решите уравнение В ответе напишите наибольший отрицательный корень.
Значению соответствует Положительным значениям параметра соответствуют положительные значения корней, отрицательным значениям параметра соответствуют меньшие значения корней. Следовательно, наибольшим отрицательным корнем является число −1.
3. Задание 5 № 77377
Решите уравнение В ответе напишите наименьший положительный корень.
Значениям соответствуют отрицательные корни.
Если, то и
Если, то и
Значениям соответствуют большие положительные корни.
Наименьшим положительным решением является 0,5.
Преобразования числовых логарифмических выражений
1. Задание 9 № 26843
Найдите значение выражения
2. Задание 9 № 26844
Найдите значение выражения
3. Задание 9 № 26845
Найдите значение выражения
4. Задание 9 № 26846
Найдите значение выражения
5. Задание 9 № 26847
Найдите значение выражения
6. Задание 9 № 26848
Найдите значение выражения
7. Задание 9 № 26849
Найдите значение выражения
8. Задание 9 № 26850
Найдите значение выражения
9. Задание 9 № 26851
Найдите значение выражения
10. Задание 9 № 26852
Найдите значение выражения
11. Задание 9 № 26853
Найдите значение выражения
12. Задание 9 № 26854
Найдите значение выражения
13. Задание 9 № 26855
Найдите значение выражения
14. Задание 9 № 26856
Найдите значение выражения
15. Задание 9 № 26857
Найдите значение выражения
16. Задание 9 № 26858
Найдите значение выражения
17. Задание 9 № 26859
Найдите значение выражения
18. Задание 9 № 26860
Найдите значение выражения
19. Задание 9 № 26861
Найдите значение выражения
20. Задание 9 № 26862
Найдите значение выражения
21. Задание 9 № 26882
Найдите значение выражения
22. Задание 9 № 26883
Найдите значение выражения
23. Задание 9 № 26885
Найдите значение выражения
24. Задание 9 № 26889
Найдите значение выражения
25. Задание 9 № 26892
Найдите значение выражения
26. Задание 9 № 26893
Найдите значение выражения
27. Задание 9 № 26894
Найдите значение выражения
28. Задание 9 № 26896
Найдите значение выражения
29. Задание 9 № 77418
Вычислите значение выражения:
30. Задание 9 № 505097
Найдите значение выражения
31. Задание 9 № 509086
Найдите значение выражения
32. Задание 9 № 510939
Найдите значение выражения
33. Задание 9 № 525403
Найдите значение выражения
Вычисление значений тригонометрических выражений
1. Задание 9 № 26775
Найдите, если и
2. Задание 9 № 26776
Найдите, если и
3. Задание 9 № 26777
Найдите, если и
4. Задание 9 № 26778
Найдите, если и
5. Задание 9 № 26779
Найдите, если
6. Задание 9 № 26780
Найдите, если
7. Задание 9 № 26783
Найдите значение выражения, если
8. Задание 9 № 26784
Найдите, если и
9. Задание 9 № 26785
Найдите, если и
10. Задание 9 № 26786
Найдите, если
11. Задание 9 № 26787
Найдите, если
12. Задание 9 № 26788
Найдите, если
13. Задание 9 № 26789
Найдите, если
14. Задание 9 № 26790
Найдите, если
15. Задание 9 № 26791
Найдите, если
16. Задание 9 № 26792
Найдите значение выражения, если
17. Задание 9 № 26793
Найдите значение выражения, если
18. Задание 9 № 26794
Найдите, если
19. Задание 9 № 316350
Найдите, если
20. Задание 9 № 501598
Найдите значение выражения
21. Задание 9 № 502014
Найдите значение выражения
22. Задание 9 № 502045
Найдите значение выражения
23. Задание 9 № 502106
Найдите значение выражения
24. Задание 9 № 502285
Найдите значение выражения
25. Задание 9 № 502305
Найдите значение выражения если и
26. Задание 9 № 504410
Найдите значение выражения:
27. Задание 9 № 504824
Найдите значение выражения
28. Задание 9 № 508966
Найдите если
29. Задание 9 № 510424
Найдите если и
30. Задание 9 № 549336
Найдите если и
Преобразования числовых тригонометрических выражений
1. Задание 9 № 26755
Найдите значение выражения
2. Задание 9 № 26756
Найдите значение выражения
3. Задание 9 № 26757
Найдите значение выражения
4. Задание 9 № 26758
Найдите значение выражения
5. Задание 9 № 26759
Найдите значение выражения
6. Задание 9 № 26760
Найдите значение выражения
7. Задание 9 № 26761
Найдите значение выражения
8. Задание 9 № 26762
Найдите значение выражения
9. Задание 9 № 26763
Найдите значение выражения
10. Задание 9 № 26764
Найдите значение выражения
11. Задание 9 № 26765
Найдите значение выражения
12. Задание 9 № 26766
Найдите значение выражения
13. Задание 9 № 26767
Найдите значение выражения
14. Задание 9 № 26769
Найдите значение выражения
15. Задание 9 № 26770
Найдите значение выражения
16. Задание 9 № 26771
Найдите значение выражения
17. Задание 9 № 26772
Найдите значение выражения
18. Задание 9 № 26773
Найдите значение выражения
19. Задание 9 № 26774
Найдите значение выражения
20. Задание 9 № 77412
Найдите значение выражения
21. Задание 9 № 77413
Найдите значение выражения
22. Задание 9 № 77414
Найдите значение выражения:
23. Задание 9 № 245169
Найдите значение выражения
24. Задание 9 № 245170
Найдите значение выражения
25. Задание 9 № 245171
Найдите значение выражения
26. Задание 9 № 245172
Найдите значение выражения
27. Задание 9 № 501701
Найдите значение выражения
28. Задание 9 № 502994
Найдите значение выражения
29. Задание 9 № 503310
Найдите значения выражения
30. Задание 9 № 510013
Найдите если и
31. Задание 9 № 510312
Найдите значение выражения
32. Задание 9 № 510386
Найдите значение выражения
33. Задание 9 № 510405
Найдите значение выражения
34. Задание 9 № 510824
Найдите значение выражения
35. Задание 9 № 510843
Найдите значение выражения
36. Задание 9 № 525113
Найдите значение выражения
37. Задание 9 № 526009
Найдите значение выражения
Логарифмические и показательные уравнения
1. Задание 13 № 514082
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
2. Задание 13 № 517739
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
3. Задание 13 № 502094
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие промежутку
4. Задание 13 № 516760
А) Решите уравнение:
Б) Определите, какие из его корней принадлежат отрезку
5. Задание 13 № 514623
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие отрезку
6. Задание 13 № 502053
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие отрезку
7. Задание 13 № 525377
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие отрезку
8. Задание 13 № 513605
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
9. Задание 13 № 503127
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие отрезку
10. Задание 13 № 514081
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащего отрезку
11. Задание 13 № 502999
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие отрезку [−1; 2].
12. Задание 13 № 528517
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
13. Задание 13 № 550261
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие промежутку
14. Задание 13 № 555265
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
15. Задание 13 № 555583
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
16. Задание 13 № 561853
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие отрезку [−2,5; −1,5].
17. Задание 13 № 562032
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие отрезку [−0,5; 0,5].
18. Задание 13 № 562757
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие отрезку
б) Укажите корни этого уравнения, принадлежащие отрезку
Решите уравнение В ответе напишите наименьший положительный корень.
Просмотр содержимого документа «Материал для подготовки к экзамену по математике 1 курс.»
Б Укажите корни этого уравнения, принадлежащие отрезку.
Multiurok. ru
06.02.2020 18:29:01
2020-02-06 18:29:01
Источники:
Https://multiurok. ru/files/material-dlia-podgotovki-k-ekzamenu-po-matematike. html
Решение и ответы заданий варианта МА2210309 СтатГрад 28 февраля ЕГЭ 2023 по математике (профильный уровень). Тренировочная работа №3. ГДЗ профиль для 11 класса.
+Задания №1, №4, №6, №10 из варианта МА2210311.


Задание 1.
В треугольнике ABC угол C равен 90°, CH – высота, BC = 5, cosA=frac{2sqrt{6}}{5}. Найдите длину отрезка AH.
Задание 1 из варианта 2210311.
Найдите периметр прямоугольника, если его площадь равна 12, а отношение соседних сторон равно 1:3.
Задание 2.
Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 2. Объём параллелепипеда равен 3,2. Найдите высоту цилиндра.
Задание 3.
В группе 16 человек, среди них – Анна и Татьяна. Группу случайным образом делят на 4 одинаковые по численности подгруппы. Найдите вероятность того, что Анна и Татьяна окажутся в одной подгруппе.
Задание 4.
Агрофирма закупает куриные яйца только в двух домашних хозяйствах. Известно, что 40 % яиц из первого хозяйства – яйца высшей категории, а из второго хозяйства – 60 % яиц высшей категории. В этой агрофирме 50 % яиц высшей категории. Найдите вероятность того, что яйцо, купленное у этой агрофирмы, окажется из первого хозяйства.
Задание 4 из варианта 2210311.
Игральный кубик бросают дважды. Известно, что в сумме выпало 11 очков. Найдите вероятность того, что во второй раз выпало 5 очков.
Задание 5.
Решите уравнение frac{x–1}{5x+11}=frac{x–1}{3x-7}. Если уравнение имеет больше одного корня, в ответе запишите больший из корней.
Задание 6.
Найдите значение выражения frac{(4^{frac{3}{5} }cdot7^{frac{2}{3}})^{15}}{28^{9}} .
Задание 6 из варианта 2210311.
Найдите 98cos2α, если cosα = frac{4}{7}.
Задание 7.
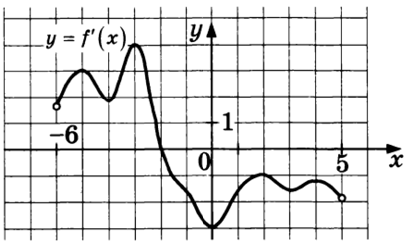
На рисунке изображён график y = f’(x) – производной функции f(x), определённой на интервале (−5; 5). В какой точке отрезка [−4; −1] функция f(x) принимает наибольшее значение?
Задание 8.
На верфи инженеры проектируют новый аппарат для погружения на небольшие глубины. Конструкция имеет кубическую форму, а значит, действующая на аппарат выталкивающая (архимедова) сила, выражаемая в ньютонах, будет определяться по формуле FA = ρgl3, где l – длина ребра куба в метрах, ρ = 1000 кг/м3 – плотность воды, а g – ускорение свободного падения (считайте, что g = 9,8 Н/кг). Какой может быть максимальная длина ребра куба, чтобы обеспечить его эксплуатацию в условиях, когда выталкивающая сила при погружении будет не больше чем 2116800 Н? Ответ дайте в метрах.
Задание 9.
Пристани A и B расположены на озере, расстояние между ними равно 280 км. Баржа отправилась с постоянной скоростью из A в B. На следующий день после прибытия она отправилась обратно со скоростью на 4 км/ч больше прежней, сделав по пути остановку на 8 часов. В результате она затратила на обратный путь столько же времени, сколько на путь из A в B. Найдите скорость баржи на пути из A в B. Ответ дайте в км/ч.
Задание 10.
На рисунке изображён график функции f(x) = ax2 + bx + c. Найдите значение f(−1).
Задание 10 из варианта 2210311.
На рисунке изображены графики функций f(x) = frac{k}{x} и g(x) = ax + b, которые пересекаются в точках A и B. Найдите абсциссу точки B.
Задание 11.
Найдите точку минимума функции y = x3 − 27x2 + 13.
Задание 12.
а) Решите уравнение 2cos3x = –sin(frac{3pi}{2} + x)
б) Найдите все корни этого уравнения, принадлежащие отрезку [3π; 4π]
Задание 13.
Основанием правильной пирамиды PABCD является квадрат ABCD. Сечение пирамиды проходит через вершину В и середину ребра PD перпендикулярно этому ребру.
а) Докажите, что угол наклона бокового ребра пирамиды к её основанию равен 60°.
б) Найдите площадь сечения пирамиды, если AB = 30.
Задание 14.
Решите неравенство frac{9^{x}–13cdot 3^{x}+30}{3^{x+2}–3^{2x+1}}ge frac{1}{3^{x}}.
Задание 15.
По вкладу «А» банк в конце каждого года планирует увеличивать на 13 % сумму, имеющуюся на вкладе в начале года, а по вкладу «Б» – увеличивать эту сумму на 7 % в первый год и на целое число n процентов за второй год. Найдите наименьшее значение n, при котором за два года хранения вклад «Б» окажется выгоднее вклада «А» при одинаковых суммах первоначальных взносов.
Задание 16.
В треугольнике ABC медианы AA1, BB1 и CC1 пересекаются в точке M. Известно, что AC = 3MB.
а) Докажите, что треугольник ABC прямоугольный.
б) Найдите сумму квадратов медиан AA1 и CC1, если известно, что AC = 22.
Задание 17.
Найдите все значения a, при каждом из которых система уравнений
begin{cases} (x-5a+1)^{2}+(y-2a-1)^{2}=a-2 \ 3x-4y=2a+3 end{cases}
не имеет решений.
Задание 18.
У Ани есть 800 рублей. Ей нужно купить конверты (большие и маленькие). Большой конверт стоит 32 рубля, а маленький – 25 рублей. При этом число маленьких конвертов не должно отличаться от числа больших конвертов больше чем на пять.
а) Может ли Аня купить 24 конверта?
б) Может ли Аня купить 29 конвертов?
в) Какое наибольшее число конвертов может купить Аня?
Источник варианта: СтатГрад/statgrad.org.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 5 / 5. Количество оценок: 2
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
ЕГЭ по математике — Профиль 2022. Открытый банк заданий с ответами.
Регистрация Форум Текущее время: 10 мар 2023, 12:44 Сообщения без ответов | Активные темы Страница 1 из 2 [ Сообщений: 12 ] На страницу 1, 2 След. Начать новую тему»> Ответить Тренировочный вариант №420
Тренировочный вариант №420
Страница 1 из 2 [ Сообщений: 12 ] На страницу 1, 2 След. Текущее время: 10 мар 2023, 12:44 | Часовой пояс: UTC + 3 часа Удалить cookies форума | Наша команда | Вернуться наверх Кто сейчас на форуме
|
Задание 1
Основания трапеции равны 7 и 14. Найдите отрезок, соединяющий середины диагоналей трапеции.
Ответ: 3,5
Скрыть
Отрезок, соединяющий середины диагоналей трапеции равен полуразности большего и меньшего оснований. Поэтому он равен
$$frac{14-7}{2}=3,5$$
Задание 2
Длины двух ребер прямоугольного параллелепипеда равны 4 и 10, а площадь поверхности параллелепипеда равна 304. Найдите объем параллелепипеда.
Ответ: 320
Скрыть
Рассчитаем скольким условным единицам будет равняться третье измерение (обозначив его за $$c$$) заданной фигуры, если нам известно, согласно условиям этого задания, что первые два измерения равняются 4 и 10, в то время как площадь поверхности составляет 304:
$$2(4cdot c + 4cdot10 + 10cdot c) = 304$$
$$80+28c=304$$
$$28c=224$$
$$c=8$$
Рассчитаем скольким кубическим условным единицам будет равняться объем заданного параллелепипеда:
$$4cdot10cdot8 = 320$$
Задание 3
Из пруда, в котором плавают 40 щук, выловили 5 щук, пометили их и пустили обратно в пруд. Во второй раз выловили 9 щук. Какова вероятность того, что среди них окажутся только две помеченные щуки? Ответ округлите до тысячных.
Ответ: 0,246
Скрыть
После того как выловили и пометили 5 щук в пруде оказалось 5 помеченных щук и 35 без метки.
Количество исходов при выборе 2 щук из 5 помеченных: $$C^2_5 = frac{5!}{2!cdot(5-2)!} = 10$$
Количество исходов при вылове 7 щук из 35 без метки: $$C^{7}_{35}=frac{35!}{7!cdot(35-7)!)}=29cdot30cdot…cdotfrac{35}{1cdot2cdot…cdot7)} = 6724520$$
Общее количество исходов при вылове 9 щук из 40: $$C^9_{40}=frac{40!}{9!cdot(40 — 9)!}=32cdot33cdot…cdotfrac{40}{1cdot2cdot…cdot9} = 273438880$$
Вероятность выловить 2 помеченные щуки: $$P(2) = C^2_5cdotfrac{C_{35}^7}{C_{40}^9} = 10cdotfrac{6724520}{273438880} = 0,246.$$
Задание 4
На участке кросса для мотоциклиста-гонщика имеется три препятствия. Вероятность успешного прохождения первого препятствия равна 0,4, второго — 0,5, третьего — 0,6. Найдите вероятность успешного преодоления не менее двух препятствий.
Ответ: 0,5
Скрыть
$$p=p_1cdot p_2cdot q_3+p_1cdot q_2cdot p_3+q_1cdot p_2cdot p_3+p_1cdot p_2cdot p_3=$$
$$=0,4cdot0,5cdot0,4+0,4cdot0,5cdot0,6+0,6cdot0,5cdot0,6+0,4cdot0,5cdot0,6=$$
$$=0,08+0,12+0,18+0,12=0,5$$
Задание 5
Решите уравнение $$log_4(1,6-6x)=log_4(16x-0,6)-1.$$
Ответ: 0,175
Скрыть
ОДЗ:
$$1,6-6x>0$$
$$-6x>-1,6$$
$$x<frac{-1,6}{-6}$$
$$x<frac{4}{15}$$
$$16x-0,6>0$$
$$16>0,6$$
$$x>frac{3}{80}$$
$$xin(frac{3}{80};frac{4}{15})$$
Решение:
$$log_4(1,6-6x)=log_4(16x-0,6)-1$$
$$log_4(1,6-6x)=log_4(16x-0,6)-log_4 4$$
$$log_4(1,6-6x)=log_4((16x-0,6):4)$$
$$log_4(1,6-6x)=log_4(4x-0,15)$$
$$1,6-6x=4x-0,15$$
$$-4x-6x=-1,6-0,15$$
$$-10x=-1,75$$
$$x=0,175$$
$$frac{3}{80}<0,175<frac{4}{15}$$
Задание 6
Найдите значение выражения $$log_{0,8}log_{144}(288sqrt{3}).$$
Ответ: -1
Скрыть
$$log_{0,8}log_{144}288sqrt{3}=log_{0,8}log_{12^2}144cdot2sqrt{3}=log_{0,8}log_{12^2}12^2cdot(4cdot3)^{frac{1}{2}}=$$
$$=log_{0,8}log_{12^2}12^2cdot12^{frac{1}{2}}=log_{0,8}log_{12^2}12^{2,5}=log_{0,8}frac{2,5}{2}=log_{frac{4}{5}}frac{5}{4}=-1$$
Задание 7
На рисунке изображен график $$y=f'(x)$$ производной функции $$f(x),$$ определенной на интервале $$(-6;5).$$ Найдите точку экстремума функции $$f(x),$$ принадлежащую отрезку $$[-3; 4].$$
Ответ: -2
Скрыть
Точка экстремума на графике производной – точка пересечения с осью Ox: -2.
Задание 8
Уравнение процесса, в котором участвовал газ, записывается в виде $$Рcdot V^a=const,$$ где $$P$$ — давление в газе (в Па), $$V$$ — объем газа (в м3), а $$const$$ и $$a$$ — постоянные величины. Найдите минимальное значение $$a$$ при котором уменьшение объема газа в 16 раз приводит к увеличению давления не менее, чем в 32 раза.
Ответ: 1,25
Скрыть
Согласно понятиям термодинамики, в каждом состоянии газ характеризуется определенными параметрами – давлением, объемом, температурой.
По условию задачи, газ переходит из одного состояния в другое так, что $$pV^a=const$$
Это значит, что
$$p_1V_1^a=p_2V_2^a$$
$$frac{p_1}{p_2}=(frac{V_2}{V_1})^2$$
Давление уменьшилось не менее чем в 32 раза, то есть
$$frac{p_1}{p_2}geq32$$
Значит,
$$(frac{V_2}{V_1})^2geq32$$
$$16^ageq32,$$ отсюда $$аgeq1,25$$
Наименьшее значение для а записываем в ответ.
Задание 9
Бассейн можно наполнить через четыре трубы. Если открыты вторая, третья и четвертая трубы, то бассейн наполняется за 1 час, если открыты первая, третья и четвертая трубы — за 1 час 15 минут, а если только первая и вторая — за 1 час 40 минут. За сколько минут наполнится бассейн, если открыть все четыре трубы?
Ответ: 50
Скрыть
Пусть производительность труб $$а,в,с,х$$ литров в час соответственно. Примем объем всего бассейна за 1.
Тогда $$в+с+х=1$$
$$(а+с+х)cdotfrac{1}{4} = 1$$
$$(а+в)cdotfrac{2}{3} = 1$$
Получили систему:
$$в+с+х=1$$
$$а+с+х= frac{4}{5}$$
$$а+в=frac{3}{5}$$
Сложим все уравнения:
$$2(а+в+с+х)= 1+frac{3}{5}+frac{4}{5}$$
$$2(а+в+с+х) = frac{12}{5}$$
$$а+в+с+х = frac{6}{5}$$ литров в час — совместная производительность
$$1:frac{6}{5}=frac{5}{6} ч=frac{5}{6}cdot60=50$$ минут
Задание 10
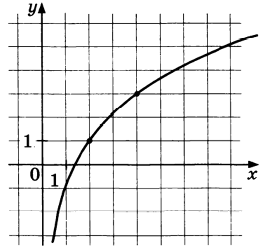
На рисунке изображен график функции $$f(x)=b+log_a x.$$ Найдите $$f(0,5).$$
Ответ: -3
Скрыть
График проходит через $$(2;1)$$ и $$(4;3).$$ Тогда:
$$left{begin{matrix} 1=b+log_a 2\ 3=b+log_a 4 end{matrix}right.Leftrightarrowleft{begin{matrix} 1=b+log_a 2\ 2=log_a 4-log_a 2 end{matrix}right.Leftrightarrowleft{begin{matrix} 1=b+2\ log_a 2=2 end{matrix}right.Leftrightarrowleft{begin{matrix} b=-1\ a=sqrt{2} end{matrix}right.$$
Получим:
$$f(x)=-1+log_{sqrt{2}} xRightarrow f(0,5)=-1+log_{sqrt{2}}frac{1}{2}=-1-2=-3$$
Задание 11
Найдите наибольшее значение функции $$y=x^3-frac{48}{x^2}$$ на отрезке $$[-3;2].$$
Ответ: -4
Скрыть
$$(x^3-frac{48}{x^2})’ = frac{3(x^5+32)}{x^3}$$
Точки экстремума:
$$frac{3(x^5+32)}{x^3} = 0$$
$$x^5+32 = 0$$
$$x^5= -32$$
$$x= — 2$$ входит в отрезок $$[-3;2]$$
Значение функции в точке экстремума $$y(-2)=(-2)^3-frac{48}{(-2)^2} = -20$$
Значение функции на концах отрезка $$[-3;2]:$$
$$y(-3)=(-2)^3-frac{48}{(-2)^2} = -frac{97}{3} =-32frac{1}{3}$$
$$y(2)=2^3-frac{48}{2^2}= -4$$
Наибольшее значение функции в точке $$x=2 ; y= -4$$
Задание 12
А) Решите уравнение $$sin^4x+(sin x-2)^4=2$$
Б) Найдите все корни уравнения, принадлежащие отрезку $$[4pi;5pi]$$
Ответ: А)$$frac{pi}{2}+2pi n,nin Z$$ Б)$$frac{9pi}{2}$$
Задание 13
В правильной треугольной пирамиде $$МАВС$$ двугранный угол при основании равен $$arctg3.$$ Через точку $$К$$ ребра $$МС$$ и вершины $$А$$ и $$В$$ проходит плоскость $$alpha$$ так, что площадь сечения пирамиды плоскостью $$alpha$$ относится к площади основания как $$3:sqrt{13}.$$
А) Докажите, что прямая $$МС$$ перпендикулярна плоскости $$alpha.$$
Б) Найдите объем пирамиды $$МАВК,$$ если объем пирамиды $$МАВС$$ равен $$52sqrt{5}.$$
Ответ: $$28sqrt{5}$$
Задание 14
Решите неравенство: $$frac{2x^3-11x^2+12x+9}{3^{2x+1}-7cdot3^x+2}leq0$$
Ответ: $$(-infty;-1),[-frac{1}{2};log_3 2),left{3right}$$
Задание 15
15 января планируется взять кредит в банке на 24 месяца. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца.
Известно, что в течение первого года кредитования нужно вернуть банку 2466 тыс. рублей. Какую сумму (в тыс. рублей) нужно выплатить банку за последние 12 месяцев?
Ответ: 2034
Задание 16
Внутри окружности с центром О построен правильный шестиугольник KOFPDL так, что его вершина D лежит на окружности. Из точки В, диаметрально противоположной точке D, проведены две хорды АВ и ВС, проходящие через вершины К и F шестиугольника соответственно.
А) Докажите, что АК : КВ = 3 : 7.
Б) Найдите площадь треугольника АВС, если радиус окружности равен 14.
Ответ: $$125sqrt{3}$$
Задание 17
Найдите все значения параметра $$a,$$ при каждом из которых система:
$$left{begin{matrix} sqrt{x}(x^2-x+2)-yx^3=yx(2-x),\ y^2+(2a-7)y+(a+2)(5-3a)=0 end{matrix}right.$$
имеет ровно 2 решения.
Ответ: $$left{frac{3}{4}right}$$
Задание 18
Первый член геометрической прогрессии, состоящей из трехзначных натуральных чисел, равен 368. Известно, что в прогрессии не меньше трех чисел.
A) Может ли число 575 являться членом такой прогрессии?
Б) Может ли число 920 являться членом такой прогрессии?
В) Какое наибольшее число может являться членом такой прогрессии?
Ответ: А) да, Б) нет, В) 828


















































































































































 Для печати
Для печати
 Предыдущая тема | Следующая тема
Предыдущая тема | Следующая тема