52227 решу егэ


Образовательный портал для подготовки к экзаменам

Математика профильного уровня

Математика профильного уровня

Сайты, меню, вход, новости

Задания

Версия для печати и копирования в MS Word

Найдите угол ACO, если его сторона CA касается окружности, O  — центр окружности, а большая дуга AD окружности, заключенная внутри этого угла, равна 152°. Ответ дайте в градусах.

Спрятать решение

Решение.

Заметим, что DB  — диаметр окружности, поэтому дуга AB, не содержащая точки D, равна 180° − 152°  =  28°. На эту дугу опирается центральный угол AOB, поэтому он равен 28°. Радиус, проведённый в точку касания, перпендикулярен касательным, поэтому треугольник AOC прямоугольный. Тогда angle ACO = 90 градусов минус angle COA = 90 градусов минус 28 градусов = 62 градусов.

Ответ: 62.

Спрятать решение

·

Прототип задания

·

·

Курс Д. Д. Гущина

·

Екатерина Волженская 28.10.2018 08:35

«…БОЛЬШАЯ дуга AD окружности, заключённая внутри этого угла равна 152»

Разве здесь имеется ввиду не меньшая дуга?

Александр Иванов

Из двух дуг, заключённых внутри угла, дуга АD является большей

Источник

Установите соответствие между характеристиками и структурами, обозначенными на рисунке выше цифрами 1, 2, 3: к каждой позиции, данной в первом столбце, подберите соответствующую позицию из второго столбца.

ХАРАКТЕРИСТИКИ

А)  Центральный орган эндокринной системы

Б)  Передача информации из спинного мозга

В)  Включает в себя мозолистое тело

Г)  Секреция гормона роста

Д)  Связан с мозжечком

Е)  Отвечает за формирование речи и абстрактного мышления

Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:

А Б В Г Д Е
           

Рассмотрите рисунок и выполните задания 13 и 14.

Источник

Новые тренировочные варианты ЕГЭ 2023 по математике базовый и профильный уровень с ответами и решением для 10 и 11 класса, больше 100 вариантов в формате реального экзамена ФИПИ вы можете решать онлайн или скачать.

Тренировочные варианты ЕГЭ 2023 по математике база и профиль

13.09.2022 Тренировочный вариант №1 ЕГЭ 2023 по математике профиль с ответами

20.09.2022 Тренировочный вариант №2 ЕГЭ 2023 по математике профиль с ответами

20.09.2022 Тренировочный вариант №2 ЕГЭ 2023 база по математике с ответами

27.09.2022 Математика 11 класс профиль входная мониторинговая работа 3 варианта с ответами

28.09.2022 Тренировочный вариант №3 ЕГЭ 2023 база по математике с ответами

28 сентября 2022 Статград математика 11 класс ЕГЭ 2023 база и профиль варианты и ответы

29 сентября 2022 Тренировочный вариант №3 ЕГЭ 2023 по математике профиль с ответами

1 октября 2022 Ларин вариант 399 ЕГЭ 2023 по математике профиль решение с ответами

6 октября Тренировочный вариант №4 ЕГЭ 2023 база по математике с ответами

6 октября Тренировочный вариант №4 ЕГЭ 2023 по математике профиль с ответами

8 октября Ларин вариант 400 ЕГЭ 2023 по математике профиль решение с ответами

12 октября Тренировочный вариант №5 ЕГЭ 2023 база по математике с ответами

12 октября Тренировочный вариант №5 ЕГЭ 2023 по математике профиль с ответами

14 октября Вариант 1 Ященко ЕГЭ 2023 математика профиль с ответами и решением

14 октября Вариант 2 Ященко ЕГЭ 2023 математика профиль с ответами и решением

15 октября Ларин вариант 401 ЕГЭ 2023 по математике профиль решение с ответами

15 октября Ларин вариант 402 ЕГЭ 2023 по математике профиль решение с ответами

16 октября Вариант 3 Ященко ЕГЭ 2023 математика профиль с ответами и решением

16 октября Вариант 4 Ященко ЕГЭ 2023 математика профиль с ответами и решением

23 октября Тренировочный вариант №6 ЕГЭ 2023 база по математике с ответами

24 октября Тренировочный вариант №6 ЕГЭ 2023 по математике профиль с ответами

25 октября Тренировочный вариант №7 ЕГЭ 2023 база по математике с ответами

26 октября Тренировочный вариант №7 ЕГЭ 2023 по математике профиль с ответами

28 октября Ларин вариант 403 ЕГЭ 2023 по математике профиль решение с ответами

29 октября Ларин вариант 404 ЕГЭ 2023 по математике профиль решение с ответами

1 ноября 2022 Тренировочный вариант №8 решу ЕГЭ 2023 база по математике с ответами

1 ноября 2022 Тренировочный вариант №8 решу ЕГЭ 2023 по математике профиль с ответами

5 ноября 2022 Вариант 1-2 распечатай и реши ЕГЭ 2023 база по математике 11 класс с ответами

6 ноября 2022 Ларин вариант 405 ЕГЭ 2023 профиль по математике решение с ответами

9 ноября 2022 Тренировочный вариант №9 решу ЕГЭ 2023 база по математике с ответами

12 ноября 2022 Тренировочный вариант №9 решу ЕГЭ 2023 по математике профиль с ответами

13 ноября 2022 Ларин вариант 406 ЕГЭ 2023 профиль по математике решение с ответами

15 ноября 2022 Тренировочный вариант №10 решу ЕГЭ 2023 база по математике 11 класс с ответами

15 ноября 2022 Тренировочный вариант №10 решу ЕГЭ 2023 по математике профиль с ответами

21 ноября 2022 Ларин вариант 407 ЕГЭ 2023 профиль по математике решение с ответами

23 ноября 2022 Тренировочный вариант №11 решу ЕГЭ 2023 база по математике 11 класс с ответами

23 ноября 2022 Тренировочный вариант №11 решу ЕГЭ 2023 по математике профиль с ответами

27 ноября 2022 Ларин вариант 408 ЕГЭ 2023 профиль по математике решение с ответами

28 ноября 2022 Вариант 3-4 распечатай и реши ЕГЭ 2023 база по математике 11 класс с ответами

30 ноября 2022 Мониторинговая работа по математике 11 класс ЕГЭ 2023 профиль 1 полугодие

3 декабря 2022 Тренировочный вариант №12 решу ЕГЭ 2023 база по математике 11 класс с ответами

3 декабря 2022 Тренировочный вариант №12 решу ЕГЭ 2023 по математике профиль с ответами

3 декабря 2022 Пробник ЕГЭ 2023 Москва по математике профиль задания и ответы

5 декабря 2022 Ларин вариант 409 ЕГЭ 2023 профиль по математике решение с ответами

9 декабря 2022 Тренировочный вариант №13 решу ЕГЭ 2023 база по математике 11 класс с ответами

10 декабря 2022 Тренировочный вариант №13 решу ЕГЭ 2023 профиль по математике 11 класс с ответами

12 декабря 2022 Ларин вариант 410 ЕГЭ 2023 профиль по математике решение с ответами

13 декабря 2022 Статград математика 11 класс профиль ЕГЭ 2023 варианты МА2210209-МА2210212 и ответы

13 декабря 2022 Математика 11 класс база ЕГЭ 2023 статград варианты и ответы

15 декабря 2022 Тренировочный вариант №14 решу ЕГЭ 2023 профиль по математике 11 класс с ответами

15 декабря 2022 Тренировочный вариант №14 решу ЕГЭ 2023 база по математике 11 класс с ответами

20 декабря 2022 Вариант 5-6 распечатай и реши ЕГЭ 2023 база по математике 11 класс с ответами

20 декабря 2022 Ларин вариант 411 ЕГЭ 2023 профиль по математике решение с ответами

3 января 2023 Ларин вариант 412 ЕГЭ 2023 профиль по математике решение с ответами

6 января 2023 Тренировочный вариант 1-2 ЕГЭ 2023 профиль математика задания и ответы

8 января 2023 Вариант 3-4 ЕГЭ 2023 профиль математика задания и ответы

9 января 2023 Вариант 7-8 распечатай и реши ЕГЭ 2023 база по математике 11 класс с ответами

10 января 2023 Тренировочный вариант №15 и №16 решу ЕГЭ 2023 профиль по математике 11 класс с ответами

11 января 2023 ЕГЭ 2023 математика тренировочные задания и ответы Ященко, Семенов

11 января 2023 Тренировочный вариант №15 и №16 база ЕГЭ 2023 по математике 11 класс с ответами

19 января 2023 Тренировочные варианты №17 и №18 решу ЕГЭ 2023 профиль по математике 11 класс с ответами

22 января 2023 Ларин вариант 413 и 414 ЕГЭ 2023 профиль по математике решение и ответы

22 января 2023 Тренировочный 19 вариант решу ЕГЭ 2023 профиль по математике 11 класс с ответами

22 января 2023 База ЕГЭ 2023 математика 11 класс тренировочный вариант 19 с ответами

25 января 2023 База ЕГЭ 2023 математика 11 класс тренировочный вариант 20 с ответами

27 января 2023 Тренировочный вариант №20 решу ЕГЭ 2023 профиль по математике 11 класс с ответами

28 января 2023 Вариант 415 Ларина ЕГЭ 2023 по математике 11 класс задания и ответы

2 февраля 2023 Вариант 21 база ЕГЭ 2023 математика 11 класс тренировочный вариант с ответами

2 февраля 2023 Тренировочный вариант №21 решу ЕГЭ 2023 профиль по математике 11 класс с ответами

8 февраля 2023 Математика 10-11 класс ЕГЭ 2023 статград варианты база и профиль МА2200101-МА2200110 и ответы

11 февраля 2023 Тренировочный вариант №22 решу ЕГЭ 2023 профиль по математике 11 класс с ответами

11 февраля 2023 Тренировочный вариант №22 решу ЕГЭ 2023 база по математике 11 класс с ответами

12 февраля 2023 Вариант 416 Ларина ЕГЭ 2023 по математике 11 класс задания и ответы

12 февраля 2023 Вариант 417 Ларина ЕГЭ 2023 по математике 11 класс задания и ответы

13 февраля 2023 Вариант 9 и вариант 10 ЕГЭ 2023 база математика распечатай и реши задания

13 февраля 2023 Вариант 11 и вариант 12 ЕГЭ 2023 база математика распечатай и реши

16 февраля 2023 Тренировочный вариант №23 решу ЕГЭ 2023 база по математике 11 класс с ответами

16 февраля 2023 Тренировочный вариант №23 решу ЕГЭ 2023 профиль по математике 11 класс с ответами

18 февраля 2023 Вариант 418 Ларина ЕГЭ 2023 по математике 11 класс задания и ответы

22 февраля 2023 Пробный ЕГЭ 2023 вариант 24 база по математике 11 класс с ответами

22 февраля 2023 Пробный ЕГЭ 2023 вариант 24 профиль по математике 11 класс с ответами

25 февраля 2023 Вариант 419 Ларина ЕГЭ 2023 по математике 11 класс задания и ответы

28 февраля 2023 Статград математика 11 класс ЕГЭ 2023 база и профиль и ответы

4 марта 2023 Пробник ЕГЭ 2023 вариант 25 база по математике 11 класс с ответами

4 марта 2023 Вариант 420 Ларин ЕГЭ 2023 по математике 11 класс задания и ответы

5 марта 2023 Пробник ЕГЭ 2023 вариант 25 профиль по математике 11 класс с ответами

8 марта 2023 Пробник ЕГЭ 2023 вариант 26 профиль по математике 11 класс с ответами

8 марта 2023 Пробник ЕГЭ 2023 вариант 26 база по математике 11 класс 100 баллов с ответами

Смотрите также на нашем сайте:

Сборник Ященко ЕГЭ 2023 математика профильный уровень 36 вариантов

ПОДЕЛИТЬСЯ МАТЕРИАЛОМ

Источник

ОГЭ по математике 9 класс 2023. Новый тренировочный вариант №25 — №220912 (задания и ответы)ОГЭ 2023. Экзаменационная работа состоит из двух частей,  включающие в себя 25 заданий. Часть 1 содержит 19 заданий, часть 2 содержит 6 заданий с развернутым ответом. На выполнение экзаменационной работы по математике отводится 3 часа 55 минут (235 минут).

В конце варианта приведены правильные ответы ко всем заданиям. Вы можете свериться с ними и найти у себя ошибки.

Скачать тренировочный вариант ОГЭ: Скачать

Интересные задания:

На плане изображено домохозяйство по адресу с. Иволгино, 5-й Заречный пер, д. 3 (сторона каждой клетки на плане равна 1 м). Участок имеет прямоугольную форму. Выезд и въезд осуществляются через единственные ворота. При входе на участок слева от ворот находится сарай, а справа – гараж. Площадь, занятая гаражом, равна 48 кв. м. Жилой дом находится в глубине территории. Помимо гаража, жилого дома и сарая, на участке имеется теплица, расположенная на территории огорода (огород отмечен на плане цифрой 5). Перед гаражом имеется площадка, вымощенная тротуарной плиткой размером 0,2 м × 0,1 м и отмеченная на плане цифрой 6.

1. Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, а в бланк перенесите последовательность четырёх цифр.
Ответ: 2143

2. Тротуарная плитка продаётся в упаковках по 40 штук. Сколько упаковок плитки понадобилось, чтобы выложить площадку перед гаражом?
Ответ: 68

3. Найдите расстояние между противоположными углами гаража (длину диагонали) в метрах.
Ответ: 10

4. Найдите площадь, которую занимает жилой дом. Ответ дайте в квадратных метрах.
Ответ: 108

5. Хозяин участка хочет сделать пристройку к дому. Для этого он планирует купить 15 тонн силикатного кирпича. Один кирпич весит 3 кг. Цена кирпича и условия доставки всей покупки приведены в таблице. Во сколько рублей обойдётся наиболее дешёвый вариант?
Ответ: 66300

7. На координатной прямой отмечены точки 𝐴, 𝐵, 𝐶, 𝐷. Одна из них соответствует числу √95. Какая это точка?
Ответ: 2

10. В среднем из 150 карманных фонариков, поступивших в продажу, три неисправных. Найдите вероятность того, что выбранный наудачу в магазине фонарик окажется исправен.
Ответ: 0,98

12. Мощность постоянного тока (в ваттах) вычисляется по формуле 𝑃 = 𝐼 2𝑅, где 𝐼 − сила тока (в амперах), 𝑅 − сопротивление (в омах). Пользуясь этой формулой, найдите сопротивление 𝑅, если мощность составляет 29,25 Вт, а сила тока равна 1,5 А. Ответ дайте в омах.
Ответ: 13

14. Известно, что на высоте 2205 м над уровнем моря атмосферное давление составляет 550 мм рт. ст. Считая, что при подъёме на каждые 10,5 м давление уменьшается примерно на 1 мм рт. ст., определите атмосферное давление на высоте 1890 м над уровнем моря.
Ответ: 580

15. Диагональ 𝐴𝐶 параллелограмма 𝐴𝐵𝐶𝐷 образует с его сторонами углы, равные 30° и 45°. Найдите больший угол этого параллелограмма. Ответ дайте в градусах.
Ответ: 105

16. Угол 𝐴 трапеции 𝐴𝐵𝐶𝐷 с основаниями 𝐴𝐷 и 𝐵𝐶, вписанной в окружность, равен 81°. Найдите угол 𝐶 этой трапеции. Ответ дайте в градусах.
Ответ: 99

17. В треугольнике 𝐴𝐵𝐶 известно, что 𝐴𝐵 = 6, 𝐵𝐶 = 10, sin ∠𝐴𝐵𝐶 = 1 3 . Найдите площадь треугольника 𝐴𝐵𝐶.
Ответ: 10

18. На клетчатой бумаге с размером клетки 1 × 1 отмечены три точки: 𝐴, 𝐵 и 𝐶. Найдите расстояние от точки 𝐴 до середины отрезка 𝐵𝐶.
Ответ: 3

19. Какое из следующих утверждений верно?
1) Через точку, не лежащую на данной прямой, можно провести прямую, перпендикулярную этой прямой.
2) В любой прямоугольник можно вписать окружность.
3) Каждая из биссектрис равнобедренного треугольника является его медианой.
Ответ: 1

21. Первый рабочий за час делает на 10 деталей больше, чем второй, и выполняет заказ, состоящий из 60 деталей, на 3 часа быстрее, чем второй рабочий, выполняющий такой же заказ. Сколько деталей в час делает второй рабочий?
Ответ: 10

23. Окружность пересекает стороны 𝐴𝐵 и 𝐴𝐶 треугольника 𝐴𝐵𝐶 в точках 𝐾 и 𝑃 соответственно и проходит через вершины 𝐵 и 𝐶. Найдите длину отрезка 𝐾𝑃, если 𝐴𝑃 = 36, а сторона 𝐵𝐶 в 1,8 раза меньше стороны 𝐴𝐵.
Ответ: 20

24. Биссектрисы углов 𝐴 и 𝐷 параллелограмма 𝐴𝐵𝐶𝐷 пересекаются в точке 𝐾, лежащей на стороне 𝐵𝐶. Докажите, что 𝐾 − середина 𝐵𝐶.

25. В треугольнике 𝐴𝐵𝐶 известны длины сторон 𝐴𝐵 = 84, 𝐴𝐶 = 98, точка 𝑂 − центр окружности, описанной около треугольника 𝐴𝐵𝐶. Прямая 𝐵𝐷, перпендикулярная прямой 𝐴𝑂, пересекает сторону 𝐴𝐶 в точке 𝐷. Найдите 𝐶𝐷.
Ответ: 26

Вам будет интересно:

ОГЭ по Математике 9 класс 2023. Новый типовой тренировочный вариант №3 — №221003 (задания и ответы)

* Олимпиады и конкурсы
* Готовые контрольные работы
* Работы СтатГрад
* Официальные ВПР

Поделиться:

Источник

Решение и ответы заданий варианта МА2210309 СтатГрад 28 февраля ЕГЭ 2023 по математике (профильный уровень). Тренировочная работа №3. ГДЗ профиль для 11 класса.
+Задания №1, №4, №6, №10 из варианта МА2210311.

❗Все материалы получены из открытых источников и публикуются после окончания тренировочного экзамена в ознакомительных целях.

❗Задания №13,16,17,18 долго оформлять, решу их позже, если будет время и желание. Решены те задания, у которых кнопка «Смотреть решение» зелёная.

Задание 1.
В треугольнике ABC угол C равен 90°, CH – высота, BC = 5, cosA=frac{2sqrt{6}}{5}. Найдите длину отрезка AH.

В треугольнике ABC угол C равен 90°, CH – высота, BC = 5

Задание 1 из варианта 2210311.
Найдите периметр прямоугольника, если его площадь равна 12, а отношение соседних сторон равно 1:3.
Найдите периметр прямоугольника, если его площадь равна 12, а отношение соседних сторон равно 13.

Задание 2.
Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 2. Объём параллелепипеда равен 3,2. Найдите высоту цилиндра.

Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 2.

Задание 3.
В группе 16 человек, среди них – Анна и Татьяна. Группу случайным образом делят на 4 одинаковые по численности подгруппы. Найдите вероятность того, что Анна и Татьяна окажутся в одной подгруппе.

Задание 4.
Агрофирма закупает куриные яйца только в двух домашних хозяйствах. Известно, что 40 % яиц из первого хозяйства – яйца высшей категории, а из второго хозяйства – 60 % яиц высшей категории. В этой агрофирме 50 % яиц высшей категории. Найдите вероятность того, что яйцо, купленное у этой агрофирмы, окажется из первого хозяйства.

Задание 4 из варианта 2210311.
Игральный кубик бросают дважды. Известно, что в сумме выпало 11 очков. Найдите вероятность того, что во второй раз выпало 5 очков.

Задание 5.
Решите уравнение frac{x–1}{5x+11}=frac{x–1}{3x-7}. Если уравнение имеет больше одного корня, в ответе запишите больший из корней.

Задание 6.
Найдите значение выражения frac{(4^{frac{3}{5} }cdot7^{frac{2}{3}})^{15}}{28^{9}} .

Задание 6 из варианта 2210311.
Найдите 98cos2α, если cosα = frac{4}{7}.

Задание 7.
На рисунке изображён график y = f’(x) – производной функции f(x), определённой на интервале (−5; 5). В какой точке отрезка [−4; −1] функция f(x) принимает наибольшее значение?

На рисунке изображён график y = f'(x) – производной функции f(x), определённой на интервале (−5; 5).

Задание 8.
На верфи инженеры проектируют новый аппарат для погружения на небольшие глубины. Конструкция имеет кубическую форму, а значит, действующая на аппарат выталкивающая (архимедова) сила, выражаемая в ньютонах, будет определяться по формуле FA = ρgl3, где l – длина ребра куба в метрах, ρ = 1000 кг/м3 – плотность воды, а g – ускорение свободного падения (считайте, что g = 9,8 Н/кг). Какой может быть максимальная длина ребра куба, чтобы обеспечить его эксплуатацию в условиях, когда выталкивающая сила при погружении будет не больше чем 2116800 Н? Ответ дайте в метрах.

Задание 9.
Пристани A и B расположены на озере, расстояние между ними равно 280 км. Баржа отправилась с постоянной скоростью из A в B. На следующий день после прибытия она отправилась обратно со скоростью на 4 км/ч больше прежней, сделав по пути остановку на 8 часов. В результате она затратила на обратный путь столько же времени, сколько на путь из A в B. Найдите скорость баржи на пути из A в B. Ответ дайте в км/ч.

Задание 10.
На рисунке изображён график функции f(x) = ax2 + bx + c. Найдите значение f(−1).

На рисунке изображён график функции f(x) = ax2 + bx + c.

Задание 10 из варианта 2210311.
На рисунке изображены графики функций f(x) = frac{k}{x} и g(x) = ax + b, которые пересекаются в точках A и B. Найдите абсциссу точки B.

Найдите абсциссу точки B.

Задание 11.
Найдите точку минимума функции y = x3 − 27x2 + 13.

Задание 12.
а) Решите уравнение 2cos3x = –sin(frac{3pi}{2} + x)
б) Найдите все корни этого уравнения, принадлежащие отрезку [3π; 4π]

Задание 13.
Основанием правильной пирамиды PABCD является квадрат ABCD. Сечение пирамиды проходит через вершину В и середину ребра PD перпендикулярно этому ребру.
а) Докажите, что угол наклона бокового ребра пирамиды к её основанию равен 60°.
б) Найдите площадь сечения пирамиды, если AB = 30.

Задание 14.
Решите неравенство frac{9^{x}–13cdot 3^{x}+30}{3^{x+2}–3^{2x+1}}ge frac{1}{3^{x}}.

Задание 15.
По вкладу «А» банк в конце каждого года планирует увеличивать на 13 % сумму, имеющуюся на вкладе в начале года, а по вкладу «Б» – увеличивать эту сумму на 7 % в первый год и на целое число n процентов за второй год. Найдите наименьшее значение n, при котором за два года хранения вклад «Б» окажется выгоднее вклада «А» при одинаковых суммах первоначальных взносов.

Задание 16.
В треугольнике ABC медианы AA1, BB1 и CC1 пересекаются в точке M. Известно, что AC = 3MB.
а) Докажите, что треугольник ABC прямоугольный.
б) Найдите сумму квадратов медиан AA1 и CC1, если известно, что AC = 22.

Задание 17.
Найдите все значения a, при каждом из которых система уравнений 

begin{cases} (x-5a+1)^{2}+(y-2a-1)^{2}=a-2 \ 3x-4y=2a+3 end{cases}

не имеет решений.

Задание 18.
У Ани есть 800 рублей. Ей нужно купить конверты (большие и маленькие). Большой конверт стоит 32 рубля, а маленький – 25 рублей. При этом число маленьких конвертов не должно отличаться от числа больших конвертов больше чем на пять.
а) Может ли Аня купить 24 конверта?
б) Может ли Аня купить 29 конвертов?
в) Какое наибольшее число конвертов может купить Аня?

Источник варианта: СтатГрад/statgrad.org.

Есть три секунды времени? Для меня важно твоё мнение!

Насколько понятно решение?

Средняя оценка: 5 / 5. Количество оценок: 2

Оценок пока нет. Поставь оценку первым.

Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️

Вступай в группу vk.com 😉

Расскажи, что не так? Я исправлю в ближайшее время!

В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.

Источник

Синус, косинус и тангенс острого угла прямоугольного треугольника

Изучение тригонометрии мы начнем с прямоугольного треугольника. Определим, что такое синус и косинус, а также тангенс и котангенс острого угла. Это основы тригонометрии.

Напомним, что прямой угол — это угол, равный 90 градусов. Другими словами, половина развернутого угла.

Острый угол — меньший 90 градусов.

Тупой угол — больший 90 градусов. Применительно к такому углу «тупой» — не оскорбление, а математический термин :-)

Развёрнутый, прямой, острый и тупой углы

Нарисуем прямоугольный треугольник. Прямой угол обычно обозначается C. Обратим внимание, что сторона, лежащая напротив угла, обозначается той же буквой, только маленькой. Так, сторона, лежащая напротив угла A, обозначается a.

Угол A обозначается соответствующей греческой буквой alpha.

Гипотенуза и катеты

Гипотенуза прямоугольного треугольника — это сторона, лежащая напротив прямого угла.

Катеты — стороны, лежащие напротив острых углов.

Катет a, лежащий напротив угла alpha, называется противолежащим (по отношению к углу alpha). Другой катет b, который лежит на одной из сторон угла alpha, называется прилежащим.

Синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе:

sin A=genfrac{}{}{}{0}{displaystyle a}{displaystyle c}.

Косинус острого угла в прямоугольном треугольнике — отношение прилежащего катета к гипотенузе:

cos A=genfrac{}{}{}{0}{displaystyle b}{displaystyle c}.

Тангенс острого угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему:

tg A =genfrac{}{}{}{0}{displaystyle a}{displaystyle b}.

Другое (равносильное) определение: тангенсом острого угла называется отношение синуса угла к его косинусу:

tg A=genfrac{}{}{}{0}{displaystyle sin A}{displaystyle cos A}.

Котангенс острого угла в прямоугольном треугольнике — отношение прилежащего катета к противолежащему (или, что то же самое, отношение косинуса к синусу):

ctg A =genfrac{}{}{}{0}{displaystyle cos A}{displaystyle sin A}.

Обратите внимание на основные формулы для синуса, косинуса, тангенса и котангенса, которые приведены ниже. Они пригодятся нам при решении задач.

sin displaystyle alpha = frac{a}{c} sin{}^2 alpha +cosdisplaystyle {}^2 alpha =frac{1}{cos^2 alpha} alpha + beta = 90 ^{circ} 
cos displaystyle alpha = frac{b}{c} 1+tg displaystyle {}^2 alpha =frac{1}{cos ^2 alpha} cosalpha = sin beta
tg displaystyle alpha = frac{a}{b} 1+ctg displaystyle {}^2 alpha =frac{1}{sin ^2 alpha} sinalpha = cosbeta
ctg displaystyle alpha = frac{b}{a} tgalpha = ctgbeta

Давайте докажем некоторые из них.

  1. Сумма углов любого треугольника равна 180^{circ}. Значит, сумма двух острых углов прямоугольного треугольника равнa 90^{circ}.
  2. С одной стороны, sin A =genfrac{}{}{}{0}{displaystyle a}{displaystyle c} как отношение противолежащего катета к гипотенузе. С другой стороны, cos B =genfrac{}{}{}{0}{displaystyle a}{displaystyle c}, поскольку для угла beta катет а будет прилежащим. Получаем, что cos beta =sin alpha. Иными словами, cos left( 90^{circ}-A right) = sin A.
  3. Возьмем теорему Пифагора: a^2+b^2=c^2. Поделим обе части на c^2, получаем displaystyle left ( frac{a}{c} right )^2+left ( frac{b}{c} right )^2=left ( frac{c}{c} right )^2 , то есть sin ^2 A+cos^2 A=1.
    Мы получили основное тригонометрическое тождество.
  4. Поделив обе части основного тригонометрического тождества на cos^2 A, получим: 1+tg ^2 A = genfrac{}{}{}{0}{displaystyle 1}{displaystyle cos ^2 A }. Это значит, что если нам дан тангенс острого угла alpha, то мы сразу можем найти его косинус. Аналогично,1+ctg ^2 A =genfrac{}{}{}{0}{1}{sin ^2 A }.

Хорошо, мы дали определения и записали формулы. А для чего все-таки нужны синус, косинус, тангенс и котангенс?

Мы знаем, что сумма углов любого треугольника равна 180^{circ}.

Знаем соотношение между сторонами прямоугольного треугольника. Это теорема Пифагора: a^2+b^2=c^2.

Получается, что зная два угла в треугольнике, можно найти третий. Зная две стороны в прямоугольном треугольнике, можно найти третью. Значит, для углов — свое соотношение, для сторон — свое. А что делать, если в прямоугольном треугольнике известен один угол (кроме прямого) и одна сторона, а найти надо другие стороны?

С этим и столкнулись люди в прошлом, составляя карты местности и звездного неба. Ведь не всегда можно непосредственно измерить все стороны треугольника.

Синус, косинус и тангенс — их еще называют тригонометрическими функциями угла — дают соотношения между сторонами и углами треугольника. Зная угол, можно найти все его тригонометрические функции по специальным таблицам. А зная синусы, косинусы и тангенсы углов треугольника и одну из его сторон, можно найти остальные.

Мы тоже нарисуем таблицу значений синуса, косинуса, тангенса и котангенса для «хороших» углов от 0^{circ} до 90^{circ}.

varphi 0 genfrac{}{}{}{0}{displaystyle pi}{displaystyle 6} genfrac{}{}{}{0}{displaystyle pi}{displaystyle 4} genfrac{}{}{}{0}{displaystyle pi}{displaystyle 3} genfrac{}{}{}{0}{displaystyle pi}{displaystyle 2}
sinvarphi 0 displaystyle frac{1}{2} displaystyle frac{sqrt{2}}{2} displaystyle frac{sqrt{3}}{2} 1
cosvarphi 1 displaystyle frac{sqrt{3}}{2} displaystyle frac{sqrt{2}}{2} displaystyle frac{1}{2} 0
tgvarphi 0 genfrac{}{}{}{0}{displaystyle 1}{displaystyle sqrt{3}} 1 sqrt{3} −
ctgvarphi − sqrt{3} 1 genfrac{}{}{}{0}{displaystyle 1}{displaystyle sqrt{3}} 0

Обратите внимание на два прочерка в таблице. При соответствующих значениях углов тангенс и котангенс не существуют.

Докажем теорему:

Если острый угол одного прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то синусы этих углов равны, косинусы этих углов равны и тангенсы этих углов равны.

В самом деле, пусть АВС и A_1B_1C_1 — два прямоугольных треугольника с прямыми углами С и C_1 и равными острыми углами А и A_1.

Треугольники АВС и A_1B_1C_1 подобны по первому признаку подобия треугольников, поэтому displaystyle frac{AB}{A_1 B_1}=frac{BC}{B_1 C_1}=frac{AC}{A_1 C_1 } .

Из этих равенств следует, что displaystyle frac{BC}{AB}=frac{B_1 C_1}{A_1 B_1} , т. е. sin А = sin A_1.

Аналогично, displaystyle frac{AC}{AB}=frac{A_1C_1}{A_1 B_1}, т. е. cos А = cosA_1, и displaystyle frac{BC}{AC}=frac{B_1C_1}{A_1 C_1}, т. е. tg A = tg A_1.

Это значит, что синус, косинус и тангенс зависят только от величины угла.

Разберем несколько задач по тригонометрии из Банка заданий ФИПИ.

Задача 1. В треугольнике ABC угол C равен 90^{circ}, sin A = 0,1. Найдите cos B.

Задача решается за четыре секунды.

Поскольку A+B = 90^{circ}, sin A = cos B = 0,1.

Задача 2. В треугольнике ABC угол C равен 90^{circ}, AB=5, sin A = genfrac{}{}{}{0}{displaystyle 7}{displaystyle 25}.

Найдите AC.

Решение:

sin A = genfrac{}{}{}{0}{displaystyle a}{displaystyle c} = genfrac{}{}{}{0}{displaystyle BC}{displaystyle AB} = genfrac{}{}{}{0}{displaystyle 7}{displaystyle 25}.

Отсюда

BC= genfrac{}{}{}{0}{displaystyle 7}{displaystyle 25} cdot AB = genfrac{}{}{}{0}{displaystyle 7}{displaystyle 5}.

Найдем AC по теореме Пифагора.

AC=sqrt{AB^2-BC^2} = genfrac{}{}{}{0}{displaystyle 24}{displaystyle 5} = 4,8.

Ответ: 4,8.

Задача 3. В треугольнике АВС угол С равен 90^circ , AВ = 13, ВС = 5. Найдите косинус и тангенс острого угла А. Ответ округлите до сотых.

Решение:

Для угла А противолежащий катет – это ВС,

АВ является гипотенузой треугольника, лежит против angle C. Значит, sin A displaystyle = frac{BC}{AB}= frac{5}{13}.

Катет, прилежащий к angle A – это катет АС, следовательно, cos⁡ А displaystyle = frac{AC}{AB}=frac{AC}{13}.

Длину катета АС найдем по теореме Пифагора: AC^2+BC^2=AB^2.

Тогда AC = sqrt{AB^2-BC^2}=sqrt{(13)^2-5^2}=sqrt{144}=12.

cos⁡ А displaystyle = frac{12}{13}=0,923 ... approx 0,92 ;

tg A displaystyle = frac{BC}{AC} = frac{5}{12}=0,416...approx 0,42.

Ответ: 0,92; 0,42.

Заметим, что если катеты прямоугольного треугольника равны 5 и 12, то гипотенуза равна 13. Это одна из так называемых Пифагоровых троек. О них мы расскажем в других статьях сайта.

Задача 4. В треугольнике АВС угол С равен 90^circ , AC = 2, sin A= displaystyle frac{sqrt{17}}{17} .

Найдите BC.
Решение:

AC = b = 2, BC = a, AB = c.

Так как sin A displaystyle = frac{a}{c} = frac{BC}{AB} = frac{sqrt{17}}{17}, displaystyle frac{a}{c} = frac{sqrt{17}}{17} , displaystyle c = frac{17a}{sqrt{17}}=sqrt{17}a.

По теореме Пифагора a^2+b^2=c^2, получим

a^2+2^2=(sqrt{17} a)^2;

a^2+4=17a^2;

16a^2=4, displaystyle a= frac{1}{2}=0,5;

BC = 0,5.

Ответ: 0,5.

Задача 5. В треугольнике АВС угол С равен 90^circ , AC = 4, tg A = displaystyle frac{33}{4sqrt{33}} . Найдите AB.

Решение:

AC = b = 4, tg A displaystyle = frac{a}{b}=frac{33}{4sqrt{33}},

displaystyle frac{a}{4}=frac{33}{4sqrt{33}}, displaystyle a=frac{4 cdot 33}{4 cdot sqrt{33}}=sqrt{33},

AB = c = sqrt{a^2+b^2}=sqrt{(sqrt{33})^2+4^2}=sqrt{33+16} =7.

Ответ: 7.

Задача 6.

В треугольнике АВС угол С равен 90^ circ, CH – высота, AB = 13, tg A = displaystyle frac{1}{5} . Найдите AH.

Решение:

AВ = с = 13, tg A = displaystyle frac{a}{b}=frac{1}{5} , тогда b = 5a.

По теореме Пифагора triangleABC: a^2+b^2=c^2,

a^2+(5a)^2=13^2,

26 a^2=169,

displaystyle a=sqrt{frac{169}{26}}=frac{13}{sqrt{26}}, тогда displaystyle b = 5a=5cdot frac{13}{sqrt{26}}=frac{65}{sqrt{26}}.

triangle AHC approx triangle ACB (по двум углам), следовательно displaystyle frac{AH}{AC}=frac{AC}{AB} , откуда

displaystyle AH = frac{AC^2}{AB}=frac{b^2}{c}=left ( frac{65}{sqrt{26}}right )^2:13=12,5.

Ответ: 12,5.

Задача 7. В треугольнике АВС угол С равен 90^circ,

CH – высота, BC = 3, sin A = displaystyle frac{1}{6} .

Найдите AH.

Решение:

Так как sin A = displaystyle frac{a}{c} = frac{BC}{AB} = frac{1}{6}, тогда displaystyle frac{3}{c} = frac{1}{6} , c = АВ = 18.

sin A = displaystyle frac{a}{c} = cos⁡ B = displaystyle frac{1}{6} .

Рассмотрим triangle BHC:

{cos B= }displaystyle frac{BH}{BC} = displaystyle frac{1}{6} , получим displaystyle frac{BH}{3}=displaystyle frac{1}{6},

тогда BH = displaystyle frac{3}{6}=displaystyle frac{1}{2} = 0,5,

AH = AB — BH = 18 — 0,5 = 17,5.

Ответ: 17,5.

Задача 8. В треугольнике АВС угол С равен 90{}^circ, CH — высота, BC = 3, cos A = displaystyle frac{sqrt{35}}{6}.

Найдите АH.

Решение:

Так как для triangle АВС: cos A = displaystyle frac{AC}{AB}= sin В = displaystyle frac{sqrt{35}}{6},

а для triangle ВНС: sin В = displaystyle frac{CH}{BC} = displaystyle frac{sqrt{35}}{6} , откуда СН = displaystyle frac{BC cdot sqrt{35}}{6}=displaystyle frac{3 cdot sqrt{35}}{6}=displaystyle frac{sqrt{35}}{2},

По теореме Пифагора найдем ВН:

BH = sqrt{{BC}^2-{CH}^2}=sqrt{3^2-{left(displaystyle frac{sqrt{35}}{2}right)}^2}=

=sqrt{9-displaystyle frac{35}{4}}=sqrt{displaystyle frac{1}{4}}=displaystyle frac{1}{2}=0,5.

Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой. Поэтому для triangle АВС получим:

{CH}^2=AH cdot BH, тогда AH= displaystyle frac{ {CH}^2}{BH}, ; AH= displaystyle frac{ {left(displaystyle frac{sqrt{35}}{2}right)}^2}{0,5}=displaystyle frac{35 cdot 2}{4}=17,5.

Ответ: 17,5.

Задача 9. В треугольнике АВС угол С равен 90{}^circ, CH — высота, СН = 24 и BН = 7. Найдите sin A.

Решение:

По определению sin A= displaystyle frac{a}{c} = displaystyle frac{BC}{AB} = {cos B}.

Рассмотрим triangle BHC : {cos B= }displaystyle frac{BH}{BC}.

ВС найдем по теореме Пифагора:

ВС= sqrt{{BH}^2+{CH}^2}=sqrt{7^2+{24}^2}=sqrt{49+576}=sqrt{625}=25,

тогда {cos B= }displaystyle frac{BH}{BC}=displaystyle frac{7}{25}=0,28, а значит и sin A = {cos B }= 0,28.

Ответ: 0,28.

Задача 10. В треугольнике АВС угол С равен 90{}^circ, CH — высота, СН = 8 и BН = 4. Найдите tg A.

Решение:

По определению sin A = displaystyle frac{a}{c} = displaystyle frac{BC}{AB} = ; cos A = displaystyle frac{b}{c} = displaystyle frac{AC}{AB} = {sin B },

тогда tg A = displaystyle frac{sin A}{{cos A }}=displaystyle frac{cosB}{sinB}=ctgB, который найдем из triangle BHC:

ctgB=displaystyle frac{BH}{CH}=displaystyle frac{4}{8}=0,5.

Ответ: 0,5.

Задача 11. В треугольнике АВС угол С равен 90{}^circ, CH — высота, BН = 12, tg A = displaystyle frac{2}{3}. Найдите АН.

Решение:

По определению tg A= displaystyle frac{BC}{AC}=ctgB=displaystyle frac{2}{3}.

Для triangle BHC: ctgB=displaystyle frac{BH}{CH}=displaystyle frac{2}{3} , значит displaystyle frac{12}{CH}=displaystyle frac{2}{3}, СН = displaystyle frac{12 cdot 3}{2}=18.

Для triangle АHC: tg A= displaystyle frac{CH}{AH}=displaystyle frac{2}{3}, то displaystyle frac{18}{AH}=displaystyle frac{2}{3}, AH = displaystyle frac{18 cdot 3}{2}=27.

Ответ: 27.

Задача 12. В треугольнике АВС угол С равен 90{}^circ, CH — высота, BН = 12, sin A = displaystyle frac{2}{3}. Найдите АВ.

Решение:

Так как cos В = displaystyle frac{BC}{AB} = sin A = displaystyle frac{2}{3}.

Из triangle СВН имеем cos В = displaystyle frac{HB}{BC} = displaystyle frac{2}{3}, тогда ВС = displaystyle frac{3 cdot HB}{2}=displaystyle frac{3 cdot 12}{2}=18.

В triangle АВС имеем sinA = displaystyle frac{BC}{AB} = displaystyle frac{2}{3}, тогда AВ = displaystyle frac{3 cdot BC}{2}=displaystyle frac{3 cdot 18}{2}=27.

Ответ: 27.

Задача 13. В треугольнике АВС угол С равен 90{}^circ, из вершины прямого угла к гипотенузе проведена высота СН. Найдите cos A, AC и AB, если СН = 12, ВС = 20.

Решение:

Найдем НВ по теореме Пифагора из triangle ВСН:

HB = sqrt{BC^2-BH^2}=sqrt{20^2-12^2}=sqrt{(20-12)(20+12)}=

sqrt{8 cdot 32}= sqrt{8 cdot 2 cdot 16}=16.

sin В = displaystyle frac{CH}{BC} = displaystyle frac{12}{20}=displaystyle frac{3}{5}.

Для triangle АВС: cos A = displaystyle frac{AC}{AB}=sin B=displaystyle frac{3}{5}, получили cos A = 0,6.

Найдем АС и АВ несколькими способами.

1-й способ.

Так как cos A = displaystyle frac{AC}{AB}=displaystyle frac{3}{5}, то пусть АС = 3х, АВ = 5х,

тогда по теореме Пифагора {AC}^2+{BC}^2= {AB}^2, получим {(3x)}^2+{(20)}^2= {(5x)}^2
{25x}^2-{9x}^2= {20}^2 ,

{16x}^2= {20}^2,

x^2= {left(displaystyle frac{20}{4}right)}^2,
х = 5 ( так как хtextgreater 0). Значит, AC=15, AB=25.

2-й способ.

triangle HBC approx triangle CBA (по двум углам), значит displaystyle frac{HB}{CB}=frac{HC}{AC}=frac{BC}{AB} или displaystyle frac{16}{20}={12}{AC}={20}{AB} = k,

k = displaystyle frac{16}{20}=displaystyle frac{4}{5} , тогда displaystyle frac{12}{AC}=displaystyle frac{4}{5}, АС = displaystyle frac{12 cdot 5}{4}=15; displaystyle frac{20}{AB}=displaystyle frac{4}{5}, АВ = displaystyle frac{20 cdot 5}{4}=25.

3-й способ.

{CH}^2=AH cdot HB (высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой) , тогда {12}^2=AH cdot 16, АН = 144:16 = 9.

АВ = АН + НВ = 9 + 16 = 25.

По теореме Пифагора найдем АС:

AC = sqrt{{AB}^2-{BC}^2}=sqrt{{25}^2-{20}^2}=sqrt{(25-20)(25+20)} = sqrt{5cdot 45}=sqrt{5cdot 5cdot 9}=15.

Ответ: cos A = 0,6; АС = 15, АВ = 25.

Задача 14.

Высота ВН прямоугольного треугольника АВС, проведенная из вершины прямого угла В, равна 24 и отсекает от гипотенузы АС отрезок НС, равный 18.

Найдите АВ и cos А.

Решение:

Из прямоугольного triangle ВНС по теореме Пифагора найдем гипотенузу ВС и cos C:

ВС = sqrt{{HC}^2+{BH}^2}=sqrt{{18}^2+{24}^2}=sqrt{324+576}= sqrt{900}=30;

cos C = displaystyle frac{HC}{BC}=displaystyle frac{18}{30}=displaystyle frac{3}{5}.

Для triangle АВС: sin А = displaystyle frac{BC}{AC} = cos C = displaystyle frac{3}{5}.

Для triangle АНВ: sin А = displaystyle frac{BH}{AB} = displaystyle frac{3}{5}, то displaystyle frac{24}{AB} = displaystyle frac{3}{5}, АВ = displaystyle frac{24 cdot 5}{3}=40.

Из основного тригонометрического тождества найдем

cos A = sqrt{1-{sin}^2A}=sqrt{1-0,36}=sqrt{0,64}=0,8.

Ответ: АВ = 40, cos A = 0,8.

Задача 15.

Гипотенуза АС прямоугольного треугольника АСЕ равна 50, sin А = displaystyle frac{7}{25}.

Найдите площадь треугольника.

Решение:

В прямоугольном triangle АСЕ sin А = displaystyle frac{CE}{AC},

значит CE=AC cdot sinA=50 cdot displaystyle frac{7}{25} = 14.

Второй катет найдем, используя теорему Пифагора: AE= sqrt{{AC}^2-{CE}^2};

AE = sqrt{{50}^2-{14}^2}=sqrt{(50-14)(50+14)} =sqrt{36cdot 64}=6cdot8=48.

Площадь прямоугольного треугольника равна S = displaystyle frac{1}{2}ab,

поэтому S_{ACE}= displaystyle frac{1}{2} AEcdot CE=displaystyle frac{48cdot 14}{2}=336.

Ответ: 336.

Задача 16.

В треугольнике АВС угол С — прямой, катеты АВ = 13 и ВС = 12, СК — высота.

Найдите sin angle ACK. Результат округлите до сотых.

Решение:

triangle CAK approx triangle BAC ( angle A-общий, angle AKC=angle ACB=90{}^circ ),

значит angle ACK=angle ABC, sin angle ACK=displaystyle frac{AK}{AC}=displaystyle frac{AC}{AB}.

Найдем АС по теореме Пифагора из triangle САВ:

AC = sqrt{{AB}^2-{BC}^2}=sqrt{{13}^2-{12}^2}=

=sqrt{(13-12)(13+12)}=sqrt{25}= 5.

Тогда sin angle ACK=displaystyle frac{5}{13}=0,384..approx 0,38.

Ответ: 0,38.

Задача 17. В треугольнике АВС АС = ВС, АВ = 72, cos A = displaystyle frac{12}{13}. Найдите высоту СН.

Решение:

Так как АС = ВС, то triangle АВС — равнобедренный с основанием АВ, тогда

высота СН является медианой, то есть АН = НВ = displaystyle frac{1}{2}AB=36.

Поскольку triangle АСН — прямоугольный,

cos A = displaystyle frac{AH}{AC}= displaystyle frac{12}{13}, то есть displaystyle frac{36}{AC}= displaystyle frac{12}{13} Rightarrow АС = displaystyle frac{36 cdot 13}{12}=39.

По теореме Пифагора {AH}^2+{CH}^2={AC}^2, тогда

CH = sqrt{{AC}^2-{AH}^2} = sqrt{{39}^2-{36}^2}=

=sqrt{(39-36)(39+36)}=sqrt{3cdot 3cdot 25}=15.

Ответ: 15.

Задача 18. В треугольнике АВС угол С равен 90{}^circ, sin A = displaystyle frac{11}{14}, AC = 10sqrt{3}. Найдите АВ.

Решение:

1-й способ.

Поскольку sin A = displaystyle frac{BC}{AB}= displaystyle frac{11}{14}, то можно обозначить

ВС = 11х, АВ = 14х.

По теореме Пифагора AC^2+{BC}^2={AB}^2;

{(10sqrt{3})}^2+{(11x)}^2={(14x)}^2;

{(14x)}^2-{(11x)}^2 = 3 cdot 100;

(14х- 11х)(14х + 11х) = 3 cdot 100;

3cdot 25 x^2 = 3 cdot 100.

x^2=4, учитывая, что длина стороны положительна, х = 2,

следовательно, АВ = 14 cdot 2 = 28.

2-й способ.

Воспользуемся основным тригонометрическим тождеством {sin}^2A+{cos}^2A=1;

cos A = sqrt{1-{sin}^2A}=sqrt{1-{left(displaystyle frac{11}{14}right)}^2}=sqrt{displaystyle frac{196-121}{196}}=sqrt{displaystyle frac{75}{196}}=displaystyle frac{5sqrt{3}}{14}.

По определению cos A = displaystyle frac{AC}{AB}, значит displaystyle frac{AC}{AB}= displaystyle frac{5sqrt{3}}{14}.

Так как АС=10sqrt{3}, то displaystyle frac{10sqrt{3}}{AB}= displaystyle frac{5sqrt{3}}{14}, откуда АВ = displaystyle frac{10sqrt{3} cdot 14}{5sqrt{3}} = 28.

Ответ: 28.

Задача 19. Найдите углы ромба АВСD, если его диагонали АС и ВD равны 4sqrt{3} и 4.

Решение:

Пусть angle ВАО = alpha .

Диагонали ромба делят его углы пополам, значит, angle DAO=angle BAO = alpha .

Диагонали ромба взаимно перпендикулярны и точкой пересечения делятся пополам, следовательно, в прямоугольном треугольнике АВО катет АО = displaystyle frac{1}{2} AC=2sqrt{3}, а катет ВО = displaystyle frac{1}{2}BD =2.

Поэтому tgalpha =displaystyle frac{BO}{AO}=displaystyle frac{2}{2sqrt{3}}=displaystyle frac{1}{sqrt{3}}, откуда alpha =30{}^circ .

angle BAD=2alpha =60{}^circ , ; angle ADC=angle ABC=180{}^circ -60{}^circ =120{}^circ .

Ответ: {60}^circ, {120}^circ, {60}^circ, {120}^circ .

Часто в задачах встречаются треугольники с углами 90^{circ},, 30^{circ} и 60^{circ} или с углами 90^{circ},, 45^{circ} и 45^{circ}. Основные соотношения для них запоминайте наизусть!

Прямоугольные треугольники с углами 30, 60, 90 и 45, 45, 90 градусов

Для треугольника с углами 90^{circ},, 30^{circ} и 60^{circ} катет, лежащий напротив угла в 30^{circ}, равен половине гипотенузы.

Треугольник с углами 90^{circ},, 45^{circ} и 45^{circ} — равнобедренный. В нем гипотенуза в sqrt{2} раз больше катета.

Задача 20.

В треугольнике АВС угол С равен 90{}^circ, угол А равен 30{}^circ, АВ = 2sqrt{3} .

Найдите высоту CH.

Решение:

Рассмотрим triangle АВС:

По свойству катета, лежащего против угла {30}^circ, имеем ВС = displaystyle frac{1}{2} АВ = sqrt{3}.

В triangle BHC: angle BHC=90{}^circ ,; angle B=60{}^circ , то angle HCB=30{}^circ , следовательно, ВН = displaystyle frac{1}{2} BC = displaystyle frac{sqrt{3}}{2}.

По теореме Пифагора найдем НС:

HC = sqrt{{BC}^2-{BH}^2}=sqrt{{left(sqrt{3}right)}^2-{left(displaystyle frac{sqrt{3}}{2}right)}^2}=sqrt{3-displaystyle frac{3}{4}}=

=sqrt{2displaystyle frac{1}{4}}=sqrt{displaystyle frac{9}{4}}=displaystyle frac{3}{2}=1,5.

Ответ: 1,5.

Задача 21.

В треугольнике АВС угол С равен 90{}^circ, CH — высота, АВ = 2, angle A=30{}^circ . Найдите АH.

Решение:

Из triangle АВС найдем ВС = displaystyle frac{1}{2} АВ = 1 (по свойству катета, лежащего против угла 30{}^circ),

angle A=30{}^circ , то angle B=60{}^circ .

Из triangle ВСН: angle BHC=90{}^circ , angle B=60{}^circ , то angle HCB=30{}^circ , следовательно,

ВН = displaystyle frac{1}{2} ВС = displaystyle frac{1}{2}.

АН = АВ — НВ = 2 — displaystyle frac{1}{2} = 1,5.

Ответ: 1,5.

Еще раз повторим, что такое синус, косинус и тангенс угла в прямоугольном треугольнике.

Как запомнить эти соотношения? Лучший способ – решать много задач, и на уроках геометрии, и готовясь к ЕГЭ. Тогда все формулы, равенства, соотношения запомнятся сами собой.

Мы рассмотрели задачи на решение прямоугольных треугольников — то есть на нахождение неизвестных сторон или углов. Но это не всё! В вариантах ЕГЭ по математике множество задач, где фигурирует синус, косинус, тангенс или котангенс внешнего угла треугольника. Об этом — в следующей статье.

Если вам понравился разбор данной темы — записывайтесь на курсы подготовки к ЕГЭ по математике онлайн

Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Синус, косинус и тангенс острого угла прямоугольного треугольника» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
09.03.2023

Источник

Задание 1

В треугольнике $$ABC$$ известно, что $$AC=BC$$, высота $$AH$$ равна $$6sqrt{6}$$, $$BH=3$$ Найдите $$cos BAC$$.

Ответ: 0,2

Скрыть

Задание 2

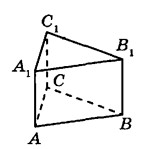
Найдите объём многогранника, вершинами которого являются точки $$B$$, $$C$$, $$A_1$$, $$C_1$$ правильной треугольной призмы $$ABCA_1B_1C_1$$ площадь основания которой равна 5, а боковое ребро равно 6.

Ответ: 10

Скрыть

Задание 3

В группе туристов 25 человек. Их вертолётом доставляют в труднодоступный район, перевозя по 5 человек за рейс. Порядок, в котором вертолёт перевозит туристов, случаен. Найдите вероятность того, что турист 3. полетит третьим рейсом вертолёта.

Ответ: 0,2

Скрыть

Номер рейса в этой задаче не имеет значения. Важно, что за один рейс перевозятся 5 человек. То есть, вероятность попасть туристу З. на какой-либо рейс (в том числе и 3-й), равна:

$$P=frac{m}{n}=frac{5}{25}=frac{1}{5}=0,2$$

Задание 4

Игральную кость бросали до тех пор, пока сумма всех выпавших очков не превысила число 5. Какова вероятность того, что для этого потребовалось два броска? Ответ округлите до сотых.

Ответ: 0,56

Скрыть

Задание 5

Найдите корень уравнения $$(frac{1}{4})^{x+2}=256^{x}$$

Ответ: -0,4

Скрыть

Задание 6

Найдите значение выражения $$log_{2,5}6cdot log_{6} 0,4$$

Ответ: -1

Скрыть

Задание 7

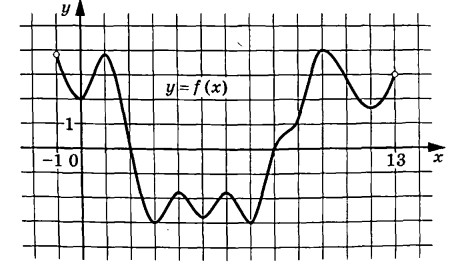
На рисунке изображён график функции $$y=f(x)$$, определённой на интервале $$(-1; 13)$$. Найдите количество точек, в которых касательная к графику функции $$y=f(x)$$ параллельна прямой $$y=-2$$.

Ответ: 9

Скрыть

Задание 8

Высота над землёй подброшенного вверх мяча меняется по закону $$y=1,4+11t-5t^2$$, где $$h$$ — высота в метрах, $$t$$ — время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее 7 метров?

Ответ: 0,6

Скрыть

Задание 9

Смешав 8-процентный и 26-процентный растворы кислоты и добавив 10 кг чистой воды, получили 16-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 20-процентный раствор кислоты. Сколько килограммов 8-процентного раствора использовали для получения смеси? Сколько секунд мяч будет находиться на высоте не менее 7 метров?

Ответ: 55

Скрыть

Задание 10

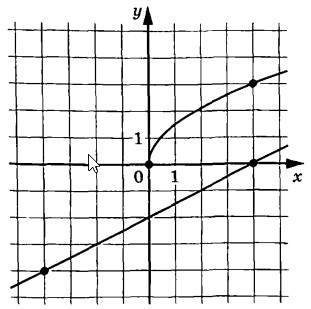
На рисунке изображены графики функций $$f(x)=asqrt{x}$$ и $$g(x)=kx+b$$, которые пересекаются в точке $$A(x_0; y_0)$$. Найдите $$y_0$$.

Ответ: 6

Скрыть

Задание 11

Найдите точку максимума функции промежутку $$y=(2x-1)cos x-2sin x+9$$, принадлежащую промежутку $$(0;frac{pi}{2})$$

Ответ: 0,5

Скрыть

Задание 12

а) Решите уравнение $$log^{2}_{2}(4x^{2})+3log_{0,5}(8x)=1$$

б) Найдите все корни этого уравнения, принадлежащие отрезку $$[0,15;1,5]$$

Ответ: а)$$0,25;sqrt[4]{8}$$ б)$$0,25$$

Скрыть

Задание 13

Сторона основания правильной четырёхугольной пирамиды $$SABCD$$ относится к боковому ребру как $$1:sqrt{2}$$. Через вершину $$D$$ проведена плоскость $$alpha$$, перпендикулярная боковому ребру $$SB$$ и пересекающая его в точке $$M$$.

а) Докажите, что $$M$$ — середина $$SB$$.

б) Найдите расстояние между прямыми $$AC$$ и $$DM$$, если высота пирамиды равна $$6sqrt{3}$$.

Ответ: 3

Скрыть

Задание 14

Решите неравенство $$frac{sqrt{x+4}(8-3^{2+x^{2}})}{4^{x-1}-3}leq 0$$

Ответ: $$-4;(log_{4}12;+infty)$$

Скрыть

Задание 15

15 июня 2025 года Сергей Данилович планирует взять кредит в банке на 4 года в размере целого числа миллионов рублей. Условия его возврата таковы:

— в январе каждого года действия кредита долг увеличивается на 15 % от суммы долга на конец предыдущего года;

— в период с февраля по июнь в каждый из 2026 и 2027 годов необходимо выплатить только начисленные в январе проценты по кредиту;

— в период с февраля по июнь в каждый из 2028 и 2029 годов выплачиваются равные суммы, причём последний платёж должен погасить долг по кредиту полностью.

Найдите наименьший размер кредита, при котором общая сумма выплат по кредиту превысит 12 млн рублей.

Ответ: 8 млн. руб.

Скрыть

Задание 16

Окружность с центром в точке $$C$$ касается гипотенузы $$AB$$ прямоугольного треугольника $$ABC$$ и пересекает его катеты $$AC$$ и $$BC$$ в точках $$E$$ и $$F$$. Точка $$D$$ — основание высоты, опущенной из вершины $$C$$. $$I$$ и $$J$$ — центры окружностей, вписанных в треугольники $$BCD$$ и $$ACD$$.

а) Докажите, что $$I$$ и $$J$$ лежат на отрезке $$EF$$.

б) Найдите расстояние от точки $$C$$ до прямой $$IJ$$, если $$AC=15$$, $$BC = 20$$.

Ответ: $$6sqrt{2}$$

Скрыть

Задание 17

Найдите все значения $$a$$, при каждом из которых оба уравнения $$a+frac{x}{2}=|x|$$ и $$asqrt{2}+x=sqrt{2asqrt{2}-x^{2}+12}$$ имеют ровно по 2 различных корня, и строго между корнями каждого из уравнений лежит корень другого уравнения.

Ответ: $$[sqrt{2};frac{3sqrt{6}}{sqrt{13}})$$

Скрыть

Задание 18

Трёхзначное число, меньшее 910, поделили на сумму его цифр и получили натуральное число $$n$$.

а) Может ли $$n$$ равняться 68?

б) Может ли $$n$$ равняться 86?

в) Какое наибольшее значение может принимать $$n$$, если все цифры ненулевые?

Ответ: а)да б)нет в)79

Скрыть

Источник

Понравилась статья? Поделить с друзьями:
  • 520825 решу егэ
  • 520824 решу егэ
  • 520803 решу егэ
  • 520802 решу егэ
  • 541376 решу егэ