В треугольнике ABC известно, что AC=BC, высота AH=6√6, BH=3. Найдите cos∠BAC.
Найдите объём многогранника, вершинами которого являются вершины B,C,A₁,C₁ правильной треугольной призмы ABCA₁B₁C₁, площадь основания которой равна 5, а боковое ребро равно 6.
В группе туристов 25 человек. Их вертолётом доставляют в труднодоступный район, перевозя по 5 человек за рейс. Порядок, в котором вертолёт перевозит туристов, случаен. Найдите вероятность того, что турист Н. полетит вторым рейсом вертолёта.
Игральную кость бросают до тех пор, пока сумма всех выпавших очков не превысит число 5. Какова вероятность, что для этого потребовалось два броска? Ответ округлите до сотых.
Найдите корень уравнения (left(dfrac14right)^{x+2}=256^x)
Найдите значение выражения (log_{2{,}5}6cdotlog_60{,}4)
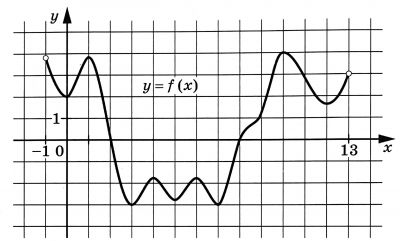
На рисунке изображен график функции y=f(x), определенной на интервале (-1;13). Найдите количество точек, в которых касательная к графику функции y=f(x) параллельна прямой y=-2.
Высота над землей подброшенного вверх мяча меняется по закону (h(t)=1{,}4+11t-5t^2), где (h) – высота в метрах, (t) – время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее 7 метров?
Смешав 8-процентный и 26-процентный растворы кислоты и добавив 10 кг чистой воды, получили 16‐процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 20-процентный раствор кислоты. Сколько килограммов 8-процентного раствора использовали для получения смеси?
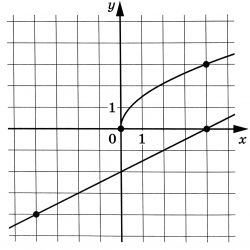
На рисунке изображены графики функций (f(x)=asqrt{x}) и (g(x)=kx+b), которые пересекаются в точке (A(x_0;y_0)). Найдите (y_0)
Найдите точку максимума функции (y=(2x-1)cos x-2sin x+9) принадлежащую промежутку (left(0;dfrac{pi}{2}right)).
а) Решите уравнение (log^2_2(4x^2)+3log_{0{,}5}(8x)=1)
б) Найдите все корни этого уравнения, принадлежащие отрезку ([0{,}15;1{,}5])
Сторона основания правильной четырехугольной пирамиды SABCD относится к боковому ребру как 1:√2. Через вершину D проведена плоскость α, перпендикулярная боковому ребру SB и пересекающая его в точке M.
а) Докажите, что M – середина SB.
б) Найдите расстояние между прямыми AC и DM, если высота пирамиды равна 6√3.
Решите неравенство (dfrac{sqrt{x+4}left(8-3^{2+x^2}right)}{4^{x-1}-3}leqslant0)
15 июня 2025 года Сергей Данилович планирует взять кредит в банке на 4 года в размере целого числа миллионов рублей. Условия его возврата таковы:
– в январе каждого года действия кредита долг увеличивается на 15% от суммы долга на конец предыдущего года;
– в период с февраля по июнь в каждый из 2026 и 2027 годов необходимо выплатить только начисленные в январе проценты по кредиту;
– в период с февраля по июнь в каждый из 2028 и 2029 годов выплачиваются равные суммы, причем последний платеж должен погасить долг по кредиту полностью.
Найдите наименьший размер кредита, при котором общая сумма выплат по кредиту превысит 12 млн рублей. В ответ запишите количество миллионов.
Окружность с центром в точке C касается гипотенузы AB прямоугольного треугольника ABC и пересекает его катеты AC и BC в точках E и F. Точка D – основание высоты, опущенной из вершины C. I и J – центры окружностей, вписанных в треугольники BCD и ACD.
а) Докажите, что I и J лежат на отрезке EF.
б) Найдите расстояние от точки C до прямой IJ, если AC=15, BC=20.
Найдите все значения (a), при каждом из которых оба уравнения (a+dfrac{x}2=|x|) и (asqrt2+x=sqrt{2asqrt2x-x^2+12}) имеют ровно 2 различных корня, и строго между корнями каждого из уравнений лежит корень другого уравнения.
Трёхзначное число, меньшее 910, поделили на сумму его цифр и получили натуральное число n.
а) Может ли n равняться 68?
б) Может ли n равняться 86?
в) Какое наибольшее значение может принимать n, если все цифры ненулевые?
Введите ответ в форме строки «да;да;1234». Где ответы на пункты разделены «;», и первые два ответа с маленькой буквы.
Задание 1
Площадь ромба равна 9. Одна из его диагоналей в 8 раз больше другой. Найдите меньшую диагональ.
Ответ: 1,5
Скрыть
Задание 2
Длина окружности основания конуса равна 6, образующая равна 4. Найдите площадь боковой поверхности конуса.
Ответ: 12
Скрыть
Задание 3
Из районного центра в деревню ежедневно ходит автобус. Вероятность того, что в понедельник в автобусе окажется меньше 18 пассажира, равна 0,9. Вероятность того, что окажется меньше 9 пассажиров, равна 0,66. Найдите вероятность того, что число пассажиров будет от 9 до 17 включительно.
Ответ: 0,24
Скрыть
Задание 4
Перед началом волейбольного матча капитаны команд тянут честный жребий, чтобы определить, какая из команд начнёт игру с мячом. Команда «Стартер» по очереди играет с командами «Ротор», «Мотор» и «Монтёр». Найдите вероятность того, что «Стартер» будет начинать только вторую игру.
Ответ: 0,125
Скрыть
Задание 5
Решите уравнение $$cos frac{pi(8x+8)}{3}=frac{1}{2}$$. В ответе запишите наибольший отрицательный корень.
Ответ: 0,375
Скрыть
Задание 6
Найдите значение выражения $$frac{125^{3,2}}{25^{3,3}}$$
Ответ: 125
Скрыть
Задание 7
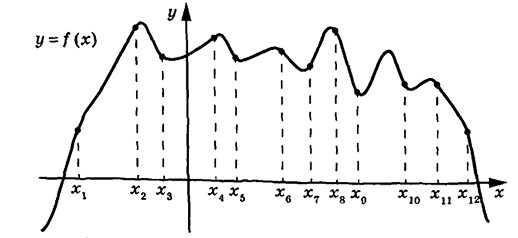
На рисунке изображён график функции $$y=f(x)$$. На оси абсцисс отмечено двенадцать точек: $$x_1$$, $$x_2$$, $$x_3$$, $$x_4$$, $$x_5$$, $$x_6$$, $$x_7$$, $$x_8$$, $$x_9$$, $$x_{10}$$, $$x_{11}$$, $$x_{12}$$. В ответе укажите количество точек (из отмеченных), в которых производная функции $$f(x)$$ отрицательна.
Ответ: 8
Скрыть
Задание 8
Наблюдатель находится на высоте $$h$$, выраженной в метрах. Расстояние от наблюдателя до наблюдаемой им линии горизонта, выраженное в километрах, вычисляется по формуле $$l=sqrt{frac{Rh}{500}}$$, где $$R=6400$$ км — радиус Земли. На какой высоте находится наблюдатель, если он видит линию горизонта на расстоянии 60 километров? Ответ дайте в метрах.
Ответ: 281,25
Скрыть
Задание 9
Заказ на изготовление 216 деталей первый рабочий выполняет на 6 часов быстрее, чем второй. Сколько деталей за час изготавливает первый рабочий, если известно, что он за час изготавливает на 6 деталей больше?
Ответ: 18
Скрыть
Задание 10
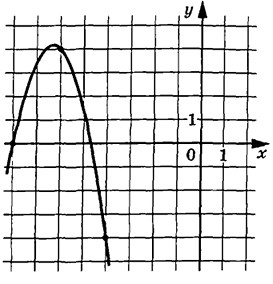
На рисунке изображён график функции $$f(x)=ax^2+bx+c$$. Найдите ординату точки пересечения графика функции $$y=f(x)$$ с осью ординат.
Ответ: -56
Скрыть
Задание 11
Найдите точку минимума функции $$y=10x-ln (x+11)+3$$.
Ответ: -10,9
Скрыть
Задание 12
а) Решите уравнение $$5^{x+sqrt{x}-1}+6cdot 5^{x-sqrt{x}+1}-5^{x+1}=0$$
б) Найдите все корни этого уравнения, принадлежащие отрезку $$[1;2,56]$$
Ответ: а)$$log^{2}_{5}10;log^{2}_{5}15$$ б)$$log^{2}_{5}10$$
Скрыть
Задание 13
В прямой пятиугольной призме $$ABCDEA_1B_1C_1D_1E_1$$ высота равна $$2sqrt{3}$$ , треугольник $$BCD$$ — правильный, со стороной 6, а четырёхугольник $$ABDE$$ — равнобедренная трапеция со сторонами $$AB=DE=2$$, $$BD=6$$ и $$AE=4$$.
а) Докажите, что плоскости $$CA_1E_1$$ и $$AED_1$$ перпендикулярны.
б) Найдите объём многогранника $$CAED_1B_1$$.
Ответ: 40
Скрыть
Задание 14
Решите неравенство $$log_{tg 0,9}(log_{frac{1}{4}}(x^2-2))leq 0$$
Ответ: $$(-sqrt{3};-1,5];[1,5;sqrt{3})$$
Скрыть
Задание 15
В июле Борис планирует взять кредит в банке на некоторую сумму. Банк предложил Борису два варианта кредитования.
1-й вариант:
— кредит предоставляется на 3 года;
— в январе каждого года действия кредита долг увеличивается на 10 % от суммы долга на конец предыдущего года;
— в период с февраля по июнь каждого года действия кредита выплачиваются равные суммы, причём последний платёж должен погасить долг по кредиту полностью,
2-й вариант:
— кредит предоставляется на 2 года; — в январе каждого года действия кредита долг увеличивается на 16 %;
— в период с февраля по июнь каждого года действия кредита выплачиваются равные суммы, причём последний платёж должен погасить долг по кредиту полностью.
Когда Борис подсчитал, то выяснил, что по 1-му варианту кредитования ему придётся выплачивать на 353 740 рублей меньше, чем по 2-му варианту. Какую сумму Борис планирует взять в кредит?
Ответ: 8937 тыс. руб.
Скрыть
Задание 16
Четырёхугольник $$ABCD$$ со сторонами $$BC=14$$ и $$AB=CD=40$$ вписан в окружность радиусом $$R=25$$.
а) Докажите, что прямые $$BC$$ и $$AD$$ параллельны.
б) Найдите $$AD$$.
Ответ: 42,16
Скрыть
Задание 17
Найдите все значения $$а$$, при каждом из которых уравнение $$frac{log_{0,2}(6x^2+13ax+7x+8a^2+2a-2)}{sqrt{4-3a-2x}}=0$$ имеет единственный корень.
Ответ: $$(-infty;-7];[2;+infty);-frac{11}{8}$$
Скрыть
Задание 18
Все члены конечной последовательности являются натуральными числами. Каждый член этой последовательности, начиная со второго, либо в 8 раз больше, либо в 7 раз меньше предыдущего. Сумма всех членов последовательности равна 4040.
а) Может ли последовательность состоять из трёх членов?
б) Может ли последовательность состоять из пяти членов?
в) Какое наибольшее количество членов может быть в последовательности?
Ответ: а)да б)нет в)897
Скрыть
ЕГЭ 2023
Варианты ЕГЭ 2023 базового уровня
ЕГЭбаз 2023 №01-12
ЕГЭбаз 2023 №13-24 в VK по платной подписке
Задачники ЕГЭ 2023 базового уровня
Задание 01. Текстовые задачи (простейшие)
Задание 02. Размеры и единицы измерения
Задание 03. Графики и диаграммы
Задание 04. Преобразование выражений (формулы)
Задание 05. Теория вероятностей
Задание 06. Выбор оптимального варианта
Задание 07. Анализ графиков и таблиц
Задание 08. Анализ утверждений
Задание 09. Площадь
Задание 10. Прикладная планиметрия
Задание 11. Прикладная стереометрия
Задание 12. Планиметрия
Задание 13. Стереометрия
Задание 14. Действия с дробями
Задание 15. Текстовые задачи (проценты)
Задание 16. Вычисления и преобразования
Задание 17. Уравнения
Задание 18. Числа и неравенства
Задание 19. Цифровая запись числа
Задание 20. Текстовая задача
Внимание!
Скачивая материалы с этого сайта, Вы принимаете условия
Пользовательского Соглашения!
Варианты ЕГЭ 2023 профильного уровня
ЕГЭпроф 2023 №01-10
ЕГЭпроф 2023 №11-24 в VK по платной подписке
Задачники ЕГЭ 2023 профильного уровня
Задание 01. Планиметрия
Задание 02. Стереометрия
Задание 03. Теория вероятностей
Задание 04. Теория вероятностей (повыш. сложность)
Задание 05. Простейшие уравнения
Задание 06. Значение выражения
Задание 07. Производная и первообразная
Задание 08. Задачи с прикладным содержанием
Задание 09. Текстовые задачи
Задание 10. Функции
Задание 11. Исследование функций
Задание 12. Уравнения
Задание 13. Стереометрия
Задание 14. Неравенства
Задание 15. Финансовая математика
Задание 16. —-
Задание 17. —-
Задание 18. —-
ОТВЕТЫ к Задачникам ЕГЭ 2023 года
МАТЕРИАЛЫ прошлых лет (ЕГЭ АРХИВ)
Задание 21. Задачи на смекалку
551737 решу егэ математика профиль
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
—>
Задание 6 № 551781
Функция определена и непрерывна на отрезке На рисунке изображен график её производной. Найдите промежутки убывания функции В ответе укажите сумму целых точек, входящих в эти промежутки.
Промежутки убывания данной функции F(X) соответствуют промежуткам, на которых её производная неположительна, то есть полуинтервалам (−5; −3,5] и [3,5; 6). В силу непрерывности функция F(X) убывает на отрезках [−5; −3,5] и [3,5; 6]. Данные промежутки содержат целые точки −5, −4, 4, 5 и 6. Их сумма равна 6.
Напомним, что если функция непрерывна на каком-либо из концов промежутка возрастания или убывания, то граничную точку присоединяют к этому промежутку. В частности, если функция непрерывна на отрезке и монотонна на интервале то функция монотонна на всем отрезке
Обобщением этого утверждения служит следующая теорема: функция монотонна на промежутке, если ее производная сохраняет знак всюду на этом промежутке, за исключением конечного числа точек, в которых функция непрерывна. Например, производная функции
Не существует в точке и положительна во всех остальных точках. Функция F в точке непрерывна, следовательно, она возрастает на
—>
Задание 6 № 551781
Их сумма равна 6.
Ege. sdamgia. ru
04.06.2019 12:20:54
2019-06-04 12:20:54
Источники:
Https://ege. sdamgia. ru/problem? id=551781
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword { color: red; } 551737 решу егэ математика профиль
551737 решу егэ математика профиль
551737 решу егэ математика профиль
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
—>
Задание 14 № 507736
Вернёмся к исходной переменной:
Таким образом, решение исходного неравенства
Насколько я могу судить, в результате приведения к общему знаменателю после перехода к новой переменной и после переноса 2у в левую часть уравнения, знак там не меняется.
—>
Задание 14 № 507736
Вернёмся к исходной переменной.
Ege. sdamgia. ru
11.03.2020 23:18:06
2020-03-11 23:18:06
Источники:
Https://ege. sdamgia. ru/problem? id=507736
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword { color: red; } 551737 решу егэ математика профиль
551737 решу егэ математика профиль
551737 решу егэ математика профиль
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
—>
При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
На одну порцию рисовой каши требуется 40 грамм риса и 0,12 литра молока. Какое наибольшее количество порций каши может приготовить столовая, если в ее распоряжении есть 900 грамм риса и 3 литра молока?
В аэропорту чемоданы пассажиров поднимают в зал выдачи багажа по транспортерной ленте. При проектировании транспортера необходимо учитывать допустимую силу натяжения ленты транспортера. На рисунке изображена зависимость натяжения ленты от угла наклона транспортера к горизонту при расчетной нагрузке. На оси абсцисс откладывается угол подъема в градусах, на оси ординат — сила натяжения транспортерной ленты (в килограммах силы). При каком угле наклона сила натяжения достигает 150 кгс? Ответ дайте в градусах.
Найдите величину угла ABC. Ответ дайте в градусах.
Ковбой Джон попадает в муху на стене с вероятностью 0,9, если стреляет из пристрелянного револьвера. Если Джон стреляет из непристрелянного револьвера, то он попадает в муху с вероятностью 0,2. На столе лежит 10 револьверов, из них только 4 пристрелянные. Ковбой Джон видит на стене муху, наудачу хватает первый попавшийся револьвер и стреляет в муху. Найдите вероятность того, что Джон промахнётся.
Около окружности, радиус которой равен 3, описан многоугольник, периметр которого равен 20. Найдите его площадь.
Функция определена и непрерывна на отрезке На рисунке изображен график её производной. Найдите промежутки возрастания функции В ответе укажите сумму целых точек, входящих в эти промежутки.
Прямоугольный параллелепипед описан около сферы радиуса 1. Найдите его площадь поверхности.
Найдите значение выражения
Независимое агентство намерено ввести рейтинг новостных интернет-изданий на основе оценок информативности In, оперативности Op, объективности публикаций Tr, а также качества сайта Q. Каждый отдельный показатель − целое число от –2 до 2.
Составители рейтинга считают, что объективность ценится втрое, а информативность публикаций — впятеро дороже, чем оперативность и качество сайта. Таким образом, формула приняла вид
Если по всем четырем показателям какое-то издание получило одну и ту же оценку, то рейтинг должен совпадать с этой оценкой. Найдите число A, при котором это условие будет выполняться.
Бригада маляров красит забор длиной 240 метров, ежедневно увеличивая норму покраски на одно и то же число метров. Известно, что за первый и последний день в сумме бригада покрасила 60 метров забора. Определите, сколько дней бригада маляров красила весь забор.
Найдите точку максимума функции
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
Дана правильная четырехугольная призма ABCDA1B1C1D1. На ребре AA1 отмечена точка K так, что AK : KA1 = 1 : 2. Плоскость α проходит через точки B и K параллельно прямой AC. Эта плоскость пересекает ребро DD1 в точке M.
А) Докажите, что MD : MD1 = 2 : 1.
Б) Найдите площадь сечения, если AB = 4, AA1 = 6.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
Две окружности касаются внешним образом в точке K. Прямая AB касается первой окружности в точке A, а второй — в точке B. Прямая BK пересекает первую окружность в точке D, прямая AK пересекает вторую окружность в точке C.
А) Докажите, что прямые AD и BC параллельны.
Б) Найдите радиус окружности, описанной около треугольника BCD, если известно, что радиус первой окружности равен 4, а радиус второй окружности равен 1.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
В июле планируется взять кредит в банке на сумму 18 млн рублей на некоторый срок (целое число лет). Условия его возврата таковы:
— каждый январь долг возрастает на 10% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
На сколько лет был взят кредит, если общая сумма выплат после полного погашения кредита составила 27 млн рублей?
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
При каких значениях параметра A уравнение
Имеет ровно 2 различных решения.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
На конкурсе «Мисс−261» выступление каждой участницы оценивают шесть судей. Каждый судья выставляет оценку — целое число баллов от 0 до 10 включительно. Известно, что за выступление участницы С все члены жюри выставили различные оценки. По старой системе оценивания итоговый балл за выступление определяется как среднее арифметическое всех оценок судей. По новой системе оценивания итоговый балл вычисляется следующим образом: отбрасываются две наибольшие оценки, и считается среднее арифметическое четырех оставшихся оценок.
А) Может ли разность итоговых баллов, вычисленных по старой и новой системам оценивания, быть равной 18?
Б) Может ли разность итоговых баллов, вычисленных по старой и новой системам оценивания, быть равной
В) Найдите наименьшее возможное значение разности итоговых баллов, вычисленных по старой и новой системам оценивания.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
—>
Дана правильная четырехугольная призма ABCDA 1 B 1 C 1 D 1.
Math-ege. sdamgia. ru
16.03.2019 6:43:59
2019-03-16 06:43:59
Источники:
Https://math-ege. sdamgia. ru/test? id=38005132