551780 решу егэ математика профиль - Помощь в подготовке к экзаменам и поступлению

Профиль математика 551780

Задание 6 № 551780

Функция определена и непрерывна на интервале На рисунке изображен график её производной. Найдите промежутки возрастания функции В ответе укажите сумму целых точек, входящих в эти промежутки.

Промежутки возрастания данной функции F(X) соответствуют промежуткам, на которых её производная неотрицательна, то есть интервалам (−3; 1) и (1; 4). В силу непрерывности функция F(X) возрастает на интервале (−3; 4). Данный промежуток содержит целые точки −2, −1, 0, 1, 2 и 3. Их сумма равна 3.

Напомним, что если функция непрерывна на каком-либо из концов промежутка возрастания или убывания, то граничную точку присоединяют к этому промежутку. В частности, если функция непрерывна на отрезке и монотонна на интервале то функция монотонна на всем отрезке

Обобщением этого утверждения служит следующая теорема: функция монотонна на промежутке, если ее производная сохраняет знак всюду на этом промежутке, за исключением конечного числа точек, в которых функция непрерывна. Например, производная функции

Не существует в точке и положительна во всех остальных точках. Функция F в точке непрерывна, следовательно, она возрастает на

Рекомендуем сравнить данную задачу с задачами 551782 и 551783 и обратить внимание на границы промежутка задания функции.

Задание 6 № 551780

Например, производная функции.

Math-ege. sdamgia. ru

09.03.2020 22:12:09

2020-03-09 22:12:09

Источники:

Https://math-ege. sdamgia. ru/problem? id=551780

Математика егэ на рисунке изображен график функции — Математика и Английский » /> » /> .keyword { color: red; } Профиль математика 551780

Математика егэ на рисунке изображен график функции

Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!

Задание 6 № 551780

Их сумма равна 3.

Источники:

ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword Математика егэ на рисунке изображен график функции

Математика егэ на рисунке изображен график функции

Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!

Задание 6 № 27500

На рисунке изображен график производной функции F(x), определенной на интервале (−2; 12). Найдите промежутки убывания функции F(x). В ответе укажите длину наибольшего из них.

Если функция непрерывна на отрезке [A; B], а её производная положительна (отрицательна) на интервале (A; B), то функция возрастает (убывает) на отрезке [A; B].

Производная функции отрицательна, на интервалах (−1; 5) и (7; 11). Значит, функция убывает на отрезках [−1; 5] длиной 6 и [7; 11] длиной 4. Длина наибольшего из них 6.

Задание 6 № 27500

Уско рен ная под го тов ка к ЕГЭ с ре пе ти то ра ми Учи.

Источники:

Математика егэ на рисунке изображен график функции

Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!

При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.

Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.

На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите где — одна из первообразных функции

Источники:

Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!

Задание 6 № 27500

Уско рен ная под го тов ка к ЕГЭ с ре пе ти то ра ми Учи.

Источники:

Тесты ЕГЭ по математике базового уровня 2022 » /> » /> .keyword < color: red; >Вариант 12154529 математика егэ база

Привет! Это онлайн школа Умскул

Привет! Это онлайн школа «Умскул»

Легендарный курс — Предбанник. Повтори весь материал ЕГЭ и ОГЭ за 5-9 дней!

Математика Базовый уровень

Об экзамене

Базовая математика – для слабаков, скажут одни, другие – для тупых гуманитариев, а третьи (те, что не снобы) просто используют ее в качестве разминки перед математикой профильной. Пусть гуманитарии не обижаются и не принимают все так близко к сердцу, самоирония должна быть. Просто, чтобы сдать базу, надо лишь ходить на уроки по математике и хотя бы немного слушать учителя. Никаких проблем не возникнет.

Структура

Экзаменационная работа состоит из одной части, включающей 20 заданий с кратким ответом базового уровня сложности. Ответом к каждому из заданий 1–20 является целое число или конечная десятичная дробь, или последовательность цифр.

На выполнение экзаменационной работы отводится 3 часа (180 минут).

Пояснения к оцениванию заданий

Правильное решение каждого из заданий 1–20 оценивается 1 баллом. Задание считается выполненным верно, если экзаменуемый дал правильный ответ в виде целого числа или конечной десятичной дроби, или последовательности цифр. Максимальный первичный балл за всю работу – 20.

Математика Базовый уровень

На выполнение экзаменационной работы отводится 3 часа (180 минут).

На выполнение экзаменационной работы отводится 3 часа 180 минут.

Источники:

ЕГЭ–2022, математика базовый уровень: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword < color: red; >Вариант 12154529 математика егэ база

Вариант 12154529 математика егэ база

Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!

При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв слов или цифр.

Источники:

Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!

На рисунке изображён график некоторой функции два луча с общей начальной точкой.

Dankonoy. com

08.11.2018 11:38:10

2018-11-08 11:38:10

Источники:

Https://dankonoy. com/ege/ege11/archives/10582

Профиль математика 551780 — Математика и Английский » /> » /> .keyword { color: red; } Профиль математика 551780

Профиль математика 551780

Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!

Задание 6 № 551780

Например, производная функции.

Источники:

ЕГЭ по математике 2022 варианты база и профиль с ответами » /> » /> .keyword < color: red; >Профиль математика 551780

ЕГЭ по математике

Единый государственный экзамен по математике 2022 года в 11 классе пройдет в следующие даты:

3 июня — базовый уровень — основной период

2 июня — профильный уровень — основной период

—

Тренировочные варианты ЕГЭ по математике на 2021 год

Пробные варианты ЕГЭ по математике 2021 базового уровня с ответами и решениями от Школы Пифагора:

Пробные варианты ЕГЭ по математике 2021 профильного уровня с ответами и решениями от Школы Пифагора:

Варианты ЕГЭ по математике от Решу ЕГЭ

Тренировочные варианты по математике базового уровня с ответами и решениями от портала Решу ЕГЭ (Сдам ГИА):

Все варианты ЕГЭ по математике представлены в формате pdf — вы легко можете скачать их и распечатать.

Реальные варианты ЕГЭ по математике

Варианты досрочного экзамена официально предоставлены ФИПИ.

Новости

Результаты итогового сочинения 2021-2022 Итоговое сочинение 2021-2022 года Обновлен проект расписания ЕГЭ в 2021 году Досрочный период ЕГЭ-2021 отменен Итоговое сочинение перенесено на апрель 2021 года Проекты расписаний ЕГЭ и ОГЭ 2021 Осенние каникулы в школах Москвы Порядок приема на обучение по программам высшего образования Направления итогового сочинения 2020-2021 учебного года

Важно знать

Ресурс носит неофициальный информационно-справочный характер, персональные данные не собирает и не обрабатывает, на интеллектуальные права третьих лиц не претендует.

Пробные варианты ЕГЭ по математике 2021 профильного уровня с ответами и решениями от Школы Пифагора.

Источники:

Профиль математика 551780 » /> » /> .keyword < color: red; >Профиль математика 551780

Профиль математика 551780

На рисунке изображён график — производной функции определенной на интервале (−8; 3). В какой точке отрезка [−3; 2] функция принимает наибольшее значение?

Решение. На заданном отрезке производная функции отрицательна, поэтому функция на этом отрезке убывает. Поэтому наибольшее значение функции достигается на левой границе отрезка, т. е. в точке −3.

На рисунке изображен график производной функции F(X), определенной на интервале (−8; 4). В какой точке отрезка [−7; −3] F(X) принимает наименьшее значение?

Решение. На заданном отрезке производная функции положительна, поэтому функция на этом отрезке возрастает. Поэтому наименьшее значение функции достигается на левой границе отрезка, т. е. в точке

На рисунке изображен график производной функции F(x), определенной на интервале (−7; 14). Найдите количество точек максимума функции F(x) на отрезке [−6; 9].

Решение. Точки максимума соответствуют точкам смены знака производной с положительного на отрицательный. На отрезке [−6; 9] функция имеет одну точку максимума X = 7.

На рисунке изображен график производной функции F(X), определенной на интервале (−18; 6). Найдите количество точек минимума функции F(X) на отрезке [−13;1].

Решение. Точки минимума соответствуют точкам смены знака производной с минуса на плюс. На отрезке [−13;1] функция имеет одну точку минимума X = −9.

На рисунке изображен график производной функции F(x), определенной на интервале (−11; 11). Найдите количество точек экстремума функции F(x) на отрезке [−10; 10].

Решение. Точки экстремума соответствуют точкам смены знака производной. Производная меняет знак в точках −6, −2, 2, 6, 9. Тем самым, на отрезке [−10; 10] функция имеет 5 точек экстремума.

На рисунке изображен график производной функции F(x), определенной на интервале (−5; 7). Найдите промежутки убывания функции F(x). В ответе укажите сумму целых точек, входящих в эти промежутки.

Решение. Промежутки убывания функции F(x) соответствуют промежуткам, на которых производная функции отрицательна, то есть интервалу (−2,5; 6,5). Данный интервал содержит следующие целые точки: –2, –1, 0, 1, 2, 3, 4, 5, 6 сумма которых равна 18.

На рисунке изображен график производной функции F(x), определенной на интервале (−11; 3). Найдите промежутки возрастания функции F(x). В ответе укажите длину наибольшего из них.

Решение. Промежутки возрастания функции F(x) соответствуют промежуткам, на которых производная функции неотрицательна, то есть промежуткам (−11; −10], [−7; −1], [2; 3). Наибольший из них — отрезок [−7; −1], длина которого 6.

Решение. Если функция непрерывна на отрезке [A; B], а её производная положительна (отрицательна) на интервале (A; B), то функция возрастает (убывает) на отрезке [A; B].

На рисунке изображен график производной функции F(x), определенной на интервале (−4; 8). Найдите точку экстремума функции F(x) на отрезке [−2; 6].

Решение. Если производная в некоторой точке равна нулю и меняет знак, то это точка экстремума. На отрезке [–2; 6] график производной пересекает ось абсцисс, производная меняет знак с плюса на минус. Следовательно, точка 4 является точкой экстремума.

На рисунке изображен график функции Y = F(X), определенной на интервале (−3; 9) . Найдите количество точек, в которых производная функции F(X) равна 0.

Решение. Производная изображенной на рисунке функции F(X) равна нулю в точках экстремумов: −2; −1; 1; 4 и 6. Производная равна нулю в 5 точках.

На рисунке изображён график — производной функции F(X). На оси абсцисс отмечены восемь точек: X1, X2, X3, . X8. Сколько из этих точек лежит на промежутках возрастания функции F(X)?

Решение. Возрастанию дифференцируемой функции F(X) соответствуют положительные значения её производной. Производная положительна в точках X4, X5 X6. Таких точек 3.

На рисунке изображён график производной функции и восемь точек на оси абсцисс: В скольких из этих точек функция убывает?

Решение. Убыванию дифференцируемой функции соответствуют отрицательные значения её производной. Производная отрицательна в точках : точки лежат ниже оси абсцисс, их ординаты отрицательны. Таких точек 5.

На рисунке изображен график функции и отмечены точки −2, −1, 1, 4. В какой из этих точек значение производной наименьшее? В ответе укажите эту точку.

Решение. Значение производной в точке касания равно угловому коэффициенту касательной, который в свою очередь равен тангенсу угла наклона данной касательной к оси абсцисс. Производная отрицательна в точках −1 и 4. Модуль тангенса угла наклона касательной явно больше в точке 4, поэтому тангенс в этой точке наименьший.

На рисунке изображён график дифференцируемой функции Y = F(X). На оси абсцисс отмечены девять точек: X1, X2, X3, . X9. Среди этих точек найдите все точки, в которых производная функции F(X) отрицательна. В ответе укажите количество найденных точек.

Решение. Две из отмеченных точек являются точками экстремума функции F(X). Это точки X3 и X6 (выделены красным). В них производная функции F(X) равна нулю.

В точках X1, X2, X7 и X8 функция F(X) возрастает (выделены синим). В этих четырёх точках производная функции F(X) положительна.

В точках X4, X5 и X9 функция F(X) убывает (выделены оранжевым). В этих Трёх точках производная функции F(X) отрицательна.

Источник: Демонстрационная версия ЕГЭ—2013 по математике., Проект демонстрационной версии ЕГЭ—2014 по математике.

На рисунке изображён график функции — производной функции F(X) определённой на интервале (1; 10). Найдите точку минимума функции F(X).

Решение. Точки минимума соответствуют точкам смены знака производной с отрицательного на положительный. На интервале (1; 10) функция имеет одну точку минимума X = 9.

На рисунке изображён график функции Y = f(X) и отмечены семь точек на оси абсцисс: X1, X2, X3, X4, X5, X6, X7. В скольких из этих точек производная функции F(X) отрицательна?

Решение. Производная функции отрицательна в тех точках, которые принадлежат участкам убывания функции. Это точки X3, X4, X7 — всего 3 точки.

Функция Y = F (X) определена и непрерывна на отрезке [−5; 5]. На рисунке изображён график её производной. Найдите точку X0, в которой функция принимает наименьшее значение, если F (−5) ≥ F (5).

Решение. Напомним, что если функция непрерывна на отрезке [A; B], а её производная положительна (отрицательна) на интервале (A; B), то функция возрастает (убывает) на отрезке [A; B].

Тем самым, функция F, график производной которой дан в условии, возрастает на отрезках [−5; −3] и [3; 5] и убывает на отрезке [−3; 3].

Из этого следует, что F принимает наименьшее значение на левой границе отрезка, в точке −5, или в точке минимума ХMin = 3. В силу возрастания F на отрезке [3; 5] справедливо неравенство F (5) > F (3). Поскольку по условию F (−5) не меньше, чем F (5), справедлива оценка F (−5) > F (3).

Тем самым, наименьшего значения функция F достигает в точке 3. График одной из функций, удовлетовряющих условию, приведён на рисунке.

Примечание Б. М. Беккера (Санкт-Петербург).

Непрерывность функции на концах отрезка существенна. Действительно, если бы функция F имела в точке 5 разрыв первого рода (см. рис.), значение F (5) могло оказаться меньше значения F (3), а тогда наименьшим значением функции на отрезке [−5; 5] являлось бы значение функции в точке 5.

Примечание портала РЕШУ ЕГЭ.

Мы были удивлены, обнаружив это задание в экзаменационной работе досрочного ЕГЭ по математике 28.04.2014 г. Это непростое задание отсутствует в Открытых банках заданий, что, несомненно, оказалось неприятным сюрпризом для выпускников.

Примечание Александра Ларина (Москва).

В этой задачке весь ужас «выстрелил вхолостую», 99,9999% решающих даже и не обратят внимание на потенциальную угрозу — ответ-то получается такой же. А про соотношение значений на границах и уж тем более про непрерывность никто читать и не собирается 🙂 А вот если условие слегка поменять, то «минус балл» всей стране обеспечен будет.

Из этого следует, что f принимает наименьшее значение на левой границе отрезка, в точке 5, или в точке минимума х min 3.

Источники:

ЕГЭ по математике 2022 варианты база и профиль с ответами » /> » /> .keyword < color: red; >Профиль математика 551780

Единый государственный экзамен по математике 2022 года в 11 классе пройдет в следующие даты:

3 июня — базовый уровень — основной период

2 июня — профильный уровень — основной период

—

Если функция непрерывна на отрезке A ; B, а её производная положительна отрицательна на интервале A ; B, то функция возрастает убывает на отрезке A ; B.

Dankonoy. com

22.01.2019 22:58:36

2019-01-22 22:58:36

Источники:

Https://dankonoy. com/ege/ege12/archives/3895

Источник

Информация о генераторе вариантов:

На данный момент в базе заданий 838 заданий (обновление было 20.09.2022) – только те, которые могут выпасть на экзамене. Варианты максимально приближены к вариантам реального ЕГЭ.

Источники заданий:

1) Прототипы из fipi.ru;
2) Прототипы из os.fipi.ru;
3) Прототипы с реальных ЕГЭ всех лет;
4) Прототипы с mathege.ru.
На каждую позицию рандомно выпадает случайное задание из базы заданий.

Описание каждой из позиций №1–18:

Задание 1. Планиметрия – все 160 прототипов темы, выпадающие на ЕГЭ.
Задание 2. Стереометрия – все 183 прототипа темы, выпадающие на ЕГЭ.
Задание 3. Начала теории вероятностей – все 40 прототипов темы, выпадающие на ЕГЭ.
Задание 4. Вероятности сложных событий – все 37 прототипов темы, выпадающие на ЕГЭ.
Задание 5. Простейшие уравнения – все 38 прототипов темы, выпадающие на ЕГЭ.
• Задание 6. Вычисления и преобразования – на данный момент 10 прототипов.
Задание 7. Производная и первообразная – все 44 прототипа темы, выпадающие на ЕГЭ.
Задание 8. Задачи с прикладным содержанием – все 71 прототип темы, выпадающие на ЕГЭ.
Задание 9. Текстовые задачи – все 93 прототипа темы, выпадающие на ЕГЭ.
Задание 10. Функции и их свойства – все 54 прототипа темы, выпадающие на ЕГЭ.
Задание 11. Наибольшее и наименьшее значение функции – все 54 прототипа темы, выпадающие на ЕГЭ.
Условия прототипов заданий первой части взяты у Евгения Пифагора из его видеокурса: «1–11 задания ЕГЭ профиль (первая часть с нуля)».

• Задание 12. Уравнения – на данный момент 10 прототипов.
• Задание 13. Стереометрическая задача – на данный момент 4 прототипа.
• Задание 14. Неравенства – на данный момент 10 прототипов.
• Задание 15. Финансовая математика – на данный момент 9 прототипов.
• Задание 16. Планиметрическая задача – на данный момент 4 прототипа.
• Задание 17. Задача с параметром – на данный момент 7 прототипов.
• Задание 18. Числа и их свойства – на данный момент 9 прототипов.

База заданий постоянно дополняется, в течение года будут добавлены все необходимые для подготовки прототипы.

Примеры заданий, тестовая часть.

Примеры заданий, развёрнутая часть.

На выполнение экзаменационной работы отводится 3 часа 55 минут.

Время выполнения варианта.

Тестовая часть проверяется автоматически, а развёрнутая часть самостоятельно вами по решениям и их критериям.

Пример критерия задания из развёрнутой части на 2 балла.

Пример задания из развёрнутой части на 4 балла.

В итоге выводится количество набранных баллов и ссылки на решения задач варианта:

Итог работы, ссылки на подробные решения всех задач.

Теги: тренировочные варианты, 11 класс, 2021, с ответами, новый вариант, профиль, пробный егэ.

Источник

4 июня 2022

В закладки

Обсудить

Жалоба

Полный вариант профильного уровня по математике от 2 июня с подробным разбором.

02_06_2022.pdf

00:00 — Введение
00:53 — Задание №1
01:49 — Задание №2
03:00 — Задание №3
05:29 — Задание №4
08:41 — Задание №5
11:11 — Задание №6
17:12 — Задание №7
22:27 — Задание №8
31:12 — Задание №9
39:00 — Задание №10
45:16 — Задание №11
51:10 — Задание №12
1:15:20 — Задание №13
1:34:35 — Задание №14 (1 тип задания)
1:43:40 — Задание №15
1:56:56 — Задание №16 (1 тип задания)
2:10:25 — Задание №16 (2 тип задания)
2:31:12 — Задание №16 (3 тип задания)
2:41:03 — Задание №16 (4 тип задания)
2:50:13 — Задание №16 (5 тип задания)
3:02:31 — Задание №17 (1 способ решения)
3:27:40 — Задание №17 (2 способ решения)
3:43:26 — Задание №14 (2 тип задания)
3:55:38 — Задание №18 (1 способ решения, 1 тип задания)
4:09:30 — Задание №18 (2 способ решения, 1 тип задания)
4:12:17 — Задание №18 (2 тип задания)

Источник: youtube.com/c/Профиматика

Источник

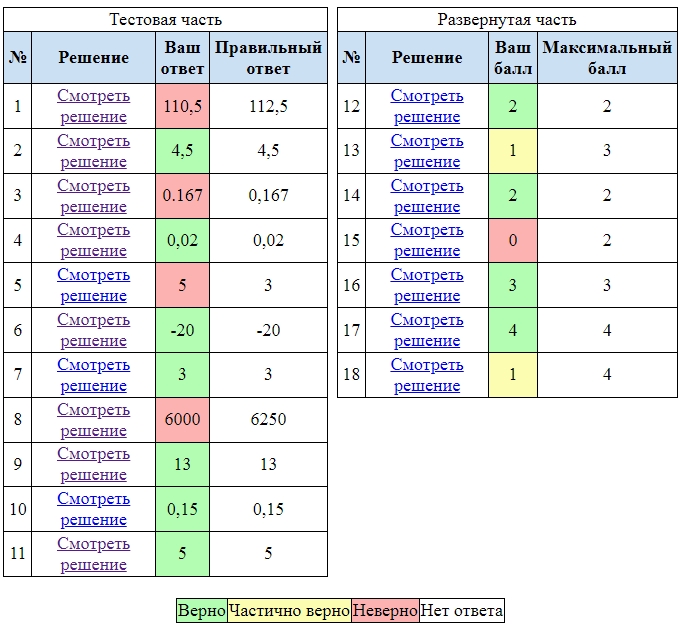
Задание 1

Альбом для рисования стоит 30 рублей. Какое наибольшее число таких альбомов можно будет купить на 500 рублей во время акции, где на все канцтовары действует скидка 15%?

Ответ: 19

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

1) Скидка действует 15%, значит заплатить придется 100-15=85% от основной суммы: 30 — 100% x — 85% x = 30 * 85 / 100 = 25.5 2) 500/25.5=19.6 ( если округлить ) , значит можно купить 19 тетрадей

Задание 2

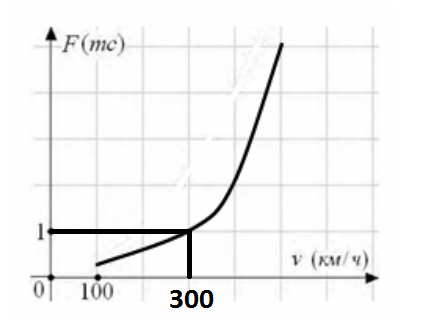
Когда самолет находится в горизонтальном полете, подъемная сила, действующая на крылья, зависит только от скорости. На рисунке изображена эта зависимость для некоторого самолета. На оси абсцисс откладывается скорость (в километрах в час), на оси ординат – сила (в тоннах силы). Определите по рисунку, чему равна подъемная сила (в тоннах силы) при скорости 300 км/ч?

Ответ: 1

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

На рисунке видно, что подъемная сила в данном случае будет равна 1

Задание 3

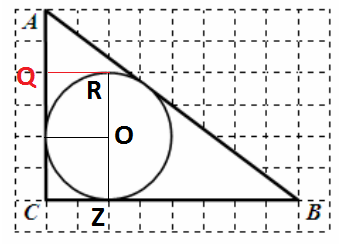
Найдите радиус окружности, вписанной в треугольник АВС, если размер клетки 1 см х 1 см. Ответ дайте в сантиметрах.

Ответ: 2

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

1 Вариант

Находим диаметр — RZ, он равен QZ = 4 . Значит радиус вписанной равен 2

2 Вариант

По теореме Пифаогора найдем AB = 10

Найдем полупериметр $$p = frac{10+8+6}{2}=12$$

Найдем площадь через половину произведения катетов $$S = frac{1}{2}6*8=24$$

Найдем радиус вписанной окружности $$ r = frac{S}{p}=frac{24}{12}=2$$

Задание 4

В супермаркете стоят три банкомата. Каждый из них может быть неисправен с вероятностью 0,2 независимо от других. Найдите вероятность того, что в супермаркете ровно два банкомата окажутся в рабочем состоянии .

Ответ: 0.384

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

Вероятность того, что банкомат окажется в рабочем состоянии, противоположна нерабочему состоянию, а значит равна 1 — 0,2 = 0,8

Так как у нас независимо друг от друга вероятности банкоматов существуют, то вероятность того, что два исправны выглядит так ( И — исправен, Н — неисправен, 1,2,3 — номера банкоматов ):

1	2	3	вероятность
И	И	Н	0,80,80,2=0,128
И	Н	И	0,80,20,8=0,128
Н	И	И	0,20,80,8=0,128

Следовательно, конечная вероятность равна сумме полученных: 0.128 * 3 = 0.384

Задание 5

В прямоугольном треугольнике АВС угол С – прямой. СН – высота, СL – биссектриса, ∠ А = 39. Найдите ∠ НСL. Ответ дайте в градусах.

Ответ: 6

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

Так как CH — высота, то треугольники ACH и CBH подобны, а значит ∠HCB=∠CAH=39

В таком случае ∠ACH = 90 — ∠HCB = 90 — 39 = 51

∠ ACL = 90 / 2 = 45 ( так как CL биссектриса )

Тогда ∠LCH = ∠ACH — ∠ACL = 51 — 45 = 6

Задание 6

На рисунке приведен график f ‘ (x) – производной функции у = f (x). Определите абсциссу точки графика функции у = f (x), в которой касательная параллельна прямой у = 2х – 1 или совпадает с ней.

Ответ: -3

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

Так как касательная к графику параллельна или совпадает с прямой y = 2x — 1, и при этом значение производной равно коэффициенту k линейной функции ( в нашем случае этот коэффициент равен 2 ), то и значение производной, которое мы ищем, равно 2. А так как нам дан график производной, то мы смело находим точку с ординатой (ось Оу) равную 2 и ищем абсциссу этой точки. Она равна -3

Задание 7

В кубе с ребром, равным 3, сделано сквозное отверстие размером 1 х 1. Найдите площадь полной поверхности полученного многогранника.

Ответ: 64

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

Площадь поверхности самого куба равна 3*3*6=54. Из него вычитаем два окошка , каждое из которых 1*1 = 1. То есть остается 54 — 2 = 52.

Но так же надо прибавить площади появившихся граней внутри куба. Каждая из них прямоугольник со сторонами 3 и 1 . Значит площадь 3*1=3. Их 4 штуки, а значит 3*1*4=12

В итоге площадь поверхности многогранника будет 52+12=64

Задание 8

Известно, что $$ tg x = frac{2}{sqrt{21}}$$ и $$pi < x< frac{3pi }{2}$$. Найдите sin x

Ответ: -0.4

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

Угол располагается в третьей четверти, поэтому sin будет отрицательный. Найдем сначала ctg x: $$ ctg x = frac {1}{tg x}= frac {1}{frac{2}{sqrt{21}}}=frac{sqrt{21}}{2}$$ Выразим sin x из формулы $$ 1 + ctg^{2} x = frac{1}{sin^{2} x} $$ $$ frac{1}{1 + ctg^{2} x} =sin^{2} x $$ $$sin x = — sqrt{ frac{1}{1 + ctg^{2} x} } $$ $$sin x = — sqrt{ frac{1}{1 + (frac{sqrt{21}}{2})^{2}} }=- sqrt{ frac{1}{1 + frac{21}{4}}}=-frac{2}{5}=-0.4 $$

Задание 9

На верфи инженеры проектируют новый аппарат для погружения на небольшие глубины. Конструкция имеет форму сферы, а значит, действующая на аппарат выталкивающая (архимедова) сила, выражаемая в ньютонах, будет определяться по формуле: F_A= αρgr³, где α=4,2 – постоянная, r – радиус аппарата в метрах, ρ=1000 кг/м³ – плотность воды, а g – ускорение свободного падения (считайте g=10 Н/кг). Каков может быть максимальный радиус аппарата, чтобы выталкивающая сила при погружении была не больше, чем 336000 Н? Ответ выразите в метрах.

Ответ: 2

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

Подставим имеющиеся значения в формулу: $$336000=4.2*1000*10*r^{3}$$ $$r^{3}=frac{336000}{4.2*1000*10}=8$$ r = 2

Задание 10

Первые пять часов автомобиль ехал со скоростью 60 км/ч, следующие 246 км он преодолел за 3 часа, а последние 130 км проехал со скоростью 65 км/ч. Найдите среднюю скорость (в км/ч) автомобиля на всем пути.

Ответ: 67.6

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

За первые пять часов он проехал 60 * 5 = 300 км

Последние 130 км он ехал $$frac{130}{65}=2$$ ч

Тогда средняя скорость будет равна $$frac{300+246+130}{5+3+2}=67.6$$

Задание 11

Найдите точку максимума функции $$f(x)=24-3x^{4}-8x{3}$$

Ответ: -2

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

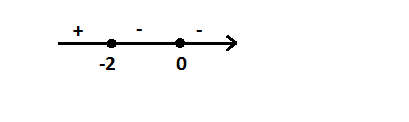
Найдем производную функции и приравняем ее к нулю:

$$f'(x)=-12x^{3}-24x^{2}=0$$

$$f'(x)=-12x^{2}(x+2)=0$$

Получаем или x = 0, или x = -2.

Отметим эти точки на координатной прямой и расставим знаки производной:

Как видим, точка максимум -2

Задание 12

Дано уравнение $$cos^{2}x(tg(frac{9pi}{2}+x)-3tg^{2}(pi-x))=cos 2x-1$$

А) Решите уравнение.

Б) Найдите его корни, принадлежащие промежутку $$[-4;-1]$$.

Ответ: А)$$-frac{pi}{4}+pi n,n in Z$$ Б)$$-frac{5pi}{4}$$

Задание 13

В основании прямой призмы $$ABCA_{1}B_{1}C_{1}$$ лежит равнобедренный треугольник $$ABC$$, в котором $$AB=AC$$.

А) Докажите, что объем пирамиды $$A_{1}BCC_{1}B_{1}$$ составляет 2/3 объема призмы.

Б) Найдите радиус сферы, описанной около пирамиды $$A_{1}BCC_{1}B_{1}$$, если известно, что $$AB=5$$, $$BC=6$$, $$AA_{1}=15$$.

Ответ: $$frac{65}{8}$$

Задание 14

Решите неравенство $$4cdotlog_{2}(8-2^{1+x^{2}})-log_{2}^{2}(2^{3-x^{2}}-2)leq 4x^{2}+3$$

Ответ: $$(-sqrt{2};-1];[1;sqrt{2})$$

Задание 15

В треугольнике $$ABC$$ проведена биссектриса $$BK$$ и на сторонах $$BA$$ и $$BC$$ взяты соответственно точки $$M$$ и $$P$$Р так, что $$angle AKM=angle CKP=frac{1}{2}angle ABC$$

а) Докажите, что прямая $$AC$$ касается окружности, описанной около треугольника $$MBP$$.

б) Найдите радиус окружности, описанной около треугольника $$MBP$$, если известно, что $$AB=10$$, $$BC=15$$, $$AC=20$$.

Ответ: $$frac{24sqrt{15}}{25}$$

Задание 16

1 мая 2017 г. Татьяна Константиновна положила 10 000 000 рублей в банк сроком на 1 год с ежемесячным начислением процентов и капитализацией под а % годовых. Это означает, что первого числа каждого месяца сумма вклада увеличивается на одно и то же количество процентов, рассчитанное таким образом, что за 12 месяцев она увеличится ровно на $$a$$ %. Найдите $$a$$, если известно, что через 6 месяцев сумма вклада Татьяны Константиновны составила 10 400 000 рублей.

Ответ: 8,16

Задание 17

Найдите все $$a$$, при каждом из которых система $$left{begin{matrix} y^2-2x^2+xy+9x-9=0\ ax^2+2ax-y-3+a=0 end{matrix}right.$$ имеет ровно четыре различных решения

Ответ: $$(-frac{1}{8};0);(0;frac{2}{9});(frac{2}{9};frac{1}{4})$$

Задание 18

Государство Новая Анчурия расположено на острове, имеющем форму круга. В стране 11 городов, расположенных на побережье. Каждый город напрямую соединен с каждым из остальных городов автотрассой.

А) Сколько автотрасс в государстве Новая Анчурия?

Б) После наводнения несколько автотрасс в стране закрыли на ремонт. Могло ли оказаться так, что теперь каждый город острова стал напрямую соединен автотрассой ровно с пятью другими городами?

В) Какое наибольшее число автотрасс в Новой Анчурии можно одновременно закрыть на ремонт, чтобы из каждого города можно было добраться на автомобиле до любого другого?

Ответ: А)55 Б)Нет В)45

Скрыть

а) Из каждого города выходит 10 дорог, поэтому всего есть 10 умножить на 11=110 концов дорог. Значит, дорог 55.

б) Если теперь из каждого города выходит 5 дорог, то всего есть 5 умножить на 11=55 концов дорог. Значит, дорог 27,5, что невозможно.

в) Можно оставить 10 дорог (например, соединяющих столицу со всеми городами, тогда откуда угодно куда угодно можно будет проехать через столицу), поэтому удастся закрыть 45.

Если оставить всего n-2 или меньше дорог на n городов, то это будет невозможно. В самом деле, у n-2 дорог 2n-4 конца, поэтому найдется город (на самом деле даже минимум 4 таких города) из которых выходит по одной дороге (0 дорог быть не может, из него тогда никуда нельзя доехать). Ясно, что проезжать транзитом через такой город нельзя. Поэтому если мысленно убрать с карты этот город и эту дорогу, на остальной карте можно будет проехать от любого города до любого другого. При этом число дорог снова на 2 меньше числа городов. Продолжая эти действия, придем к ситуации 0 дорог и 2 города, которая нам не подходит.

Источник