562032 решу егэ математика - Помощь в подготовке к экзаменам и поступлению

Решу егэ профиль математика 517739

Задание 12 № 517746

А) Решите уравнение

Б) Укажите корни этого уравнения, принадлежащие отрезку

А) Из уравнения получаем:

Б) Заметим, что Значит, указанному отрезку принадлежит корень −3.

Ответ: а) −3 и 27; б) −3.

Аналоги к заданию № 517739: 517746 517747 Все

Задание 12 № 517747

Задание 12 № 517746

Задание 12 № 517747

Ответ а 3 и 27; б 3.

Ege. sdamgia. ru

12.01.2020 13:48:01

2020-01-12 13:48:01

Источники:

Https://ege. sdamgia. ru/test? likes=517739

Решу егэ профиль математика 517739 — Математика и Английский » /> » /> .keyword { color: red; } Решу егэ профиль математика 517739

Решу егэ профиль математика 517739

Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!

Задание 12 № 517746

А) Решите уравнение

Б) Укажите корни этого уравнения, принадлежащие отрезку

А) Из уравнения получаем:

Б) Заметим, что Значит, указанному отрезку принадлежит корень −3.

Ответ: а) −3 и 27; б) −3.

Аналоги к заданию № 517739: 517746 517747 Все

Задание 12 № 517747

Задание 12 № 517746

Б Заметим, что Значит, указанному отрезку принадлежит корень 3.

Источники:

ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword < color: red; >Решу егэ профиль математика 517739

Решу егэ профиль математика 517739

Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!

Задание 12 № 514082

А) Решите уравнение

Б) Укажите корни этого уравнения, принадлежащие отрезку

А) Запишем исходное уравнение в виде:

Б) Поскольку отрезку принадлежит единственный корень −2.

Ответ: а) −2; 1, б) −2.

Почему такое странное ОДЗ?? Где 2-х>0, х>0, следовательно х0; тогда х (0;2)

Екатерина, в решении не находили ОДЗ.

В решении было использован равносильный переход, при котором условия достаточно для решения примера

А у Вас ОДЗ найдено с ошибкой.

Задание 12 № 517739

А) Решите уравнение

Б) Укажите корни этого уравнения, принадлежащие отрезку

А) Из уравнения получаем:

Б) Заметим, что Значит, указанному отрезку принадлежит только корень −2.

Ответ: а) −2 и 16; б) −2.

В пункте «а» ответ только 16,вы не проверили ОДЗ

В этом уравнении не нужно искать ОДЗ. Это лишнее действие

Задание 12 № 502094

А) Решите уравнение

Б) Найдите все корни этого уравнения, принадлежащие промежутку

А) Заметим, что преобразуем исходное уравнение:

Пусть тогда уравнение запишется в виде откуда или

При получим: откуда

Б) Корень не принадлежит промежутку Поскольку и корень принадлежит промежутку

Источник: ЕГЭ по математике 19.06.2013. Основная волна, резервный день. Центр. Вариант 502., Задания 13 (С1) ЕГЭ 2013

В строчке а) откуда-то взялась «3»

Путём каких преобразований мы получили ответ log(3)5 ?

1) Уравнение начинается с числе 9 в степени. Т. е. Мы раскладываем 9 как 3*3. Однако в первой строке решения мы видим 9*3. От туда и дальнейшее неверное вычисление.

2) Когда мы возвращаем замену (четвёртая строчка решения) вместо этого (если, допустим, t и правда равно 5/3) должно получиться Х-1= логорифм 5/3 по основанию 3. Верно?

Так ли это? Ибо мне свойственно ошибаться. Это правда ошибка, или я чего-то не понимаю? Если второе, то объясните, если можно.

Задание 12 № 517739

Задание 12 № 502094

Задание 12 502094.

Источники:

Решу егэ профиль математика 517739

Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!

При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.

Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.

Диагональ экрана телевизора равна 64 дюймам. Выразите диагональ экрана в сантиметрах, если в одном дюйме 2,54 см. Результат округлите до целого числа сантиметров.

Источники:

Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!

Задание 12 № 514082

А) Решите уравнение

Б) Укажите корни этого уравнения, принадлежащие отрезку

А) Запишем исходное уравнение в виде:

Б) Поскольку отрезку принадлежит единственный корень −2.

Ответ: а) −2; 1, б) −2.

Почему такое странное ОДЗ?? Где 2-х>0, х>0, следовательно х0; тогда х (0;2)

Екатерина, в решении не находили ОДЗ.

В решении было использован равносильный переход, при котором условия достаточно для решения примера

А у Вас ОДЗ найдено с ошибкой.

Задание 12 № 517739

А) Решите уравнение

Б) Укажите корни этого уравнения, принадлежащие отрезку

А) Из уравнения получаем:

Б) Заметим, что Значит, указанному отрезку принадлежит только корень −2.

Ответ: а) −2 и 16; б) −2.

В пункте «а» ответ только 16,вы не проверили ОДЗ

В этом уравнении не нужно искать ОДЗ. Это лишнее действие

Задание 12 № 502094

А) Решите уравнение

Б) Найдите все корни этого уравнения, принадлежащие промежутку

А) Заметим, что преобразуем исходное уравнение:

Пусть тогда уравнение запишется в виде откуда или

При получим: откуда

Б) Корень не принадлежит промежутку Поскольку и корень принадлежит промежутку

Источник: ЕГЭ по математике 19.06.2013. Основная волна, резервный день. Центр. Вариант 502., Задания 13 (С1) ЕГЭ 2013

В строчке а) откуда-то взялась «3»

Путём каких преобразований мы получили ответ log(3)5 ?

Задание 12 № 517739

Задание 12 № 502094

Задание 12 502094.

Уско рен ная под го тов ка к ЕГЭ с ре пе ти то ра ми Учи.

Dankonoy. com

16.06.2020 6:45:22

2020-06-16 06:45:22

Источники:

Https://dankonoy. com/ege/ege11/archives/10087

Материал для подготовки к экзамену по математике 1 курс. » /> » /> .keyword { color: red; } Решу егэ профиль математика 517739

Материал для подготовки к экзамену по математике 1 курс

Материал для подготовки к экзамену по математике 1 курс.

Материал для подготовки к экзамену по математике для 1 курса СПО.

Просмотр содержимого документа
«Материал для подготовки к экзамену по математике 1 курс.»

Логарифмические уравнения

1. Задание 5 № 26646

Найдите корень уравнения

2. Задание 5 № 26647

Найдите корень уравнения

3. Задание 5 № 26648

Найдите корень уравнения

4. Задание 5 № 26649

Найдите корень уравнения

5. Задание 5 № 26657

Найдите корень уравнения

6. Задание 5 № 26658

Найдите корень уравнения

7. Задание 5 № 26659

Найдите корень уравнения

8. Задание 5 № 77380

Решите уравнение

9. Задание 5 № 77381

Решите уравнение

10. Задание 5 № 77382

Решите уравнение Если уравнение имеет более одного корня, в ответе укажите меньший из них.

11. Задание 5 № 315120

Найдите корень уравнения

12. Задание 5 № 315535

Найдите корень уравнения

13. Задание 5 № 525399

Решите уравнение

Тригонометрические уравнения

1. Задание 5 № 26669

Найдите корни уравнения: В ответ запишите наибольший отрицательный корень.

Значениям соответствуют положительные корни.

Если, то и

Значениям соответствуют меньшие значения корней.

Следовательно, наибольшим отрицательным корнем является число

2. Задание 5 № 77376

Решите уравнение В ответе напишите наибольший отрицательный корень.

Значению соответствует Положительным значениям параметра соответствуют положительные значения корней, отрицательным значениям параметра соответствуют меньшие значения корней. Следовательно, наибольшим отрицательным корнем является число −1.

3. Задание 5 № 77377

Решите уравнение В ответе напишите наименьший положительный корень.

Значениям соответствуют отрицательные корни.

Если, то и

Значениям соответствуют большие положительные корни.

Наименьшим положительным решением является 0,5.

Преобразования числовых логарифмических выражений

1. Задание 9 № 26843

Найдите значение выражения

2. Задание 9 № 26844

Найдите значение выражения

3. Задание 9 № 26845

Найдите значение выражения

4. Задание 9 № 26846

Найдите значение выражения

5. Задание 9 № 26847

Найдите значение выражения

6. Задание 9 № 26848

Найдите значение выражения

7. Задание 9 № 26849

Найдите значение выражения

8. Задание 9 № 26850

Найдите значение выражения

9. Задание 9 № 26851

Найдите значение выражения

10. Задание 9 № 26852

Найдите значение выражения

11. Задание 9 № 26853

Найдите значение выражения

12. Задание 9 № 26854

Найдите значение выражения

13. Задание 9 № 26855

Найдите значение выражения

14. Задание 9 № 26856

Найдите значение выражения

15. Задание 9 № 26857

Найдите значение выражения

16. Задание 9 № 26858

Найдите значение выражения

17. Задание 9 № 26859

Найдите значение выражения

18. Задание 9 № 26860

Найдите значение выражения

19. Задание 9 № 26861

Найдите значение выражения

20. Задание 9 № 26862

Найдите значение выражения

21. Задание 9 № 26882

Найдите значение выражения

22. Задание 9 № 26883

Найдите значение выражения

23. Задание 9 № 26885

Найдите значение выражения

24. Задание 9 № 26889

Найдите значение выражения

25. Задание 9 № 26892

Найдите значение выражения

26. Задание 9 № 26893

Найдите значение выражения

27. Задание 9 № 26894

Найдите значение выражения

28. Задание 9 № 26896

Найдите значение выражения

29. Задание 9 № 77418

Вычислите значение выражения:

30. Задание 9 № 505097

Найдите значение выражения

31. Задание 9 № 509086

Найдите значение выражения

32. Задание 9 № 510939

Найдите значение выражения

33. Задание 9 № 525403

Найдите значение выражения

Вычисление значений тригонометрических выражений

1. Задание 9 № 26775

Найдите, если и

2. Задание 9 № 26776

Найдите, если и

3. Задание 9 № 26777

Найдите, если и

4. Задание 9 № 26778

Найдите, если и

5. Задание 9 № 26779

Найдите, если

6. Задание 9 № 26780

Найдите, если

7. Задание 9 № 26783

Найдите значение выражения, если

8. Задание 9 № 26784

Найдите, если и

9. Задание 9 № 26785

Найдите, если и

10. Задание 9 № 26786

Найдите, если

11. Задание 9 № 26787

Найдите, если

12. Задание 9 № 26788

Найдите, если

13. Задание 9 № 26789

Найдите, если

14. Задание 9 № 26790

Найдите, если

15. Задание 9 № 26791

Найдите, если

16. Задание 9 № 26792

Найдите значение выражения, если

17. Задание 9 № 26793

Найдите значение выражения, если

18. Задание 9 № 26794

Найдите, если

19. Задание 9 № 316350

Найдите, если

20. Задание 9 № 501598

Найдите значение выражения

21. Задание 9 № 502014

Найдите значение выражения

22. Задание 9 № 502045

Найдите значение выражения

23. Задание 9 № 502106

Найдите значение выражения

24. Задание 9 № 502285

Найдите значение выражения

25. Задание 9 № 502305

Найдите значение выражения если и

26. Задание 9 № 504410

Найдите значение выражения:

27. Задание 9 № 504824

Найдите значение выражения

28. Задание 9 № 508966

Найдите если

29. Задание 9 № 510424

Найдите если и

30. Задание 9 № 549336

Найдите если и

Преобразования числовых тригонометрических выражений

1. Задание 9 № 26755

Найдите значение выражения

2. Задание 9 № 26756

Найдите значение выражения

3. Задание 9 № 26757

Найдите значение выражения

4. Задание 9 № 26758

Найдите значение выражения

5. Задание 9 № 26759

Найдите значение выражения

6. Задание 9 № 26760

Найдите значение выражения

7. Задание 9 № 26761

Найдите значение выражения

8. Задание 9 № 26762

Найдите значение выражения

9. Задание 9 № 26763

Найдите значение выражения

10. Задание 9 № 26764

Найдите значение выражения

11. Задание 9 № 26765

Найдите значение выражения

12. Задание 9 № 26766

Найдите значение выражения

13. Задание 9 № 26767

Найдите значение выражения

14. Задание 9 № 26769

Найдите значение выражения

15. Задание 9 № 26770

Найдите значение выражения

16. Задание 9 № 26771

Найдите значение выражения

17. Задание 9 № 26772

Найдите значение выражения

18. Задание 9 № 26773

Найдите значение выражения

19. Задание 9 № 26774

Найдите значение выражения

20. Задание 9 № 77412

Найдите значение выражения

21. Задание 9 № 77413

Найдите значение выражения

22. Задание 9 № 77414

Найдите значение выражения:

23. Задание 9 № 245169

Найдите значение выражения

24. Задание 9 № 245170

Найдите значение выражения

25. Задание 9 № 245171

Найдите значение выражения

26. Задание 9 № 245172

Найдите значение выражения

27. Задание 9 № 501701

Найдите значение выражения

28. Задание 9 № 502994

Найдите значение выражения

29. Задание 9 № 503310

Найдите значения выражения

30. Задание 9 № 510013

Найдите если и

31. Задание 9 № 510312

Найдите значение выражения

32. Задание 9 № 510386

Найдите значение выражения

33. Задание 9 № 510405

Найдите значение выражения

34. Задание 9 № 510824

Найдите значение выражения

35. Задание 9 № 510843

Найдите значение выражения

36. Задание 9 № 525113

Найдите значение выражения

37. Задание 9 № 526009

Найдите значение выражения

Логарифмические и показательные уравнения

1. Задание 13 № 514082

А) Решите уравнение

Б) Укажите корни этого уравнения, принадлежащие отрезку

2. Задание 13 № 517739

А) Решите уравнение

Б) Укажите корни этого уравнения, принадлежащие отрезку

3. Задание 13 № 502094

А) Решите уравнение

Б) Найдите все корни этого уравнения, принадлежащие промежутку

4. Задание 13 № 516760

А) Решите уравнение:

Б) Определите, какие из его корней принадлежат отрезку

5. Задание 13 № 514623

А) Решите уравнение

Б) Найдите все корни этого уравнения, принадлежащие отрезку

6. Задание 13 № 502053

А) Решите уравнение

Б) Найдите все корни этого уравнения, принадлежащие отрезку

7. Задание 13 № 525377

А) Решите уравнение

Б) Найдите все корни этого уравнения, принадлежащие отрезку

8. Задание 13 № 513605

А) Решите уравнение

Б) Укажите корни этого уравнения, принадлежащие отрезку

9. Задание 13 № 503127

А) Решите уравнение

Б) Найдите все корни этого уравнения, принадлежащие отрезку

10. Задание 13 № 514081

А) Решите уравнение

Б) Укажите корни этого уравнения, принадлежащего отрезку

11. Задание 13 № 502999

А) Решите уравнение

Б) Найдите все корни этого уравнения, принадлежащие отрезку [−1; 2].

12. Задание 13 № 528517

А) Решите уравнение

Б) Укажите корни этого уравнения, принадлежащие отрезку

13. Задание 13 № 550261

А) Решите уравнение

Б) Укажите корни этого уравнения, принадлежащие промежутку

14. Задание 13 № 555265

А) Решите уравнение

Б) Укажите корни этого уравнения, принадлежащие отрезку

15. Задание 13 № 555583

А) Решите уравнение

Б) Укажите корни этого уравнения, принадлежащие отрезку

16. Задание 13 № 561853

А) Решите уравнение

Б) Найдите все корни этого уравнения, принадлежащие отрезку [−2,5; −1,5].

17. Задание 13 № 562032

А) Решите уравнение

Б) Найдите все корни этого уравнения, принадлежащие отрезку [−0,5; 0,5].

18. Задание 13 № 562757

А) Решите уравнение

Б) Найдите все корни этого уравнения, принадлежащие отрезку

б) Укажите корни этого уравнения, принадлежащие отрезку

Решите уравнение В ответе напишите наименьший положительный корень.

Просмотр содержимого документа «Материал для подготовки к экзамену по математике 1 курс.»

Б Укажите корни этого уравнения, принадлежащие отрезку.

Multiurok. ru

06.02.2020 18:29:01

2020-02-06 18:29:01

Источники:

Https://multiurok. ru/files/material-dlia-podgotovki-k-ekzamenu-po-matematike. html

Источник

Вчера, 22:23

В закладки

Обсудить

Жалоба

Теория и практика.

Содержание

1) Прямые
2) Параболы
3) Как искать пересечение параболы и прямой, двух парабол
4) Гипербола. Асимптотические точки гиперболы
5) Пересечение гиперболы и прямой
6) Иррациональные функции
7) Пересечение корня и прямой
Тригонометрические функции
9) Показательные функции
10) Логарифмические функции

10_zadacha.pdf

Источник: vk.com/profimatika

Источник

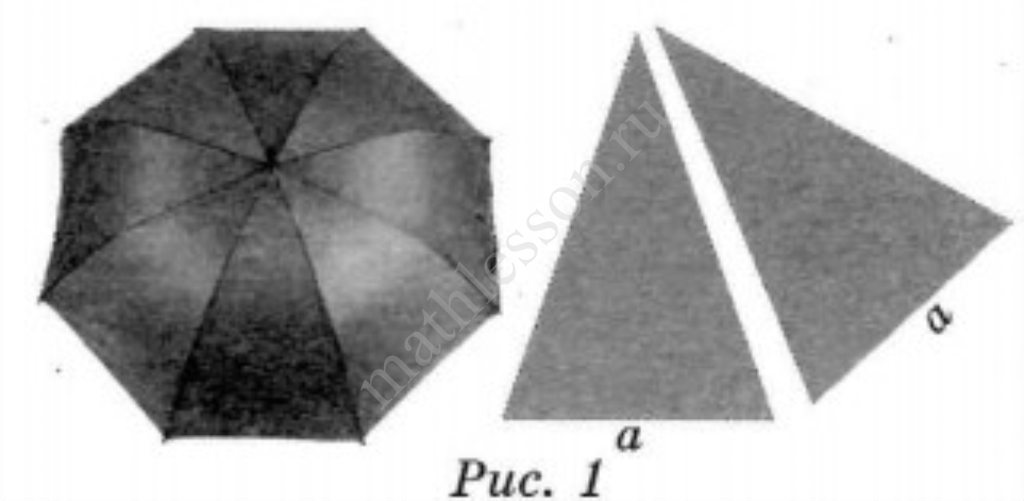
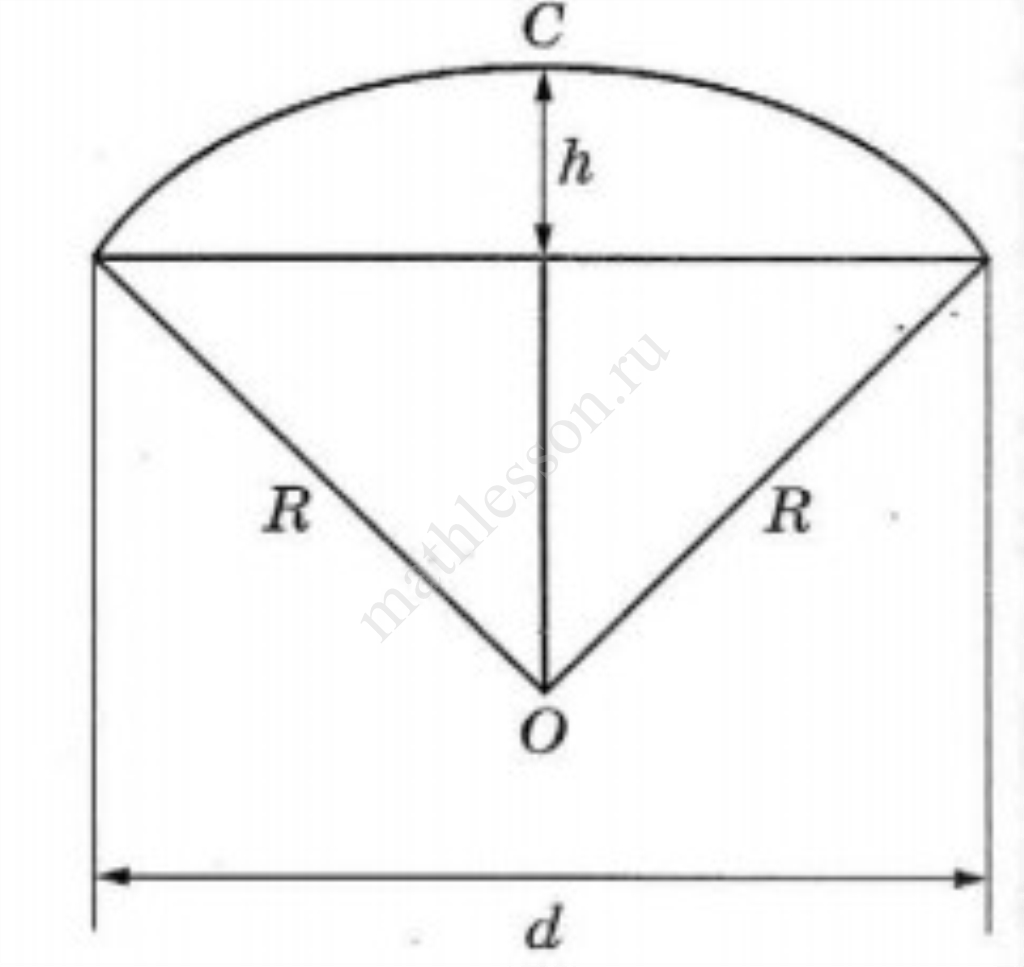
Два друга Петя и Вася задумались о том, как рассчитать площадь поверхности зонта. На первый взгляд зонт кажется круглым, а его купол напоминает часть сферы (сферический сегмент). Но если присмотреться, то видно, что купол зонта состоит из восьми отдельных клиньев, натянутых на каркас из восьми спиц (рис. 1). Сферическая форма в раскрытом состоянии достигается за счёт гибкости спиц и эластичности ткани, из которой изготовлен зонт. Петя и Вася сумели измерить расстояние между концами соседних спиц а. Оно оказалось равно 38 см. Высота купола зонта h (рис. 2) оказалась равна 25 см, а расстояние d между концами спиц, образующих дугу окружности, проходящей через вершину зонта, — ровно 100 см.

1. Длина зонта в сложенном виде равна 20 см и складывается из длины ручки (рис. 3) и трети длины спицы (зонт в три сложения). Найдите длину спицы, если длина ручки зонта равна 5,9 см.

2. Поскольку зонт сшит из треугольников, рассуждал Петя, площадь его поверхности можно найти как сумму площадей треугольников. Вычислите площадь поверхности зонта методом Пети, если высота каждого равнобедренного треугольника, проведённая к основанию, равна 53,1 см. Ответ дайте в квадратных сантиметрах с округлением до десятков.

3. Вася предположил, что купол зонта имеет форму сферического сегмента. Вычислите радиус $$R$$ сферы купола, зная, что $$ОС = R$$ (рис. 2). Ответ дайте в сантиметрах.

4. Вася нашёл площадь купола зонта как площадь поверхности сферического сегмента по формуле $$S = 2pi Rh$$, где R — радиус сферы, a h — высота сегмента. Рассчитайте площадь поверхности купола способом Васи. Число $$pi$$ округлите до 3,14. Ответ дайте в квадратных сантиметрах с округлением до целого.

5. Рулон ткани имеет длину 35 м и ширину 80 см. На фабрике из этого рулона были вырезаны треугольные клинья для 29 зонтов, таких же, как зонт, который был у Пети и Васи. Каждый треугольник с учётом припуска на швы имеет площадь 1050 кв. см. Оставшаяся ткань пошла в обрезки. Сколько процентов ткани рулона пошло в обрезки?

Источник

Синус, косинус и тангенс острого угла прямоугольного треугольника

Изучение тригонометрии мы начнем с прямоугольного треугольника. Определим, что такое синус и косинус, а также тангенс и котангенс острого угла. Это основы тригонометрии.

Напомним, что прямой угол — это угол, равный 90 градусов. Другими словами, половина развернутого угла.

Острый угол — меньший 90 градусов.

Тупой угол — больший 90 градусов. Применительно к такому углу «тупой» — не оскорбление, а математический термин

Нарисуем прямоугольный треугольник. Прямой угол обычно обозначается C. Обратим внимание, что сторона, лежащая напротив угла, обозначается той же буквой, только маленькой. Так, сторона, лежащая напротив угла A, обозначается .

Угол A обозначается соответствующей греческой буквой alpha .

Гипотенуза прямоугольного треугольника — это сторона, лежащая напротив прямого угла.

Катеты — стороны, лежащие напротив острых углов.

Катет , лежащий напротив угла alpha , называется противолежащим (по отношению к углу alpha ). Другой катет , который лежит на одной из сторон угла alpha , называется прилежащим.

Синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе:

sin A $=genfrac{}{}{}{0}{displaystyle a}{displaystyle c}.$

Косинус острого угла в прямоугольном треугольнике — отношение прилежащего катета к гипотенузе:

cos A $=genfrac{}{}{}{0}{displaystyle b}{displaystyle c}.$

Тангенс острого угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему:

tg A $=genfrac{}{}{}{0}{displaystyle a}{displaystyle b}.$

Другое (равносильное) определение: тангенсом острого угла называется отношение синуса угла к его косинусу:

tg A $=genfrac{}{}{}{0}{displaystyle sin A}{displaystyle cos A}.$

Котангенс острого угла в прямоугольном треугольнике — отношение прилежащего катета к противолежащему (или, что то же самое, отношение косинуса к синусу):

ctg A $=genfrac{}{}{}{0}{displaystyle cos A}{displaystyle sin A}.$

Обратите внимание на основные формулы для синуса, косинуса, тангенса и котангенса, которые приведены ниже. Они пригодятся нам при решении задач.

sin $displaystyle alpha = frac{a}{c}$	sin ${}^2 alpha +$ cos $displaystyle {}^2 alpha =frac{1}{cos^2 alpha}$	$alpha + beta = 90 ^{circ}$
cos $displaystyle alpha = frac{b}{c}$	1+tg $displaystyle {}^2 alpha =frac{1}{cos ^2 alpha}$	cos = sin
tg $displaystyle alpha = frac{a}{b}$	1+ctg $displaystyle {}^2 alpha =frac{1}{sin ^2 alpha}$	sin = cos
ctg $displaystyle alpha = frac{b}{a}$		tg = ctg

Давайте докажем некоторые из них.

Сумма углов любого треугольника равна $180^{circ}$ . Значит, сумма двух острых углов прямоугольного треугольника равнa $90^{circ}$ .
С одной стороны, $sin A =genfrac{}{}{}{0}{displaystyle a}{displaystyle c}$ как отношение противолежащего катета к гипотенузе. С другой стороны, $cos B =genfrac{}{}{}{0}{displaystyle a}{displaystyle c}$ , поскольку для угла катет а будет прилежащим. Получаем, что . Иными словами, $cos left( 90^{circ}-A right) = sin A$ .
Возьмем теорему Пифагора: . Поделим обе части на получаем $displaystyle left ( frac{a}{c} right )^2+left ( frac{b}{c} right )^2=left ( frac{c}{c} right )^2 ,$ то есть
Мы получили основное тригонометрическое тождество.
Поделив обе части основного тригонометрического тождества на , получим: $1+tg ^2 A = genfrac{}{}{}{0}{displaystyle 1}{displaystyle cos ^2 A }.$ Это значит, что если нам дан тангенс острого угла , то мы сразу можем найти его косинус. Аналогично, $1+ctg ^2 A =genfrac{}{}{}{0}{1}{sin ^2 A }.$

Хорошо, мы дали определения и записали формулы. А для чего все-таки нужны синус, косинус, тангенс и котангенс?

Мы знаем, что сумма углов любого треугольника равна $180^{circ}$ .

Знаем соотношение между сторонами прямоугольного треугольника. Это теорема Пифагора: .

Получается, что зная два угла в треугольнике, можно найти третий. Зная две стороны в прямоугольном треугольнике, можно найти третью. Значит, для углов — свое соотношение, для сторон — свое. А что делать, если в прямоугольном треугольнике известен один угол (кроме прямого) и одна сторона, а найти надо другие стороны?

С этим и столкнулись люди в прошлом, составляя карты местности и звездного неба. Ведь не всегда можно непосредственно измерить все стороны треугольника.

Синус, косинус и тангенс — их еще называют тригонометрическими функциями угла — дают соотношения между сторонами и углами треугольника. Зная угол, можно найти все его тригонометрические функции по специальным таблицам. А зная синусы, косинусы и тангенсы углов треугольника и одну из его сторон, можно найти остальные.

Мы тоже нарисуем таблицу значений синуса, косинуса, тангенса и котангенса для «хороших» углов от $0^{circ}$ до $90^{circ}$ .

	0	$genfrac{}{}{}{0}{displaystyle pi}{displaystyle 6}$	$genfrac{}{}{}{0}{displaystyle pi}{displaystyle 4}$	$genfrac{}{}{}{0}{displaystyle pi}{displaystyle 3}$	$genfrac{}{}{}{0}{displaystyle pi}{displaystyle 2}$
sin	0	$displaystyle frac{1}{2}$	$displaystyle frac{sqrt{2}}{2}$	$displaystyle frac{sqrt{3}}{2}$
cos		$displaystyle frac{sqrt{3}}{2}$	$displaystyle frac{sqrt{2}}{2}$	$displaystyle frac{1}{2}$	0
tg	0	$genfrac{}{}{}{0}{displaystyle 1}{displaystyle sqrt{3}}$			−
ctg	−			$genfrac{}{}{}{0}{displaystyle 1}{displaystyle sqrt{3}}$	0

Обратите внимание на два прочерка в таблице. При соответствующих значениях углов тангенс и котангенс не существуют.

Докажем теорему:

Если острый угол одного прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то синусы этих углов равны, косинусы этих углов равны и тангенсы этих углов равны.

В самом деле, пусть АВС и — два прямоугольных треугольника с прямыми углами С и C_1 и равными острыми углами А и A_1.

Треугольники АВС и подобны по первому признаку подобия треугольников, поэтому $displaystyle frac{AB}{A_1 B_1}=frac{BC}{B_1 C_1}=frac{AC}{A_1 C_1 } .$

Из этих равенств следует, что $displaystyle frac{BC}{AB}=frac{B_1 C_1}{A_1 B_1} ,$ т. е. sin А = sin A_1.

Аналогично, $displaystyle frac{AC}{AB}=frac{A_1C_1}{A_1 B_1},$ т. е. cos А = cos A_1, и $displaystyle frac{BC}{AC}=frac{B_1C_1}{A_1 C_1},$ т. е. tg A = tg A_1.

Это значит, что синус, косинус и тангенс зависят только от величины угла.

Разберем несколько задач по тригонометрии из Банка заданий ФИПИ.

Задача 1. В треугольнике ABC угол C равен $90^{circ}$ , sin A = 0,1. Найдите cos B.

Задача решается за четыре секунды.

Поскольку $A+B = 90^{circ}$ , sin A = cos B = 0,1.

Задача 2. В треугольнике ABC угол равен $90^{circ}$ , AB=5 , $sin A = genfrac{}{}{}{0}{displaystyle 7}{displaystyle 25}$ .

Найдите .

Решение:

$sin A = genfrac{}{}{}{0}{displaystyle a}{displaystyle c} = genfrac{}{}{}{0}{displaystyle BC}{displaystyle AB} = genfrac{}{}{}{0}{displaystyle 7}{displaystyle 25}.$

Отсюда

$BC= genfrac{}{}{}{0}{displaystyle 7}{displaystyle 25} cdot AB = genfrac{}{}{}{0}{displaystyle 7}{displaystyle 5}.$

Найдем AC по теореме Пифагора.

$AC=sqrt{AB^2-BC^2} = genfrac{}{}{}{0}{displaystyle 24}{displaystyle 5} = 4,8.$

Ответ: 4,8.

Задача 3. В треугольнике АВС угол С равен AВ = 13, ВС = 5. Найдите косинус и тангенс острого угла А. Ответ округлите до сотых.

Решение:

Для угла А противолежащий катет – это ВС,

АВ является гипотенузой треугольника, лежит против Значит, sin A $displaystyle = frac{BC}{AB}= frac{5}{13}.$

Катет, прилежащий к angle A – это катет АС, следовательно, cos⁡ А $displaystyle = frac{AC}{AB}=frac{AC}{13}.$

Длину катета АС найдем по теореме Пифагора:

Тогда $AC = sqrt{AB^2-BC^2}=sqrt{(13)^2-5^2}=sqrt{144}=12.$

cos⁡ А $displaystyle = frac{12}{13}=0,923 ... approx 0,92 ;$

tg A $displaystyle = frac{BC}{AC} = frac{5}{12}=0,416...approx 0,42.$

Ответ: 0,92; 0,42.

Заметим, что если катеты прямоугольного треугольника равны 5 и 12, то гипотенуза равна 13. Это одна из так называемых Пифагоровых троек. О них мы расскажем в других статьях сайта.

Задача 4. В треугольнике АВС угол С равен AC = 2, sin A= $displaystyle frac{sqrt{17}}{17} .$

Найдите BC.
Решение:

AC = b = 2, BC = a, AB = c.

Так как sin A $displaystyle = frac{a}{c} = frac{BC}{AB} = frac{sqrt{17}}{17},$ $displaystyle frac{a}{c} = frac{sqrt{17}}{17} ,$ $displaystyle c = frac{17a}{sqrt{17}}=sqrt{17}a.$

По теореме Пифагора получим

$a^2+2^2=(sqrt{17} a)^2;$

$displaystyle a= frac{1}{2}=0,5;$

Ответ: 0,5.

Задача 5. В треугольнике АВС угол С равен AC = 4, tg A = $displaystyle frac{33}{4sqrt{33}} .$ Найдите AB.

Решение:

AC = b = 4, tg A $displaystyle = frac{a}{b}=frac{33}{4sqrt{33}},$

$displaystyle frac{a}{4}=frac{33}{4sqrt{33}},$ $displaystyle a=frac{4 cdot 33}{4 cdot sqrt{33}}=sqrt{33},$

$AB = c = sqrt{a^2+b^2}=sqrt{(sqrt{33})^2+4^2}=sqrt{33+16} =7.$

Ответ: 7.

Задача 6.

В треугольнике АВС угол С равен CH – высота, AB = 13, tg A = $displaystyle frac{1}{5} .$ Найдите AH.

Решение:

AВ = с = 13, tg A = $displaystyle frac{a}{b}=frac{1}{5} ,$ тогда b = 5a.

По теореме Пифагора ABC:

$displaystyle a=sqrt{frac{169}{26}}=frac{13}{sqrt{26}},$ тогда $displaystyle b = 5a=5cdot frac{13}{sqrt{26}}=frac{65}{sqrt{26}}.$

(по двум углам), следовательно $displaystyle frac{AH}{AC}=frac{AC}{AB} ,$ откуда

$displaystyle AH = frac{AC^2}{AB}=frac{b^2}{c}=left ( frac{65}{sqrt{26}}right )^2:13=12,5.$

Ответ: 12,5.

Задача 7. В треугольнике АВС угол С равен

CH – высота, BC = 3, sin A = $displaystyle frac{1}{6} .$

Найдите AH.

Решение:

Так как sin A = $displaystyle frac{a}{c} = frac{BC}{AB} = frac{1}{6},$ тогда $displaystyle frac{3}{c} = frac{1}{6} ,$ c = АВ = 18.

sin A = $displaystyle frac{a}{c}$ = cos⁡ B = $displaystyle frac{1}{6} .$

Рассмотрим BHC:

${cos B= }displaystyle frac{BH}{BC}$ = $displaystyle frac{1}{6} ,$ получим $displaystyle frac{BH}{3}=displaystyle frac{1}{6},$

тогда BH = $displaystyle frac{3}{6}=displaystyle frac{1}{2}$ = 0,5,

AH = AB — BH = 18 — 0,5 = 17,5.

Ответ: 17,5.

Задача 8. В треугольнике АВС угол С равен 90 ${}^circ,$ CH — высота, BC = 3, cos A = $displaystyle frac{sqrt{35}}{6}.$

Найдите АH.

Решение:

Так как для АВС: cos A = $displaystyle frac{AC}{AB}=$ sin В = $displaystyle frac{sqrt{35}}{6},$

а для ВНС: sin В = $displaystyle frac{CH}{BC}$ = $displaystyle frac{sqrt{35}}{6}$ , откуда СН = $displaystyle frac{BC cdot sqrt{35}}{6}=displaystyle frac{3 cdot sqrt{35}}{6}=displaystyle frac{sqrt{35}}{2},$

По теореме Пифагора найдем ВН:

$BH = sqrt{{BC}^2-{CH}^2}=sqrt{3^2-{left(displaystyle frac{sqrt{35}}{2}right)}^2}=$

$=sqrt{9-displaystyle frac{35}{4}}=sqrt{displaystyle frac{1}{4}}=displaystyle frac{1}{2}=0,5.$

Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой. Поэтому для АВС получим:

${CH}^2=AH cdot BH,$ тогда $AH= displaystyle frac{ {CH}^2}{BH}, ; AH= displaystyle frac{ {left(displaystyle frac{sqrt{35}}{2}right)}^2}{0,5}=displaystyle frac{35 cdot 2}{4}=17,5.$

Ответ: 17,5.

Задача 9. В треугольнике АВС угол С равен 90 ${}^circ,$ CH — высота, СН = 24 и BН = 7. Найдите sin A.

Решение:

По определению sin A= $displaystyle frac{a}{c}$ = $displaystyle frac{BC}{AB}$ =

Рассмотрим BHC : ${cos B= }displaystyle frac{BH}{BC}.$

ВС найдем по теореме Пифагора:

ВС= $sqrt{{BH}^2+{CH}^2}=sqrt{7^2+{24}^2}=sqrt{49+576}=sqrt{625}=25,$

тогда ${cos B= }displaystyle frac{BH}{BC}=displaystyle frac{7}{25}=0,28,$ а значит и sin A = = 0,28.

Ответ: 0,28.

Задача 10. В треугольнике АВС угол С равен 90 ${}^circ,$ CH — высота, СН = 8 и BН = 4. Найдите tg A.

Решение:

По определению sin A = $displaystyle frac{a}{c}$ = $displaystyle frac{BC}{AB}$ = cos A = $displaystyle frac{b}{c}$ = $displaystyle frac{AC}{AB}$ =

тогда tg A = $displaystyle frac{sin A}{{cos A }}=displaystyle frac{cosB}{sinB}=ctgB,$ который найдем из BHC:

$ctgB=displaystyle frac{BH}{CH}=displaystyle frac{4}{8}=0,5.$

Ответ: 0,5.

Задача 11. В треугольнике АВС угол С равен 90 ${}^circ,$ CH — высота, BН = 12, tg A = $displaystyle frac{2}{3}.$ Найдите АН.

Решение:

По определению tg A= $displaystyle frac{BC}{AC}=ctgB=displaystyle frac{2}{3}.$

Для BHC: $ctgB=displaystyle frac{BH}{CH}=displaystyle frac{2}{3}$ , значит $displaystyle frac{12}{CH}=displaystyle frac{2}{3},$ СН = $displaystyle frac{12 cdot 3}{2}=18.$

Для АHC: tg A= $displaystyle frac{CH}{AH}=displaystyle frac{2}{3},$ то $displaystyle frac{18}{AH}=displaystyle frac{2}{3},$ AH = $displaystyle frac{18 cdot 3}{2}=27.$

Ответ: 27.

Задача 12. В треугольнике АВС угол С равен 90 ${}^circ,$ CH — высота, BН = 12, sin A = $displaystyle frac{2}{3}.$ Найдите АВ.

Решение:

Так как cos В = $displaystyle frac{BC}{AB}$ = sin A = $displaystyle frac{2}{3}.$

Из СВН имеем cos В = $displaystyle frac{HB}{BC}$ = $displaystyle frac{2}{3},$ тогда ВС = $displaystyle frac{3 cdot HB}{2}=displaystyle frac{3 cdot 12}{2}=18.$

В АВС имеем sinA = $displaystyle frac{BC}{AB}$ = $displaystyle frac{2}{3},$ тогда AВ = $displaystyle frac{3 cdot BC}{2}=displaystyle frac{3 cdot 18}{2}=27.$

Ответ: 27.

Задача 13. В треугольнике АВС угол С равен 90 ${}^circ,$ из вершины прямого угла к гипотенузе проведена высота СН. Найдите cos A, AC и AB, если СН = 12, ВС = 20.

Решение:

Найдем НВ по теореме Пифагора из ВСН:

$HB = sqrt{BC^2-BH^2}=sqrt{20^2-12^2}=sqrt{(20-12)(20+12)}=$

sin В = $displaystyle frac{CH}{BC}$ = $displaystyle frac{12}{20}=displaystyle frac{3}{5}.$

Для АВС: cos A = $displaystyle frac{AC}{AB}=sin B=displaystyle frac{3}{5},$ получили cos A = 0,6.

Найдем АС и АВ несколькими способами.

1-й способ.

Так как cos A = $displaystyle frac{AC}{AB}=displaystyle frac{3}{5},$ то пусть АС = 3х, АВ = 5х,

тогда по теореме Пифагора ${AC}^2+{BC}^2= {AB}^2,$ получим ${(3x)}^2+{(20)}^2= {(5x)}^2$
${25x}^2-{9x}^2= {20}^2 ,$

${16x}^2= {20}^2,$

$x^2= {left(displaystyle frac{20}{4}right)}^2,$
х = 5 ( так как х0). Значит,

2-й способ.

(по двум углам), значит $displaystyle frac{HB}{CB}=frac{HC}{AC}=frac{BC}{AB}$ или $displaystyle frac{16}{20}={12}{AC}={20}{AB} = k,$

k = $displaystyle frac{16}{20}=displaystyle frac{4}{5} ,$ тогда $displaystyle frac{12}{AC}=displaystyle frac{4}{5},$ АС = $displaystyle frac{12 cdot 5}{4}=15$ ; $displaystyle frac{20}{AB}=displaystyle frac{4}{5},$ АВ = $displaystyle frac{20 cdot 5}{4}=25.$

3-й способ.

${CH}^2=AH cdot HB$ (высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой) , тогда ${12}^2=AH cdot 16,$ АН = 144:16 = 9.

АВ = АН + НВ = 9 + 16 = 25.

По теореме Пифагора найдем АС:

$AC = sqrt{{AB}^2-{BC}^2}=sqrt{{25}^2-{20}^2}=sqrt{(25-20)(25+20)}$ =

Ответ: cos A = 0,6; АС = 15, АВ = 25.

Задача 14.

Высота ВН прямоугольного треугольника АВС, проведенная из вершины прямого угла В, равна 24 и отсекает от гипотенузы АС отрезок НС, равный 18.

Найдите АВ и cos А.

Решение:

Из прямоугольного ВНС по теореме Пифагора найдем гипотенузу ВС и cos C:

ВС = $sqrt{{HC}^2+{BH}^2}=sqrt{{18}^2+{24}^2}=sqrt{324+576}$ =

cos C = $displaystyle frac{HC}{BC}=displaystyle frac{18}{30}=displaystyle frac{3}{5}.$

Для АВС: sin А = $displaystyle frac{BC}{AC}$ = cos C = $displaystyle frac{3}{5}.$

Для АНВ: sin А = $displaystyle frac{BH}{AB}$ = $displaystyle frac{3}{5},$ то $displaystyle frac{24}{AB}$ = $displaystyle frac{3}{5},$ АВ = $displaystyle frac{24 cdot 5}{3}=40.$

Из основного тригонометрического тождества найдем

cos A = $sqrt{1-{sin}^2A}=sqrt{1-0,36}=sqrt{0,64}=0,8.$

Ответ: АВ = 40, cos A = 0,8.

Задача 15.

Гипотенуза АС прямоугольного треугольника АСЕ равна 50, sin А = $displaystyle frac{7}{25}.$

Найдите площадь треугольника.

Решение:

В прямоугольном АСЕ sin А = $displaystyle frac{CE}{AC},$

значит $displaystyle frac{7}{25}$ = 14.

Второй катет найдем, используя теорему Пифагора: $AE= sqrt{{AC}^2-{CE}^2};$

$AE = sqrt{{50}^2-{14}^2}=sqrt{(50-14)(50+14)} =sqrt{36cdot 64}=6cdot8=48.$

Площадь прямоугольного треугольника равна S = $displaystyle frac{1}{2}ab,$

поэтому $S_{ACE}= displaystyle frac{1}{2} AEcdot CE=displaystyle frac{48cdot 14}{2}=336.$

Ответ: 336.

Задача 16.

В треугольнике АВС угол С — прямой, катеты АВ = 13 и ВС = 12, СК — высота.

Найдите sin Результат округлите до сотых.

Решение:

A-общий, $angle AKC=angle ACB=90{}^circ$ ),

значит sin $angle ACK=displaystyle frac{AK}{AC}=displaystyle frac{AC}{AB}.$

Найдем АС по теореме Пифагора из САВ:

$AC = sqrt{{AB}^2-{BC}^2}=sqrt{{13}^2-{12}^2}=$

Тогда sin $angle ACK=displaystyle frac{5}{13}=0,384..approx 0,38.$

Ответ: 0,38.

Задача 17. В треугольнике АВС АС = ВС, АВ = 72, cos A = $displaystyle frac{12}{13}.$ Найдите высоту СН.

Решение:

Так как АС = ВС, то АВС — равнобедренный с основанием АВ, тогда

высота СН является медианой, то есть АН = НВ = $displaystyle frac{1}{2}AB=36.$

Поскольку АСН — прямоугольный,

cos A = $displaystyle frac{AH}{AC}=$ $displaystyle frac{12}{13},$ то есть $displaystyle frac{36}{AC}=$ $displaystyle frac{12}{13}$ АС = $displaystyle frac{36 cdot 13}{12}=39.$

По теореме Пифагора ${AH}^2+{CH}^2={AC}^2,$ тогда

$CH = sqrt{{AC}^2-{AH}^2} = sqrt{{39}^2-{36}^2}=$

Ответ: 15.

Задача 18. В треугольнике АВС угол С равен 90 ${}^circ,$ sin A = $displaystyle frac{11}{14},$ AC = 10 Найдите АВ.

Решение:

1-й способ.

Поскольку sin A = $displaystyle frac{BC}{AB}=$ $displaystyle frac{11}{14},$ то можно обозначить

ВС = 11х, АВ = 14х.

По теореме Пифагора $AC^2+{BC}^2={AB}^2;$

${(10sqrt{3})}^2+{(11x)}^2={(14x)}^2;$

${(14x)}^2-{(11x)}^2 = 3 cdot 100;$

(14х- 11х)(14х + 11х) = 3 cdot 100;

x^2=4, учитывая, что длина стороны положительна, х = 2,

следовательно, АВ = 14 cdot 2 = 28.

2-й способ.

Воспользуемся основным тригонометрическим тождеством ${sin}^2A+{cos}^2A=1;$

cos A = $sqrt{1-{sin}^2A}=sqrt{1-{left(displaystyle frac{11}{14}right)}^2}=sqrt{displaystyle frac{196-121}{196}}=sqrt{displaystyle frac{75}{196}}=displaystyle frac{5sqrt{3}}{14}.$

По определению cos A = $displaystyle frac{AC}{AB},$ значит $displaystyle frac{AC}{AB}= displaystyle frac{5sqrt{3}}{14}.$

Так как АС=10 то $displaystyle frac{10sqrt{3}}{AB}= displaystyle frac{5sqrt{3}}{14},$ откуда АВ = $displaystyle frac{10sqrt{3} cdot 14}{5sqrt{3}}$ = 28.

Ответ: 28.

Задача 19. Найдите углы ромба АВСD, если его диагонали АС и ВD равны 4 sqrt{3} и 4.

Решение:

Пусть angle ВАО = alpha .

Диагонали ромба делят его углы пополам, значит, = alpha .

Диагонали ромба взаимно перпендикулярны и точкой пересечения делятся пополам, следовательно, в прямоугольном треугольнике АВО катет АО = $displaystyle frac{1}{2} AC=2sqrt{3},$ а катет ВО = $displaystyle frac{1}{2}BD =2.$

Поэтому tg $alpha =displaystyle frac{BO}{AO}=displaystyle frac{2}{2sqrt{3}}=displaystyle frac{1}{sqrt{3}},$ откуда $alpha =30{}^circ .$

$angle BAD=2alpha =60{}^circ , ; angle ADC=angle ABC=180{}^circ -60{}^circ =120{}^circ .$

Ответ: ${60}^circ,$ ${120}^circ,$ ${60}^circ,$ ${120}^circ .$

Часто в задачах встречаются треугольники с углами $90^{circ},, 30^{circ}$ и $60^{circ}$ или с углами $90^{circ},, 45^{circ}$ и $45^{circ}$ . Основные соотношения для них запоминайте наизусть!

Для треугольника с углами $90^{circ},, 30^{circ}$ и $60^{circ}$ катет, лежащий напротив угла в $30^{circ}$ , равен половине гипотенузы.

Треугольник с углами $90^{circ},, 45^{circ}$ и $45^{circ}$ — равнобедренный. В нем гипотенуза в sqrt{2} раз больше катета.

Задача 20.

В треугольнике АВС угол С равен 90 ${}^circ,$ угол А равен 30 ${}^circ,$ АВ = 2

Найдите высоту CH.

Решение:

Рассмотрим АВС:

По свойству катета, лежащего против угла ${30}^circ,$ имеем ВС = $displaystyle frac{1}{2}$ АВ =

В BHC: $angle BHC=90{}^circ ,; angle B=60{}^circ ,$ то $angle HCB=30{}^circ ,$ следовательно, ВН = $displaystyle frac{1}{2}$ BC = $displaystyle frac{sqrt{3}}{2}.$

По теореме Пифагора найдем НС:

$HC = sqrt{{BC}^2-{BH}^2}=sqrt{{left(sqrt{3}right)}^2-{left(displaystyle frac{sqrt{3}}{2}right)}^2}=sqrt{3-displaystyle frac{3}{4}}=$

$=sqrt{2displaystyle frac{1}{4}}=sqrt{displaystyle frac{9}{4}}=displaystyle frac{3}{2}=1,5.$

Ответ: 1,5.

Задача 21.

В треугольнике АВС угол С равен 90 ${}^circ,$ CH — высота, АВ = 2, $angle A=30{}^circ .$ Найдите АH.

Решение:

Из АВС найдем ВС = $displaystyle frac{1}{2}$ АВ = 1 (по свойству катета, лежащего против угла 30 ${}^circ$ ),

$angle A=30{}^circ ,$ то $angle B=60{}^circ .$

Из ВСН: $angle BHC=90{}^circ , angle B=60{}^circ ,$ то $angle HCB=30{}^circ ,$ следовательно,

ВН = $displaystyle frac{1}{2}$ ВС = $displaystyle frac{1}{2}.$

АН = АВ — НВ = 2 — $displaystyle frac{1}{2}$ = 1,5.

Ответ: 1,5.

Еще раз повторим, что такое синус, косинус и тангенс угла в прямоугольном треугольнике.

Как запомнить эти соотношения? Лучший способ – решать много задач, и на уроках геометрии, и готовясь к ЕГЭ. Тогда все формулы, равенства, соотношения запомнятся сами собой.

Мы рассмотрели задачи на решение прямоугольных треугольников — то есть на нахождение неизвестных сторон или углов. Но это не всё! В вариантах ЕГЭ по математике множество задач, где фигурирует синус, косинус, тангенс или котангенс внешнего угла треугольника. Об этом — в следующей статье.

Если вам понравился разбор данной темы — записывайтесь на курсы подготовки к ЕГЭ по математике онлайн

Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Синус, косинус и тангенс острого угла прямоугольного треугольника» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
09.03.2023

Источник