В основании правильной треугольной призмы ABCA1B1C1 лежит треугольник ABC. На прямой AA1 отмечена точка D так, что A1 — середина AD. На прямой B1C1 отмечена точка E так, что C1 — середина B1E.
а) Докажите, что прямые A1B1 и DE перпендикулярны.
б) Найдите расстояние между прямыми AB и DE, если AB = 4, а AA1 = 1.
Спрятать решение
Решение.
а) Прямая AD перпендикулярна плоскости A1B1C1, поэтому проекцией прямой DE на эту плоскость является прямая A1E. Заметим, что в треугольнике A1EB1 медиана A1C1 равна половине стороны B1E, поэтому треугольник A1EB1 прямоугольный с прямым углом A1. Отсюда, по теореме о трех перпендикулярах, получаем, что ребро A1B1 перпендикулярно прямой DE.
б) В прямоугольном треугольнике A1EB1 найдем катет Далее, пусть L — точка пересечения прямой DE и плоскости ABC. Тогда отрезки AL и A1E параллельны, следовательно,
по теореме о средней линии треугольника. Так как
угол
прямой, следовательно, прямая AB перпендикулярна плоскости ADE, поэтому расстояние между прямыми DE и AB равно расстоянию от точки A до прямой DE, то есть высоте AF прямоугольного треугольника с катетами AD = 2 и
Далее вычислим расстояние между прямыми AB и DE:
Ответ:
Спрятать критерии
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Имеется верное доказательство утверждения пункта a) и обоснованно получен верный ответ в пункте б) | 3 |
| Получен обоснованный ответ в пункте б)
ИЛИ имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки |
2 |
| Имеется верное доказательство утверждения пункта а)
ИЛИ при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, ИЛИ обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен |
1 |
| Решение не соответствует ни одному из критериев, приведённых выше | 0 |
| Максимальный балл | 3 |
Источник: ЕГЭ по математике 29.06.2021. Резервная волна. Центр. Вариант 401, Задания 14 ЕГЭ–2021
ЕГЭ по математике — Профиль 2022. Открытый банк заданий с ответами.
Новые тренировочные варианты ЕГЭ 2023 по математике базовый и профильный уровень с ответами и решением для 10 и 11 класса, больше 100 вариантов в формате реального экзамена ФИПИ вы можете решать онлайн или скачать.
Тренировочные варианты ЕГЭ 2023 по математике база и профиль
13.09.2022 Тренировочный вариант №1 ЕГЭ 2023 по математике профиль с ответами
20.09.2022 Тренировочный вариант №2 ЕГЭ 2023 по математике профиль с ответами
20.09.2022 Тренировочный вариант №2 ЕГЭ 2023 база по математике с ответами
27.09.2022 Математика 11 класс профиль входная мониторинговая работа 3 варианта с ответами
28.09.2022 Тренировочный вариант №3 ЕГЭ 2023 база по математике с ответами
28 сентября 2022 Статград математика 11 класс ЕГЭ 2023 база и профиль варианты и ответы
29 сентября 2022 Тренировочный вариант №3 ЕГЭ 2023 по математике профиль с ответами
1 октября 2022 Ларин вариант 399 ЕГЭ 2023 по математике профиль решение с ответами
6 октября Тренировочный вариант №4 ЕГЭ 2023 база по математике с ответами
6 октября Тренировочный вариант №4 ЕГЭ 2023 по математике профиль с ответами
8 октября Ларин вариант 400 ЕГЭ 2023 по математике профиль решение с ответами
12 октября Тренировочный вариант №5 ЕГЭ 2023 база по математике с ответами
12 октября Тренировочный вариант №5 ЕГЭ 2023 по математике профиль с ответами
14 октября Вариант 1 Ященко ЕГЭ 2023 математика профиль с ответами и решением
14 октября Вариант 2 Ященко ЕГЭ 2023 математика профиль с ответами и решением
15 октября Ларин вариант 401 ЕГЭ 2023 по математике профиль решение с ответами
15 октября Ларин вариант 402 ЕГЭ 2023 по математике профиль решение с ответами
16 октября Вариант 3 Ященко ЕГЭ 2023 математика профиль с ответами и решением
16 октября Вариант 4 Ященко ЕГЭ 2023 математика профиль с ответами и решением
23 октября Тренировочный вариант №6 ЕГЭ 2023 база по математике с ответами
24 октября Тренировочный вариант №6 ЕГЭ 2023 по математике профиль с ответами
25 октября Тренировочный вариант №7 ЕГЭ 2023 база по математике с ответами
26 октября Тренировочный вариант №7 ЕГЭ 2023 по математике профиль с ответами
28 октября Ларин вариант 403 ЕГЭ 2023 по математике профиль решение с ответами
29 октября Ларин вариант 404 ЕГЭ 2023 по математике профиль решение с ответами
1 ноября 2022 Тренировочный вариант №8 решу ЕГЭ 2023 база по математике с ответами
1 ноября 2022 Тренировочный вариант №8 решу ЕГЭ 2023 по математике профиль с ответами
5 ноября 2022 Вариант 1-2 распечатай и реши ЕГЭ 2023 база по математике 11 класс с ответами
6 ноября 2022 Ларин вариант 405 ЕГЭ 2023 профиль по математике решение с ответами
9 ноября 2022 Тренировочный вариант №9 решу ЕГЭ 2023 база по математике с ответами
12 ноября 2022 Тренировочный вариант №9 решу ЕГЭ 2023 по математике профиль с ответами
13 ноября 2022 Ларин вариант 406 ЕГЭ 2023 профиль по математике решение с ответами
15 ноября 2022 Тренировочный вариант №10 решу ЕГЭ 2023 база по математике 11 класс с ответами
15 ноября 2022 Тренировочный вариант №10 решу ЕГЭ 2023 по математике профиль с ответами
21 ноября 2022 Ларин вариант 407 ЕГЭ 2023 профиль по математике решение с ответами
23 ноября 2022 Тренировочный вариант №11 решу ЕГЭ 2023 база по математике 11 класс с ответами
23 ноября 2022 Тренировочный вариант №11 решу ЕГЭ 2023 по математике профиль с ответами
27 ноября 2022 Ларин вариант 408 ЕГЭ 2023 профиль по математике решение с ответами
28 ноября 2022 Вариант 3-4 распечатай и реши ЕГЭ 2023 база по математике 11 класс с ответами
30 ноября 2022 Мониторинговая работа по математике 11 класс ЕГЭ 2023 профиль 1 полугодие
3 декабря 2022 Тренировочный вариант №12 решу ЕГЭ 2023 база по математике 11 класс с ответами
3 декабря 2022 Тренировочный вариант №12 решу ЕГЭ 2023 по математике профиль с ответами
3 декабря 2022 Пробник ЕГЭ 2023 Москва по математике профиль задания и ответы
5 декабря 2022 Ларин вариант 409 ЕГЭ 2023 профиль по математике решение с ответами
9 декабря 2022 Тренировочный вариант №13 решу ЕГЭ 2023 база по математике 11 класс с ответами
10 декабря 2022 Тренировочный вариант №13 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
12 декабря 2022 Ларин вариант 410 ЕГЭ 2023 профиль по математике решение с ответами
13 декабря 2022 Статград математика 11 класс профиль ЕГЭ 2023 варианты МА2210209-МА2210212 и ответы
13 декабря 2022 Математика 11 класс база ЕГЭ 2023 статград варианты и ответы
15 декабря 2022 Тренировочный вариант №14 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
15 декабря 2022 Тренировочный вариант №14 решу ЕГЭ 2023 база по математике 11 класс с ответами
20 декабря 2022 Вариант 5-6 распечатай и реши ЕГЭ 2023 база по математике 11 класс с ответами
20 декабря 2022 Ларин вариант 411 ЕГЭ 2023 профиль по математике решение с ответами
3 января 2023 Ларин вариант 412 ЕГЭ 2023 профиль по математике решение с ответами
6 января 2023 Тренировочный вариант 1-2 ЕГЭ 2023 профиль математика задания и ответы
8 января 2023 Вариант 3-4 ЕГЭ 2023 профиль математика задания и ответы
9 января 2023 Вариант 7-8 распечатай и реши ЕГЭ 2023 база по математике 11 класс с ответами
10 января 2023 Тренировочный вариант №15 и №16 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
11 января 2023 ЕГЭ 2023 математика тренировочные задания и ответы Ященко, Семенов
11 января 2023 Тренировочный вариант №15 и №16 база ЕГЭ 2023 по математике 11 класс с ответами
19 января 2023 Тренировочные варианты №17 и №18 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
22 января 2023 Ларин вариант 413 и 414 ЕГЭ 2023 профиль по математике решение и ответы
22 января 2023 Тренировочный 19 вариант решу ЕГЭ 2023 профиль по математике 11 класс с ответами
22 января 2023 База ЕГЭ 2023 математика 11 класс тренировочный вариант 19 с ответами
25 января 2023 База ЕГЭ 2023 математика 11 класс тренировочный вариант 20 с ответами
27 января 2023 Тренировочный вариант №20 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
28 января 2023 Вариант 415 Ларина ЕГЭ 2023 по математике 11 класс задания и ответы
2 февраля 2023 Вариант 21 база ЕГЭ 2023 математика 11 класс тренировочный вариант с ответами
2 февраля 2023 Тренировочный вариант №21 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
8 февраля 2023 Математика 10-11 класс ЕГЭ 2023 статград варианты база и профиль МА2200101-МА2200110 и ответы
11 февраля 2023 Тренировочный вариант №22 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
11 февраля 2023 Тренировочный вариант №22 решу ЕГЭ 2023 база по математике 11 класс с ответами
12 февраля 2023 Вариант 416 Ларина ЕГЭ 2023 по математике 11 класс задания и ответы
12 февраля 2023 Вариант 417 Ларина ЕГЭ 2023 по математике 11 класс задания и ответы
13 февраля 2023 Вариант 9 и вариант 10 ЕГЭ 2023 база математика распечатай и реши задания
13 февраля 2023 Вариант 11 и вариант 12 ЕГЭ 2023 база математика распечатай и реши
16 февраля 2023 Тренировочный вариант №23 решу ЕГЭ 2023 база по математике 11 класс с ответами
16 февраля 2023 Тренировочный вариант №23 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
18 февраля 2023 Вариант 418 Ларина ЕГЭ 2023 по математике 11 класс задания и ответы
22 февраля 2023 Пробный ЕГЭ 2023 вариант 24 база по математике 11 класс с ответами
22 февраля 2023 Пробный ЕГЭ 2023 вариант 24 профиль по математике 11 класс с ответами
25 февраля 2023 Вариант 419 Ларина ЕГЭ 2023 по математике 11 класс задания и ответы
28 февраля 2023 Статград математика 11 класс ЕГЭ 2023 база и профиль и ответы
4 марта 2023 Пробник ЕГЭ 2023 вариант 25 база по математике 11 класс с ответами
4 марта 2023 Вариант 420 Ларин ЕГЭ 2023 по математике 11 класс задания и ответы
5 марта 2023 Пробник ЕГЭ 2023 вариант 25 профиль по математике 11 класс с ответами
8 марта 2023 Пробник ЕГЭ 2023 вариант 26 профиль по математике 11 класс с ответами
8 марта 2023 Пробник ЕГЭ 2023 вариант 26 база по математике 11 класс 100 баллов с ответами
Смотрите также на нашем сайте:
Сборник Ященко ЕГЭ 2023 математика профильный уровень 36 вариантов
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
508780 решу егэ математика
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
—>
Задание 14 № 508380
Воспользуемся тем, что для суммы возможны четыре случая раскрытия модулей, откуда заключаем:
Приведем другое решение:
Как и в первом решении запишем неравенство в виде:
Заметим, что левая часть представляет из себя кусочно-линейную функцию, которая возрастает при и убывает при Это означает, что в точке –3 она достигает минимума равного 5. Таким образом, правая часть Тогда неравенство принимает вид:
Задание 14 № 508380
—>
508780 решу егэ математика.
Ege. sdamgia. ru
07.03.2017 0:00:13
2017-03-07 00:00:13
Источники:
Https://ege. sdamgia. ru/problem? id=508380
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword { color: red; } 508780 решу егэ математика
508780 решу егэ математика
508780 решу егэ математика
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
—>
Задание 10 № 508781
Симметричную монету бросают 11 раз. Во сколько раз вероятность события «выпадет ровно 5 орлов» больше вероятности события «выпадет ровно 4~орла»?
Задание 10 № 508782
Симметричную монету бросают 12 раз. Во сколько раз вероятность события «выпадет ровно 4 орла» меньше вероятности события «выпадет ровно 5~орлов»?
Задание 10 № 508783
Симметричную монету бросают 8 раз. Во сколько раз вероятность события «выпало ровно 4 орла» больше вероятности события «выпадет ровно 3~орла»?
Задание 10 № 508784
Симметричную монету бросают 9 раз. Во сколько раз вероятность события «выпадет ровно 4 орла» больше вероятности события «выпадет ровно 3~орла»?
Задание 10 № 508785
Симметричную монету бросают 10 раз. Во сколько раз вероятность события «выпадет ровно 4 орла» больше вероятности события «выпадет ровно 3~орла»?
Задание 10 № 508786
Симметричную монету бросают 16 раз. Во сколько раз вероятность события «выпадет ровно 8 орлов» больше вероятности события «выпадет ровно 7~орлов»?
Задание 10 № 508787
Симметричную монету бросают 17 раз. Во сколько раз вероятность события «выпадет ровно 8 орлов» больше вероятности события «выпадет ровно 7~орлов»?
Задание 10 № 508788
Симметричную монету бросают 20 раз. Во сколько раз вероятность события «выпадет ровно 10 орлов» больше вероятности события «выпадет ровно 9~орлов»?
Задание 10 № 508789
Симметричную монету бросают 21 раз. Во сколько раз вероятность события «выпадет ровно 10 орлов» больше вероятности события «выпадет ровно 9~орлов»?
Задание 10 № 508790
Симметричную монету бросают 22 раза. Во сколько раз вероятность события «выпадет ровно 10 орлов» больше вероятности события «выпадет ровно 9~орлов»?
Задание 10 № 508786
Задание 10 № 508781
Задание 10 508786.
Ege. sdamgia. ru
14.05.2019 20:28:53
2019-05-14 20:28:53
Источники:
Https://ege. sdamgia. ru/test? likes=508780
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword { color: red; } 508780 решу егэ математика
508780 решу егэ математика
508780 решу егэ математика
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
—>
Задание 10 № 508780
Симметричную монету бросают 10 раз. Во сколько раз вероятность события «выпадет ровно 5 орлов» больше вероятности события «выпадет ровно 4 орла»?
Воспользуемся формулой Бернулли. Найдем вероятность события А, состоящего в том, что при десяти бросаниях выпадет ровно 5 орлов:
Аналогично найдем вероятность события B, состоящего в том, что при десяти бросаниях выпадет ровно 4 орла:
Приведем решение Ирины Шраго.
Вероятность того, что выпадет ровно 5 орлов, равна отношению количества вариантов, при которых выпадает ровно 5 орлов, к общему количеству вариантов: Вероятность того, что выпадет ровно 4 орла, равна отношению количества вариантов, при которых выпадает ровно 4 орла, к общему количеству вариантов: Тогда отношение этих вероятностей
—>
Задание 10 № 508780
Уско рен ная под го тов ка к ЕГЭ с ре пе ти то ра ми Учи.
Ege. sdamgia. ru
09.08.2017 16:57:34
2017-08-09 16:57:34
Источники:
Https://ege. sdamgia. ru/problem? id=508780
В США тоже есть ЕГЭ — причём он был задолго до нас. Вот одна задачка оттуда. Мы перевели её на русский и заменили центы на привычные рубли. Сама задача звучит так:
Эту задачку можно решить на листочке за несколько минут. Попробуйте сами, а если не получится — кат в помощь ↓
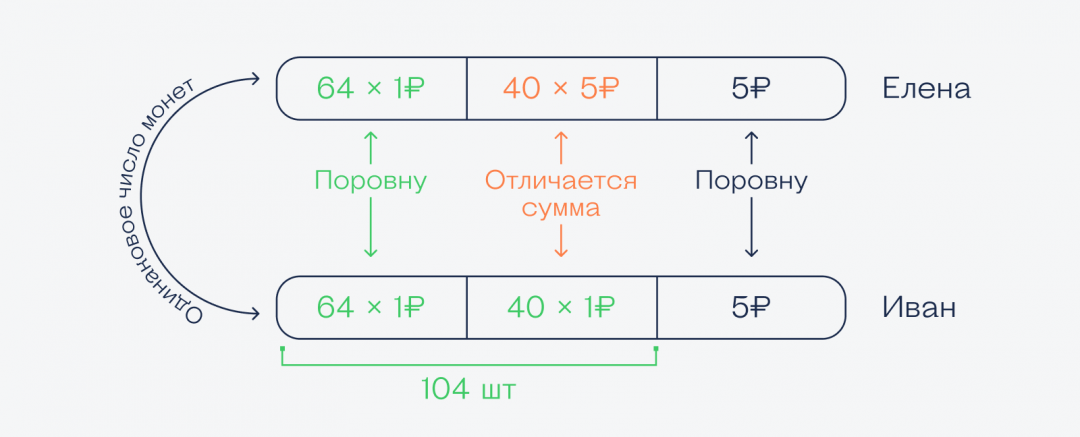
Это звучит удивительно, но для решения нам не нужно считать точное количество монет обоих видов у каждого (хотя никто не мешает вам попробовать это сделать). Вместо этого мы применим хитрость и смекалку.
Нам неважно, сколько у кого монет, главное, что их одинаковое количество и у Елены, и у Ивана, а вот количество рублёвых монет разное. Зная это, достаточно нарисовать простую картинку, по которой легко найти ответ на этот вопрос:
Глядя на неё становится понятно, что общую часть из 64 рублёвых монет можно выкинуть у обоих, потому что и там и там одинаковая сумма. А то, что осталось, и даст нужную разницу.
👉 Так как количество монет у каждого одинаковое, то у Ивана вместо 40 пятирублёвок лежит 40 рублёвых монет, а остальные пятирублёвки снова у обоих в одинаковом количестве, и их тоже можно отбросить. Получается, разница в деньгах такая:
- у Елены — 40 × 5 ₽ = 200 ₽
- у Ивана — 40 × 1 ₽ = 40 ₽
Значит, у Елены на 200 − 40 = 160 ₽ больше.
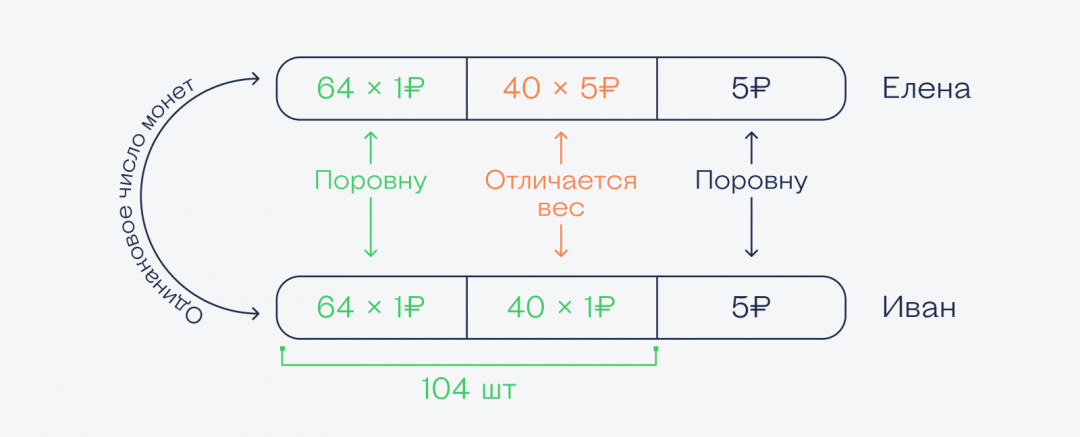
На этом этапе спотыкается большинство решающих, потому что они пытаются найти точное количество монет Ивана. Но мы-то с вами уже знаем, что это необязательно — достаточно найти разницу в весе и по ней посчитать вес монет.
Используем тот же рисунок, но уже в разрезе веса монет:
Получается, что разница в весе зависит от тех же монет, что мы считали в первой части.
Так как одна рублёвая монета легче одной пятирублёвой на 2,7 грамма, то у 40 монет разница в весе будет 40 × 2,7 = 108 грамм. А раз у Ивана пятирублёвок меньше, чем у Елены, то и монеты будут весить как раз на эти 108 грамм легче: 1,134 − 0,108 = 1,026 килограмма.
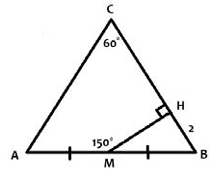
Задание 1
В треугольнике АВС из середины М стороны АВ опущен перпендикуляр МН на стороны ВС, $$angle ACB = 60^{circ}, angle AMH = 150^{circ}, BH = 2.$$ Найдите длину стороны АС.
Ответ: 8
Скрыть
$$angle HMB=180^{circ}-150^{circ}=30^{circ}Rightarrow angle MBH=90^{circ}-30^{circ}=60^{circ}Rightarrow Delta ABC$$ — равносторонний.
Из $$Delta HMB: MB=frac{HB}{sinangle HMB}=frac{2}{sin30^{circ}}=4Rightarrow AB=8Rightarrow AC=8$$
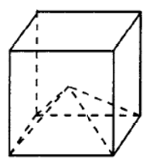
Задание 2
Объём куба равен 72. Найдите объём четырёхугольной пирамиды, основанием которой является грань куба, а вершиной — центр куба.
Ответ: 12
Скрыть
$$V_{куба}=72$$
$$V_{пирамиды}=frac{1}{3}cdot S_{ocн}cdot h$$
$$V_{пирамиды}=frac{1}{6}cdot S_{куба}=frac{1}{6}cdot72=12$$
Задание 3
В Волшебной стране бывает два типа погоды: дождливая и солнечная, причём погода, установившаяся утром, держится неизменной весь день. Известно, что с вероятностью 0,7 погода завтра будет такой же, как и сегодня.
Сегодня, 3 мая, погода в стране солнечная. Найдите вероятность того, что 5 мая в стране будет дождливая погода.
Ответ: 0,42
Скрыть
Имеем два варианта расклада с разным промежуточным состоянием 4-го мая:
а) 3-го мая солнечно, 4-го мая солнечно, 5-го мая дождливо:
$$0,7cdot0,3=0,21,$$
б) 3-го мая солнечно, 4-го мая дождливо, 5-го мая дождливо:
$$0,3cdot0,7=0,21$$
$$0,21+0,21=0,42$$
Задание 4
Аня коллекционирует принцесс из Киндер-сюрпризов. Всего в коллекции 10 разных принцесс, и они равномерно распределены, то есть в каждом очередном Киндер-сюрпризе может с равными вероятностями оказаться любая из 10 принцесс.
У Ани уже есть шесть разных принцесс из коллекции. Какова вероятность того, что для получения следующей принцессы Ане придётся купить ещё 1 или 2 шоколадных яйца?
Ответ: 0,64
Скрыть
Ане нужны 4 принцессы из 10, то есть вероятность обнаружить одну из нужных принцесс при покупке равна $$0,4.$$
Вероятность того, что в очередной покупке не будет нужной принцессы равна
$$1-0,4 = 0,6.$$
Тогда вероятность того, что нужной принцессы не будет в первой покупке, но она будет в следующей равна $$0,6cdot0,4 = 0,24.$$
Таким образом, искомая вероятность получения нужной принцессы после одной или двух покупок:
$$0,4+0,24 = 0,64.$$
Задание 5
Решите уравнение $$frac{x}{x^2+1}+frac{x^2+1}{x}=2,9.$$ Если уравнение имеет несколько корней, в ответе укажите их сумму.
Ответ: 2,5
Скрыть
Пусть $$frac{x}{x^2+1}=y$$. Получим: $$y+frac{1}{y}=frac{29}{10}Rightarrowfrac{10y^2-29y+10}{10y}=0Rightarrow 10y^2-29y+10=0$$
$$D=841-400=441$$
$$y_1=frac{29+21}{20}=2,5$$
$$y_2=frac{29-21}{20}=0,4$$
Обратная замена:
$$frac{x}{x^2+1}=frac{5}{2}Leftrightarrow5x^2-2x+5=0: D<0$$ — решений нет.
$$frac{x}{x^2+1}=frac{2}{5}Rightarrow2x^2-5x+2=0Rightarrow x^2-2,5x+1=0Rightarrow x_1+x_2=2,5$$
Задание 6
Найдите значение выражения
$$log_4cos0^{circ}+log_4cos20^{circ}+log_4cos40^{circ}+log_4cos80^{circ}.$$
Ответ: -1,5
Скрыть
Получим $$log_4(cos0^{circ}cos20^{circ}cos40^{circ}cos80^{circ})$$
Учтём, что $$cos20^{circ}cos40^{circ}cos80^{circ}=frac{sin20cos20cos40cos80}{sin20}=frac{frac{1}{2}sin40cos40cos80}{sin20}=$$
$$=frac{frac{1}{4}sin80cos80}{sin20}=frac{frac{1}{8}sin160}{sin20}=frac{frac{1}{8}sin(180-20)}{sin20}=frac{frac{1}{8}sin20}{sin20}=frac{1}{8}$$
$$cos0=1$$
Получим: $$log_4(1cdotfrac{1}{8})=log_{2^2}2^{-3}=-frac{3}{2}=-1,5$$
Задание 7
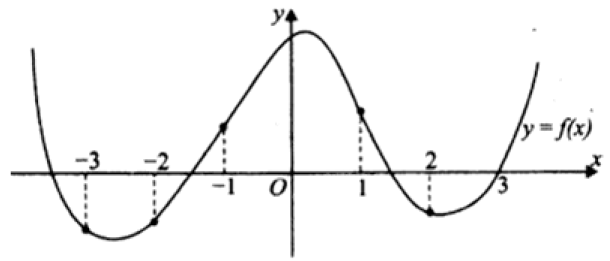
На рисунке изображен график функции $$y=f(x)$$ и отмечены точки -3, -2, -1, 1, 2, 3. В какой из этих точек значение производной наименьшее? В ответе укажите эту точку.
Ответ: 1
Скрыть
Производная отрицательная там, где функция убывает: -3; 1; 2. При этом, чем ближе тупой угол между касательной в эти точки и Ox, тем меньше значение производной $$Rightarrow 1$$.
Задание 8
В боковой стенке цилиндрического бака вблизи дна закреплен кран. После его открытия вода начинает вытекать из бака по закону $$H(t)=at^2+bt+H_0,$$ где
$$H_0 = 5$$ м — начальная высота уровня вода, $$a = frac{1}{500}; b = -frac{21}{50}$$ — постоянные величины, $$t$$ — время в минутах с момента открытия крана. Найдите наибольшее время в минутах с момента открытия крана, через которое следует закрыть кран, чтобы в баке осталось не менее 1 метра уровня воды.
Ответ: 10
Скрыть
Очевидно, что вода будет вытекать из бака пока высота воды в баке отлична от нуля. Следовательно, чтобы найти время вытекания воды, нужно величину $$H(t)$$ приравнять к (т.к. не менее 1 метра) и из полученного уравнения найти время $$t$$:
$$at^2+bt+H_0=1$$
$$frac{1}{500}t^2-frac{21}{50}t+5=1$$
$$x^2-210x+2000=0$$
Решая уравнение, получаем
$$x_1=10$$
$$x_2=200$$
200 нам не подходит, значит, ответ 10
Задание 9
К некоторому количеству сплава меди с цинком, в котором эти металлы находятся в отношении 2 : 3, добавили 4 кг чистой меди. В результате получили новый сплав, в котором медь и цинк относятся как 2 : 1. Сколько килограммов нового сплава получилось?
Ответ: 9
Скрыть
Чтобы из отношения $$2:3$$ получить отношение $$2:1,$$ нужно добавить четыре части меди:
$$(2 + 4):3 = 6:3 = 2:1,$$
а добавлено было 4 кг меди, следовательно, одна часть добавленной меди имела массу 1 кг.
Значит, меди было изначально 2 кг, а цинка 3 кг, всего 5 кг, а после добавления меди масса сплава стала равной 9 кг
Задание 10
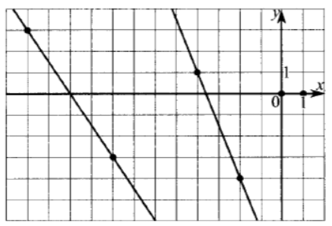
На рисунке изображены графики двух линейных функций. Найти ординату точки пересечения графиков.
Ответ: -24
Скрыть
f(x) проходит через (-12;3) и (-8;-3).
Получим: $$left{begin{matrix} 3=-12k+b\ -3=-8k+b end{matrix}right.Rightarrowleft{begin{matrix} 6=-4k\ -3=-8k+b end{matrix}right.Rightarrowleft{begin{matrix} k=-1,5\ -15=b end{matrix}right.$$
$$f(x)=-1,5x-15$$
g(x) проходит через (-4;1) и (-2;-4):
$$left{begin{matrix} 1=-4k+b\ -4=-2k+b end{matrix}right.Rightarrowleft{begin{matrix} 5=-2k\ -4=-2k+b end{matrix}right.Rightarrowleft{begin{matrix} k=-2,5\ b=-9 end{matrix}right.$$
$$g(x)=-2,5x-9$$
Тогда: $$-1,5x-15=-2,5x-9Rightarrow x=6Rightarrow y=-1,5cdot6-15=-24$$
Задание 11
Найдите наименьшее значение функции $$y=e^{4x}-4e^x+8$$ на отрезке $$[-2;2]$$
Ответ: 5
Скрыть
1. Вычисляем производную функции:
$$y = e^{4x} — 4e^x + 8;$$
$$y’ = 4e^{4x} — 4e^x = 4(e^{4x}-e^x).$$
2. Находим стационарные точки:
$$4(e^{4x} — e^x) = 0;$$
$$e^{3x + x} — e^x = 0;$$
$$e^xcdot e^{3x} — e^x = 0;$$
$$e^xcdot(e^{3x} — 1) = 0;$$
$$left[begin{matrix} e^x=0;-;нет, решений\ e^{3x}-1=0 end{matrix}right.$$
$$e^{3x} = 1;$$
$$3x = 0;$$
$$x = 0.$$
В точке $$x = 0$$ происходит переход от убывания к возрастанию, значит, это — точка минимума.
3. Наименьшее значение функции:
$$y = e^{4x} — 4e^x + 8;$$
$$x_{min} = 0;$$
$$y_{min} = y(0) = e^{4cdot0}-4cdot e^0 + 8 = 1 — 4 + 8 = 5.$$
Задание 12
А) Решите уравнение $$3cosfrac{x}{4}cosfrac{x}{2}sinfrac{x}{4}=frac{1-ctg x}{1-ctg^2x}$$
Б) Найдите все корни уравнения, принадлежащие интервалу $$(-2pi;-frac{3pi}{2})$$
Ответ: А)$$frac{pi}{4}pmarccosfrac{2sqrt{2}}{3}+2pi n,nin Z$$ Б)$$-frac{7pi}{4}pmarccosfrac{2sqrt{2}}{3}$$
Задание 13
Трапеция KLMN является основанием пирамиды PKLMN, $$angle KLM + angle LMN = 270^{circ},$$ Q — точка пересечения прямых KL и MN. Плоскости KPL и PMN перпендикулярны плоскости основания.
А) Докажите, что плоскости KPL и PMN взаимно перпендикулярны.
Б) Найдите площадь полной поверхности пирамиды PLQM, если KL=LM=MN=12, а высота пирамиды PKLMN равна 8.
Ответ: $$96+48sqrt{2}$$
Задание 14
Решите неравенство: $$lg(5x^2-15)-lg x<lg(5x^2+frac{5}{x}-10x)$$
Ответ: $$(sqrt{3};2),(2;infty)$$
Задание 15
Банк выдает кредиты под 10% годовых при условии погашения кредита ежегодными равными платежами. На какой срок (целое число лет) следует взять кредит, чтобы ежегодный платеж не превосходил 20% от суммы кредита, а полная сумма выплат превосходила сумму кредита не более чем на 50%?
Ответ: 8
Задание 16
Две окружности касаются внутренним образом. Третья окружность касается первых двух и их линии центров.
А) Докажите, что периметр треугольника с вершинами в центрах трёх окружностей равен диаметру наибольшей из этих окружностей.
Б) Найдите радиус третьей окружности, если известно, что радиусы первых двух равны 4 и 1.
Ответ: $$frac{48}{25}$$
Задание 17
Найдите все значения параметра $$a,$$ при каждом из которых система
$$left{begin{matrix} |x^2-x-6|=(y-1)^2+x-7\ 3y=2x+a end{matrix}right.$$
имеет ровно один или ровно два корня.
Ответ: $$(-infty;-10),(-9;-2],[3;infty)$$
Задание 18
На множестве натуральных чисел введем новую операцию «квазиумножения» $$(*)$$: квазипроизведением чисел $$m$$ и $$n$$ будем называть $$m*n=frac{m}{d}cdotfrac{n}{d},$$ где $$d=НОД (m, n).$$
А) Решить уравнение $$2*x=3$$$$
Б) Сколько решений может иметь уравнение $$a*x=p,$$ где $$p$$ — простое число?
В) Последовательность натуральных чисел $$left{a_nright}$$ называется квазигеометрической прогрессией со знаменателем $$q,$$ если $$a_{n+1}=a_n * q$$ для всех $$ngeq1.$$ Сколько элементов в самой длинной возрастающей квазигеометрической прогрессии?
Ответ: А) 6, Б) 1 и 2, В) 2
11:29 10.03.2023
(обновлено: 12:21 10.03.2023)
https://ria.ru/20230310/ekzameny-1856951080.html
Вице-спикер Госдумы призвал обсудить отмену ЕГЭ
Вице-спикер Госдумы призвал обсудить отмену ЕГЭ — РИА Новости, 10.03.2023
Вице-спикер Госдумы призвал обсудить отмену ЕГЭ
Тема отмены ЕГЭ нуждается во всестороннем обсуждении, и чем скорее оно начнется, тем лучше, заявил вице-спикер Госдумы Петр Толстой («Единая Россия»). РИА Новости, 10.03.2023
2023-03-10T11:29
2023-03-10T11:29
2023-03-10T12:21
общество
россия
петр толстой
анзор музаев
единая россия
госдума рф
федеральная служба по надзору в сфере образования и науки (рособрнадзор)
единый государственный экзамен (егэ)
/html/head/meta[@name=’og:title’]/@content
/html/head/meta[@name=’og:description’]/@content
https://cdnn21.img.ria.ru/images/07e6/06/08/1794077403_0:97:3072:1825_1920x0_80_0_0_8fb2880b77c924e87b1e22d2dbd1a31e.jpg
МОСКВА, 10 мар — РИА Новости. Тема отмены ЕГЭ нуждается во всестороннем обсуждении, и чем скорее оно начнется, тем лучше, заявил вице-спикер Госдумы Петр Толстой («Единая Россия»). Ранее глава Рособрнадзора Анзор Музаев заявил журналистам, что отмена ЕГЭ в России в связи с выходом из Болонской системы не обсуждается. Толстой, комментируя сообщение, тогда отметил, что тема отмены ЕГЭ обсуждается, систему будут «демонтировать» постепенно. «Тема отмены ЕГЭ нуждается во всестороннем обсуждении. И чем раньше оно начнется, тем лучше», — написал он в телеграм-канале. По словам политика, у системы на практике оказалось больше недостатков, чем достоинств. При этом он назвал попыткой «чиновников ничего не менять» отрицание того, что ЕГЭ появилось в результате «так называемых реформ образования». «А менять эту систему надо, такова воля большинства наших избирателей», — резюмировал он.
https://ria.ru/20230307/ege-1856449728.html
https://ria.ru/20230304/ege-1855788901.html
россия
РИА Новости
internet-group@rian.ru
7 495 645-6601
ФГУП МИА «Россия сегодня»
https://xn--c1acbl2abdlkab1og.xn--p1ai/awards/
2023
Новости
ru-RU
https://ria.ru/docs/about/copyright.html
https://xn--c1acbl2abdlkab1og.xn--p1ai/
РИА Новости
internet-group@rian.ru
7 495 645-6601
ФГУП МИА «Россия сегодня»
https://xn--c1acbl2abdlkab1og.xn--p1ai/awards/
https://cdnn21.img.ria.ru/images/07e6/06/08/1794077403_0:0:2732:2048_1920x0_80_0_0_40dd2897d8e6452d54553e41bdd5df84.jpg
РИА Новости
internet-group@rian.ru
7 495 645-6601
ФГУП МИА «Россия сегодня»
https://xn--c1acbl2abdlkab1og.xn--p1ai/awards/
общество, россия, петр толстой, анзор музаев, единая россия, госдума рф, федеральная служба по надзору в сфере образования и науки (рособрнадзор), единый государственный экзамен (егэ)
Общество, Россия, Петр Толстой, Анзор Музаев, Единая Россия, Госдума РФ, Федеральная служба по надзору в сфере образования и науки (Рособрнадзор), Единый государственный экзамен (ЕГЭ)
Вице-спикер Госдумы призвал обсудить отмену ЕГЭ
Вице-спикер Госдумы Толстой призвал не медлить с обсуждением отмены ЕГЭ
МОСКВА, 10 мар — РИА Новости. Тема отмены ЕГЭ нуждается во всестороннем обсуждении, и чем скорее оно начнется, тем лучше, заявил вице-спикер Госдумы Петр Толстой («Единая Россия»).
Ранее глава Рособрнадзора Анзор Музаев заявил журналистам, что отмена ЕГЭ в России в связи с выходом из Болонской системы не обсуждается. Толстой, комментируя сообщение, тогда отметил, что тема отмены ЕГЭ обсуждается, систему будут «демонтировать» постепенно.
Рособрнадзор заявил, что не обсуждает отмену ЕГЭ
«Тема отмены ЕГЭ нуждается во всестороннем обсуждении. И чем раньше оно начнется, тем лучше», — написал он в телеграм-канале.
По словам политика, у системы на практике оказалось больше недостатков, чем достоинств. При этом он назвал попыткой «чиновников ничего не менять» отрицание того, что ЕГЭ появилось в результате «так называемых реформ образования».
«А менять эту систему надо, такова воля большинства наших избирателей», — резюмировал он.
В Госдуме попросили Голикову рассмотреть возможность отмены ЕГЭ