Задания
Версия для печати и копирования в MS Word
Тип 10 № 564552
На рисунке изображён график функции вида
где числа a, b, c и d — целые. Найдите
Спрятать решение
Решение.
По графику
тогда
и
По графику тогда, если
то
— не имеет целочисленных решений,
если то
Значит, и
Найдём наименьший положительный период функции
Наименьший положительный период функции равен
а по графику наименьший положительный период равен 4, тогда
Таким образом, Найдём
Ответ: −3.
Аналоги к заданию № 564531: 564543 564555 564542 564551 564552 564553 564554 564556 564578 564579 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 3.1.5 Преобразования графиков, 3.2.3 Периодичность функции, 3.3.5 Тригонометрические функции, их графики
Спрятать решение
·
Прототип задания
·
·
Сообщить об ошибке · Помощь
Задания
Версия для печати и копирования в MS Word
Тип 10 № 564552
На рисунке изображён график функции вида
где числа a, b, c и d — целые. Найдите
Спрятать решение
Решение.
По графику
тогда
и
По графику тогда, если
то
— не имеет целочисленных решений,
если то
Значит, и
Найдём наименьший положительный период функции
Наименьший положительный период функции равен
а по графику наименьший положительный период равен 4, тогда
Таким образом, Найдём
Ответ: −3.
Аналоги к заданию № 564531: 564543 564555 564542 564551 564552 564553 564554 564556 564578 564579 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 3.1.5 Преобразования графиков, 3.2.3 Периодичность функции, 3.3.5 Тригонометрические функции, их графики
Спрятать решение
·
Прототип задания
·
·
Сообщить об ошибке · Помощь
Новые тренировочные варианты в формате решу ЕГЭ 2022 по математике профильный уровень 11 класс для подготовки к экзамену, каждый вариант составлен по новой демоверсии ФИПИ ЕГЭ 2022 года, к тренировочным заданиям прилагаются правильные ответы и пояснения.
-
Тренировочный вариант №41054170 с ответами
-
Тренировочный вариант №41054171 с ответами
-
Тренировочный вариант №41054172 с ответами
-
Тренировочный вариант №41054173 с ответами
-
Тренировочный вариант №41054174 с ответами
-
Тренировочный вариант №41054175 с ответами
-
Тренировочный вариант №41054176 с ответами
-
Тренировочный вариант №41054177 с ответами
-
Тренировочный вариант №41054178 с ответами
-
Тренировочный вариант №41054179 с ответами
-
Тренировочный вариант №41054180 с ответами
-
Тренировочный вариант №41054181 с ответами
-
Тренировочный вариант №41054182 с ответами
-
Тренировочный вариант №41054183 с ответами
-
Тренировочный вариант №41054184 с ответами
Другие тренировочные варианты ЕГЭ 2022 по математике:
Тренировочные варианты ЕГЭ по математике 11 класс задания с ответами
Пробный вариант ЕГЭ 2022 №211004 по математике 11 класс с ответами
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
Целое положительное
число 564552
является составным числом.
27 — сумма всех цифр данного числа.
Число имеет следующие делители: 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72, 7841, 15682, 23523, 31364, 47046, 62728, 70569, 94092, 141138, 188184, 282276, 564552.
И сумма этих делителей: 1529190.
Обратным числом является 0.0000017713160169479516.
Число 564552 представляется произведением простых чисел: 2 * 2 * 2 * 3 * 3 * 7841.
Представление числа в других системах счисления:
двоичный вид: 10001001110101001000, троичный вид: 1001200102100, восьмеричный вид: 2116510, шестнадцатеричный вид: 89D48.
Число 564552 в байтах это 551 килобайт 328 байтов .
Кодирование азбукой Морзе: ….. -…. ….- ….. ….. ..—
Синус 564552: 0.9986, косинус 564552: 0.0538, тангенс 564552: 18.5585.
Число 564552 имеет натуральный логарифм: 13.2438.
Число 564552 имеет десятичный логарифм: 5.7517.
Квадратный корень числа 564552: 751.3668, а кубический: 82.6484.
Квадрат числа 564552: 3.1872e+11.
Число секунд 564552 – это 6 дней 12 часов 49 минут 12 секунд .
В нумерологии число 564552 означает цифру 9.
hex: #564552
rgb(86, 69, 82)
hsl(314, 11%, 30%)
В аддитивной цветовой модели RGB цвет #564552 (шестнадцатеричный код – hexadecimal triplet code) состоит на 34% (86) из красного (red), на 27% (69) из зеленого (green) и на 32% (82) из синего (blue). Аналогично, в моделе CMYK, цвет состоит из 0% сине-зелёного (cyan), 20% маджента (magenta), 5% жёлтого (yellow) и 66% чёрного (black). В цветовой модели HSL представлен значениями: тон (hue) – 314°, насыщеность (brightness) – 11% и светлота (lightness/intensity) – 30%. Представление #564552 в Win32 имеет вид: DWORD COLORREF C=0x00255465. В десятичном виде имеет значение 5653842.
Ближайшим цветом из безопасной палитры “Netspace” (web-safe colors) для #564552 является #663366. #564552 не входит в список цветов X11, ближайший X11-цвет – DarkSlateGray (#2f4f4f).
RGB
зелёный / green = 69 (27%)
HSL
насыщенность / saturation = 0.110 (11%)
светлота / lightness = 0.304 (30%)
CMYK
сине-зелёный (циан) / cyan = 0.000
маджента / magenta = 0.198
Ближайшие похожие, альтернативные цвета: Quartz, RAL 360 30 10, RAL 330 30 15, Purple Taupe, RAL 300 30 10, RAL 020 30 10, Dark Reddish Gray, RAL 340-M, RAL 010 30 15, RAL 330 30 20.
Цветовые пространства #564552, преобразование значений
В таблице представлены значения основных (наиболее часто используемых) цветовых моделей: RGB (аддитивная модель цветовоспроизведения); CMY, CMYK (субтрактивная модель); HSL, HSI, CIE XYZ (стандартные модели). Данные доступны для загрузки в виде JSON (564552.json) и CSV (564552.csv).
RGB и CMY — цветовая модель CMY являются противоположной RGB. Цвета CMY являются дополнительными (комплементарным) цветам модели RGB.
R = 86
G = 69
B = 82
33.73%
27.06%
32.16%
C = 66.27%
M = 72.94%
Y = 67.84%
0.66274509803922
0.72941176470588
0.67843137254902
HSL (HSI) — тон, насыщенность, светлота (hue, saturation, lightness/intensity)
H = 314°
S = 10.97%
L = 30.39%
0.87254901960784
0.10967741935484
0.30392156862745
HSV (HSB) — тон, насыщенность, яркость (hue, saturation, brightness/value)
H = 314°
S = 19.77%
V = 33.73%
0.87254901960784
0.19767441860465
0.33725490196078
CMYK — циан, маджента, жёлтый, чёрный (cyan, magenta, yellow, key/black)
C = 0.00
M = 19.77
Y = 4.65
K = 66.27
0
0.19767441860465
0.046511627906977
0.66274509803922
Международная комиссия по освещению (МКО) — International Commission on Illumination (CIE)
CIE XYZ
X = 7.489
Y = 6.844
Z = 8.909
CIE 1931 XYZ color space
7.4888641228775
6.8438735508857
8.9089366644682
Yxy
Y = 6.844
x = 0.322
y = 0.294
CIE (x, y, Y)
6.8438735508857
0.32221706637368
0.29446559878984
Hunter-Lab
L = 26.16
a = 5.32
b = -1.88
Hunter 1948 color space
26.160798059092
5.31651879329
-1.8783718357261
CIELAB
L = 31.45
a = 9.83
b = -5.02
CIE 1976 (L*, a*, b*)
31.448808895227
9.8320831202909
-5.01813520514
CIELUV
L = 31.45
u = 8.59
v = -7.49
CIE 1976 (L*, u*, v*)
31.448808895227
8.591567500185
-7.4915488148071
CIELCH
L = 31.45
C = 11.04
H = 332.96
Cylindrical representation
31.448808895227
11.038638476795
332.96097344817
Монохроматические цвета #564552: оттенки, тени, тональности
Сочетание цветов с #564552 – цветовые гармонии
Примеры использования #564552 в HTML и CSS
Возможные варианты задания значения цвета #564552 в свойствах CSS:
color: #564552;
color: rgb(86, 69, 82);
color: rgb(34%, 27%, 32%);
color: rgba(86, 69, 82, 1);
color: hsl(314, 11%, 30%);
color: hsla(314, 11%, 30%, 1);
#564552 в качестве цвета текста (color) и границы элемента (border):
div {
border: 4px solid #564552;
color: #564552;
}
font color & element border color
Цвет фона элемента (background-color):
div { background-color: #564552; }
Пример использования CSS свойств для создания тени текста (text-shadow) и тени элемента (box-shadow):
div {
box-shadow: 7px 7px 10px 0px rgba(86, 69, 82, 1);
text-shadow: #564552 4px 4px 3px;
}
Использования линейного (linear-gradient) и радиального (radial-gradient) градиентов с цветами #564552 и #fff:
div.linear-gradient { background: linear-gradient(129deg, #564552, #564552, #fff); }
div.radial-gradient { background: radial-gradient(ellipse farthest-corner, #564552 0%, #fff 90%); }
Оцените, насколько полезна предоставленная информация о цвете #564552
ЕГЭ по математике — Профиль 2022. Открытый банк заданий с ответами.
БАЗА ЗАДАНИЙ
Задание № 1. Планиметрия.
1. У треугольника со сторонами 12 и 15 проведены высоты к этим сторонам. Высота, проведённая к первой стороне, равна 10. Найдите длину высоты, проведенной ко второй стороне.
Ответ: 8
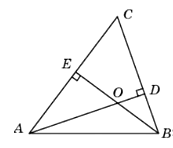
2. В треугольнике ABC угол A равен 56°, углы B и C – острые, высоты BD и CE пересекаются в точке O. Найдите угол DOE. Ответ дайте в градусах.
Ответ: 124°
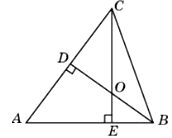
3. В треугольнике ABC угол C равен 66°, биссектрисы AD и BE пересекаются в точке O. Найдите угол AOB. Ответ дайте в градусах.
Ответ: 123°
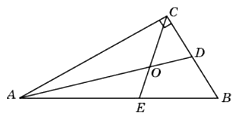
4. Угол A прямоугольного треугольника равен 64°. Найдите угол AOE, образованный биссектрисами этого и прямого углов треугольника. Ответ дайте в градусах.
Ответ: 77°
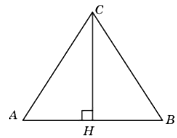
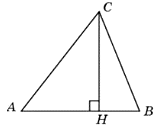
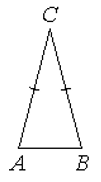
5. В треугольнике ABC AC=BC, AB=20, высота AH равна 8. Найдите синус угла BAC.
Ответ: 0,4
6. В треугольнике ABC AC = BC, AB = 8, sin∠BAC = 0,5. Найдите высоту AH.
Ответ: 4
7. В треугольнике ABC известно, что AC = BC, AH – высота, sin∠BAC=7/25. Найдите sin∠BAH.
Ответ: 0,96
8. В треугольнике ABC известно, что AC = BC, AH – высота, tg∠BAC=7/24. Найдите cos∠BAH.
Ответ: 0,28
9. В треугольнике ABC известно, что AC = BC=4√15, cos∠BAC=0,25. Найдите высоту AH.
Ответ: 7,5
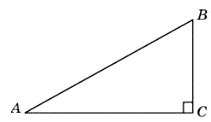
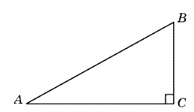
10. В треугольнике ABC угол C равен 90°, AB=10, AC=√51. Найдите sin∠A.
Ответ: 0,7
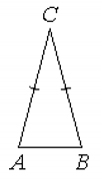
11. Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 30°. Боковая сторона треугольника равна 11. Найдите площадь этого треугольника.
Ответ: 30,25
12. В прямоугольном треугольнике угол между высотой и биссектрисой, проведёнными из вершины прямого угла, равен 14°. Найдите меньший угол прямоугольного треугольника. Ответ дайте в градусах.
Ответ: 31°
13. Острые углы прямоугольного треугольника равны 84° и 6°. Найдите угол между высотой и медианой, проведёнными из вершины прямого угла. Ответ дайте в градусах.
Ответ: 78°
14. Угол между биссектрисой и медианой прямоугольного треугольника, проведёнными из вершины прямого угла, равен 14°. Найдите меньший угол прямоугольного треугольника.
Ответ: 31°
15. В треугольнике ABC CD — медиана, угол C равен 90°, угол B равен 35°. Найдите угол ACD. Ответ дайте в градусах.
Ответ: 55°
16. В треугольнике ABC AC=BC=20, AB=28. Найдите косинус угла A.
Ответ: 0,7
17. В треугольнике ABC известно, что AC=BC=7, tg∠A=
√33/4 . Найдите AB.
Ответ: 8
18. В треугольнике ABC AC = BC = 5, sin∠A =0,8. Найдите АВ.
Ответ: 6
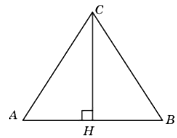
19. В равностороннем треугольнике ABC высота CH равна 45√3. Найдите AB.
Ответ: 90
20. В треугольнике ABC известно, что AC = BC, AB = 1, cos∠A=
√17/17. Найдите высоту CH.
Ответ: 2
21. В треугольнике ABC известно, что AC = BC, AB = 16, tg∠A=0,5. Найдите высоту CH.
Ответ: 4
22. В треугольнике ABC известно, что AC = BC, AB = 4, высота CH=2√3. Найдите угол С.
Ответ: 60°
23. В треугольнике ABC угол C равен 90°, AC=6, tg∠A=√5/2. Найдите AB.
Ответ: 9
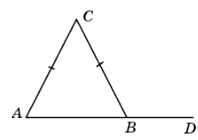
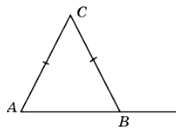
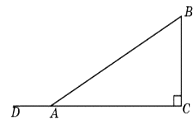
24. В треугольнике ABC стороны AC и BC равны, угол C равен 156°, угол CBD – внешний. Найдите угол CBD. Ответ дайте в градусах.
Ответ: 168°
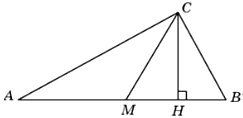
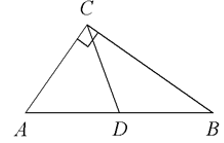
25. В прямоугольном треугольнике АВС из вершины прямого угла проведена медиана CD, причем величины углов BDC и ADC относятся как 4:5. Найдите величину угла А в градусах.
Ответ: 40°
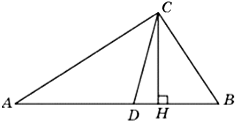
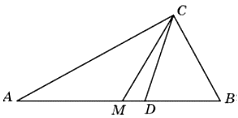
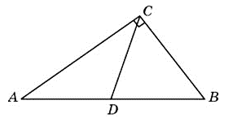
26. Высота AD треугольника АВС делит противоположную сторону на части: CD = 4, BD =1,5. Найдите длину стороны АC, если tg∠B = 2.
Ответ: 5
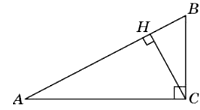
27. В треугольнике ABC угол C равен 90°, CH — высота, BC = 8, sin∠A=0,5. Найдите BH.
Ответ: 4
28. В треугольнике ABC угол C равен 90°, AB = 5, cos∠A = 0,6. Найдите высоту CH.
Ответ: 2,4
29. В треугольнике ABC угол C равен 90°, угол A равен 30°, AB=2√3. Найдите высоту CH.
Ответ: 1,5
30. В треугольнике ABC угол C равен 90°, CH — высота, BC = 3, cos∠A=
√35/6. Найдите AH.
Ответ: 17,5
31. В треугольнике ABC угол C равен 90°, CH — высота, AB = 13, tg∠A = 1/5. Найдите AH.
Ответ: 12,5
32. В треугольнике ABC угол C равен 90°, AB = 13, tg∠A = 1/5. Найдите высоту CH.
Ответ: 2,5
33. В треугольнике ABC угол C равен 90°, CH — высота, BC = 25, BH = 20. Найдите cos∠A.
Ответ: 0,6
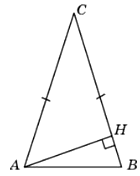
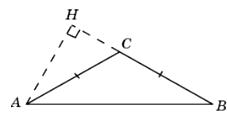
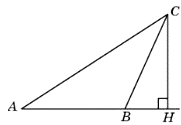
34. В тупоугольном треугольнике ABC AC = BC=8, высота AH равна 4. Найдите sin∠ACB.
Ответ: 0,5
35. В тупоугольном треугольнике ABC AC = BC, AB = 10, высота AH равна 8. Найдите sin∠BAC.
Ответ: 0,8
36. В тупоугольном треугольнике ABC AC = BC, AB = 5, высота AH равна 4. Найдите cos∠BAC.
Ответ: 0,6
37. В треугольнике ABC угол C равен 90°, синус
∠В=7/25. Найдите синус внешнего угла при вершине А.
Ответ: 0,96
38. В треугольнике ABC угол C равен 90°, косинус угла В=0,6. Найдите косинус внешнего угла при вершине А.
Ответ: -0,8
39. В треугольнике ABC угол C равен 90°, косинус внешнего угла при вершине A равен -0,1. Найдите синус ∠B.
Ответ: 0,1
40. В треугольнике ABC угол C равен 90°, тангенс внешнего угла при вершине A равен -2. Найдите тангенс ∠B.
Ответ: 0,5
41. В треугольнике ABC AC=BC=√17, AB=8. Найдите тангенс внешнего угла при вершине В.
Ответ: -0,25
42. В треугольнике ABC AC=BC=8, косинус внешнего угла при вершине В равен -0,5. Найдите AB.
Ответ: 8
43. Один из внешних углов треугольника равен 85°. Углы, не смежные с данным внешним углом, относятся как 2:3. Найдите наибольший из них. Ответ дайте в градусах.
Ответ: 51°
44. В треугольнике ABC угол A равен 60°, угол B равен 70°, CH — высота. Найдите разность углов ACH и BCH. Ответ дайте в градусах.
Ответ: 10°
45. В треугольнике ABC угол A равен 30°, CH — высота, угол BCH равен 22°. Найдите угол ACB. Ответ дайте в градусах.
Ответ: 38°
46. В треугольнике ABC AD — биссектриса, угол C равен 30°, угол BAD равен 22°. Найдите угол ADB. Ответ дайте в градусах.