6 диаграммы в электронных таблицах егэ ответы - Помощь в подготовке к экзаменам и поступлению

На уроке рассмотрен материал для подготовки к ЕГЭ по информатике, разбор 9 задания. Объясняется тема о работе в электронных таблицах и базах данных.

Содержание:

ЕГЭ по информатике 9 задания объяснение
- Анализ диаграмм и графиков в электронных таблицах
- Типы ссылок в ячейках
- Построение диаграмм
Тренировочные задания 9 ЕГЭ по информатике и их решение
- Встроенные функции в электронных таблицах
- Задания с диаграммами (задания прошлых лет для тренировки)

9-е задание: «Электронные таблицы»

Уровень сложности

— базовый,

Требуется использование специализированного программного обеспечения

— да,

Максимальный балл

— 1,

Примерное время выполнения

— 6 минут.

Проверяемые элементы содержания: Умение обрабатывать числовую информацию в электронных таблицах

До ЕГЭ 2021 года — определенные типы этого задания были заданием № 7 ЕГЭ

Ниже рассмотрены наиболее часто встречающиеся функции и их смысл. Наводите курсор на пример для просмотра ответа.

Таблица: Наиболее часто используемые функции

русский	англ.	действие	синтаксис
СУММ	SUM	Суммирует все числа в интервале ячеек	СУММ(число1;число2)
Пример:
=СУММ(3; 2) =СУММ(A2:A4)
СЧЁТ	COUNT	Подсчитывает количество всех непустых значений указанных ячеек	СЧЁТ(значение1, [значение2],…)
Пример:
=СЧЁТ(A5:A8)
СРЗНАЧ	AVERAGE	Возвращает среднее значение всех непустых значений указанных ячеек	СРЕДНЕЕ(число1, [число2],…)
Пример:
=СРЗНАЧ(A2:A6)
МАКС	MAX	Возвращает наибольшее значение из набора значений	МАКС(число1;число2; …)
Пример:
=МАКС(A2:A6)
МИН	MIN	Возвращает наименьшее значение из набора значений	МИН(число1;число2; …)
Пример:
=МИН(A2:A6)
ЕСЛИ	IF	Проверка условия. Функция с тремя аргументами: первый аргумент — логическое выражение; если значение первого аргумента — истина, то результатом выполнения функции является второй аргумент. Если ложно — третий аргумент.	ЕСЛИ(лог_выражение; значение_если_истина; значение_если_ложь)
Пример:
=ЕСЛИ(A2>B2;»Превышение»;»ОК»)
СЧЁТЕСЛИ	COUNTIF	Количество непустых ячеек в указанном диапазоне, удовлетворяющих заданному условию.	СЧЁТЕСЛИ(диапазон, критерий)
Пример:
=СЧЁТЕСЛИ(A2:A5;»яблоки»)
СУММЕСЛИ	SUMIF	Сумма непустых ячеек в указанном диапазоне, удовлетворяющих заданному условию.	СУММЕСЛИ (диапазон, критерий, [диапазон_суммирования])
Пример:
=СУММЕСЛИ(B2:B25;»>5″)

следует иметь в виду, что при использовании функции СРЗНАЧ не учитываются пустые ячейки и текстовые ячейки; например, после ввода формулы в C2 появится значение 2 (не учитывается пустая А2):

Анализ диаграмм и графиков в электронных таблицах

Типы ссылок в ячейках

Формулы, записанные в ячейках таблицы, бывают относительными, абсолютными и смешанными.

Имена ячеек в относительной формуле автоматически меняются при переносе или копировании ячейки с формулой в другое место таблицы:

Относительная адресация:
имя столбца вправо на 1
номер строки вниз на 1

Имена ячеек в абсолютной формуле не меняются при переносе или копировании ячейки с формулой в другое место таблицы.
Для указания того, что не меняется столбец, ставится знак $ перед буквой столбца. Для указания того, что не меняется строка, ставится знак $ перед номером строки:

Абсолютная адресация:
имена столбцов и строк при копировании формулы остаются неизменными

В смешанных формулах меняется только относительная часть:

Смешанные формулы

Построение диаграмм

Диаграммы используются для наглядного представления табличных данных.
Разные типы диаграмм используются в зависимости от необходимого эффекта визуализации.
Так, круговая и кольцевая диаграммы отображают соотношение находящихся в выбранном диапазоне ячеек данных к их общей сумме. Иными словами, эти типы служат для представления доли отдельных составляющих в общей сумме.
Соответствие секторов круговой диаграммы (если она намеренно НЕ перевернута) начинается с «севера»: верхний сектор соответствует первой ячейке диапазона.

Типы диаграмм Линейчатая и Гистограмма (на левом рис.), а также График и Точечная (на рис. справа) отображают абсолютные значения в выбранном диапазоне ячеек.

Егифка ©:

* Некоторые изображения, представленные в изложении теоретического материала, заимствованны с сайта К. Полякова

Тренировочные задания 9 ЕГЭ по информатике и их решение

Плейлист видеоразборов задания на YouTube:
Задание демонстрационного варианта 2022 года ФИПИ

Встроенные функции в электронных таблицах

9_00: 9 задание. Демоверсия варианта ЕГЭ по информатике 2021, ФИПИ:

Задание выполняется с использованием прилагаемых файлов

Откройте файл электронной таблицы, содержащей вещественные числа – результаты ежечасного измерения температуры воздуха на протяжении трёх месяцев.
Найдите разность между максимальным значением температуры и её средним арифметическим значением.
В ответе запишите только целую часть получившегося числа.

Типовые задания для тренировки

9_01: Задание 1:

Задание выполняется с использованием прилагаемых файлов

Найдите разность между максимальным и минимальным числом в диапазоне C48:Y360. В ответе запишите только целую часть числа.

✍ Решение:

Ячейка A502 = МАКС(C48:Y360)
Ячейка B502 = МИН(C48:Y360)
любая пустая ячейка =A502-B502
Оставляем только целую часть (отсекаем дробную, не округляя число).

Ответ: 920

9_02: Задание:

Задание выполняется с использованием прилагаемых файлов

Откройте файл 9-J1.xls электронной таблицы, содержащей вещественные числа – показатели высот над уровнем моря географических точек.

Найдите среднее значение всех отрицательных показателей и максимальное положительное значение.

В качестве ответа укажите целую часть суммы найденных значений.

✍ Решение:

Перейдите в пустую ячейку (например, АО1).
Поскольку для вычисления среднего арифметического используется дополнительное условие (только отрицательные показатели), то проще использовать формулу СРЗНАЧЕСЛИ. Внесите формулу в заготовленную ячейку:

=СРЗНАЧЕСЛИ(A1:AN500;"<0")

Здесь условие обязательно должно быть в кавычках.

Таким же образом вычислим максимальное положительное значение, используя функцию МАКСЕСЛИ.
Добавьте формулу в пустую ячейку AO2:

=МАКСЕСЛИ(A1:AN500;A1:AN500;">0")

Вычислим сумму в ячейке АО3:

=СУММ(AO1;AO2)

Получилось 502,531856

Отбрасывая дробную часть, получаем 502.

Ответ: 502

9_03: Задание:

Задание выполняется с использованием прилагаемых файлов

Откройте файл 9-j2.xl s электронной таблицы, содержащей вещественные числа – успеваемость учеников школ города по учебным дисциплинам за четвертую четверть.

Найдите школы с максимальным и минимальным средними показателями.
В качестве ответа укажите два числа – номера найденных школ, сначала с наименьшим показателем, затем с наибольшим.

✍ Решение:

Поскольку средние значения по дисциплинам расставлены по столбцам, то необходимо выполнить вычисление общего среднего арифметического по каждой школе в каждом столбце.
Для этого в пустой ячейке B18 для школы №1 напишите формулу вычисления среднего арифметического:

=СРЗНАЧ(B2:B16)

Скопируйте формулу на всю строку вправо (во все столбцы школ).
Для поиска максимального значения из всех средних значений будем рассуждать следующим образом: если максимальное значение из диапазона всех найденных средних значений совпадает со средним значением конкретной школы, то выводим значение ячейки номера школы, иначе – оставляем значение пустым.
Т.е. поставьте курсор на ячейку B20 и введите формулу:

=ЕСЛИ(МАКС($B$18:$AI$18)=B18;B1;"")

Здесь обязательно для диапазона необходимо использовать абсолютную адресацию (знаки $), иначе при копировании диапазон изменится, а нам этого не надо.
Скопируйте формулу на всю строку вправо. В строке появилось значение 8.
Для поиска минимального значения будем придерживаться таких-же рассуждений.
Т.е. поставьте курсор на ячейку B21 и введите формулу:

=ЕСЛИ(МИН($B$18:$AI$18)=B18;B1;"")

Скопируйте формулу на всю строку вправо. В строке появилось значение 32.

Ответ: 32 8

9_04: Задание:

Задание выполняется с использованием прилагаемых файлов

Откройте файл электронной таблицы 9-0.xls (в заголовке задания), содержащей вещественные числа – результаты ежечасного измерения температуры воздуха на протяжении трёх месяцев.
Найдите разность между максимальным значением температуры и её средним арифметическим значением в первой половине дня (до 12:00 включительно).
В ответе запишите только целую часть получившегося числа.

✍ Решение:

Ячейка A94 = МАКС(B2:N92) = 35,6
Ячейка A95 =СРЗНАЧ(B2:N92) = 21,4
любая пустая ячейка =A94-A95 = 14,2
Оставляем только целую часть (отсекаем дробную, не округляя число).

Ответ: 14

9_05: Задание:

Задание выполняется с использованием прилагаемых файлов

Откройте файл электронной таблицы 9-0.xls (в заголовке задания), содержащей вещественные числа – результаты ежечасного измерения температуры воздуха на протяжении трёх месяцев.
Найдите разность между максимальным значением температуры в апреле и её средним арифметическим значением во второй половине дня (с 12:00) за тот же период.
В ответе запишите только целую часть получившегося числа.

✍ Решение:

04 месяц

12.00

Ячейка A94 = МАКС(B2:Y31) = 26,0
Ячейка A95 = СРЗНАЧ(N2:Y31) = 21,0
любая пустая ячейка =A94-A95 = 5,0
Оставляем только целую часть (отсекаем дробную, не округляя число).

Ответ: 5

9_06: Задание:

Задание выполняется с использованием прилагаемых файлов

Откройте файл электронной таблицы 9-0.xls (в заголовке задания), содержащей вещественные числа – результаты ежечасного измерения температуры воздуха на протяжении трёх месяцев.
Найдите разность между максимальным и минимальным значением температуры среди измерений, сделанных в 17:00.
В ответе запишите только целую часть получившегося числа, округлять не нужно.

✍ Решение:

17.00

Ячейка A94 =МАКС(S2:S92) = 37,8
Ячейка A95 =МИН(S2:S92) = 22,4
любая пустая ячейка =A94-A95 = 15,4
Оставляем только целую часть (отсекаем дробную, не округляя число).

Ответ: 15

9_07: Задание:

Задание выполняется с использованием прилагаемых файлов

Откройте файл электронной таблицы 9-0.xls (в заголовке задания), содержащей вещественные числа – результаты ежечасного измерения температуры воздуха на протяжении трёх месяцев.
Посчитайте сумму средних арифметических значений температур в 16:00 и в 23:00.
Округлите полученное число до целого и запишите его в ответ.

✍ Решение:

16.00

23.00

Ячейка A94 =СРЗНАЧ(R2:R92) = 29,9
Ячейка A95 =СРЗНАЧ(Y2:Y92) = 20,8
любая пустая ячейка =A94+A95 = 50,7
После округления получаем 51.
Можно также решить данное задание, записав все в одну строку:

 = СРЗНАЧ(R2:R92)+СРЗНАЧ(Y2:Y92)

Ответ: 51

9_08: Задание:

Задание выполняется с использованием прилагаемых файлов

Откройте файл электронной таблицы 9-0.xls (в заголовке задания), содержащей вещественные числа – результаты ежечасного измерения температуры воздуха на протяжении трёх месяцев.
Найдите результат деления суммы всех значений температуры на максимальное значение.
В ответе запишите только целую часть получившегося числа, округлять не нужно.

✍ Решение:

B2

Y92

B2:Y92

Ячейка A94 =МАКС(B2:Y92) = 38,0
Ячейка A95 =СУММ(B2:Y92) = 51807,0
любая пустая ячейка (поделим сумму на максимальное значение) =A95/A94 = 1363,3
Оставляем только целую часть = 1363.

Ответ: 1363

9_09: Задание:

Задание выполняется с использованием прилагаемых файлов

Откройте файл электронной таблицы 9-0.xls (в заголовке задания), содержащей вещественные числа – результаты ежечасного измерения температуры воздуха на протяжении трёх месяцев.
Посчитайте чему будет равно самое часто встречаемое значение температуры и среднее арифметическое значений температуры за всё время измерений. Найдите разницу между самым встречаемым значением и средним арифметическим значением.
В ответе запишите только целую часть числа (разницы).

✍ Решение:

B2

Y92

B2:Y92

Для более достоверных расчетов будем использовать числа с тремя знаками после десятичной запятой. Воспользуемся кнопкой
Ячейка A94 =СРЗНАЧ(B2:Y92) = 23,721
Ячейка A95 =МОДА(B2:Y92) = 25,700

Для нахождения наиболее часто встречаемого значения используется функция МОДА ()

любая пустая ячейка =A95-A94 = 1,979
Оставляем только целую часть = 1.

Ответ: 1

9_14: Задание:

Задание выполняется с использованием прилагаемых файлов

Откройте файл электронной таблицы 9-0.xls (в заголовке задания), содержащей вещественные числа – результаты ежечасного измерения температуры воздуха на протяжении трёх месяцев.

В каком количестве измерений температура оказалась выше 25 градусов?

✍ Решение:

Поскольку нам необходимо посчитать количество, то будем использовать функцию СЧЁТ(). Но так как считать надо количество измерений температуры выше 25 градусов, то нужно использовать функцию с критерием, а именно, СЧЁТЕСЛИ().
Введите формулу в любую пустую ячейку:

=СЧЁТЕСЛИ(B2:Y92;">25")

Обратите внимание, что так как с условием сравнивается диапазон, а не единственная ячейка, то само условие необходимо разместить в кавычках.

Ответ: 942

9_15: Задание:

Задание выполняется с использованием прилагаемых файлов

Откройте файл электронной таблицы 9-j5.xls, содержащей вещественные числа – количество баллов, которое набрали участники тестирования. В первой строке указаны дисциплины, во второй – максимальный балл за тест по дисциплине, в левом столбце – фамилии участников. Считается, что тест пройден, если участник тестирования набрал больше 60% от максимального балла. В качестве ответа укажите, сколько участников тестирования прошли больше трёх тестов.

✍ Решение:

Для начала будем сравнивать максимальный балл * 0,6 с баллом, набранным участником. Если балл участника больше, будем ставить в ячейку цифру 1, иначе — 0.
В ячейку B35 введем формулу:

=ЕСЛИ(B4>B$2*0,6;1;0)

Скопируем формулу на всю 35-ю строку. И затем вниз до 64 строки (так как нумерация не сначала).
Затем выделим полностью столбец с формулой и скопируем его вправо, до столбца О включительно (последний столбец с данными).
Теперь необходимо посчитать кол-во единиц в каждой строке: если их больше трех, то считаем такой вариант. Будем использовать функцию ЕСЛИ().
В ячейку А35:

=ЕСЛИ(СУММ(B35:O35)>3;1;"")

Копируем формулу до ячейки B64.
Выделяем часть столбца c рассчитанными значениями и в нижней части экрана смотрим сумму – 18.

Ответ: 18

9_16: Задание:

Задание выполняется с использованием прилагаемых файлов

В электронной таблице в файле 9-j10.xls хранятся вещественные числа – результаты ежечасного измерения скорости ветра на протяжении трех месяцев.

Найдите количество дней, когда максимальная скорость ветра составляла не менее 90% от максимального значения за весь период.

✍ Решение:

Сначала найдем максимальную скорость ветра за весь период. Введем формулу в ячейку AB2:

=МАКС(B2:Y91)

Теперь посчитаем количество дней по всему диапазону дней с условием, что скорость ветра составляла бы не менее 90% от максимального значения за весь период, т.е. рассчитанного значения в ячейке AB2. Будем использовать функцию СЧЁТЕСЛИ(), так как считаем при условии.
Введем формулу в любую пустую ячейку:

=СЧЁТЕСЛИ($Z$2:$Z$91;">="&AB2*0,9)

Обратите внимание, что в условии используются кавычки, но для добавления к условию рассчитанного значения в ячейке AB2, необходимо «приклеить» это значение с помощью знака &

Ответ: 80

Также можно посмотреть некоторые аналогичные задания ОГЭ

Задания с диаграммами (задания прошлых лет для тренировки)

9_7:

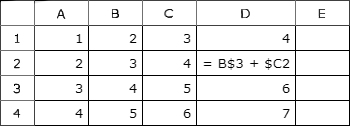
Задан фрагмент электронной таблицы:

Как изменится значение ячейки C3, если после ввода формул переместить содержимое ячейки B2 в B3?
(«+1» означает увеличение на 1, «-1» означает уменьшение на 1):

Варианты:
1) -2
2) -1
3) 0
4) +1

✍ Решение:

В ячейке C2 будет находиться число 4, так как функция СЧЁТ подсчитывает количество непустых ячеек указанного диапазона.
В ячейке С3 будет находиться число 3:

(1 + 2 + 2 + 6 + 4) / 5 = 3

Теперь посмотрим, что произойдет после перемещения:

Перемещение содержимого ячейки означает, что ячейка B2 окажется пустой, а в ячейке B3 появится число 6.
Тогда расчёт формулы в ячейке C2 поменяется: количество непустых ячеек диапазона A1:B2 станет равным 3.
Соответственно изменится и значение после расчёта формулы ячейки C3: среднее значение содержимого диапазона ячеек A1:C2 станет равным:

(1 + 2 + 2 + 3) / 4 = 2

(нужно не забывать, что функция СРЗНАЧ не учитывает пустые ячейки, поэтому ячейка B2 не учтена).

Таким образом, значение после перемещения формулы изменилось, уменьшившись на 1. Верный ответ 2

Результат: 2

Подробное решение задания на видео:

📹 YouTube здесь (теоретическое решение)

📹 Видеорешение на RuTube здесь (теоретическое решение)

Задание:

В электронной таблице значение формулы =СРЗНАЧ(С2:С5) равно 3.

Чему равно значение формулы =СУММ(С2:С4), если значение ячейки С5 равно 5?

✍ Решение:

Функция СРЗНАЧ предназначена для вычисления среднего арифметического значения указанного диапазона ячеек. Т.е. в нашем случае среднее значение ячеек C2, C3, C4, C5.
Результат функции =СРЗНАЧ(С2:С5) задан по условию, подставим его в формулу:

(C2 + C3 + C4 + C5)/4 = 3

Примем неизвестную сумму в за x и получим по формуле вычисления среднего значения:

x / 4 = 3

Найдем x:

x = 3 * 4 = 12  ->  C2 + C3 + C4 + C5 = 12

По заданию необходимо найти =СУММ(С2:С4). Зная значение в ячейке С5, вычтем его из полученной суммы и найдем ответ:

C2 + C3 + C4 = C2 + C3 + C4 + C5 - C5 = 
= 12 - 5 = 7

Результат: 7

Подробное решение смотрите на видео:

📹 YouTube здесь

Рассмотрим еще один пример решения 9 задания ЕГЭ по информатике:

9_10:

Дан фрагмент электронной таблицы:

Какое целое число должно быть записано в ячейке C1, чтобы построенная после выполнения вычислений диаграмма по значениям диапазона ячеек А2:С2 соответствовала рисунку?
Известно, что все значения диапазона, по которым построена диаграмма, имеют один и тот же знак.

✍ Решение:

Круговая диаграмма отображает доли отдельных частей в общей сумме. В нашем случае в диаграмме отражаются результаты вычисления формул в ячейках А2:С2
По диаграмме можно судить о том, что, скорее всего, полученные значения в формулах во всех ячейках должны быть равны (секторы диаграммы визуально равны).
Получим выражения из формул ячеек, подставив вместо С1 -> x:

А2: х + 2
В2: 8/2 = 4
С2: х * 2

Так как секторы диаграммы равны, то приравняем два из полученных выражений (например, С2 = В2):

2 * х = 4 => x = 2

Результат: 2

Детальный разбор можно посмотреть в видеоуроке решения данного 9 задания ЕГЭ по информатике:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь (теоретическое решение)

9_11:

Задан фрагмент электронной таблицы:

Какое число должно быть записано в ячейке B1, чтобы построенная после выполнения вычислений диаграмма по значениям диапазона ячеек A2:C2 соответствовала рисунку:

✍ Решение:

По диаграмме можно судить только о следующем: если она не перевернута, то значения в ячейках A2 и B2 должны быть равны, а значение ячейки C2 — в два раза больше каждой из них.
Поскольку у нас неизвестны значения двух ячеек, то обозначим B1 за x, а C1 за y.
Подставим неизвестные в формулы и получим:

Исходя из первого пункта, получаем:

A2 = B2 = C2/2

Составим систему уравнений:

4y = x - y
2 * 4y = x - y + 4

Первое уравнение нам дает x = 5y. Подставим это значение во второе уравнение:

8y = 5y - y + 4  ->  y = 1

Таким образом, x=5. А значения ячеек A2 = B2 = 4, C2 = 8. Т.е. изображение диаграммы действительно сходится с полученными значениями.

Результат: 5

Подробное теоретическое решение смотрите на видео:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь (теоретическое решение)

9_12:

Дан фрагмент электронной таблицы в режиме отображения формул:

После копирования диапазона ячеек АЗ:ЕЗ в диапазон А4:Е6 была построена диаграмма (график) по значениям столбцов диапазона ячеек В2:Е6.
1_11

Значениям D2:D6 соответствует график:

Варианты:
1) А 2) Б 3) В 4) Г

✍ Решение:

Копирование диапазона ячеек АЗ:ЕЗ в диапазон А4:Е6 буквально означает выделение диапазона АЗ:ЕЗ и протягивание маркера копирования до конца указанного блока ячеек.
Поскольку нас интересует только столбец D, то посмотрим, что там за формула, и что с ней произойдет при копировании:

в ячейке D3 значение зависит от ячейки A3 и оно равно 2;
при копировании формулы столбец остается тот же (D), поэтому и в формуле буквы остаются теми же (D и A), а вот строки копируются вниз, т.е. цифры в формуле увеличиваются на единицу при движении вниз на каждую строку; соответственно, нас интересуют еще ячейки A4, A5, A6;
формулы ячеек A4, A5, A6 зависят от ячеек столбца B, поэтому рассмотрим получившиеся при копировании формулы столбцов A и B:

1_11

Теперь вычислим значения в этих столбцах:

Получаем точки по столбцу D: 1, -1, -1, -7, -15, что соответствует графику Г (ответ 4)

Результат: 4

Разбор задания смотрите на видео:

📹 YouTube здесьздесь (теоретическое решение)

9_13:

Дан фрагмент электронной таблицы:

Какое целое число должно быть записано в ячейке C1, чтобы построенная после выполнения вычислений диаграмма по значениям диапазона ячеек A2:D2 соответствовала рисунку? Известно, что все значения диапазона, по которым построена диаграмма, положительные.

✍ Решение задания 7:

На изображенной диаграмме (если она преднамеренно не перевернута) секторы соответствуют указанному диапазону ячеек при движении по часовой стрелке с «севера на юг»: т.е. А2 — синий сектор, B2 — красный и т.п. Таким образом, делаем следующий вывод:

А2 = B2 = 2 * C2 = 2 * D2

Поскольку необходимо найти C1, и оно встречается в формулах, то примем его за x.
Перепишем формулы согласно введенному обозначению:

1_11

Приравняем формулы в ячейках B2 и D2 (см. п.1) и получим:

B2 = 2 * D2
2(x + 5) = x + 21
2x - x = 21 - 10
x = 11

Т.е. С1 = 11

Результат: 11

Видеоразбор задания:

📹 YouTube здесьздесь (теоретическое решение)

Источник

Это задание в 2021 году изменилось, поэтому здесь можете посмотреть статью в новом формате!

Добрый день! Разбираемся с 7 (седьмым) заданием из ЕГЭ по информатике.

Седьмое задание обычно связано с диаграммами и таблицами. Некоторые задачи данной категории из ЕГЭ по информатике удобно решать или проверять в программе Excel.

Задача (классика)

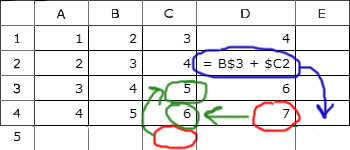
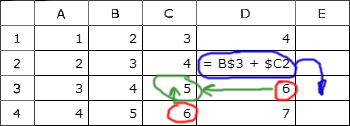
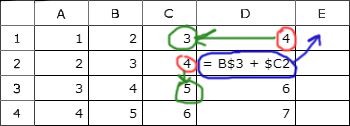
Дан фрагмент электронной таблицы. Из ячейки B2 в ячейку C3 была скопирована формула. При копировании адреса ячеек в формуле автоматически изменились. Какое числовое значение находится в ячейке C3 ?

Примечание: знак $ обозначает абсолютную адресацию.

Решение:

Первый шаг при решении данной задачи из ЕГЭ по информатике — не обращать внимание на значки доллара($).

Посмотрим, какие ячейки участвуют в формуле до её копирования, записывая себе на черновик их положение относительно первоначальной ячейки B2

A2, находится от начальной ячейки B2: 1 шаг влево.
D4, находится от начальной ячейки B2: 2 шага вправо, 2 вниз.

Следующий шаг. Переносим мысленно формулу из B2 в ячейку C3. Отсчитываем от С3 те координаты, которые мы записали в предыдущем пункте.

Для A2: отсчитываем от нового положения формулы (ячейки C3) 1 шаг влево. Попадаем на ячейку B3

Для D4: отсчитываем от нового положения формулы (ячейки C3) 2 шага вправо, 2 вниз. Попадаем на ячейку E5

Мы бы использовали значения ячеек B3 и E5 в формуле, если бы не было значков доллара($).

Знак «$» «цементирует» либо столбец (если $ стоит перед названием столбца), либо строчку (если $ стоит перед названием строки).

Например, в первом выражении нашей формулы $ стоит перед столбцом A, значит, вычисленная после копирования ячейка B3 превратится в $A3. Столбец A должен обязательно остаться!

Во втором выражении $ стоит перед четвёртой строчкой. Значит, в данном выражении обязательно должна остаться четвёртая строчка! Ячейка E5 превращается в ячейку E$4.

Таким образом, численный результат формулы после копирования можно записать следующим образом $A3 + E$4 = 3 + 20 = 23.

Ответ: 23.

Ещё один тип задач задания номер 7 из ЕГЭ по информатике.

Задача (встречается в тренировочных вариантах ЕГЭ по информатике)
В электронной таблице значение формулы =CPЗHAЧ(C2:D5) равно 4. Чему равно значение формулы =CУMM(C5:D5), если значение формулы =CPЗHAЧ(C2:D4) равно 5? Пустых ячеек в таблице нет.

Решение:

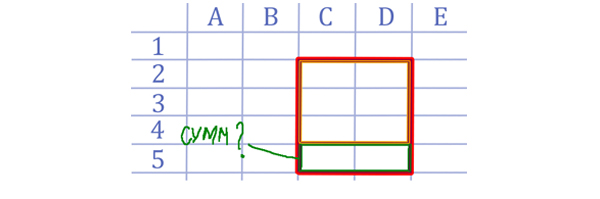
Для начала нам нужно в черновике нарисовать ячейки таблицы, как в программе Excel, чтобы там были С2 и D5.

Теперь отметим разными цветами то, что нам дано в условии задачи.

=CPЗHAЧ(C2:D5) — Отметим красным цветом (Равно 4)
=CPЗHAЧ(C2:D4) — Отметим оранжевым цветом (Равно 5)
=CУMM(C5:D5) — Отметим зелёным цветом (Нужно найти)

Важно, что действие формулы =CPЗHAЧ(C2:D5) именно прямоугольная область. В левом верхнем углу ячейка С2, в правом нижнем углу ячейка D5. Аналогично и для других формул.

Распишем формулы подробно.

CPЗHAЧ — это среднее значение! (Сумма всех ячеек, делённое на их количество)

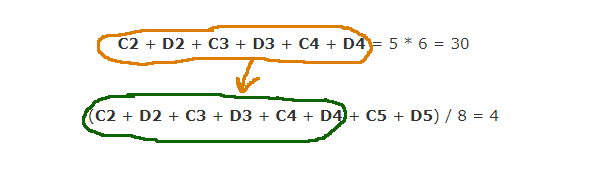
CPЗHAЧ(C2:D5) = (C2 + D2 + C3 + D3 + C4 + D4 + C5 + D5) / 8 = 4 (1)

CPЗHAЧ(C2:D4) = (C2 + D2 + C3 + D3 + C4 + D4) / 6 = 5 (2)

Нужно найти сумму двух ячеек C5 + D5.

Из второго (2) уравнения выразим сумму всех ячеек и подставим в первое (1) уравнение.

Тогда

(30 + C5 + D5) / 8 = 4

(30 + C5 + D5) = 8 * 4 = 32

C5 + D5 = 32 — 30 = 2

Ответ: 2.

Задание на диаграммы из тренировочного варианта ЕГЭ по информатике.

Задача (диаграммы)

Дан фрагмент электронной таблицы.

Какое целое число должно быть записано в ячейке A1, чтобы диаграмма, построенная по значениям ячеек A2:C2, соответствовала рисунку ? Известно, что все значения ячеек из рассматриваемого диапазона неотрицательны.

Решение:

Подставим в каждую формулу из второй строчки таблицы те значения, которые мы уже знаем.

Ячейка A2 : 2 * 4 / (A1 + 1) = 8 / (A1 + 1)
Ячейка B2 : (A1 + 1) / (5 — 4) = A1 + 1
Ячейка C2 : A1 / (5 — 4) + 1 = A1 + 1

В формулах осталась только ячейка A1, которую и нужно найти.

Посмотрим на диаграмму справа, которая соответствует второй строчке (три ячейки A2, B2, C2). Видим, что на диаграмме 2 части имеют одинаковое значение, а третья часть в два раз больше, чем остальные.

При упрощении выражений, у нас тоже получились две ячейки одинаковые: B2 и C2, и каждая равна A1 + 1.
Значит, ячейка A2 будет больше, чем C2 и B2 в 2 раза.

Составим уравнение:

2 * (A1 + 1) = 8 / (A1 + 1)
A1 + 1 = 4 / (A1 + 1)

(A1 + 1)² = 4
(A1 + 1) = 2 или (A1 + 1) = -2
A1 = 1 или A1 = -3

В условии задачи сказано, что все ячейки неотрицательные. Значит, ответ будет 1.

Ответ: 1.

В последнее время всё чаще встречается в тренировочных вариантах ЕГЭ по информатике такой вид задания 7.

Задача (редкая, не сложная)

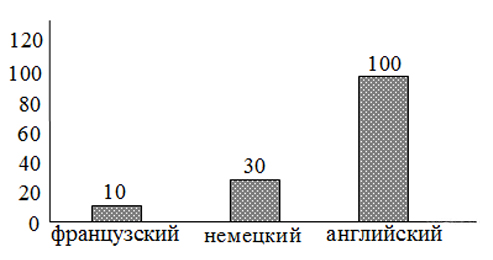
На предприятии работают 100 человек. Каждый из них владеет как минимум одним иностранным языком (английским, немецким или французским), На следующей диаграмме отражено количество человек, владеющих каждым из языков.

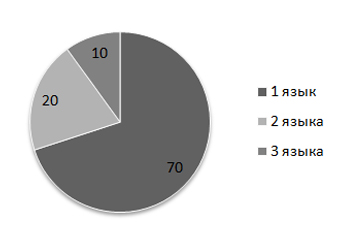
Вторая диаграмма отражает количество человек, знающих только один язык, только два языка или все три иностранных языка.

Определите количество человек, владеющих одновременно английским и немецким, но не говорящих по-французски.

Решение:

Десять человек знают только французский язык (это видно из первой диаграммы), но из второй диаграммы видно, что 10 человек знают все три языка! Значит, на второй диаграмме 10 человек, которые будут французский и ещё два.

На второй диаграмме показано, что 20 человек знают 2 языка, но те кто знаю французский язык уже вошли в предыдущий сектор. Следовательно, 20 человек знают два языка: английский и немецкий, но не знают французский.

Ответ: 20.

Ещё один тип задач задания 7 ЕГЭ по информатике, похожий на 1-ю из разобранных нами в этой статье. Отличается данная задача вопросом.

Задача (редкая)

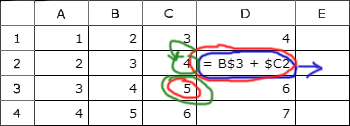
Дан фрагмент электронной таблицы. Из ячейки D2 в одну из ячеек диапазона E1:E4 была скопирована формула. При копировании адреса ячеек в формуле автоматически изменились, и значение формулы стало равным 8. В какую ячейку была скопирована формула? В ответе укажите только одно число – номер строки, в которой расположена ячейка.

Примечание. Знак $ обозначает абсолютную адресацию.

Решение:

Нам сказано, что формулу скопировали в одну из четырёх ячеек E1, E2, E3, E4. Значит, нам нужно проверить каждую из них, и посмотреть, где будет формула иметь значение 8.

Запишем координаты для двух ячеек, участвующих в формуле.

B3, находится от начальной ячейки D2: 2 шага влево, 1 шаг вниз.
C2, находится от начальной ячейки D2: 1 шаг влево.

Проверяем ячейку E4

Отсчитываем от E4 записанные координаты. На рисунке отмечены красным цветом отсчитанные ячейки относительно E4:

Т.к. в формуле в первом выражении (B$3) перед 3 (тройкой) стоит знак $, то мы должны обязательно брать значение из третьей строчки. Поднимаемся на третью строчку, и теперь будем брать значение для этого выражения из ячейки C$3. На рисунке отмечено зелёным цветом.

Тоже самое будет и для второго выражения ($C2), но теперь «цементируется» столбец С. Тогда численное значение берём из ячейки $С4.

Получается, что численное значение формулы в ячейке E4 будет С$3+$С4 = 11. А нам нужно 8. Значит, данная ячейка не подходит.

Проверяем ячейку E3

Аналогичным образом проверяем и остальные ячейки.

В этом случае, при попадании формулы в ячейку E3 два выражения в формуле будут ссылаться на численное значение из ячейки C3.

Получается, что численное значение формулы в ячейке E3 будет С$3+$С3 = 5 + 5 = 10. А нам нужно 8. Значит, данная ячейка не подходит.

Проверяем ячейку E2

Как всегда, красным цветом отмечены ячейки, на которые бы ссылалась формула, если бы не было знака $. При использовании формулы со знаком $, ячейки, отмеченные красным цветом, «превращаются» в ячейки, отмеченные зелёным цветом.

Получается, что численное значение формулы в ячейке E2 будет С$3 + $C2 = 4 + 5 = 9. А нам нужно 8. Значит, данная ячейка не подходит.

Проверяем ячейку E1

Получается, что численное значение формулы в ячейке E1 будет С$3 + $C1 = 3 + 5 = 8. Нам и нужно 8. Значит, данная ячейка подходит!

В ответе нужно записать только строчку нужной ячейки.

Ответ: 1.

Забористая задача седьмого задания ЕГЭ по информатике, но встречается не часто.

Задача (редкая)

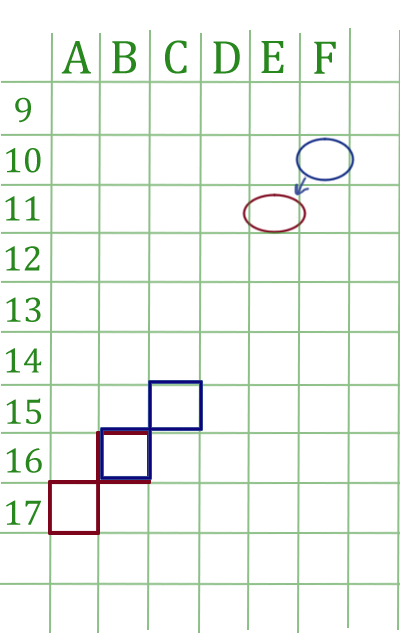
В ячейке F10 электронной таблицы записана формула. Эту формулу скопировали в ячейку Е11. В соответствии с формулой, полученной в ячейке Е11, значение в этой ячейке равно сумме значений в ячейках В16 и А17.

Напишите, сколько из следующих четырёх утверждений не противоречат этим данным.

A)Значение в ячейке F10 равно х+у, где х — значение в ячейке В16, а у — значение в ячейке А17.

Б)Значение в ячейке F10 равно х+у, где х — значение в ячейке С15, а у — значение в ячейке А17.

В)Значение в ячейке F10 вычисляется по формуле х+у, где х — значение в ячейке С16, а у — значение в ячейке A16.

Г)Значение в ячейке F10 равно 2 · х, где х — значение в ячейке В16.

Решение:

Нарисуем примерную сетку, чтобы были ячейки, которые описаны в условии задачи.

Синим цветом овальным знаком показано начальное положение формулы, а овал бордового цвета — копия этой формулы.

В условии сказано, что численное значение для новой копии равно сумме В16 и А17. Эти ячейки обозначены так же бордовым цветом. Тогда мы можем вычислить местоположение ячеек, которые были бы задействованы в первоначальной формуле, если бы совсем не использовалась абсолютная адресация (т.е. без использования знака $).

Т.к. первоначальная формула расположена от новой копии на расстоянии: одного шага вправо и одного шага вверх, то и от каждой бордовой ячейки тоже нужно отступить один шаг вправо и один вверх. Получим ячейки, которые обозначим синим цваетом!

Ещё раз подчеркну, данный рисунок сделан исходя из того, что в формуле не было знаков $ для более ясного представления ситуации.

Теперь нужно разобрать каждое из 4-х утверждений (А-Г) на противоречние!

1. A)Значение в ячейке F10 равно х+у, где х — значение в ячейке В16, а у — значение в ячейке А17

В этом утверждении говорится, что в первоначальной ячейке F10 были использованы значения B16 и A17. Но мы знаем, что эти ячейки используются в новой копии формулы. Т.е получается копирование формулы не изменило значения её аргументов ? Да, такое возможно, если мы «зацементируем» в наших ячейках и столбцы, и строчки. Т.е. если прописать в первоначальной формуле =$A$17 + $B$16. Значит, данное утверждение не противоречит условию задаче!

2. Б)Значение в ячейке F10 равно х+у, где х — значение в ячейке С15, а у — значение в ячейке А17.

Теперь утверждается, что в первоначальной ячейке F10 суммировались значения из С15 и A17. Но С15, у нас отмечена синим квадратом! Значит, эта ячейка нами предполагалась, как участник данной формулы, только без использования абсолютной адресации $.

Воторой компонент (Ячейка A17) остался в неизменном виде, что до копирования, что после! Такое может быть, если строка и столбец этой ячейки «зацементированы».

Получается, что утверждение обосновано, если в первоначальной формуле будет формула =С15 + $A$17.

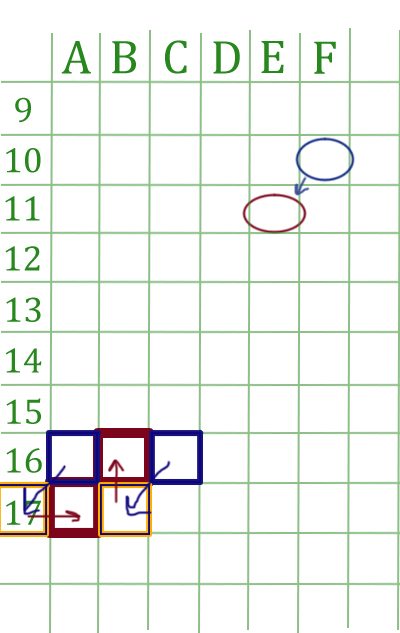
3. В)Значение в ячейке F10 вычисляется по формуле х+у, где х — значение в ячейке С16, а у — значение в ячейке A16

Синим цветом отмечены те ячейки, которые в утверждении участвуют в сумме для первоначальной формулы в F10 (рисунок ниже). Если бы в них не было бы абсолютной адресации ($), то они бы перешли при копировании в те ячейки, которые отмечены оранжевым цветом. (Одна ячейка ушла за пределы таблицы, такое не допускается!). Но по условию задачи, при копировании у нас получились те ячейки, которые отмечены бордовым цветом. Как такое могло произойти ? Дело в том, что у нас присутствовала абсолютная адресация!

Получается, чтобы всё было нормально, в ячейке C16 «зацементируем» 16 строчку, а в ячейке A16, столбец A.

Тогда, в первоначальной формуле будет значение =С$16 + $A16. И это утверждение не противоречит условию задачи!

4. Г) Значение в ячейке F10 равно 2 · х, где х — значение в ячейке В16

Последнюю формулу можно составить для F10 следующим образом = B16 + $B$16. Тогда после копирования ячейка B16 превратится в A17, а $B$16 полностью «зацементирована», так и останется на значении B16. Таким образом, утверждение так же не противоречит условию задачи.

Все четыре утверждения подходят под условия задачи.

Ответ: 4.

Источник

(Старый формат ЕГЭ) 7. Электронные таблицы

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

Простейший анализ диаграмм

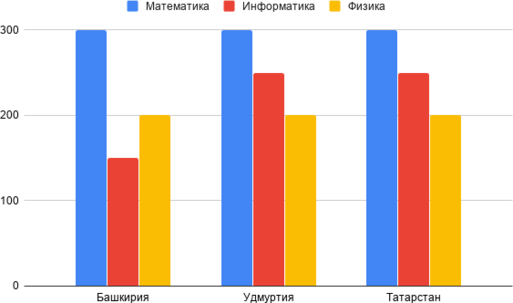
На диаграмме отображено количество участников марафона из разных регионов России по предметам.

Какая из диаграмм правильно отражает соотношение общего количества участников (из всех трех регионов) по каждому из предметов?

Так как на круговых диаграммах отображается процентное соотношение, вычислим его для наших данных, представленных в виде столбчатой диаграммы.

Для начала посчитаем общее количество участников по всем регионам и всем предметам: (300+150+200+300+250+200+300+250+200=2150)

Далее разделим суммарное количество участников марафона из региона на общее количество, которые мы нашли до этого:

Башкирия: (150+250+350=750)

(750/2150=15/43approx0.34approx34%)

Удмуртия: (300+250+200=750)

(750/2150=15/43approx0.34approx34%)

Татрстан: (300+250+200=750)

(750/2150=15/43approx0.34approx34%)

Как мы можем заметить, процентные соотношения равны, значит и секторы диаграммы долдны быть равны, значит, наш ответ 1.

Ответ: 1

Дан фрагмент электронной таблицы:

Какое целое число должно быть записано в ячейке А1, чтобы диаграмма, построенная по значениям ячеек А2:С2, соответствовала рисунку? Известно, что все значения ячеек из рассматриваемого диапазона неотрицательны.

Для начала посчитаем значения формул в ячейках:

(A2: x+6-3=x+3)

(B2: (5x+5)/5=x+1)

(C2: (x+1)*(x-4)=x^2-4x+x-4=x^2-3x-4)

Из диаграммы видно, что секторы равны, значит, приравняем два любых уравнения и найдем ответ:

(x^2-3x-4=x+1)

(x^2-4x-5=0)

(D=16+20=6^2)

(x_1=(4+6)/2=5)

(x_2=(4-6)/2=-1)

Так как по условию все числа неотрицательные, наш ответ — 5.

Ответ: 5

Дан фрагмент электронной таблицы:

Для начала посчитаем значения формул в ячейках:

(A2: x+5-4=x+1)

(B2: (6x+6)/6=x+1)

(C2: (x+1)*(x-4)=x^2-4x+x-4=x^2-3x-4)

Из диаграммы видно, что секторы равны, значит, приравняем два любых уравнения и найдем ответ:

(x^2-3x-4=x+1)

(x^2-4x-5=0)

(D=16+20=6^2)

(x_1=(4+6)/2=5)

(x_2=(4-6)/2=-1)

Так как по условию все числа неотрицательные, наш ответ — 5.

Ответ: 5

Дан фрагмент электронной таблицы:

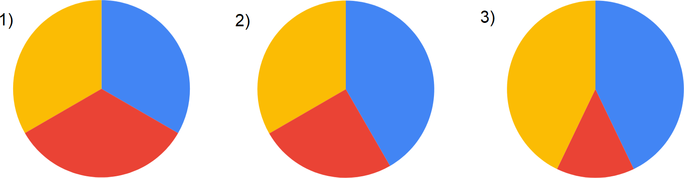
Какое целое число должно быть записано в ячейке C1, чтобы диаграмма, построенная по значениям ячеек А2:С2, соответствовала рисунку? Известно, что все значения ячеек из рассматриваемого диапазона неотрицательны.

Для начала посчитаем значения формул в ячейках:

(A2: x-1)

(B2: (9+1)/5=2)

(C2: 2x)

Из диаграммы видно, что секторы равны, значит, приравняем два любых уравнения и найдем ответ:

(2x=2)

(x=1)

Ответ: 1

Дан фрагмент электронной таблицы:

Какое целое число должно быть записано в ячейке С1, чтобы диаграмма, построенная по значениям ячеек A2:C2, соответствовала рисунку? Известно, что все значения ячеек из рассматриваемого диапазона неотрицательны.

Для начала посчитаем значения формул в ячейках:

(A2: x+3)

(B2: (4x-4)/4=x-1)

(C2: 7x)

Из диаграммы видно, что секторы равны, значит, приравняем два любых уравнения и найдем ответ:

(7x=x+3)

(6x=3)

(x=2)

Ответ: 2

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ

Источник