Привет! Сегодня разберём новый тип 6 задания из ЕГЭ по информатике 2023! Добавим недостающий пазл в видеокурс по подготовке к ЕГЭ по информатике.
Так же Вы можете посмотреть разбор 6 задания из ДЕМОВЕРСИИ 2023.
На мой взгляд, на экзамене скорее всего будет задача, похожая именно на демонстрационный вариант. Т.к. это задание нового образца, то выпускникам необходимо привыкнуть к нему.
Вспомним, когда в прошлом году была введена новая формулировка для 3 задания, то на экзамене дали очень похожую задачу на ту, которая была в демоверсии.
Рассмотрим первую тренировочную задачу из 6 задания ЕГЭ по информатике 2023.
Задача (Элегантный способ)
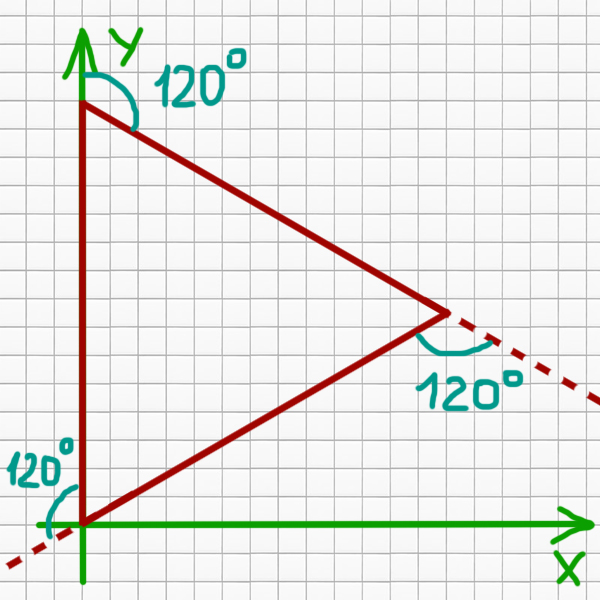
Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует две команды: Вперёд n (где n – целое число), вызывающая передвижение Черепахи на n единиц в том направлении, куда указывает её голова, и Направо m (где m – целое число), вызывающая изменение направления движения на m градусов по часовой стрелке. Запись
Повтори k [Команда1 Команда2 … КомандаS]
означает, что последовательность из S команд повторится k раз. Черепахе был дан для исполнения следующий алгоритм:
Повтори 15 [Вперёд 15 Направо 120]
Определите, сколько точек с целочисленными координатами будут находиться внутри области, ограниченной линией, заданной данным алгоритмом. Точки на линии учитывать не следует.
Решение:
В начале нужно понять, какая фигура получится в результате действий Исполнителя Черепахи.
Черепаха идёт вверх на 15 единиц. Потом поворачивает направо на 120 градусов. Потом идёт на 15 единиц по заданному курсу и снова поворачивает на 120 градусов, идёт на 15 единиц ещё и попадает в исходную точку. В итоге получается равносторонний треугольник! Дальнейшие повторения не имеют смысла, т.к. нового больше ничего не нарисуется.
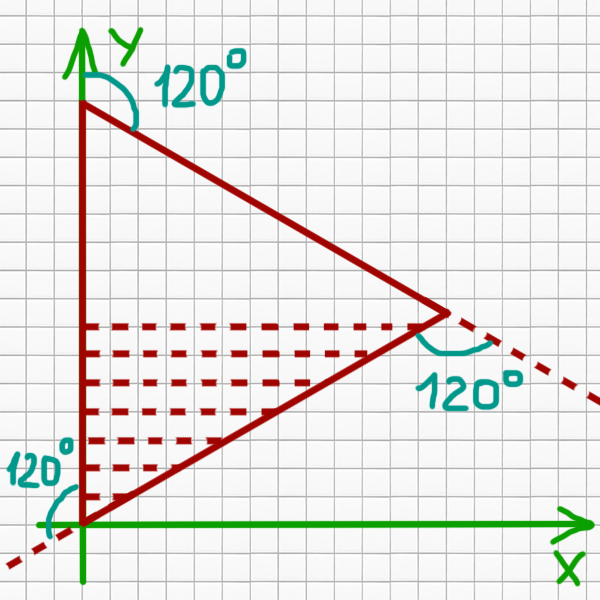
Проведём перпендикуляры от каждой точки с целыми координатами на оси Y внутри треугольника.
Для каждой точки на оси Y мы можем найти этот перпендикуляр. Это и есть искомое количество точек на каждой такой линии, если округлить это значение в меньшую сторону.
Посмотрим, как найти такой перпендикуляр, если точка на оси Y находится до середины стороны. Пусть есть точка (0, yn), а dn — это перпендикуляр для этой точки. Тогда
tg(60o) = dn / yn
dn = tg(60o) * yn
Для второй половины длины перпендикуляров будут такие же.
Напишем программу на Питоне, которая подсчитает все точки.
import math s=0 for y in range(0, 8): s = s + int(math.tan(math.pi / 3) * y ) s = 2*s print(s)
Нам необходимо взять первые 7 точек, дальше ситуация симметричная. Пишем в цикле for 8, потому что последнее число не проходится в Питоне.
Вычисляем по формуле длину каждого перпендикуляра. Тангенс вычисляется с помощью функции math.tan. Для неё нужна математическая библиотека math. Функция должна получить градусы в радианах, поэтому ей передаём π/3 = 60o.
В цикле суммируем все точки для каждой линии. Результат нужно умножить на 2, чтобы учесть вторую половину треугольника.
Ответ: 90
Задача(Считаем точки вручную)
Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует две команды: Вперёд n (где n – целое число), вызывающая передвижение Черепахи на n единиц в том направлении, куда указывает её голова, и Налево m (где m – целое число), вызывающая изменение направления движения на m градусов против часовой стрелки. Запись
Повтори k [Команда1 Команда2 … КомандаS]
означает, что последовательность из S команд повторится k раз. Черепахе был дан для исполнения следующий алгоритм:
Повтори 16 [Налево 36 Вперёд 4 Налево 36]
Определите, сколько точек с целочисленными координатами будут находиться внутри области, ограниченной линией, заданной данным алгоритмом. Точки на линии следует учитывать.
Решение:
В это задачке достаточно не просто составить уравнения прямых полученной фигуры. В таких случаях можно попробовать вручную посчитать точки с помощью известной программы Кумир от НИИСИ РАН. Скачать её можно с официального сайта НИИСИ РАН.
Вероятно, это программа окажется на компьютере на экзамене.
Запустим программу Кумир-Стандарт. В начале нужно подключить модуль Черепаха.
После того, как модуль Черепаха подключён, можно написать программу на языке Кумир.
использовать Черепаха
алг
нач
опустить хвост
нц 16 раз
влево(36)
вперед(4)
влево(36)
кц
кон
В начале нужно подключить модуль Черепаха. Слово алг обозначает начало алгоритма. Слово нач — это начало программы.
Опускаем хвост у Черепахи. Цикл пишем с помощью команды нц — начало цикла. Команда кц — это конец цикла. Команда влево — это аналог команды Налево (видим, что эти команды пишутся по-разному). Аналогично есть команда вправо в программе Кумир. Команда вперед пишется без буквы ё.
После того, как алгоритм перенесли в программу Кумир, запускаем программу, нажав на кнопку F9 (или кнопка плей в виде треугольника).
После этого появится окно в правом нижнем углу. Это окно можно расширить до приемлемых размеров, чтобы нам было удобно анализировать рисунок.
Необходимо настроить масштабирование на 1.
После этого можно сделать скриншот и перенести рисунок в программу Paint, где и посчитать точки вручную.
Получается в ответе 31 точка. Обратите внимание, что в этой задачи просили подсчитать точки, которые находятся на линиях в том числе.
Даже если нет программы Кумир, можно подсчитать точки вручную через Python. Напишем программу.
from turtle import * left(90) for i in range(16): left(36) forward(4*40) left(36) penup() for x in range(-10, 10): for y in range(-10, 10): setpos(x*40, y*40) dot(4, 'red')
Программа выведет такую картину.
В программе подключаем модуль turtle. В начале повернём Черепаху на 90 градусов налево, с помощью команды left. Это делается из-за того, в Python Черепаха смотрит вдоль положительного направления оси абсцисс.
Далее идёт цикл, который указан в задаче. Он должен повторится 16 раз. Внутри цикла пишем программу для Черепахи. Команда left() — поворот налево (аналогично right() — поворот направо), команда forward() — это движение верёд.
4 единицы внутри команды forward() умножаются на 40. Число 40 — это коэффициент размера нашего рисунка. Попробуйте «поиграть» с этим числом, чтобы посмотреть эффект уменьшения или увеличения рисунка.
Команда penup() позволяет поднять кисть, чтобы проставить точки, которые будут символизировать точки с целыми координатами.
Далее идут вложенные циклы, с помощью них мы проставим точки с целыми координатами. Выбираем диапазон, чтобы наша фигура точно уместилась.
Команда setpos() ставим точки. Умножаем координаты x и y на тот же коэффициент, что использовали ранее.
Команда dot() устанавливает жирность и цвет точки.
Ответ: 31
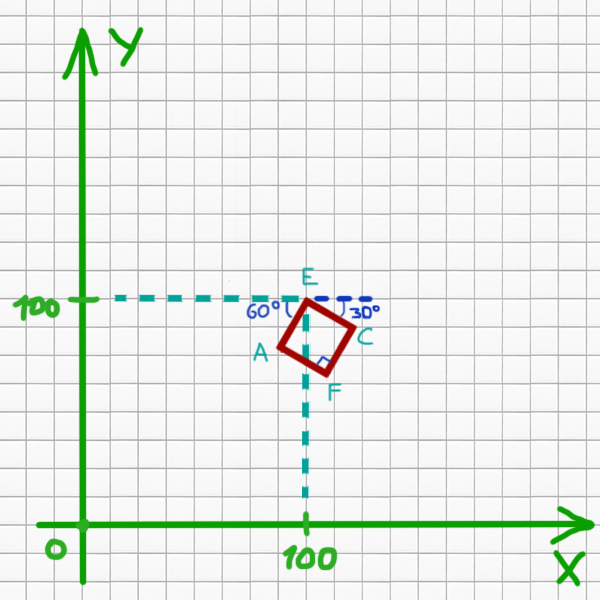
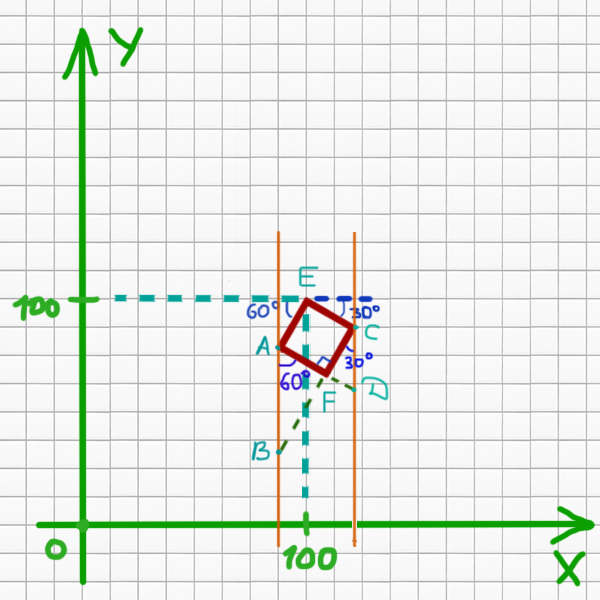
Задача (Составляем уравнения)
Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост поднят. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует три команды: Вперёд n (где n — целое число), вызывающая передвижение Черепахи на n единиц в том направлении, куда указывает её голова; Направо m (где m — целое число), вызывающая изменение направления движения на m градусов по часовой стрелке; Опусти, принуждающая Черепаху опустить хвост.
Запись Повтори k [Команда 1 Команда 2 … Команда S] означает, что последовательность из S команд повторится k раз.
Черепахе был дан для исполнения следующий алгоритм:
Вперёд 100 Направо 90 Вперёд 100 Направо 30 Опусти Повтори 10 [Вперёд 25 Направо 90]
Определите, сколько точек с целочисленными координатами будут находиться внутри области, ограниченной линией, заданной данным алгоритмом. Точки на линии учитывать не следует.
Решение:
Нарисуем общий рисунок.
Здесь уже не очень удобно пользоваться элегантным способом. Составим уравнения прямых, которые образуют квадрат. Общий вид уравнения прямой выглядит так:
y=k*x+b
Коэффициент k — это тангенс угла наклона α к оси X ( 0 ≤ α < π, но α ≠ π/2). Число b — это смещение прямой по оси Y относительно нуля.
Для прямой AE k1=tan(60o)=√3. Так же она проходит через точку (100, 100).
Найдём число b. Подставим в общее уравнение координаты точки (100, 100):
y = k*x+b = √3*100 + b = 100
b=100*(1 — √3)
Получается уравнение прямой AE:
y= √3*x + 100(1 — √3)
Найдём на сколько смещена FC по оси Y относительно AE.
cos(60o) = 25 (сторона квадрата) / AB
AB = 25 / cos(60o) = 25 / 0,5 = 50
Получается, что уравнение для прямой FC:
y=√3*x + 100(1 — √3) — 50
Для прямой EC k2=-tan(30o) = — √3/3. Эта прямая тоже проходит через точку (100, 100). Подставим эти координаты в уравнение и найдём b.
y = (-√3/3) * x + b = (-√3/3) * 100 + b = 100
b = 100(1 + √3/3)
Тогда уравнение для прямой EC получается:
y = (-√3/3) * x + 100(1 + √3/3)
Найдём на сколько смещена прямая AF относительно EC по оси Y.
cos(30o) = 25 (длина стороны) / CD
CD = 25 / cos(30o) = 25 / (√3/2) = 50/√3
Тогда для прямой AF:
y = (- √3/3) * x + 100(1 + √3/3) — 50/√3
Пробежимся с помощью Питона для переменной x от 0 до 150. Для переменной y от 0 до 100. Чтобы получить точку, используем вложенные циклы!
s=0
for x in range(1, 200):
for y in range(1, 200):
if (y < (3**0.5)*x + 100*(1-3**0.5)) and (y > (3**0.5)*x + 100*(1-3**0.5) - 50) and (y < (- 3**0.5 / 3)*x + 100*(1+ 3**0.5 / 3)) and (y > (-3**0.5/3)*x + 100*(1 + 3**0.5 /3) - 50 / 3**0.5 ):
s=s+1
print(s)
Точки, которые лежат в квадрате должны удовлетворять следующим условиям:
Точки должны быть ниже прямых AE и EC, но выше AF и FC
Проверить выше или ниже некоторая точка M(xm, ym), чем прямая y=k*x+b, можно следующим образом:
Если ym > k*xm + b, то точка лежит выше прямой.
Если ym < k*xm + b, то точка лежит ниже прямой.
Данный принцип и был использован в программе.
Ответ: 625
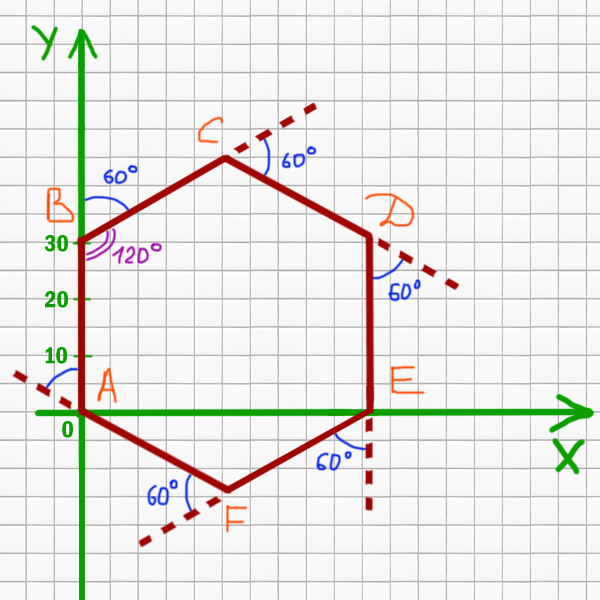
Задача (Закрепление)
Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует три команды: Вперёд n (где n — целое число), вызывающая передвижение Черепахи на n единиц в том направлении, куда указывает её голова; Направо m (где m — целое число), вызывающая изменение направления движения на m градусов по часовой стрелке; Опусти, принуждающая Черепаху опустить хвост.
Запись Повтори k [Команда 1 Команда 2 … Команда S] означает, что последовательность из S команд повторится k раз.
Черепахе был дан для исполнения следующий алгоритм:
Повтори 21 [Вперёд 31 Направо 60]
Определите, сколько точек с целочисленными координатами будут находиться внутри области, ограниченной линией, заданной данным алгоритмом. Точки на линии учитывать не следует.
Копирование прямо
Решение:
Попробуем понять, какая фигура получится в итоге.
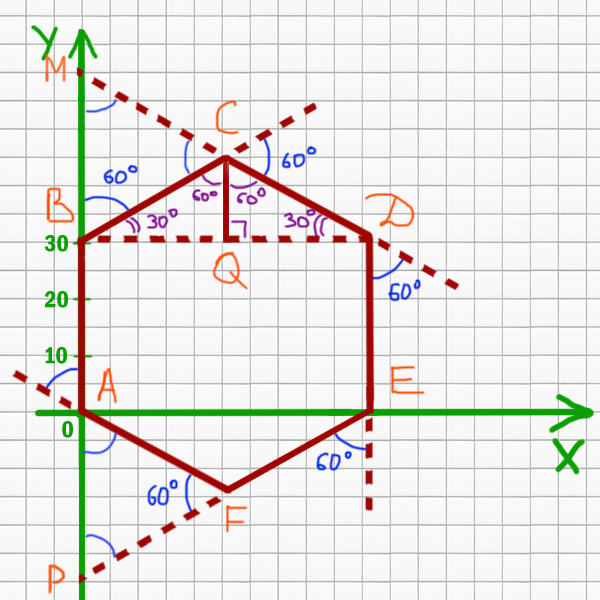
Получается правильный шестиугольник. Угол ∠СВА = 120o. Как раз угол правильного n-угольника равен (n-2)*180o/n. Для шестиугольника получается (6-2)*180o/6 = 120o.
Будем решать методом составления уравнений.
Рассмотрим прямую BC. Если провести от точки B прямую параллельную оси X, то мы увидим, что угол наклона прямой BC равен 30o.
y = tan(30o)*x + 31
y = (√3/3) * x + 31
Прямая DC имеет угол наклона -30o к оси X. Она расположена выше, чем BC на МВ. Треугольник BCM равносторонний. Значит, МВ=31. Тогда уравнение для DC будет:
y = -(√3/3) * x + 62
Уравнение для AF будет:
y = -(√3/3) * x
Прямая EF имеет угол наклона 30o относительно оси X. Смещена она вниз на AP. Треугольник AFP так же является равносторонним. Следовательно, AP = 31. Тогда для EF получается:
y=tan(30o)*x — 31
y=(√3/3)*x — 31
Прямая AB это x=0. Найдём так же ED.
cos(30o) = BQ / BC
BQ = BC * cos(30o)
BQ = 31 * (√3/2)
BD = 2 * BQ = 2 * 31 * (√3/2) = 31 * √3
Значит, уравнение для ED: x = 31 * √3.
Когда уравнения готовы, можно написать программу.
k=0
for x in range(-100, 100):
for y in range(-100, 100):
if (y < 3**0.5 / 3 * x + 31) and (y < -(3**0.5) / 3 * x + 62) and (y > -(3**0.5) / 3 * x) and (y > 3**0.5 / 3 * x - 31) and (x > 0) and (x < 31 * 3**0.5):
k=k+1
print(k)
Точки должны быть ниже прямых BC и CD, но выше прямых AF и EF. Так же координаты x должны быть 0 < x < 31 * √3.
Важно не забыть для y пробежаться и по отрицательным значениям, т.к. фигура находится меньше оси X.
Ответ: 2476
На сегодня всё. Удачи при решение 6 задания из ЕГЭ по информатике 2023.
Зачем это делать? Авторы задания предполагают, что ученики просто воспользуются КуМир и все там получат.
В Кумире не удобно считать.
Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует две команды: Вперёд n (где n — целое число), вызывающая передвижение Черепахи на n единиц в том направлении, куда указывает её голова, и Направо m (где m — целое число), вызывающая изменение направления движения на m градусов по часовой стрелке. Запись
Повтори k [Команда1 Команда2 … КомандаS]
означает, что последовательность из S команд повторится k раз. Черепахе был дан для исполнения следующий алгоритм:
Повтори 4 [Вперёд 9 Направо 90]
Повтори 3 [Вперёд 9 Направо 120]
Определите, сколько точек с целочисленными координатами будут находиться внутри области, ограниченной линией, заданной данным алгоритмом: Повтори 4 [Вперёд 9 Направо 90] и находиться вне области, ограниченной линией, заданной данным алгоритмом: Повтори 3 [Вперёд 9 Направо 120]. Точки на линии учитывать не следует.
мой код:
| Python | ||
|
Выходит как-то не так, помогите пожалуйста!
__________________
Помощь в написании контрольных, курсовых и дипломных работ, диссертаций здесь
Задания для подготовки
Версия для печати и копирования в MS Word
1
Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует две команды: Вперёд n (где n — целое число), вызывающая передвижение Черепахи на n единиц в том направлении, куда указывает её голова, и Направо m (где m — целое число), вызывающая изменение направления движения на m градусов по часовой стрелке.
Запись Повтори k [Команда1 Команда2 … КомандаS] означает, что последовательность из S команд повторится k раз.
Черепахе был дан для исполнения следующий алгоритм: Повтори 7 [Вперёд 10 Направо 120].
Определите, сколько точек с целочисленными координатами будут находиться внутри области, ограниченной линией, заданной данным алгоритмом. Точки на линии учитывать не следует.
Источник: Демонстрационная версия ЕГЭ−2023 по информатике
2
Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и
его движения. У исполнителя существует две команды: Вперёд n (где n — целое число), вызывающая передвижение Черепахи на n единиц в том направлении, куда указывает её голова, и Направо m (где m — целое число), вызывающая изменение направления движения на m градусов по часовой стрелке. Запись
Повтори k [Команда1 Команда2 … КомандаS]
означает, что последовательность из S команд повторится k раз. Черепахе был дан для исполнения следующий алгоритм:
Повтори 5 [Вперёд 9 Направо 120]
Определите, сколько точек с целочисленными координатами будут находиться внутри области, ограниченной линией, заданной данным алгоритмом. Точки на линии учитывать не следует.
3
Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует две команды: Вперёд n (где n — целое число), вызывающая передвижение Черепахи на n единиц в том направлении, куда указывает её голова, и Направо m (где m — целое число), вызывающая изменение направления движения на m градусов по часовой стрелке. Запись
Повтори k [Команда1 Команда2 … КомандаS]
означает, что последовательность из S команд повторится k раз. Черепахе был дан для исполнения следующий алгоритм:
Повтори 4 [Вперёд 14 Направо 120]
Определите, сколько точек с целочисленными координатами будут находиться внутри области, ограниченной линией, заданной данным алгоритмом. Точки на линии учитывать не следует.
4
Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует две команды: Вперёд n (где n — целое число), вызывающая передвижение Черепахи на n единиц в том направлении, куда указывает её голова, и Направо m (где m — целое число), вызывающая изменение направления движения на m градусов по часовой стрелке. Запись
Повтори k [Команда1 Команда2 … КомандаS]
означает, что последовательность из S команд повторится k раз. Черепахе был дан для исполнения следующий алгоритм:
Повтори 8 [Вперёд 6 Направо 120]
Определите, сколько точек с целочисленными координатами будут находиться внутри области, ограниченной линией, заданной данным алгоритмом. Точки на линии учитывать не следует.
5
Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует две команды: Вперёд n (где n — целое число), вызывающая передвижение Черепахи на n единиц в том направлении, куда указывает её голова, и Направо m (где m — целое число), вызывающая изменение направления движения на m градусов по часовой стрелке. Запись
Повтори k [Команда1 Команда2 … КомандаS]
означает, что последовательность из S команд повторится k раз. Черепахе был дан для исполнения следующий алгоритм:
Повтори 4 [Вперёд 10 Направо 90]
Определите, сколько точек с целочисленными координатами будут находиться внутри области, ограниченной линией, заданной данным алгоритмом. Точки на линии учитывать не следует.
6
Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует две команды: Вперёд n (где n — целое число), вызывающая передвижение Черепахи на n единиц в том направлении, куда указывает её голова, и Направо m (где m — целое число), вызывающая изменение направления движения на m градусов по часовой стрелке. Запись
Повтори k [Команда1 Команда2 … КомандаS]
означает, что последовательность из S команд повторится k раз. Черепахе был дан для исполнения следующий алгоритм:
Повтори 6 [Вперёд 13 Направо 120]
Определите, сколько точек с целочисленными координатами будут находиться внутри области, ограниченной линией, заданной данным алгоритмом. Точки на линии учитывать не следует.
7
Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует две команды: Вперёд n (где n — целое число), вызывающая передвижение Черепахи на n единиц в том направлении, куда указывает её голова, и Направо m (где m — целое число), вызывающая изменение направления движения на m градусов по часовой стрелке. Запись
Повтори k [Команда1 Команда2 … КомандаS]
означает, что последовательность из S команд повторится k раз. Черепахе был дан для исполнения следующий алгоритм:
Повтори 5 [Вперёд 7 Направо 120]
Определите, сколько точек с целочисленными координатами будут находиться внутри области, ограниченной линией, заданной данным алгоритмом. Точки на линии учитывать не следует.
8
Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует две команды: Вперёд n (где n — целое число), вызывающая передвижение Черепахи на n единиц в том направлении, куда указывает её голова, и Направо m (где m — целое число), вызывающая изменение направления движения на m градусов по часовой стрелке. Запись
Повтори k [Команда1 Команда2 … КомандаS]
означает, что последовательность из S команд повторится k раз. Черепахе был дан для исполнения следующий алгоритм:
Повтори 4 [Вперёд 5 Направо 90 Вперёд 10 Направо 90]
Определите количество точек с целочисленными координатами, лежащих внутри и на границе области, которую ограничивает заданная алгоритмом линия.
9
Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует две команды: Вперёд n (где n — целое число), вызывающая передвижение Черепахи на n единиц в том направлении, куда указывает её голова, и Направо m (где m — целое число), вызывающая изменение направления движения на m градусов по часовой стрелке. Запись
Повтори k [Команда1 Команда2 … КомандаS]
означает, что последовательность из S команд повторится k раз. Черепахе был дан для исполнения следующий алгоритм:
Повтори 4 [Вперёд 7 Направо 90 Вперёд 8 Направо 90]
Определите, сколько точек с целочисленными координатами будут находиться внутри области, ограниченной линией, заданной данным алгоритмом. Точки на линии учитывать не следует.
10
Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует две команды: Вперёд n (где n — целое число), вызывающая передвижение Черепахи на n единиц в том направлении, куда указывает её голова, и Направо m (где m — целое число), вызывающая изменение направления движения на m градусов по часовой стрелке. Запись
Повтори k [Команда1 Команда2 … КомандаS]
означает, что последовательность из S команд повторится k раз. Черепахе был дан для исполнения следующий алгоритм:
Повтори 4 [Вперёд 9 Направо 90 Вперёд 7 Направо 90]
Определите, сколько точек с целочисленными координатами будут находиться внутри области, ограниченной линией, заданной данным алгоритмом. Точки на линии учитывать не следует.
11
Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует две команды: Вперёд n (где n — целое число), вызывающая передвижение Черепахи на n единиц в том направлении, куда указывает её голова, и Направо m (где m — целое число), вызывающая изменение направления движения на m градусов по часовой стрелке. Запись
Повтори k [Команда1 Команда2 … КомандаS]
означает, что последовательность из S команд повторится k раз. Черепахе был дан для исполнения следующий алгоритм:
Повтори 4 [Вперёд 8 Направо 90 Вперёд 8 Направо 90]
Определите, сколько точек с целочисленными координатами будут находиться внутри области, ограниченной линией, заданной данным алгоритмом. Точки на линии учитывать не следует.
12
Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует две команды: Вперёд n (где n — целое число), вызывающая передвижение Черепахи на n единиц в том направлении, куда указывает её голова, и Направо m (где m — целое число), вызывающая изменение направления движения на m градусов по часовой стрелке. Запись
Повтори k [Команда1 Команда2 … КомандаS]
означает, что последовательность из S команд повторится k раз. Черепахе был дан для исполнения следующий алгоритм:
Повтори 4 [Вперёд 10 Направо 60 Вперёд 10 Направо 120]
Определите, сколько точек с целочисленными координатами будут находиться внутри области, ограниченной линией, заданной данным алгоритмом. Точки на линии учитывать не следует.
13
Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует две команды: Вперёд n (где n — целое число), вызывающая передвижение Черепахи на n единиц в том направлении, куда указывает её голова, и Направо m (где m — целое число), вызывающая изменение направления движения на m градусов по часовой стрелке. Запись
Повтори k [Команда1 Команда2 … КомандаS]
означает, что последовательность из S команд повторится k раз. Черепахе был дан для исполнения следующий алгоритм:
Повтори 5 [Вперёд 8 Направо 60 Вперёд 8 Направо 120]
Определите, сколько точек с целочисленными координатами будут находиться внутри области, ограниченной линией, заданной данным алгоритмом. Точки на линии учитывать не следует.
14
Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси абсцисс, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует две команды: Вперёд n (где n — целое число), вызывающая передвижение Черепахи на n единиц в том направлении, куда указывает её голова, и Направо m (где m — целое число), вызывающая изменение направления движения на m градусов по часовой стрелке. Запись
Повтори k [Команда1 Команда2 … КомандаS]
означает, что последовательность из S команд повторится k раз. Черепахе был дан для исполнения следующий алгоритм:
Повтори 4 [Вперёд 8 Направо 150 Вперёд 8 Направо 30]
Определите, сколько точек с целочисленными координатами будут находиться внутри области, ограниченной линией, заданной данным алгоритмом. Точки на линии учитывать не следует.
15
Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси абсцисс, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует две команды: Вперёд n (где n — целое число), вызывающая передвижение Черепахи на n единиц в том направлении, куда указывает её голова, и Направо m (где m — целое число), вызывающая изменение направления движения на m градусов по часовой стрелке. Запись
Повтори k [Команда1 Команда2 … КомандаS]
означает, что последовательность из S команд повторится k раз. Черепахе был дан для исполнения следующий алгоритм:
Повтори 4 [Вперёд 6 Направо 150 Вперёд 6 Направо 30]
Определите, сколько точек с целочисленными координатами будут находиться внутри области, ограниченной линией, заданной данным алгоритмом. Точки на линии учитывать не следует.
16
Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует две команды: Вперёд n (где n — целое число), вызывающая передвижение Черепахи на n единиц в том направлении, куда указывает её голова, и Направо m (где m — целое число), вызывающая изменение направления движения на m градусов по часовой стрелке. Запись
Повтори k [Команда1 Команда2 … КомандаS]
означает, что последовательность из S команд повторится k раз. Черепахе был дан для исполнения следующий алгоритм:
Повтори 4 [Вперёд 12 Направо 150 Вперёд 12 Направо 30]
Определите, сколько точек с целочисленными координатами будут находиться внутри области, ограниченной линией, заданной данным алгоритмом. Точки на линии учитывать не следует.
17
Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует две команды: Вперёд n (где n — целое число), вызывающая передвижение Черепахи на n единиц в том направлении, куда указывает её голова, и Направо m (где m — целое число), вызывающая изменение направления движения на m градусов по часовой стрелке. Запись
Повтори k [Команда1 Команда2 … КомандаS]
означает, что последовательность из S команд повторится k раз. Черепахе был дан для исполнения следующий алгоритм:
Повтори 4 [Вперёд 5 Направо 90 Вперёд 7 Направо 90]
Определите количество точек с целочисленными координатами, лежащих внутри или на границе области, которую ограничивает заданная алгоритмом линия.
18
Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует две команды: Вперёд n (где n — целое число), вызывающая передвижение Черепахи на n единиц в том направлении, куда указывает её голова, и Направо m (где m — целое число), вызывающая изменение направления движения на m градусов по часовой стрелке. Запись
Повтори k [Команда1 Команда2 … КомандаS]
означает, что последовательность из S команд повторится k раз. Черепахе был дан для исполнения следующий алгоритм:
Повтори 10 [Вперёд 9 Направо 90 Вперёд 2 Направо 90]
Определите количество точек с целочисленными координатами, лежащих внутри или на границе области, которую ограничивает заданная алгоритмом линия.
19
Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует две команды: Вперёд n (где n — целое число), вызывающая передвижение Черепахи на n единиц в том направлении, куда указывает её голова, и Направо m (где m — целое число), вызывающая изменение направления движения на m градусов по часовой стрелке. Запись
Повтори k [Команда1 Команда2 … КомандаS]
означает, что последовательность из S команд повторится k раз. Черепахе был дан для исполнения следующий алгоритм:
Повтори 5 [Вперёд 7 Направо 90 Вперёд 4 Направо 90]
Определите количество точек с целочисленными координатами, лежащих внутри или на границе области, которую ограничивает заданная алгоритмом линия.
20
Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует две команды: Вперёд n (где n — целое число), вызывающая передвижение Черепахи на n единиц в том направлении, куда указывает её голова, и Направо m (где m — целое число), вызывающая изменение направления движения на m градусов по часовой стрелке. Запись
Повтори k [Команда1 Команда2 … КомандаS]
означает, что последовательность из S команд повторится k раз. Черепахе был дан для исполнения следующий алгоритм:
Повтори 6 [Вперёд 7 Направо 90 Вперёд 7 Направо 90]
Определите количество точек с целочисленными координатами, лежащих внутри или на границе области, которую ограничивает заданная алгоритмом линия.
21
Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует две команды: Вперёд n (где n — целое число), вызывающая передвижение Черепахи на n единиц в том направлении, куда указывает её голова, и Направо m (где m — целое число), вызывающая изменение направления движения на m градусов по часовой стрелке. Запись
Повтори k [Команда1 Команда2 … КомандаS]
означает, что последовательность из S команд повторится k раз. Черепахе был дан для исполнения следующий алгоритм:
Повтори 5 [Вперёд 9 Направо 90 Вперёд 3 Направо 90]
Определите количество точек с целочисленными координатами, лежащих внутри или на границе области, которую ограничивает заданная алгоритмом линия.
22
Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует две команды: Вперёд n (где n — целое число), вызывающая передвижение Черепахи на n единиц в том направлении, куда указывает её голова, и Направо m (где m — целое число), вызывающая изменение направления движения на m градусов по часовой стрелке. Запись
Повтори k [Команда1 Команда2 … КомандаS]
означает, что последовательность из S команд повторится k раз. Черепахе был дан для исполнения следующий алгоритм:
Повтори 12 [Направо 60 Вперёд 1 Направо 60 Вперёд 1 Направо 270]
Определите, сколько точек с целочисленными координатами будут находиться внутри области, ограниченной линией, заданной данным алгоритмом. Точки на линии учитывать не следует.
23
Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует две команды: Вперёд n (где n — целое число), вызывающая передвижение Черепахи на n единиц в том направлении, куда указывает её голова, и Направо m (где m — целое число), вызывающая изменение направления движения на m градусов по часовой стрелке. Запись
Повтори k [Команда1 Команда2 … КомандаS]
означает, что последовательность из S команд повторится k раз. Черепахе был дан для исполнения следующий алгоритм:
Повтори 14 [Направо 60 Вперёд 2 Направо 60 Вперёд 2 Направо 270]
Определите, сколько точек с целочисленными координатами будут находиться внутри области, ограниченной линией, заданной данным алгоритмом. Точки на линии учитывать не следует.
24
Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует две команды: Вперёд n (где n — целое число), вызывающая передвижение Черепахи на n единиц в том направлении, куда указывает её голова, и Направо m (где m — целое число), вызывающая изменение направления движения на m градусов по часовой стрелке. Запись
Повтори k [Команда1 Команда2 … КомандаS]
означает, что последовательность из S команд повторится k раз. Черепахе был дан для исполнения следующий алгоритм:
Повтори 6 [Вперёд 10 Направо 60]
Определите количество точек с целочисленными координатами, лежащих внутри или на границе области, которую ограничивает заданная алгоритмом линия.
25
Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует две команды: Вперёд n (где n — целое число), вызывающая передвижение Черепахи на n единиц в том направлении, куда указывает её голова, и Направо m (где m — целое число), вызывающая изменение направления движения на m градусов по часовой стрелке. Запись
Повтори k [Команда1 Команда2 … КомандаS]
означает, что последовательность из S команд повторится k раз. Черепахе был дан для исполнения следующий алгоритм:
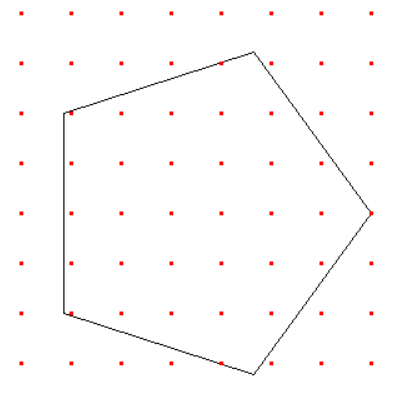
Повтори 6 [Направо 36 Вперёд 10 Направо 36]
Определите, сколько точек с целочисленными координатами будут находиться внутри области, ограниченной линией, заданной данным алгоритмом. Точки на линии учитывать не следует.
26
Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует две команды: Вперёд n (где n — целое число), вызывающая передвижение Черепахи на n единиц в том направлении, куда указывает её голова, и Направо m (где m — целое число), вызывающая изменение направления движения на m градусов по часовой стрелке. Запись
Повтори k [Команда1 Команда2 … КомандаS]
означает, что последовательность из S команд повторится k раз. Черепахе был дан для исполнения следующий алгоритм:
Повтори 10 [Вперёд 5 Направо 60]
Определите, сколько точек с целочисленными координатами будут находиться внутри области, ограниченной линией, заданной данным алгоритмом. Точки на линии учитывать не следует.
27
Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует две команды: Вперёд n (где n — целое число), вызывающая передвижение Черепахи на n единиц в том направлении, куда указывает её голова, и Направо m (где m — целое число), вызывающая изменение направления движения на m градусов по часовой стрелке. Запись
Повтори k [Команда1 Команда2 … КомандаS]
означает, что последовательность из S команд повторится k раз. Черепахе был дан для исполнения следующий алгоритм:
Повтори 4 [Вперёд 12 Направо 90]
Направо 30
Повтори 3 [Вперёд 8 Направо 60 Вперёд 8 Направо 120]
Определите, сколько точек с целочисленными координатами будут находиться внутри области, ограниченной линией, заданной данным алгоритмом: Повтори 4 [Вперёд 12 Направо 90]
и находиться вне области, ограниченной линией, заданной данным алгоритмом: Повтори 3 [Вперёд 8 Направо 60 Вперёд 8 Направо 120]. Точки на линии учитывать не следует.
28
Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует две команды: Вперёд n (где n — целое число), вызывающая передвижение Черепахи на n единиц в том направлении, куда указывает её голова, и Направо m (где m — целое число), вызывающая изменение направления движения на m градусов по часовой стрелке. Запись
Повтори k [Команда1 Команда2 … КомандаS]
означает, что последовательность из S команд повторится k раз. Черепахе был дан для исполнения следующий алгоритм:
Повтори 4 [Вперёд 10 Направо 90]
Направо 30
Повтори 5 [Вперёд 6 Направо 60 Вперёд 6 Направо 120]
Определите, сколько точек с целочисленными координатами будут находиться внутри области, ограниченной линией, заданной данным алгоритмом: Повтори 4 [Вперёд 10 Направо 90] и находиться вне области, ограниченной линией, заданной данным алгоритмом: Повтори 5 [Вперёд 6 Направо 60 Вперёд 6 Направо 120]. Точки на линии учитывать не следует.
29
Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует две команды: Вперёд n (где n — целое число), вызывающая передвижение Черепахи на n единиц в том направлении, куда указывает её голова, и Направо m (где m — целое число), вызывающая изменение направления движения на m градусов по часовой стрелке. Запись
Повтори k [Команда1 Команда2 … КомандаS]
означает, что последовательность из S команд повторится k раз. Черепахе был дан для исполнения следующий алгоритм:
Повтори 4 [Вперёд 9 Направо 90]
Повтори 3 [Вперёд 9 Направо 120]
Определите, сколько точек с целочисленными координатами будут находиться внутри области, ограниченной линией, заданной данным алгоритмом: Повтори 4 [Вперёд 9 Направо 90] и находиться вне области, ограниченной линией, заданной данным алгоритмом: Повтори 3 [Вперёд 9 Направо 120]. Точки на линии учитывать не следует.
30
Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует две команды: Вперёд n (где n — целое число), вызывающая передвижение Черепахи на n единиц в том направлении, куда указывает её голова, и Направо m (где m — целое число), вызывающая изменение направления движения на m градусов по часовой стрелке. Запись
Повтори k [Команда1 Команда2 … КомандаS]
означает, что последовательность из S команд повторится k раз. Черепахе был дан для исполнения следующий алгоритм:
Повтори 4 [Вперёд 12 Направо 90]
Повтори 3 [Вперёд 12 Направо 120]
Определите, сколько точек с целочисленными координатами будут находиться внутри области, ограниченной линией, заданной данным алгоритмом: Повтори 4 [Вперёд 12 Направо 90]
и находиться вне области, ограниченной линией, заданной данным алгоритмом: Повтори 3 [Вперёд 12 Направо 120]. Точки на линии учитывать не следует.
31
Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует две команды: Вперёд n (где n — целое число), вызывающая передвижение Черепахи на n единиц в том направлении, куда указывает её голова, и Направо m (где m — целое число), вызывающая изменение направления движения на m градусов по часовой стрелке. Запись
Повтори k [Команда1 Команда2 … КомандаS]
означает, что последовательность из S команд повторится k раз. Черепахе был дан для исполнения следующий алгоритм:
Повтори 4 [Вперёд 8 Направо 90]
Повтори 3 [Вперёд 12 Направо 120]
Определите, сколько точек с целочисленными координатами будут находиться внутри области, ограниченной линией, заданной данным алгоритмом:Повтори 4 [Вперёд 8 Направо 90]
и находиться вне области, ограниченной линией, заданной данным алгоритмом: Повтори 3 [Вперёд 12 Направо 120]. Точки на линии учитывать не следует.
В Python есть встроенный модуль (turtle), можно решать задание (6) с помощью него.
|
Команда |
Комментарии |
| left((90)) | Поворачивает Черепаху налево на (90) градусов |
| right((90)) | Поворачивает Черепаху направо на (90) градусов |
| forward (Х) | Черепаха перемещается в указанном направлении на Х пикселей |
| up() | Черепаха поднимает хвост |
| goto((x), (y)) | Черепаха перемещается в точку с координатами ((x), (y)) |
| dot((5)) | Черепаха рисует точку толщиной (5) |
Программа для решения демоверсии (2023)
Рис. (1). Примерная программа
Результат работы программы
Рис. (2). Результат работы программы
Обрати внимание!
Правильно считать точки, не учитывая те, что на линии.
Ответ: 38.
Источники:
Рис. 1. Примерная программа. © ЯКласс.
Рис. 2. Результат работы программы. © ЯКласс.
ЕГЭ информатика 6 задание разбор, теория, как решать.
Анализ программ с циклами, (Б) — 1 балл
Е6.10 сколько различных точек с целочисленными координатами будет находиться на линиях
Определите, сколько различных точек с целочисленными координатами будет находиться на линиях, полученных при выполнении данной программы. Черепаха выполнила следующую программу: Повтори 3 [Вперёд 7 Направо 90] Вперёд 10 Повтори 3 [Налево 90 Вперёд 6] Исполнитель Черепаха передвигается по плоскости и оставляет след в виде линии. Черепаха может выполнять три команды: Вперёд n (n – число), …
Читать далее
Е6.9 Определите, сколько точек с целочисленными положительными координатами будут
Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует две команды: Вперёд …
Читать далее
Е6.8 при котором Черепаха оставит след в виде замкнутой ломанной линии.
Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует две команды: Вперёд …
Читать далее
Е6.7 Сколько раз черепаха пройдет через начало координат?
Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует две команды: Вперёд …
Читать далее
Е6.6 Сколько существует точек с целочисленными координатами, лежащими на получившемся контуре?
Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует две команды: Вперёд …
Читать далее
Е6.5 Определите, сколько точек с целочисленными координатами будут находиться внутри области
Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует две команды: Вперёд …
Читать далее
Е6.4 Определите, из какого количества отрезков будет состоять фигура, заданная данным алгоритмом.
Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует две команды: Вперёд …
Читать далее
Е6.3 сколько точек с целочисленными координатами будут находиться внутри пересечения фигур
Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует две команды: Вперёд …
Читать далее
Е6.2 Определите периметр фигуры, построенной Черепахой после выполнения данного алгоритма.
Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует две команды: Вперёд …
Читать далее
Е6.1 Исполнитель Черепаха действует на плоскости с декартовой системой координат.
Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует две команды: Вперёд …
Читать далее
Практика: Черепаха
Введение
Данный курс будет посвящен изучению программирования с использованием языка Python. Python — это современный язык
программирования, работающий на всех распространённых операционных системах.
В настоящее время существует две версии языка Python: более старая, но пока ещё более распространённая версия 2 и
современная версия 3. Мы будем использовать версию 3 данного языка. Именно её необходимо установить дома, скачав данную
версию с сайта www.python.org.
Запустить интерпретатор python можно из командной строки:
Будьте внимательны — команда python запустит интерпретатор версии 2, с которым мы работать не будем. В системе
Windows можно использовать пункт меню «Python (command line)».
Интерактивный режим
Откройте командную строку и напишите команду python3.
Вы увидите примерно следующее приглашение командной строки:
Python 3.1.2 (r312:79147, Jun 12 2010, 15:29:06) [GCC 4.4.3 20100316 (ALT Linux 4.4.3-alt2)] on linux2 Type "help", "copyright", "credits" or "license" for more information. >>>
Вводите команды и наслаждайтесь результатом. А что можно вводить? Несколько примеров:
>>> 2 + 2 4 >>> 2 ** 100 1267650600228229401496703205376 >>> 'Hello' + 'World' 'HelloWorld' >>> 'ABC' * 10 'ABCABCABCABCABCABCABCABCABCABC'
Первая команда вычисляет сумму двух чисел, вторая команда вычисляет 2 в степени 100, третья команда выполняет операцию
конкатенации для строк, а четвертая команда печатает строку 'ABC', повторенную 10 раз.
Хотите закончить работу с питоном? Введите команду exit() (именно так, со скобочками, так как это — функция)
или нажмите Ctrl+D.
Программируемый режим
В предыдущей главе мы использовали Python для простых разовых вычислений, используя интерактивный режим.
Теперь создадим программу и выполним её целиком.
a = 179 b = 197 c = (a ** 2 + b ** 2) ** 0.5 print (c)
Здесь мы используем переменные — объекты, в которых можно сохранять различные (числовые, строковые и прочие)
значения. В первой строке переменной a присваивается значение 179, затем переменной b присваивается значение
971, затем переменной c присваивается значение арифметического выражения, равного длине гипотенузы. После этого
значение переменной c выводится на экран.
Упражнение №1: первая программа
Откройте произвольный текстовый редактор, например, gedit. Скопируйте туда текст программы, написанной выше.
Сохраните текст в файле с именем hypot.py.
Запустите терминал, перейдите в каталог, где лежит файл hypot.py и выполните эту программу:
Интерпретатор языка Python вместо интерактивного режима выполнит последовательность команд из файла.
При этом значения вычисленных выражений не выводятся на экран (в
отличии от интерактивного режима), поэтому для того, чтобы вывести результат работы программы, то есть значение
переменной c, нужна функция print().
Базовый синтаксис языка Python 3
Типы данных
Итак, мы видим, что Python умеет работать как минимум с двумя видами данных — числами и строками. Числа записываются
последовательностью цифр, также перед числом может стоять знак минус, а строки записываются в одинарных кавычках. 2
и '2' — это разные объекты, первый объект — число, а второй — строка. Операция + для целых чисел и для строк
работает по-разному: для чисел это сложение, а для строк — конкатенация.
Кроме целых чисел есть и другой класс чисел: действительные (вещественные числа), представляемые в виде десятичных
дробей. Они записываются с использованием десятичной точки, например, 2.0.
Определить тип объекта можно при помощи функции type:
>>> type(2) <class 'int'> >>> type('2') <class 'str'> >>> type(2.0) <class 'float'>
Обратите внимание — type является функцией, аргументы функции указываются в скобках после ее имени.
Операции с числами
Вот список основных операций для чисел:
A+B— сумма;A-B— разность;A*B— произведение;A/B— частное;A**B— возведение в степень.
Полезно помнить, что квадратный корень из числа x — это x**0.5, а корень степени n — это x**(1/n).
Есть также унарный вариант операции -, то есть операция с одним аргументом. Она возвращает число, противоположное
данному. Например: -A.
В выражении может встречаться много операций подряд. Как в этом случае определяется порядок действий? Например, чему
будет равно 1+2*3**1+1? В данном случае ответ будет 8, так как сначала выполняется возведение в степень, затем —
умножение, затем — сложение.
Более общие правила определения приоритетов операций такие:
- Выполняются возведения в степень справа налево, то есть
3**3**3это 3²⁷. - Выполняются унарные минусы (отрицания).
- Выполняются умножения и деления слева направо. Операции умножения и деления имеют одинаковый приоритет.
- Выполняются сложения и вычитания слева направо. Операции сложения и вычитания имеют одинаковый приоритет.
Операции над строками
A+B— конкатенация;A*n— повторение n раз, значение n должно быть целого типа.
Ветвление
Ветвление (или условная инструкция) в Python имеет следующий синтаксис:
if Условие: Блок_инструкций_1 else: Блок_инструкций_2
Блок_инструкций_1 будет выполнен, если Условие истинно. Если Условие ложно, будет выполнен Блок_инструкций_2.
В условной инструкции может отсутствовать слово else и последующий блок. Такая инструкция называется неполным
ветвлением. Например, если дано число x и мы хотим заменить его на абсолютную величину x, то это можно сделать
следующим образом:
if x < 0: x = -x print(x)
В этом примере переменной x будет присвоено значение -x, но только в том случае, когда x<0. А вот инструкция
print(x) будет выполнена всегда, независимо от проверяемого условия.
Для выделения блока инструкций, относящихся к инструкции if или else в языке Python используются отступы. Все
инструкции, которые относятся к одному блоку, должны иметь равную величину отступа, то есть одинаковое число пробелов в
начале строки. Рекомендуется использовать отступ в 4 пробела.
Вложенные условные инструкции
Внутри условных инструкций можно использовать любые инструкции языка Python, в том числе и условную инструкцию. Вложенное ветвление — после одной развилки в ходе исполнения программы появляется другая развилка. При этом вложенные блоки имеют больший размер отступа (например, 8 пробелов).
Примере программы, которая по данным ненулевым
числам x и y определяет, в какой из четвертей координатной плоскости находится точка (x,y):
x = int(input()) y = int(input()) if x > 0: if y > 0: # x>0, y>0 print("Первая четверть") else: # x>0, y<0 print("Четвертая четверть") else: if y > 0: # x<0, y>0 print("Вторая четверть") else: # x<0, y<0 print("Третья четверть")
В этом примере мы использовали комментарии – текст, который интерпретатор игнорирует. Комментариями в Pythonе
является символ # и весь текст после этого символа до конца строки.
Операторы сравнения
Как правило, в качестве проверяемого условия используется результат вычисления одного из следующих операторов сравнения:
| Оператор | Значение |
|---|---|
< |
Меньше — условие верно, если первый операнд меньше второго. |
> |
Больше — условие верно, если первый операнд больше второго. |
<= |
Меньше или равно — условие верно, если первый операнд меньше или равен второму. |
>= |
Больше или равно — условие верно, если первый операнд больше или равен второму. |
== |
Равенство. Условие верно, если два операнда равны. |
Например, условие (x * x < 1000) означает «значение x * x меньше 1000», а условие (2 * x != y) означает «удвоенное
значение переменной x не равно значению переменной y».
Операторы сравнения в можно объединять в цепочки, например, a == b == c или 1 <= x <= 10.
Тип данных bool
Операторы сравнения возвращают значения специального логического типа bool. Значения логического типа могут принимать
одно из двух значений: True (истина) или False (ложь). Если преобразовать логическое True к типу int, то
получится 1, а преобразование False даст 0. При обратном преобразовании число 0 преобразуется в False, а любое
ненулевое число в True. При преобразовании str в bool пустая строка преобразовывается в False, а любая непустая
строка в True.
Каскадные условные инструкции
Пример программы, определяющий четверть координатной плоскости, можно переписать используя «каскадную«
последовательность операцией if... elif... else:
x = int(input()) y = int(input()) if x > 0 and y > 0: print("Первая четверть") elif x > 0 and y < 0: print("Четвертая четверть") elif y > 0: print("Вторая четверть") else: print("Третья четверть")
В такой конструкции условия if, …, elif проверяются по очереди, выполняется блок, соответствующий первому из
истинных условий. Если все проверяемые условия ложны, то выполняется блок else, если он присутствует.
Цикл while
Цикл while («пока») позволяет выполнить одну и ту же последовательность действий, пока проверяемое условие истинно.
Условие записывается до тела цикла и проверяется до выполнения тела цикла. Как правило, цикл while используется, когда
невозможно определить точное значение количества проходов исполнения цикла.
Синтаксис цикла while в простейшем случае выглядит так:
while Условие: Блок_инструкций
При выполнении цикла while сначала проверяется условие. Если оно ложно, то выполнение цикла прекращается и управление
передается на следующую инструкцию после тела цикла while. Если условие истинно, то выполняется инструкция, после чего
условие проверяется снова и снова выполняется инструкция. Так продолжается до тех пор, пока условие будет истинно. Как
только условие станет ложно, работа цикла завершится и управление передастся следующей инструкции после цикла.
Например, следующий фрагмент программы напечатает на экран всех целые числа, не превосходящие n:
a = 1 while a <= n: print(a) a += 1
Общая схема цикла while в данном случае для перебора всех подходящих значений такая:
a = начальное_значение while а_является_подходящим_числом: обработать_a перейти_к_следующему_a
Выводем все степени двойки, не превосходящие числа n:
a = 1 while a <= n: print(a) a *= 2
Цикл for
Цикл for может быть использован как более краткая альтернатива циклу while.
Для последовательного перебора целых чисел из диапазона [0; n) можно использовать цикл for:
for i in range(10): print(i)
Этот код по выполняемым действиям полностью соответствуют циклу while:
i = 0 while i < 10: print(i) i += 1
Можно задавать начальные и конечные значения для переменной цикла, а также шаг:
for i in range(20, 10, -2): print(i)
Аналогичный цикл while
i = 20 while i > 10: print(i) i -= 2
Черепаха
Стандартная библиотека Python содержит модуль turtle, предназначенный для обучения программированию. Этот модуль
содержит набор функций, позволяющих управлять черепахой. Черепаха умеет выполнять небольшой набор команд, а именно:
| Команда | Значение |
|---|---|
| forward(X) | Пройти вперёд X пикселей |
| backward(X) | Пройти назад X пикселей |
| left(X) | Повернуться налево на X градусов |
| right(X) | Повернуться направо на X градусов |
| penup() | Не оставлять след при движении |
| pendown() | Оставлять след при движении |
| shape(X) | Изменить значок черепахи (“arrow”, “turtle”, “circle”, “square”, “triangle”, “classic”) |
| stamp() | Нарисовать копию черепахи в текущем месте |
| color() | Установить цвет |
| begin_fill() | Необходимо вызвать перед рисованием фигуры, которую надо закрасить |
| end_fill() | Вызвать после окончания рисования фигуры |
| width() | Установить толщину линии |
| goto(x, y) | Переместить черепашку в точку (x, y) |
Например, следующая программа рисует букву S:
import turtle turtle.shape('turtle') turtle.forward(50) turtle.left(90) turtle.forward(50) turtle.left(90) turtle.forward(50) turtle.right(90) turtle.forward(50) turtle.right(90) turtle.forward(50)
Упражнение №2: буква S
Сохраните и выполните предыдущую программу. Убедитесь в том, что черепаха работает.
Упражнение №3: квадрат
Нарисуйте квадрат. Пример:
Упражнение №4: окружность
Нарисуйте окружность. Воспользуйтесь тем фактом, что правильный многоугольник с большим числом сторон будет выглядеть
как окружность. Пример:

Упражнение №5: больше квадратов
Нарисуйте 10 вложенных квадратов.

Упражнение №6: паук
Нарисуйте паука с n лапами. Пример n = 12:

Упражнение №8: квадратная «спираль»
Нарисуйте «квадратную» спираль. Пример:

Написание функций
Как было сказано раньше, функции — это своего рода готовые кирпичики, из которых строится программа. До этого момента мы
использовали стандартные функции (print, input, функции модуля turtle), теперь настало время написать функцию:
>>> def hello(name): ... print('Hello, ', name, '!') ... >>> hello('world') Hello, world!
Это простейший пример функции, которая принимает в качестве параметра имя, а затем выводит на экран сообщение
Hello, <имя>. Как видно из примера, функции в языке Python описываются при помощи ключевого слова def:
def Имя_функции(параметр_1, параметр_2, ...): Блок_операций
Так же, как и в случае циклов и условных операторов, тело функции выделяется при помощи отступов.
Вызов функции осуществляется по имени с указанием параметров:
Внутри функции можно использовать те же синтаксические конструкции, что и вне её — циклы, ветвления, можно даже
описывать новые функции. Естественно, внутри функции можно работать и с переменными.
Написанная ранее функция имеет особенность — она просто просто выводит текст на экран и не возвращает никакого
результата. Многие функции, напротив, занимаются вычислением какого-либо значения, а затем возвращают его тому, кто
эту функцию вызвал. В качестве примера можно рассмотреть функцию для сложения двух чисел:
>>> def sum(a, b): ... return a + b ... >>> sum(1, 2) 3 >>> sum(5, -7) -2
Для возврата значения из функции используется оператор return: в качестве параметра указывается значение, которое
требуется вернуть.
Упражнение №9: правильные многоугольники
Нарисуйте 10 вложенных правильных многоугольников. Используйте функцию, рисующую правильный n-угольник. Формулы для
нахождения радиуса описанной окружности. Пример:

Упражнение №10: «цветок»
Нарисуйте «цветок» из окружностей. Используйте функцию, рисующую окружность. Пример:

Упражнение №11: «бабочка»
Нарисуйте «бабочку» из окружностей. Используйте функцию, рисующую окружность. Пример:

Упражнение №12: пружина
Нарисуйте пружину. Используйте функцию, рисующую дугу. Пример:

Упражнение №13: смайлик
Нарисуйте смайлик с помощью написанных функций рисования круга и дуги. Пример:

Упражнение №14: звезды
Нарисуйте две звезды: одну с 5 вершинами, другую — с 11. Используйте функцию, рисующую звезду с n вершинами. Пример:

Красивый код на Python
Важная мысль создателя языка Python, Гвидо ван Россума: код читается намного больше раз, чем пишется.
Поэтому существуют рекомендации о стиле кодирования PEP8. Они направлены на то, чтобы улучшить читаемость и сделать его согласованным между большим числом проектов. В идеале, весь код будет написан в едином стиле, и любой сможет легко его прочесть.
На русском можно прочитать про PEP8 тут, на английском — здесь.
Условие задачи:
Исполнитель Черепаха действует на плоскости с
декартовой системой координат. В начальный момент Черепаха находится в начале
координат, её голова направлена вдоль положительного направления оси ординат,
хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде
линии. В каждый конкретный момент известно положение исполнителя и направление
его движения. У исполнителя существует две команды: Вперёд n (где
n – целое число), вызывающая передвижение Черепахи на n единиц в том
направлении, куда указывает её голова, и Направо m (где m –
целое число), вызывающая изменение направления движения на m градусов по
часовой стрелке.
Запись Повтори k [Команда1 Команда2 …
КомандаS] означает, что последовательность из S команд
повторится k раз.
Черепахе был дан для исполнения следующий алгоритм:
Повтори
7 [Вперёд 10 Направо 120].
Определите, сколько точек с целочисленными
координатами будут находиться внутри области, ограниченной линией, заданной
данным алгоритмом. Точки на линии учитывать не следует.
Решение: С
этого сайта https://www.niisi.ru/kumir/dl.htm скачиваем
программу Загрузить версию 2.1.0
(rc11)
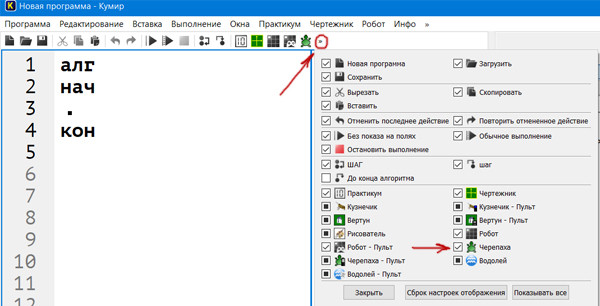
Запускаем
Кумир-Стандарт Пишем алгоритм:
использовать Черепаха
алг нач
. опустить хвост
. нц
7 раз
. .
вперед (10)
. .
вправо (120)
. кц
кон
Появляется
вот такой значок:

Нажимаем
на черепашку и появляется клетчатое поле:

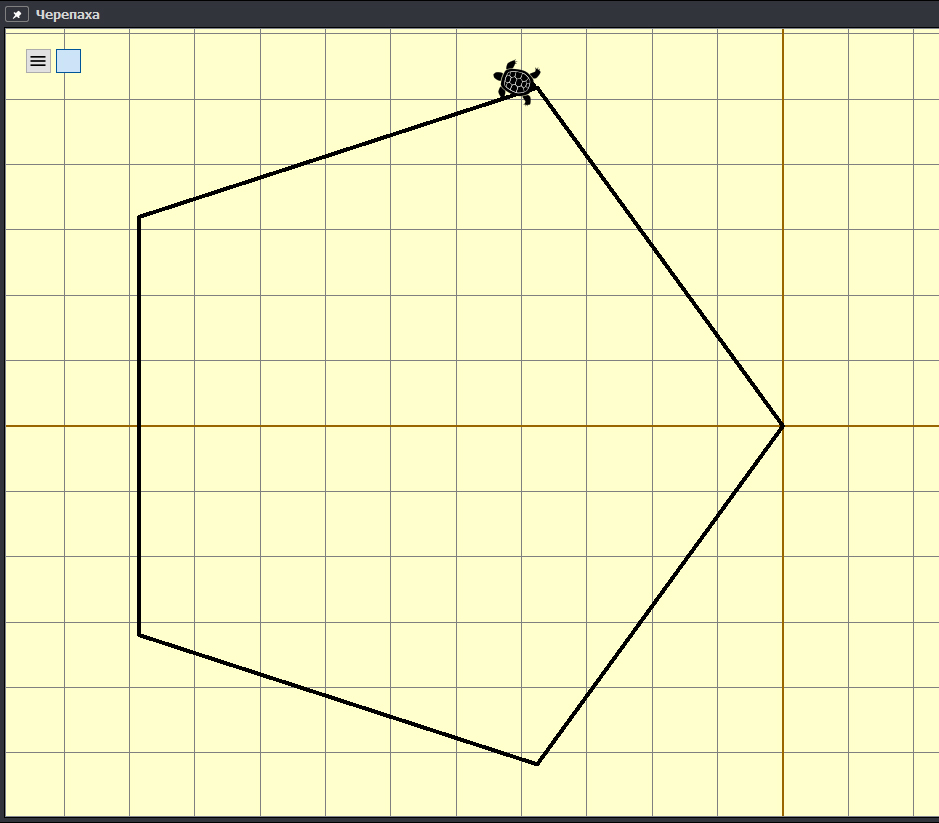
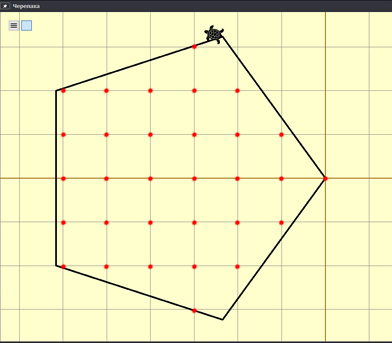
Далее
нажимаем выполнение. И черепашка нарисует треугольник.
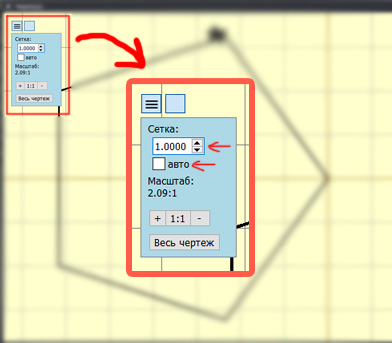
Обязательно
нужно настроить поле. Для этого нажимаем значок 

Убираем
галочку с авто и значение ставим 1.0000 (как на рисунке выше) и нажимаем кнопку
«Весь чертеж».
После
этого подсчитываем количество точек внутри треугольника.