600 ppi что это егэ - Помощь в подготовке к экзаменам и поступлению

Урок посвящен разбору задания 7 ЕГЭ по информатике

Содержание:

Объяснение заданий 7 ЕГЭ по информатике
- Кодирование текстовой информации
- Кодирование графической информации
- Кодирование звуковой информации
- Определение скорости передачи информации
Решение заданий 7 ЕГЭ по информатике
- Тема: Кодирование изображений
- Тема: Кодирование звука
- Тема: Кодирование видео
- Тема: Скорость передачи данных

7-е задание: «Кодирование графической и звуковой информации, объем и передача информации»

Уровень сложности

— базовый,

Требуется использование специализированного программного обеспечения

— нет,

Максимальный балл

— 1,

Примерное время выполнения

— 5 минут.

Проверяемые элементы содержания: Умение определять объём памяти, необходимый для хранения графической и звуковой информации

До ЕГЭ 2021 года — это было задание № 9 ЕГЭ

Типичные ошибки и рекомендации по их предотвращению:

«Если вычисления получаются слишком громоздкими, значит, Вы неправильно решаете задачу. Удобно выделить во всех множителях степени двойки, тогда умножение сведётся к сложению
показателей степеней, а деление – к вычитанию»

ФГБНУ «Федеральный институт педагогических измерений»

Кодирование текстовой информации

I = n * i

где:

n — количество символов

i — количество бит на 1 символ (кодировка)

Кодирование графической информации

Рассмотрим некоторые понятия и формулы, необходимые для решения ЕГЭ по информатике данной темы.

Пиксель – это наименьший элемент растрового изображения, который имеет определенный цвет.
Разрешение – это количество пикселей на дюйм размера изображения.
Глубина цвета — это количество битов, необходимое для кодирования цвета пикселя.
Если глубина кодирования составляет i битов на пиксель, код каждого пикселя выбирается из 2ⁱ возможных вариантов, поэтому можно использовать не более 2ⁱ различных цветов.

Формула для нахождения количества цветов в используемой палитре:

i = log₂N

N — количество цветов
i — глубина цвета
В цветовой модели RGB (красный (R), зеленый (G), синий (B)): R (0..255) G (0..255) B (0..255) -> получаем 2⁸ вариантов на каждый из трех цветов.
R G B: 24 бита = 3 байта — режим True Color (истинный цвет)

Найдем формулу объема памяти для хранения растрового изображения:

I = M * N * i

где:

I — объем памяти, требуемый для хранения изображения
M — ширина изображения в пикселях
N — высота изображения в пикселях
i — глубина кодирования цвета или разрешение

Или можно формулу записать так:

I = N * i битов

где N – количество пикселей (M * N) и i – глубина кодирования цвета (разрядность кодирования)

* для указания объема выделенной памяти встречаются разные обозначения (V или I).

Следует также помнить формулы преобразования:

1 Мбайт = 2²⁰ байт = 2²³ бит,
1 Кбайт = 2¹⁰ байт = 2¹³ бит

Кодирование звуковой информации

Познакомимся с понятиями и формулами, необходимыми для решения заданий 7 ЕГЭ по информатике.

Оцифровка или дискретизация – это преобразование аналогового сигнала в цифровой код.

Дискретизация, объяснение задания 7 ЕГЭ

T – интервал дискретизации (измеряется в с)
ƒ — частота дискретизации (измеряется в Гц, кГц)

* Изображение взято из презентации К. Полякова

Частота дискретизации определяет количество отсчетов, т.е. отдельных значений сигнала, запоминаемых за 1 секунду. Измеряется в герцах, 1 Гц (один герц) – это один отсчет в секунду, а, например, 7 кГц – это 7000 отсчетов в секунду.
Разрядность кодирования (глубина, разрешение) — это число битов, используемое для хранения одного отсчёта.

Разрядность кодирования

* Изображение взято из презентации К. Полякова

Получим формулу объема звукового файла:

Для хранения информации о звуке длительностью t секунд, закодированном с частотой дискретизации ƒ Гц и глубиной кодирования β бит требуется бит памяти:

I = β * ƒ * t * S

I — объем
β — глубина кодирования
ƒ — частота дискретизации
t — время
S — количество каналов

S для моно = 1, для стерео = 2, для квадро = 4

Пример: при ƒ=8 кГц, глубине кодирования 16 бит на отсчёт и длительности звука 128 с. потребуется:

✍ Решение:

I = 8000*16*128 = 16384000 бит
I = 8000*16*128/8 = 2³ * 1000 * 2⁴ * 2⁷ / 2³ = 2¹⁴ / 2³ =2¹¹ =
= 2048000 байт

Определение скорости передачи информации

Канал связи всегда имеет ограниченную пропускную способность (скорость передачи информации), которая зависит от свойств аппаратуры и самой линии связи(кабеля)

Объем переданной информации I вычисляется по формуле:

I = V * t

I — объем информации
v — пропускная способность канала связи (измеряется в битах в секунду или подобных единицах)
t — время передачи

* Вместо обозначения скорости V иногда используется q
* Вместо обозначения объема сообщения I иногда используется Q

Скорость передачи данных определяется по формуле:

V = I/t

и измеряется в бит/с

Егифка ©:

Решение заданий 7 ЕГЭ по информатике

Плейлист видеоразборов задания на YouTube:
Задание демонстрационного варианта 2022 года ФИПИ

Тема: Кодирование изображений

7_1:

Какой минимальный объем памяти (в Кбайт) нужно зарезервировать, чтобы можно было сохранить любое растровое изображение размером 160 х 160 пикселей при условии, что в изображении могут использоваться 256 различных цветов? В ответе запишите только целое число, единицу измерения писать не нужно.

Типовые задания для тренировки

✍ Решение:

Используем формулу нахождения объема:
Подсчитаем каждый сомножитель в формуле, стараясь привести числа к степеням двойки:
M x N:

160 * 160 = 20 * 2³ *  20 * 2³ = 400 * 2⁶ = 
= 25 * 2⁴ * 2⁶

Нахождение глубины кодирования i:

256 = 2⁸ 
т.е. 8 бит на пиксель  (из формулы кол-во цветов = 2ⁱ)

Находим объем:

I = 25 * 2⁴ * 2⁶ * 2³ = 25 * 2¹³ - всего бит на всё изображение

Переводим в Кбайты:

(25 * 2¹³) / 2¹³ = 25 Кбайт

Результат: 25

Детальный разбор задания 7 ЕГЭ по информатике предлагаем посмотреть в видео:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

Тема: Кодирование изображений:

ЕГЭ по информатике задание 7.2:

Рисунок размером 128 на 256 пикселей занимает в памяти 24 Кбайт (без учёта сжатия). Найдите максимально возможное количество цветов в палитре изображения.

Типовые задания для тренировки

✍ Решение:

По формуле объема файла изображения имеем:
где M * N — общее количество пикселей. Найдем это значение, используя для удобства степени двойки:

128 * 256 = 2⁷ * 2⁸ = 2¹⁵

В вышеуказанной формуле i — это глубина цвета, от которой зависит количество цветов в палитре:
Найдем i из той же формулы:

i = I / (M*N)

Учтем, что 24 Кбайт необходимо перевести в биты. Получим:

2³ * 3 * 2¹⁰ * 2³:
i = (2³ * 3 * 2¹⁰ * 2³) / 2¹⁵ = 
= 3 * 2¹⁶ / 2¹⁵ = 6 бит

Теперь найдем количество цветов в палитре:

2⁶ = 64 вариантов цветов в цветовой палитре

Результат: 64

Смотрите видеоразбор задания:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

Тема: Кодирование изображений:

ЕГЭ по информатике задание 7.3:

После преобразования растрового 256-цветного графического файла в 4-цветный формат его размер уменьшился на 18 Кбайт. Каков был размер исходного файла в Кбайтах?

Типовые задания для тренировки

✍ Решение:

По формуле объема файла изображения имеем:

где N — общее количество пикселей,
а i — глубина кодирования цвета (количество бит, выделенное на 1 пиксель)

i можно найти, зная количество цветов в палитре:

до преобразования: i = 8 (2⁸ = 256)
после преобразования: i = 2 (2² = 4)

Составим систему уравнений на основе имеющихся сведений, примем за x количество пикселей (разрешение):

I = x * 8
I - 18 = x * 2

Выразим x в первом уравнении:

x = I / 8

Подставим во второе уравнение и найдем I (объем файла):

I - 18 = I / 4
4I - I = 72
3I = 72
I = 24

Результат: 24

Подробный разбор 7 задания ЕГЭ смотрите на видео:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

Тема: Кодирование изображений:

ЕГЭ по информатике задание 7.4:

Цветное изображение было оцифровано и сохранено в виде файла без использования сжатия данных. Размер полученного файла – 42 Мбайт. Затем то же изображение было оцифровано повторно с разрешением в 2 раза меньше и глубиной кодирования цвета увеличили в 4 раза больше по сравнению с первоначальными параметрами. Сжатие данных не производилось. Укажите размер файла в Мбайт, полученного при повторной оцифровке.

Типовые задания для тренировки

✍ Решение:

По формуле объема файла изображения имеем:

где N — общее количество пикселей или разрешение,
а i — глубина цвета (количество бит, выделенное на 1 пиксель)

В такого рода задачах необходимо учесть, что уменьшение разрешения в 2 раза, подразумевает уменьшение в 2 раза пикселей отдельно по ширине и по высоте. Т.е. в целом N уменьшается в 4 раза!
Составим систему уравнений на основе имеющихся сведений, в которой первое уравнение будет соответствовать данным до преобразования файла, а второе уравнение — после:

42 = N * i
I = N / 4 * 4i

Выразим i в первом уравнении:

i = 42 / N

Подставим во второе уравнение и найдем I (объем файла):

[ I= frac {N}{4} * 4* frac {42}{N} ]

После сокращений получим:

I = 42

Результат: 42

Тема: Кодирование изображений:

ЕГЭ по информатике задание 7.5:

Изображение было оцифровано и сохранено в виде растрового файла. Получившийся файл был передан в город А по каналу связи за 72 секунды. Затем то же изображение было оцифровано повторно с разрешением в 2 раза больше и глубиной кодирования цвета в 3 раза меньше, чем в первый раз. Сжатие данных не производилось. Полученный файл был передан в город Б, пропускная способность канала связи с городом Б в 3 раза выше, чем канала связи с городом А.
Сколько секунд длилась передача файла в город Б?

Типовые задания для тренировки

✍ Решение:

По формуле скорости передачи файла имеем:

где I — объем файла, а t — время

По формуле объема файла изображения имеем:

где N — общее количество пикселей или разрешение,
а i — глубина цвета (количество бит, выделенное на 1 пиксель)

Для данной задачи, необходимо уточнить, что разрешение на самом деле имеет два сомножителя (пикселей по ширине * пикселей по высоте). Поэтому при увеличении разрешения в два раза, увеличатся оба числа, т.е. N увеличится в 4 раза вместо двух.
Изменим формулу получения объема файла для города Б:

[ I= frac {2*N * i}{3} ]

Для города А и Б заменим значения объема в формуле для получения скорости:

Город А:

[ V= frac {N*i}{72} ]

Город Б:

[ 3*V= frac{frac {4*N*i}{3}}{t} ]

или:

[ t*3*V= frac {4*N*i}{3} ]

Подставим значение скорости из формулы для города А в формулу для города Б:

[ frac {t*3*N*i}{72}= frac {4*N*i}{3} ]

Выразим t:

t = 4 * 72 / (3 * 3) = 32 секунды

Результат: 32

Другой способ решения смотрите в видеоуроке:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

Тема: Кодирование изображений:

ЕГЭ по информатике задание 7.6:

Камера делает фотоснимки размером 1024 х 768 пикселей. На хранение одного кадра отводится 900 Кбайт.
Найдите максимально возможное количество цветов в палитре изображения.

Типовые задания для терировки

✍ Решение:

Количество цветов зависит от глубины кодирования цвета, которая измеряется в битах. Для хранения кадра, т.е. общего количества пикселей выделено 900 Кбайт. Переведем в биты:

900 Кбайт = 2² * 225 * 2¹⁰ * 2³ = 225 * 2¹⁵

Посчитаем общее количество пикселей (из заданного размера):

1024 * 768 = 2¹⁰ * 3 * 2⁸

Определим объем памяти, необходимый для хранения не общего количества пикселей, а одного пикселя ([память для кадра]/[кол-во пикселей]):

[ frac {225 * 2^{15}}{3 * 2^{18}} = frac {75}{8} approx 9 ]

9 бит на 1 пиксель

9 бит — это i — глубина кодирования цвета. Количество цветов = 2ⁱ:

2⁹ = 512

Результат: 512

Смотрите подробное решение на видео:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

Тема: Кодирование изображений:

7_8: Демоверсия ЕГЭ 2018 информатика:

Автоматическая фотокамера производит растровые изображения размером 640×480 пикселей. При этом объём файла с изображением не может превышать 320 Кбайт, упаковка данных не производится.
Какое максимальное количество цветов можно использовать в палитре?

✍ Решение:

По формуле объема файла изображения имеем:

I = N * i

где N — общее количество пикселей или разрешение, а i — глубина кодирования цвета (количество бит, выделенное на 1 пиксель)

Посмотрим, что из формулы нам уже дано:

I = 320 Кбайт, 
N = 640 * 420 = 307200 = 75 * 2¹² всего пикселей, 
i - ?

Количество цветов в изображении зависит от параметра i, который неизвестен. Вспомним формулу:

количество цветов = 2ⁱ

Поскольку глубина цвета измеряется в битах, то необходимо объем перевести из Килобайт в биты:

320 Кбайт = 320 * 2¹⁰ * 2³ бит  = 320 * 2¹³ бит

Найдем i:

[ i = frac {I}{N} = frac {320 * 2^{13}}{75 * 2^{12}} approx 8,5 бит ]

Найдем количество цветов:

2ⁱ = 2⁸ = 256

Результат: 256

Подробное решение данного 7 (9) задания из демоверсии ЕГЭ 2018 года смотрите на видео:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

7_21: : ЕГЭ по информатике задание 7.21:

Для хранения в информационной системе документы сканируются с разрешением 300 ppi. Методы сжатия изображений не используются. Средний размер отсканированного документа составляет 5 Мбайт. В целях экономии было решено перейти на разрешение 150 ppi и цветовую систему, содержащую 16 цветов. Средний размер документа, отсканированного с изменёнными параметрами, составляет 512 Кбайт.

Определите количество цветов в палитре до оптимизации.

Типовые задания для тренировки

✍ Решение:

По формуле объема файла изображения имеем:

I = N * i

где N — общее количество пикселей или разрешение, а i — глубина кодирования цвета (количество бит, выделенное на 1 пиксель).

Так как по заданию имеем разрешение, выраженное в пикселях на дюйм, то фактически это означает:

I = значение ppi² * N * i

Формула количества цветов:

количество цветов = 2ⁱ

Посмотрим, что из формулы нам уже дано до экономного варианта и при экономном варианте:

Неэкономный вариант:
I = 5 Мбайт = 5 * 2²³ бит, 
N - ?, 
i - ?
300 ppi

Экономный вариант:
I = 512 Кбайт = 2⁹ * 2¹³ бит = 2²² бит, 
N - ?, 
i = 4 бит (2⁴ = 16)
150 ppi

Так как в экономном режиме нам известны все составляющие формулы, кроме разрешения (N), то найдем разрешение:

N = I / (i * 150*150 ppi)
N = 2²² / (4 * 22500)

Подставим все известные значения, включая найденное N, в формулу для неэкономного режима:

I = N * 300*300 ppi * i
5 * 2²³ = (2²² * 300 * 300 * i) / (22500 * 4);

Выразим i и вычислим его значение:

i = (5 * 2²³ * 22500 * 4) / (2²² * 300 * 300) = 9000 / 900 = 10 бит

По формуле нахождения количества цветов в палитре имеем:

2¹⁰ = 1024

Результат: 1024

Тема: Кодирование звука

7_7:

На студии при четырехканальной (квадро) звукозаписи с 32-битным разрешением за 30 секунд был записан звуковой файл. Сжатие данных не производилось. Известно, что размер файла оказался 7500 Кбайт.

С какой частотой дискретизации (в кГц) велась запись? В качестве ответа укажите только число, единицы измерения указывать не нужно.

Типовые задания для тренировки

✍ Решение:

По формуле объема звукового файла получим:

I = β * t * ƒ * S

Из задания имеем:

I= 7500 Кбайт
β= 32 бита
t= 30 секунд
S= 4 канала

ƒ — частота дискретизации — неизвестна, выразим ее из формулы:

[ ƒ = frac {I}{S*B*t} = frac {7500 * 2^{10} * 2^3 бит}{2^7 * 30}Гц = frac { 750 * 2^6}{1000}КГц = 2^4 = 16 ]

2⁴ = 16 КГц

Результат: 16

Для более детального разбора предлагаем посмотреть видео решения данного 7 задания ЕГЭ по информатике:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

Тема: Кодирование звука:

ЕГЭ по информатике задание 7_9:

Музыкальный фрагмент был оцифрован и записан в виде файла без использования сжатия данных. Получившийся файл был передан в город А по каналу связи. Затем тот же музыкальный фрагмент был оцифрован повторно с разрешением в 2 раза выше и частотой дискретизации в 3 раза меньше, чем в первый раз. Сжатие данных не производилось. Полученный файл был передан в город Б за 15 секунд; пропускная способность канала связи с городом Б в 4 раза выше, чем канала связи с городом А.

Сколько секунд длилась передача файла в город A? В ответе запишите только целое число, единицу измерения писать не нужно.

Типовые задания для тренировки

✍ Решение:

Для решения понадобится формула нахождения скорости передачи данных формулы:

V = I/t

Вспомним также формулу объема звукового файла:

I = β * ƒ * t * s

где:
I — объем
β — глубина кодирования
ƒ — частота дискретизации
t — время
S — кол-во каналов (если не указывается, то моно)

Выпишем отдельно, все данные, касающиеся города Б (про А практически ничего не известно):

город Б: 
β - в 2 раза выше
ƒ - в 3 раза меньше
t - 15 секунд, 
пропускная способность (скорость V) - в 4 раза выше

Исходя из предыдущего пункта, для города А получаем обратные значения:

город А: 
β_Б / 2
ƒ_Б * 3
I_Б / 2
V_Б / 4
t_Б / 2, t_Б * 3, t_Б * 4  -  ?

Дадим объяснения полученным данным:
так как глубина кодирования (β) для города Б выше в 2 раза, то для города А она будет ниже в 2 раза, соответственно, и t уменьшится в 2 раза:

t = t/2

так как частота дискретизации (ƒ) для города Б меньше в 3 раза, то для города А она будет выше в 3 раза; I и t изменяются пропорционально, значит, при увеличении частоты дискретизации увеличится не только объем, но и время:

t = t * 3

скорость (V)(пропускная способность) для города Б выше в 4 раза, значит, для города А она будет ниже в 4 раза; раз скорость ниже, то время выше в 4 раза (t и V — обратно пропорциональная зависимость из формулы V = I/t):

t = t * 4

Таким образом, с учетом всех показателей, время для города А меняется так:

[ t_А = frac {15}{2} * 3 * 4 ]

90 секунд

Результат: 90

Подробное решение смотрите на видео:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

Тема: Кодирование звука:

ЕГЭ по информатике задание 7.10:

Музыкальный фрагмент был записан в формате стерео (двухканальная запись), оцифрован и сохранён в виде файла без использования сжатия данных. Размер полученного файла – 30 Мбайт. Затем тот же музыкальный фрагмент был записан повторно в формате моно и оцифрован с разрешением в 2 раза выше и частотой дискретизации в 1,5 раза меньше, чем в первый раз. Сжатие данных не производилось.

Укажите размер файла в Мбайт, полученного при повторной записи. В ответе запишите только целое число, единицу измерения писать не нужно.

Типовые задания для тренировки

✍ Решение:

Вспомним формулу объема звукового файла:

I = β * ƒ * t * S

I — объем
β — глубина кодирования
ƒ — частота дискретизации
t — время
S -количество каналов

Выпишем отдельно, все данные, касающиеся первого состояния файла, затем второго состояния — после преобразования:

1 состояние:
S = 2 канала
I = 30 Мбайт

2 состояние:
S = 1 канал
β = в 2 раза выше
ƒ = в 1,5 раза ниже
I = ?

Так как изначально было 2 канала связи (S), а стал использоваться один канал связи, то файл уменьшился в 2 раза:

I = I / 2

Глубина кодирования (β) увеличилась в 2 раза, то и объем (I) увеличится в 2 раза (пропорциональная зависимость):

I = I * 2

Частота дискретизации (ƒ) уменьшилась в 1,5 раза, значит, объем (I) тоже уменьшится в 1,5 раза:

I = I / 1,5

Рассмотрим все изменения объема преобразованного файла:

I = 30 Мбайт / 2 * 2 / 1,5 = 20 Мбайт

Результат: 20

Смотрите видеоразбор данной задачи:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

Тема: Кодирование звуковых файлов:

ЕГЭ по информатике задание 7_11:

Музыкальный фрагмент был оцифрован и записан в виде файла без использования сжатия данных. Получившийся файл был передан в город А по каналу связи за 100 секунд. Затем тот же музыкальный фрагмент был оцифрован повторно с разрешением в 3 раза выше и частотой дискретизации в 4 раз меньше, чем в первый раз. Сжатие данных не производилось. Полученный файл был передан в город Б за 15 секунд.

✍ Решение:

Вспомним формулу объема звукового файла:

I = β * ƒ * t * S

I — объем
β — глубина кодирования
ƒ — частота дискретизации
t — время

Выпишем отдельно, все данные, касающиеся файла, переданного в город А, затем преобразованного файла, переданного в город Б:

А:
t = 100 c.

Б:
β = в 3 раза выше
ƒ = в 4 раза ниже
t = 15 c.

✎ 1 способ решения:

Скорость передачи данных (пропускная способность) зависит от времени передачи файла: чем больше время, тем ниже скорость. Т.е. во сколько раз увеличится время передачи, во столько раз уменьшится скорость и наоборот.
Из предыдущего пункта видим, что если мы вычислим, во сколько раз уменьшится или увеличится время передачи файла в город Б (по сравнению с городом А), то мы поймем, во сколько раз увеличится или уменьшится скорость передачи данных в город Б (обратная зависимость).
Соответственно, представим, что преобразованный файл передается в город А. Объем файла изменился в 3/4 раза (глубина кодирования (β) в 3 раза выше, частота дискретизации (ƒ) в 4 раза ниже). Объем и время изменяются пропорционально. Значит и время изменится в 3/4 раза:

 t_{A для преобразов.} = 100 секунд * 3 / 4 = 75 секунд

Т.е. преобразованный файл передавался бы в город А 75 секунд, а в город Б 15 секунд. Вычислим, во сколько раз снизилось время передачи:

75 / 15 = 5

Раз время передачи в город Б снизилось в 5 раз, соответственно, скорость увеличилась в 5 раз.

Ответ: 5

✎ 2 способ решения:

Выпишем отдельно все данные, касающиеся файла, переданного в город А:
```
А:
t_А = 100 c.
V_А = I / 100
```
Поскольку увеличение или уменьшение во сколько-то раз разрешения и частоты дискретизации приводит к соответствующему увеличению или уменьшению объема файла (пропорциональная зависимость), то запишем известные данные для преобразованного файла, переданного в город Б:

Б:
β = в 3 раза выше
ƒ = в 4 раза ниже
t = 15 c.
I_Б = (3 / 4) * I
V_Б = ((3 / 4) * I) / 15

Теперь найдем соотношение V_Б к V_А:

[ frac {V_Б}{V_А} = frac {3/_4 * I}{15} * frac {100}{I} = frac {3/_4 * 100}{15} = frac {15}{3} = 5 ]

(((3/4) * I) / 15) * (100 / I)= (3/4 * 100) / 15 = 15/3 = 5

Результат: 5

Подробный видеоразбор задания:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

Тема: Кодирование звука:

ЕГЭ по информатике задание 7_12:

Производится четырёхканальная (квадро) звукозапись с частотой дискретизации 32 кГц и 32-битным разрешением. Запись длится 2 минуты, её результаты записываются в файл, сжатие данных не производится.

Определите приблизительно размер полученного файла (в Мбайт). В качестве ответа укажите ближайшее к размеру файла целое число, кратное 10.

✍ Решение:

Вспомним формулу объема звукового файла:

I — объем
β — глубина кодирования
ƒ — частота дискретизации
t — время
S — количество каналов

Для простоты расчетов пока не будем брать во внимание количество каналов. Рассмотрим, какие данные у нас есть, и какие из них необходимо перевести в другие единицы измерения:

β = 32 бита
ƒ = 32кГц = 32000Гц
t = 2 мин = 120 с

Подставим данные в формулу; учтем, что результат необходимо получить в Мбайтах, соответственно, произведение будем делить на 2²³ (2³ (байт) * 2¹⁰ (Кбайт) * 2¹⁰(Мбайт)):

(32 * 32000 * 120) / 2²³ = 
=( 2⁵ * 2⁷ * 250 * 120) / 2²³ = 
= (250*120) / 2¹¹ = 
= 30000 / 2¹¹ = 
= (2⁴ * 1875) / 2¹¹ =
= 1875 / 128 ~ 14,6

Полученный результат значения объема умножим на 4 с учетом количества каналов связи:

 14,6 * 4 = 58,5

Ближайшее число, кратное 10 — это 60.

Результат: 60

Смотрите подробное решение:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

Тема: Кодирование звука:

7_19: Государственный выпускной экзамен ГВЭ 2018 (информатика ГВЭ ФИПИ, задание 7):

Производится двухканальная (стерео) цифровая звукозапись. Значение сигнала фиксируется 48 000 раз в секунду, для записи каждого значения используется 32 бит. Запись длится 5 минут, её результаты записываются в файл, сжатие данных не производится.

Какая из приведённых ниже величин наиболее близка к размеру полученного файла?

1) 14 Мбайт
2) 28 Мбайт
3) 55 Мбайт
4) 110 Мбайт

✍ Решение:

По формуле объема звукового файла имеем:

I — объем
β — глубина кодирования = 32 бита
ƒ — частота дискретизации = 48000 Гц
t — время = 5 мин = 300 с
S — количество каналов = 2

Подставим в формулу имеющиеся значения:

I = 48000 * 32 * 300 * 2

Поскольку значения большие, необходимо числа 48000 и 300 выразить в степенях двойки:

48000 | 2
24000 | 2
12000 | 2
 6000 | 2     = 375 * 2⁷
 3000 | 2
 1500 | 2
  750 | 2 
  375 | 2 - уже не делится
 187,5

300 | 2     = 75 * 2²
150 | 2
 75 | 2 - уже не делится 
37,5

Получим:

I = 375 * 75 * 2¹⁵

В предложенных вариантах ответа видим, что результат везде в Мбайт. Значит, необходимо разделить полученный нами результат на 2²³ (2³ * 2¹⁰ * 2¹⁰):

I = 375 * 75 * 2¹⁵ / 2²³ = 28125 / 2⁸

Найдем приближенное к числу 28125 значение в степени двойки:

Получаем:

2¹⁰ * 2⁵ = 2¹⁵ = 32768
2¹⁰ * 2⁴ = 2¹⁴ = 16384

Число 28125 лежит между этими значениями, значит берем их:

2¹⁵ / 2⁸ = 2⁷ = 128
2¹⁴ / 2⁸ = 2⁶ = 64

Выбираем ответ, значение в котором находится между двумя этими числами: вариант 4 (110 Мбайт)

Результат: 4

Подробное решение ГВЭ задания 7 2018 года смотрите на видео:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

Тема: Кодирование звука:

7_20:

Производится двухканальная (стерео) звукозапись с частотой дискретизации 4 кГц и 64-битным разрешением. Запись длится 1 минуту, ее результаты записываются в файл, сжатие данных не производится.

Определите приблизительно размер получившегося файла (в Мбайтах). В качестве ответа укажите ближайшее к размеру файла целое число, кратное 2.

✍ Решение:

По формуле объема звукового файла имеем:

I — объем
β — глубина кодирования = 32 бита
ƒ — частота дискретизации = 48000 Гц
t — время = 5 мин = 300 с
S — количество каналов = 2

Подставим в формулу имеющиеся значения. Для удобства будем использовать степени двойки:

ƒ = 4 кГЦ = 4 * 1000 Гц ~ 2² * 2¹⁰
B = 64 бит = 2⁶ / 2²³ Мбайт
t = 1 мин = 60 c = 15 * 2² c
S = 2

Подставим значения в формулу объема звукового файла:

I = 2⁶ * 2² * 2¹⁰ * 15 * 2² * 2¹ / 2²³ = 15/4 ~ 3,75

Ближайшее целое, кратное двум — это число 4

Результат: 4

Видеоразбор задания:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

Тема: Кодирование видео

7_22:

Камера снимает видео без звука с частотой 120 кадров в секунду, при этом изображения используют палитру, содержащую 2²⁴ = 16 777 216 цветов. При записи файла на сервер полученное видео преобразуют так, что частота кадров уменьшается до 20, а изображения преобразуют в формат, использующий палитру из 256 цветов. Другие преобразования и иные методы сжатия не используются. 10 секунд преобразованного видео в среднем занимают 512 Кбайт.

Сколько Мбайт в среднем занимает 1 минута исходного видео?

Типовые задания для тренировки

✍ Решение:

Посмотрим, как изменялись параметры файла до преобразования и после:

ДО:
ƒ = 120, 
i = 24 бит

ПОСЛЕ:
ƒ = 20, 
i = 8 бит (2⁸ = 256)
t = 10 секунд
I = 512 Кбайт = 2⁹ Кбайт

Поскольку после преобразования количество кадров в секунду уменьшилось в 6 раз (120 / 20 = 6), а количество бит на пиксель уменьшилось в 3 раза (24 / 8 = 3), то и объем уменьшился в целом в 18 раз (6 * 3 = 18).
Вычислим объем файла, передаваемого за 10 секунд, до его преобразования:

за 10 секунд: I * 18 = 2⁹ * 18 Кбайт = (2⁹ * 18) . 2¹⁰ Мбайт = 9 Мбайт

Чтобы получить объем, переданный за 1 минуту, необходимо полученное значение умножить на 6:

за 1 мин: 9 * 6 = 54 Мбайт

Результат: 54

Тема: Скорость передачи данных

ЕГЭ по информатике задание 7_13:

Скорость передачи данных через ADSL-соединение равна 128000 бит/с. Передача текстового файла через это соединение заняла 1 минуту.

Определите, сколько символов содержал переданный текст, если известно, что он был представлен в 16-битной кодировке Unicode.

Типовые задания для тренировки

✍ Решение:

Вспомним формулу скорости передачи данных:

* Вместо Q можно использовать обозначение I (для объема файла)

V - скорость
Q - объем
t - время

Что нам известно из формулы (для удобства решения будем использовать степени двойки):

V = 128000 бит/с = 2¹⁰ * 125 бит/с
t = 1 мин = 60 с = 2² * 15 с
1 символ кодируется 16-ю битами
всего символов - ?

Если мы найдем, сколько бит необходимо для всего текста, тогда, зная что на 1 символ приходится 16 бит, мы сможем найти сколько всего символов в тексте. Таким образом, найдем объем:

Q = 2¹⁰ * 125 * 2² * 15 = 
= 2¹² * 1875 бит на все символы

Когда мы знаем, что на 1 символ необходимо 16 бит, а на все символы 2¹² * 1875 бит, то можем найти общее количество символов:

кол-во символов = 2¹² * 1875 / 16 = 2¹² * 1875 / 2⁴ = 
= 2⁸ * 1875 = 480000

Результат: 480000

Разбор 7 задания:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

Тема: Скорость передачи информации:

ЕГЭ по информатике задание 7_14:

У Васи есть доступ к Интернет по высокоскоростному одностороннему радиоканалу, обеспечивающему скорость получения им информации 2¹⁷ бит в секунду. У Пети нет скоростного доступа в Интернет, но есть возможность получать информацию от Васи по низкоскоростному телефонному каналу со средней скоростью 2¹⁶ бит в секунду. Петя договорился с Васей, что тот будет скачивать для него данные объемом 8 Мбайт по высокоскоростному каналу и ретранслировать их Пете по низкоскоростному каналу. Компьютер Васи может начать ретрансляцию данных не раньше, чем им будут получены первые 1024 Кбайт этих данных.

Каков минимально возможный промежуток времени (в секундах), с момента начала скачивания Васей данных, до полного их получения Петей?

Типовые задания для тренировки

✍ Решение:

Вспомним формулу скорости передачи данных:

* Вместо Q можно использовать обозначение I (для объема файла)

V - скорость
Q - объем
t - время

Определим, что нам известно:

Вася: V = 2¹⁷ бит/с
Петя: V = 2¹⁶ бит/с
Общий объем Q = 8 Мбайт

Для начала переведем объем в биты:

Q = 8Мбайт = 8 * 2²³ бит = 2³ * 2²³ = 2²⁶ бит

Также известно, что сначала 1024 Кбайта будут передаваться по скоростному каналу Васи со скоростью 2¹⁷ бит/с (примем за t1), а затем все 8 Мбайт будут передаваться по низкоскоростному каналу (примем за t2). Найдем время по двум промежуткам:

t1 = 1024 Кбайт / 2¹⁷ = 2¹⁰ * 2¹³ бит / 2¹⁷ = 
= 2¹⁰ / 2⁴ = 64 с

t2 = 2²⁶ / 2¹⁶ = 2¹⁰ = 1024 c

Найдем общее время:

t = t1 + t2 = 64 + 1024 = 1088

Результат: 1088

Подробный разбор смотрите на видео:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

Тема: Скорость передачи информации:

ЕГЭ по информатике задание 7_15:

Сколько секунд потребуется модему, передающему сообщения со скоростью 32000 бит/с, чтобы передать 16-цветное растровое изображение размером 800 x 600 пикселей, при условии, что в каждом байте закодировано максимально возможное число пикселей?

Типовые задания для тренировки

✍ Решение:

Вспомним формулу скорости передачи данных:

* Вместо Q можно использовать обозначение I (для объема файла)

V - скорость
Q - объем
t - время

Отсюда получаем формулу для времени:
Для нахождения времени вычислим объем сообщения по формуле:

N — общее количество пикселей или разрешение, 
i — глубина кодирования цвета (количество бит, выделенное на 1 пиксель)

Q = 4 * 480000

Теперь найдем время:

t = 4 * 480000 / 32000 = 60 секунд

Результат: 60

Тема: Скорость передачи информации:

ЕГЭ по информатике задание 7_16:

Каково время (в минутах) передачи полного объема данных по каналу связи, если известно, что передано 9000 Мбайт данных, причем треть времени передача шла со скоростью 60 Мбит в секунду, а остальное время – со скоростью 90 Мбит в секунду?

✍ Решение:

Формула скорости передачи данных:

* Вместо Q можно использовать обозначение I (для объема файла)

V - скорость
Q - объем
t - время

При 1/3 t скорость (V) равна 60 Мбит/c
При 2/3 t скорость(V) равна 90 Мбит/c
Объем переданных данных выразим в Мбитах:

1 Мбайт = 8 Мбит

 Q = 9000 Мбайт * 8 = 72000 Мбит

Из формулы выразим объем:
Так как общий объем данных у нас известен, получим уравнение:

(60 * 1/3t)  + (90 * 2/3t) = 72000
вынесем t за скобки, получим уравнение:
t * (20 + 60) = 72000
выразим t:
t = 72000 / 80 = 900 с = 15 мин

Результат: 15

Решение задания можно посмотреть и на видео:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

Тема: Скорость передачи информации:

ЕГЭ по информатике задание 7.17:

Документ объемом 5 Мбайт можно передать с одного компьютера на другой двумя способами:
А) Сжать архиватором, передать архив по каналу связи, распаковать
Б) Передать по каналу связи без использования архиватора.

Какой способ быстрее и насколько, если

средняя скорость передачи данных по каналу связи составляет 2¹⁸ бит в секунду,
объем сжатого архиватором документа равен 20% от исходного,
время, требуемое на сжатие документа – 7 секунд, на распаковку – 1 секунда?

В ответе напишите букву А, если способ А быстрее или Б, если быстрее способ Б. Сразу после буквы напишите количество секунд, насколько один способ быстрее другого.

Так, например, если способ Б быстрее способа А на 23 секунды, в ответе нужно написать Б23.

Типовые задания для тренировки

✍ Решение:

Рассмотрим способ А:

Сначала найдем объем документа, зная, что он составляет 20% от исходного:

Q (объем) = 5 Мбайт * 0.2 = 1 Мбайт = 1 * 2²³ бит

Формула времени передачи данных:

V - скорость
Q - объем
t - время

Получим t с учетом времени на сжатие и распаковку:

t = Q / V + 7 + 1 = 8 + 2²³ / 2¹⁸ = 8 + 2⁵ = 40 c

Рассмотрим способ Б:

Для этого способа можно сразу найти время (по формуле):

t = Q / V = 5 * 2²³ / 2¹⁸ = 5 * 2⁵ = 5 * 32 = 160 c

Получаем, что способ А быстрее; вычислим насколько быстрее:

160 с - 40 с = 120 с

Результат: А120

Решение также можно посмотреть в видеоуроке:

📹 YouTube здесьздесь

Тема: Скорость передачи информации:

ЕГЭ по информатике задание 7_18:

Документ объёмом 20 Мбайт можно передать с одного компьютера на другой двумя способами:
А) сжать архиватором-1, передать архив по каналу связи, распаковать;
Б) сжать архиватором-2, передать архив по каналу связи, распаковать;

Какой способ быстрее и насколько, если

средняя скорость передачи данных по каналу связи составляет 2²⁰ бит в секунду,
объём документа, сжатого архиватором-1, равен 20% от исходного,
на сжатие документа архиватором-1 требуется 15 секунд, на распаковку — 2 секунды,
объём документа, сжатого архиватором-2, равен 10% от исходного,
на сжатие документа архиватором-2 требуется 20 секунд, на распаковку — 4 секунды?

В ответе напишите букву А, если способ А быстрее или Б, если быстрее способ Б. Сразу после буквы напишите количество секунд, насколько один способ быстрее другого.

Так, например, если способ Б быстрее способа А на 23 секунды, в ответе нужно написать Б23.

✍ Решение:

Рассмотрим способ А:

Сначала найдем объем документа, зная, что он составляет 20% от исходного:

Q (объем) = 20 Мбайт * 0.2  = 4 Мбайт = 2² * 2²³ бит  = 2²⁵ бит

Формула времени передачи данных:

V - скорость
Q - объем
t - время

Найдем время для способа А с учетом времени на сжатие и распаковку:

t_A = 2²⁵ / 2²⁰ + 17 с = 2⁵ + 17 = 49 с

Рассмотрим способ Б:

Сначала найдем объем документа, зная, что он составляет 10% от исходного:

Q (объем) = 20 Мбайт * 0.1  = 2 Мбайт = 2¹ * 2²³ бит  = 2²⁴ бит

Найдем общее время с учетом потраченного времени на сжатие и распаковку:

t_Б = 2²⁴ / 2²⁰ + 24 с = 2⁴ + 24 = 40 с

Получили, что второй способ (Б) быстрее. Выясним насколько быстрее:

49 - 40 = 9 с

Результат: Б9

Тема: Скорость передачи информации:

Решение 7 ЕГЭ по информатике, задание 7_19:

Документ (без упаковки) можно передать по каналу связи с одного компьютера на другой за 1 минуту и 40 секунд. Если предварительно упаковать документ архиватором, передать упакованный документ, а потом распаковать на компьютере получателя, то общее время передачи (включая упаковку и распаковку) составит 30 секунд. При этом на упаковку и распаковку данных всего ушло 10 секунд. Размер исходного документа 45 Мбайт.

Чему равен размер упакованного документа (в Мбайт)?

✍ Решение:

Выпишем исходные данные для двух состояний документа, используя неизвестное x для искомого параметра — объема:

неупакованный:

I₁ = 45 Мбайт
t₁ = 100 секунд (60 секунд + 40 секунд = 100)

упакованный:

I₂ = x Мбайт
t₂ = 20 секунд (30 секунд - 10 секунд = 20)

Получим систему уравнений:

45 = 100
х = 20

Выразим x, т.е. объем упакованного документа:

х = (45 * 20) / 100 = 9 Мбайт

Результат: 9

Источник

Определение объёма памяти, необходимого для хранения графической информации

Различают три вида компьютерной графики:

растровая графика;
векторная графика;
фрактальная графика.

Они различаются принципами формирования изображения при отображении на экране монитора или при печати на бумаге. Наименьшим элементом растрового изображения является точка (пиксель), векторное изображение строится из геометрических примитивов, фрактальная графика задаётся математическими уравнениями.

Расчёт информационного объёма растрового графического изображения основан на подсчёте количества пикселей в этом изображении и на определении глубины цвета (информационного веса одного пикселя).

Глубина цвета зависит от количества цветов в палитре:

N=2i

.
(N) — это количество цветов в палитре,
(i) — глубина цвета (или информационный вес одной точки, измеряется в битах).

Чтобы найти информационный объём растрового графического изображения (I) (измеряется в битах), воспользуемся формулой

I=i⋅k

.
(k) — количество пикселей (точек) в изображении;
(i) — глубина цвета (бит).

Пример:

Полина увлекается компьютерной графикой. Для конкурса она создала рисунок размером (1024*768) пикселей, на диске он занял (900) Кбайт. Найди максимально возможное количество цветов в палитре изображения.

Дано

(k=1024*768);

(I=900) Кбайт.

Найти: (N).

Решение

Чтобы найти (N), необходимо знать (i):

N=2i

Из формулы

I=i⋅k

выразим

i=Ik

, подставим числовые значения. Не забудем перевести (I) в биты.

Получим

i=900∗1024∗81024∗768≈9,3

Возьмём (i=9) битам. Обрати внимание, нельзя взять (i=10) битам, так как в этом случае объём файла (I) превысит (900) Кбайт. Тогда

N=29=512.

Ответ: (512) цветов.

На качество изображения влияет также разрешение монитора, сканера или принтера.

Разрешение — величина, определяющая количество точек растрового изображения на единицу длины.

Получается, если увеличить разрешение в (3) раза, то увеличится в (3) раза количество пикселей по горизонтали и увеличится в (3) раза количество пикселей по вертикали, т. е. количество пикселей в изображении увеличится в (9) раз.

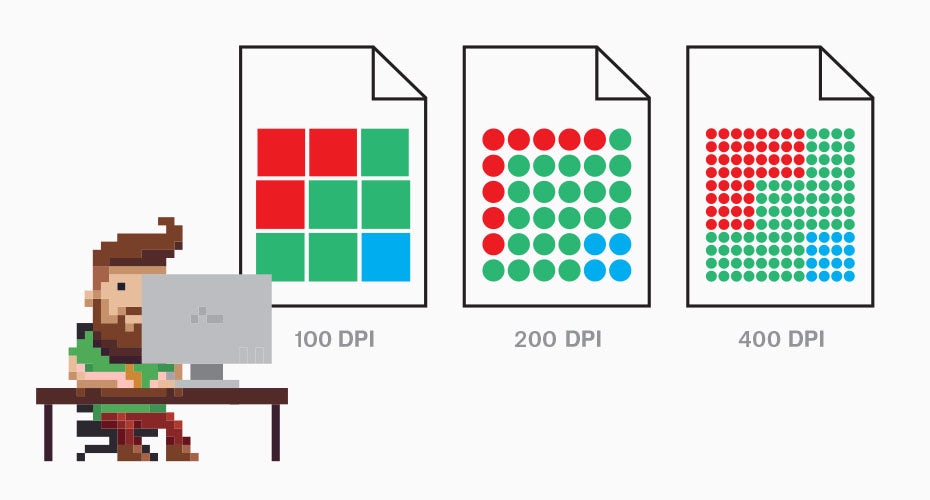
Параметры PPI и DPI определяют разрешение или чёткость изображения, но каждый относится к отдельным носителям:
• цифровой (монитор) — PPI;
• печать (бумага) — DPI.
При решении задач величины PPI и DPI имеют одинаковый смысл.

При расчётах используется формула

I=k⋅i⋅ppi2

.
(I) — это информационный объём растрового графического изображения (бит);
(k) — количество пикселей (точек) в изображении;
(i) — глубина цвета (бит),
ppi (или dpi) — разрешение.

Пример:

для обучения нейросети распознаванию изображений фотографии сканируются с разрешением (600) ppi и цветовой системой, содержащей (16 777 216) цветов. Методы сжатия изображений не используются. Средний размер отсканированного документа составляет (18) Мбайт. В целях экономии было решено перейти на разрешение (300) ppi и цветовую систему, содержащую (65 536) цветов. Сколько Мбайт будет составлять средний размер документа, отсканированного с изменёнными параметрами?

Решение

Заметим, что

16777216=224

, значит,

i1=24

бита.

65536=216

, значит,

i2=16

бит.

Воспользуемся формулой

I=k⋅i⋅ppi2

I1=24⋅k⋅6002;I2=16⋅k⋅3002;I1I2=24⋅k⋅600216⋅k⋅3002=6;18I2=6;I2=186=3.

Ответ: (3) Мбайта.

Определение объёма памяти, необходимого для хранения звуковой информации

Звук — это распространяющиеся в воздухе, воде или другой среде волны с непрерывно меняющейся амплитудой и частотой.
Чтобы компьютер мог обрабатывать звук, непрерывный звуковой сигнал должен быть преобразован в цифровую дискретную форму. Для этого его подвергают временной дискретизации и квантованию: параметры звукового сигнала измеряются не непрерывно, а через определённые промежутки времени (временная дискретизация); результаты измерений записываются в цифровом виде с ограниченной точностью (квантование).
Сущность временной дискретизации заключается в том, что через равные промежутки времени мы измеряем уровень аналогового сигнала. Количество таких измерений за одну секунду называется частотой дискретизации.

Частота дискретизации ((H)) — это количество измерений громкости звука за одну секунду.

Частота дискретизации измеряется в герцах (Гц) и килогерцах (кГц). (1) кГц (=) (1000) Гц. Частота дискретизации, равная (100) Гц, означает, что за одну секунду проводилось (100) измерений громкости звука.
Качество звукозаписи зависит не только от частоты дискретизации, но также и от глубины кодирования звука.

Глубина кодирования звука или разрешение ((i)) — это количество информации, которое необходимо для кодирования дискретных уровней громкости цифрового звука.

В результате измерений звукового сигнала будет получено некоторое значение громкости, при этом все результаты измерений будут лежать в некотором диапазоне — количество уровней дискретизации.

Обозначим за (N) количество уровней дискретизации, тогда глубину кодирования можно найти по формуле:

N=2i

Для решения задач на нахождение объёма памяти, необходимого для хранения звуковой информации, воспользуемся формулой:

I=H⋅i⋅t⋅k

, где
(I) — информационный объём звукового файла (бит);
(H) — частота дискретизации (Гц);
(i) — глубина кодирования информации (бит);
(k) — количество каналов (моно — (1) канал, стерео — (2) канала, квадро — (4) канала).

Пример:

для распределения птиц по категориям обучают нейросеть. Для этого загружают звуки, издаваемые птицами. Каждый файл записан в формате монозвукозаписи с частотой дискретизации (128) Гц. При записи используется (64) уровня дискретизации. Запись длится (6) минут (24) секунды. Определи размер загружаемого файла в килобайтах.

Дано

(k=1);

(H=128) Гц;

(N=64);

(t=384) секунды.

Найти: (I) (Кбайт).

Решение

Воспользуемся формулой

N=2i

, (i=6) бит.

Подставим числовые значения в формулу

I=H⋅i⋅t⋅k

и переведём биты в килобайты:

Ответ: (36) килобайт.

Любой файл может быть передан по каналу связи, тогда объём переданной информации вычисляется по формуле:

I=V⋅t

, где
(I) — объём информации (бит);
(V) — пропускная способность канала связи (бит/секунду);
(t) — время передачи (секунды).

Пример:

в дельте Волги орнитологи оцифровывают звуки птиц и записывают их в виде файлов без использования сжатия данных. Получившийся файл передают в Астраханский биосферный заповедник по каналу связи за (56) секунд. Затем тот же файл оцифровывают повторно с разрешением в (8) раз ниже и частотой дискретизации в (3) раза выше, чем в первый раз. Сжатие данных не производится. Полученный файл передают в Кавказский природный заповедник; пропускная способность канала связи с Кавказским заповедником в (2) раза ниже, чем канала связи с Астраханским заповедником. Сколько секунд длилась передача файла в Кавказский заповедник?

Решение

Воспользуемся формулой

I=H⋅i⋅t⋅k

I1=k⋅i⋅t⋅H;I2=k⋅i8⋅t⋅3⋅H;I2I1=38.По условиюV2=V12.

Выразим (V) из формулы

I=V⋅t

, получим

V=It

, учтём, что

t1=56 секунд.Тогда I2t2=I156⋅2;t2=56⋅2⋅I2I1=56⋅2⋅38=42.

Ответ: (42) секунды.

Обрати внимание!

1 Мбайт=220 байт=223 бит.1 Кбайт=210 байт=213 бит.

Источник

Е7.30 Сколько Мбайт составлял средний размер документа до оптимизации?

Сколько Мбайт составлял средний размер документа до оптимизации? Для хранения в информационной системе документы сканируются с разрешением 600 ppi и цветовой системой, содержащей 2²⁴ = 16 777 216 цветов. Методы сжатия изображений не используются.

В целях экономии было решено перейти на разрешение 300 ppi и цветовую систему, содержащую 16 цветов. Средний размер документа, отсканированного с изменёнными параметрами, составляет 128 Кбайт. Сколько Мбайт составлял средний размер документа до оптимизации?

Ответ:

Тренировочный вариант от 09.11.2020 «Евгений Джобс»

Источник

Канал видеоролика: Елена Сергеевна

Смотреть видео:

#информатика #егэинформатика #икт #экзамены #егэ_2020 #мгту #школьникам #помощь_студентам #поступление

Свежая информация для ЕГЭ и ОГЭ по Информатике (листай):

С этим видео ученики смотрят следующие ролики:

№11-2 КЕГЭ информатика. Разбор задачи с подвохом

Елена Сергеевна

7 номер ЕГЭ. Кодирование информации. Разбор задачи 1827 с сайта К.Ю. Полякова

Физика Информатика

#2 ЕГЭ разбор задачи от 4 05 18

Елена Сергеевна

#6 ЕГЭ. Разбор задачи первого типа

Елена Сергеевна

Облегчи жизнь другим ученикам — поделись! (плюс тебе в карму):

13.02.2021

Источник

PPI и DPI — это два важных термина, которые должен знать каждый, кто работает с изображениями. Оба определяют разрешение или четкость изображения, но каждый относится к отдельным носителям, то есть цифровой по сравнению с печатью .

PPI и DPI часто используются взаимозаменяемо, когда их не должно быть. Понимание того, как они различаются и как применять каждый из них в ваших проектах, даст вам возможность производить качественную печать, оптимизировать цифровые изображения для Интернета и, в конечном итоге, сэкономить драгоценное время. С учетом вышесказанного, давайте разберемся, что означают эти термины, и разберем различия между PPI и DPI.

Содержание статьи

1 В чем разница между PPI и DPI?
—
2 Разрешение PPI
—
- 2.1 Что означает PPI
- 2.2 Когда вы используете PPI?
- 2.3 Как установить или изменить разрешение PPI
3 DPI печать
—
- 3.1 Что означает DPI
- 3.2 Когда вы используете DPI?
4 Разрешение изображения имеет значение
—
- - - 4.0.0.1
      Хотите идеальное разрешение изображения в ваших дизайнерских проектах?
      - 4.0.0.1.1
        Найдите дизайнера сегодня!

PPI описывает разрешение в пикселях цифрового изображения, тогда как DPI описывает количество точек чернил на напечатанном изображении.

Хотя PPI в значительной степени относится к экранному дисплею, он также влияет на размер отпечатка вашего дизайна и, следовательно, на качество вывода. DPI, с другой стороны, не имеет ничего общего с цифровыми технологиями и в первую очередь касается печати.

Разрешение PPI
—

Что означает PPI

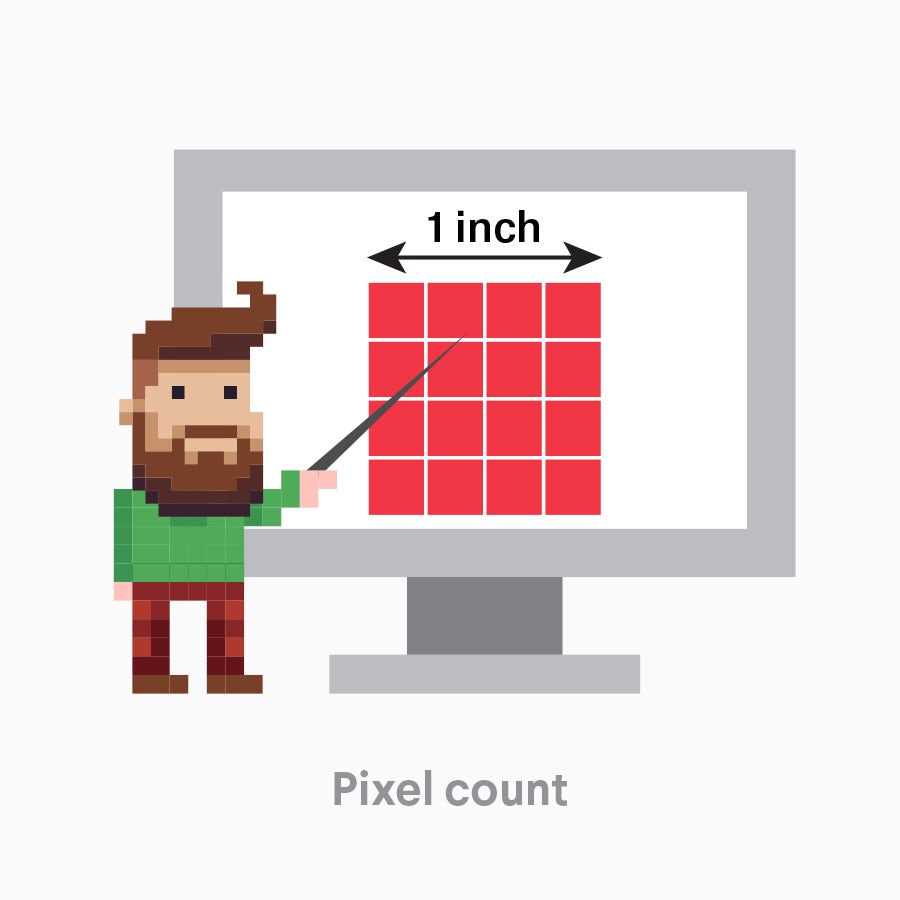
PPI, или пикселей на дюйм относится как к фиксированному количеству пикселей, которое может отображать экран, так и к плотности пикселей в цифровом изображении. Число пикселей с другой стороны, относится к количеству пикселей по длине и ширине цифрового изображения, то есть к размерам изображения в пикселях. Пиксели или «элементы изображения», представляют собой наименьшие строительные блоки цифрового изображения. Увеличьте любое изображение на вашем, и вы увидите, что оно разбивается на цветные квадраты — это пиксели.

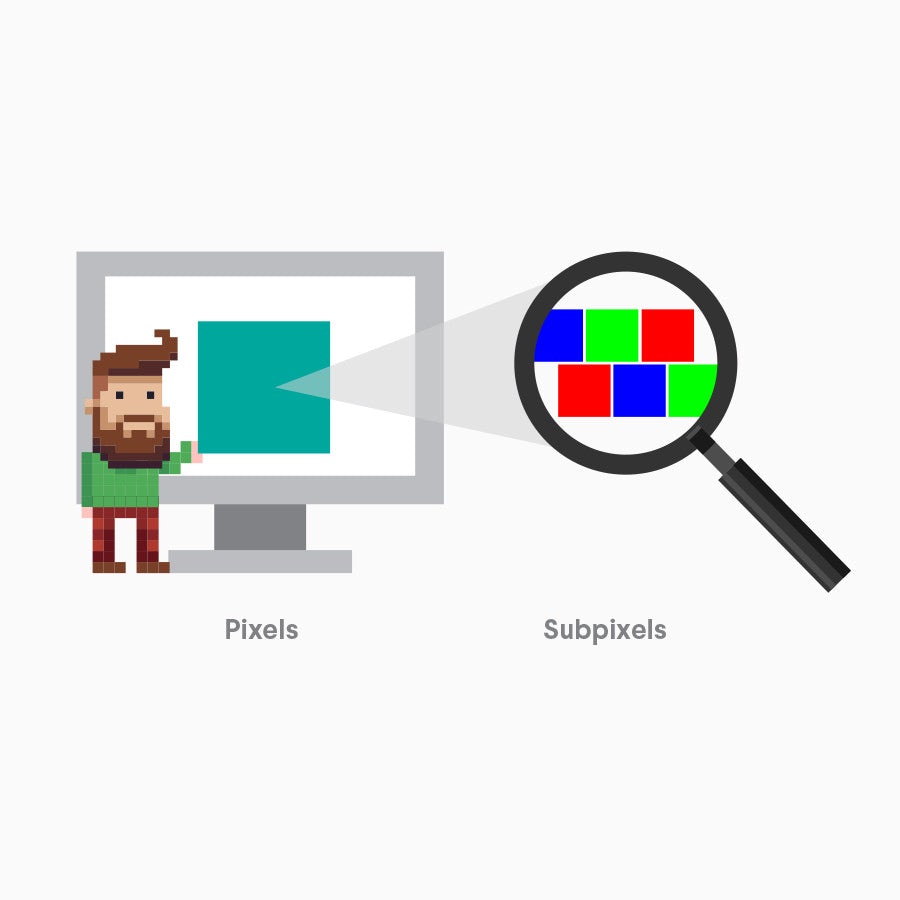
Внутри пикселей находятся подпиксели, красный, зеленый и элементы синего света, которые человеческий глаз не может видеть, потому что аддитивная обработка цвета смешивает их в один оттенок, который появляется на уровне пикселей. Вот почему PPI использует цветовую модель RGB (красный, зеленый и синий) также известную как аддитивная цветовая модель. Это не существует в печати — только в электронном отображении изображений, таких как телевизионные экраны, компьютерные мониторы и цифровая фотография.

Когда вы используете PPI?

Используйте PPI всякий раз, когда вы работаете с цифровыми изображениями. PPI наиболее полезен при подготовке файлов к печати (хотя DPI будет использоваться физическим принтером — см. Больше в разделе DPI ниже). Изображение с более высоким PPI, как правило, имеет более высокое качество, потому что оно имеет большую плотность пикселей, но экспорт в 300 PPI обычно считается отраслевым стандартом качества.

Поскольку увеличение PPI увеличивает размер вашего файла, вы захотите использовать высокий PPI только при необходимости. Например, когда печать содержит много мелких деталей на глянцевой поверхности, лучше использовать более высокое разрешение. Печать изображения на холсте не требует такого высокого разрешения, потому что детали теряются в текстуре материала. PPI не имеет большого значения для распространения в Интернете, поскольку плотность пикселей вашего монитора фиксирована. Изображение 72 PPI и изображение 3000 PPI будут одинаковыми на вашем экране. Именно размеры в пикселях (количество пикселей слева направо, сверху вниз) будут определять размер и детализацию вашего изображения.

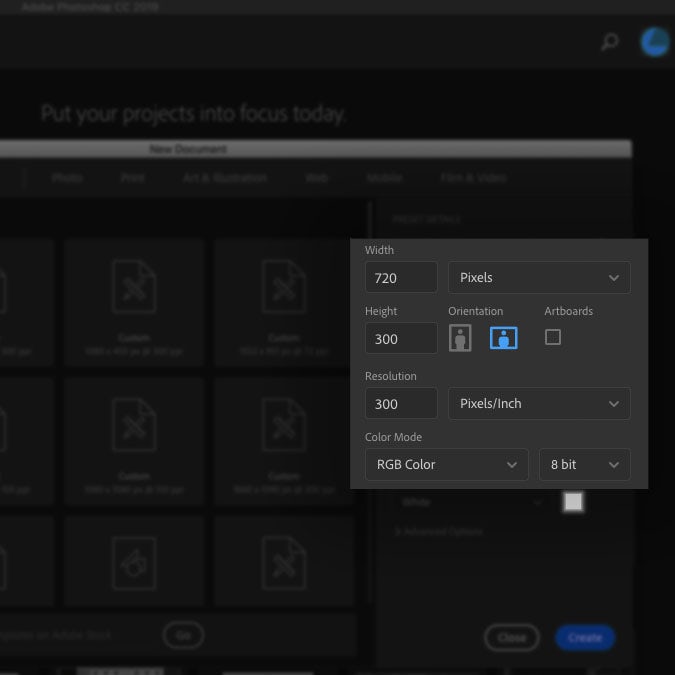
Как установить или изменить разрешение PPI

В окне «Новый документ» в Photoshop вы вначале задали разрешение в пикселях на дюйм

Растровые программы (программы, работающие с пиксельными носителями), такие как Photoshop, позволяют устанавливать разрешение PPI в самом начале, когда вы создаете документ. Вы найдете разрешение в списке с другими параметрами в окне «Новый документ».

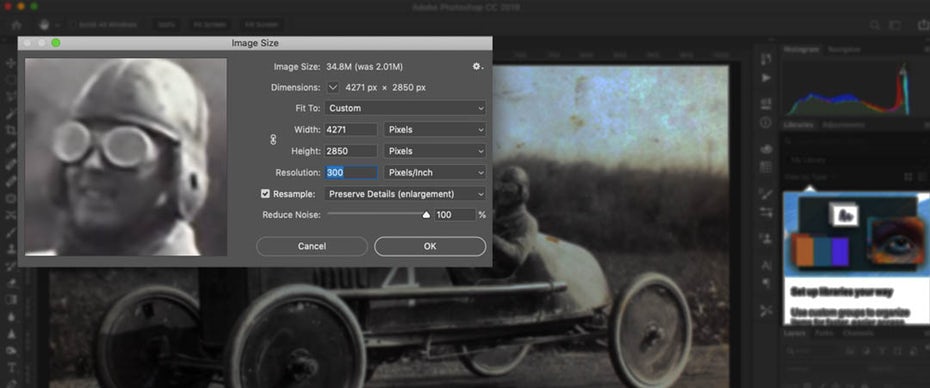
Если вам нужно увеличить разрешение на уже созданном изображении, вы можете повторно сэмплировать его. Повторная выборка — это процесс изменения количества пикселей в изображении, при котором программа создает или удаляет пиксели для сохранения качества изображения.

В Photoshop вы можете сделать это, перейдя к Изображение> Размер изображения . В окне «Размер изображения» у вас будут параметры для изменения ширины, высоты и разрешения PPI вашего изображения. Установите флажок «Resample» и установите для него «Preservation Details», чтобы выбрать, как Photoshop заполняет новые пиксели.

В окне «Размер изображения» можно настроить разрешение в Photoshop

Вы можете уменьшить разрешение, если установите PPI на более низкое значение. По мере уменьшения количества пикселей размер и размеры изображения также уменьшаются. Вы увеличиваете разрешение, когда устанавливаете PPI на более высокое значение. Это позволяет печатать изображение в большем размере.

Тем не менее, лучше по возможности избегать изменения PPI для существующего изображения. Процесс пересэмплирования требует, чтобы Photoshop генерировал новые пиксели с нуля. Хотя Photoshop способен считывать окружающие пиксели и делать несколько точные предположения о том, каким должен быть цвет каждого нового пикселя, компьютеры, как известно, плохо «видят» изображения так, как это могут делать люди. Таким образом, сгенерированные компьютером пиксели могут привести к непреднамеренным результатам на вашем изображении.

DPI печать
—

Что означает DPI

DPI, или число точек на дюйм, относится к значению разрешения физического принтера. Принтеры воспроизводят изображение, выплевывая крошечные точки, а количество точек на дюйм влияет на количество деталей и общее качество печати.

DPI использует цветовую модель CMYK (голубой, пурпурный, желтый и ключевой / черный) контролировать количество красного, зеленого и синего света, который отражается от белой бумаги. Это также называется субтрактивной цветовой моделью. Точки каждого цвета напечатаны узорами, что позволяет человеческому глазу воспринимать определенный цвет, созданный из этой комбинации. DPI — это измерение этой плотности. Эти точки имеют фиксированный размер, и на разрешение влияет только количество точек на дюйм.

Когда вы используете DPI?

Когда ваш дизайн будет напечатан физически, принтер будет использовать DPI. Каждая модель и стиль принтера создает свой уникальный DPI на основе своих настроек. Струйные принтеры обеспечивают разрешение от 300 до 720 DPI, а лазерные принтеры — от 600 до 2400 DPI.

Более высокое значение DPI может означать более высокое разрешение, но размеры точек зависят от принтера

Не существует стандартного размера или формы точки, поэтому более высокое значение DPI не всегда означает более высокое качество печати. Точки одного производителя могут выглядеть так же хорошо при 1200 DPI, как точки другого производителя при 700 DPI. Книги и журналы часто используют 150 DPI для фотографического воспроизведения, а газеты часто используют 85 DPI. Обратитесь в типографию или ознакомьтесь со спецификациями принтера, чтобы найти подходящий DPI для вашего проекта.

Разрешение изображения имеет значение
—

Знание того, как использовать PPI, позволит вам каждый раз получать высококачественные изображения. А знание навигации DPI поможет вам эффективно общаться с печатными машинами и профессионалами в полиграфической промышленности. Если вы не принтер, ваше основное внимание будет уделено PPI. Но важно понимать процесс физической печати, если ваша работа требует этого регулярно.

В конце концов, даже самый лучший дизайн может быть разрушен из-за плохого разрешения изображения. Вот почему, если вы хотите кристально чистого качества в ваших проектах, убедитесь, что вы работаете с профессиональным дизайнером.

Ознакомьтесь с этой статьей об основах графического дизайна для получения дополнительных знаний о дизайне.

Хотите идеальное разрешение изображения в ваших дизайнерских проектах?

Найдите дизайнера сегодня!

Эта статья была первоначально написана Алексом Бингманом и опубликована в 2013 году. В нее были добавлены новые примеры и информация.

Сообщение PPI против DPI: в чем разница? впервые появился на 99designs.

Источник

A pixel (the word was originally coined, iirc, by IBM and derives from «picture element») is the smallest indivisible unit of information in a digital image. Pixels may be displayed, or they may be printed, but you can’t divide pixels into smaller pieces to get more information. How many channels and bits per channel make up one pixel is the measure of how subtle the information in a pixel may be, but the basic fact is that 1 pixel the smallest increment of information in an image. If you do video, you know that pixels don’t have to be square — they are non-square in all older video formats. Square or not, a pixel is still the smallest unit of a picture.

An inch (okay, so you know this already — bear with me) is a unit of linear measurement on a surface, which could be a screen or a piece of paper.

A dot is, well, a dot. It can be a dot on a screen, or it can be a dot produced by a printhead. Like pixels, dots are atomic. They’re either there, or they’re not. How much fine detail a screen can display depends on how close the dots are (what they used to call «dot pitch» in the old CRT days). How small the dots are from an inkjet, a laser printer or an imagesetter determines how much fine detail it can reproduce.

Dots per inch is fairly easy. A screen has so many dots (each comprising R, G and B elements) per inch of screen. It’s the same on paper. A 1200 dpi printer can lay down 1200 dots in one linear inch. In describing screen detail or printer output, dots per inch is the correct term.

PPI is where the confusion comes in. An image has so many pixels. Its metadata contains an output size in inches, cm, mm, M&Ms, whatever. It’s the width in pixels divided by the output width in the metadata that «per inch» comes from. So the same image with different metadata may be 72 ppi, 150 ppi or 8000 ppi. The image information is the same; all that’s changed is the metadata.

A quick and easy demo that somewhat illustrates the point is to make some marks on a piece of elastic, say five to an inch. Stretch the elastic to twice its length. The number of marks hasn’t changed, even though the «marks per inch» is now 2.5.

You can see this in Photoshop if you turn off Resample Image and change the size. The ppi value changes to reflect how small the pixels must be reproduced in order to hit the measurement value in inches/cm/mm etc. Note that in this case the Pixels fields are disabled. You can’t change those values unless you resample.

Mass confusion entered in when image pixels were mapped to screen dots in web browsers. A 200 pixel image shows up as 200 pixels in a browser. How large it is, measured with a ruler, depends on the dots per inch of the screen. The image metadata might say it’s 200 ppi or 72 ppi or 1 ppi, it will still occupy exactly 200 screen dots. The world remains fixated on «72 ppi for the web,» so the question of «what’s the right resolution for web images» keeps coming up, and the correct answer, «it doesn’t matter,» keeps being supplied ad nauseam.

If you’re still with me, there’s one last step that brings the two together.

A 720-pixels-wide image at 10 physical inches wide has a resolution of 72 pixels per inch. If you print it on a 1200 dpi printer, there will be 1200 dots per inch on the paper, but the image is still 72 pixels per inch. That’s why it looks like crap. On the other hand, a 7200 pixels wide image printed at 1 inch wide will exceed the resolution of our 1200 dpi printer. Photoshop (let’s say) and the printer driver decide which pixels to throw away and which to actually print. Some of the printed dots will be averaged among adjacent image pixels, but, regardless, some of the image information has to be thrown away. The output will be 1200 dpi, but the resolution of the printed image will have been reduced to at most 1200 dpi by the software.

answered Feb 21, 2012 at 1:04

Alan GilbertsonAlan Gilbertson

47.3k5 gold badges75 silver badges147 bronze badges

Alan covered most of the basics quite nicely. I would also like to highlight not just the difference between DPI and PPI, but also the relationship between PPI and display resolution (which is just the raw numbers of pixels in a display).

I think many remember those heady days when we got to move from VGA to SVGA to XGA resolutions. It was nice for a while when most consumers had monitors with specs similar to 1024px X 768px @ 72 PPI and we had a pretty safe target for display graphics.

This complacency is still evident, but ever more unrealistic. Many mobile manufacturers have been focusing on increasing resolution while the physical screens change slightly, if at all. The result is PPIs that are on the rise in small hand-held form-factors. This provides many opportunities to accidentally create graphics that simply aren’t useful (or, nearly as bad, get automatically scaled-up by the operating systems at the expense of those clean edges you worked so hard on).

An easy real-world example is Apple’s iPhone. The first 3 editions had an 89mm (diagonal) screen, with 320px X 480px (163 PPI). Then they introduced «Retina» display (hello, Marketing) which bumped the resolution up to 640px X 480px but was still only 89mm in physical size (326 PPI!). BlackBerry has made similar moves (though without the marketing panache) and it looks like the same is about to happen with iPad as well.

One other term that may also be of interest is DIP or DP. Microsoft refers to them as «Device Independent Pixels» and on the Android platform they are «Density-independent Pixels». They have slightly different names, but are the same core concept. The goal is to allow apps to be «DPI aware» and scale text/objects around constant conventions. Density-aware applications are aware of the display’s PPI and your desired «DPI», and then scale text and objects appropriately.

Taking this back to our ever-increasing-PPI scenario, if you designed a website or app with a 80px font, you may think that’s pretty large on your 163 PPI screen. Your text would be nearly a half-inch tall, which is reasonably large on a phone. But then the next version of the phone comes out and suddenly your text is only 1/4″ tall at 326 PPI. This would be especially bad if some of your text was scaled in another unit of measurement and suddenly body text is larger than header text. (Sometimes I still run across websites that made this mistake.) If instead you were using DIP/DP for scale, you could hold both phones side-by-side and the text would be the same physical dimensions (though perhaps noticeably sharper on the higher-DPI model).

At any rate, while PPI may be the most confusing of the measurements, it is incredibly important to pay attention to it. If you have the option of designing with DIP or DP units, it should handle some of the guesswork for you and allow you to target a wider array of displays without increasing your technical burden.

_{My apologies that this answer is so screen-centric, I rarely dabble in print.}

answered Feb 21, 2012 at 3:15

FarrayFarray

7,5884 gold badges32 silver badges43 bronze badges

DPI = how many distinct dots a printing device and render per inch.

PPI = the number of pixels in an inch of a video display device.

A lot of software, namely photoshop, uses DPI for both definitions.

UPDATE:

e100 has me now questioning my opinions on this (which is a good thing!) and in doing some more research, I need to update my opinion a bit.

HISTORICALLY, DPI refers to the print process…namely how many discreet dots a printer can produce on paper. PPI referred to the number of pixels per inch of your monitor.

So, one is about the process of printing on paper, the other is about your display hardware.

Neither is directly about the ‘resolution per inch’ of your digital image, though both seem to have correlations to the point of being almost identical in many ways.

So, let’s say you have a 1200dpi laser printer. That means for every inch of paper, that printer can create 1200 unique dots.

Now…on to the issue of assigning a DPI/PPI setting to a digital image.

A digital image is composed of pixels. As long as the image remains digital, it doesn’t care what PPI you tell it it is, as it will always render based on the total pixels. For isntance, a 1000px x 1000px image, by default, in a web browser, will be 1000px wide.

Where giving an image a DPI/PPI setting matters is when printing…that’s how the software calculates the physical size of the analog output. So your 1000px x 1000px image with a DPI setting of 500dpi will result in am image printed 2″ in size.

Where things get confusing is that IIRC, Photoshop historically used ‘DPI’ as the term for this. Though it clearly looks like it now uses the term ‘PPI’.

Because of that, I’d say either term is appropriate when referring to the output resolution meta-information in your graphics editing software.

So, in summary, my definitions would be:

DPI = a spec for your printer explaining how detailed an image it can print
PPI = a spec for your monitor explaining how detailed an image it can display for a given physical size

In terms of setting up an image for printing = either PPI or DPI is an appropriate term. I think PPI makes more sense for the person dealing with creating the digital file. In the end, you will need so many pixels for decent output. DPI makes more sense for the person printing the digital file, as that is a term that makes sense in the service bureau/printer world.

answered Feb 21, 2012 at 6:27

DA01DA01

50k3 gold badges76 silver badges160 bronze badges

Starting to answer my own question, I think one of the problems with explaining this is that only parts of the full story are relevant to anyone’s day-to-day work, unless you cover the gamut from web/app designer to print designer to prepress expert. So I’ll probably come back to this and tune it for different audiences.

Pixels per inch (ppi) is a measure of resolution in two different contexts.

(a) the resolution of a image printed at a specific physical size

This is not an intrinsic property of an image file. Pixels have no real-world dimensions, and so ppi has no meaning until the image is printed, or at least specified in a print layout which uses physical (inches or mm) measurements.

e.g. 1. You have a 1000px square image in Photoshop and you print it so it’s 3 inches square. The resolution of the print is 333ppi.

e.g. 2. You then put it in an InDesign layout at 1.5 inches square and PDF it. Acrobat’s prepress tools tell you it’s 666dpi — when printed.

e.g 3. You view it in a web browser on various devices. It’s 1000px square, whatever size or resolution your screen is; the physical dimensions vary widely however.

e.g. 4. You go back into Photoshop and notice the image has been set as 72ppi all along, and it didn’t make any difference to any of these cases. You change it to 144ppi (without resampling, i.e the number of pixels is unchanged) and find it makes no difference to any of the cases either.

e.g. 5. After a bit of experimentation, you find that ppi does make a difference when you print from Photoshop at 100% scale. But so does changing print dimensions — they are directly (and inversely) related, and both are just metadata which specify how the image should be printed, and can be easily overridden.

(b) the physical resolution of a display device

Going back to e.g. 3, the image displayed at different physical sizes because the screens have a fixed hardware grid of pixels. So PPI in this case is an intrinsic property of the hardware.

You can measure the PPI of a screen easily if you know its pixel dimensions, just divide its height (or width) in pixels by its height (or width) measured with a ruler. The first Macs had 72ppi; laptops are up to about 130ppi; current smartphones 200ppi+, up to the iPhone 4’s 330ppi.

Dots per inch (dpi) is a physical measure of a print device’s output resolution.

The dots are individual blobs of ink.

(to be continued)

NB The term is very commonly used to mean ppi in both senses above.

Personally, I regard this as incorrect, however entrenched it may be, and the source of continued confusion.

answered Feb 21, 2012 at 20:00

e100e100

9,7825 gold badges44 silver badges72 bronze badges

I will not answer what is the difference between DPI and PPI. I’ll make a more fundamental answer.

What is the difference between a dot and a pixel?

A dot

I will leave the mathematical, geometrical and conceptual definitions out of this answer. I am only referring to graphic arts.

A dot is a tiny little spot of something (a droplet of ink, a dust particle) used on a physically printed medium. Normally it is the smallest amount of stuff you can have on that medium. Either you have a dot or you do not have one.

A dot has a binary nature. Either it exists or does not exist. In a printed medium you either print it or not. That is the nature of a dot.

A pixel

A pixel defines different things. Yes, we probably should call some of them in a different way)

I. A little block of information on a digital image file.

It is a tiny block of information, not a dot. A dot can be either there or not. On the contrary, a pixel can store one of several million values. But another important part of the nature of a pixel is that it has its space reserved. A pixel is always there, but you can change its values to make it transparent or white or black, but always has a value.

Imagine a store where you can either buy one nail or not buy it. That is a dot.

Now imagine a store where you can choose potentially among several millions of shapes of nails or even «nails with helixes», aka screws. That is a pixel.

The amount of options to choose from on this store is given by the depth of the store, in this case, the bit depth. From only on-off to several million options.

One thing about a pixel is that it is there. It has a defined position, what can change is its value of it.

II. The smallest portion of a screen that can be changed to render different shades of color.

Yes we can get how many of these screen pixels we have on a physical monitor, but lucky for us people give the total number; FullHD, 4K on a 50″ screen.

(This element tho should have to be named differently than the «pixel» of a digital image. The neologism I propose to reduce the confusion is to call a display element as dixel, not pixel)

Note one thing. A dot can be used in the realm of mathematics, geometry, painting, graphic arts, etc. A pixel on a digital file, a screen or a projection. You only need to know what is the context.

answered Dec 18, 2017 at 20:07

RafaelRafael

34.7k2 gold badges35 silver badges93 bronze badges

DPI used for Print
PPI used for anything on screen for things such as games or online banners ETC.

answered Apr 11, 2015 at 21:04