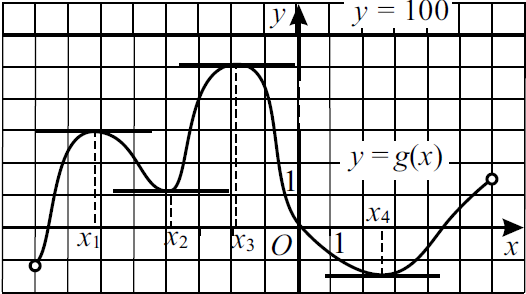| Выделите в таблице ячейки, соответствующие тем типам задач, которые вас интересуют. | |||||
| B1 | B2 | B3 | B4 | B5 | B6 |
| B7 | B8 | B9 | B10 | B11 | B12 |
Версия для печати и копирования в MS WordВерсия для печати и копирования в MS Word
1
Найдите значение выражения при
2
Найдите значение выражения:
Раздел: Алгебра
Кодификатор ФИПИ/Решу ЕГЭ: 1.2.3 Синус, косинус, тангенс и котангенс числа, 1.2.4 Основные тригонометрические тождества, 1.4.4 Преобразования тригонометрических выражений, 1.2.1 Синус, косинус, тангенс, котангенс произвольного угла, 1.2.2 Радианная мера угла, 1.2.5 Формулы приведения, 1.2.6 Синус, косинус и тангенс суммы и разности двух углов, 1.2.7 Синус и косинус двойного угла
3
Найдите значение выражения
4
5
Найдите значение выражения:
6
Найдите значение выражения
7
Найдите значение выражения:
8
Найдите значение выражения при
9
Найдите значение выражения при
10
Найдите значение выражения
6ое задание егэ математика профиль
Это одно из сложных заданий первой части профильного ЕГЭ по математике. Здесь очень много различных типов задач, в том числе непростых. Необходимо отличное знание формул планиметрии, определений и основных теорем.
Bесь необходимый теоретический материал — формулы собраны в презентациях
Автор: Алькаева Лариса Рахимовна
Основные типы заданий № 6 профильного ЕГЭ по математике.
Задание 6. Планиметрия
Окружность вписанная и описанная
Окружность (углы, касательная, хорда)
Если вы выучили все необходимые формулы, определения и теоремы, у вас намного больше шансов решить на ЕГЭ задачу 16 (часть 2), также посвященную планиметрии. Многие задания № 6 являются схемами для решения более сложных геометрических задач.
Окружность углы, касательная, хорда.
Vpr-ege. ru
13.05.2020 15:22:53
2020-05-13 15:22:53
Источники:
Https://vpr-ege. ru/ege/matematika/1055-zadanie-6-ege-profilnaya-matematika-teoriya-i-praktika
Задание 6 ЕГЭ по математике профильного уровня 2022: теория и практика » /> » /> .keyword { color: red; } 6ое задание егэ математика профиль
Задание 6. Функции. Производная и первообразная. ЕГЭ 2022 по математике профильного уровня
Задание 6. Функции. Производная и первообразная. ЕГЭ 2022 по математике профильного уровня
За это задание ты можешь получить 1 балл. На решение дается около 5 минут. Уровень сложности: Базовый.
Средний процент выполнения: 61.5%
Ответом к заданию 6 по математике (профильной) может быть Целое число или конечная десятичная дробь.
Задачи для практики
Задача 1
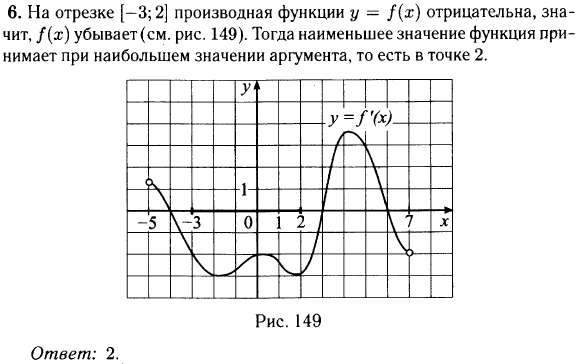
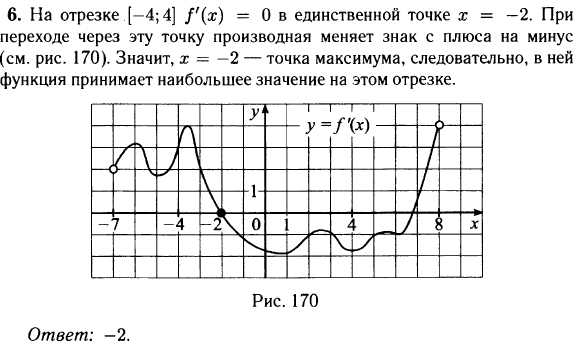
На рисунке изображён график функции $y=f'(x)$ производной функции $f(x)$, определённой на интервале $(-7;4)$. В какой точке отрезка $[-3;2]$ функция $f(x)$ принимает наибольшее значение?
Решение
На отрезке $[-3; 2]$ производная $y = f′(x)$ равна нулю в точке $x = -2$ и при переходе через неё меняет свой знак с «+» на «-», поэтому точка $x = -2$ — точка максимума функции на отрезке $[−3; 2]$. Так как она, кроме того, единственная точка экстремума на отрезке $[−3; 2]$, то в ней функция принимает наибольшее значение на данном отрезке.
Задача 2
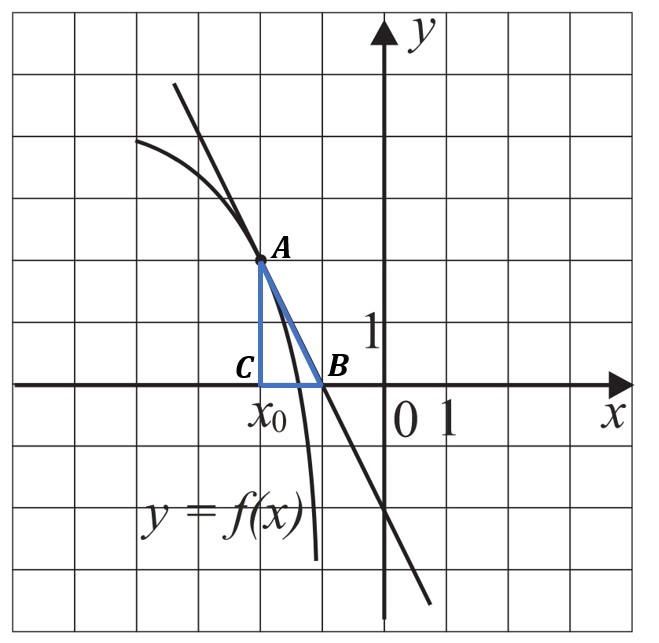
На рисунке изображён график функции $y=f(x)$ и касательная к нему в точке с абсциссой $x_0$. Найдите значение производной функции $f(x)$ в точке $x_0$.
Решение
По рисунку определяем, что касательная проходит через точки $A(-2; 2)$ и $B(-1; 0)$. Построим прямоугольный треугольник $ABC$ , где $C$ имеет координаты (-2; 0). Заметим, что прямая AB образует с положительным направлением оси Ox тупой уголα. Учитывая, что $f′(x_0) = tgα$, имеем $tgα = tg(180° — ∠ABC ) = — tg ∠ABC = -/ = -/ = -2$.
Задача 3
На рисунке изображён график функции $y=f(x)$ и отмечены точки $-7$; $-5$; $-1$;$1$. В какой из этих точек значение производной наибольшее?
Решение
Проводим касательные к графику в точках с указанными абсциссами (см. рис.).
Определяем, под каким углом $α$ они наклонены к положительному направлению оси $Ox$.
Согласно геометрическому смыслу производной $f'(x_0)=tg α$, то есть значения тангенсов построенных углов — это и есть значения производной в указанных точках
Замечаем, в точках $-7$ и $1$ касательные наклонены под острым углом, поэтому в этих точках значение производной положительно.
Учитывая, что касательная, проведённая к графику функции в точке с абсциссой $1$, образует больший угол с положительным направлении оси $Ox$, значит, значение производной в этой точке наибольшее.
Задача 4
На рисунке изображён график $y=f'(x)$ — производной функции $f(x)$, определённой на интервале $(-6;9)$. Найдите промежутки возрастания функции $f(x)$. В ответе укажите длину наибольшего из них.
Решение
Так как производная функции $y = f′(x)$ положительна на промежутках $(-6; -3)$ и $(8,5; 9)$, то функция $y = f(x$) возрастает на этих промежутках. Длина наибольшего из них $(-6; -3)$ равна $-3 — (-6) = 3$
Задача 5
На рисунке изображён график $y=f'(x)$ — производной функции $f(x)$, определённой на интервале $(-6;9)$. Найдите промежутки убывания функции $f(x)$. В ответе укажите длину наибольшего из них.
Решение
Так как на промежутке $(-3;8)$ производная функции $y=f'(x)$ отрицательна, то на этом промежутке функция $y=f(x)$ убывает. Длина этого промежутка равна $8-(-3)=11$.
Задача 6
На рисунке изображён график $y=f'(x)$ — производной функции $f(x)$, определённой на интервале $(-8;5)$. Найдите промежутки убывания функции $f(x)$. В ответе укажите сумму целых точек, входящих в эти промежутки.
Решение
Так как на промежутке (-6.5; -3.5) производная функции y = f′(x) отрицательна, то на этом промежутке функция y = f (x) убывает. В этот промежуток входят целые точки: -6; -5; -4. Их сумма равна -15.
Задача 7
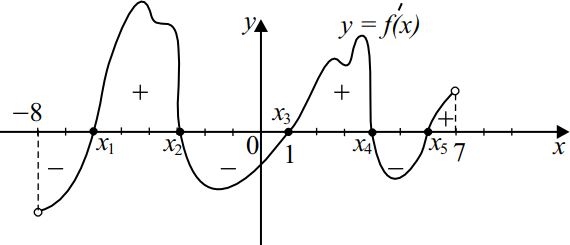
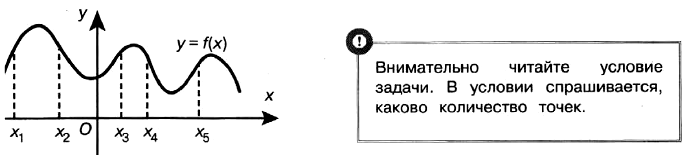
На рисунке изображён график $y=f'(x)$ — производной функции $f(x)$, определённой на интервале $(-8;7)$. Найдите количество точек экстремума функции $f(x)$ на заданном интервале.
Решение
Из графика видно, что производная $f′(x)$ функции $f(x)$ равна нулю в пяти точках причём при переходе через эти точки она меняет знак. То есть на заданном промежутке таких точек $5: x_1 , x_2 , x_3 , x_4 , x_5$. Таким образом, функция $f (x)$ имеет $5$ точек экстремума на заданном промежутке.
Задача 8
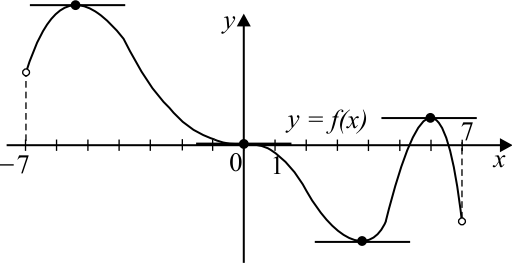
На рисунке изображён график функции $y=f(x)$, определённой на интервале $(-7;7)$. Найдите количество решений уравнения $f'(x)=0$.
Решение
Производная функции y = f′(x) на интервале (-7; 7) равна нулю в 4-х точках, в которых касательная к графику функции y = f(x) параллельна оси абсцисс.
Задача 9
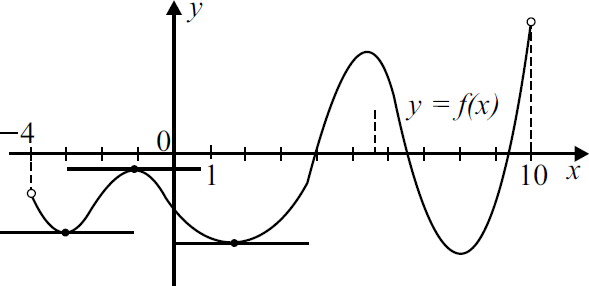
На рисунке изображён график функции $y=f(x)$, определённой на интервале $(-4;10)$. Найдите количество решений уравнения $f'(x)=0$ на интервале $(-4;3)$.
Решение
Так как угловой коэффициент касательной $k = tg α = f′(x_0) = 0$, то это означает, что касательная к графику данной функции параллельна оси абсцисс.
На интервале $(-4; 3)$ построены три касательные, параллельные оси абсцисс.
Задача 10
Прямая $y=38x-28$ параллельна касательной к графику функции $y=3x^2+8x-2$. Найдите абсциссу точки касания.
Решение
Угловой коэффициент касательной к графику функции $y = 3x^2+8x-2$ в некоторой точке $x_0$ равен $y′(x_0). y′ = (3x^2 + 8x — 2)′ = 6x + 8$, значит, $y′(x_0) = 6x_0+8$. Угловой коэффициент прямой $y = 38x-28$ равен $38$. По условию, эта прямая параллельна касательной, значит, их угловые коэффициенты равны. Найдём значение $x_0$ из условия $6x_0 + 8 = 38, x_0 = 5$.
Задача 11
На рисунке изображён график $y=f'(x)$ — производной функции $f(x)$. На оси абсцисс отмечено десять точек: $x_1$, $x_2$, $x_3$, … , $x_8$, $x_9$, $x_$. Сколько из этих точек лежит на промежутках убывания функции $f(x)$?
Решение
Так как производная функции $y = f′(x)$ отрицательна в точках $x_1, x_2, x_3$ и $x_8, x_9, x_$, то на промежутках убывания лежат $6$ точек.
Задача 12
На рисунке изображён график $y=f'(x)$ — производной функции $f(x)$. На оси абсцисс отмечено десять точек: $x_1$, $x_2$, $x_3$, … , $x_8$, $x_9$, $x_$. Сколько из этих точек лежит на промежутках возрастания функции $f(x)$?
Решение
Так как производная $y=f'(x)$ положительна в точках $x_4$, $x_5$, $x_6$, $x_7$, а в остальных точках — отрицательна, то на промежутке возрастания лежат $4$ точки.
Задача 13
На рисунке изображён график функции $y=f(x)$ и восемь точек на оси абсцисс: $x_1$, $x_2$, $x_3$, … ,$x_8$. В скольких из этих точек производная функции $f(x)$ отрицательна?
Решение
Производная отрицательна только в тех точках, которые принадлежат промежуткам убывания функции, если касательные в них не горизонтальны. Таких точек $3: x_3, x_5, x_8$.
Задача 14
Материальная точка движется прямолинейно по закону
$x(t)= / t^3- / t^2-3t+5$, где $x$ — расстояние от точки отсчёта в метрах, $t$ — время в секундах, измеренное с начала движения. В какой момент времени (в секундах) её скорость была равна $5$ м/с?
Решение
Найдём скорость движения материальной точки $v(t) = x′(t) = t^2-7t-3$.
Найдём в какой момент времени (в секундах) её скорость была равна $5$ м/с, решив уравнение $t^2-7t-3 = 5$.
$t_1 = 8, t_2 = -1$ не удовлетворяет условию задачи.
Скорость материальной точки была равна $5$ м/с в момент времени $8$ секунд.
Задача 15
Материальная точка движется прямолинейно по закону
$x(t)=t^2-t-12$, где $x$ — расстояние от точки отсчёта в метрах, $t$ — время в секундах, измеренное с начала движения. Найдите её скорость (в метрах в секунду) в момент времени $t=7$ с.
Решение
Согласно физическому смыслу производной, мгновенная скорость равна $v(t) = x′(t). v(t) = (t^2-t-12)′ = 2t-1. v(7) = 2·7-1 = 13$. Скорость материальной точки была $13$ м/с в момент времени $7$ секунд.
Задача 16
На рисунке изображён график функции $y=g(x)$, определённой и дифференцируемой на интервале $(-8; 6)$. Найдите количество точек, в которых касательная к графику этой функции параллельна прямой $y=100$.
Решение
Построим прямую y = 100. По графику определяем, что касательная к графику функции y = g(x) параллельна прямой y = 100 в четырёх точках.
Задача 17
На рисунке изображён график функции $y=f(x)$, определённой и дифференцируемой на интервале $(-6;7)$. Найдите количество точек, в которых касательная к графику функции $f(x)$ параллельна прямой $y=4$.
Решение
Построим прямую $y=4$. По графику находим, что касательная к графику функции $y=f(x)$ параллельна прямой $y=4$ в $6$ точках (см. рис.).
Задание 6. Функции. Производная и первообразная. ЕГЭ 2022 по математике профильного уровня
За это задание ты можешь получить 1 балл. На решение дается около 5 минут. Уровень сложности: Базовый.
Средний процент выполнения: 61.5%
Ответом к заданию 6 по математике (профильной) может быть Целое число или конечная десятичная дробь.
На рисунке изображён график функции $y=f'(x)$ производной функции $f(x)$, определённой на интервале $(-7;4)$. В какой точке отрезка $[-3;2]$ функция $f(x)$ принимает наибольшее значение?
Решение
На отрезке $[-3; 2]$ производная $y = f′(x)$ равна нулю в точке $x = -2$ и при переходе через неё меняет свой знак с «+» на «-», поэтому точка $x = -2$ — точка максимума функции на отрезке $[−3; 2]$. Так как она, кроме того, единственная точка экстремума на отрезке $[−3; 2]$, то в ней функция принимает наибольшее значение на данном отрезке.
Найдите значение производной функции f x в точке x_0.
Egeturbo. ru
12.08.2017 19:17:26
2017-08-12 19:17:26
Источники:
Https://egeturbo. ru/ege/math/tasks/6
Задание 6 из ЕГЭ по математике | Функции. Производная и первообразная » /> » /> .keyword { color: red; } 6ое задание егэ математика профиль
Задание 6 из ЕГЭ по математике (профильной)
Задание 6 из ЕГЭ по математике (профильной)
На рисунке изображён график $y=f'(x)$ — производной функции $f(x)$, определённой на интервале $(-5;8)$. Найдите точку экстремума функции $f(x)$, принадлежащую отрезку $[-3;7]$.
На рисунке изображён график функции $y=F(x)$, которая является первообразной для функции $y=f(x)$. Найдите площадь под графиком функции $y=f(x)$ на отрезке $[2; 6]$.
На рисунке изображён график $y=f'(x)$ производной функции $f(x)$. Найдите абсциссу точки, в которой касательная к графику $y=f(x)$ параллельна оси абсцисс или совпадает с ней.
На рисунке изображён график $y=f'(x)$ производной функции $f(x)$. Найдите абсциссу точки, в которой касательная к графику $y=f(x)$ параллельна прямой $y=2x+2$ или совпадает с ней.
На рисунке изображён график функции $y=f(x)$ и касательная к нему в точке с абсциссой $x_0$. Найдите значение производной функции $f(x)$ в точке $x_0$.
На рисунке изображён график $y=f'(x)$ — производной функции $f(x)$, определённой на интервале $(-8;6)$. В какой точке отрезка $[-5;-4]$ функция принимает наименьшее значение?
На рисунке изображён график $y=f'(x)$ — производной функции $f(x)$, определённой на интервале $(-8;5)$. Найдите промежутки возрастания функции $f(x)$. В ответе укажите сумму целых точек, в…
На рисунке изображён график $y=f'(x)$ — производной функции $f(x)$, определённой на интервале $(-6;9)$. Найдите количество точек максимума функции $f(x)$ на заданном интервале.
На рисунке изображён график функции $y=f(x)$, определённой на интервале $(-7;7)$. Найдите количество точек, в которых касательная к графику функции параллельна прямой $y=5$.
Прямая $y=4x+4$ параллельна касательной к графику функции $y=2x^2-5x+10$. Найдите абсциссу точки касания.
Материальная точка движется прямолинейно по закону
$x(t)= / t^3- / t^2-3t+7$, где $x$ — расстояние от точки отсчёта в метрах, $t$ — время в секундах, измеренное с начала дви…
Материальная точка движется прямолинейно по закону
$x(t)=3t^2-10t+3$, где $x$ — расстояние от точки отсчёта в метрах, $t$ — время в секундах, измеренное с начала движения. Найдите её ск…
На рисунке изображен график функции $y=f(x)$. Прямая, проходящая через начало координат, касается графика этой функции в точке с абсциссой $5$. Найдите $f'(5)$.
Материальная точка движется прямолинейно по закону $x(t) = /t^3 + 2t^2 + 5t$, где $x$ — расстояние от точки отсчета в метрах, $t$ — время в секундах, измеренное с начала движения. В…
Материальная точка движется прямолинейно по закону $x(t) = /t^3 — 4t^2 + t$, где $x$ — расстояние от точки отсчёта в метрах, $t$ — время в секундах, измеренное с начала движения. В…
Материальная точка движется прямолинейно по закону $x(t) = — t^ +7t^ +6t+16$, где $x$ — расстояние от точки отсчёта в метрах, $t$ — время в секундах, измеренное с начала движения. Н…
Материальная точка движется прямолинейно по закону $x(t) = /t^ — 4t^ + t$, где $x$ — расстояние от точки отсчета в метрах, $t$ — время в секундах, измеренное с начала движен…
На рисунке изображены график функции $y=f(x)$ и касательная к нему в точке с абсциссой $x_0$. Найдите значение производной функции $f(x)$ в точке $x_0$.
Найдите тангенс угла наклона касательной, проведённой к графику функции $f(x)=77x^2+202x-814$ в точке с абсциссой $x_0=7$.
Материальная точка движется прямолинейно по закону $x(t)=4t^2+53t+161$, где $x$ — расстояние от точки отсчёта в метрах, $t$ — время в секундах, измеренное с начала движения. Найдите её с…
Материальная точка движется прямолинейно по закону x t t 3 — 4t 2 t, где x — расстояние от точки отсчёта в метрах, t — время в секундах, измеренное с начала движения.
Examer. ru
24.03.2020 8:43:27
2020-03-24 08:43:27
Источники:
Https://examer. ru/ege_po_matematike/2022/zadanie_6/
ЕГЭ по математике Профиль. Задание 6: Уметь выполнять действия с функциями. Материалы для подготовки к итоговой аттестации. Алгоритм выполнения задания. Примеры с объяснением выбора правильного ответа. Анализ типичных ошибок.
Вернуться к Оглавлению раздела «Анализ заданий ЕГЭ по математике».
ЕГЭ Профиль. Задание № 6
АЛГОРИТМ ВЫПОЛНЕНИЯ
Задание № 6 ЕГЭ профиль проверяет умение применять производную для решения прикладных задач. Такие задачи часто встречаются в физике и технических областях науки.
Задание состоит из текстовой задачи на определение физического, геометрического смысла производной, промежутков возрастания и убывания функции по её графику и графику её производной или первообразной. Ответом является целое число или конечная десятичная дробь.
При подготовке необходимо повторить правила нахождения производной, физический и геометрический смысл производной, понятие возрастания и убывания функции, понятие первообразной.
План выполнения задания № 6:
- Внимательно прочитайте задачу.
- Рассмотрите график. Определите, какой из графиков вам дан: функции, производной функции или первообразной функции. От ответа на данный вопрос зависит ход решения задачи.
- Определите по графику необходимые значения.
- Запишите полученное число в поле ответа КИМ и бланк ответов № 1.
1) Задачи на Физический смысл производной
Задачи на применение физического смысла производной состоят из текста и выражения, описывающего уравнение движения материальной точки или тела.
Производная перемещения по времени выражает скорость движения: v(t) = x'(t) = at + v0.
Производная скорости по времени выражает ускорение движения: a(t) = v'(t).
Задача № 6 (1). Материальная точка движется прямолинейно по закону x(t) = 2t2 – 8t – 9, где х — расстояние от точки отсчёта в метрах, t — время в секундах, измеренное с начала движения. Найдите её скорость (в м/с) в момент времени t = 5с.
Решение: Найдём закон изменения скорости: v(t) = x'(t) = 4t – 8.
При t = 5 имеем: v(5) = 4 • 5 – 8 = 12.
Ответ: 12.
Комментарий. Иногда в ответе получаются отрицательные числа, которые учащиеся рассматривают как ошибочный ответ.
Задача № 6 (2). Тело движется прямолинейно по закону: x(t) = 2t3 + t – 1. В какой момент времени (в секундах) его ускорение будет равно 12 м/с2?
Решение: Найдём закон изменения скорости: v(t) = x'(t) = 6t2 + 1.
Ускорение — это производная скорости по времени: a(t) = v'(t) = 12t.
Чтобы найти, в какой момент времени ускорение было 12 м/с2, решим уравнение: 12t = 12. Отсюда t = 1 c.
Ответ: 1.
Комментарий. Обратите внимание: в задании нужно найти, в какой момент времени ускорение (не скорость!) будет равно 12 м/с2.
2) Задачи на Геометрический смысл производной
Задание ориентировано на умение выпускников читать и анализировать графики, содержит задачи на определение или вычисление величин по графику, рассчитано на умение использовать знания в практической деятельности. При подготовке нужно повторить понятия: точка максимума, точка минимума, точки экстремума, убывание и возрастание функции, уравнение касательной к графику функции.
Геометрический смысл производной: угловой коэффициент касательной к графику функции в точке с абсциссой х0 равен производной этой функции в точке х0.
Геометрический смысл производной: k = tg a = f'(x)
Производная функции в точке с абсциссой х есть тангенс угла наклона касательной, проведённой к графику этой функции в точке (х0; f(x0)). При tg a > 0 производная функции положительна, при tg a < 0 производная отрицательна. При tg a = 0 производная равна нулю.
Точка х0 называется точкой максимума (минимума) функции, если существует такая окрестность точки х0, что для любого х из этой окрестности верно неравенство f(x) < f(x0) (f(x) > f(x0)).
Задача № 6 (3). На рисунке изображён график функции y = f(x) и отмечены пять точек на оси абсцисс: х1, х2, х3, х4, х5. В скольких из этих точек производная функции f(x) отрицательна?
Решение: Производная функции отрицательна в тех точках, которые принадлежат участкам убывания функции. Это точки х2, х4 — всего 2 точки.
Ответ: 2.
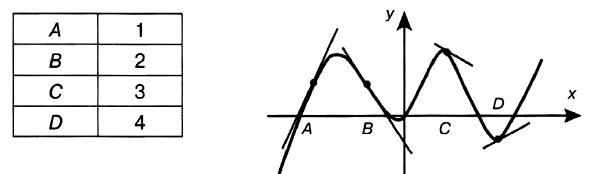
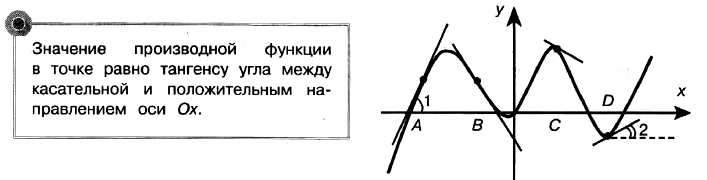
Задача № 6 (4). На рисунке изображены график функции и касательные, проведённые к нему в точках с абсциссами А, В, С и D. Пользуясь графиком, определите, в какой из данных точек значение производной наибольшее. В ответе укажите число, которое ей соответствует по таблице.
Решение: Производная функции положительна в точках А и D, так как в данных точках функция возрастает.
Угол 1 больше угла 2, значит, тангенс первого угла больше тангенса второго угла, соответственно, значение производной в точке А больше значения производной в точке D.
Ответ: 1.
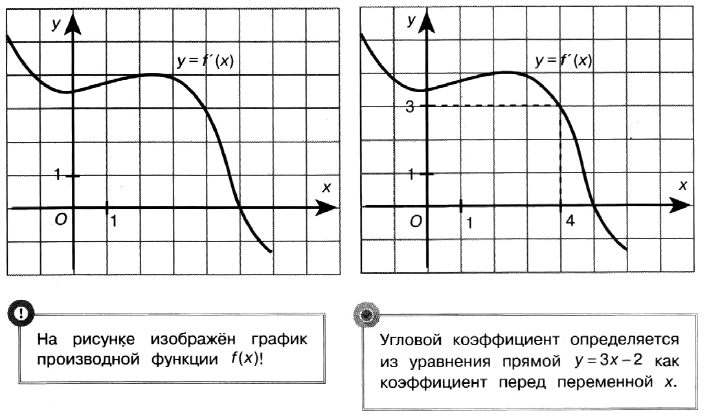
Задача № 6 (5). На рисунке изображён график производной функции f(x). Найдите абсциссу точки, в которой касательная к графику параллельна прямой у = 3х–2 или совпадает с ней.
Решение: Поскольку касательная параллельна прямой у = 3х – 2 или совпадает с ней, она имеет угловой коэффициент, равный 3 (у’ = 3). Найдём, при каких х производная принимает значение 3. Из графика видно, что значению у = 3 соответствует точка х = 4.
Ответ: 4.
3) Задачи на Применение
производной к исследованию функций
Задание содержит задачи на определение или вычисление величин по графику, рассчитано на умение использовать знания в практической деятельности. При подготовке нужно повторить понятия: точка максимума, точка минимума, точки экстремума, убывание и возрастание функции, уравнение касательной к графику функции.
- Если функция y = f(x) имеет экстремум в точке х0, то в этой точке производная равна нулю или не существует.
- Если f'(x) = 0 и при переходе через точку х0 значения производной меняют знак с «+» на «–», то х0 — точка максимума.
- Если f'(x) = 0 и при переходе через точку х0 значения производной меняют знак с «–» на «+», то х0 — точка минимума.
- Если f'(x) = 0 и при переходе через точку х0 значения производной не меняют знак, то х0 не является точкой экстремума.
- Если в каждой точке х некоторого промежутка f'(х) > 0, то функция f(x) возрастает на этом промежутке.
- Если в каждой точке х некоторого промежутка f'(х) < 0, то функция f{x) убывает на этом промежутке.
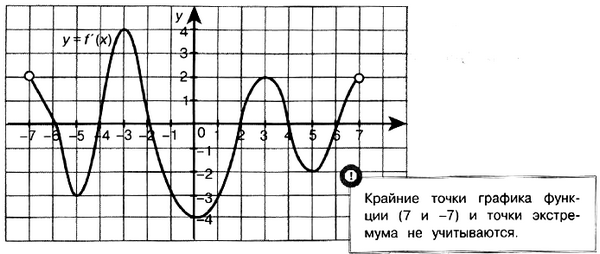
Задача № 6 (6). На рисунке изображён график производной функции f(x), определённой на интервале (–7; 7). Найдите промежутки возрастания функции f(x). В ответе укажите сумму целых точек, входящих в эти промежутки.
Решение: Промежутки возрастания данной функции f(x) соответствуют промежуткам, на которых её производная положительна, то есть промежуткам (–7; –6); (–4; –2); (2; 4); (6; 7). Данные промежутки содержат целые числа –3; 3. Их сумма равна 0.
Ответ: 0.
ПРИМЕЧАНИЕ: В ответе нужно указать сумму целых точек, входящих в промежутки возрастания.
4) Задачи на Первообразную
Функцию y = F(x) называют первообразной для функции y = f(x) на заданном промежутке х, если для всех х из этого промежутка верно равенство F'(x) = f(x).
Если функция y = F(x) является первообразной для функции y = f(x) на некотором промежутке, то и функция y = F(x) + C (С — постоянная) является первообразной для функции f на этом промежутке.
Пусть функция f(x) непрерывна на отрезке [а; b]. Тогда площадь трапеции, ограниченной линиями y = f(x); у = а; у = b и у = 0, равна F(b) – F(a), где F(x) — первообразная функции f(x).
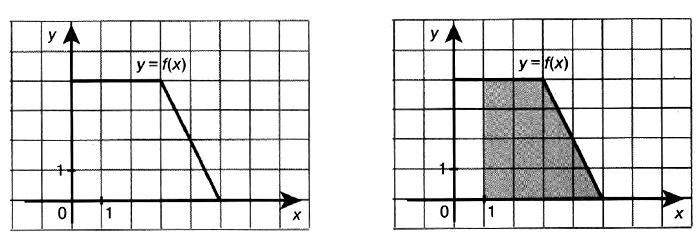
Задача № 6 (7). На рисунке изображён график некоторой функции y = f(x). Пользуясь рисунком, вычислите F(5) – F(1), где F(x) — одна из первообразных функции f(x).
Решение: Разность значений первообразной в точках 5 и 1 равна площади выделенной на рисунке трапеции.
Площадь трапеции ограничена точками 1 и 5.
Площадь трапеции вычисляется по формуле S = h • (a + b)/2.
Из рисунка видно, что а =2, b = 4, h = 4. Значит, F(5) – F(1) = 4 • (2 + 4)/2 = 12.
Ответ: 12.
ПРИМЕЧАНИЕ: Если результат отрицательный или равен нулю, значит, в вычислениях была допущена ошибка.
Тренировочные задания с самопроверкой
№ 6.1. На рисунке изображён график у = f’(x) – производной функции f(x), определённой на интервале (–5; 7). В какой точке отрезка [–3; 2] f(x) принимает наименьшее значение?
Открыть ОТВЕТ
№ 6.2. Прямая у = 5х + 4 параллельна касательной к графику функции у = х2 – 4х – 12. Найдите абсциссу точки касания.
Открыть ОТВЕТ
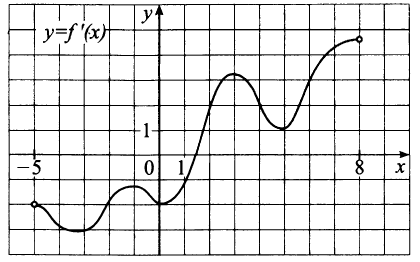
№ 6.3. На рисунке изображён график у = f‘(х) – производной функции f(х), определённой на интервале (–5; 8). Найдите количество точек, в которых касательная к графику функции f(х) параллельна прямой у = 2х – 4 или совпадает с ней.
Открыть ОТВЕТ
№ 6.4. На рисунке изображён график у = f‘(x) – производной функции f(x), определённой на интервале (–7; 8). Найдите, в какой точке отрезка [–4; 4] функция принимает наибольшее значение.
Открыть ОТВЕТ
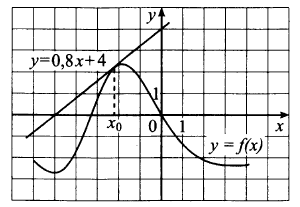
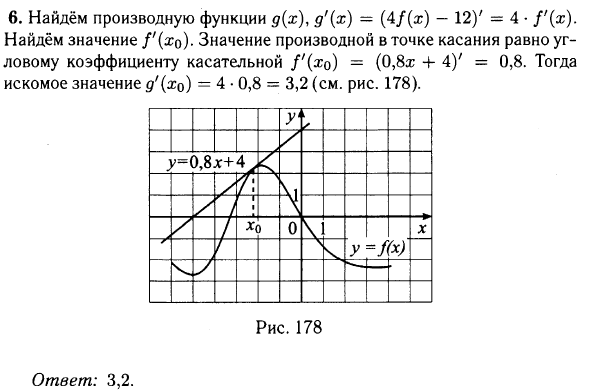
№ 6.5. На рисунке изображены график функции у = f(x) и касательная к этому графику, проведённая в точке x0. Уравнение касательной показано на рисунке. Найдите значение производной функции g(х) = 4f(x) – 12 в точке x0.
Открыть ОТВЕТ
Вы смотрели: ЕГЭ по математике Профиль. Задание 6: Уметь выполнять действия с функциями. Материалы для подготовки к итоговой аттестации. Алгоритм выполнения задания. Примеры с объяснением выбора правильного ответа. Анализ типичных ошибок.
Вернуться к Оглавлению раздела «Анализ заданий ЕГЭ по математике».
Просмотров:
20 975
- ЕГЭ по математике профиль
Прототипы задания №6 ЕГЭ по математике профильного уровня — производная и первообразная. Практический материал для подготовки к экзамену в 11 классе.
Для успешного выполнения задания №6 необходимо уметь выполнять действия с функциями.
Практика
Примеры заданий:
Коды проверяемых элементов содержания (по кодификатору) — 4.1–4.3
Уровень сложности задания — базовый.
Примерное время выполнения задания выпускником, изучавшим математику на профильном уровне (в мин.) — 4
Связанные страницы:
ЕГЭ Профиль №6. Вычисление значений тригонометрических выражений
Скачать файл в формате pdf.
ЕГЭ Профиль №6. Вычисление значений тригонометрических выражений
| Задача 1. Найдите значение выражения (frac{{50sin {{179}^ circ } cdot cos {{179}^ circ }}}{{sin {{358}^ circ }}})
Ответ
ОТВЕТ: 25. Решение
Воспользуемся формулой синуса двойного угла: (sin 2alpha = 2sin alpha cos alpha ) (frac{{50sin {{179}^ circ } cdot cos {{179}^ circ }}}{{sin {{358}^ circ }}} = frac{{50sin {{179}^ circ } cdot cos {{179}^ circ }}}{{sin left( {2 cdot {{179}^ circ }} right)}} = frac{{50sin {{179}^ circ } cdot cos {{179}^ circ }}}{{2sin {{179}^ circ } cdot cos {{179}^ circ }}} = 25.) Ответ: 25. |
| Задача 2. Найдите значение выражения (8sin frac{{5{\pi }}}{{12}} cdot cos frac{{5{\pi }}}{{12}})
Ответ
ОТВЕТ: 2. Решение
Воспользуемся формулой синуса двойного угла: (sin 2alpha = 2sin alpha cos alpha ) (8sin frac{{5pi }}{{12}}cos frac{{5pi }}{{12}} = 4 cdot 2 cdot sin frac{{5pi }}{{12}}cos frac{{5pi }}{{12}} = 4 cdot sin left( {2 cdot frac{{5pi }}{{12}}} right) = 4 cdot sin frac{{5pi }}{6} = 4 cdot frac{1}{2} = 2.) Ответ: 2. |
| Задача 3. Найдите значение выражения (frac{{24left( {{{sin }^2}{{17}^ circ } — {{cos }^2}{{17}^ circ }} right)}}{{cos {{34}^ circ }}})
Ответ
ОТВЕТ: — 24. Решение
Воспользуемся формулой косинус двойного угла: (cos 2alpha = {cos ^2}alpha — {sin ^2}alpha ) (frac{{24left( {{{sin }^2}{{17}^ circ } — {{cos }^2}{{17}^ circ }} right)}}{{cos {{34}^ circ }}} = frac{{ — 24left( {{{cos }^2}{{17}^ circ } — {{sin }^2}{{17}^ circ }} right)}}{{cos {{34}^ circ }}} = frac{{ — 24cos {{34}^ circ }}}{{cos {{34}^ circ }}} = — 24.) Ответ: — 24. |
| Задача 4. Найдите значение выражения (sqrt 3 {cos ^2}frac{{5{pi }}}{{12}} — sqrt 3 {sin ^2}frac{{5pi }}{{12}})
Ответ
ОТВЕТ: — 1,5. Решение
Воспользуемся формулой косинус двойного угла: (cos 2alpha = {cos ^2}alpha — {sin ^2}alpha ) (sqrt 3 {cos ^2}frac{{5pi }}{{12}} — sqrt 3 {sin ^2}frac{{5pi }}{{12}} = sqrt 3 left( {{{cos }^2}frac{{5pi }}{{12}} — {{sin }^2}frac{{5pi }}{{12}}} right) = sqrt 3 cos left( {2 cdot frac{{5pi }}{{12}}} right) = ) ( = sqrt 3 cos frac{{5pi }}{6} = sqrt 3 cdot left( { — frac{{sqrt 3 }}{2}} right) = — 1,5.) Ответ: — 1,5. |
| Задача 5. Найдите значение выражения (sqrt {12} {cos ^2}frac{{5{pi }}}{{12}} — sqrt 3 )
Ответ
ОТВЕТ: — 1,5. Решение
Воспользуемся формулой косинус двойного угла: (cos 2alpha = 2{cos ^2}alpha — 1) (sqrt {12} {cos ^2}frac{{5pi }}{{12}} — sqrt 3 = sqrt 3 left( {2{{cos }^2}frac{{5pi }}{{12}} — 1} right) = sqrt 3 cdot cos left( {2 cdot frac{{5pi }}{{12}}} right) = ) ( = sqrt 3 cos frac{{5pi }}{6} = sqrt 3 cdot left( { — frac{{sqrt 3 }}{2}} right) = — 1,5.) Ответ: — 1,5. |
| Задача 6. Найдите значение выражения (sqrt 3 — sqrt {12} {sin ^2}frac{{5{pi }}}{{12}})
Ответ
ОТВЕТ: — 1,5. Решение
Воспользуемся формулой косинус двойного угла: (cos 2alpha = 1 — 2{sin ^2}alpha ) (sqrt 3 — sqrt {12} {sin ^2}frac{{5pi }}{{12}} = sqrt 3 left( {1 — 2{{sin }^2}frac{{5pi }}{{12}}} right) = sqrt 3 cos left( {2 cdot frac{{5pi }}{{12}}} right) = ) ( = sqrt 3 cos frac{{5pi }}{6} = sqrt 3 cdot left( { — frac{{sqrt 3 }}{2}} right) = — 1,5.) Ответ: — 1,5. |
| Задача 7. Найдите ( — 47cos 2alpha ), если (cos alpha = — 0,4)
Ответ
ОТВЕТ: 31,96. Решение
Воспользуемся формулой косинус двойного угла: (cos 2alpha = 2{cos ^2}alpha — 1) ( — 47cos 2alpha = — 47 cdot left( {2{{cos }^2}alpha — 1} right) = — 47 cdot left( {2 cdot {{left( { — 0,4} right)}^2} — 1} right) = ) ( = — 47 cdot left( {0,32 — 1} right) = — 47 cdot left( { — 0,68} right) = 31,96.) Ответ: 31,96. |
| Задача 8. Найдите значение выражения (frac{{5cos {{29}^ circ }}}{{sin {{61}^ circ }}})
Ответ
ОТВЕТ: 5. Решение
(frac{{5cos {{29}^ circ }}}{{sin {{61}^ circ }}} = frac{{5cos left( {{{90}^ circ } — {{61}^ circ }} right)}}{{sin {{61}^ circ }}} = frac{{5sin {{61}^ circ }}}{{sin {{61}^ circ }}} = 5.) При решении воспользовались формулой приведения: (cos left( {{{90}^ circ } — alpha } right) = sin alpha .) Ответ: 5. |
| Задача 9. Найдите значение выражения (36sqrt 3 {text{tg}}frac{{\pi }}{3}sin frac{{\pi }}{6})
Ответ
ОТВЕТ: 54. Решение
(36sqrt 3 ,,tgfrac{pi }{3} cdot sin frac{pi }{6} = 36sqrt 3 cdot sqrt 3 cdot frac{1}{2} = 18 cdot 3 = 54.) Ответ: 54. |
| Задача 10. Найдите значение выражения (4sqrt 2 cos frac{{\pi }}{4}cos frac{{7{\pi }}}{3})
Ответ
ОТВЕТ: 2. Решение
(4sqrt 2 cos frac{pi }{4}cos frac{{7pi }}{3} = 4sqrt 2 cdot frac{{sqrt 2 }}{2}cos left( {frac{{7pi }}{3} — 2pi } right) = 4 cdot cos frac{pi }{3} = 4 cdot frac{1}{2} = 2.) При решении воспользовались периодичностью косинуса: (cos left( {alpha — 2pi } right) = cos alpha .) Ответ: 2. |
| Задача 11. Найдите значение выражения (frac{8}{{sin left( { — frac{{27{\pi }}}{4}} right)cos left( {frac{{31{\pi }}}{4}} right)}})
Ответ
ОТВЕТ: — 16. Решение
(sin left( { — frac{{27pi }}{4}} right) = sin left( { — frac{{27pi }}{4} + 8pi } right) = sin frac{{5pi }}{4} = — frac{{sqrt 2 }}{2}) (cos left( {frac{{31pi }}{4}} right) = cos left( {frac{{31pi }}{4} — 8pi } right) = cos left( { — frac{pi }{4}} right) = cos frac{pi }{4} = frac{{sqrt 2 }}{2}) (frac{8}{{sin left( { — frac{{27pi }}{4}} right) cdot cos left( {frac{{31pi }}{4}} right)}} = frac{8}{{ — frac{{sqrt 2 }}{2} cdot frac{{sqrt 2 }}{2}}} = — 16.) Ответ: — 16. |
| Задача 12. Найдите значение выражения (33sqrt 2 cos left( {{{495}^ circ }} right))
Ответ
ОТВЕТ: — 33. Решение
(33sqrt 2 cos left( {{{495}^ circ }} right) = 33sqrt 2 cos left( {{{495}^ circ } — {{360}^ circ }} right) = 33sqrt 2 cos {135^ circ } = 33sqrt 2 cdot left( { — frac{{sqrt 2 }}{2}} right) = — 33.) Ответ: — 33. |
| Задача 13. Найдите значение выражения (2sqrt 3 {text{tg}}left( { — {{300}^ circ }} right))
Ответ
ОТВЕТ: 6. Решение
(2sqrt 3 tgleft( { — {{300}^ circ }} right) = 2sqrt 3 tgleft( { — {{300}^ circ } + {{360}^ circ }} right) = 2sqrt 3 tg{60^ circ } = 2sqrt 3 cdot sqrt 3 = 6.) Ответ: 6. |
| Задача 14. Найдите значение выражения ( — 18sqrt 2 sin left( { — {{135}^ circ }} right))
Ответ
ОТВЕТ: 18. Решение
( — 18sqrt 2 sin left( { — {{135}^ circ }} right) = 18sqrt 2 sin {135^ circ } = 18sqrt 2 cdot frac{{sqrt 2 }}{2} = 18.) Ответ: 18. |
| Задача 15. Найдите значение выражения (24sqrt 2 cos left( { — frac{{\pi }}{3}} right)sin left( { — frac{{\pi }}{4}} right))
Ответ
ОТВЕТ: — 12. Решение
(24sqrt 2 cos left( { — frac{pi }{3}} right)sin left( { — frac{pi }{4}} right) = — 24sqrt 2 cos frac{pi }{3}sin frac{pi }{4} = — 24sqrt 2 cdot frac{1}{2} cdot frac{{sqrt 2 }}{2} = — 12.) Ответ: — 12. |
| Задача 16. Найдите значение выражения (frac{{14sin {{19}^ circ }}}{{sin {{341}^ circ }}})
Ответ
ОТВЕТ: — 14. Решение
(frac{{14sin {{19}^ circ }}}{{sin {{341}^ circ }}} = frac{{14sin {{19}^ circ }}}{{sin left( {{{341}^ circ } — {{360}^ circ }} right)}} = frac{{14sin {{19}^ circ }}}{{sin left( { — {{19}^ circ }} right)}} = frac{{14sin {{19}^ circ }}}{{ — sin {{19}^ circ }}} = — 14.) Ответ: — 14. |
| Задача 17. Найдите значение выражения (frac{{36cos {{93}^ circ }}}{{cos {{87}^ circ }}})
Ответ
ОТВЕТ: — 36. Решение
(frac{{36cos {{93}^ circ }}}{{cos {{87}^ circ }}} = frac{{ — 36cos left( {{{180}^ circ } — {{93}^ circ }} right)}}{{cos {{87}^ circ }}} = frac{{ — 36cos {{87}^ circ }}}{{cos {{87}^ circ }}} = — 36.) Ответ: — 36. |
| Задача 18. Найдите значение выражения (frac{{ — 37{text{tg6}}{{text{3}}^ circ }}}{{{text{tg11}}{{text{7}}^ circ }}})
Ответ
ОТВЕТ: 37. Решение
(frac{{ — 37tg{{63}^ circ }}}{{tg{{117}^ circ }}} = frac{{ — 37tg{{63}^ circ }}}{{ — tgleft( {{{180}^ circ } — {{117}^ circ }} right)}} = frac{{37tg{{63}^ circ }}}{{tg{{63}^ circ }}} = 37.) Ответ: 37. |
| Задача 19. Найдите значение выражения (frac{{14sin {{409}^ circ }}}{{sin {{49}^ circ }}})
Ответ
ОТВЕТ: 14. Решение
(frac{{14sin {{409}^ circ }}}{{sin {{49}^ circ }}} = frac{{14sin left( {{{409}^ circ } — {{360}^ circ }} right)}}{{sin {{49}^ circ }}} = frac{{14sin {{49}^ circ }}}{{sin {{49}^ circ }}} = 14.) Ответ: 14. |
| Задача 20. Найдите значение выражения (5{text{tg1}}{{text{7}}^ circ } cdot {text{tg10}}{{text{7}}^ circ })
Ответ
ОТВЕТ: — 5. Решение
(5,tg{17^ circ } cdot tg{107^ circ } = 5,tg{17^ circ } cdot tgleft( {{{90}^ circ } + {{17}^ circ }} right) = — 5,tg{17^ circ } cdot ctg{17^ circ } = — 5.) При решении воспользовались формулой приведения: (tgleft( {{{90}^ circ } + alpha } right) = — tgalpha ) и формулой: (tgalpha cdot ctgalpha = 1.) Ответ: — 5. |
| Задача 21. Найдите значение выражения ( — 6{text{tg3}}{{text{1}}^ circ } cdot {text{tg5}}{{text{9}}^ circ })
Ответ
ОТВЕТ: — 6. Решение
( — 6,,tg{31^ circ } cdot tg{59^ circ } = — ,6,tg{31^ circ } cdot tgleft( {{{90}^ circ } — {{59}^ circ }} right) = — ,6,tg{31^ circ } cdot ctg{31^ circ } = — 6.) При решении воспользовались формулой приведения: (tgleft( {{{90}^ circ } — alpha } right) = ctgalpha .) Ответ: — 6. |
| Задача 22. Найдите значение выражения (frac{{ — 12}}{{{{sin }^2}{{131}^ circ } + {{sin }^2}{{221}^ circ }}})
Ответ
ОТВЕТ: — 12. Решение
(frac{{ — 12}}{{{{sin }^2}{{131}^ circ } + {{sin }^2}{{221}^ circ }}} = frac{{ — 12}}{{{{sin }^2}{{131}^ circ } + {{sin }^2}left( {{{90}^ circ } + {{131}^ circ }} right)}} = frac{{ — 12}}{{{{sin }^2}{{131}^ circ } + {{cos }^2}{{131}^ circ }}} = — frac{{12}}{1} = — 12.) Ответ: — 12. |
| Задача 23. Найдите значение выражения (frac{{27}}{{{{cos }^2}{{116}^ circ } + {{cos }^2}{{206}^ circ }}})
Ответ
ОТВЕТ: 27. Решение
(frac{{27}}{{{{cos }^2}{{116}^ circ } + {{cos }^2}{{206}^ circ }}} = frac{{27}}{{{{cos }^2}{{116}^ circ } + {{cos }^2}left( {{{90}^ circ } + {{116}^ circ }} right)}} = frac{{27}}{{{{cos }^2}{{116}^ circ } + {{left( { — sin {{116}^ circ }} right)}^2}}} = ) ( = frac{{27}}{{{{cos }^2}{{116}^ circ } + {{sin }^2}{{116}^ circ }}} = frac{{27}}{1} = 27.) Ответ: 27. |
| Задача 24. Найдите значение выражения (frac{{ — 5}}{{{{sin }^2}{{16}^ circ } + {{cos }^2}{{196}^ circ }}})
Ответ
ОТВЕТ: — 5. Решение
(frac{{ — 5}}{{{{sin }^2}{{16}^ circ } + {{cos }^2}{{196}^ circ }}} = frac{{ — 5}}{{{{sin }^2}{{16}^ circ } + {{cos }^2}left( {{{180}^ circ } + {{16}^ circ }} right)}} = frac{{ — 5}}{{{{sin }^2}{{16}^ circ } + {{left( { — cos {{16}^ circ }} right)}^2}}} = ) ( = frac{{ — 5}}{{{{sin }^2}{{16}^ circ } + {{cos }^2}{{16}^ circ }}} = frac{{ — 5}}{1} = — 5.) Ответ: — 5. |
| Задача 25. Найдите значение выражения (frac{{ — 14sin {{84}^ circ }}}{{sin {{42}^ circ } cdot sin {{48}^ circ }}})
Ответ
ОТВЕТ: — 28. Решение
Воспользуемся формулой синуса двойного угла: (sin 2alpha = 2sin alpha cos alpha ) (frac{{ — 14sin {{84}^ circ }}}{{sin {{42}^ circ } cdot sin {{48}^ circ }}} = frac{{ — 14sin left( {2 cdot {{42}^ circ }} right)}}{{sin {{42}^ circ }sin {{48}^ circ }}} = frac{{ — 14 cdot 2 cdot sin {{42}^ circ } cdot cos {{42}^ circ }}}{{sin {{42}^ circ } cdot cos left( {{{90}^ circ } — {{48}^ circ }} right)}} = frac{{ — 28cos {{42}^ circ }}}{{cos {{42}^ circ }}} = — 28.) При решении воспользовались формулой приведения: (cos left( {{{90}^ circ } — alpha } right) = sin alpha .) Ответ: — 28. |
| Задача 26. Найдите значение выражения (frac{{5sin {{74}^ circ }}}{{cos {{37}^ circ } cdot cos {{53}^ circ }}})
Ответ
ОТВЕТ: 10. Решение
Воспользуемся формулой синуса двойного угла: (sin 2alpha = 2sin alpha cos alpha ) (frac{{5sin {{74}^ circ }}}{{cos {{37}^ circ } cdot cos {{53}^ circ }}} = frac{{5 cdot sin left( {2 cdot {{37}^ circ }} right)}}{{cos {{37}^ circ }cos {{53}^ circ }}} = frac{{5 cdot 2 cdot sin {{37}^ circ }cos {{37}^ circ }}}{{cos {{37}^ circ } cdot sin left( {{{90}^ circ } — {{53}^ circ }} right)}} = frac{{10sin {{37}^ circ }}}{{sin {{37}^ circ }}} = 10.) При решении воспользовались формулой приведения: (sin left( {{{90}^ circ } — alpha } right) = cos alpha .) Ответ: 10. |
| Задача 27. Найдите значение выражения (20sin {135^ circ } cdot cos {45^ circ })
Ответ
ОТВЕТ: 10. Решение
(20sin {135^ circ } cdot cos {45^ circ } = 20frac{{sqrt 2 }}{2} cdot frac{{sqrt 2 }}{2} = 10.) Ответ: 10. |
| Задача 28. Найдите ({text{tg}}alpha ), если (cos alpha = frac{1}{{sqrt {10} }}) и (a in left( {frac{{3{\pi }}}{2};;2{\pi }} right))
Ответ
ОТВЕТ: — 3. Решение
1 Вариант Воспользуемся формулой: (1 + t{g^2}alpha = frac{1}{{{{cos }^2}alpha }}). Тогда: (1 + t{g^2}alpha = frac{1}{{{{left( {frac{1}{{sqrt {10} }}} right)}^2}}},,,,,, Leftrightarrow ,,,,,1 + t{g^2}alpha = 10,,,,,, Leftrightarrow ,,,,,t{g^2}alpha = 9) Следовательно, (tgalpha = 3) или (tgalpha = — 3). Так как (alpha ,, in ,,left( {frac{{3pi }}{2};2pi } right)), то есть лежит в четвертой четверти, то его тангенс отрицательный. Поэтому (tgalpha = — 3.) 2 Вариант Воспользуемся основным тригонометрическим тождеством: ({sin ^2}alpha + {cos ^2}alpha = 1) ({sin ^2}alpha + {left( {frac{1}{{sqrt {10} }}} right)^2} = 1,,,,, Leftrightarrow ,,,,,,{sin ^2}alpha = 1 — frac{1}{{10}},,,,, Leftrightarrow ,,,,,{sin ^2}alpha = frac{9}{{10}}) Следовательно, (sin alpha = frac{3}{{sqrt {10} }}) или (sin alpha = — frac{3}{{sqrt {10} }}). Так как (alpha ,, in ,,left( {frac{{3pi }}{2};2pi } right)), то есть лежит в четвертой четверти, то его синус отрицательный. Поэтому (sin alpha = — frac{3}{{sqrt {10} }}). Воспользуемся тем, что: (tgalpha = frac{{sin alpha }}{{cos alpha }} = frac{{ — frac{3}{{sqrt {10} }}}}{{frac{1}{{sqrt {10} }}}} = — 3.) Ответ: — 3. |
| Задача 29. Найдите ({text{tg}}alpha ), если (sin alpha = — frac{5}{{sqrt {26} }}) и (alpha in left( {{\pi };;frac{{3{\pi }}}{2}} right))
Ответ
ОТВЕТ: 5. Решение
1 Вариант Воспользуемся формулой: (1 + ct{g^2}alpha = frac{1}{{{{sin }^2}alpha }}) Тогда: (1 + ct{g^2}alpha = frac{1}{{{{left( { — frac{5}{{sqrt {26} }}} right)}^2}}},,,,,,, Leftrightarrow ,,,,,,,1 + ct{g^2}alpha = frac{{26}}{{25}},,,,,,, Leftrightarrow ,,,,,,,ct{g^2}alpha = frac{1}{{25}}) Следовательно, (ctgalpha = frac{1}{5}) или (ctgalpha = — frac{1}{5}). Так как (alpha ,, in ,,left( {pi ;frac{{3pi }}{2}} right)), то есть лежит в третьей четверти, то его котангенс положительный. Поэтому (ctgalpha = frac{1}{5}.) Так как (tgalpha cdot ctgalpha = 1), то (tgalpha = frac{1}{{ctgalpha }} = frac{1}{{frac{1}{5}}} = 5.) 2 Вариант Воспользуемся основным тригонометрическим тождеством: ({sin ^2}alpha + {cos ^2}alpha = 1.) ({left( { — frac{5}{{sqrt {26} }}} right)^2} + {cos ^2}alpha = 1,,,,,, Leftrightarrow ,,,,,,{cos ^2}alpha = 1 — frac{{25}}{{26}},,,,,, Leftrightarrow ,,,,,,{cos ^2}alpha = frac{1}{{26}}.) Следовательно, (cos alpha = frac{1}{{sqrt {26} }}) или (cos alpha = — frac{1}{{sqrt {26} }}). Так как (alpha ,, in ,,left( {pi ;frac{{3pi }}{2}} right)), то есть лежит в третьей четверти, то косинус отрицательный. Поэтому (cos alpha = — frac{1}{{sqrt {26} }}). Воспользуемся тем, что: (tgalpha = frac{{sin alpha }}{{cos alpha }} = frac{{ — frac{5}{{sqrt {26} }}}}{{ — frac{1}{{sqrt {26} }}}} = 5.) Ответ: 5. |
| Задача 30. Найдите (3cos alpha ), если (sin alpha = — frac{{2sqrt 2 }}{3}) и (alpha in left( {frac{{3{\pi }}}{2};;2{\pi }} right))
Ответ
ОТВЕТ: 1. Решение
Воспользуемся основным тригонометрическим тождеством: ({sin ^2}alpha + {cos ^2}alpha = 1.) ({left( { — frac{{2sqrt 2 }}{3}} right)^2} + {cos ^2}alpha = 1,,,,,, Leftrightarrow ,,,,,{cos ^2}alpha = 1 — frac{8}{9},,,,,, Leftrightarrow ,,,,,,{cos ^2}alpha = frac{1}{9}) Следовательно, (cos alpha = frac{1}{3}) или (cos alpha = — frac{1}{3}). Так как (alpha ,, in ,,left( {frac{{3pi }}{2};2pi } right)), то есть лежит в четвертой четверти, то его косинус положительный. Поэтому (cos alpha = frac{1}{3}.) Тогда: (3cos alpha = 3 cdot frac{1}{3} = 1.) Ответ: 1. |
| Задача 31. Найдите (7sin alpha ), если (cos alpha = frac{{3sqrt 5 }}{7}) и (alpha in left( {1,5{\pi };;2{\pi }} right))
Ответ
ОТВЕТ: — 2. Решение
Воспользуемся основным тригонометрическим тождеством: ({sin ^2}alpha + {cos ^2}alpha = 1.) ({sin ^2}alpha + {left( {frac{{3sqrt 5 }}{7}} right)^2} = 1,,,,,, Leftrightarrow ,,,,,{sin ^2}alpha = 1 — frac{{45}}{{49}},,,,,, Leftrightarrow ,,,,,,{sin ^2}alpha = frac{4}{{49}}) Следовательно: (sin alpha = frac{2}{7}) или (sin alpha = — frac{2}{7}). Так как (alpha ,, in ,,left( {1,5pi ;2pi } right)), то есть лежит в четвертой четверти, то его синус отрицательный. Поэтому (sin alpha = — frac{2}{7}.) Тогда: (7sin alpha = 7 cdot left( { — frac{2}{7}} right) = — 2.) Ответ: — 2. |
| Задача 32. Найдите (24cos 2alpha ), если (sin alpha = — 0,2)
Ответ
ОТВЕТ: 22,08. Решение
Воспользуемся формулой косинус двойного угла: (cos 2alpha = 1 — 2{sin ^2}alpha ) (24cos 2alpha = 24 cdot left( {1 — 2{{sin }^2}alpha } right) = 24 cdot left( {1 — 2 cdot {{left( { — 0,2} right)}^2}} right) = 24 cdot left( {1 — 0,08} right) = 24 cdot 0,92 = 22,08) Ответ: 22,08. |
| Задача 33. Найдите (frac{{10sin 6alpha }}{{3cos 3alpha }}), если (sin 3alpha = 0,6)
Ответ
ОТВЕТ: 4. Решение
Воспользуемся формулой синуса двойного угла: (sin 2alpha = 2sin alpha cos alpha ) (frac{{10sin 6alpha }}{{3cos 3alpha }} = frac{{10 cdot sin left( {2 cdot 3alpha } right)}}{{3cos 3alpha }} = frac{{10 cdot 2 cdot sin 3alpha cdot cos 3alpha }}{{3cos 3alpha }} = frac{{20 cdot sin 3alpha }}{3} = frac{{20 cdot 0,6}}{3} = 4.) Ответ: 4. |
| Задача 34. Найдите значение выражения (frac{{3cos left( {{\pi } — beta } right) + sin left( {frac{{\pi }}{2} + beta } right)}}{{cos left( {beta + 3{\pi }} right)}})
Ответ
ОТВЕТ: 2. Решение
(frac{{3cos left( {pi — beta } right) + sin left( {frac{pi }{2} + beta } right)}}{{cos left( {beta + 3pi } right)}} = frac{{ — 3cos beta + cos beta }}{{ — cos beta }} = frac{{ — 2cos beta }}{{ — cos beta }} = 2.) Ответ: 2. |
| Задача 35. Найдите значение выражения (frac{{2sin left( {alpha — 7{\pi }} right) + cos left( {frac{{3{\pi }}}{2} + alpha } right)}}{{sin left( {a + {\pi }} right)}})
Ответ
ОТВЕТ: 1. Решение
(frac{{2sin left( {alpha — 7pi } right) + cos left( {frac{{3pi }}{2} + alpha } right)}}{{sin left( {alpha + pi } right)}} = frac{{ — 2sin alpha + sin alpha }}{{ — sin alpha }} = frac{{ — sin alpha }}{{ — sin alpha }} = 1.) Ответ: 1. |
| Задача 36. Найдите значение выражения (5{text{tg}}left( {5{\pi } — gamma } right) — {text{tg}}left( { — gamma } right)), если ({text{tg}}gamma {text{ = 7}})
Ответ
ОТВЕТ: — 28. Решение
(5,tgleft( {5pi — gamma } right) — tgleft( { — gamma } right) = — 5,tggamma + tggamma = — 4,tggamma = — 4 cdot 7 = — 28.) Ответ: — 28. |
| Задача 37. Найдите (sin left( {frac{{7{\pi }}}{2} — alpha } right)), если (sin alpha = 0,8) и (a in left( {frac{{\pi }}{2};;{\pi }} right))
Ответ
ОТВЕТ: 0,6. Решение
(sin left( {frac{{7pi }}{2} — alpha } right) = — cos alpha ) Воспользуемся основным тригонометрическим тождеством: ({sin ^2}alpha + {cos ^2}alpha = 1) ({0,8^2} + {cos ^2}alpha = 1,,,,, Leftrightarrow ,,,,,{cos ^2}alpha = 1 — 0,64,,,,, Leftrightarrow ,,,,,{cos ^2}alpha = 0,36) Следовательно, (cos alpha = 0,6) или (cos alpha = — 0,6). Так как (alpha ,, in ,,left( {frac{pi }{2};pi } right)), то есть лежит во второй четверти, то его косинус отрицательный. Поэтому: (sin left( {frac{{7pi }}{2} — alpha } right) = — cos alpha = — left( { — 0,6} right) = 0,6.) Ответ: 0,6. |
| Задача 38. Найдите (26cos left( {frac{{3{\pi }}}{2} + alpha } right)), если (cos alpha = frac{{12}}{{13}}) и (alpha in left( {frac{{3{\pi }}}{2};;2{\pi}} right))
Ответ
ОТВЕТ: — 10. Решение
(26cos left( {frac{{3pi }}{2} + alpha } right) = 26sin alpha ) Воспользуемся основным тригонометрическим тождеством: ({sin ^2}alpha + {cos ^2}alpha = 1) ({sin ^2}alpha + {left( {frac{{12}}{{13}}} right)^2} = 1,,,,,, Leftrightarrow ,,,,,,{sin ^2}alpha = 1 — frac{{144}}{{169}},,,,,,, Leftrightarrow ,,,,,{sin ^2}alpha = frac{{25}}{{169}}) Следовательно, (sin alpha = frac{5}{{13}}) или (sin alpha = — frac{5}{{13}}). Так как (alpha ,, in ,,left( {frac{{3pi }}{2};2pi } right)), то есть лежит в четвертой четверти, то его синус отрицательный. Поэтому: (26cos left( {frac{{3pi }}{2} + alpha } right) = 26sin alpha = 26 cdot left( { — frac{5}{{13}}} right) = — 10.) Ответ: — 10. |
| Задача 39. Найдите ({text{tg}}left( {alpha + frac{{5{\pi }}}{2}} right)), если ({text{tg}}alpha {text{ = 0}}{text{,4}})
Ответ
ОТВЕТ: — 2,5. Решение
(tgleft( {alpha + frac{{5pi }}{2}} right) = — ctgalpha ) Воспользуемся тем, что: (tgalpha cdot ctgalpha = 1.) Тогда: (ctgalpha = frac{1}{{tgalpha }} = frac{1}{{0,4}} = 2,5.) Поэтому: (tgleft( {alpha + frac{{5pi }}{2}} right) = — ctgalpha = — 2,5.) Ответ: — 2,5. |
| Задача 40. Найдите ({text{t}}{{text{g}}^2}alpha ), если (4{sin ^2}alpha + 9{cos ^2}alpha = 6)
Ответ
ОТВЕТ: 1,5. Решение
Выполним следующее преобразование: (6 = 6 cdot 1 = 6left( {{{sin }^2}alpha + {{cos }^2}alpha } right) = 6{sin ^2}alpha + 6{cos ^2}alpha ) Тогда: (4{sin ^2}alpha + 9{cos ^2}alpha = 6,,,,, Leftrightarrow ,,,,,4{sin ^2}alpha + 9{cos ^2}alpha = 6{sin ^2}alpha + 6{cos ^2}alpha ,,,,, Leftrightarrow ) ( Leftrightarrow ,,,,,2{sin ^2}alpha = 3{cos ^2}alpha ,,,,, Leftrightarrow ,,,,,frac{{{{sin }^2}alpha }}{{{{cos }^2}alpha }}, = frac{3}{2},,,,,, Leftrightarrow ,,,,,t{g^2}alpha = 1,5.) Ответ: 1,5. |
| Задача 41. Найдите (frac{{3cos alpha — 4sin alpha }}{{2sin alpha — 5cos alpha }}), если ({text{tg}}alpha {text{ = 3}})
Ответ
ОТВЕТ: — 9. Решение
1 Вариант Разделим числитель и знаменатель дроби на (cos alpha ). Тогда: (frac{{3cos alpha — 4sin alpha }}{{2sin alpha — 5cos alpha }} = frac{{frac{{3cos alpha }}{{cos alpha }} — frac{{4sin alpha }}{{cos alpha }}}}{{frac{{2sin alpha }}{{cos alpha }} — frac{{5cos alpha }}{{cos alpha }}}} = frac{{3 — 4,,tgalpha }}{{2,,tgalpha — 5}} = frac{{3 — 4 cdot 3}}{{2 cdot 3 — 5}} = frac{{ — 9}}{1} = — 9.) 2 Вариант Так как (tgalpha = 3), то (frac{{sin alpha }}{{cos alpha }} = 3) и (sin alpha = 3cos alpha ). Тогда: (frac{{3cos alpha — 4sin alpha }}{{2sin alpha — 5cos alpha }} = frac{{3cos alpha — 4 cdot 3cos alpha }}{{2 cdot 3cos alpha — 5cos alpha }} = frac{{3cos alpha — 12cos alpha }}{{6cos alpha — 5cos alpha }} = frac{{ — 9cos alpha }}{{cos alpha }} = — 9.) Ответ: — 9. |
| Задача 42. Найдите (frac{{10cos alpha + 4sin alpha + 15}}{{2sin alpha + 5cos alpha + 3}}), если ({text{tg}}alpha {text{ = }} — {text{2}}{text{,5}})
Ответ
ОТВЕТ: 5. Решение
1 Вариант Разделим числитель и знаменатель дроби на (cos alpha ). Тогда: (frac{{10cos alpha + 4sin alpha + 15}}{{2sin alpha + 5cos alpha + 3}} = frac{{frac{{10cos alpha }}{{cos alpha }} + frac{{4sin alpha }}{{cos alpha }} + frac{{15}}{{cos alpha }}}}{{frac{{2sin alpha }}{{cos alpha }} + frac{{5cos alpha }}{{cos alpha }} + frac{3}{{cos alpha }}}} = frac{{10 + 4,,tgalpha + frac{{15}}{{cos alpha }}}}{{2,,tgalpha + 5 + frac{3}{{cos alpha }}}} = ) ( = frac{{10 + 4 cdot left( { — 2,5} right) + frac{{15}}{{cos alpha }}}}{{2 cdot left( { — 2,5} right) + 5 + frac{3}{{cos alpha }}}} = frac{{10 — 10 + frac{{15}}{{cos alpha }}}}{{ — 5 + 5 + frac{3}{{cos alpha }}}} = frac{{frac{{15}}{{cos alpha }}}}{{frac{3}{{cos alpha }}}} = frac{{15}}{{cos alpha }} cdot frac{{cos alpha }}{3} = 5.) 2 Вариант Так как (tgalpha = — 2,5), то (frac{{sin alpha }}{{cos alpha }} = — 2,5) и (sin alpha = — 2,5cos alpha ). Тогда: (frac{{10cos alpha + 4sin alpha + 15}}{{2sin alpha + 5cos alpha + 3}} = frac{{10cos alpha + 4 cdot left( { — 2,5cos alpha } right) + 15}}{{2 cdot left( { — 2,5cos alpha } right) + 5cos alpha + 3}} = frac{{10cos alpha — 10cos alpha + 15}}{{ — 5cos alpha + 5cos alpha + 3}} = frac{{15}}{3} = 5.) Ответ: 5. |
| Задача 43. Найдите ({text{tg}}alpha ), если (frac{{6sin alpha — 2cos alpha }}{{4sin alpha — 4cos alpha }} = — 1)
Ответ
ОТВЕТ: 0,6. Решение
Разделим числитель и знаменатель левой части на (cos alpha ): (frac{{frac{{6sin alpha }}{{cos alpha }} — frac{{2cos alpha }}{{cos alpha }}}}{{frac{{4sin alpha }}{{cos alpha }} — frac{{4cos alpha }}{{cos alpha }}}} = — 1,,,,, Leftrightarrow ,,,,,frac{{6,,tgalpha — 2}}{{4,,tgalpha — 4}} = frac{{ — 1}}{1},,,,, Leftrightarrow ,,,,,6,,tgalpha — 2 = — 4,tgalpha + 4,,,,, Leftrightarrow ) ( Leftrightarrow ,,,,,10,,tgalpha = 6,,,,, Leftrightarrow ,,,,,tgalpha = 0,6.) Ответ: 0,6. |
| Задача 44. Найдите ({text{tg}}alpha ), если (frac{{3sin alpha — 5cos alpha + 2}}{{sin alpha + 3cos alpha + 6}} = frac{1}{3})
Ответ
ОТВЕТ: 2,25. Решение
Воспользуемся свойством пропорции: (frac{{3sin alpha — 5cos alpha + 2}}{{sin alpha + 3cos alpha + 6}} = frac{1}{3},,,,,, Leftrightarrow ,,,,,,3left( {3sin alpha — 5cos alpha + 2} right) = sin alpha + 3cos alpha + 6,,,,,, Leftrightarrow ) ( Leftrightarrow ,,,,,,9sin alpha — 15cos alpha + 6 = sin alpha + 3cos alpha + 6,,,,, Leftrightarrow ,,,,,8sin alpha = 18cos alpha ,,,,, Leftrightarrow ) ( Leftrightarrow ,,,,,frac{{sin alpha }}{{cos alpha }} = frac{{18}}{8},,,,, Leftrightarrow ,,,,,tgalpha = 2,25.) Ответ: 2,25. |
| Задача 45. Найдите значение выражения (7cos left( {{\pi } + beta } right) — 2sin left( {frac{{\pi }}{2} + beta } right)), если (cos beta = — frac{1}{3})
Ответ
ОТВЕТ: 3. Решение
(7cos left( {pi + beta } right) — 2sin left( {frac{pi }{2} + beta } right) = — 7cos beta — 2cos beta = — 9cos beta = — 9 cdot left( { — frac{1}{3}} right) = 3.) Ответ: 3. |
| Задача 46. Найдите значение выражения (5sin left( {alpha — 7{\pi }} right) — 11cos left( {frac{{3{\pi }}}{2} + alpha } right)), если (sin alpha = — 0,25)
Ответ
ОТВЕТ: 4. Решение
(5sin left( {alpha — 7pi } right) — 11cos left( {frac{{3pi }}{2} + alpha } right) = — 5sin alpha — 11sin alpha = — 16sin alpha = — 16 cdot left( { — 0,25} right) = 4.) Ответ: 4. |
| Задача 47. Найдите (3cos 2alpha ), если (cos alpha = frac{1}{2})
Ответ
ОТВЕТ: — 1,5. Решение
Воспользуемся формулой косинус двойного угла: (cos 2alpha = 2{cos ^2}alpha — 1) (3cos 2alpha = 3left( {2{{cos }^2}alpha — 1} right) = 3 cdot left( {2 cdot {{left( {frac{1}{2}} right)}^2} — 1} right) = 3 cdot left( {2 cdot frac{1}{4} — 1} right) = 3 cdot left( { — frac{1}{2}} right) = — 1,5.) Ответ: — 1,5. |
Открытый банк заданий mathege.ru — тренажер задания 6 профильного ЕГЭ по математике-2022 (с ответами). Все прототипы задания 6 на исследование функций. Это задание на использование свойств производной при анализе функций, либо на геометрический смысл производной, либо на физический смысл производной, либо на первообразную функции. Номер заданий соответствует номеру заданий в базе mathege.ru.
Использование свойств производной для исследования функций
27487 На рисунке изображен график функции y = f(x), определенной на интервале (-6; 8). Определите количество целых точек, в которых производная функции положительна.
27488. На рисунке изображён график функции y = f(x), определенной на интервале (-5;5). Определите количество целых точек, в которых производная функции отрицательна.
27490. На рисунке изображен график функции y = f(x), определенной на интервале (-2; 12). Найдите сумму точек экстремума функции f(x).
27491. На рисунке изображён график y = f'(x) — производной функции f(x), определенной на интервале (-8; 3). В какой точке отрезка [-3; 2] функция f(x) принимает наибольшее значение?
27492. На рисунке изображён график y = f'(x) — производной функции f(x), определенной на интервале (-8; 4). В какой точке отрезка [-7;-3] функция f(x) принимает наименьшее значение?
27494. На рисунке изображен график y = f'(x) — производной функции f(x), определенной на интервале (-7; 14). Найдите количество точек максимума функции f(x), принадлежащих отрезку [-6;9].
27495. На рисунке изображен график y = f'(x) — производной функции f(x), определенной на интервале (-18; 6). Найдите количество точек минимума функции f(x), принадлежащих отрезку [-13;1].
27496. На рисунке изображен график y = f'(x) — производной функции f(x), определенной на интервале (-11; 11). Найдите количество точек экстремума функции f(x), принадлежащих отрезку [-10;10].
27497. На рисунке изображен график y = f'(x) — производной функции f(x), определенной на интервале (-7; 4). Найдите промежутки возрастания функции f(x). В ответе укажите сумму целых точек, входящих в эти промежутки.
27498. На рисунке изображен график y = f'(x) — производной функции f(x), определенной на интервале (-5; 7). Найдите промежутки убывания функции f(x). В ответе укажите сумму целых точек, входящих в эти промежутки.
27499. На рисунке изображен график y = f'(x) — производной функции f(x), определенной на интервале (-11; 3). Найдите промежутки возрастания функции f(x). В ответе укажите длину наибольшего из них.
27500. На рисунке изображен график y = f'(x) — производной функции f(x), определенной на интервале (-2; 12). Найдите промежутки убывания функции f(x). В ответе укажите длину наибольшего из них.
27502. На рисунке изображен график y = f'(x) — производной функции f(x), определенной на интервале (-4; 8). Найдите точку экстремума функции f(x), принадлежащую отрезку [-2; 6 ].
119971. На рисунке изображен график функции f(x), определенной на интервале (-5;5). Найдите количество точек, в которых производная функции f(x) равна 0.
317539. На рисунке изображён график функции y = f(x) и восемь точек на оси абсцисс: x1, x2, x3, x4, x5, x6, x7, x8. В скольких из этих точек производная функции f(x) положительна?
317540. На рисунке изображён график функции y = f(x) и двенадцать точек на оси абсцисс: x1, x2, x3, x4, x5, x6, x7, x8, x9, x10, x11, x12. В скольких из этих точек производная функции f(x) отрицательна?
317541. На рисунке изображён график y = f'(x) — производной функции f(x). На оси абсцисс отмечены восемь точек: x1, x2, x3, x4, x5, x6, x7, x8. Сколько из этих точек лежит на промежутках возрастания функции f(x)?
317542. На рисунке изображён график y = f'(x) — производной функции f(x). На оси абсцисс отмечены восемь точек: x1, x2, x3, x4, x5, x6, x7, x8. Сколько из этих точек лежит на промежутках убывания функции f(x)?
Геометрический смысл производной
27485. Прямая y = 7x — 5 параллельна касательной к графику функции y = x2 + 6x — 8. Найдите абсциссу точки касания.
27486. Прямая y = -4x — 11 является касательной к графику функции y = x3 + 7x2 + 7x — 6. Найдите абсциссу точки касания.
27489. На рисунке изображен график функции y = f(x), определенной на интервале (-5;5). Найдите количество точек, в которых касательная к графику функции параллельна прямой y = 6 или совпадает с ней.
27501. На рисунке изображен график y = f'(x) — производной функции f(x), определенной на интервале (-10; 2). Найдите количество точек, в которых касательная к графику функции f(x) параллельна прямой y = -2x -11 или совпадает с ней.
27503. На рисунке изображены график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
27504. На рисунке изображены график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
27505. На рисунке изображены график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
27506. На рисунке изображены график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
40130. На рисунке изображен график y = f'(x) — производной функции f(x). Найдите абсциссу точки, в которой касательная к графику y = f(x) параллельна прямой y = 2x — 2 или совпадает с ней.
40131. На рисунке изображен график y = f'(x) — производной функции f(x). Найдите абсциссу точки, в которой касательная к графику y = f(x) параллельна оси абсцисс или совпадает с ней.
119972. Прямая y = 3x +1 является касательной к графику функции ax2 + 2x + 3. Найдите a.
119973. Прямая y = -5x + 8 является касательной к графику функции 28x2 + bx + 15. Найдите b, учитывая, что абсцисса точки касания больше 0.
119974. Прямая y = 3x + 4 является касательной к графику функции 3x2 — 3x + c. Найдите c.
317543. На рисунке изображён график функции y = f(x). На оси абсцисс отмечены точки −2, −1, 1, 2. В какой из этих точек значение производной наибольшее? В ответе укажите эту точку.
317544. На рисунке изображён график функции y = f(x). На оси абсцисс отмечены точки −2, −1, 1, 4. В какой из этих точек значение производной наименьшее? В ответе укажите эту точку.
[s60u_expand more_text=»Ответ» less_text=»Свернуть» height=»1″ hide_less=»no» text_color=»#333333″ link_color=»#0088FF» link_style=»default» link_align=»left» more_icon=»» less_icon=»» class=»»]
4
[/su_expand]
Физический смысл производной
119975. Материальная точка движется прямолинейно по закону x(t) = 6t2 — 48t +17, где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t = 9 с.
119976. Материальная точка движется прямолинейно по закону x(t) = 1/2t3 — 3t2 + 2t, где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t = 6 с.
119977. Материальная точка движется прямолинейно по закону x(t) = -t4 + 6t3 + 5t + 23, где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t = 3 с.
119978. Материальная точка движется прямолинейно по закону x(t) = t2 -13t +23, где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. В какой момент времени (в секундах) ее скорость была равна 3 м/с?
119979. Материальная точка движется прямолинейно по закону x(t) = 1/3t3 — 3t2 — 5t + 3, где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. В какой момент времени (в секундах) ее скорость была равна 2 м/с?
Первообразная
323077. На рисунке изображён график функции y = F(x) — одной из первообразных функции f(x), определённой на интервале (-3;5). Найдите количество решений уравнения f(x) = 0 на отрезке [-2;4].
323078. На рисунке изображён график функции y = f(x) (два луча с общей начальной точкой). Пользуясь рисунком, вычислите F(8) — F(2), где F(x) — одна из первообразных функции f(x).
323079. На рисунке изображён график некоторой функции y = f(x). Функция F(x) = x3 + 30x2 + 302x — 15/8 — одна из первообразных функции f(x). Найдите площадь закрашенной фигуры.
323080. На рисунке изображён график некоторой функции y = f(x). Функция F(x)= -x3 — 27x2 — 240x — 8 — одна из первообразных функции f(x). Найдите площадь закрашенной фигуры.