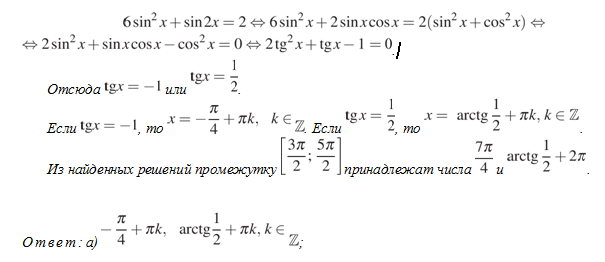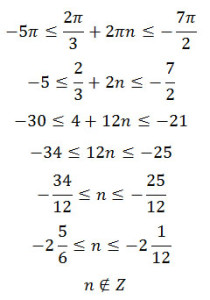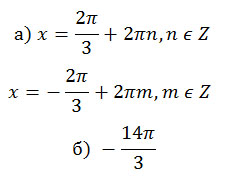Задать свой вопрос
*более 50 000 пользователей получили ответ на «Решим всё»
Задача 543 Решите уравнение…
Условие
slava191
30.01.2014
Решите уравнение 6sin^2x+sin2x=2
Укажите корни, принадлежащие промежутку [3Pi/2;5Pi/2]
математика 10-11 класс
39680
Решение
Ответ: в решение
Вопросы к решению (4)
Написать комментарий
Меню
- Решим всё
- Найти задачу
- Категории
- Статьи
- Тесты
- Архив задач
Присоединяйся в ВК
Вы не ошибаетесь. В решении действительно обе части уравнения поделили на .
И в общем случае при делении на выражение содержащее неизвестное могут потеряться корни. Но…
Здесь перед нами один из частных случаев − полное однородное тригонометрическое уравнение второй степени. В школьном курсе доказано, что такие уравнения можно делить на (или
), и при этом корни не теряются.
Если же Вам хочется в решении это пояснить, то рассмотрите два случая:
1. , и тогда получится, что решений нет.
2. , и тогда можно делить на
Ответ оставил Гость
Sin2x=1-2sin^2 x
Подставляем это в место sin2x
6sin^2 x+1-2sin^2 x=2
4sin^2 x=1
sin^2 x=1/4
sinx=1/2 и sinx=-1/2
x1=(-1)^n *arcsin(1/2)+pi*n,n-любое целое x2=(-1)^k *arcsin(-1/2)+pi*k,k- любое целое
x2=(-1)^k *(-pi/6)+pi*k
Внесем — в степень (-1)
x2=(-1)^(k+1) *pi/6+pi*k
x1=(-1)^n *pi/6+pi*n
Оцени ответ
Задание 13. Математика ЕГЭ. Решите уравнение 6sin^2x + 5sin(π/2-x) – 2 = 0
Задание.
а) Решите уравнение 6sin2x + 5sin(π/2-x) – 2 = 0.
б) Укажите корни этого уравнения, принадлежащие отрезку [- 5π; — 7π/2].
Решение:
а) Решите уравнение
ОДЗ уравнения – все числа.
Преобразуем sin(π/2 — x), воспользуемся формулами приведения.
Так как под знаком преобразуемой тригонометрической функции содержится выражение (π/2 — x), то наименование тригонометрической функции меняем на родственное, т. е. синус — на косинус.
Так как (π/2 — x) — аргумент из первой четверти, то в ней преобразуемая функция синус имеет знак плюс. Получим:
sin (π/2 — x) = cosx
Воспользуемся основным тригонометрическим тождеством:
sin2x + cos2x = 1
sin2x = 1 – cos2x
Тогда данное уравнение примет вид:
6sin2x + 5sin(π/2-x) – 2 = 0
6·(1 – cos2x) + 5cosx – 2 = 0
6 – 6cos2x + 5cosx – 2 = 0
– 6cos2x + 5cosx + 4 = 0
6cos2x – 5cosx – 4 = 0
Введем новую переменную, пусть cosx = a, тогда получим
6a2 – 5a – 4 = 0
D = 121
a1 = 4/3, a2 = — 1/2
Вернемся к первоначальной переменной, получим два уравнения.
Решим 1 уравнение:
cosx = 4/3
Уравнение не имеет решения, так как — 1 ≤ cosx ≤ 1.
Решим 2 уравнение:
cosx = — 1/2
(1)
(2)
б) Найдем корни уравнения, принадлежащие отрезку [- 5π; — 7π/2].
Для первого корня:
Для второго корня:
Ответ:
Дан 1 ответ
Vas61_zn
Бакалавр
(10.4k баллов)
28 Май, 20
Ответ:
Пошаговое объяснение:
6sin2x+2cos2x=2 |÷2
3sin2x+cos2x=1
3·2sinxcosx+cos²x-sin²x-cos²x-sin²x=0
6sinxcosx-2sin²x=0
2sinx(3cosx-sinx)=0
sinx=0 x=πn n принадлежит Z
3cosx-sinx=0 |÷cosx
3-tgx=0
tgx=3 x=arctg3+πm m принадлежит Z
Сдается мне, что тут нужно понизить степень синуса?
`6*sin^2 x = 6*((1-cos 2x)/2)` ?
ДОБРЫЙВЕЧЕР, если начинать с формулы понижения степени — то получите что-то такое: `sin(2x) -3*cos(2x) +1 =0` — и надо будет потом брать дополнительный угол (делить обе части ур-ия на `sqrt(10)`— решить так можно, но значения углов будут …=(( «плохо узнаваемые» ; вобщем, если не очень любите этот «метод дополнительного угла», то лучше так не делайте);
лучше распишите `sin(2x) =…`( обычная ф-ла синуса двойного угла), и `2=2*((sinx)^2 + (cosx)^2)` — уравнение сведется к однородному
~ghost, после указанных рокировок `2*sin^2 x+sin x*cos x-cos^2 x=0`
да, такое)
что дальше делать — знаете ?
Делим на cos^2 и получаем квадратное уравнение
Получаются корни `x=-arctg (1/2)+pi*n` и `x=pi/4 +pi*n`. Нужно отобрать корни на промежутке [3pi/2;5pi/2]
От второго икса попадает корень 9pi/4. А от арктангенса как найти?
а там не наоборот `tgx = -1` и `tgx = +1/2` ?
к интервалу `(-pi/2; pi/2)` {к области значений арктангенсов} добавили `+2*pi`,
т.е. в `(3*pi/2; 5*pi/2)` попадают `x= -pi/4 +2*pi = 7*pi/4` и `x=arctg(1/2) + 2*pi`
Белый и пушистый (иногда)
ДОБРЫЙВЕЧЕР, после приведения к уравнению `3cos2x-sin2x=1` можно поступить так. Обозначим `sin2x=v`, `cos2x=u` и перейдем к системе уравнений `{(3u-v=1),(u^2+v^2=1):}`. Решение этой системы почти очевидно: `(0;-1)` и `(0.6;0.8)`. Отсюда можно найти x.
красиво))
VEk, извините, я о Вашем решении..)) а то сама видела только самое «стандартное»: «привести к однородному»