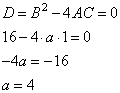7 задание егэ математика профиль теория шпаргалка

Предварительный просмотр:

• Мне нравится 

 

---

Производная и первообразные функции

---

В задании №7 профильного уровня ЕГЭ по математике необходимо продемонстрировать знания функции производной и первообразной. В большинстве случаев достаточно просто определения понятий и понимания значений производной.

---

Разбор типовых вариантов заданий №7 ЕГЭ по математике профильного уровня

---

Первый вариант задания (демонстрационный вариант 2018)

[su_note note_color=”#defae6″]

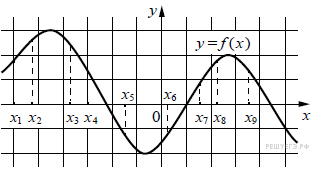
На рисунке изображён график дифференцируемой функции y = f(x). На оси абсцисс отмечены девять точек: x₁, x₂, …, x₉. Среди этих точек найдите все точки, в которых производная функции y = f(x) отрицательна. В ответе укажите количество найденных точек.

[/su_note]

Алгоритм решения:

1. Рассматриваем график функции.
2. Ищем точки, в которых функция убывает.
3. Подсчитываем их количество.
4. Записываем ответ.

Решение:

1. На графике функция периодически возрастает, периодически убывает.

2. В тех интелвалах, где функция убывает, производная имеет отрицательные значения.

3. В этих интервалах лежат точки x₃, x₄, x₅, x₉. Таких точек 4.

Ответ: 4.

---

Второй вариант задания (из Ященко, №4)

[su_note note_color=”#defae6″]

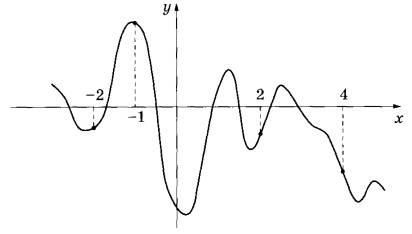
На рисунке изображён график функции у = f(x). На оси абсцисс отмечены точки -2, -1, 2, 4. В какой из этих точек значение производной наибольшее? В ответе укажите эту точку.

[/su_note]

Алгоритм решения:

1. Рассматриваем график функции.
2. Рассматриваем поведение функции в каждой из точек и знак производной в них.
3. Находим точки в наибольшим значением производной.
4. Записываем ответ.

Решение:

1. Функция имеет несколько промежутков убывания и возрастания.

2. Там, где функция убывает. Производная имеет знак минус. Такие точки есть среди указанных. Но на графике есть точки, в которых функция возрастает. В них производная положительная. Это точки с абсциссами -2 и 2.

3. Рассмотрим график в точках с х=-2 и х=2. В точке х=2 функция круче уходит вверх, значит касательная в этой точке имеет больший угловой коэффициент. Следовательно, в точке с абсциссой 2. Производная имеет наибольшее значение.

Ответ: 2.

---

Третий вариант задания (из Ященко, №21)

[su_note note_color=”#defae6″]

Прямая  является касательной к графику функции . Найдите а.

[/su_note]

Алгоритм решения:

1. Приравняем уравнения касательной и функции.
2. Упрощаем полученное равенство.
3. Находим дискриминант.
4. Определяем параметр а, при котором решение единственное.
5. Записываем ответ.

Решение:

1. Координаты точки касания удовлетворяют обоим уравнениям: касательной и функции. Поэтому мы можем приравнять уравнения. Получим:

2. Упрощаем равенство, перенеся все слагаемые в одну сторону:

3. В точке касания должно быть одно решение, поэтому дискриминант полученного уравнения должен равняться нулю. Таково условие единственности корня квадратного уравнения.

4. Получаем:

Ответ: 4.

Даниил Романович | Просмотров: 11.9k

6 задача ЕГЭ – на понимание производной функции. Задание проверяет знание связи между графиком функции и значением ее производной в различных точках, и наоборот – графиком производной и возрастанием/убыванием функции на интервалах и в точках.

Хотя это задание относится к сложному разделу (математический анализ), само по себе оно довольно простое. Решается в одно действие и знать нужно немного — для решения большинства задач хватит информации написанной на этих двух картинках:

Более подробно об этом теме – рассказано в этих видео:

Что такое производная | Наглядное объяснение на графиках
Разбор задач на поиск экстремумов, минимумов и максимумов
Геометрический смысл производной | Теория + разбор задач ЕГЭ

Задачи, которые были на экзамене за последние 10 лет

2011:

2012:

2013:

2014:

2015:

2016:

2017:

2018:

2019:

2020:

2021:

В открытом банке есть и другие типы заданий (на первообразную, физический смысл производной и условия касания), но в вариантах реальных ЕГЭ я таких задачи не нашла. Хотя это и не значит, что в будущем на ЕГЭ такого никогда не будет, так что лучше разберитесь и в них тоже. Вот примеры таких задач:

Процент выполнения

Сколько процентов пишущих экзамен решили задачу на производные в разные годы:

Сколько процентов из тех, кто решал экзамен в 2021 году, набрал в задаче хотя бы 1 балл:

Какой вывод можно сделать? Шестую задачу решает примерно 6 человек из 10 и это третья задача по потерянным баллам (в первой части). Для меня это несколько удивительно, потому что 6 задача не требует большого количества знаний и решается в одно действие. В чем же может быть причина таких результатов?

Типичные ошибки

1. Перепутать производную и функцию

Многие начинают в этой задаче отвечать так будто перед ними график функции и выбирают точки – (x_1), (x_4), (x_7), (x_8). Хотя правильные точки (x_4), (x_5), (x_6) и ответ (3).

Вот, что авторы ЕГЭ написали в Методических рекомендациях по итогам ЕГЭ об этой задаче: «Выполнение – около 69%. Типичные ошибки связаны в первую очередь с невнимательным чтением условия – почти 24% участников указали количество точек, в которых значение функции положительно, а еще около 2% участников пытались перечислить номера точек, в которых производная принимает положительные значения.»

2. Не ограничить график данным отрезком

Если забыть про отрезок, который указан в конце условия, то в ответ задаче (3). Если не забывать про отрезок, то ответ в задаче (2). Составители ЕГЭ пишут, что около (31)% экзаменуемых делают такую ошибку, а правильный ответ дают лишь (43)%. Поэтому Ященко, Семенов и Высоцкий советуют начинать решение задачи с отмечания данного отрезка в КИМе. Напомню, что вы МОЖЕТЕ рисовать на выданных вам бланках КИМ.

3. Неправильно вычислить тангенс или не учесть убывание/возрастание функции

Чтобы найти производную в точке, нужно вычислить тангенс угла наклона касательной с положительным направлением оси (Ox). На практике задача решается в 2 этапа:

1. Определить убывает касательная или возрастает и соответственно поставить знак минус или плюс.

2. Определить тангенс угла в треугольнике, в котором гипотенуза является частью касательной, а вершины треугольника совпадали с вершинами клеточек.

В этой задаче многие, во-первых, забывали про первый пункт, а во-вторых, путались в определении тангенса и вместо (frac{AC}{BC}) считали (frac{BC}{AC}).

• Главная

  
  

• Теория ЕГЭ

  
  

• Математика — теория ЕГЭ

  
  

• 
  Задание 7 ЕГЭ 2021 по математике, теория

08.10.2018

Необходимая теория для успешного освоения и решения заданий №7 по математике профильного уровня на ЕГЭ в 2021 году.

Представлена вся теория и алгоритм решения различных заданий такого типа.

• Тренировочные кимы ЕГЭ по математике
• Практика — примеры для решения каждого типа заданий

Обсудить решение конкретных заданий вы можете в комментариях ниже.

Смотреть в PDF:

Или прямо сейчас: cкачать в pdf файле.

Сохранить ссылку:

Комментарии (0)
Добавить комментарий

Добавить комментарий

Комментарии без регистрации. Несодержательные сообщения удаляются.

Имя (обязательное)

E-Mail

Подписаться на уведомления о новых комментариях

Отправить

Таблица производных некоторых элементарных функций

Функция	Производная
$c$	$0$
$x$	$1$
$x^n$	$nx^{n-1}$
${1}/{x}$	$-{1}/{x^2}$
$√x$	${1}/{2√x}$
$e^x$	$e^x$
$lnx$	${1}/{x}$
$sinx$	$cosx$
$cosx$	$-sinx$
$tgx$	${1}/{cos^2x}$
$ctgx$	$-{1}/{sin^2x}$

Основные правила дифференцирования

1. Производная суммы (разности) равна сумме (разности) производных

$(f(x) ± g(x))’= f'(x)±g'(x)$

2. Производная произведения

$(f(x) · g(x))’= f'(x) · g(x)+ f(x) · g(x)’$

3. Производная частного

$({f(x)}/{g(x)})’={f'(x)·g(x)-f(x)·g(x)’}/{g^2(x)}$

4. Производная сложной функции равна произведению производной внешней функции на производную внутренней функции

$f(g(x))’=f'(g(x))·g'(x)$

Физический смысл производной

Геометрический смысл производной

Напомним, что уравнение прямой, не параллельной осям координат, можно записать в виде $y = kx + b$, где $k$ – угловой коэффициент прямой. Коэффициент $k$ равен тангенсу угла наклона между прямой и положительным направлением оси $Ох$.

$k = tgα$

Производная функции $f(x)$ в точке $х_0$ равна угловому коэффициенту $k$ касательной к графику в данной точке:

$f'(x_0) = k$

Следовательно, можем составить общее равенство:

$f'(x_0) = k = tgα$

На рисунке касательная к функции $f(x)$ возрастает, следовательно, коэффициент $k > 0$. Так как $k > 0$, то $f'(x_0) = tgα > 0$. Угол $α$ между касательной и положительным направлением $Ох$ острый.

На рисунке касательная к функции $f(x)$ убывает, следовательно, коэффициент $k < 0$, следовательно, $f'(x_0) = tgα < 0$. Угол $α$ между касательной и положительным направлением оси $Ох$ тупой.

На рисунке касательная к функции $f(x)$ параллельна оси $Ох$, следовательно, коэффициент $k = 0$, следовательно, $f'(x_0) = tg α = 0$. Точка $x_0$, в которой $f ‘(x_0) = 0$, называется экстремумом.

Производная так же применяется для нахождения промежутков возрастания и убывания функции:

Если $f'(x) > 0$ на промежутке, то функция $f(x)$ возрастает на этом промежутке.

Если $f'(x) < 0$ на промежутке, то функция $f(x)$ убывает на этом промежутке.