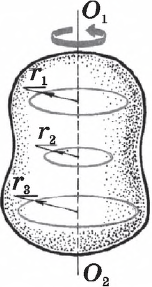
В сосуд высотой 20 см налита вода, уровень которой ниже края сосуда на 2 см. Чему равна сила давления воды на дно сосуда, если площадь дна 0,01 м2? (Ответ дайте в ньютонах.) Атмосферное давление не учитывать. Ускорение свободного падения принять равным 10 м/с2.
Спрятать решение
Решение.
Сила давления воды равна давлению воды, умноженному на площадь дна. Давление воды равно произведению ускорению свободного падения, плотности и высоты воды. В итоге получаем:
Ответ: 18.
Примечание.
В вертикальном сосуде сила давления жидкости на дно равна весу жидкости.
Источник: Демонстрационная версия ЕГЭ−2017 по физике
Тренировочный вариант №2 КИМ №210927 ЕГЭ 2022 по физике 11 класс для подготовки на 100 баллов от 27 сентября 2021 года.
Вариант с ответами: скачать
Данный вариант составлен по новой демоверсии ФИПИ экзамена ЕГЭ 2022 года, к тренировочным заданиям прилагаются решения и правильные ответы.
Для выполнения экзаменационной работы по физике отводится 3 часа 55 минут (235 минут). Работа состоит из двух частей, включающих в себя 30 заданий.
Решу ЕГЭ 2022 по физике 11 класс вариант 100 баллов №210927:
Сложные задания и ответы с варианта
1)Выберите все верные утверждения о физических явлениях, величинах и закономерностях. Запишите цифры, под которыми они указаны.
- 1) При неупругом столкновении двух тел механическая энергия не сохраняется.
- 2) Равномерное движение – это такое движение, при котором тело за равные промежутки времени проходит равные расстояния.
- 3) Электрический ток – направленное движение электронов.
- 4) При преломлении электромагнитных волн на границе воздух-вода скорость волны уменьшается.
- 5) Удельная теплота плавления показывает какое количество теплоты надо подвести к телу массой 1 кг, чтобы расплавить его.
Ответ: 14
2)Даны следующие зависимости величин: А) зависимость температуры идеального газа от объема при изотермическом процессе; Б) зависимость количества нераспавшихся частиц при радиоактивном распаде; В) зависимость координаты х при движении тела, брошенного под углом к горизонту. Установите соответствие между этими зависимостями и видами графиков, обозначенных цифрами 1–5. Для каждой зависимости А–В подберите соответствующий вид графика и запишите в таблицу выбранные цифры под соответствующими буквами.
Ответ: 345
3)На рисунке приведены графики зависимости проекции скорости от времени для легкового автомобиля (I) и микроавтобуса (II), движущихся по прямой дороге, вдоль которой и направлена ось Ох. Определите отношение модулей.
Ответ: 2
4)Пластилиновый шар массой 0,1 кг имеет скорость 1 м/с. Он налетает на неподвижную тележку массой 0,1 кг, прикрепленную к пружине, и прилипает к тележке (см. рисунок). Чему равна полная механическая энергия системы при ее дальнейших колебаниях? Трением пренебречь.
Ответ: 0,025
5)Два груза массами 2m и m закреплены на невесомом стержне длиной 60 см. Чтобы стержень оставался в равновесии, его следует подвесить в точке О, находящейся на расстоянии Х от левого груза. Определите, чему равно Х.
Ответ: 20
6)При подвешивании груза массой m к стальному тросу длина троса возрастает на ∆L. Из приведенного ниже списка выберите все верные утверждения, соответствующих данным графикам. 1) Величина ∆L не изменится, если L будет вдвое больше, а m – вдвое меньше. 2) Величина ∆L не изменится, если L и m будут вдвое меньше. 3) Величина ∆L увеличится в четыре раза, если L и m будут вдвое больше. 4) Величина ∆L уменьшится в четыре раза, если L и m – вдвое больше. 5) Величина ∆L уменьшится в два раза, если L будет вчетверо меньше, а m – вдвое меньше.
Ответ: 13
7)На поверхности воды плавает сплошной деревянный брусок. Как изменятся глубина погружения бруска и сила Архимеда, действующая на брусок, если его заменить сплошным бруском той же плотности и высоты, но большей массы? Для каждой величины определите соответствующий характер изменения: 1) увеличивается 2) уменьшается 3) не изменится
Ответ: 31
8)Тело массой 100 г движется вдоль оси Ох, при этом его координата изменяется во времени в соответствии с формулой х(t) = 10 + 5t – 3t2 (все величины выражены в СИ). Установите соответствие между физическими величинами и формулами, выражающими их зависимости от времени в условиях данной задачи. К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
Ответ: 12
9)В одном из опытов стали закачивать воздух в стеклянный сосуд, одновременно охлаждая его. При этом температура воздуха в сосуде понизилась в 2 раза, а его давление возросло в 3 раза. Во сколько раз увеличилась масса воздуха в сосуде?
Ответ: 6
10)В кубическом метре воздуха в помещении при температуре 20 °С находится 1,1245⋅10-2 г водяных паров. Пользуясь таблицей плотности насыщенных паров воды, определите относительную влажность воздуха.
Ответ: 65
11)На графике показана зависимость давления одноатомного идеального газа от объема. Газ совершает работу, равную 3 кДж. Определите количество теплоты, полученное газом при переходе из состояния 1 в состояние 2.
Ответ: 3000
12)При переводе идеального газа из состояния 1 в состояние 2 концентрация молекул n пропорциональна давлению р (см. рисунок). Масса газа в процессе остаётся постоянной. Выберите из предложенного перечня все верные утверждения, которые сделать анализируя данный график:
- 1) Плотность газа возрастает.
- 2) Происходит изотермическое расширение газа.
- 3) Газ совершает работу без изменения внутренней энергии.
- 4) Плотность газа уменьшается.
- 5) Внутренняя энергия газа уменьшается.
Ответ: 234
13)В ходе адиабатного процесса внутренняя энергия одного моля разреженного гелия увеличивается. Как изменяются при этом температура гелия и его объём? Для каждой величины определите соответствующий характер изменения: 1) увеличивается 2) уменьшается 3) не изменится
Ответ: 12
14)По участку цепи, состоящему из резистора R = 4 кОм, течёт постоянный ток I = 100мА. За какое время на этом участке выделится количество теплоты Q = 2,4 кДж?
Ответ: 60
16)Если ключ находится в положении 1, то период собственных электромагнитных колебаний в контуре (см. рисунок) равен 6 мс. Насколько увеличится период собственных электромагнитных колебаний в контуре, если ключ перевести из положения 1 в положение 2?
Ответ: 6
17)Ученик, изучая законы геометрической оптики, провел опыт по преломлению света (см. рисунок). Для этого он направил узкий пучок света на стеклянную пластину. Пользуясь приведенной таблицей, выберите из приведенного ниже списка два правильных утверждения, описывающих наблюдаемое явление.
Ответ: 14
18)Электрический колебательный контур радиоприемника настроен на длину волны λ. Как изменятся частота колебаний в контуре и соответствующая им длина волны, если площадь пластин конденсатора уменьшить? Для каждой величины определите соответствующий характер изменения: 1) увеличится 2) уменьшится 3) не изменится
Ответ: 12
19)Конденсатор колебательного контура длительное время подключён к источнику постоянного напряжения (см. рисунок). В момент времени t = 0 переключатель К переводят из положения 1 в положение 2. Графики А и Б представляют изменения физических величин, характеризующих колебания в контуре после этого. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять. К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.
Ответ: 21
20)Какая доля радиоактивных атомов распадется через интервал времени, равный двум периодам полураспада? Ответ выразите в процентах.
Ответ: 75
21)В опытах по фотоэффекту взяли пластину из металла с работой выхода 3,5 эВ и стали освещать ее светом частоты 3⋅1015Гц. Затем частоту падающей на пластину световой волны уменьшили в 4 раза, увеличив в 2 раза интенсивность светового пучка. Как изменится в результате этого число фотоэлектронов, покидающих пластину за 1 с и их скорость. Для каждой величины определите соответствующий характер изменения: 1) увеличивается 2) уменьшается 3) не изменится
Ответ: 33
22)С помощью линейки с миллиметровыми делениями измерили толщину стопки из 25 шайб. Толщина стопки оказалась равной примерно 45 мм. Определите толщину одной шайбы, если погрешность измерений равна половине цены деления линейки. Запишите ответ с учетом погрешности.
Ответ: 1,800,04
23)Пучок белого света, пройдя через призму, разлагается в спектр. Была выдвинута гипотеза, что ширина спектра, получаемого на стоящем за призмой экране, зависит от угла при вершине призмы. Необходимо экспериментально проверить эту гипотезу. Какие два опыта нужно провести для такого исследования?
Ответ: 13
24)Намагниченный стальной стержень начинает свободное падение с нулевой начальной скоростью из положения, изображённого на рис. 1. Пролетая сквозь закреплённое проволочное кольцо, стержень создаёт в нём электрический ток, сила которого изменяется со временем так, как показано на рис. 2. Почему в моменты времени t1 и t2 ток в кольце имеет различные направления? Ответ поясните, указав, какие физические явления и закономерности Вы использовали для объяснения. Влиянием тока в кольце на движение магнита пренебречь.
25)Небольшой камень, брошенный с ровной горизонтальной поверхности земли под углом к горизонту, упал обратно на землю в 20 метрах от места броска. Сколько времени прошло от броска до того момента, когда его скорость была направлена горизонтально и равна 10 м/с?
26)Напряжение на концах первичной обмотки трансформатора 220 В, сила тока в ней 1 А. Напряжение на концах вторичной обмотки 22 В. Какой была бы сила тока во вторичной обмотке при коэффициенте полезного действия трансформатора 95 %?
27)В водонепроницаемый мешок, лежащий на дне моря на глубине 73,1 м закачивается сверху воздух. Вода вытесняется из мешка через нижнее отверстие, и когда объём воздуха в мешке достигает 28,0 м3 , мешок всплывает вместе с прикреплённым к нему грузом. Масса оболочки 2710 кг. Опреде-лите массу груза. Температура воды равна 7°С. Атмосферное давление на уровне моря равно 105 Па. Объёмом груза и стенок мешка пренебречь.
28)К конденсатору С1 через диод и катушку индуктивности L подключён конденсатор ёмкостью С2 = 2 мкФ. До замыкания ключа К конденсатор С1 был заряжен до напряжения U = 50 В, а конденсатор С2 не заряжен. После замыкания ключа система перешла в новое состояние равновесия, в котором напряжение на конденсаторе С2 оказалось равным U2 = 20 В. Какова ёмкость конденсатора С1? (Активное сопротивление цепи пренебрежимо мало.)
29)На поверхности воды плавает надувной плот шириной 4 м и длиной б м. Небо затянуто сплошным облачным покровом, полностью рассеивающим солнечный свет. На какой максимальной глубине под плотом должна находиться маленькая рыбка, чтобы ее не увидели плавающие вокруг плота хищники? Глубиной погружения плота, рассеиванием света водой и его отражением от дна водоема пренебречь. Показатель преломления воды относительно воздуха принять равным 4/3.
30)В изображенной на рисунке системе нижний брусок может двигаться по наклонной плоскости, составляющей с горизонтом угол α = 30°, а верхний брусок — вдоль наклонной плоскости, составляющей с горизонтом некоторый угол β. Коэффициент трения между нижним бруском и плоскостью равен μ = 0,2, трение между верхним бруском и наклонной плоскостью отсутствует. Считая соединяющую бруски нить очень легкой и нерастяжимой, и пренебрегая массой блока и трением в его оси найдите, при каких значениях угла β нить будет натянута.
Другие тренировочные варианты ЕГЭ 2022 по физике:
Физика 11 класс итоговая контрольная работа 2 варианта с ответами
12.07.2021 Тест по физике для 11 класса повторение 1 четверть 4 варианта с ответами
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
- 09.03.2023
Пятый тренировочный вариант, составленный на основе демоверсии ЕГЭ 2023 года по физике от ФИПИ. Вариант включает все задания кодификатора 2023 года и учитывает все изменения, которые произошли в 2023 году (полный список изменений). Вариант содержит правильные ответы и подробные разборы для второй части теста — задания повышенной сложности. Ответы сохранены в конце варианта.
- Другие тренировочные варианты по физике
В варианте присутствуют задания на знание физических законов и явлений, на проведение простых физических экспериментов, на расчет физических величин, а также на решение задач. Сам тренировочный вариант состоит из нескольких частей. В первой части обычно представлены задания на знание физических законов и явлений, а также на проведение простых физических экспериментов. Вторая часть содержит задания на расчет физических величин, таких как скорость, ускорение, работа, мощность и т.д. Третья часть включает задания на решение задач, в которых учащиеся должны применить свои знания физики для решения конкретной задачи.
Задания из тренировочного варианта №5
Задание 1. Материальная точка движется вдоль оси OX. Её координата изменяется с течением времени по закону x=3+3t-2t2 (все величины даны в СИ). Чему равна проекция скорости материальной точки на ось OX в момент времени t = 2 с?
Задание 2. Тело массой 1,5 кг лежит на горизонтальном столе. На него почти мгновенно начинает действовать сила, направленная вертикально вверх. Через 3 с после начала действия силы модуль скорости этого тела равен 9 м/с. Чему равен модуль приложенной к телу силы?
Задание 3. Координата тела массой 8 кг, движущегося вдоль оси x, изменяется по закону x=x0 + vxt, где . x0 = 6 м; vx = 8 м/с. Чему равна кинетическая энергия тела в момент времени t = 10 с?
Задание 4. Два одинаковых бруска толщиной 5 см и массой 1 кг каждый, связанные друг с другом, плавают в воде так, что уровень воды приходится на границу между ними (см. рисунок). Из приведенного ниже списка выберите все правильные утверждения.
- Плотность материала, из которого сделаны бруски, равна 500 кг/м3.
- Если на верхний брусок положить груз массой 0,7 кг, то бруски утонут..
- Если воду заменить на керосин, то глубина погружения брусков уменьшится.
- Сила Архимеда, действующая на бруски, равна 20 Н.
- Если в стопку добавить еще 2 таких же бруска, то глубина её погружения увеличится на 10 см.
Задание 7. Какое изменение температуры Δt (в градусах Цельсия) соответствует нагреву на 27 К?
Задание 8. Рабочее тело тепловой машины с КПД 40% за цикл получает от нагревателя количество теплоты, равное 50 Дж. Какое количество теплоты рабочее тело за цикл отдает холодильнику?
Задание 9. Кусок свинца, находившийся при температуре +27,5 °C, начали нагревать, подводя к нему постоянную тепловую мощность. Через 39 секунд после начала нагревания свинец достиг температуры плавления +327,5 °C. Через сколько секунд после этого момента кусок свинца расплавится? Потери теплоты отсутствуют.
Задание 13. На сколько отличаются наибольшее и наименьшее значения модуля силы, действующей на прямой провод длиной 20 см с током 10 А, при различных положениях провода водородном магнитном поле, индукция которого равна 1 Тл?
Задание 14. На какой частоте корабли передают сигнал SOS, если по Международному соглашению длина радиоволн должна быть равна 600м?
Задание 20. Выберите все верные утверждения о физических явлениях, величинах и закономерностях. Запишите цифры, под которыми они указаны.
- При увеличении частоты звуковой волны скорость ее распространения увеличивается.
- При изотермическом сжатии идеального газа его давление уменьшается.
- Сопротивление резистора не зависит от силы тока через него.
- При переходе света из воздуха в стекло угол падения меньше, чем угол преломления.
- Работа выхода электронов из металла при фотоэффекте не зависит от энергии падающих фотонов.
Задание 26. Поток фотонов выбивает из металла электроны. Энергия фотона равна 2 эВ. Если длину волны падающего излучения уменьшить в 2,5 раза, то максимальная скорость фотоэлектронов, вылетающих из этого металла, увеличится в 2 раза. Определите работу выхода электронов из металла.
Задание 27. В горизонтальном цилиндрическом сосуде, закрытым поршнем, находится одноатомный идеальный газ. Первоначальное давление газа p1 = 4105 Па. Расстояние от дна сосуда до поршня L = 0,3 м. Площадь поперечного сечения поршня S. В результате медленного нагревания газ получил количество теплоты Q = 1,65 кДж, а поршень сдвинулся на расстояние x = 10 см. При движении поршня на него со стороны стенок сосуда действует сила трения величиной Fтр = 3103 Н. Найдите S. Считать, что сосуд находится в вакууме.
Задание 29. В плоскости, параллельной плоскости тонкой собирающей линзы, по окружности со скоростью v = 5 м/с движется точечный источник света. Расстояние между плоскостями d = 15 см. Центр окружности находится на главной оптической оси линзы. Фокусное расстояние линзы F = 10 см. Найдите скорость движения изображения точечного источника света. Сделайте пояснительный чертеж, указав ход лучей в линзе.
Смотреть в PDF:
Или прямо сейчас: cкачать в pdf файле.
Ускорение материальной точки
Ускорение — величина, характеризующая быстроту изменения скорости. Как правило, движение является неравномерным, т. е. происходит с переменной скоростью. На одних участках траектории тела могут иметь большую скорость, на других — меньшую. Например, поезд, отходящий от станции, со временем двигается все быстрее и быстрее. Подъезжая к станции, он, наоборот, замедляет свое движение.
Ускорение (или мгновенное ускорение) — векторная физическая величина, равная пределу отношения изменения скорости к промежутку времени, за который это изменение произошло, при стремлении $∆t$ к нулю, (т. е. производной $υ↖{→}$ по $t$):
$a↖{→}=lim↙{∆t→0}{∆υ↖{→}}/{∆t}=υ↖{→}_t’$
Составляющие $a↖{→} (а_х, а_у, а_z)$ равны соответственно:
$a_x=υ_x’;a_y=υ_y’;a_z=υ_z’$
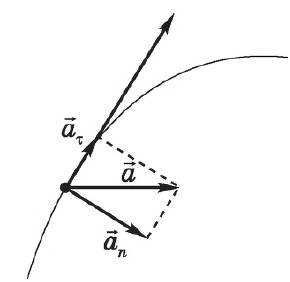
Ускорение, как и изменение скорости, направлено в сторону вогнутости траектории и может быть разложено на две составляющие — тангенциальную — по касательной к траектории движения — и нормальную — перпендикулярно к траектории.
В соответствии с этим проекцию ускорения $а_х$ на касательную к траектории называют касательным, или тангенциальным ускорением, проекцию $a_n$ на нормаль — нормальным, или центростремительным ускорением.
Касательное ускорение определяет величину изменения численного значения скорости:
$a_t=lim↙{∆t→0}{∆υ}/{∆t}$
Нормальное, или центростремительное ускорение характеризует изменение направления скорости и определяется по формуле:
$a_n={v^2}/{R}$
где R — радиус кривизны траектории в соответствующей ее точке.
Модуль ускорения определяется по формуле:
$a=√{a_t^2+a_n^2}$
При прямолинейном движении полное ускорение $а$ равно тангенциальному $a=a_t$, т. к. центростремительное $a_n=0$.
Единицей ускорения в СИ является такое ускорение, при котором за каждую секунду скорость тела изменяется на 1 м/с. Эту единицу обозначают 1 м/с2 и называют «метр на секунду в квадрате».
Равноускоренное прямолинейное движение
Равноускоренным называется движение с постоянным ускорением ($a↖{→}=const$) при $a↖{→}↑↑υ↖{→}$. Когда вектор ускорения направлен против вектора скорости $a↖{→}↑↓υ↖{→}$, движение называется равнозамедленным.
Поскольку ускорение постоянно, оно равно изменению скорости за любой конечный интервал времени:
$a↖{→}={∆υ↖{→}}/{∆t}={υ↖{→}-{υ_0}↖{→}}/{∆t}$
При прямолинейном движении векторы $υ↖{→}$ и ${υ_0}↖{→}$, а следовательно, и вектор а направлены вдоль одной прямой, которая является траекторией движения. Вдоль этой же прямой удобно направить координатную ось X.
Тогда из последнего уравнения следует:
$a_x={∆υ_x}/{t}={υ_x-υ_{0x}}/{t}$
где $υ_{0x}$ — скорость в начальный момент времени, принятый за нуль; $υ_x$ — текущее значение скорости (в момент времени $t$). Формула для определения ускорения из состояния покоя (равноускоренное движение, начальная скорость равна нулю: $υ_{0x}=0$) имеет вид:
$a_x={υ_x}/{t}$
Если же нулю равна не начальная, а конечная скорость ($υ_x=0$, торможение при равнозамедленном движении), то формула ускорения принимает вид:
$a_x=-{υ_{0x}}/{t}$
Из формулы находим выражение для скорости при $υ_{0x}≠0$
$υ_x=υ_{0x}+a_{x}t$
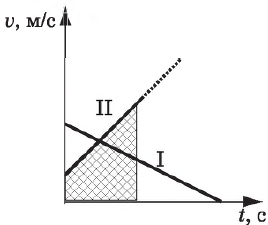
Графики скорости при равноускоренном движении имеют вид прямых линий, наклон которых показывает, как быстро меняется скорость с течением времени. На рис. приведены графики для модуля скорости с ненулевой начальной скоростью для равноускоренного (II) и равнозамедленного (I) движений.
Путь, пройденный точкой за некоторое время $t$ (в данном случае совпадающий с перемещением $∆x↖{→}$ за то же время), легко определяется из рис.. Он равен площади трапеции, образованной графиком $υ(t)$, осями координат и прямой, восстановленной из заданной точки $t$ параллельно оси ординат. Аналитически эта площадь определяется, как известно, интегрированием функции $υ(t)$:
$∆x(t)=x(t)-x_0=∫↙{0}↖{t}υ(t)dt=∫↙{0}↖{t}(υ_0+at)dt=(υ_0t+{at^2}/{2})|↙{0}↖{t}=υ_0t+{at^2}/{2}$
Отсюда получаем закон прямолинейного равноускоренного движения:
$x=x_0+υ_0t+{at^2}/{2}$
Из этого уравнения при известных начальных условиях: координате тела в момент начала движения $х_0$, начальной скорости $υ_{0х}$, а также ускорению $а_х$ можно определить координату тела $х$ в любой момент времени $t$. В векторной форме:
$r↖{→}={r_0}↖{→}+{υ_0}↖{→}+{a↖{→}t^2}/{2}$
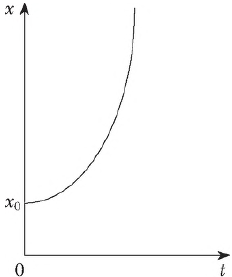
График зависимости координаты от времени прямолинейного равноускоренного движения представлен на рис.
Решая систему уравнений для двух точек траектории, соответствующих моментам времени $t_1$ и $t_2$, получим выражение, связывающее скорости тела в этих точках и ускорение с перемещением на участке $1→2$:
$υ_2^2-υ_1^2=2a(x_2-x_1)$
Эта формула часто бывает полезной при решении различных практических задач.
Равномерное движение точки по окружности
Наряду с равномерным прямолинейным движением очень часто приходится встречаться с равномерным движением по окружности. Такое движение могут совершать точки вращающихся колес, валов и роторов турбин, искусственные спутники, обращающиеся по круговым орбитам, и т. д. При равномерном движении по окружности численное значение скорости остается постоянным. Однако направление скорости при таком движении непрерывно изменяется.
В каждой точке круговой траектории скорость точки направлена по касательной к траектории в этой точке. В этом нетрудно убедиться, коснувшись вращающегося точильного камня, имеющего форму диска, стальным резцом: раскаленные частицы камня, имеющие в момент отрыва от него определенную скорость, будут отлетать от диска по касательной к нему. Эта скорость называется линейной скоростью вращения.
Равномерное движение по окружности характеризуют периодом и частотой обращения.
Период обращения — это время, за которое совершается один оборот.
Известно, что при равномерном движении время определяется делением пройденного пути, т. е. длины окружности — $l_{окр}$, на скорость движения. Таким образом,
$T={l_{окр}}/{υ}={2πr}/{υ}.$
Величина, обратная периоду, называется частотой обращения и обозначается буквой $v$:
$v={1}/{T}$
Угловой скоростью точки $ω$ называется отношение угла поворота к интервалу времени, в течение которого этот поворот совершен:
$ω={φ}/{∆t}$
Угловая скорость выражается в радианах в секунду (рад/с).
Угловая скорость связана с периодом $Т$ и частотой $v$ вращения следующим соотношением:
$ω={2π}/{T}=2πv$
Центростремительное ускорение
Из-за непрерывного изменения направления скорости тело, движущееся по окружности, обладает ускорением. Это ускорение характеризует не быстроту изменения численного значения скорости (которое в данном случае не меняется), а быстроту изменения ее направления.
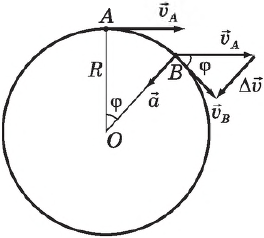
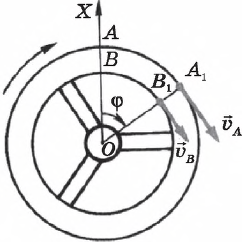
При равномерном движении по окружности ускорение тела все время направлено к ее центру и называется центростремительным ускорением. Чтобы найти его значение, рассмотрим отношение изменения вектора скорости $∆υ$ к малому интервалу времени $∆t$, за который это изменение произошло.
В силу малости угла $φ$ имеем:
$∆υ=υφ$
Так как угол $φ$ между векторами скорости в точках $А$ и $В$ равен углу $АОВ$ между радиусами, который, в свою очередь, равен отношению длины дуги $АВ$ к радиусу $R$, получим:
$φ={υ∆t}/{R}$
Из уравнений получим выражение для модуля вектора ускорения:
$a={∆υ}/{∆t}={υ^2}/{R}$
Из формул следует, что $a={4π^2R}/{T^2}$ и $a=4π^2Rv^2$
Поступательное и вращательное движение твердого тела
Поступательное движение — это движение твердого тела, при котором прямая, соединяющая две любые точки тела, перемещается параллельно своему начальному направлению.
При поступательном движении все точки тела описывают одинаковые (при наложении совпадающие) траектории и имеют в каждый момент времени одинаковые по модулю направления скорости и ускорения.
Поступательное движение может быть как криволинейным, так и прямолинейным. Например, поступательно движется кабина колеса обозрения. Человек, стоящий на ступеньке движущегося эскалатора, также движется поступательно. Для описания его движения (т. е. определения изменения скорости со временем, пути) достаточно рассмотреть движение только одной его точки.
Другими словами, изучение поступательного движения твердого тела сводится к задаче кинематики точки.
Вращательное движение абсолютно твердого тела вокруг неподвижной оси — один из самых простых (после поступательного) видов движения. Оно характеризуется углом поворота точек тела вокруг оси $O_1O_2$, жестко связанной с телом.
Угол поворота $φ$ отсчитывается между двумя лучами, выходящими из одной точки на оси $O_1O_2$ и перпендикулярными к ней: один из лучей (ОХ) неподвижен, другой (ОА) жестко связан с телом.
При вращении тела вокруг неподвижной оси все его точки поворачиваются на одинаковый угол, но описывают окружности разных радиусов в зависимости от степени удаленности точки тела от оси вращения.
Равномерное вращение твердого тела или точки его окружности характеризуется постоянной угловой скоростью.
При равномерном вращении, если известна угловая скорость в начальный момент времени $t_0=0$, можно определить угол поворота тела за время $t$ и тем самым положение точек тела:
$φ=ωt$
При ненулевом значении угла поворота $φ_0$ в начальный момент времени ($t=0$) закон вращательного движения описывается уравнением:
$φ=φ_0+ωt$
Связь между линейной $υ$ и угловой $ω$ скоростями и центростремительным ускорением $а$ определяется соотношениями:
$υ={2πR}/{T}=2πRv; υ=ωR; a={υ^2}/{R}=ω^2R$
За это задание ты можешь получить 2 балла. Уровень сложности: повышенный.
Средний процент выполнения: 67.9%
Ответом к заданию 4 по физике может быть последовательность цифр, чисел или слов. Порядок записи имеет значение.
Разбор сложных заданий в тг-канале
Задачи для практики
Задача 1
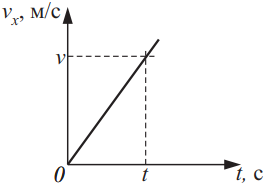
На рисунке изображён график зависимости проекции скорости тела массой m от времени (t). На основании графика выберите два верных утверждения из приведённого ниже списка для момента времени t. Укажите их номера.
- Движущаяся сила вычисляется по формуле F = m · v · t.
- Работу силы можно найти по формуле $A = {m· v}/{2t}$.
- Движущаяся сила вычисляется по формуле $F = {mv}/{t}$.
- Работу силы можно найти по формуле $A = {m·v^2}/{2}$.
- Работу силы можно найти по формуле $A = {m·v^2}/{2t^2}$.
Решение
3) Движущаяся сила $F=ma$, где $a={υ-υ_0}/{y}={υ}/{t}$, поскольку $υ_0=0$, что видно графика. Тогда $F=ma={mυ}/{t}$.
4) Работа силы равна изменению кинетической энергии, т.е. $A=∆E_к={mυ^2}/{2}-{mυ_0^2}/{2}$, поскольку $υ_0=0$, то $A={mυ^2}/{2}-0={mυ^2}/{2}$.
Ответ: 34
Задача 2
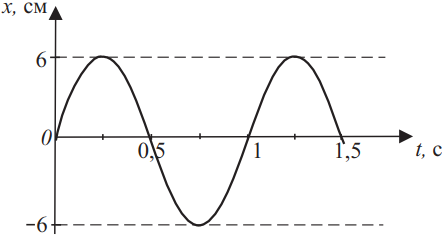
По экспериментальным данным построен график зависимости координаты колебания от времени на рисунке. Из приведённого ниже списка на основании анализа представленного графика выберите все верные утверждения и укажите их номера.
- В момент времени, равный 10 периодам колебаний, тело находится в точке с координатой x = 6 см.
- Координату тела в момент времени t можно найти по формуле x = 6 sin(π · t).
- В момент времени, равный 10 периодам колебаний, тело находится в точке с координатой x = 0 см.
- Координату тела в момент времени t можно найти по формуле x = 6 cos(2π · t).
- Координату тела в момент времени t можно найти по формуле x = 6 sin(2π · t).
Решение
1) Из графика видно, что период колебаний тела $T=1с$, амплитудное значение координаты $x_m=6$см. Значит, угловая частота тела $ω={2π}/{T}={2π}/{1}=2π$. Запишем уравнение колебаний в общем виде: $x=x_m·sin({2π}/{T}·t)$. Подставим наши данные, имеем: $x=6·sin({2πt}/{1})=6·sin(2π·t)$. Координата колебания подчиняется закону синуса, следовательно, в момент времени, равный 10 периодам колебаний, тело находится в точке с координатой $х=0$ см.
Ответ: 35
Задача 3
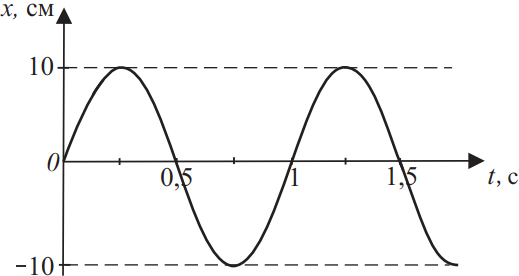
Координата колеблющегося тела меняется так, как показано на графике рисунке. Из приведённого ниже списка на основании анализа представленного графика выберите все верные утверждения и укажите их номера.
- Период колебаний тела равен 1 с.
- Координату тела в момент времени t можно найти по формуле x = 0,1 sin(π · t + π/4).
- Тело совершает колебания с периодом 0,1 с.
- Координату тела в момент времени t можно найти по формуле x = 10 sin(2π · t).
- Координату тела в момент времени t можно найти по формуле x = 10 cos(2π · t + π/4).
Решение
1) Из графика видно, что период колебаний тела равен 1с.
4) Поскольку координата колеблющегося тела изменяется по закону синуса, $x_m=10$см — амплитудное значение координаты и начальная фаза $ϕ_0=0$, то координату тела в момент времени $t$ можно найти по формуле $x=10·sin(2π·t)$.
Ответ: 14
Задача 4
Ученик исследовал зависимость модуля силы упругости F пружины от её растяжения x. Результаты эксперимента приведены в таблице. Из приведённого ниже списка выберите два правильных утверждения и укажите их номера.
| F, H | 0 | 0,5 | 1 | 1,5 | 2 | 2,5 |
| x, м | 0 | 0,02 | 0,04 | 0,06 | 0,08 | 0,10 |
- Коэффициент упругости пружины равен 2,5 Н/м.
- При увеличении массы груза растяжение пружины уменьшается.
- Потенциальная энергия пружины пропорциональна растяжению пружины.
- Потенциальная энергия пружины при её растяжении на 0,08 м равна 0,08 Дж.
- При подвешенном к пружине грузе массой 100 г её удлинение составит 4 см.
Решение
Исходя из теории упругости и результатов опыта, определим $E_n={kx^2}/{2}={25·0.08^2}/{2}=0.08$Дж. $k={E}/{x}={2}/{0.08}=25$н/м, а при $F_т=1H; x=0.04$м.
Ответ: 45
Задача 5
Грузик, подвешенный на нити, совершает гармонические колебания. В таблице представлены значения координаты грузика через одинаковые промежутки времени. Из приведённого ниже списка выберите все правильные утверждения и укажите их номера.
| t, c | 0 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 |
| x, см | 6 | 3 | 0 | 3 | 6 | 3 | 0 | 3 |
- Максимальная скорость грузика равна 0,15 м/с.
- Период колебаний шарика равен 0,4 с.
- В момент времени 0,1 с кинетическая энергия шарика максимальна.
- Полная механическая энергия шарика остаётся неизменной.
- Амплитуда колебаний шарика равна 6 мм.
Решение
Исходя из теории о гармонических колебаниях и данной таблицы, полная механическая энергия шарика остается неизменной. (4 — верно).
Период колебании — время за которое происходит одно полное колебание — 0,4 с (2 — верно)
Максимальная скорость шарика связана с амплитудой ( $υ_{max}=А ω ={А2π}/{T}= {0,03* 2*3.14}/{0,4}=0,471$м/с. (1 — неверно)
Максимальная кинетическая энергия будет в момент прохождения шариком положения равновесия x=3 см, это соответствует времени t=0,1 с (3 — верно)
Амплитуда колебания — это максимальное отклонение от положения равновесия, так как координата колеблется между значениями 6 см и 0, положению равновесия будет соответствовать координата х=3 см, значит амплитуда: А=6-3=3 см (5 — неверно)
Ответ: 234
Задача 6
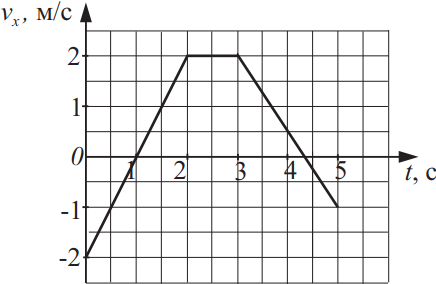
Тело массой 15 кг движется вдоль оси Ox в инерциальной системе отсчёта. График зависимости проекции скорости vx этого тела на ось Ox от времени представлен на рисунке. Из приведённого ниже списка выберите два верных утверждения на основании анализа представленного графика и укажите их номера.
- В течение первых двух секунд перемещение тела равно 2 м.
- Модуль ускорения тела в промежутке времени от 1 с до 2 с на 25% больше модуля ускорения тела в промежутке времени от 3 с до 4 с.
- В течение первой секунды кинетическая энергия тела увеличилась на 30 Дж.
- В промежутке времени от 1 с до 2 с импульс тела увеличился в 2 раза.
- В момент времени 4 с модуль равнодействующей сил, действующих на тело, равен 22,5 Н.
Решение
Из теории кинематики и данного графика можно сказать, что модуль ускорения тела с 1 до 2 на 25% больше 3-4, т.е. $a_{1-2}=2м/с^2; a_{3-4}=1.5м/с^2$. В момент времени 4с модуль равнодействующих сил, $F=22.5H$, т.к. $a_4=1.5м/с^2$, $F_p=ma_4=15·1.5=22.5H$
Ответ: 25
Задача 7
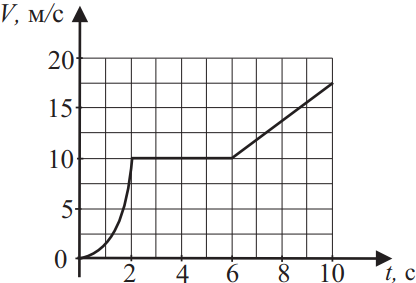
На рисунке представлен график зависимости скорости V от времени t для тела, движущегося прямолинейно. Используя данные графика, выберите из приведённого ниже списка все верные утверждения и укажите их номера.
- Первые две секунды тело двигалось равноускоренно.
- Со 2-й по 6-ю секунду тело переместилось на 40 м.
- Со 2-й по 6-ю секунду тело переместилось на меньшее расстояние, чем за первые две секунды.
- Средняя скорость тела во время движения со 2-й по 10-ю секунду равна 12,5 м/с.
- С 6-й по 10-ю секунду тело двигалось равноускоренно.
Решение
1) Неверно, так как равноускоренному движению соответствует линейный график: $v(t)=v_0+at$.
2)Верно. Из данного рисунка видно, что с 2 по 6 сек, тело прошло 40 м (площадь под графиком)
3) Неверно. Площадь под графиком со 2 по 6-ю секунды гораздо больше, чем площадь под графиком за первые две секунды.
4)Чтобы найти среднюю скорость, нужно разделить весь путь со 2-й по 10-ю секунду на всё соответствующее время, т.е. на 8 с. При этом путь определяем как площадь под графиком, так как у нас есть график в координатах v(t):
$S=S_1+S_2=8·10+{4·7,5}/2=110$ м.
Тогда $v_{ср}={110}/8=13,75$. Утверждение 4 — неверно.
5) Верно. С 6 по 10 сек, тело двигалось равноускоренно, т.к. за равные промежутки времени скорость увеличивается на одну ту же величину (линейная зависимость v(t)).
Ответ: 25
Задача 8

Математический маятник совершает незатухающие колебания между точками А и Б. Точка О соответствует положению равновесия маятника. Используя текст и рисунок, выберите из предложенного ниже списка все верные утверждения. Укажите их номера.
- За время, равное периоду колебаний, маятник проходит путь, равный длине дуги АБ.
- При перемещении маятника из положения О в положение В потенциальная энергия уменьшается, а кинетическая энергия увеличивается.
- В точке О кинетическая энергия маятника максимальна.
- Расстояние АБ соответствует амплитуде колебаний координаты.
- В точках А и Б потенциальная энергия маятника принимает максимальное значение.
Решение
- За время, равное периоду колебаний, маятник проходит путь, равный ДВУМ длинам дуги АБ — «туда и обратно». 1 — неверно.
- При перемещении маятника из положения О в положение В потенциальная энергия УВЕЛИЧИВАЕТСЯ (т.к. высота растёт), а кинетическая энергия УМЕНЬШАЕТСЯ (т.к. маятник замедляется). 2 — неверно
- В точке О кинетическая энергия маятника максимальна, так как положение равновесия груз маятника проходит с наибольшей скоростью — верно
- Амплитуда колебаний координаты — это половина расстояния АБ — отклонение от положения равновесия. 4 — неверно.
- В точках А и Б потенциальная энергия маятника принимает максимальное значение, так как груз находится на наибольшей высоте. 5 — верно.
В точке О кинетическая энергия максимальна. Потенциальная энергия принимает максимальное значение в точках А и Б.
Ответ: 35
Задача 9
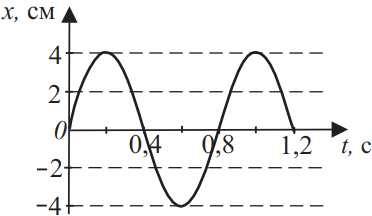
Координата колеблющегося тела меняется так, как показано на графике рисунка. Из приведённого ниже списка выберите все верные утверждения на основании анализа представленного графика и укажите их номера.
- Период колебаний тела равен 1 с.
- Амплитуда колебаний равна 8 см.
- Частота колебаний равна 1,25 Гц.
- Амплитуда колебаний равна 4 см.
- Период колебаний тела равен 0,4 с.
Решение
Из данного графика очевидно, что $A=4$см (2 — неверно, 4 — верно), период колебаний T=0.8 c (1, 5 — неверно), а частота $v={1}/{T}={1}/{0.8}=1.25$Гц.(3 — верно)
Ответ: 34
Задача 10
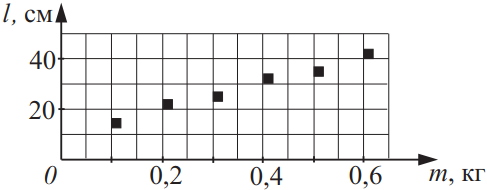
На рисунке приведён график зависимости длины пружины от величины нагрузки. Из приведённого ниже списка выберите два утверждения, соответствующих результатам этого эксперимента, и укажите их номера.
- Коэффициент упругости пружины примерно равен 20 Н/м.
- Коэффициент упругости пружины примерно равен 30 Н/м.
- Коэффициент упругости пружины примерно равен 50 Н/м.
- Коэффициент упругости пружины примерно равен 10 Н/м.
- Для данного эксперимента выполняется закон Гука.
Решение
$k=F/(l-l_0)$
Если продолжить прямую, видно, что длина недеформированной пружины 10 см
$k=2/(0.2-0.1)=20$ Н/м
Ответ: 15
Задача 11
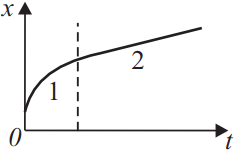
Бусинка скользит по неподвижной горизонтальной спице. На графике изображена зависимость координаты бусинки от времени. Ось Ox параллельна спице. Из приведённого ниже списка на основании графика выберите два верных утверждения о движении бусинки и укажите их номера.
- На участке 1 проекция ускорения ax бусинки отрицательна.
- На участке 1 модуль скорости остаётся неизменным, а на участке 2 — уменьшается.
- На участке 1 модуль скорости увеличивается, а на участке 2 — уменьшается.
- На участке 1 модуль скорости уменьшается, а на участке 2 — остаётся неизменным.
- В процессе движения вектор скорости бусинки менял направление на противоположное.
Решение
Скорость — это производная координаты по времени. Графически это $tgα$ наклонной графика зависимости координаты от времени. Заметим, что координата все время растет, но на участке 1 — скорость уменьшается, следовательно, проекция ускорения отрицательна. На участке 2, скорость неизменна, а координата растет, тело не меняет направление движения.
Ответ: 14
Задача 12
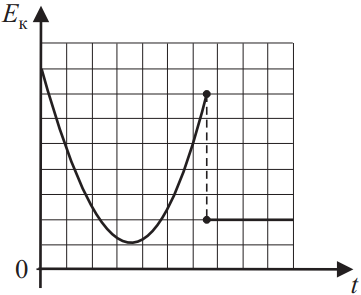
На рисунке представлен схематичный вид графика изменения кинетической энергии тела с течением времени. Выберите два верных утверждения, описывающих движение в соответствии с данным графиком.
- В конце наблюдения кинетическая энергия тела равна нулю.
- Кинетическая энергия тела в течение всего времени наблюдения увеличивается.
- Кинетическая энергия тела в начальный момент времени максимальна.
- Тело брошено вертикально вверх с балкона и упало на Землю.
- В конце наблюдения скорость тела не равна нулю.
Решение
1) В конце наблюдения $E_к=0$, неверно, т.к. при $t=t_к⇒E_к≠0$, если $E_к=0$, то график должен проходить через ось ординат.
2) $E_к$, в течении всего времени увеличивается, неверно, т.к. при $t={t_к}/{2}$ $E_к=min$, в середине пути кинетическая энергия минимальна.
3) Исходя из графика $E_к$ максимальная в момент (верно) $t=0$.
4) Неверно, т.к. график вертикально брошенного тела, выглядит иначе.
5) При $t_к=t; E_к≠0$ (верно), т.к. $υ≠0⇔E_к≠0$.
Ответ: 35
Задача 13
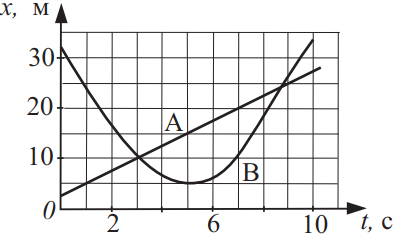
На рисунке приведены графики зависимости координаты от времени для двух тел A и B, движущихся по прямой, вдоль которой и направлена ось Ox. Из приведённого ниже списка выберите два верных утверждения о характере движения тел и укажите их номера.
- Тело A движется равномерно.
- Тело A движется с постоянным ускорением, равным 5 м/с2.
- Первый раз тела A и B встретились в момент времени, равный 3 с.
- Вторично тела A и B встретились в момент времени, равный 7 с.
- В момент времени t = 5 с тело B достигло максимальной скорости движения.
Решение
1) Тело А движется равномерно, т.к. равномерное движение — это движение, при котором тело за равные промежутки времени проходит одинаковые расстояния (подходит).
2) Ускорение тела А равно нулю, т.к. оно движется с постоянной скоростью $υ={20-10}/{7-3}=2.5м/с$ (не подходит).
3) Графики зависимости координаты от времени для двух тел А и В пересекаются в момент времени $t=3c$, значит, первый раз тела А и В встретились в момент времени, равный 3с (подходит).
Ответ: 13
Задача 14
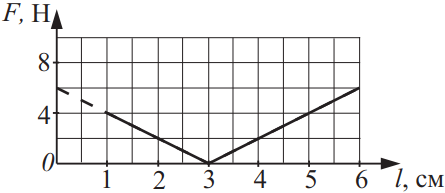
При проведении эксперимента ученик исследовал зависимость модуля силы упругости пружины, которая выражается формулой F (l) = k|l − l0|, где l0 — длина пружины в недеформированном состоянии, от её длины. График полученной зависимости приведён на рисунке. Из приведённого ниже списка выберите все верные утверждения на основании анализа графика и укажите их номера.
- Длина пружины в недеформированном состоянии равна 6 см.
- Длина пружины в недеформированном состоянии равна 3 см.
- При действии силы 2 Н деформация пружины равна 2 см.
- При действии силы 4 Н деформация пружины равна 2 см.
- Коэффициент жёсткости пружины равен 50 Н/м.
Решение
1) Из графика видно, что длина пружины в не деформированном состоянии равна 3 см, т.к. при l=3см сила упругости $F=OH$(не подходит).
2) Длина пружины в не деформированном состоянии равна 3 см (подходит).
3) При действии сила 2Н деформация пружины равна |2см-3см|=|-1см|=1см или |4см-3см|=1см (не подходит).
4) При действии сила 4Н пружина сжимается или растягивается на 2см, поскольку |1см-3см|=|-2см|=1см или |5см-3см|=2см (подходит).
Ответ: 24
Задача 15
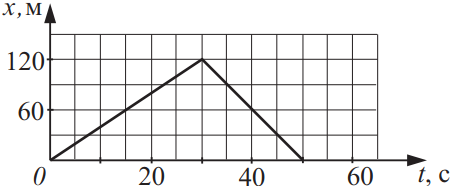
На рисунке приведена зависимость координаты движущегося тела от времени. Из приведённого ниже списка выберите два верных утверждения
- Скорость движения тела в интервале времени от 30 до 50 с на 2 м/с больше, чем скорость в интервале времени от 0 до 30 с.
- Скорость тела возрастала в интервале времени от 0 до 30 с и убывала в интервале от 30 до 50 с.
- Максимальная скорость движения на всём пути равна 2,4 м/с.
- За всё время движения тело прошло путь 120 м.
- За всё время движения тело прошло путь 240 м.
Решение
1) $υ_1[30-50c]={x_к-x_н}/{t_к-t_н}={0-120}/{50-30}=-{120}/{20}=-6м/с$. Знак «минус» говорит о том, что тело движется в обратном направлении, поэтому возьмем по модулю $υ[30-50c]=6м/с; υ_2[0-30c]={x_к-x_н}/{t_к-t_н}={120-0}/{30-0}={120}/{30}=4м/с; ∆υ=υ_1[30-50c]-υ_2[0-30c]=6-4=2м/с$(подходит).
2) Скорость тела возрастала в интервале времени от 0 до 30с и в интервале от 30 до 50с (не подходит).
3) Максимальная скорость на всем пути равна 6м/с (не подходит).
4) За все время движения тело прошло путь: $S=S_1+S_2=υ_1·∆t_1+υ_1·∆t_2=6·(50-30)+4·(30-0)=6·20+4·30=120+120=240$м (не подходит).
5) За все время движения тело прошло путь 240м (подходит).
Ответ: 15
Задача 16
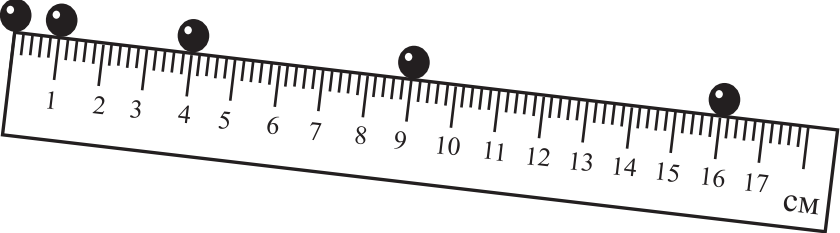
На рисунке приведена стробоскопическая фотография движущегося шарика по жёлобу, образующему некоторый угол с горизонтом. Положения шарика на фотографии показаны через равные промежутки времени. Из приведённого ниже списка выберите два верных утверждения на основании анализа стробоскопической фотографии и укажите их номера.
- Движение шарика равномерное.
- Скорость шарика увеличивается.
- Шарик движется под действием переменной силы.
- Если промежуток времени между двумя последовательными положениями шарика равен 2 с, то его ускорение равно 0,5 см/с2.
- Импульс шарика в процессе движения остаётся постоянным.
Решение
1) Шарик за одинаковые промежутки времени проходит разные расстояния, значит, его движение неравномерное (не подходит).
2) Движение шарика равноускоренное, значит, скорость шарика увеличивается (подходит).
3) Шарик движется под действием постоянной силы $F↖{→}=ma↖{→}$ (не подходит).
4) $S=0.16м; t=4·2=8c; υ_0=0м/с; a=0.005м/с^2$. При равноускоренном движении перемещение равно: $S=υ_0е+{at^2}/{2}=0·8+{0.005·(8)^2}/{2}={0.005·64}/{2}=32·0.005=0.16=16$см (подходит).
Ответ: 24
Задача 17
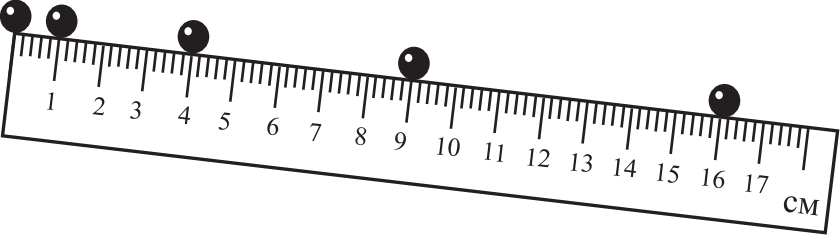
На рисунке приведена стробоскопическая фотография движущегося шарика по жёлобу, образующему некоторый угол с горизонтом. Положения шарика на фотографии показаны через равные промежутки времени. Из приведённого ниже списка выберите два верных утверждения на основании анализа стробоскопической фотографии и укажите их номера.
- Шарик движется с переменным ускорением.
- Скорость шарика уменьшается.
- Шарик движется под действием постоянной силы.
- Если промежуток времени между двумя последовательными положениями шарика равен 2 с и он начинал движение из состояния покоя, то его скорость в точке с координатой 9 см равна 3 см/с.
- Импульс шарика в процессе движения уменьшается.
Решение
1) Шарик движется с постоянным ускорением (не подходит).
2) Скорость шарика увеличивается, т.к. за равные промежутки времени он проходит все больше расстояния (не подходит).
3) Шарик движется под действием постоянной силы $F=m·a$ (подходит).
4) $υ_k=υ_0+at$(1), т.к. $υ_0=0$м/с, поскольку начинает движение из состояния покоя, то $υ_k=at$(2). Перемещение $S={at^2}/{2}⇒a={2·S}/{t^2}$(3), где $S=0.09$м, $t=6c$ (т.к. 3 вспышки стробослота), тогда $a={2·0.09}/{36}=0.005$, тогда $υ=at=0.005·6=0.03=3$см/с (подходит).
Ответ: 34
Задача 18
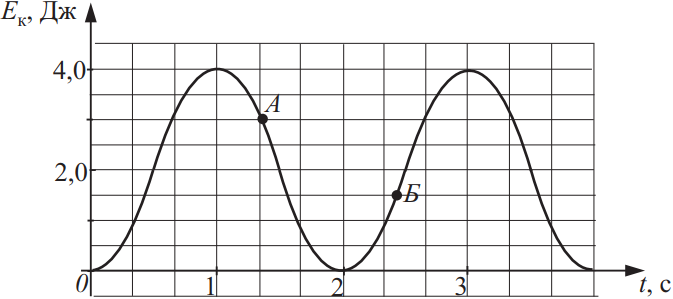
На рисунке приведён график зависимости кинетической энергии тела от времени t. Выберите все верные утверждения на основании анализа представленного графика.
- Тело движется под действием постоянной силы.
- Потенциальная энергия тела в точке Б равна 1,5 Дж.
- Период колебаний тела равен 4 с.
- Максимальное значение потенциальной энергии равно значению потенциальной энергии в точке А.
- Полная механическая энергия тела равна 4 Дж.
Решение
1. Из графика видно, что время одного полного колебания равно 4с, т.к. в течение одного полного колебания тело проходит три максимальных значения (или три минимальных значения) кинетической энергии, т.е. период колебаний тела равен 4с (верно).
2. Поскольку полная механическая энергия тела равна: $E=E_{к,max}=E_{к,max}=E_к+Е_п$(1), а максимальная кинетическая энергия тела равна 4 Дж, то полная механическая энергия тела равна 4 Дж (верно).
Ответ: 35
Задача 19
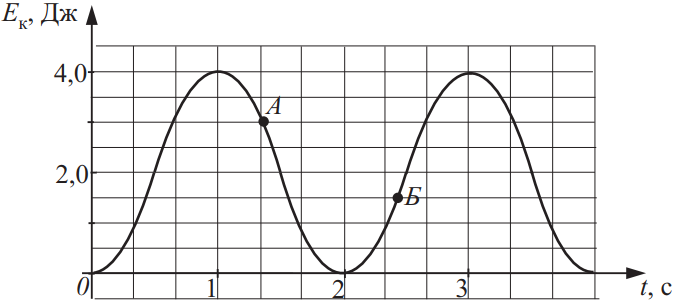
На рисунке приведён график зависимости кинетической энергии тела от времени t. Из приведённого ниже списка выберите все верные утверждения на основании анализа представленного графика и укажите их номера.
- Тело совершает гармонические колебания.
- Потенциальная энергия тела в точке A равна 1 Дж.
- Период колебаний тела равен 2 с.
- Максимальное значение потенциальной энергии равно потенциальной энергии в точке Б.
- Частота колебаний тела равна 4 Гц.
Решение
1. Тело совершает гармонические колебания, т.к. гармонические колебания — это колебания, подчиняющиеся закону синуса или косинуса, а на графике мы видим синусоиду (1 — верно).
2. Поскольку полная механическая энергия тела равна: $E=E_{п,max}=E_{п,max}=E_к+Е_п$(1), где $E_к$ — кинетическая энергия тела, $E_{к,max}=4$Дж, $E_п$ — потенциальная энергия тела. В точке А $E_к=3$Дж, значит, $E_п=E-E_к=E_{к,max}-E_к=4-3=1$Дж (2 — верно)
3. За один период колебаний тела, успевает произойти два колебания кинетической энергии, поэтому период колебаний тела равен 4с, а не 2. (3 — неверно)
4. Максимальное значение потенциальной энергии будет в той точке, в которой кинетическая энергия минимальна. Точка Б под это условие не подходит (4 — неверно)
5. Частота колебания тела равна: $v=1/T=1/4=0,25$ Гц (5 — неверно)
Ответ: 12
Задача 20
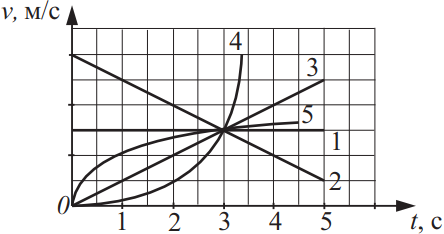
На рисунке представлены графики зависимости проекции скорости v на некоторую ось от времени t для пяти тел. Из приведённого ниже списка выберите два верных утверждения на основании анализа представленных графиков и укажите их номера.
- Наибольшей начальной скоростью обладало второе тело.
- Первое тело покоится.
- Наименьший путь за первые три секунды прошло второе тело.
- Третье тело движется равноускоренно.
- Пятое тело совершает равнопеременное движение.
Решение
Из графика видно, что в момент времени t=0с наибольшей начальной скоростью обладает тело 2.
Третье тело движется равноускоренно, т.к. график скорости напрвлен вверх.
Ответ: 14
Рекомендуемые курсы подготовки
ОГЭ
Освоение образовательных программ основного общего образования завершается обязательной государственной итоговой аттестацией (далее – ГИА 9) по русскому языку и математике.
Нормативно-правовые документы
Приказы и методические документы
Демоверсии, спецификации, кодификаторы
В данном разделе представлены документы, определяющие структуру и содержание контрольных измерительных материалов основного государственного экзамена.
Для предметных комиссий субъектов РФ
Открытый банк заданий ОГЭ
Новая версия открытого банка заданий
Варианты ЕГЭ по химии 2022/2023
В этой категории
1195 заданий и
423 видео.
Дацук и Степенин. Варианты ЕГЭ-2023В течение 2022/2023 учебного годы мы будем выкладывать здесь наши варианты ЕГЭ-2023 по химии. |
|
|
Вариант 1 |
|
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
|
|
Вариант 2 |
|
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
|
|
Вариант 3 |
|
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
|
|
Вариант 4 |
|
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
|
|
Вариант 5 |
|
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
|
|
Вариант 6 |
|
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
|
|
Вариант 7 |
|
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
|
|
Вариант 8 |
|
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
|
|
Вариант 9 |
|
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
|
|
Вариант 10 |
|
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
|
|
Вариант 11 |
|
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
|
|
Вариант 12 |
|
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
|
|
Вариант 13 |
|
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
|
|
Вариант 14 |
|
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
|
ФИПИДемоверсия содержит больше вопросов, чем стандартный вариант, потому что включает в себя альтернативные примеры заданий. Это открытый вариант, который ФИПИ публикует в начале учебного года |
|
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 |
|
СтатГрад |
|
|
Вариант ХИ2110101 |
|
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
|
|
Вариант ХИ2110102 |
|
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
|
|
Вариант ХИ2110201 |
|
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
|
|
Вариант ХИ2110202 |
|
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
|
|
Вариант ХИ2110204 |
|
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
|
|
Вариант ХИ2110301 |
|
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
|
|
Вариант ХИ2110302 |
|
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
|
|
Вариант ХИ2110303 |
|
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
|
|
Вариант ХИ2110304 |
|
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
|
|
Вариант ХИ2110401 |
|
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
|
|
Вариант ХИ2110402 |
|
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
|
|
Вариант ХИ2110501 |
|
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
|
|
Вариант ХИ2110502 |
|
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
|
|
Вариант ХИ2210101 |
|
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
|
|
Вариант ХИ2210102 |
|
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
|
Широкопояс |
|
|
Вариант 1 |
|
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
|
|
Вариант 2 |
|
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
|
|
Вариант 3 |
|
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
|
|
Вариант 4 |
|
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
|
|
Вариант 5 |
|
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
|