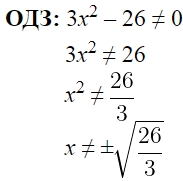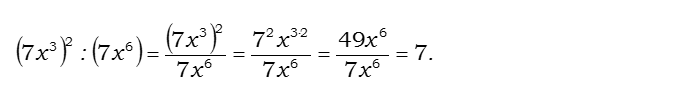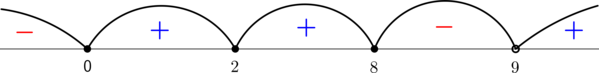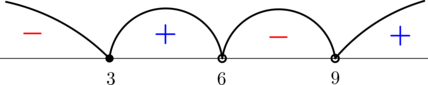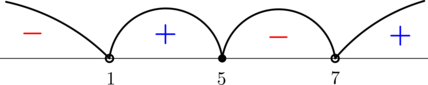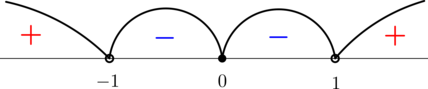Решите уравнение
frac{7x}{3x^{2}–26}=1
Если уравнение имеет более одного корня, в ответе запишите меньший из корней.
Источник: Ященко ЕГЭ 2022 (36 вар)
Решение:
ОДЗ:
3х2 – 26 ≠ 0
3х2 ≠ 26
х2 ≠ frac{26}{3}
х2 ≠ 8frac{2}{3}
х ≠ pm sqrt{8frac{2}{3}}
Решение уравнения:
frac{7x}{3x^{2}–26}=1
3x2 – 26 = 7x
3x2 – 7x – 26 = 0
D = (–7)2 – 4·3·(–26) = 361 = 192
x_{1}=frac{7+19}{2cdot 3}=frac{26}{6}=4frac{2}{6}=4frac{1}{3}\x_{2}=frac{7–19}{2cdot 3}=frac{–12}{6}=–2
Оба корня уравнения удовлетворяют ОДЗ, в ответ записываем меньший из них х = –2.
Ответ: –2.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 4 / 5. Количество оценок: 25
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
Решите уравнение (displaystyle frac{7x}{3x^2-26}=1). Если уравнение имеет более одного корня, в ответ запишите меньший из корней.
Решение
(7x=3x^2-26;)
(3z^2-7x-26=0;)
(D=b^2-4ac=49-4cdot3 cdot -26=361)
(displaystyle x_1=frac{-b+sqrt{D}}{2a}=frac{13}{3};)
(displaystyle x_2=frac{-b-sqrt{D}}{2a}=-2.)
ОДЗ: (3x^2-26 neq 0) отсюда (x neq pm sqrt{frac{26}{3}}).
Получилось, что меньший из корней равен (-2).
Ответ: (-2).
Источник: ЕГЭ 2023 Математика. Профильный уровень. Типовые экзаменационные варианты. 36 вариантов (вариант 14) (Купить книгу)
|
|
|
|
-
11 класс
- 10 класс
- 9 класс
- 7-8 классы
- 6 класс
- 5 класс
- 4 класс
-
Item
- Критерии оценивания 2 части ЕГЭ по математике профильного уровня ФИПИ ❗
ЕГЭ по математике 2023
- Математика 36 вариантов ЕГЭ 2023 ФИПИ школе Ященко 🔥
Пробные ЕГЭ 2023
- СтатГрад 28-02-2023 Тренировочная работа № 3 11 класс по математике 🔥
- СтатГрад 13-12-2022 Тренировочная работа № 2 11 класс по математике
- СтатГрад 28-09-2022 Тренировочная работа № 1 11 класс по математике
- Реальныe варианты ЕГЭ по математике ❗
Задания ЕГЭ части 1
- Задачи 1 планиметрия
- Задачи 2 стереометрия
- Задачи 3 вероятность
- Задачи 4 вероятность
- Задачи 5 уравнения
- Задачи 6 выражения
- Задачи 7 смысл производной
- Задачи 8 физические
- Задачи 9 текстовые
- Задачи 10 графики функций
- Задачи 11 исследование функции
Задания ЕГЭ части 2
- Задачи 12 с уравнениями
- Задачи 13 на стереометрию
- Задачи 14 с неравенствами
- Задачи 15 экономические
- Задачи 16 на планиметрию
- Задачи 17 с параметрами
- Задачи 18 Числа и их свойства
- Критерии
- Олимпиада 🔥
ЕГЭ по математике 2022
- ЕГЭ по математике 27-06-2022 резервный день
- ЕГЭ по математике 02-06-2022 основная волна профильный уровень
- Досрочный ЕГЭ 2022 по математике
Пробные ЕГЭ 2022
- Тренировочная работа №2 по математике 10-11 класс Статград 18-05-2022
- Тренировочная работа №5 по математике 11 класс Статград 28-04-2022
- Тренировочная работа №4 по математике 11 класс Статград 15-03-2022
- Тренировочная работа №3 по математике 11 класс Статград 16-02-2022
- Тренировочная работа №1 по математике 10-11 класс Статград 27-01-2022
- Тренировочная работа №2 по математике 11 класс Статград 15-12-2021
- Тренировочная работа №1 по математике 11 класс Статград 28-09-2021
- Диагностическая работа по математике для 11 классов МЦКО 16-11-2021
Математика 36 вариантов ЕГЭ 2022 ФИПИ школе Ященко
- Вариант 1 ( из 36 вариантов заданий ЕГЭ 2022 ФИПИ Ященко)
- Вариант 2 ( из 36 вариантов заданий ЕГЭ 2022 ФИПИ Ященко)
- Вариант 3 ( из 36 вариантов заданий ЕГЭ 2022 ФИПИ Ященко)
- Вариант 4 ( из 36 вариантов заданий ЕГЭ 2022 ФИПИ Ященко)
- Вариант 5 ( из 36 вариантов заданий ЕГЭ 2022 ФИПИ Ященко)
- Вариант 6 ( из 36 вариантов заданий ЕГЭ 2022 ФИПИ Ященко)
- Вариант 7 ( из 36 вариантов заданий ЕГЭ 2022 ФИПИ Ященко)
- Вариант 8 ( из 36 вариантов заданий ЕГЭ 2022 ФИПИ Ященко)
- Вариант 9 ( из 36 вариантов заданий ЕГЭ 2022 ФИПИ Ященко)
- Вариант 10 ( из 36 вариантов заданий ЕГЭ 2022 ФИПИ Ященко)
- Вариант 11 ( из 36 вариантов заданий ЕГЭ 2022 ФИПИ Ященко)
- Вариант 12 ( из 36 вариантов заданий ЕГЭ 2022 ФИПИ Ященко)
- Вариант 13 ( из 36 вариантов заданий ЕГЭ 2022 ФИПИ Ященко)
- Вариант 14 ( из 36 вариантов заданий ЕГЭ 2022 ФИПИ Ященко)
- Вариант 15 ( из 36 вариантов заданий ЕГЭ 2022 ФИПИ Ященко)
- Вариант 16 ( из 36 вариантов заданий ЕГЭ 2022 ФИПИ Ященко)
- Вариант 17 ( из 36 вариантов заданий ЕГЭ 2022 ФИПИ Ященко)
- Вариант 18 ( из 36 вариантов заданий ЕГЭ 2022 ФИПИ Ященко)
- Вариант 19 ( из 36 вариантов заданий ЕГЭ 2022 ФИПИ Ященко)
- Вариант 20 ( из 36 вариантов заданий ЕГЭ 2022 ФИПИ Ященко)
- Вариант 21 ( из 36 вариантов заданий ЕГЭ 2022 ФИПИ Ященко)
- Вариант 22 ( из 36 вариантов заданий ЕГЭ 2022 ФИПИ Ященко)
- Вариант 23 ( из 36 вариантов заданий ЕГЭ 2022 ФИПИ Ященко)
- Вариант 24 ( из 36 вариантов заданий ЕГЭ 2022 ФИПИ Ященко)
- Вариант 25 ( из 36 вариантов заданий ЕГЭ 2022 ФИПИ Ященко)
- Вариант 26 ( из 36 вариантов заданий ЕГЭ 2022 ФИПИ Ященко)
- Вариант 27 ( из 36 вариантов заданий ЕГЭ 2022 ФИПИ Ященко)
- Вариант 28 ( из 36 вариантов заданий ЕГЭ 2022 ФИПИ Ященко)
- Вариант 29 ( из 36 вариантов заданий ЕГЭ 2022 ФИПИ Ященко)
- Вариант 30 ( из 36 вариантов заданий ЕГЭ 2022 ФИПИ Ященко)
- Вариант 31 ( из 36 вариантов заданий ЕГЭ 2022 ФИПИ Ященко)
- Вариант 32 ( из 36 вариантов заданий ЕГЭ 2022 ФИПИ Ященко)
- Вариант 33 ( из 36 вариантов заданий ЕГЭ 2022 ФИПИ Ященко)
- Вариант 34 ( из 36 вариантов заданий ЕГЭ 2022 ФИПИ Ященко)
- Вариант 35 ( из 36 вариантов заданий ЕГЭ 2022 ФИПИ Ященко)
- Вариант 36 ( из 36 вариантов заданий ЕГЭ 2022 ФИПИ Ященко)
Математика 50 вариантов заданий ЕГЭ 2022 Ященко
- 1 Вариант ( из 50 вариантов заданий ЕГЭ 2022 Ященко)
- 2 Вариант ( из 50 вариантов заданий ЕГЭ 2022 Ященко)
- 3 Вариант ( из 50 вариантов заданий ЕГЭ 2022 Ященко)
- 4 Вариант ( из 50 вариантов заданий ЕГЭ 2022 Ященко)
- 5 Вариант ( из 50 вариантов заданий ЕГЭ 2022 Ященко)
- 6 Вариант ( из 50 вариантов заданий ЕГЭ 2022 Ященко)
- 7 Вариант ( из 50 вариантов заданий ЕГЭ 2022 Ященко)
- 8 Вариант ( из 50 вариантов заданий ЕГЭ 2022 Ященко)
- 9 Вариант ( из 50 вариантов заданий ЕГЭ 2022 Ященко)
- 10 Вариант ( из 50 вариантов заданий ЕГЭ 2022 Ященко)
- 11 Вариант ( из 50 вариантов заданий ЕГЭ 2022 Ященко)
- 12 Вариант ( из 50 вариантов заданий ЕГЭ 2022 Ященко)
- 13 Вариант ( из 50 вариантов заданий ЕГЭ 2022 Ященко)
- 14 Вариант ( из 50 вариантов заданий ЕГЭ 2022 Ященко)
- 15 Вариант ( из 50 вариантов заданий ЕГЭ 2022 Ященко)
- 16 Вариант ( из 50 вариантов заданий ЕГЭ 2022 Ященко)
- 17 Вариант ( из 50 вариантов заданий ЕГЭ 2022 Ященко)
- 18 Вариант ( из 50 вариантов заданий ЕГЭ 2022 Ященко)
- 19 Вариант ( из 50 вариантов заданий ЕГЭ 2022 Ященко)
- 20 Вариант ( из 50 вариантов заданий ЕГЭ 2022 Ященко)
- Демонстрационный вариант ЕГЭ 2022 ФИПИ по математике
ОГЭ 2022 по математике
- ОГЭ по математике 2022 основная волна 23 мая
- Тренировочная работа №1 по математике 9 класс Статград 05-10-2021
- Математика 50 вариантов заданий ОГЭ 2022 Ященко
ЕГЭ по математике 2021
- егэ по математике 2021 резервный день 29 июня
- егэ по математике профильного уровня 07-06-2021 основная волна
- открытый вариант ким егэ по математике 2021 ФИПИ
Пробные ЕГЭ 2021
- тренировочная работа №5 по математике 11 класс статград 29-04-2021
- Тренировочная работа №4 по математике 11 класс Статград 16-03-2021
- Тренировочная работа №3 по математике 11 класс Статград 10-02-2021
- Тренировочная работа №2 по математике 11 класс Статград 16-12-2020
- Тренировочная работа №1 по математике 11 класс Статград 30-09-2020
- Математика 50 вариантов заданий ЕГЭ 2021 Ященко
- Математика 36 вариантов ЕГЭ 2021 ФИПИ школе Ященко
- Математика 37 вариантов заданий 2021 Ященко профильный уровень ЕГЭ
- Демонстрационный вариант ЕГЭ 2021 ФИПИ по математике
ЕГЭ 2020
- ЕГЭ по математике 2020 резервный день
- ЕГЭ по математике 10-07-2020
- Открытые варианты досрочного отменённого ЕГЭ 2020 по математике
Пробные ЕГЭ 2020
- Тренировочная работа № 2 по математике 10 — 11 класс СтатГрад 15-05-2020
- Тренировочная работа № 5 11 класс по математике СтатГрад 22-04-2020
- Пробный ЕГЭ в Санкт-Петербурге 13-03-2020
- Тренировочная работа № 4 11 класс по математике СтатГрад 11-03-2020
- Пробный ЕГЭ по математике 29-02-2020
- Тренировочная работа № 3 11 класс по математике СтатГрад 29-01-2020
- Региональные диагностические работы по математике 2020
- СтатГрад 18-12-2019 Тренировочная работа № 2 11 класс по математике
- СтатГрад 25-09-2019 Тренировочная работа № 1 11 класс по математике
- Лысенко ЕГЭ 2020 математика профильный уровень 40 тренировочных вариантов
- Математика 50 вариантов заданий 2020 Ященко профильный уровень ЕГЭ
- Математика 36 вариантов заданий 2020 Ященко профильный уровень ЕГЭ
ЕГЭ 2019
- ЕГЭ по математике 24-06-2019 резервный день
- ЕГЭ по математике 29-05-2019 основная волна
- Резервный день Досрочного ЕГЭ по математике 10-04-2019
- Досрочный ЕГЭ 2019 математика профильный уровень 29-03-2019
Пробные ЕГЭ 2019
- СтатГрад 19-04-2019 Тренировочная работа № 5 11 класс по математике
- Пробный ЕГЭ 16-03-2019
- СтатГрад 13-03-2019 Тренировочная работа № 4 11 класс
- Пробный ЕГЭ 12-03-2019 Санкт-Петербург
- СтатГрад 24-01-2019 Диагностическая работа № 3 11 класс
- СтатГрад 20-12-2018 11 класс Тренировочная работа №2
- Тренировочная работа 20_09_2018 СтатГрад 11 класс
- Диагностическая работа 10_10_2018 Коми 11 класс
- Демонстрационный вариант КИМ ФИПИ ЕГЭ 2019
ященко егэ 2019 математика профиль 36 вариантов
- 36 вариантов ФИПИ егэ 2019 математика ященко
14 вариантов 2019 Ященко Типовые тестовые задания профильный уровень ЕГЭ
20 вариантов тестов ЕГЭ 2019 Ященко Тематическая рабочая тетрадь
- ВВ Мирошин АР Pязановский Математика Решение задач ЕГЭ 2019
ЕГЭ 2018
- Резервный день ЕГЭ 2018 профиль 25 июня
- Реальный ЕГЭ 2018 профиль 1 июня основная волна
- ДОСРОЧНЫЙ ЕГЭ 2018
- ДОСРОЧНЫЙ ЕГЭ резервный день 11-04-2018
Пробные ЕГЭ 2018
- Тренировочная работа 18_04_2018 СтатГрад 11 класс
- Пробный ЕГЭ в Санкт-Петербурге 4 апреля 2018
- Тренировочная работа 06_03_2018 СтатГрад 11 класс
- Тренировочная работа 25_01_2018 СтатГрад 11 класс
- Тренировочная работа 21_12_2017 СтатГрад 11 класс
- Демонстрационный вариант КИМ ЕГЭ 2018
30 новых вариантов ЕГЭ 2018 Математика Мирошин В.В. Тренировочные задания
36 вариантов 2018 Ященко Типовые тестовые задания профильный уровень ЕГЭ
50 вариантов 2018 Ященко Типовые тестовые задания профильный уровень ЕГЭ
2018 Математика профильный уровень Ященко 20 вариантов тестов Тематическая рабочая тетрадь
14 вариантов 2018 Ященко Типовые тестовые задания профильный уровень ЕГЭ
ЕГЭ 2017
4 класс
- ВПР по математике 4 класс март 2021
Дополнительные вступительные испытания в ВУЗы
ДВИ в МГУ
ДВИ в МГУ 2022
- ДВИ в МГУ резервный день 25-07-2022
- ДВИ в МГУ 6-й Поток 22-07-2022
- ДВИ в МГУ 5-й Поток 20-07-2022
- ДВИ в МГУ 4-й Поток 19-07-2022
- ДВИ в МГУ 3-й Поток 15-07-2022
- ДВИ в МГУ 2-й Поток 14-07-2022
- ДВИ в МГУ 1-й Поток 11-07-2022
5 класс
- ВПР по математике 5 класс 2021
- ВПР по математике 5 класс сентябрь 2020
6 класс
10 класс
7 — 8 классы
Подготовка к ОГЭ 9 класс ГИА
ОГЭ 2021
- Региональная оценка качества образования математика 9 класс 2021
- Тренировочная работа №4 по математике 9 класс Статград 10-03-2021
- Тренировочная работа №3 по математике 9 класс Статград 21-01-2021
- Мониторинговая работа за 1 полугодие в 9 классе в формате ОГЭ 19-12-2020
- Диагностическая работа по геометрии 9 класс Статград 09-12-2020
- Тренировочная работа №2 по математике 9 класс Статград 25-11-2020
- Тренировочная работа №1 по математике 9 класс Статград 02-10-2020
- Диагностическая работа по математике по разделу теория вероятностей и статистика 9 класс Сентябрь 2020
- Проверочная работа по математике 9 класс (по материалам 8 класса)
- Демонстрационный вариант ОГЭ 2021 ФИПИ по математике
ОГЭ 2020
ОГЭ 2019
- ОГЭ по математике 06-06-2019 основная волна
- Досрочный ОГЭ по математике 22-04-2019
Пробные ОГЭ 2019
ОГЭ 2018
Вступительные контрольные работы в ФМШ
- Контрольная работа на вступительном экзамене в ФМШ для 8 класса
Ларин варианты
ОГЭ(ГИА) 9 класс Ларин
- 399 тренировочный вариант от Ларина
- 398 тренировочный вариант от Ларина
- 397 тренировочный вариант от Ларина
- 368 тренировочный вариант от Ларина
- 367 тренировочный вариант от Ларина
- 366 тренировочный вариант от Ларина
- 365 тренировочный вариант от Ларина
- 364 тренировочный вариант от Ларина
- 363 тренировочный вариант от Ларина
- 362 тренировочный вариант от Ларина
- 361 тренировочный вариант от Ларина
- 360 тренировочный вариант от Ларина
- 359 тренировочный вариант от Ларина
- 358 тренировочный вариант от Ларина
- 332 тренировочный вариант от Ларина
- 331 тренировочный вариант от Ларина
- 330 тренировочный вариант от Ларина
- 329 тренировочный вариант от Ларина
- 328 тренировочный вариант от Ларина
- 327 тренировочный вариант от Ларина
- 326 тренировочный вариант от Ларина
- 325 тренировочный вариант от Ларина
- 324 тренировочный вариант от Ларина
- 323 тренировочный вариант от Ларина
- 322 тренировочный вариант от Ларина
- 321 тренировочный вариант от Ларина
- 320 тренировочный вариант от Ларина
- 319 тренировочный вариант от Ларина
- 318 тренировочный вариант от Ларина
- 317 тренировочный вариант от Ларина
- 316 тренировочный вариант от Ларина
- 315 тренировочный вариант от Ларина
- 314 тренировочный вариант от Ларина
- 313 тренировочный вариант от Ларина
- 312 тренировочный вариант от Ларина
- 311 тренировочный вариант от Ларина
- 310 тренировочный вариант от Ларина
- 309 тренировочный вариант от Ларина
- 308 тренировочный вариант от Ларина
- 307 тренировочный вариант от Ларина
- 306 тренировочный вариант от Ларина
- 305 тренировочный вариант от Ларина
- 304 тренировочный вариант от Ларина
- 303 тренировочный вариант от Ларина
- 302 тренировочный вариант от Ларина
- 301 тренировочный вариант от Ларина
- 300 тренировочный вариант от Ларина
- 297 тренировочный вариант от Ларина
- 296 тренировочный вариант от Ларина
- 295 тренировочный вариант от Ларина
- 293 тренировочный вариант от Ларина
- 292 тренировочный вариант от Ларина
- 291 тренировочный вариант от Ларина
- 290 тренировочный вариант от Ларина
- 286 тренировочный вариант от Ларина
- 285 тренировочный вариант от Ларина
- 284 тренировочный вариант от Ларина
- 283 тренировочный вариант от Ларина
- 282 тренировочный вариант от Ларина
- 281 тренировочный вариант от Ларина
- 280 тренировочный вариант от Ларина
- 279 тренировочный вариант от Ларина
- 278 тренировочный вариант от Ларина
- 277 тренировочный вариант от Ларина
- 276 тренировочный вариант от Ларина
- 275 тренировочный вариант от Ларина
- 274 тренировочный вариант от Ларина
- 273 тренировочный вариант от Ларина
- 271 тренировочный вариант от Ларина
- 270 тренировочный вариант от Ларина
- 269 тренировочный вариант от Ларина
- 268 тренировочный вариант от Ларина
- 267 тренировочный вариант от Ларина
- 266 тренировочный вариант от Ларина
- 265 тренировочный вариант от Ларина
- 264 тренировочный вариант от Ларина
- 263 тренировочный вариант от Ларина
- 262 тренировочный вариант от Ларина
- 261 тренировочный вариант от Ларина
- 260 тренировочный вариант от Ларина
- 259 тренировочный вариант от Ларина
- 258 тренировочный вариант от Ларина
- 257 тренировочный вариант от Ларина
- 256 тренировочный вариант от Ларина
- 255 тренировочный вариант от Ларина
- 254 тренировочный вариант от Ларина
- 253 тренировочный вариант от Ларина
- 252 тренировочный вариант от Ларина
- 251 тренировочный вариант от Ларина
- 250 тренировочный вариант от Ларина
- 249 тренировочный вариант от Ларина
- 248 тренировочный вариант от Ларина
- 247 тренировочный вариант от Ларина
- 246 тренировочный вариант от Ларина
- 150 тренировочный вариант от Ларина
- 149 тренировочный вариант от Ларина
- 130 тренировочный вариант от Ларина
- 93 тренировочный вариант от Ларина
- 92 тренировочный вариант от Ларина
- 91 тренировочный вариант от Ларина
- 90 тренировочный вариант от Ларина
- 89 тренировочный вариант от Ларина
- 88 тренировочный вариант от Ларина
- 87 тренировочный вариант от Ларина
- 86 тренировочный вариант от Ларина
- 85 тренировочный вариант от Ларина
- 84 тренировочный вариант от Ларина
- 82 тренировочный вариант от Ларина
- 72 тренировочный вариант от Ларина
Теория вероятностей в 9-11 классах
- Комбинаторика в школьной программе
Алгебра
- Графический способ
- Функция
Логарифм
- Метод Рационализации
- Метод логарифмирования
- Модуль
- Схема Горнера
- Обобщённый метод интервалов
Числовая последовательность
- Арифметическая прогрессия
- Геометрическая прогрессия
- Параметры
Система
- Теорема Крамера
Уравнение
- Иррациональные уравнения
Неравенство
- Иррациональные неравенства
- Формула сложных радикалов
- Способ неопределённых коэффициентов
Геометрия
Стереометрия
- Пирамида
- Призма
- Куб
Теоремы стереометрии
- теорема О трёх перпендикулярах
- признак Перпендикулярности прямой и плоскости
- признак Параллельности плоскостей
- Скрещивающиеся прямые
- Линейный угол двугранного угла
- Угол между прямой и плоскостью
- Перпендикулярность плоскостей
- признак Параллельности прямых
- Свойство параллельных плоскостей
- Расстояние между скрещивающимися прямыми
- Параллельность прямой и плоскости
- Свойство транзитивности паралельных плоскостей
- Параллелепипед
- Правильный тэтраэдр
- Сфера
- способ Вспогательного объёма
- Цилиндр
- Конус
- Шар
- Расстояние от точки до плоскости
- Угол между плоскостями
- Площадь проекции плоской фигуры
Планиметрия
Теоремы планиметрии
- Свойство высоты гипотенузы
- свойство Вписанных углов
- Подобие треугольников
- свойство Медиан
- свойство Биссектрис
- свойство Касательной и Секущей
- свойство Касательных
- свойство Секущих
- теорема Косинусов
- теорема Синусов
- свойство Пересекающихся хорд
- свойство Вписанного четырёхугольника
- свойство Описанного четырёхугольника
- свойство Диагоналей параллелограмма
- свойство Средней линии треугольника
- свойство Средней линии трапеции
- Теорема Фалеса
- Свойство углов с взаимно перпендикулярными сторонами
- Теорема Менелая
- Свойство медианы гипотенузы
- Свойство Диаметра перпендикулярного к хорде
- Свойства параллельных прямых
- Признаки параллельных прямых
- свойство Вневписанной окружности
- Формула Герона
- Свойство угла между касательной и хордой
- Лемма о трезубце
- Теорема Птолемея
- свойство Диагоналей выпуклого четырёхугольника
- Теорема Чевы
- Круг
- Сектор
- Треугольник
- Окружность
Четырёхугольник
- Дельтоид
- Трапеция
- Параллелограмм
- Ромб
- Прямоугольник
- Координатный метод
Вектор
- Нормальный вектор
Тригонометрия
- Тригонометрическая подстановка
МатАнализ
- Уравнение касательной
- Производная
- Предел
- Свойство монотонности
- Экстремум
- первообразная
Аналитическая Геометрия
- Расстояние от точки до прямой
Задачники Пособия
- Геометрия 10-11 класс Атанасян
- Подсыпанин (2001)
- Зив
- Самара 2011 Учебное пособие Тренировочные материалы для подготовки к ЕГЭ
- Видео решения
- Изюминка
- Ошибки в ответах пособий
- Подготовка к экзамену по математике
Найти
ЧИТАТЬ ВСЕ НОВОСТИ
|
|||
|
|||
|
Решите уравнение 7x / 3×2 — 26 =1
36 вариантов ФИПИ Ященко 2023 Вариант 14 Задание 5 № задачи в базе 3554
Решите уравнение
(7x)/(3x^2-26)=1
. Если уравнение имеет более одного корня, в ответе запишите меньший из корней
Ответ: -2
Ключевые слова:
Задания ЕГЭ части 1 | Задачи 5 уравнения | Алгебра | ЕГЭ по математике 2023 | Математика 36 вариантов ЕГЭ 2023 ФИПИ школе Ященко |
ФИПИ 2023 🔥 …
Примечание: Решите уравнение 7x / 3×2 — 26 =1 ! 36 вариантов ФИПИ Ященко 2023 Вариант 14 Задание 5
10%
Рейтинг сложности задачи:
Графическое решение
X
Найдите значение выражения при
Спрятать решение
Решение.
Выполним преобразования:
При имеем
Тогда
Ответ: 12.
Решите уравнениеЕсли уравнение имеет более одного корня, в ответе запишите меньший из корней.
Источник: Ященко ЕГЭ 2022 (36 вар)
Решение:
Решение уравнения:
3x2 – 26 = 7x
3x2 – 7x – 26 = 0
D = (–7)2 – 4·3·(–26) = 361 = 192
Оба корня уравнения удовлетворяют ОДЗ, в ответ записываем меньший из них х = –2.
Ответ: –2.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 3.6 / 5. Количество оценок: 14
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время
В отзыве оставь контакт для связи, если хочешь, что бы я тебе ответил.
Найдите значение выражения: (7x^3)^2 : (7x^6)
Матемаматика ОГЭ: решения задач | Дата: 29.10.2016 |
Условие задачи:
Найдите значение выражения: (7x3)2 : (7x6)
Ответ: 7
Решение:
- 1
- 2
- 3
- 4
- 5
Оценка: 5.0 из 1
Комментарии
Всего комментариев
: 0
Войдите:
Страница 1 из 1 [ Сообщений: 3 ]
| ÐвÑÐ¾Ñ | СообÑение | ||
|---|---|---|---|
|
LyudmilaSN |
Ðаголовок ÑообÑениÑ: `sqrt(3x^2-7x+3)-sqrt(x^2-2)=sqrt(3x^2-5x-1)-sqrt(x^2-3x+4)` |
||
ÐаÑегиÑÑÑиÑован: 23 дек 2014, 15:07 |
ÐдÑавÑÑвÑйÑе! |
||
  |
|||
|
Ischo_Tatiana |
Ðаголовок ÑообÑениÑ: Re: `sqrt(3x^2-7x+3)-sqrt(x^2-2)=sqrt(3x^2-5x-1)-sqrt(x^2-3x |
||
ÐаÑегиÑÑÑиÑован: 08 май 2013, 17:36 |
`sqrt(3x^2-7x+3)-sqrt(3x^2-5x-1)=sqrt(x^2-2)-sqrt(x^2-3x+4)` |
||
  |
|||
|
LyudmilaSN |
Ðаголовок ÑообÑениÑ: Re: `sqrt(3x^2-7x+3)-sqrt(x^2-2)=sqrt(3x^2-5x-1)-sqrt(x^2-3x |
||
ÐаÑегиÑÑÑиÑован: 23 дек 2014, 15:07 |
CпаÑибо. |
||
  |
|||
| ÐоказаÑÑ ÑообÑÐµÐ½Ð¸Ñ Ð·Ð°: СоÑÑиÑоваÑÑ Ð¿Ð¾: |
СÑÑаниÑа 1 из 1 [ СообÑений: 3 ]
Задание
17
#2830
Уровень задания: Равен ЕГЭ
Решите неравенство
[begin{aligned}
8^x — 3cdot 4^x + dfrac{9cdot 4^x — 288}{2^x — 9}leqslant 32
end{aligned}]
(ЕГЭ 2016, основная волна)
Сделаем замену (2^x = t > 0):
[begin{aligned}
t^3 — 3t^2 + dfrac{9t^2 — 288}{t — 9}leqslant 32
end{aligned}]
ОДЗ:
[begin{aligned}
tneq 9
end{aligned}]
Перенесём всё влево и приведём к общему знаменателю
[begin{aligned}
dfrac{t^4 — 12t^3 + 36t^2 — 32t}{t — 9}leqslant 0qquadLeftrightarrowqquad tcdotdfrac{t^3 — 12t^2 + 36t — 32}{t — 9}leqslant 0
end{aligned}]
Разложим многочлен третьей степени в числителе левой части последнего неравенства на множители. Можно угадать его корень (t = 2). Знание корня многочлена позволяет поделить его столбиком на (t — t_0), где (t_0) – корень, тогда [begin{array}{rr|l}
t^3-12t^2+36t-32&&negthickspaceunderline{qquad t-2 qquad}
underline{t^3- , 2t^2} phantom{0000000000}&&negthickspace t^2 — 10t + 16[-3pt]
-10t^2 + 36t,phantom{0000}&&
underline{-10t^2 + 20t,}phantom{0000}&&[-3pt]
16t — 32! &&
underline{16t — 32! }&&[-3pt]
0&&
end{array}] тогда последнее неравенство равносильно
[begin{aligned}
dfrac{t(t — 2)^2(t — 8)}{t — 9}leqslant 0
end{aligned}]
По методу интервалов
откуда (tin(-infty; 0]cup{2}cup[8; 9))
с учётом ОДЗ и условия (t > 0): (tin{2}cup[8; 9))
в исходных переменных: [xin{1}cup[3; log_2 9)]
Ответ:
({1}cup[3; log_2 9))
Задать свой вопрос
*более 50 000 пользователей получили ответ на «Решим всё»
Условие
Укажите решение неравенства -3-3x > 7x-9
1) (0,6; +бесконечность)
2) (-бесконечность; 1,2)
3) (1,2; +бесконечность)
4) (-бесконечность; 0,6)
математика 8-9 класс
9301
Решение
-3-3x > 7x-9
-3x — 7x > -9 + 3
-10x > -6
x < -6/(-10)
x < 0,6
(-бесконечность; 0,6)
Ответ: 4
Написать комментарий
Меню
- Решим всё
- Найти задачу
- Категории
- Статьи
- Тесты
- Архив задач
Присоединяйся в ВК
ЕГЭ Профиль №10. Парабола
Скачать файл в формате pdf.
ЕГЭ Профиль №10. Парабола
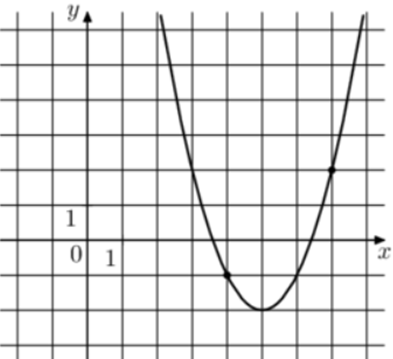
| Задача 1. На рисунке изображён график функции (fleft( x right) = 2{x^2} + b,x + c.) Найдите (fleft( { — 5} right).)
Ответ
ОТВЕТ: 31. |
 |
|
Решение
Парабола проходит через точки (left( {1;1} right)) и (left( { — 2; — 2} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{1 = 2 + b + c,,,,}\{ — 2 = 8 — 2b + c}end{array}} right.) Вычтем из первого уравнения второе: (3 = — 6 + 3b,,,,,,, Leftrightarrow ,,,,,,,b = 3.) Тогда: (1 = 2 + 3 + c,,,,,,,, Leftrightarrow ,,,,,,,,c = — 4.) Следовательно, уравнение параболы имеет вид: (fleft( x right) = 2{x^2} + 3x — 4) и (fleft( { — 5} right) = 2 cdot {left( { — 5} right)^2} + 3 cdot left( { — 5} right) — 4 = 31.) Ответ: 31. |
|
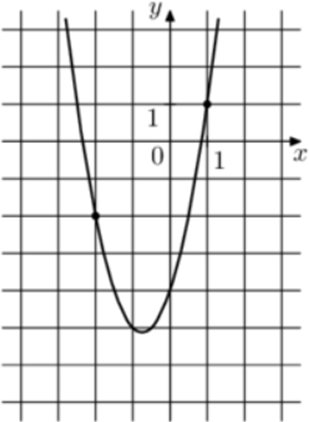
| Задача 2. На рисунке изображён график функции (fleft( x right) = {x^2} + b,x + c.) Найдите (fleft( { — 1} right).)
Ответ
ОТВЕТ: 34. |
 |
|
Решение
1 Способ Парабола проходит через точки (left( {4; — 1} right)) и (left( {6; — 1} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{ — 1 = 16 + 4b + c,,,,}\{ — 1 = 36 + 6b + c,,,}end{array}} right.) Вычтем из первого уравнения второе: (0 = — 20 — 2b,,,,,,, Leftrightarrow ,,,,,,,b = — 10.) Тогда: ( — 1 = 16 — 40 + c,,,,,,,, Leftrightarrow ,,,,,,,,c = 23.) Следовательно, уравнение параболы имеет вид: (fleft( x right) = {x^2} — 10x + 23) и (fleft( { — 1} right) = {left( { — 1} right)^2} — 10 cdot left( { — 1} right) + 23 = 34.) Ответ: 34. 2 Способ Заметим, что графиком является парабола (fleft( x right) = {x^2}), вершина которой находится в точке (left( {5; — 2} right)). Следовательно, ее уравнение будет иметь вид: (fleft( x right) = {left( {x — 5} right)^2} — 2) и (fleft( { — 1} right) = {left( { — 1 — 5} right)^2} — 2 = 34.) Ответ: 34. |
|
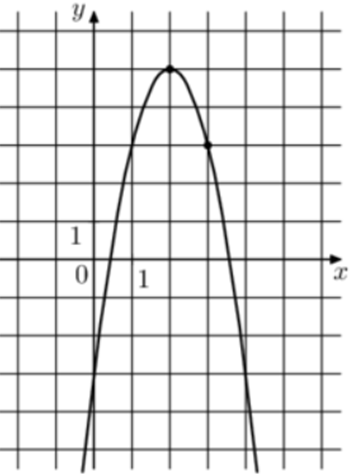
| Задача 3. На рисунке изображён график функции (fleft( x right) = — 2{x^2} + b,x + c.) Найдите (fleft( 6 right).)
Ответ
ОТВЕТ: — 27. |
 |
|
Решение
1 Способ Парабола проходит через точки (left( {1;3} right)) и (left( {3;3} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{3 = — 2 + b + c,,,,,,,,}\{3 = — 18 + 3b + c,,,}end{array}} right.)Вычтем из первого уравнения второе: (0 = 16 — 2b,,,,,,, Leftrightarrow ,,,,,,,b = 8.)Тогда: (3 = — 2 + 8 + c,,,,,,,, Leftrightarrow ,,,,,,,,c = — 3.) Следовательно, уравнение параболы имеет вид: (fleft( x right) = — 2{x^2} + 8x — 3) и (fleft( 6 right) = — 2 cdot {6^2} + 8 cdot 6 — 3 = — 27.) Ответ: – 27. 2 Способ Заметим, что графиком является парабола (fleft( x right) = — 2{x^2}), вершина которой находится в точке (left( {2;5} right)). Следовательно, ее уравнение будет иметь вид: (fleft( x right) = — 2{left( {x — 2} right)^2} + 5) и (fleft( 6 right) = — 2 cdot {left( {6 — 2} right)^2} + 5 = — 27.) Ответ: – 27. |
|
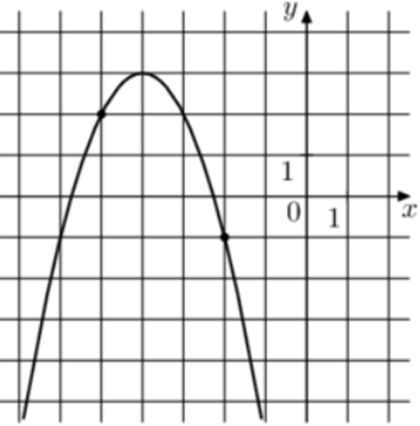
| Задача 4. На рисунке изображён график функции (fleft( x right) = — {x^2} + b,x + c.) Найдите (fleft( { — 8} right).)
Ответ
ОТВЕТ: — 13. |
 |
|
Решение
1 Способ Парабола проходит через точки (left( { — 3;2} right)) и (left( { — 5;2} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{2 = — 9 — 3b + c,,,,,,,,}\{2 = — 25 — 5b + c,,,}end{array}} right.) Вычтем из первого уравнения второе: (0 = 16 + 2b,,,,,,, Leftrightarrow ,,,,,,,b = — 8.) Тогда: (2 = — 9 + 24 + c,,,,,,,, Leftrightarrow ,,,,,,,,c = — 13.) Следовательно, уравнение параболы имеет вид: (fleft( x right) = — {x^2} — 8x — 13) и (fleft( { — 8} right) = — {left( { — 8} right)^2} + 8 cdot left( { — 8} right) — 13 = — 13.) Ответ: – 13. 2 Способ Заметим, что графиком является парабола (fleft( x right) = — {x^2}), вершина которой находится в точке (left( { — 4;3} right)). Следовательно, ее уравнение будет иметь вид: (fleft( x right) = — {left( {x + 4} right)^2} + 3) и (fleft( { — 8} right) = — {left( { — 8 + 4} right)^2} + 3 = — 13.) Ответ: – 13. |
|
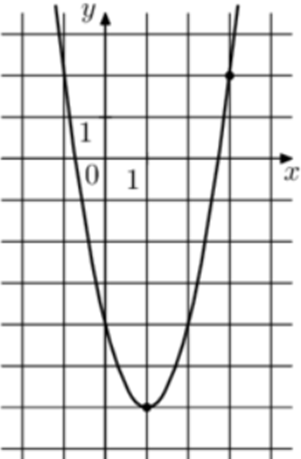
| Задача 5. На рисунке изображён график функции (fleft( x right) = a,{x^2} — 4,x + c.) Найдите (fleft( { — 3} right).)
Ответ
ОТВЕТ: 26. |
 |
|
Решение
1 Способ Парабола проходит через точки (left( {1; — 6} right)) и (left( {3;2} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{ — 6 = a — 4 + c,,,,,,,,}\{2 = 9a — 12 + c,,,}end{array}} right.) Вычтем из первого уравнения второе: ( — 8 = — 8a + 8,,,,,,, Leftrightarrow ,,,,,,,a = 2.) Тогда: ( — 6 = 2 — 4 + c,,,,,,,, Leftrightarrow ,,,,,,,,c = — 4.) Следовательно, уравнение параболы имеет вид: (fleft( x right) = 2{x^2} — 4x — 4) и (fleft( { — 3} right) = 2 cdot {left( { — 3} right)^2} — 4 cdot left( { — 3} right) — 4 = 26.) Ответ: 26. 2 Способ Заметим, что графиком является парабола (fleft( x right) = 2{x^2}), вершина которой находится в точке (left( {1; — 6} right)). Следовательно, ее уравнение будет иметь вид: (fleft( x right) = 2{left( {x — 1} right)^2} — 6) и (fleft( { — 3} right) = 2 cdot {left( { — 3 — 1} right)^2} — 6 = 26.) Ответ: 26. |
|
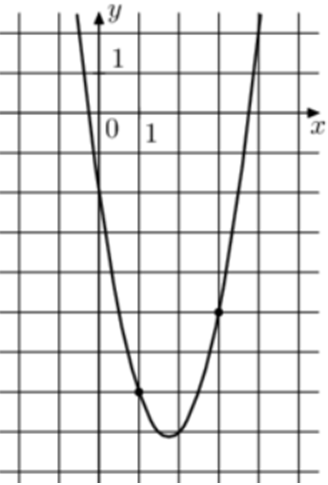
| Задача 6. На рисунке изображён график функции (fleft( x right) = a,{x^2} — 7,x + c.) Найдите (fleft( 7 right).)
Ответ
ОТВЕТ: 47. |
 |
|
Решение
Парабола проходит через точки (left( {1; — 7} right)) и (left( {3; — 5} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{ — 7 = a — 7 + c,,,,,,,,}\{ — 5 = 9a — 21 + c,,,}end{array}} right.) Вычтем из первого уравнения второе: ( — 2 = — 8a + 14,,,,,,, Leftrightarrow ,,,,,,,a = 2.) Тогда: ( — 7 = 2 — 7 + c,,,,,,,, Leftrightarrow ,,,,,,,,c = — 2.) Следовательно, уравнение параболы имеет вид: (fleft( x right) = 2{x^2} — 7x — 2) и (fleft( 7 right) = 2 cdot {7^2} — 7 cdot 7 — 2 = 47.) Ответ: 47. |
|
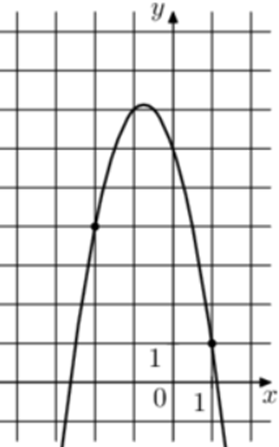
| Задача 7. На рисунке изображён график функции (fleft( x right) = a,{x^2} — 3,x + c.) Найдите (fleft( { — 4} right).)
Ответ
ОТВЕТ: — 14. |
 |
|
Решение
Парабола проходит через точки (left( {1;1} right)) и (left( { — 2;4} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{1 = a — 3 + c,,,,,,,,}\{4 = 4a + 6 + c,,,}end{array}} right.) Вычтем из первого уравнения второе: ( — 3 = — 3a — 9,,,,,,, Leftrightarrow ,,,,,,,a = — 2.) Тогда: (1 = — 2 — 3 + c,,,,,,,, Leftrightarrow ,,,,,,,,c = 6.) Следовательно, уравнение параболы имеет вид: (fleft( x right) = — 2{x^2} — 3x + 6) и (fleft( { — 4} right) = — 2 cdot {left( { — 4} right)^2} — 3 cdot left( { — 4} right) + 6 = — 14.) Ответ: – 14. |
|
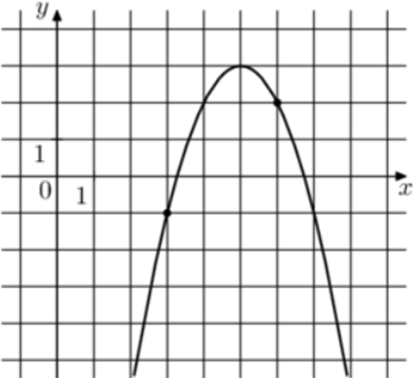
| Задача 8. На рисунке изображён график функции (fleft( x right) = a,{x^2} + 10,x + c.) Найдите (fleft( { — 1} right).)
Ответ
ОТВЕТ: — 33. |
 |
|
Решение
1 Способ Парабола проходит через точки (left( {3; — 1} right)) и (left( {4;2} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{ — 1 = 9a + 30 + c}\{2 = 16a + 40 + c}end{array}} right.) Вычтем из первого уравнения второе: ( — 3 = — 7a — 10,,,,,,, Leftrightarrow ,,,,,,,a = — 1.) Тогда: ( — 1 = — 9 + 30 + c,,,,,,,, Leftrightarrow ,,,,,,,,c = — 22.) Следовательно, уравнение параболы имеет вид: (fleft( x right) = — {x^2} + 10x — 22) и (fleft( { — 1} right) = — {left( { — 1} right)^2} + 10 cdot left( { — 1} right) — 22 = — 33.) Ответ: – 33. 2 способ Заметим, что графиком является парабола (fleft( x right) = — {x^2}), вершина которой находится в точке (left( {5;3} right)). Следовательно, ее уравнение будет иметь вид: (fleft( x right) = — {left( {x — 5} right)^2} + 3) и (fleft( { — 1} right) = — {left( { — 1 — 5} right)^2} + 3 = — 33.) Ответ: – 33. |
|
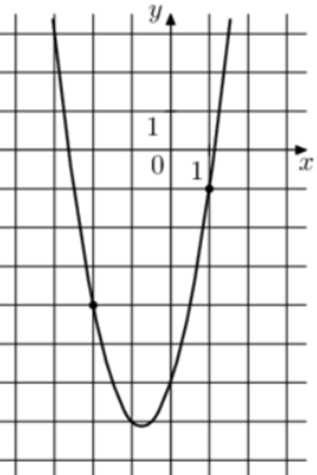
| Задача 9. На рисунке изображён график функции (fleft( x right) = a,{x^2} + b,x — 6.) Найдите (fleft( { — 6} right).)
Ответ
ОТВЕТ: 48. |
 |
|
Решение
Парабола проходит через точки (left( {1; — 1} right)) и (left( { — 2; — 4} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{ — 1 = a + b — 6,,,,,,,,,,,,,,,,,,,,,}\{ — 4 = 4a — 2b — 6left| {:left( { — 2} right)} right.,,,}end{array}} right.,,,,,,, Leftrightarrow ,,,,,,,,,left{ {begin{array}{*{20}{c}}{ — 1 = a + b — 6}\{2 = — 2a + b + 3}end{array}} right.) Вычтем из первого уравнения второе: ( — 3 = 3a — 9,,,,,,, Leftrightarrow ,,,,,,,a = 2.) Тогда: ( — 1 = 2 + b — 6,,,,,,,, Leftrightarrow ,,,,,,,,b = 3.) Следовательно, уравнение параболы имеет вид: (fleft( x right) = 2{x^2} + 3x — 6) и (fleft( { — 6} right) = 2 cdot {left( { — 6} right)^2} + 3 cdot left( { — 6} right) — 6 = 48.) Ответ: 48. |
|
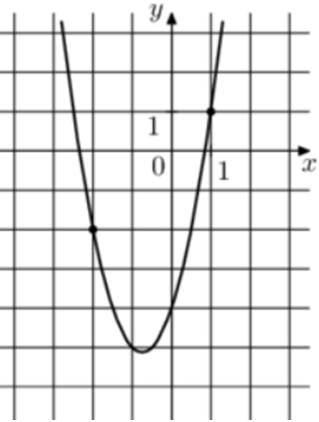
| Задача 10. На рисунке изображён график функции (fleft( x right) = a,{x^2} + b,x — 4.) Найдите (fleft( { — 4} right).)
Ответ
ОТВЕТ: 16. |
 |
|
Решение
Парабола проходит через точки (left( {1;1} right)) и (left( { — 2; — 2} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{1 = a + b — 4,,,,,,,,,,,,,,,,,,,,,,,,,}\{-2 = 4a — 2b — 4left| {:left( { — 2} right)} right.,,,}end{array},,,,, Leftrightarrow ,,,,,,,,,left{ {begin{array}{*{20}{c}}{1 = a + b — 4,,,,,,,}\{1 = — 2a + b + 2}end{array}} right.} right.) Вычтем из первого уравнения второе: (0 = 3a — 6,,,,,,, Leftrightarrow ,,,,,,,a = 2.) Тогда: (1 = 2 + b — 4,,,,,,,, Leftrightarrow ,,,,,,,,b = 3.) Следовательно, уравнение параболы имеет вид: (fleft( x right) = 2{x^2} + 3x — 4) и (fleft( { — 4} right) = 2 cdot {left( { — 4} right)^2} + 3 cdot left( { — 4} right) — 4 = 16.) Ответ: 16. |
|
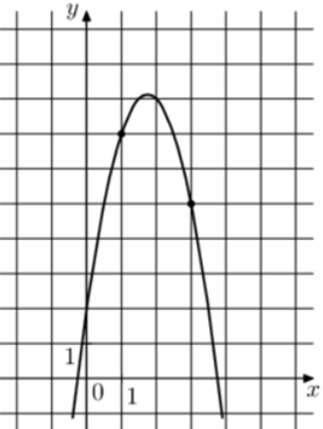
| Задача 11. На рисунке изображён график функции (fleft( x right) = a,{x^2} + b,x + 2.) Найдите (fleft( { — 3} right).)
Ответ
ОТВЕТ: — 37. |
 |
|
Решение
Парабола проходит через точки (left( {1;7} right)) и (left( {3;5} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{7 = a + b + 2,,,,,,,,}\{5 = 9a + 3b + 2,,,,}end{array},,,,, Leftrightarrow ,,,,,,,,left{ {begin{array}{*{20}{c}}{5 = a + b,,,,,,,,,,,,}\{3 = 9a + 3bleft| {:3} right.}end{array}} right.} right.,,,,,,,,, Leftrightarrow ,,,,,,,,left{ {begin{array}{*{20}{c}}{5 = a + b}\{1 = 3a + b}end{array}} right.,,,,,,,,,) Вычтем из первого уравнения второе: (4 = — 2a,,,,,,, Leftrightarrow ,,,,,,,a = — 2.) Тогда: (5 = — 2 + b,,,,,,,, Leftrightarrow ,,,,,,,,b = 7.) Следовательно, уравнение параболы имеет вид: (fleft( x right) = — 2{x^2} + 7x + 2) и (fleft( { — 3} right) = — 2 cdot {left( { — 3} right)^2} + 7 cdot left( { — 3} right) + 2 = — 37.) Ответ: – 37. |
|
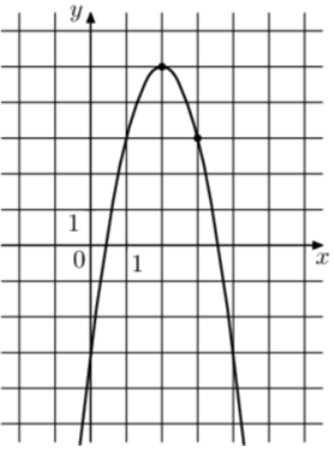
| Задача 12. На рисунке изображён график функции (fleft( x right) = a,{x^2} + b,x — 3.) Найдите (fleft( 8 right).)
Ответ
ОТВЕТ: — 67. |
 |
|
Решение
1 Способ Парабола проходит через точки (left( {1;3} right)) и (left( {3;3} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{3 = a + b — 3,,,,,,,,,,,,,,,,,,}\{3 = 9a + 3b — 3left| {:3} right.,,,,,}end{array},,,, Leftrightarrow ,,,,,,,,left{ {begin{array}{*{20}{c}}{3 = a + b — 3}\{1 = 3a + b — 1}end{array}} right.} right.) Вычтем из первого уравнения второе: (2 = — 2a — 2,,,,,,, Leftrightarrow ,,,,,,,a = — 2.) Тогда: (3 = — 2 + b — 3,,,,,,,, Leftrightarrow ,,,,,,,,b = 8.) Следовательно, уравнение параболы имеет вид: (fleft( x right) = — 2{x^2} + 8x — 3) и (fleft( 8 right) = — 2 cdot {8^2} + 8 cdot 8 — 3 = — 67.) Ответ: – 67. 2 Способ Заметим, что графиком является парабола (fleft( x right) = — 2{x^2}), вершина которой находится в точке (left( {2;5} right)). Следовательно, ее уравнение будет иметь вид: (fleft( x right) = — 2{left( {x — 2} right)^2} + 5) и (fleft( 8 right) = — 2 cdot {left( {8 — 2} right)^2} + 5 = — 67.) Ответ: – 67. |
|
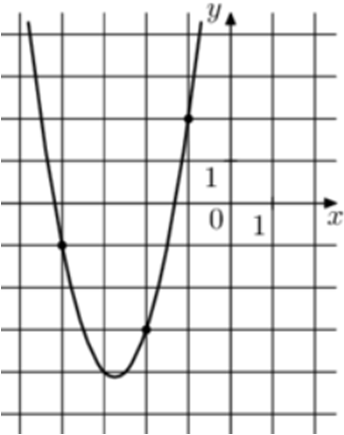
| Задача 13. На рисунке изображён график функции (fleft( x right) = a,{x^2} + b,x + c.) Найдите (fleft( { — 7} right).)
Ответ
ОТВЕТ: 32. |
 |
|
Решение
Парабола проходит через точки (left( { — 1;2} right)), (left( { — 2; — 3} right)) и (left( { — 4; — 1} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{2 = a — b + c,,,,,,,,,}\{ — 3 = 4a — 2b + c}\{ — 1 = 16a — 4b + c}end{array}} right.) Вычтем из первого уравнения второе: (5 = — 3a + b.) Вычтем из первого уравнения третье: (3 = — 15a + 3bleft| {:3,,,,,,,,,, Leftrightarrow ,,,,,,,,,,1 = — 5a + b} right..) Таким образом, получим систему уравнений: (left{ {begin{array}{*{20}{c}}{5 = — 3a + b}\{1 = — 5a + b}end{array}} right.) Вычтем из первого уравнения второе: (4 = 2a,,,,,,, Leftrightarrow ,,,,,,,,a = 2.) Тогда: (5 = — 3 cdot 2 + b,,,,,, Leftrightarrow ,,,,,,b = 11) и (2 = 2 — 11 + c,,,,, Leftrightarrow ,,,,,c = 11.) Следовательно, уравнение параболы имеет вид: (fleft( x right) = 2{x^2} + 11x + 11) и (fleft( { — 7} right) = 2 cdot {left( { — 7} right)^2} + 11 cdot left( { — 7} right) + 11 = 32.) Ответ: 32. |
|
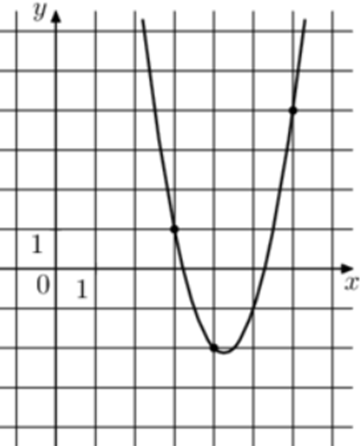
| Задача 14. На рисунке изображён график функции (fleft( x right) = a,{x^2} + b,x + c.) Найдите (fleft( {10} right).)
Ответ
ОТВЕТ: 64. |
 |
|
Решение
Парабола проходит через точки (left( {3;1} right)), (left( {4; — 2} right)) и (left( {6;4} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{1 = 9a + 3b + c,,,,,,,,,}\{ — 2 = 16a + 4b + c}\{4 = 36a + 6b + c}end{array}} right.) Вычтем из первого уравнения второе: (3 = — 7a — b) Вычтем из первого уравнения третье: ( — 3 = — 27a — 3bleft| {:left( { — 3} right),,,,,,,,, Leftrightarrow ,,,,,,,,,1 = 9a + b} right..) Таким образом, получим систему уравнений: (left{ {begin{array}{*{20}{c}}{3 = — 7a — b}\{1 = 9a + b}end{array}} right.) Прибавим к первому уравнению второе: (4 = 2a,,,,,,, Leftrightarrow ,,,,,,,,a = 2.) Тогда: (3 = — 7 cdot 2 — b,,,,,,, Leftrightarrow ,,,,,,,b = — 17) и (1 = 9 cdot 2 + 3 cdot left( { — 17} right) + c,,,,,,, Leftrightarrow ,,,,,,,c = 34.) Следовательно, уравнение параболы имеет вид: (fleft( x right) = 2{x^2} — 17x + 34) и (fleft( {10} right) = 2 cdot {10^2} — 17 cdot 10 + 34 = 64.) Ответ: 64. |
|
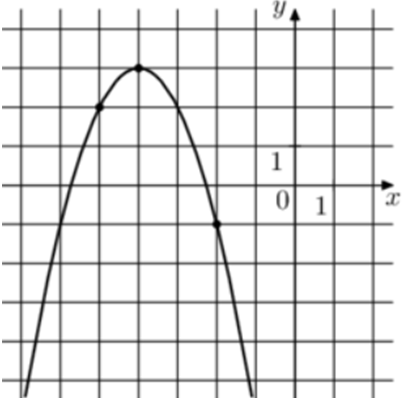
| Задача 15. На рисунке изображён график функции (fleft( x right) = a,{x^2} + b,x + c.) Найдите (fleft( 2 right).)
Ответ
ОТВЕТ: — 33. |
 |
|
Решение
1 Способ Парабола проходит через точки (left( { — 2; — 1} right)), (left( { — 5;2} right)) и (left( { — 6; — 1} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{ — 1 = 4a — 2b + c,,,,,,,,,}\{2 = 25a — 5b + c,,,,,,,}\{ — 1 = 36a — 6b + c,,,}end{array}} right.) Вычтем из первого уравнения второе: ( — 3 = — 21a + 3bleft| {:3,,,,,,,,, Leftrightarrow ,,,,,,,, — 1 = — 7a + b} right..) Вычтем из первого уравнения третье: (0 = — 32a + 4bleft| {:4,,,,,,,,,, Leftrightarrow ,,,,,,,,,,0 = — 8a + b} right..) Таким образом, получим систему уравнений: (left{ {begin{array}{*{20}{c}}{ — 1 = — 7a + b}\{0 = — 8a + b}end{array}} right.) Вычтем из первого уравнения второе: ( — 1 = a,,,,,,, Leftrightarrow ,,,,,,,,a = — 1.) Тогда: ( — 1 = — 7 cdot left( { — 1} right) + b,,,,,, Leftrightarrow ,,,,,,b = — Следовательно, уравнение параболы имеет вид: (fleft( x right) = — {x^2} — 8x — 13) и (fleft( 2 right) = -{2^2} — 8 cdot 2 — 13 = — 33.) Ответ: – 33. 2 Способ Заметим, что графиком является парабола (fleft( x right) = — {x^2}) вершина которой находится в точке (left( { — 4;3} right)). Следовательно, ее уравнение будет иметь вид: (fleft( x right) = — {left( {x + 4} right)^2} + 3) и (fleft( 2 right) = — {left( {2 + 4} right)^2} + 3 = — 33.) Ответ: – 33. |
|
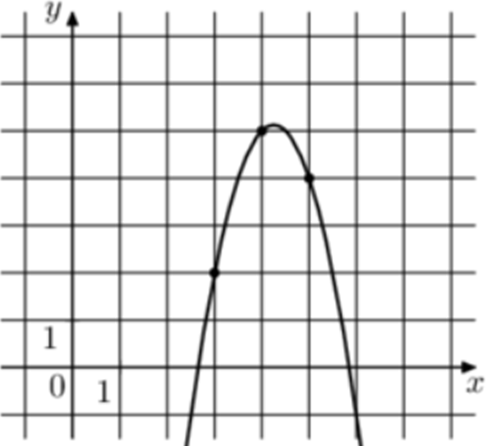
| Задача 16. На рисунке изображён график функции (fleft( x right) = a,{x^2} + b,x + c.) Найдите (fleft( { — 1} right).)
Ответ
ОТВЕТ: — 50. |
 |
|
Решение
Парабола проходит через точки (left( {3;2} right)), (left( {4;5} right)) и (left( {5;4} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{2 = 9a + 3b + c,,,,,,,,,}\{5 = 16a + 4b + c,,,,,,}\{4 = 25a + 5b + c,,,,,}end{array}} right.) Вычтем из первого уравнения второе: ( — 3 = — 7a — b.) Вычтем из первого уравнения третье: ( — 2 = — 16a — 2bleft| {:2,,,,,,,,, Leftrightarrow ,,,,,,,, — ,1 = — 8a — b} right..) Таким образом, получим систему уравнений: (left{ {begin{array}{*{20}{c}}{ — 3 = — 7a — b}\{ — 1 = — 8a — b}end{array}} right.) Прибавим к первому уравнению второе: ( — 2 = a,,,,,,, Leftrightarrow ,,,,,,,,a = — 2.) Тогда: ( — 3 = — 7 cdot left( { — 2} right) — b,,,,,,, Leftrightarrow ,,,,,,,b = 17) и (2 = 9 cdot left( { — 2} right) + 3 cdot 17 + c,,,,,, Leftrightarrow ,,,,,,c = — 31.) Следовательно, уравнение параболы имеет вид: (fleft( x right) = — 2{x^2} + 17x — 31) и (fleft( { — 1} right) = — 2 cdot {left( { — 1} right)^2} + 17 cdot left( { — 1} right) — 31 = — 50.) Ответ: – 50. |
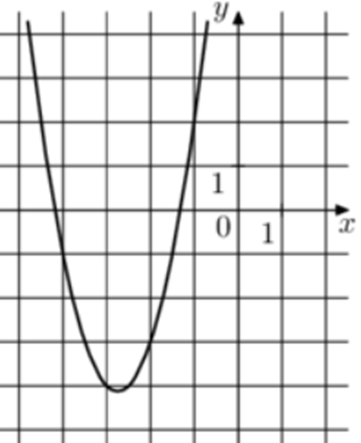
| Задача 17. На рисунке изображены графики функций (fleft( x right) = a,{x^2} + b,x + c,) где a, b и c – целые. Найдите (fleft( 2 right).)
Ответ
ОТВЕТ: 41. |
 |
|
Решение
Парабола проходит через точки (left( { — 2; — 3} right)), (left( { — 3; — 4} right)) и (left( { — 4; — 1} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{ — 3 = 4a — 2b + c,,,,,,,,,}\{ — 4 = 9a — 3b + c,,,,,,,,}\{ — 1 = 16a — 4b + c,,,,,,,}end{array}} right.) Вычтем из первого уравнения второе: (1 = — 5a + b.) Вычтем из первого уравнения третье: ( — 2 = — 12a + 2bleft| {:2,,,,,,,,, Leftrightarrow ,,,,,,,, — ,1 = — 6a + b} right..) Таким образом, получим систему уравнений: (left{ {begin{array}{*{20}{c}}{1 = — 5a + b}\{ — 1 = — 6a + b}end{array}} right.) Прибавим к первому уравнению второе: (2 = a,,,,,,, Leftrightarrow ,,,,,,,,a = 2.) Тогда: (1 = — 5 cdot 2 + b,,,,,,,, Leftrightarrow ,,,,,,,,b = 11) и ( — 3 = 4 cdot 2 — 2 cdot 11 + c,,,,,,, Leftrightarrow ,,,,,,,c = 11.) Следовательно, уравнение параболы имеет вид: (fleft( x right) = 2{x^2} + 11x + 11) и (fleft( 2 right) = 2 cdot {2^2} + 11 cdot 2 + 11 = 41.) Ответ: 41. |
|
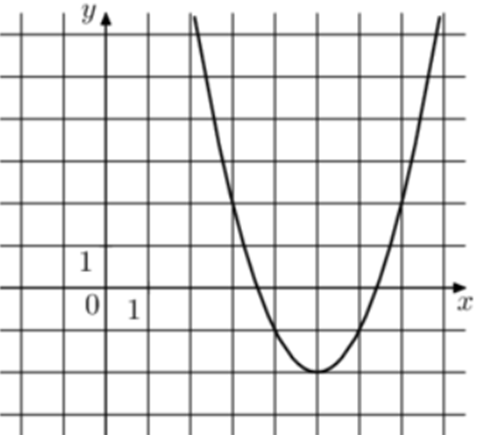
| Задача 18. На рисунке изображены графики функций (fleft( x right) = a,{x^2} + b,x + c,) где a, b и c – целые. Найдите (fleft( { — 1} right).)
Ответ
ОТВЕТ: 34. |
 |
|
Решение
1 Способ Парабола проходит через точки (left( {3;2} right)), (left( {4; — 1} right)) и (left( {5; — 2} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{2 = 9a + 3b + c,,,,,,,,,}\{ — 1 = 16a + 4b + c,,,,,,,}\{ — 2 = 25a + 5b + c,,,}end{array}} right.) Вычтем из первого уравнения второе: (3 = -7a — b.) Вычтем из первого уравнения третье: (4 = — 16a — 2bleft| {:2,,,,,,,,, Leftrightarrow ,,,,,,,,,2 = — 8a — b} right..) Таким образом, получим систему уравнений: (left{ {begin{array}{*{20}{c}}{3 = — 7a — b}\{2 = — 8a — b}end{array}} right.) Вычтем из первого уравнения второе: (1 = a,,,,,,, Leftrightarrow ,,,,,,,,a = 1.) Тогда: (3 = — 7 — b,,,,,,, Leftrightarrow ,,,,,,,b = — 10) и (2 = 9 cdot 1 + 3 cdot left( { — 10} right) + c,,,,,, Leftrightarrow ,,,,,,c = 23.) Следовательно, уравнение параболы имеет вид: (fleft( x right) = {x^2} — 10x + 23) и (fleft( { — 1} right) = {left( { — 1} right)^2} — 10 cdot left( { — 1} right) + 23 = 34.) Ответ: 34. 2 Способ Заметим, что графиком является парабола (fleft( x right) = {x^2}), вершина которой находится в точке (left( {5; — 2} right)). Следовательно, ее уравнение будет иметь вид: (fleft( x right) = {left( {x — 5} right)^2} — 2) и (fleft( { — 1} right) = {left( { — 1 — 5} right)^2} — 2 = 34.) Ответ: 34. |
|
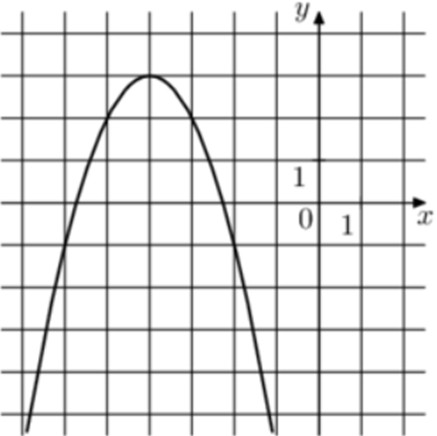
| Задача 19. На рисунке изображены графики функций (fleft( x right) = a,{x^2} + b,x + c,) где a, b и c – целые. Найдите (fleft( { — 8} right).)
Ответ
ОТВЕТ: — 13. |
 |
|
Решение
1 Способ Парабола проходит через точки (left( { — 2; — 1} right)), (left( { — 3;2} right)) и (left( { — 4;3} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{ — 1 = 4a — 2b + c,,,,,,,,,}\{2 = 9a — 3b + c,,,,,,,}\{3 = 16a — 4b + c,,,}end{array}} right.) Вычтем из первого уравнения второе: ( — 3 = — 5a + b.) Вычтем из первого уравнения третье: ( — 4 = — 12a + 2bleft| {:2,,,,,,,, Leftrightarrow ,,,,,,,, — 2 = — 6a + b} right..) Таким образом, получим систему уравнений: (left{ {begin{array}{*{20}{c}}{ — 3 = — 5a + b}\{ — 2 = — 6a + b}end{array}} right.) Вычтем из первого уравнения второе: ( — 1 = a,,,,,,, Leftrightarrow ,,,,,,,,a = — 1.) Тогда: ( — 3 = — 5 cdot left( { — 1} right) + b,,,,,,, Leftrightarrow ,,,,,,,b = — Следовательно, уравнение параболы имеет вид: (fleft( x right) = — {x^2} — 8x — 13) и (fleft( { — 8} right) = — {left( { — 8} right)^2} — 8 cdot left( { — 8} right) — 13 = — 13.) Ответ: – 13. 2 Способ Заметим, что графиком является парабола (fleft( x right) = — {x^2}), вершина которой находится в точке (left( { — 4;3} right)). Следовательно, ее уравнение будет иметь вид: (fleft( x right) = — {left( {x + 4} right)^2} + 3) и (fleft( { — 8} right) = — {left( { — 8 + 4} right)^2} + 3 = — 13.) Ответ: – 13. |
|
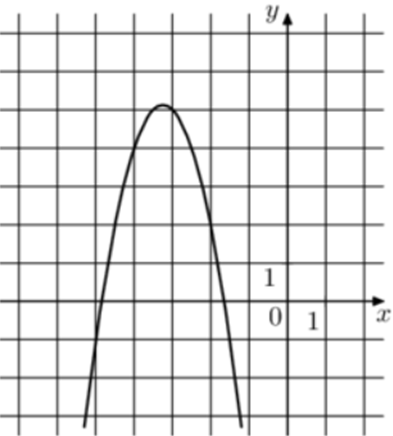
| Задача 20. На рисунке изображены графики функций (fleft( x right) = a,{x^2} + b,x + c,) где a, b и c – целые. Найдите (fleft( { — 6} right).)
Ответ
ОТВЕТ: — 10. |
 |
|
Решение
Парабола проходит через точки (left( { — 2;2} right)), (left( { — 3;5} right)) и (left( { — 4;4} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{2 = 4a — 2b + c,,,,,,,,,}\{5 = 9a — 3b + c,,,,,,,,}\{4 = 16a — 4b + c,,,,,,}end{array}} right.) Вычтем из первого уравнения второе: ( — 3 = — 5a + b.) Вычтем из первого уравнения третье: ( — 2 = — 12a + 2bleft| {:2,,,,,,,,, Leftrightarrow ,,,,,,,, — 1 = — 6a + b} right..) Таким образом, получим систему уравнений: (left{ {begin{array}{*{20}{c}}{ — 3 = — 5a + b}\{ — 1 = — 6a + b}end{array}} right.) Вычтем из первого уравнения второе: ( — 2 = a,,,,,,, Leftrightarrow ,,,,,,,,a = — 2.) Тогда: ( — 3 = — 5 cdot left( { — 2} right) + b,,,,,,, Leftrightarrow ,,,,,,b = — 13) и (2 = 4 cdot left( { — 2} right) — 2 cdot left( { — 13} right) + c,,,,,,, Leftrightarrow ,,,,,,,c = — 16.) Следовательно, уравнение параболы имеет вид: (fleft( x right) = — 2{x^2} — 13x — 16) и (fleft( { — 6} right) = — 2 cdot {left( { — 6} right)^2} — 13 cdot left( { — 6} right) — 16 = — 10.) Ответ: – 10. |
|
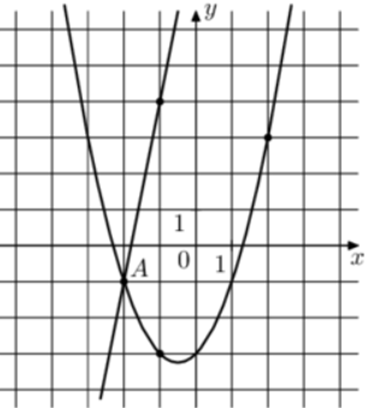
| Задача 21. На рисунке изображены графики функций (fleft( x right) = 5x + 9) и (gleft( x right) = a,{x^2} + b,x + c,) которые пересекаются в точках A и B. Найдите абсциссу точки B.
Ответ
ОТВЕТ: 6. |
 |
|
Решение
Парабола проходит через точки (left( { — 2; — 1} right)), (left( { — 1; — 3} right)) и (left( {1; — 1} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{ — 1 = 4a — 2b + c,,,,,,,,,}\{ — 3 = a — b + c,,,,,,,,,,,,,,,}\{ — 1 = a + b + c,,,,,,,,,,,,,,,}end{array}} right.) Вычтем из первого уравнения второе: (2 = 3a — b.) Вычтем из первого уравнения третье: (0 = 3a — 3bleft| {:3,,,,,,,,,, Leftrightarrow ,,,,,,,,,,0 = a — b} right..) Таким образом, получим систему уравнений: (left{ {begin{array}{*{20}{c}}{2 = 3a — b}\{0 = a — b,,,}end{array}} right.) Вычтем из первого уравнения второе: (2 = 2a,,,,, Leftrightarrow ,,,,a = 1.) Тогда: (0 = 1 — b,,,,,,,, Leftrightarrow ,,,,,,,,b = 1) и ( — 1 = 4 cdot 1 — 2 cdot 1 + c,,,,,,, Leftrightarrow ,,,,,,,c = — 3.) Следовательно, уравнение параболы имеет вид: (gleft( x right) = {x^2} + x — 3.) Чтобы найти координаты точек пересечения прямой (fleft( x right) = 5x + 9) и параболы (gleft( x right) = {x^2} + x — 3) необходимо решить систему уравнений: (left{ {begin{array}{*{20}{c}}{y = {x^2} + x — 3}\{y = 5x + 9,,,,,,,}end{array}} right.,,,,,, Leftrightarrow ,,,,,{x^2} + x — 3 = 5x + 9,,,,,, Leftrightarrow ,,,,,,{x^2} — 4x — 12 = 0,,,,, Leftrightarrow ,,,,,{x_1} = — 2,,,,{x_2} = 4.) Значение (x = — 2) является абсциссой точки А. Следовательно, абсцисса точки В равна 4. Ответ: 4. |
|
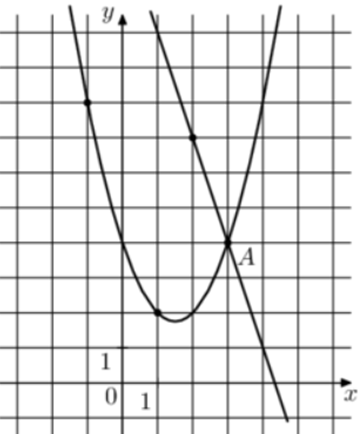
| Задача 22. На рисунке изображены графики функций (fleft( x right) = — 3x + 13) и (gleft( x right) = a,{x^2} + b,x + c,) которые пересекаются в точках A и B. Найдите абсциссу точки B.
Ответ
ОТВЕТ: — 3. |
 |
|
Решение
Парабола проходит через точки (left( {1;2} right)), (left( {2;2} right)) и (left( {3;4} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{2 = a + b + c,,,,,,,,,,,,,,,,,,,,,}\{2 = 4a + 2b + c,,,,,,,,,,,,,,,}\{4 = 9a + 3b + c,,,,,,,,,,,,,,,}end{array}} right.) Вычтем из первого уравнения второе: (0 = — 3a — b.) Вычтем из первого уравнения третье: ( — 2 = — 8a — 2bleft| {:2,,,,,,,, Leftrightarrow ,,,,,,,, — 1 = — 4a — b} right..) Таким образом, получим систему уравнений: (left{ {begin{array}{*{20}{c}}{0 = — 3a — b}\{ — 1 = — 4a — b,,,}end{array}} right.) Вычтем из первого уравнения второе: (1 = a,,,,,,,,, Leftrightarrow ,,,,,,,,a = 1.) Тогда: (0 = — 3 cdot 1 — b,,,,,,,, Leftrightarrow ,,,,,,,,b = — 3) и (2 = 1 — 3 + c,,,,,,, Leftrightarrow ,,,,,,,c = 4.) Следовательно, уравнение параболы имеет вид: (gleft( x right) = {x^2} — 3x + 4.) Чтобы найти координаты точек пересечения прямой (fleft( x right) = — 3x + 13) и параболы (gleft( x right) = {x^2} — 3x + 4) необходимо решить систему уравнений: (left{ {begin{array}{*{20}{c}}{y = {x^2} — 3x + 4}\{y = — 3x + 13,,,,,,,}end{array}} right.,,,,,,, Leftrightarrow ,,,,,{x^2} — 3x + 4 = — 3x + 13,,,,,,, Leftrightarrow ,,,,,,,{x^2} = 9,,,,,,, Leftrightarrow ,,,,,{x_1} = 3,,,,{x_2} = — 3.) Значение (x = 3) является абсциссой точки А. Следовательно, абсцисса точки В равна – 3. Ответ: – 3. |
|
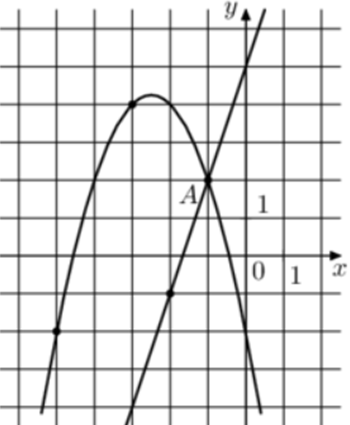
| Задача 23. На рисунке изображены графики функций (fleft( x right) = 3x + 5) и (gleft( x right) = a,{x^2} + b,x + c,) которые пересекаются в точках A и B. Найдите абсциссу точки B.
Ответ
ОТВЕТ: — 7. |
 |
|
Решение
Парабола проходит через точки (left( { — 1;2} right)), (left( { — 2;4} right)) и (left( { — 4;2} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{2 = a — b + c,,,,,,,,,,,,,,,,,,,,,}\{4 = 4a — 2b + c,,,,,,,,,,,,,,,}\{2 = 16a — 4b + c,,,,,,,,,,,,,,,}end{array}} right.) Вычтем из первого уравнения второе: ( — 2 = — 3a + b.) Вычтем из первого уравнения третье: (0 = — 15a + 3bleft| {:3,,,,,,,, Leftrightarrow ,,,,,,,0 = — 5a + b} right..) Таким образом, получим систему уравнений: (left{ {begin{array}{*{20}{c}}{ — 2 = — 3a + b}\{0 = — 5a + b,,,}end{array}} right.) Вычтем из первого уравнения второе: ( — 2 = 2a,,,,,,,,, Leftrightarrow ,,,,,,,,a = — 1.) Тогда: ( — 2 = — 3 cdot left( { — 1} right) + b,,,,,,,, Leftrightarrow ,,,,,,,,b = — 5) и (2 = — 1 + 5 + c,,,,,,, Leftrightarrow ,,,,,,,c = — 2.) Следовательно, уравнение параболы имеет вид: (gleft( x right) = — {x^2} — 5x — 2.) Чтобы найти координаты точек пересечения прямой (fleft( x right) = 3x + 5) и параболы (gleft( x right) = — {x^2} — 5x — 2) необходимо решить систему уравнений: (left{ {begin{array}{*{20}{c}}{y = — {x^2} — 5x — 2}\{y = 3x + 5,,,,,,,}end{array}} right.,,,,,,, Leftrightarrow ,,,,,, — {x^2} — 5x — 2 = 3x + 5,,,,,, Leftrightarrow ,,,,,{x^2} + 8x + 7 = 0,,,,,, Leftrightarrow ,,,,,{x_1} = — 1,,,,{x_2} = — 7.) Значение (x = — 1) является абсциссой точки А. Следовательно, абсцисса точки В равна – 7. Ответ: – 7. |
|
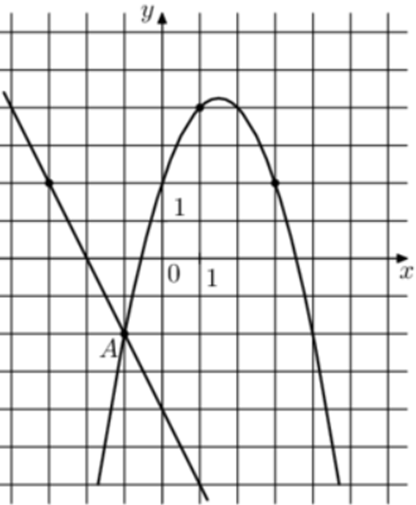
| Задача 24. На рисунке изображены графики функций (fleft( x right) = — 2x — 4) и (gleft( x right) = a,{x^2} + b,x + c,) которые пересекаются в точках A и B. Найдите абсциссу точки B.
Ответ
ОТВЕТ: 6. |
 |
|
Решение
Парабола проходит через точки (left( { — 1; — 2} right)), (left( {1;4} right)) и (left( {3;2} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{ — 2 = a — b + c,,,,,,,,,,,,,,,,,,,,,}\{4 = a + b + c,,,,,,,,,,,,,,,,,,,,,,}\{2 = 9a + 3b + c,,,,,,,,,,,,,,,}end{array}} right.) Вычтем из первого уравнения второе: ( — 6 = — 2b,,,,,,, Leftrightarrow ,,,,,,b = 3.) Вычтем из первого уравнения третье: ( — 4 = — 8a — 4bleft| {:left( { — 2} right),,,,,,,,, Leftrightarrow ,,,,,,,,2 = 4a + 2b} right..) Таким образом, получим систему уравнений: (left{ {begin{array}{*{20}{c}}{b = 3,,,,,,,,,,,,,,,,}\{2 = 4a + 2b,,,}end{array},,,,, Leftrightarrow ,,,,,,2 = 4a + 2 cdot 3,,,,,,,, Leftrightarrow ,,,,,,,,,a = — 1} right..) Тогда: ( — 2 = — 1 — 3 + c,,,,,,, Leftrightarrow ,,,,,,,,c = 2.) Следовательно, уравнение параболы имеет вид: (gleft( x right) = — {x^2} + 3x + 2.) Чтобы найти координаты точек пересечения прямой (fleft( x right) = — 2x — 4) и параболы (gleft( x right) = — {x^2} + 3x + 2) необходимо решить систему уравнений: (left{ {begin{array}{*{20}{c}}{y = — {x^2} + 3x + 2}\{y = — 2x — 4,,,,,,,,,,,}end{array}} right.,,,,, Leftrightarrow ,,,,, — ,{x^2} + 3x + 2 = — 2x — 4,,,,,, Leftrightarrow ,,,,,{x^2} — 5x — 6 = 0,,,,, Leftrightarrow ,,,,,{x_1} = — 1,,,,{x_2} = 6.) Значение (x = — 1) является абсциссой точки А. Следовательно, абсцисса точки В равна 6. Ответ: 6. |
|
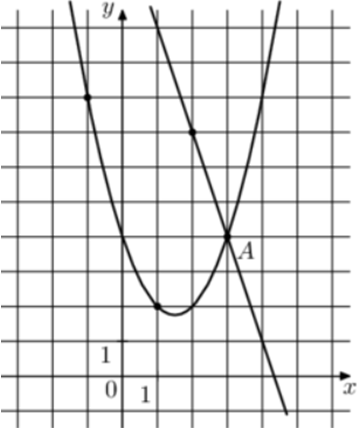
| Задача 25. На рисунке изображены графики функций (fleft( x right) = — 3x + 13) и (gleft( x right) = a,{x^2} + b,x + c,) которые пересекаются в точках A и B. Найдите ординату точки B.
Ответ
ОТВЕТ: 22. |
 |
|
Решение
Парабола проходит через точки (left( {1;2} right)), (left( {2;2} right)) и (left( {3;4} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{2 = a + b + c,,,,,,,,,,,,,,,,,,,,,,,,,,,,}\{2 = 4a + 2b + c,,,,,,,,,,,,,,,,,,,,,,}\{4 = 9a + 3b + c,,,,,,,,,,,,,,,,,,,,,}end{array}} right.) Вычтем из первого уравнения второе: (0 = — 3a — b.) Вычтем из первого уравнения третье: ( — 2 = — 8a — 2bleft| {:2,,,,,,,, Leftrightarrow ,,,,,,, — 1 = — 4a — b} right..) Таким образом, получим систему уравнений: (left{ {begin{array}{*{20}{c}}{0 = — 3a — b}\{ — 1 = — 4a — b}end{array}} right.) Вычтем из первого уравнения второе: (1 = a,,,,,,,,, Leftrightarrow ,,,,,,,,a = 1.) Тогда: (0 = — 3 cdot 1 — b,,,,,,,, Leftrightarrow ,,,,,,,,b = — 3) и (2 = 1 — 3 + c,,,,,,, Leftrightarrow ,,,,,,,c = 4.) Следовательно, уравнение параболы имеет вид: (gleft( x right) = {x^2} — 3x + 4.) Чтобы найти координаты точек пересечения прямой (fleft( x right) = — 3x + 13) и параболы (gleft( x right) = {x^2} — 3x + 4) необходимо решить систему уравнений: (left{ {begin{array}{*{20}{c}}{y = {x^2} — 3x + 4}\{y = — 3x + 13,,,,}end{array}} right.,,, Leftrightarrow ,,,{x^2} — 3x + 4 = 13 — 3x,,, Leftrightarrow ,,,{x^2} = 9,,,, Leftrightarrow ,,,{x_1} = 3,,,,{x_2} = — 3,,, Leftrightarrow ,,,{y_1} = 4,,,{y_2} = 22.) Следовательно, (Aleft( {3;4} right)) и (Bleft( { — 3;22} right)). Таким образом, ордината точки В равна 22. Ответ: 22. |
|
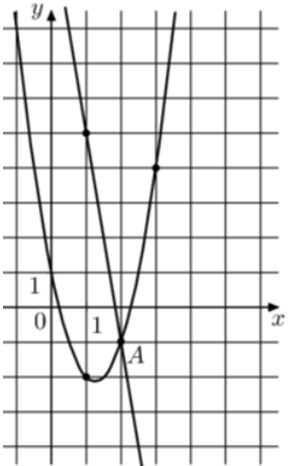
| Задача 26. На рисунке изображены графики функций (fleft( x right) = — 6x + 11) и (gleft( x right) = a,{x^2} + b,x + c,) которые пересекаются в точках A и B. Найдите ординату точки B.
Ответ
ОТВЕТ: 26. |
 |
|
Решение
Парабола проходит через точки (left( {1; — 2} right)), (left( {2; — 1} right)) и (left( {3;4} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{ — 2 = a + b + c}\{ — 1 = 4a + 2b + c}\{4 = 9a + 3b + c}end{array}} right.) Вычтем из первого уравнения второе: ( — 1 = — 3a — b.) Вычтем из первого уравнения третье: ( — 6 = — 8a — 2bleft| {:2,,,,,,,, Leftrightarrow ,,,,,,,, — 3 = — 4a — b} right..) Таким образом, получим систему уравнений: (left{ {begin{array}{*{20}{c}}{ — 1 = — 3a — b}\{ — 3 = — 4a — b}end{array}} right.) Вычтем из первого уравнения второе: (2 = a,,,,,,,,, Leftrightarrow ,,,,,,,,a = 2.) Тогда: ( — 1 = — 3 cdot 2 — b,,,,,,,, Leftrightarrow ,,,,,,,,b = — 5) и ( — 2 = 2 — 5 + c,,,,,,, Leftrightarrow ,,,,,,,c = 1.) Следовательно, уравнение параболы имеет вид: (gleft( x right) = 2{x^2} — 5x + 1.) Чтобы найти координаты точек пересечения прямой (fleft( x right) = — 6x + 11) и параболы (gleft( x right) = 2{x^2} — 5x + 1) необходимо решить систему уравнений: (left{ {begin{array}{*{20}{c}}{y = 2{x^2} — 5x + 1}\{y = — 6x + 11,,,,,,,}end{array}} right.,,,,,,,, Leftrightarrow ,,,,,,,,2{x^2} — 5x + 1 = — 6x + 11,,,,,,,,,, Leftrightarrow ,,,,,,,2{x^2} + x — 10 = 0,,,,,,,,, Leftrightarrow ,,,,,) ( Leftrightarrow ,,,,,,,,{x_1} = 2,,,,,,{x_2} = — frac{5}{2},,,,,,,,, Leftrightarrow ,,,,,,,{y_1} = — 1,,,,,{y_2} = 26.) Следовательно, (Aleft( {2; — 1} right)) и (Bleft( { — frac{5}{2};26} right)). Таким образом, ордината точки В равна 26. Ответ: 26. |
|
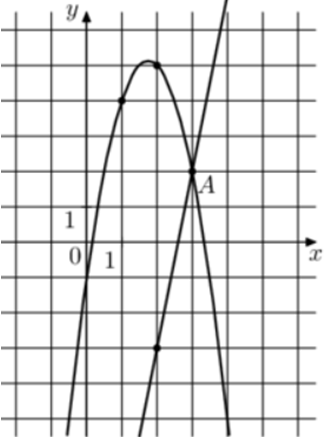
| Задача 27. На рисунке изображены графики функций (fleft( x right) = 5x — 13) и (gleft( x right) = a,{x^2} + b,x + c,) которые пересекаются в точках A и B. Найдите ординату точки B.
Ответ
ОТВЕТ: — 23. |
 |
|
Решение
Парабола проходит через точки (left( {1;4} right)), (left( {2;5} right)) и (left( {3;2} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{4 = a + b + c,,,,,,,,,,,,,,,,,,,,,,,,,,,,}\{5 = 4a + 2b + c,,,,,,,,,,,,,,,,,,,,,,}\{2 = 9a + 3b + c,,,,,,,,,,,,,,,,,,,,,,}end{array}} right.) Вычтем из первого уравнения второе: ( — 1 = — 3a — b.) Вычтем из первого уравнения третье: (2 = — 8a — 2bleft| {:2,,,,,,, Leftrightarrow ,,,,,,1 = — 4a — b} right..) Таким образом, получим систему уравнений: (left{ {begin{array}{*{20}{c}}{ — 1 = — 3a — b}\{1 = — 4a — b}end{array}} right.) Вычтем из первого уравнения второе: ( — 2 = a,,,,,,,,, Leftrightarrow ,,,,,,,,a = — 2.) Тогда: ( — 1 = — 3 cdot left( { — 2} right) — b,,,,,,,, Leftrightarrow ,,,,,,,,b = 7) и (4 = — 2 + 7 + c,,,,,,, Leftrightarrow ,,,,,,,c = — 1.) Следовательно, уравнение параболы имеет вид: (gleft( x right) = — 2{x^2} + 7x — 1.) Чтобы найти координаты точек пересечения прямой (fleft( x right) = 5x — 13) и параболы (gleft( x right) = — 2{x^2} + 7x — 1) необходимо решить систему уравнений: (left{ {begin{array}{*{20}{c}}{y = — 2{x^2} + 7x — 1}\{y = 5x — 13,,,,,,,,,,,,,,}end{array}} right.,,,,,,,, Leftrightarrow ,,,,,,,, — 2{x^2} + 7x — 1 = 5x — 13,,,,,,,,,, Leftrightarrow ,,,,,,,2{x^2} — 2x — 12 = 0,,,,,,,,, Leftrightarrow ,,,,,) ( Leftrightarrow ,,,,,,,,{x_1} = 3,,,,,,{x_2} = — 2,,,,,,,,, Leftrightarrow ,,,,,,,{y_1} = 2,,,,,{y_2} = — 23.) Следовательно, (Aleft( {3;2} right)) и (Bleft( { — 2; — 23} right)). Таким образом, ордината точки В равна – 23. Ответ: – 23. |
|
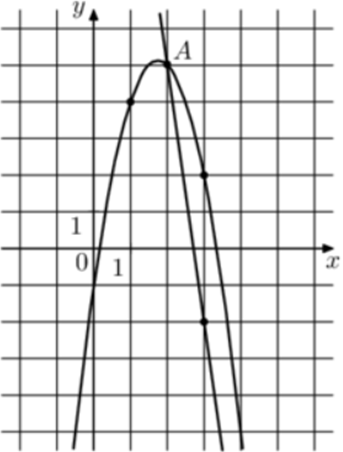
| Задача 28. На рисунке изображены графики функций (fleft( x right) = — 7x + 19) и (gleft( x right) = a,{x^2} + b,x + c,) которые пересекаются в точках A и B. Найдите ординату точки B.
Ответ
ОТВЕТ: — 16. |
 |
|
Решение
Парабола проходит через точки (left( {1;4} right)), (left( {2;5} right)) и (left( {3;2} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{4 = a + b + c,,,,,,,,,,,,,,,,,,,,,,,,,,,,}\{5 = 4a + 2b + c,,,,,,,,,,,,,,,,,,,,,,}\{2 = 9a + 3b + c,,,,,,,,,,,,,,,,,,,,,,}end{array}} right.) Вычтем из первого уравнения второе: ( — 1 = — 3a — b.) Вычтем из первого уравнения третье: (2 = — 8a — 2bleft| {:2,,,,,,,, Leftrightarrow ,,,,,,,,1 = — 4a — b} right..) Таким образом, получим систему уравнений: (left{ {begin{array}{*{20}{c}}{ — 1 = — 3a — b}\{1 = — 4a — b}end{array}} right.) Вычтем из первого уравнения второе: ( — 2 = a,,,,,,,,, Leftrightarrow ,,,,,,,,a = — 2.) Тогда: ( — 1 = — 3 cdot left( { — 2} right) — b,,,,,,,, Leftrightarrow ,,,,,,,,b = 7) и (4 = — 2 + 7 + c,,,,,,, Leftrightarrow ,,,,,,,c = — 1.) Следовательно, уравнение параболы имеет вид: (gleft( x right) = — 2{x^2} + 7x — 1.) Чтобы найти координаты точек пересечения прямой (fleft( x right) = — 7x + 19) и параболы (gleft( x right) = — 2{x^2} + 7x — 1) необходимо решить систему уравнений: (left{ {begin{array}{*{20}{c}}{y = — 2{x^2} + 7x — 1}\{y = — 7x + 19,,,,,,,}end{array}} right.,,,,,,,, Leftrightarrow ,,,,,,,, — 2{x^2} + 7x — 1 = — 7x + 19,,,,,,,,,, Leftrightarrow ,,,,,,,2{x^2} — 14x + 20 = 0,,,,,,,,, Leftrightarrow ,,,,,) ( Leftrightarrow ,,,,,,,,{x_1} = 2,,,,,,{x_2} = 5,,,,,,,, Leftrightarrow ,,,,,,,{y_1} = 5,,,,,{y_2} = — 16.) Следовательно, (Aleft( {2;5} right)) и (Bleft( {5; — 16} right)). Таким образом, ордината точки В равна – 16. Ответ: – 16. |
|
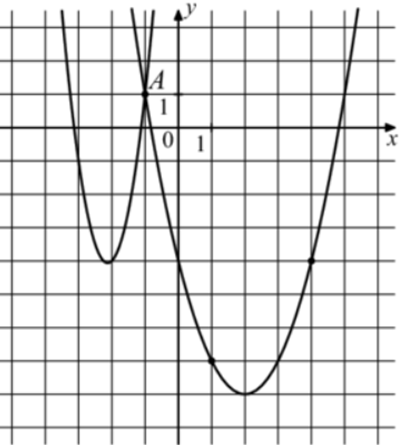
| Задача 29. На рисунке изображены графики функций (fleft( x right) = 4{x^2} + 17x + 14) и (gleft( x right) = a,{x^2} + b,x + c,) которые пересекаются в точках A и B. Найдите абсциссу точки B.
Ответ
ОТВЕТ: — 6. |
 |
|
Решение
График функции (fleft( x right) = 4{x^2} + 17x + 14) пересекает ось ординат в точке (left( {0;14} right)). Значит, график (y = fleft( x right)) изображён слева, а график (gleft( x right) = a{x^2} + bx + c) справа. Заметим, что графиком функции (y = gleft( x right)) является парабола (gleft( x right) = {x^2}), вершина которой находится в точке (left( {2; — 8} right)). Следовательно, ее уравнение будет иметь вид: (gleft( x right) = {left( {x — 2} right)^2} — 8 = {x^2} — 4x — 4.) Чтобы найти координаты точек пересечения парабол необходимо решить систему уравнений: (left{ {begin{array}{*{20}{c}}{y = 4{x^2} + 17x + 14}\{y = {x^2} — 4x — 4,,,,,,,,,}end{array}} right.,,,,,,,,, Leftrightarrow ,,,,,,4{x^2} + 17x + 14 = {x^2} — 4x — 4,,,,,,, Leftrightarrow ,,,,,,,3{x^2} + 21x + 18 = 0left| {:3,,,,, Leftrightarrow } right.) ( Leftrightarrow ,,,,,,,{x^2} + 7x + 6 = 0,,,,,,,,,, Leftrightarrow ,,,,,,,,{x_1} = — 1,,,,{x_2} = — 6.) Значение (x = — 1) является абсциссой точки А. Следовательно, абсцисса точки В равна – 6. Ответ: – 6. |
|
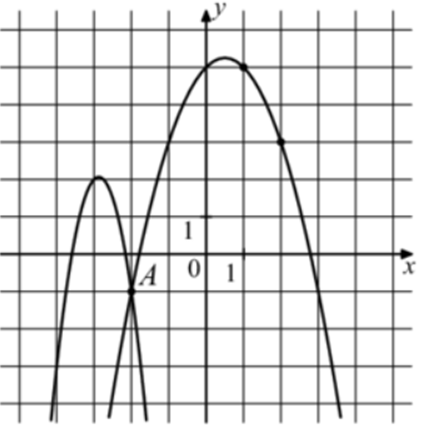
| Задача 30. На рисунке изображены графики функций (fleft( x right) = — 4{x^2} — 23x — 31) и (gleft( x right) = a,{x^2} + b,x + c,) которые пересекаются в точках A и B. Найдите абсциссу точки B.
Ответ
ОТВЕТ: — 6. |
 |
|
Решение
График функции (fleft( x right) = — 4{x^2} — 23x — 31) пересекает ось ординат в точке (left( {0; — 31} right)). Значит график функции (y = fleft( x right)) изображен слева, а график (gleft( x right) = a{x^2} + bx + c) справа, который проходит через точки (left( { — 2; — 1} right)), (left( {1;5} right)) и (left( {2;3} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{ — 1 = 4a — 2b + c}\{5 = a + b + c,,,,,,}\{3 = 4a + 2b + c}end{array}} right.) Вычтем из первого уравнения второе: ( — 6 = 3a — 3b.) Вычтем из первого уравнения третье: ( — 4 = — 4b,,,,,, Leftrightarrow ,,,,,b = 1.) Тогда: ( — 6 = 3a — 3,,,,,, Leftrightarrow ,,,,,,a = — 1) и ( — 1 = — 4 — 2 + c,,,,,, Leftrightarrow ,,,,,,,c = 5.) Следовательно: (gleft( x right) = — {x^2} + x + 5.) Чтобы найти координаты точек пересечения парабол необходимо решить систему уравнений: (left{ {begin{array}{*{20}{c}}{y = — 4{x^2} — 23x — 31}\{y = — {x^2} + x + 5,,,,,,,,,,,}end{array}} right.,,,,, Leftrightarrow ,,,,, — 4{x^2} — 23x — 31 = — {x^2} + x + 5,,,,, Leftrightarrow ,,,,,3{x^2} + 24x + 36 = 0left| {:3,,,, Leftrightarrow ,} right.) ( Leftrightarrow ,,,,,,{x^2} + 8x + 12 = 0,,,,,,,, Leftrightarrow ,,,,,,{x_1} = — 2,,,,,,{x_2} = — 6.) Значение (x = — 2) является абсциссой точки А. Следовательно, абсцисса точки В равна – 6. Ответ: – 6. |
|
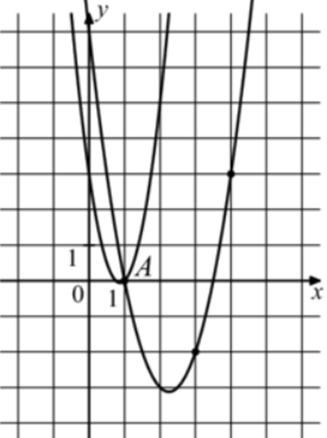
| Задача 31. На рисунке изображены графики функций (fleft( x right) = 4{x^2} — 7x + 3) и (gleft( x right) = a,{x^2} + b,x + c,) которые пересекаются в точках A и B. Найдите ординату точки B.
Ответ
ОТВЕТ: 33. |
 |
|
Решение
График функции (fleft( x right) = 4{x^2} — 7x + 3) пересекает ось ординат в точке (left( {0;3} right)). Значит график функции (y = fleft( x right)) изображен слева, а график (gleft( x right) = a{x^2} + bx + c) справа, который проходит через точки (left( {1;0} right)), (left( {3; — 2} right)) и (left( {4;3} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{0 = a + b + c,,,,,,,,}\{ — 2 = 9a + 3b + c}\{3 = 16a + 4b + c}end{array}} right.) Вычтем из первого уравнения второе: (2 = — 8a — 2bleft| {: 2,,,,,,, Leftrightarrow ,,,,,,,,1 = — 4a — b.} right.) Вычтем из первого уравнения третье: ( — 3 = — 15a — 3bleft| {:3} right.,,,,,, Leftrightarrow ,,,,, — 1 = — 5a — b.) Таким образом, получим систему уравнений: (left{ {begin{array}{*{20}{c}}{1 = — 4a — b}\{ — 1 = — 5a — b}end{array}} right.) Вычтем из первого уравнения второе: (2 = a,,,,,,, Leftrightarrow ,,,,,,,a = 2.) Тогда: (1 = — 4 cdot 2 — b,,,,,, Leftrightarrow ,,,,,,b = — 9) и (0 = 2 — 9 + c,,,,,,, Leftrightarrow ,,,,,,,c = 7.) Следовательно: (gleft( x right) = 2{x^2} — 9x + 7.) Чтобы найти координаты точек пересечения парабол необходимо решить систему уравнений: (left{ {begin{array}{*{20}{c}}{y = 4{x^2} — 7x + 3}\{y = 2{x^2} — 9x + 7}end{array},,,,,,, Leftrightarrow ,,,,,,4{x^2} — 7x + 3 = 2{x^2} — 9x + 7,,,,,,, Leftrightarrow ,,,,,,,2{x^2} + 2x — 4 = 0left| {:2,,,,, Leftrightarrow } right.} right.) ( Leftrightarrow ,,,,,,,{x^2} + x — 2 = 0,,,,,,,, Leftrightarrow ,,,,,,,,{x_1} = 1,,,,{x_2} = — 2,,,,,,,,,,,,,,{y_1} = 0,,,,{y_2} = 33.) Следовательно, (Aleft( {1;0} right)) и (Bleft( { — 2;33} right)). Таким образом, ордината точки В равна 33. Ответ: 33. |
|
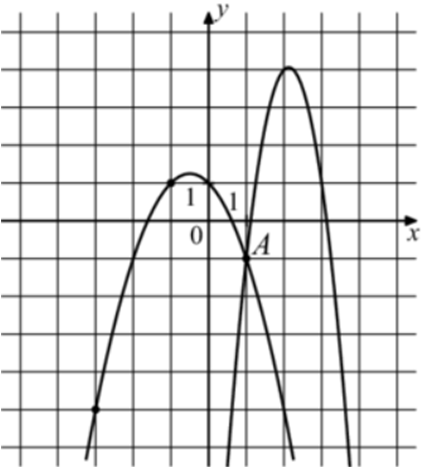
| Задача 32. На рисунке изображены графики функций (fleft( x right) = — 4{x^2} + 17x — 14) и (gleft( x right) = a,{x^2} + b,x + c,) которые пересекаются в точках A и B. Найдите ординату точки B.
Ответ
ОТВЕТ: — 29. |
 |
|
Решение
График функции (fleft( x right) = — 4{x^2} + 17x — 14) пересекает ось ординат в точке (left( {0; — 14} right)). Значит график функции (y = fleft( x right)) изображен справа, а график (gleft( x right) = a{x^2} + bx + c) слева, который проходит через точки (left( {1; — 1} right)), (left( { — 1;1} right)) и (left( { — 3; — 5} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{ — 1 = a + b + c,,,,,,}\{1 = a — b + c,,,,,,,,}\{ — 5 = 9a — 3b + c}end{array}} right.) Вычтем из первого уравнения второе: ( — 2 = 2b,,,,,,, Leftrightarrow ,,,,,,,b = — 1.) Вычтем из первого уравнения третье: (4 = — 8a + 4b,,,,, Leftrightarrow ,,,,,4 = — 8a — 4,,,,,, Leftrightarrow ,,,,,,a = — 1.) Тогда: ( — 1 = — 1 — 1 + c,,,,,, Leftrightarrow ,,,,,,,c = 1.) Следовательно: (gleft( x right) = — {x^2} — x + 1.) Чтобы найти координаты точек пересечения парабол необходимо решить систему уравнений: (left{ {begin{array}{*{20}{c}}{y = — 4{x^2} + 17x — 14}\{y = — {x^2} — x + 1,,,,,,,,,,,,,}end{array}} right.,,,,,, Leftrightarrow ,,,,, — 4{x^2} + 17x — 14 = — {x^2} — x + 1,,,,,, Leftrightarrow ,,,,,3{x^2} — 18x + 15 = 0left| {:3,,,,, Leftrightarrow } right.) ( Leftrightarrow ,,,,,,,{x^2} — 6x + 5 = 0,,,,,,,, Leftrightarrow ,,,,,,,,{x_1} = 1,,,,{x_2} = 5,,,,,,,,,{y_1} = — 1,,,,{y_2} = — 29.) Следовательно, (Aleft( {1; — 1} right)) и (Bleft( {5; — 29} right)). Таким образом, ордината точки В равна – 29. Ответ: – 29. |
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Задание
15
#1819
Уровень задания: Равен ЕГЭ
Решите неравенство
[begin{aligned}
dfrac{9^x — 3^{x + 1} — 19}{3^x — 6} + dfrac{9^{x + 1} — 3^{x + 4} + 2}{3^x — 9}leqslant 10cdot 3^x + 3
end{aligned}]
(ЕГЭ 2016, резервный день)
Сделаем замену (3^x = t > 0):
[begin{aligned}
dfrac{t^2 — 3t — 19}{t — 6} + dfrac{9t^2 — 81t + 2}{t — 9}leqslant 10t + 3
end{aligned}]
ОДЗ:
[begin{aligned}
begin{cases}
tneq 6\
tneq 9
end{cases}
end{aligned}]
Перенесём всё влево и приведём к общему знаменателю
[begin{aligned}
dfrac{t — 3}{(t — 9)(t — 6)}leqslant 0
end{aligned}]
По методу интервалов
откуда (tin(-infty; 3]cup(6; 9))
с учётом ОДЗ и условия (t > 0): (tin(0; 3]cup(6; 9))
в исходных переменных: [xin(-infty; 1]cup(log_3 6; 2).]
Ответ:
((-infty; 1]cup(log_3 6; 2))
Задание
16
#1820
Уровень задания: Равен ЕГЭ
Решите неравенство
[begin{aligned}
2log_{(x^2 — 8x + 17)^2}(3x^2 + 5)leqslant log_{x^2 — 8x + 17}(2x^2 + 7x + 5)
end{aligned}]
(ЕГЭ 2016, основная волна)
ОДЗ:
[begin{aligned}
begin{cases}
(x^2 — 8x + 17)^2 > 0\
(x^2 — 8x + 17)^2 neq 1\
3x^2 + 5 > 0\
x^2 — 8x + 17 > 0\
x^2 — 8x + 17 neq 1\
2x^2 + 7x + 5 > 0
end{cases}
qquadLeftrightarrowqquad
xin(-infty; -2,5)cup(-1; 4)cup(4; +infty)
end{aligned}]
Заметим, что [x^2 — 8x + 17 = (x — 4)^2 + 1geqslant 1,] причём на ОДЗ выполнено ((x — 4)^2 + 1 > 1), тогда
[begin{aligned}
&2log_{(x^2 — 8x + 17)^2}(3x^2 + 5)leqslant log_{x^2 — 8x + 17}(2x^2 + 7x + 5)qquadLeftrightarrow\
Leftrightarrowqquad &log_{x^2 — 8x + 17}(3x^2 + 5)leqslant log_{x^2 — 8x + 17}(2x^2 + 7x + 5)qquadLeftrightarrow\
Leftrightarrowqquad &3x^2 + 5leqslant 2x^2 + 7x + 5qquadLeftrightarrowqquad x^2 — 7x leqslant 0,
end{aligned}]
откуда (xin[0; 7])
пересечём ответ с ОДЗ: [xin[0; 4)cup(4; 7]] – итоговый ответ к задаче.
Ответ:
([0; 4)cup(4; 7])
Задание
17
#2830
Уровень задания: Равен ЕГЭ
Решите неравенство
[begin{aligned}
8^x — 3cdot 4^x + dfrac{9cdot 4^x — 288}{2^x — 9}leqslant 32
end{aligned}]
(ЕГЭ 2016, основная волна)
Сделаем замену (2^x = t > 0):
[begin{aligned}
t^3 — 3t^2 + dfrac{9t^2 — 288}{t — 9}leqslant 32
end{aligned}]
ОДЗ:
[begin{aligned}
tneq 9
end{aligned}]
Перенесём всё влево и приведём к общему знаменателю
[begin{aligned}
dfrac{t^4 — 12t^3 + 36t^2 — 32t}{t — 9}leqslant 0qquadLeftrightarrowqquad tcdotdfrac{t^3 — 12t^2 + 36t — 32}{t — 9}leqslant 0
end{aligned}]
Разложим многочлен третьей степени в числителе левой части последнего неравенства на множители. Можно угадать его корень (t = 2). Знание корня многочлена позволяет поделить его столбиком на (t — t_0), где (t_0) – корень, тогда [begin{array}{rr|l}
t^3-12t^2+36t-32&&negthickspaceunderline{qquad t-2 qquad}\
underline{t^3- , 2t^2} phantom{0000000000}&&negthickspace t^2 — 10t + 16\[-3pt]
-10t^2 + 36t,phantom{0000}&&\
underline{-10t^2 + 20t,}phantom{0000}&&\[-3pt]
16t — 32! &&\
underline{16t — 32! }&&\[-3pt]
0&&\
end{array}] тогда последнее неравенство равносильно
[begin{aligned}
dfrac{t(t — 2)^2(t — 8)}{t — 9}leqslant 0
end{aligned}]
По методу интервалов
откуда (tin(-infty; 0]cup{2}cup[8; 9))
с учётом ОДЗ и условия (t > 0): (tin{2}cup[8; 9))
в исходных переменных: [xin{1}cup[3; log_2 9)]
Ответ:
({1}cup[3; log_2 9))
Задание
18
#1822
Уровень задания: Равен ЕГЭ
Решите неравенство
[begin{aligned}
dfrac{25^x — 5^{x + 2} + 26}{5^x — 1} + dfrac{25^x — 7cdot 5^x + 1}{5^x — 7}leqslant 2cdot 5^x — 24
end{aligned}]
(ЕГЭ 2016, основная волна)
Сделаем замену (5^x = t > 0):
[begin{aligned}
dfrac{t^2 — 25t + 26}{t — 1} + dfrac{t^2 — 7t + 1}{t — 7}leqslant 2t — 24
end{aligned}]
ОДЗ:
[begin{aligned}
begin{cases}
tneq 1\
tneq 7
end{cases}
end{aligned}]
Перенесём всё влево и приведём к общему знаменателю
[begin{aligned}
dfrac{3t — 15}{(t — 1)(t — 7)}leqslant 0
end{aligned}]
По методу интервалов
откуда (tin(-infty; 1)cup[5; 7))
с учётом ОДЗ и условия (t > 0): (tin(0; 1)cup[5; 7))
в исходных переменных: [xin(-infty; 0)cup[1;log_5 7).]
Ответ:
((-infty; 0)cup[1;log_5 7))
Задание
19
#1817
Уровень задания: Равен ЕГЭ
Решите неравенство
[begin{aligned}
(4x — 7)cdotlog_{x^2 — 4x + 5}(3x — 5)geqslant 0
end{aligned}]
(ЕГЭ 2016, досрочная волна)
ОДЗ:
[begin{aligned}
begin{cases}
x^2 — 4x + 5 > 0\
x^2 — 4x + 5 neq 1\
3x — 5 > 0
end{cases}
qquadLeftrightarrowqquad
xinleft(dfrac{5}{3}; 2right)cup(2; +infty)
end{aligned}]
По методу рационализации на ОДЗ исходное неравенство равносильно неравенству
[begin{aligned}
&(4x — 7)(x^2 — 4x + 5 — 1)(3x — 5 — 1)geqslant 0quadLeftrightarrow\
Leftrightarrowquad & (4x — 7)(x^2 — 4x + 4)(3x — 6)geqslant 0quadLeftrightarrowquad (4x — 7)(x — 2)^3geqslant 0
end{aligned}]
По методу интервалов
откуда с учётом ОДЗ: [xin left(dfrac{5}{3}; dfrac{7}{4}right]cup(2; +infty),.]
Ответ:
(left(dfrac{5}{3}; dfrac{7}{4}right]cup(2; +infty))
Задание
20
#1630
Уровень задания: Равен ЕГЭ
Решите неравенство
[begin{aligned}
dfrac{5lg^2x-1}{lg^2x-1}geqslant 1.
end{aligned}]
(ЕГЭ 2015, резервный день)
ОДЗ: [x > 0.] Сделаем замену (y = lg x), тогда [dfrac{5y^2-1}{y^2-1}geqslant 1qquadLeftrightarrowqquad dfrac{5y^2-1 — (y^2 — 1)}{y^2-1}geqslant 0qquadLeftrightarrowqquad dfrac{4y^2}{y^2-1}geqslant 0.] Решим это неравенство методом интервалов:
откуда (y in (-infty; -1)cup{0}cup(1; +infty)).
(lg x in (-infty; -1)cup{0}cup(1; +infty)), что можно представить в виде
[lg x < -1qquadtext{или}qquadlg x = 0qquadtext{или}qquadlg x > 1.]
Решим первое неравенство: [lg x < -1.] Это неравенство на ОДЗ равносильно: [x < 0,1.]
Решим второе уравнение: [lg x = 0.] Это уравнение на ОДЗ равносильно: [x = 1.]
Решим третье неравенство: [lg x > 1.] Это неравенство на ОДЗ равносильно:
[x > 10.] Объединенное решение двух неравенств и уравнения: (xin(-infty; 0,1)cup{1}cup(10; +infty)).
Пересечем ответ с ОДЗ: [xin (0; 0,1)cup{1}cup(10; +infty).]
Ответ:
((0; 0,1)cup{1}cup(10; +infty))
Задание
21
#1628
Уровень задания: Равен ЕГЭ
Решите неравенство
[begin{aligned}
log^2_{5}(25 — x^2) — 3log_{5}(25 — x^2) + 2geqslant 0.
end{aligned}]
(ЕГЭ 2015)
ОДЗ: [25 — x^2 > 0 qquadLeftrightarrowqquad xin (-5; 5).] Сделаем замену (y = log_5(25 — x^2)), тогда [y^2 -3y + 2geqslant 0.] Решим это неравенство методом интервалов:
откуда (y in (-infty; 1] cup [2; +infty)).
(log_5(25 — x^2) in (-infty; 1] cup [2; +infty)), что можно представить в виде
(log_5(25 — x^2) leqslant 1) или (log_5(25 — x^2)geqslant 2).
Решим первое из этих неравенств: [log_5(25 — x^2) leqslant 1.] Это неравенство на ОДЗ равносильно: [25 — x^2 leqslant 5quadLeftrightarrowquad x^2 geqslant 20quadLeftrightarrowquad xin(-infty; -2sqrt{5}]cup[2sqrt{5}; +infty).]
Решим второе из этих неравенств: [log_5(25 — x^2) geqslant 2.] Это неравенство на ОДЗ равносильно: [25 — x^2 geqslant 25quadLeftrightarrowquad x^2 leqslant 0quadLeftrightarrowquad x = 0.]
Объединенное решение двух неравенств: (xin(-infty; -2sqrt{5}]cup{0}cup[2sqrt{5}; +infty)).
Пересечем ответ с ОДЗ: [xin(-5; -2sqrt{5}]cup{0}cup[2sqrt{5}; 5).]
Ответ:
(xin(-5; -2sqrt{5}]cup{0}cup[2sqrt{5}; 5))

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ