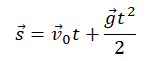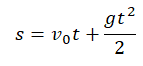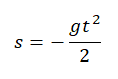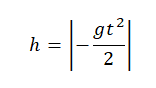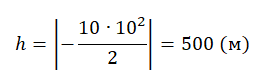При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
Версия для печати и копирования в MS Word
1
Катер плывёт по прямой реке, двигаясь относительно берега перпендикулярно береговой линии. Модуль скорости катера относительно берега равен 6 км/ч. Река течёт со скоростью 4,5 км/ч. Чему равен модуль скорости катера относительно воды? Ответ выразите в км/ч.
Ответ:
2
Чему равен модуль силы тяжести, действующей на тело массой 9 кг, на высоте, равной половине радиуса Земли?
Ответ:
3
Математический маятник, колеблющийся с циклической частотой ω = 3 с−1, в нижней точке траектории имеет ускорение, равное по модулю a = 1 м/с2. Масса груза маятника m = 900 г. Чему равен запас механической энергии маятника?
Ответ:
4
На шероховатой поверхности лежит брусок массой 1 кг. На него начинает действовать горизонтальная сила направленная вдоль поверхности и зависящая от времени так, как показано на графике слева. Зависимость работы этой силы от времени представлена на графике справа. Выберите все верные утверждения на основании анализа представленных графиков.
1) Первые 10 с брусок двигался с постоянной скоростью.
2) За первые 10 с брусок переместился на 20 м.
3) Сила трения скольжения равна 2 Н.
4) В интервале времени от 12 до 20 с брусок двигался с постоянным ускорением.
5) В интервале времени от 12 до 20 с брусок двигался с постоянной скоростью.
Ответ:
5
Пружинный маятник представляет собой груз, склеенный из двух частей и прикреплённый к лёгкой пружине. Он совершает гармонические колебания вдоль поверхности гладкого горизонтального стола. В момент, когда груз находился в крайней точке своей траектории, одна из его частей отклеилась. Как изменились в результате этого частота колебаний пружинного маятника, амплитуда колебаний пружинного маятника, максимальная кинетическая энергия пружинного маятника?
Для каждой величины определите соответствующий характер изменения:
1) увеличилась
2) уменьшилась
3) не изменилась
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ
А) частота колебаний пружинного маятника
Б) амплитуда колебаний пружинного маятника
В) максимальная кинетическая энергия пружинного маятника
ИХ ИЗМЕНЕНИЕ
1) увеличилась
2) уменьшилась
3) не изменилась
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
Ответ:
6
Груз, подвешенный к пружине с коэффициентом жесткости k совершает колебания с периодом T и амплитудой Что произойдет с периодом колебаний, максимальной потенциальной энергией пружины и частотой колебаний, если пружину заменить на другую с меньшим коэффициентом жесткости, а амплитуду колебаний оставить прежней?
Для каждой величины определите соответствующий характер изменения:
1) увеличилась
2) уменьшилась
3) не изменилась
4) может измениться любым из выше указанных способов
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Период колебаний | Максимальная потенциальная
энергия пружины |
Частота колебаний |
Ответ:
7
Температура порции идеального газа увеличилась на 773 К. На сколько возросла средняя энергия хаотического теплового движения одной молекулы, входящей в состав этой порции газа? Ответ выразите в электрон-вольтах и округлите до десятых долей.
Ответ:
8
Относительная влажность воздуха в цилиндре под поршнем равна 60%. Воздух изотермически сжали, уменьшив его объём в два раза. Какова стала относительная влажность воздуха? (Ответ дать в процентах.)
Ответ:
9
Объём идеального одноатомного газа при постоянном давлении 1,6·105 Па увеличился на 0,3 м3. Какое количество теплоты было передано газу в этом процессе? Ответ выразите в килоджоулях (кДж).
Ответ:
10
На pV-диаграммах изображены два циклических процесса 1−2−3−4−1 и 5−6−7−8−5, проводимые с одним и тем же количеством гелия.
На основании анализа приведённых графиков, выберите все верные утверждения и укажите в ответе их номера.
1) Работа газа, совершённая за каждый цикл, равна нулю.
2) Количество теплоты, полученное газом в изобарном процессе в цикле 1−2−3−4−1, больше, чем количество теплоты, полученное газом в изобарном процессе в цикле 5−6−7−8−5.
3) Количество теплоты, полученное газом в изохорном процессе в цикле 1−2−3−4−1, больше, чем количество теплоты, полученное газом в изохорном процессе в цикле 5−6−7−8−5.
4) Модуль количества теплоты, отданной газом в изобарном процессе в цикле 1−2−3−4−1, меньше, чем модуль количества теплоты, отданной газом в изобарном процессе в цикле 5−6−7−8−5.
5) Модуль количества теплоты, отданной газом в изохорном процессе в цикле 1−2−3−4−1, меньше, чем модуль количества теплоты, отданной газом в изохорном процессе в цикле 5−6−7−8−5.
Ответ:
11
В сосуде, объем которого можно изменять, находится идеальный газ. Как изменятся при адиабатическом увеличении объема сосуда следующие три величины: температура газа, его давление, концентрация молекул газа?
Для каждой величины определите соответствующий характер изменения:
1) увеличится;
2) уменьшится;
3) не изменится.
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Температура газа | Давление газа | Концентрация молекул газа |
Пояснение. Для анализа изменений, которые возникнут в газе, необходимо воспользоваться первым началом термодинамики и формулой, которая связывает давление газа с концентрацией его молекул и температурой.
Ответ:
12
Четыре точечных заряда закреплены на плоскости так, как показано на рисунке. Как направлен относительно рисунка (вправо, влево, вверх, вниз, к наблюдателю, от наблюдателя) вектор напряжённости электро-статического поля в точке О? Ответ запишите словом (словами).
Ответ:
13
Тяжёлая квадратная проволочная рамка с длиной стороны 10 см и сопротивлением 2 Ом свободно висит на горизонтальной оси, проходящей через одну из сторон рамки. В пространстве вокруг рамки создано однородное магнитное поле с индукцией 0,08 Тл, линии которого направлены горизонтально и перпендикулярны оси подвеса рамки. Рамку выводят из положения равновесия, отклонив её на угол 30° от вертикали. Какой заряд протекает через рамку в процессе её поворота из начального положения в конечное? Ответ выразите в мкКл, округлив до целого числа.
Ответ:
14
На рисунке изображены оптическая ось тонкой собирающей линзы, луч света 1, падающий на эту линзу, и луч света 2, прошедший через эту линзу. На рисунке размер одной клеточки соответствует 1 см. Каково фокусное расстояние линзы? (Ответ дать в сантиметрах.)
Ответ:
15
Две параллельные металлические пластины больших размеров расположены на расстоянии d друг от друга и подключены к источнику постоянного напряжения (рис. 1). Пластины закрепили на изолирующих подставках и спустя длительное время отключили от источника (рис. 2).
Из приведённого ниже списка выберите все правильные утверждения.
1) Напряжённость электрического поля в точке А больше, чем в точке В.
2) Потенциал электрического поля в точке А больше, чем в точке С.
3) Если увеличить расстояние между пластинами d, то напряжённость электрического поля в точке С не изменится.
4) Если уменьшить расстояние между пластинами d, то заряд правой пластины не изменится.
5) Если пластины полностью погрузить в керосин, то энергия электрического поля конденсатора останется неизменной.
Ответ:
16
Три плоскопараллельные стеклянные пластинки одинаковой толщины, но с различными показателями преломления сложены вплотную друг к другу. Из воздуха на поверхность верхней пластинки в точку А падает луч света под углом α0. В точке В луч света выходит обратно в воздух. Точки А и В смещены друг относительно друга вдоль пластинок на расстояние x. Среднюю пластинку заменяют на другую — такой же толщины, но с большим показателем преломления. Как в результате этого изменятся угол преломления света при переходе из второй пластинки в третью и расстояние x?
Для каждой величины определите соответствующий характер изменения:
1) увеличится;
2) уменьшится;
3) не изменится.
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Угол преломления света при переходе из второй пластинки в третью | Расстояние x |
Ответ:
17
Установите соответствие между разновидностями тонкой линзы и результатами преломления в ней параллельных лучей. К каждой позиции первого столбца подберите нужную позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.
РАЗНОВИДНОСТИ ТОНКОЙ ЛИНЗЫ
А) Собирающая
Б) Рассеивающая
РЕЗУЛЬТАТ ПРЕЛОМЛЕНИЯ ПАРАЛЛЕЛЬНЫХ ЛУЧЕЙ
1) Лучи, параллельные главной оптической оси линзы, пройдя через нее, пройдут затем через ее дальний фокус
2) Лучи, параллельные главной оптической оси линзы, пройдя через нее, пересекутся затем в ее ближнем фокусе
3) Лучи, параллельные главной оптической оси линзы, пройдя через нее, будут казаться расходящимися из ее ближнего фокуса
4) Лучи, параллельные главной оптической оси линзы, пройдя через нее, соберутся в ее дальнем фокусе
Ответ:
18
Электрон в атоме водорода находится в основном (самом низком, с номером n = 1) энергетическом состоянии. Атом поглощает фотон с импульсом 6,8 · 10–27 кг·м/с. Найдите номер энергетического уровня, на который в результате этого перейдёт электрон.
Ответ:
19
При переходе электрона в атоме с (n + 1)-го энергетического уровня на n-й энергетический уровень испускается фотон. Как изменятся следующие физические величины при уменьшении n на единицу: энергия испускаемого фотона, длина волны испускаемого фотона.
Для каждой величины определите соответствующий характер изменения:
1) увеличилась;
2) уменьшилась;
3) не изменилась.
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Ответ:
20
Выберите все верные утверждения о физических явлениях, величинах и закономерностях.
Запишите в ответе их номера.
1) Потенциальная энергия тела зависит от его массы и скорости движения тела.
2) Земля переизлучает падающую на её поверхность солнечную энергию, в том числе в виде инфракрасного излучения.
3) Магнитное поле индукционного тока в контуре всегда увеличивает магнитный поток сквозь контур, изменение которого привело к возникновению этого индукционного тока.
4) Гармонические колебания электрического заряда в металлических проводниках являются источниками электромагнитных волн радиодиапазона.
5) Отклонение -частиц и
-частиц в магнитном поле в противоположные стороны свидетельствует о наличии частиц, вылетающих с разными скоростями.
Ответ:
21
Даны следующие зависимости величин:
А) зависимость энергии упругой деформации пружины от её удлинения;
Б) зависимость объёма идеального газа от его абсолютной температуры при постоянном давлении;
В) зависимость модуля ускорения от времени для электрически заряженной частицы, движущейся в однородном электростатическом поле.
Установите соответствие между этими зависимостями и видами графиков, обозначенных цифрами 1−5. Для каждой зависимости А−В подберите соответствующий вид графика и запишите в таблицу выбранные цифры под соответствующими буквами.
Ответ:
Ответ:
22
При различных измерениях часто используется прибор, который называется баллистическим гальванометром. При быстром протекании электрического заряда через этот прибор максимальное отклонение его стрелки от нулевого положения пропорционально протёкшему заряду. На рисунке показана шкала баллистического гальванометра в момент, когда отклонение стрелки от нулевого положения максимально.
Зная, что коэффициент пропорциональности для этого гальванометра равен 3 · 10–4 Кл/В, определите модуль заряда, протекшего через прибор. Погрешность прямого измерения при помощи данного баллистического гальванометра составляет половину цены его деления. Запишите ответ в мкКл. В ответе запишите значение и погрешность слитно без пробела.
Ответ:
23
Школьник проводит термодинамические эксперименты, используя стакан с кипящей водой, подвешенные на нитях шарики, калориметр с водой и термометр. Сначала школьник погружает металлический шар в кипяток, а затем, дождавшись прогревания шара, переносит его в калориметр и измеряет установившуюся температуру воды в нём. Школьник зарисовал схемы оборудования, которое он использовал при проведении пяти разных опытов (калориметр школьник применял один и тот же, но воду комнатной температуры он каждый раз наливал в него заново). Какие два из этих опытов позволяют сделать вывод о наличии зависимости количества теплоты, получаемого телом при нагревании, от массы этого тела?
Ответ:
24
Широкую стеклянную трубку длиной около полуметра, запаянную с одного конца, целиком заполнили водой и установили вертикально открытым концом вниз, погрузив низ трубки на несколько сантиметров в тазик с водой (см. рис.). При комнатной температуре трубка остается целиком заполненной водой. Воду в тазике медленно нагревают. Где установится уровень воды в трубке, когда вода в тазике начнет закипать? Ответ поясните, используя физические закономерности.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
25
На следующей странице вам будет предложено проверить их самостоятельно.
26
Проволочная катушка сопротивлением 10 Ом расположена в постоянном однородном магнитном поле так, что линии его индукции направлены вдоль оси катушки. Если соединить концы проволоки друг с другом и выключить магнитное поле, то через катушку протечёт заряд 0,2 Кл. Найдите амплитуду ЭДС индукции, которая возникнет в катушке, если вновь включить прежнее магнитное поле и начать вращать в нём катушку с угловой скоростью 3 рад/с. Ось вращения перпендикулярна оси катушки. Ответ приведите в вольтах.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
27
В горизонтальной трубке постоянного сечения, запаянной с одного конца, помещен столбик ртути длиной 15 см, который отделяет воздух в трубке от атмосферы. Трубку расположили вертикально запаянным концом вниз и нагрели на 60 К. При этом объем, занимаемый воздухом, не изменился. Давление атмосферы в лаборатории — 750 мм рт. ст. Какова температура воздуха в лаборатории?
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
28
В электрической цепи, показанной на рисунке, ЭДС источника тока равна 12 В, емкость конденсатора 2 мФ, индуктивность катушки 5 мГн, сопротивление лампы 5 Ом и сопротивление резистора 3 Ом.
В начальный момент времени ключ К замкнут. Какая энергия выделится в лампе после размыкания ключа? Внутренним сопротивлением источника тока, и проводов пренебречь.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
29
На экране наблюдается спектр с помощью дифракционной решетки, имеющей 500 штрихов на миллиметр. Расстояние от решетки до экрана Спектральная линия в спектре первого порядка находится на расстоянии
от центра экрана. Определите длину волны наблюдаемой спектральной линии.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
30
Тонкий однородный стержень АВ шарнирно закреплён в точке А и удерживается горизонтальной нитью ВС (см. рис.). Трение в шарнире пренебрежимо мало. Масса стержня m = 1 кг, угол его наклона к горизонту α = 30°. Найдите модуль силы
действующей на стержень со стороны шарнира. Сделайте рисунок, на котором укажите все силы, действующие на стержень.
Какие законы Вы используете для описания равновесия стержня? Обоснуйте их применение к данному случаю.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
Завершить тестирование, свериться с ответами, увидеть решения.
Решение и ответы заданий демонстрационного варианта ВПР 5 класс по математике. Образец всероссийской проверочной работы 2023 год.
Задание 1.
Выполните сложение:
frac{2}{7}+frac{3}{7}
ИЛИ
Представьте в виде обыкновенной дроби число 2frac{3}{8}.
Задание 2.
Найдите наибольшее из чисел:
9,8 10,14 10,3 9,4
Задание 3.
В автобусе 51 место для пассажиров. Две трети мест уже заняты. Сколько свободных мест в автобусе?
Задание 4.
Каким числом нужно заменить букву А, чтобы получилось верное равенство?
А : 31 = 26
Задание 5.
Принтер печатает 72 страницы за 3 минуты. За сколько минут этот принтер напечатает 120 страниц?
Запишите решение и ответ.
Задание 6.
Найдите значение выражения 4800:24 − 4⋅(81− 63):2. Запишите решение и ответ.
Задание 7.
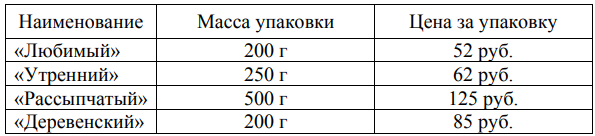
В магазине продаётся несколько видов творога в различных упаковках и по различной цене. В таблице показана масса каждой упаковки и её цена. Определите, килограмм какого творога стоит дешевле других. В ответ запишите стоимость одного килограмма этого творога.
Запишите решение и ответ.
Задание 8.
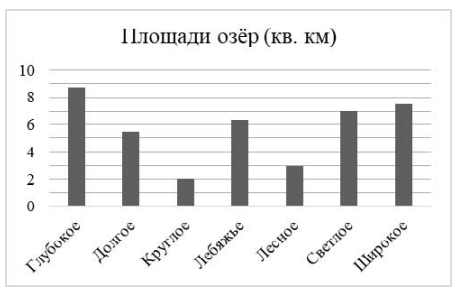
На диаграмме представлены площади нескольких озёр. Ответьте на вопросы.
1) Какое из этих озер занимает пятое место по площади?
2) На сколько квадратных километров площадь озера Светлое больше площади озера Лесное?
Задание 9.
Из одинаковых кубиков сложили параллелепипед (рис. 1). После этого сверху вытащили ровно один кубик (рис. 2).
Сколько кубиков осталось в фигуре, изображённой на рис. 2?
Задание 10.
В одном из районов города кварталы имеют форму квадратов со стороной 100 м. Ширина всех улиц равна 30 м.
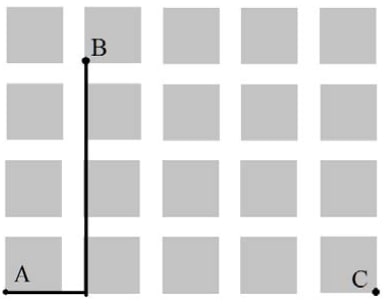
2) Нарисуйте на плане какой-нибудь маршрут, который начинается и заканчивается в точке С и имеет протяжённость не меньше 1 км, но не больше 1 км 200 м.
Источник варианта: fioco.ru
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 5 / 5. Количество оценок: 1
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
В задании №1 ЕГЭ по физике необходимо решить простую задачу по кинематике. Это может быть нахождение пути, скорости, ускорения тела или объекта по графику из условия.
Задание EF18273
Верхнюю точку моста радиусом 100 м автомобиль проходит со скоростью 20 м/с. Центростремительное ускорение автомобиля равно…
Алгоритм решения
- Записать исходные данные.
- Записать формулу для определения искомой величины.
- Подставить известные данные в формулу и произвести вычисления.
Решение
Записываем исходные данные:
- Радиус окружности, по которой движется автомобиль: R = 100 м.
- Скорость автомобиля во время движения по окружности: v = 20 м/с.
Формула, определяющая зависимость центростремительного ускорения от скорости движения тела:
Подставляем известные данные в формулу и вычисляем:
Ответ: 4
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF18741
Мальчик бросил стальной шарик вверх под углом к горизонту. Пренебрегая сопротивлением воздуха, определите, как меняются по мере приближения к Земле модуль ускорения шарика и горизонтальная составляющая его скорости?
Для каждой величины определите соответствующий характер изменения:
- увеличивается
- уменьшается
- не изменяется
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Алгоритм решения
- Сделать чертеж, иллюстрирующий ситуацию.
- Записать формулы, определяющие указанные в условии задачи величины.
- Определить характер изменения физических величин, опираясь на сделанный чертеж и формулы.
Решение
Выполняем чертеж:
Модуль ускорения шарика |g| — величина постоянная, так как ускорение свободного падения не меняет ни направления, ни модуля. Поэтому модуль ускорения не меняется (выбор «3»).
Горизонтальная составляющая скорости шарика определяется формулой:
vx = v0 cosα
Угол, под которым было брошено тело, поменяться не может. Начальная скорость броска тоже. Больше ни от каких величин горизонтальная составляющая скорости не зависит. Поэтому проекция скорости на ось ОХ тоже не меняется (выбор «3»).
Ответом будет следующая последовательность цифр — 33.
Ответ: 33
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF17519
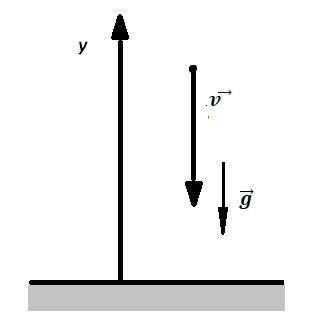
С аэростата, зависшего над Землёй, упал груз. Через 10 с он достиг поверхности Земли. На какой высоте находился аэростат? Сопротивление воздуха пренебрежимо мало.
Алгоритм решения
- Записать исходные данные.
- Сделать чертеж, иллюстрирующий ситуацию.
- Записать формулу для определения искомой величины в векторном виде.
- Записать формулу для определения искомой величины в векторном виде.
- Подставить известные данные и вычислить скорость.
Решение
Записываем исходные данные:
- Начальная скорость v0 = 0 м/с.
- Время падения t = 10 c.
Делаем чертеж:
Перемещение (высота) свободно падающего тела, определяется по формуле:
В скалярном виде эта формула примет вид:
Учтем, что начальная скорость равна нулю, а ускорение свободного падения противоположно направлено оси ОУ:
Относительно оси ОУ груз совершил отрицательное перемещение. Но высота — величина положительная. Поэтому она будет равна модулю перемещения:
Вычисляем высоту, подставив известные данные:
Ответ: 500
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF17483
Тело брошено вертикально вверх с начальной скоростью 10 м/с. Если сопротивление воздуха пренебрежимо мало, то через одну секунду после броска скорость тела будет равна…
Алгоритм решения
- Записать исходные данные.
- Сделать чертеж, иллюстрирующий ситуацию.
- Записать формулу для определения скорости тела в векторном виде.
- Записать формулу для определения скорости тела в скалярном виде.
- Подставить известные данные и вычислить скорость.
Решение
Записываем исходные данные:
- Начальная скорость v0 = 10 м/с.
- Время движения t = 1 c.
Делаем чертеж:
Записываем формулу для определения скорости тела в векторном виде:
v = v0 + gt
Теперь запишем эту формулу в скалярном виде. Учтем, что согласно чертежу, вектор скорости сонаправлен с осью ОУ, а вектор ускорения свободного падения направлен в противоположную сторону:
v = v0 – gt
Подставим известные данные и вычислим скорость:
v = 10 –10∙1 = 0 (м/с)
Ответ: 0
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF17992
Начальная скорость автомобиля, движущегося прямолинейно и равноускоренно, равна 5 м/с. После прохождения расстояния 40 м его скорость оказалась равной 15 м/c. Чему равно ускорение автомобиля?
Алгоритм решения
- Записать исходные данные.
- Записать формулу, связывающую известные из условия задачи величины.
- Выразить из формулы искомую величину.
- Вычислить искомую величину, подставив в формулу исходные данные.
Решение
Запишем исходные данные:
- Начальная скорость v0 = 5 м/с.
- Конечная скорость v = 15 м/с.
- Пройденный путь s = 40 м.
Формула, которая связывает ускорение тела с пройденным путем:
Так как скорость растет, ускорение положительное, поэтому перед ним в формуле поставим знак «+».
Выразим из формулы ускорение:
Подставим известные данные и вычислим ускорение автомобиля:
Ответ: 2,5
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF17553
На рисунке представлены графики зависимости пройденного пути от времени для двух тел. Скорость второго тела v2 больше скорости первого тела v1 в n раз, где n равно…
Алгоритм решения
- Выбрать любой временной интервал.
- Выбрать для временного интервала начальные и конечные пути для каждого из графиков.
- Записать формулу скорости и вычислить ее для 1 и 2 тела.
- Найти n — отношение скорости второго тела к скорости первого тела
Решение
Рассмотрим графики во временном интервале от 0 до 4 с. Ему соответствуют следующие данные:
- Для графика 1: начальный путь s10 = 0 м. Конечный путь равен s1 = 80 м.
- Для графика 2: начальный путь s20 = 0 м. Конечный путь равен s2 = 120 м.
Скорость определяется формулой:
Так как начальный момент времени и скорость для обоих тел нулевые, формула примет вид:
Скорость первого тела:
Скорость второго тела:
Отношение скорости второго тела к скорости первого тела:
Ответ: 1,5
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF18831
На рисунке представлен график зависимости модуля скорости υ автомобиля от времени t. Определите по графику путь, пройденный автомобилем в интервале времени от t1=20 с до t2=50 с.
Алгоритм решения
- Охарактеризовать движение тела на различных участках графика.
- Выделить участки движения, над которыми нужно работать по условию задачи.
- Записать исходные данные.
- Записать формулу определения искомой величины.
- Произвести вычисления.
Решение
Весь график можно поделить на 3 участка:
- От t1 = 0 c до t2 = 10 с. В это время тело двигалось равноускоренно (с положительным ускорением).
- От t1 = 10 c до t2 = 30 с. В это время тело двигалось равномерно (с нулевым ускорением).
- От t1 = 30 c до t2 = 50 с. В это время тело двигалось равнозамедленно (с отрицательным ускорением).
По условию задачи нужно найти путь, пройденный автомобилем в интервале времени от t1 = 20 c до t2 = 50 с. Этому времени соответствуют два участка:
- От t1 = 20 c до t2 = 30 с — с равномерным движением.
- От t1 = 30 c до t2 = 50 с — с равнозамедленным движением.
Исходные данные:
- Для первого участка. Начальный момент времени t1 = 20 c. Конечный момент времени t2 = 30 с. Скорость (определяем по графику) — 10 м/с.
- Для второго участка. Начальный момент времени t1 = 30 c. Конечный момент времени t2 = 50 с. Скорость определяем по графику. Начальная скорость — 10 м/с, конечная — 0 м/с.
Записываем формулу искомой величины:
s = s1 + s2
s1 — путь тела, пройденный на первом участке, s2 — путь тела, пройденный на втором участке.
s1 и s2 можно выразить через формулы пути для равномерного и равноускоренного движения соответственно:
Теперь рассчитаем пути s1 и s2, а затем сложим их:
s1 + s2 = 100 + 100 = 200 (м)
Ответ: 200
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF17612
Тело начинает двигаться из состояния покоя с ускорением 4 м/с2. Через 2 с его скорость будет равна…
Алгоритм решения
- Записать исходные данные в определенной системе отсчета.
- Записать формулу ускорения.
- Выразить из формулы ускорения скорость.
- Найти искомую величину.
Решение
Записываем исходные данные:
- Тело начинает двигаться из состояния покоя. Поэтому его начальная скорость v0 = 0 м/с.
- Ускорение, с которым тело начинает движение, равно: a = 4 м/с2.
- Время движения согласно условию задачи равно: t = 2 c.
Записываем формулу ускорения:
Так как начальная скорость равна 0, эта формула принимает вид:
Отсюда скорость равна:
v = at
Подставляем имеющиеся данные и вычисляем:
v = 4∙2 = 8 (м/с)
Ответ: 8
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF17727
Два автомобиля движутся по прямому шоссе, первый — со скоростью v, второй — со скоростью –4v. Найти скорость второго автомобиля относительно первого.
Алгоритм решения
- Записать данные в определенной системе отсчета.
- Изобразить графическую модель ситуации задачи.
- Записать классический закон сложения скоростей в векторном виде.
- Записать классический закон сложения скоростей в векторном виде применительно к условиям задачи.
- Найти искомую величину.
Решение
Записываем данные относительно Земли:
- Скорость первого автомобиля относительно оси ОХ: v1 = v.
- Скорость второго автомобиля относительно оси ОХ: v2 = –4v.
Изображаем графическую модель ситуации. Так как у второго автомобиля перед вектором скорости стоит знак «–», первый и второй автомобили движутся во взаимно противоположных направлениях.
Записываем закон сложения скоростей в векторном виде:
v′ = v + u
v′ — скорость второго автомобиля относительно оси ОХ (v2), v — скорость второго автомобиля относительно системы отсчета, связанной с первым автомобилем, u — скорость движения первого автомобиля относительно оси ОХ (v1).
Закон сложения скоростей в векторном виде применительно к условиям задачи будет выглядеть так:
v2 = v + v1
Отсюда:
v = v2 — v1 = –4v – v = –5v
Ответ: -5v
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF17518
Два автомобиля движутся в одном направлении. Относительно Земли скорость первого автомобиля 110 км/ч, второго 60 км/ч. Чему равен модуль скорости первого автомобиля в системе отсчёта, связанной со вторым автомобилем?
Алгоритм решения
- Записать данные в определенной системе отсчета.
- Изобразить графическую модель ситуации задачи.
- Записать классический закон сложения скоростей в векторном виде.
- Выбрать систему отсчета.
- Записать классический закон сложения скоростей в скалярном виде.
- Найти искомую величину.
Решение
Записываем данные относительно Земли:
- Скорость первого автомобиля относительно неподвижной системы отсчета: v1 = 110 км/ч;
- Скорость второго автомобиля относительно Земли: v2 = 60 км/ч.
Изображаем графическую модель ситуации:
Записываем закон сложения скоростей в векторном виде:
v′ = v + u
v′ — скорость автомобиля относительно земли (v1), v — скорость второго автомобиля относительно системы отсчета, связанной со вторым автомобилем, u — скорость движения второго автомобиля относительно земли (v2).
По условию задачи в качестве системы отсчета нужно выбрать второй автомобиль. Так как система отсчета, связанная со вторым автомобилем, и первый автомобиль движутся в одном направлении, классический закон сложения скоростей в скалярном виде будет выглядеть так:
v’ = v + u
Отсюда скорость первого автомобиля в системе отсчёта, связанной со вторым автомобилем:
v = v’ – u = v1 – v2 = 110 – 60 = 50 (км/ч).
По условию задачи ответом должен быть модуль этой скорости. Модуль числа 50 есть 50.Ответ: 50
pазбирался: Алиса Никитина | обсудить разбор | оценить
ГДЗ по математике для 5 класса Виленкина помогает ученикам справиться со сложными номерами. Автора Виленкина используют уже несколько десятков лет в пятых и шестых классах, ведь его система зарекомендовала себя в методике преподавания.
Домашняя работа по математике требует много времени и сил. Онлайн-решебник экономит нервы учеников и их родителей, которые бывают слишком заняты, чтобы заниматься с ребенком. Также нет нужны работать дополнительно с репетитором или оставаться у учителя после уроков, чтобы получать хорошие оценки. К ответам приложены полезные комментарии, объясняющие ход решения.
Издательство «Мнемозина» выпускает популярные методички, пособия, учебники по разным предметам, одним из самых успешных стало издание Виленкина, Жохова, Чеснокова, Шварцбурда. ГДЗ включает 1 часть и 2 часть, в соответствии с новой версией учебника.
1 ЧАСТЬ
Выберите номер
2 ЧАСТЬ
Выберите номер
В сборник вошли ответы и пояснения к более чем сорока темам, изучающим в курсе математики 5 класса. Раскрываются следующие темы: дроби, действия с числами, площади, периметры, объемы и так далее. Благодаря этому ребенок может не только узнать ответы и понять, как их получить, чтобы в будущем проблем не было. Ученик может вернуться в любой момент к волнующей теме и повторить ее.
Не секрет, что у школьника могут быть проблемы с учебой из-за общей сложности дисциплины, недопониманий с педагогом или одноклассниками, отсутствия мотивации и возможности у близких помогать ребенку. Родители часто не участвуют в учебе детей, потому что загружены работой и бытовыми хлопотами или в силу возраста не помнят правила решения задач и примеров.
По учебнику Виленкина и ключам к нему можно не только делать домашнюю работу, но и готовиться к самостоятельным и контрольным работам. Пробелы в темах могут быть своевременно восполнены, обращаясь к пояснениям. С помощью книги можно достичь успехов в учебе и быстро безошибочно писать любые проверочные работы.
С уверенностью можно сказать, что математика является одним из самых сложных предметов для школьников, поэтому большинство боится опозориться перед сверстниками и учителем. Если на уроке можно уточнить вопрос, то дома ребенок остается один на один с проблемой. ГДЗ по математике 5 класс Учебник Виленкин содержит много актуальной информации, замечаний, подсказок и решений, поэтому станет незаменимым помощником в обучении любого пятиклассника.
За это задание ты можешь получить 1 балл. Уровень сложности: базовый.
Средний процент выполнения: 72.6%
Ответом к заданию 3 по физике может быть целое число или конечная десятичная дробь.
Разбор сложных заданий в тг-канале
Задачи для практики
Задача 1
Малый поршень гидропресса за один ход опускается на 0,2 м, а большой поршень при этом поднимается на 1 см. С какой силой действует пресс на зажатое в нём тело, если на малый поршень действует сила 500 Н? Ответ выразите в (кН).
Решение
Дано:
$h_1=0.2$м
$h_2=0.01$м
$F_1=500H$
$F_2-?$
Решение:
Работа по перемещению малого поршня $A_м=F_1·h_1$(1), равна работе по перемещению большого поршня $A_б=F_2·h_2$(2), тогда имеем $A_м=A_б$ или $F_1·h_1=F_2·h_2$, откуда $F_2={F_1·h_1}/{h_2}={500·0.2}/{0.01}=10000=10$кН.
Ответ: 10
Задача 2
Вес тела в воде в 3 раза меньше, чем в воздухе. Какова плотность тела? Ответ выразите в (·103 кг/м3).
Решение
Дано:
$p_1=mg$
$p_2={mg}/{3}$
$ρ_в=1000{кг}/{м^3}$
$ρ_т-?$
Решение:
Сила Архимеда равна: $F_{арх}=p_1-p_2=ρ_в·g·V_т$(1). $mg-{mg}/{3}=ρ_в·g·V_т$, откуда ${2mg}/{3}=ρ_в·g·V_т⇒{m}/{V_т}={3ρ_в}/{2}$(2). Учитывая, что плотность тела $ρ_т={m}/{V_т}=1.5ρ_в=1.5·10^3{кг}/{м^3}$
Ответ: 1.5
Задача 3
Матрос, стоящий на верхней палубе корабля, определил, что расстояние между следующими друг за другом гребнями волн равно 8 м. Кроме того, он подсчитал, что за 60 с мимо него прошло 23 волновых гребня. Какова скорость распространения волн? Корабль находился на стоянке. Ответ выразите в (м/с) и округлите до десятых.
Решение
Дано:
$λ=8$м
$t=60$с
$N=23$
$υ-?$
Решение:
Расстояние между соседними гребнями называется длиной волны $λ:λ=υ·t$(1), где $υ$ — скорость волны; $T={t}/{N}$(2) — период.
Подставим (2) в (1) и найдем $υ$: $λ={υ·t}/{N}⇒υ={λN}/{t}={8·23}/{60}=3.066м/с$.
Ответ: 3.1
Задача 4
Если к некоторому грузу, колеблющемуся на пружине, подвесить дополнительно грузик массой 150 г, то частота колебаний уменьшится в 2 раза. Какой массы груз был первоначально подвешен к пружине? Ответ выразите в (г).
Решение
Дано:
$m_g=0.15$кг
$υ_2={υ_1}/{2}$
$m_0-?$
Решение:
${tableT=2π√{{m}/{K}}; T={1}/{υ};$ $⇒$ ${table.{1}/{υ_1}=2π√{{m_0}/{K}}; .{1}/{υ_2}=2π√{{m_0+m_g}/{K}};$
${υ_2}/{υ_1}=√{{m_0}/{m_0+m
_g}}; 0.25={m_0}/{m_0+m_g}$.
$0.25·m_0+0.25·m_g=m_0; m_0={0.25}/{0.75}·m_g=50$г
Ответ: 50
Задача 5
Объём плавающего в океане айсберга равен 5,1 км3. Какова плотность льда, если объём надводной части айсберга 0,4 км3, а плотность воды в океане 1,02 г/см3? Ответ выразите и округлите до сотых (г/см3).
Решение
Дано:
$V_A=5.1км^3$
$V_{возд}=0.4км^3$
$ρ_в=1.02г/см^3$
$ρ_л-?$
Решение:
1) По второму закону Ньютона $mg=F_{арх}$
$ρ_л·V_A·g=ρ_вg·(V_A-V_{возд})$
$ρ_л={ρ_вg·(V_A-V_{возд})}/{V_Ag}={1.02(5.1-0.4)}/{5.1}=0.94г/{см^3}$
Ответ: 0.94
Задача 6
Вес груза в воздухе равен 2 Н. При опускании груза в воду на него действует сила Архимеда, равная 0,5 Н. Каков вес груза в воде? Ответ выразите в (H).
Решение
Дано:
$P_{возд}=2H$
$F_{арх}=0.5H$
$P_{вода}-?$
Решение:
По закону Архимеда вычислим: $P_{вода}=P_{возд}-F_{арх}=2-0.5=1.5H$.
Ответ: 1.5
Задача 7
Аквариум кубической формы с высотой стенки 1 м полностью заполнен водой. Каково давление воды на стенку аквариума? Ответ выразите в (кПа).
Решение
Дано:
$l=1$м
$P_{на стенку}-?$
Решение:
$P_{на стенку}=P_{ср}={ρgh}/{2}={10000}/{2}=5000$Па. $P_{на стенку}=5$кПа.
Ответ: 5
Задача 8
Волна распространяется вдоль резинового шнура со скоростью 4 м/с при частоте 5 Гц. Каково минимальное расстояние между точками шнура, которые одновременно проходят через положение равновесия, двигаясь при этом в одном направлении? Ответ выразите в (м).
Решение
Дано:
$υ=4$м/с
$v=5$Гц
$λ-?$
Решение:
$λ={υ}/{v}$ — по закону о гармонических колебаниях.
$λ={4}/{5}=0.8$м.
Ответ: 0.8
Задача 9
Тело массой 40 г взвешивают на весах с разными плечами. Когда оно находится на левой чашке весов, его можно уравновесить грузом массой 20 г. Грузом какой массы можно уравновесить тело, если его положить на правую чашку весов? Ответ выразите в (г).
Решение
Дано:
$m_0=4·10^{-2}$кг
$m_1=2·10^{-2}$кг
$m_2-?$
Решение:
${tablem_0·l_1=m_1·l_2; m_0·l_2=m_2·l_1;$
Составим уравнение на первое и второе взвешивание. Выразим: $m_0·{m_0·l_2}/{m_2}=m_1l_2⇒m_2={m_0^2}/{m_1}={16·10^{-4}}/{2·10^{-2}}=80$г
Ответ: 80
Задача 10
Медный цилиндр массой 3,56 кг полностью опущен в бензин. Определите действующую на него архимедову силу. Плотность меди равна 8900 кг/м3. Плотность бензина равна 700 кг/м3. Ответ выразить в (H).
Решение
Дано:
$m_м=3.56$кг
$ρ_м=8900кг/м^3$
$ρ_б=700кг/м^3$
$F_{арх}-?$
Решение:
На погруженное в жидкость тело, действует выталкивающая сила $F_{арх}=ρ_б·g·V_м=ρ_б·g·{m_м}/{ρ_м}$
$F_{арх}={700·10·3.56}/{8900}=2.8H$
Ответ: 2.8
Задача 11
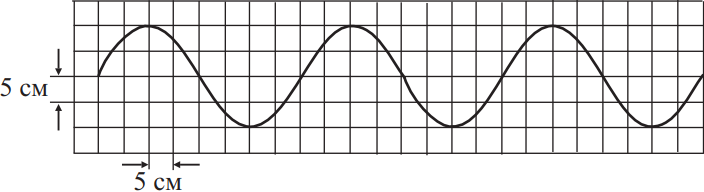
Учитель продемонстрировал распространение волны по длинному шнуру. В один из моментов времени шнур имел вид, представленный на рисунке. Скорость распространения колебаний по шнуру равна 2 м/с. С каким периодом колеблются частицы шнура? Ответ выразите в (с).
Решение
Дано:
$υ=2$м/с
$T-?$
Решение:
Из рисунка видно, что длина волны равна $λ=0.4$м. Частота колебаний равна отношению скорости распространения волны к длине волны, а период обратен частоте.
$T={λ}/{υ}={0.4}/{2}=0.2$с
Ответ: 0.2
Задача 12
Груз подвешен на лёгкой вертикальной пружине и совершает на ней колебания с циклической частотой ω = 10 рад/с, двигаясь по вертикали. Насколько растянется эта пружина, если аккуратно подвесить к ней тот же груз, не возбуждая колебаний? Ответ выразите в (см).
Решение
Дано:
$ω=10раз/с$
$g=10м/с^2$
$L-?$
Решение:
Жесткость пружины можно выразить как $k={mg}/{L}$(1), где $L$ — удлинение пружины под действием груза. Циклическая частота колебаний выражается как: $ω=√{{k}/{m}}=√{{g}/{L}}$(2). Тогда имеем: $ω^2={g}/{L}$, откуда $L={g}/{ω^2}={10}/{100}=0.1м=10см$
Ответ: 10
Задача 13
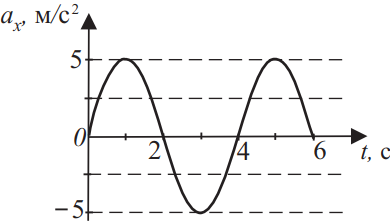
Тело массой 500 г колеблется так, что проекция его ускорения зависит от времени в соответствии с графиком, приведённом на рисунке. Чему равна проекция силы на ось Ox в момент времени 3 с? Ответ выразите в (H).
Решение
Дано:
$m=0.5$кг
$t=3с$
$a_x=-5м/с^2$
$F_x-?$
Решение:
Проекция силы на ось Ох в момент времени 3с определяется выражением: $F_x=ma_x=0.5·(-5)=-2.5H$
Ответ: -2.5
Задача 14
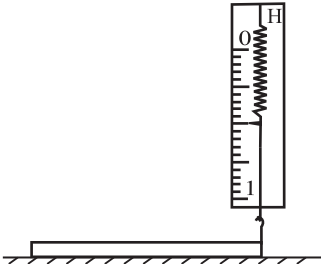
Для измерения массы однородного стержня ученик воспользовался динамометром так, как это представлено на рисунке. Чему равна масса стержня? Ответ выразите в (г).
Решение
Дано:
$F=0.5H$
$g≈10м/c^2$
$m-?$
Решение:
Согласно второго условия равновесия тел: сумма моментов сил, действующих на тело равна нулю: $∑↙{i=1}↖n{M_i}↖{→}=O$(1).
Момент силы — это произведение силы на плечо. Пусть $l$ — длина стержня. На стержень действуют две силы — сила тяжести $mg↖{→}$ и $F↖{→}$, тогда имеем: $M_1=M_2⇒{mg·l}/{2}=F·l⇒mg=2F⇒m={2F}/{g}$(2); $m={2·0.5}/{10}={1}/{10}=0.1кг=100г$
Ответ: 100
Задача 15
Какова частота звуковой волны длиной 34 см? Скорость звука в воздухе равна 340 м/с. Ответ выразите в (кГц).
Решение
Дано:
$λ=0.34$м
$υ=340$м/с
$ν-?$
Решение:
Частота звуковой волны определяется выражением: $ν={υ}/{λ}$, тогда $ν={340}/{0.34}=1000гц=1кГц$.
Ответ: 1
Задача 16
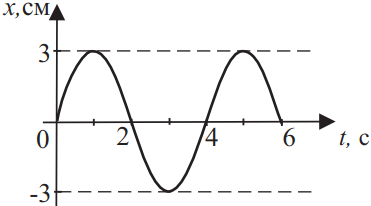
На рисунке представлена зависимость смещения пружинного маятника массой 200 г от времени. Какова потенциальная энергия в момент времени 1,5 с? В расчётах принять π2 ≈ 10. Ответ выразите в (мкДж).
Решение
Дано:
$m=0.2кг$
$t=1.5с$
$π^2=10$
$E_п-?$
Решение:
Потенциальная энергия равна: $E_п={kx^2}/{2}$(1), где $k$ — жесткость пружины, $x=x_m·sinωt=x_m·sin{2π}/{T}·t$(2), где $T$ — период колебаний пружинного маятника (из графика видно, что $T=4c$); $x_m=0.03м$ — амплитудное значение х.
Период колебаний пружинного маятника рассчитывается по формуле: $T=2π√{{m}/{R}}$(3), откуда найдем $k$: $T^2={4π^2m}/{k}⇒k={4π^2m}/{T^2}$(4)
Подставим числовые значения в (2) и в (4): $x=x_m·sin{2π}/{T}·t=0.03·sin{2π·1.5}/{4}=0.03·sin{3π}/{4}={0.03·√2}/{2}$. $k={4π^2m}/{T^2}={4·10·0.2}/{16}=0.5{Н}/{м}$.
Подставим числовые значения в (1): $E_п={kx^2}/{2}={0.5·(0.03·{√2}/{2})^2}/{2}={{0.0009·2·0.5}/{4}}/{2}={0.0009}/{8}=112.5·10^{-6}=112.5$мкДж.
Ответ: 112.5
Задача 17
Высота столба ртути ртутного барометра составляет 756 мм. Какова была бы высота столба подсолнечного масла масляного барометра при данном атмосферном давлении? Ответ выразите в (мм). Ответ запишите в целых числах. $p_p=13600{кг}/{м^3}$, $p_м=900{кг}/{м^3}$
Решение
Дано:
$h_p=756мм$
$p_p=13600{кг}/{м^3}$
$p_м=900{кг}/{м^3}$
$h_м-?$
Решение:
Давление столба ртути равно давлению столба подсолнечного масла: $p_p=p_м$(1), где $p_p=ρ_p·g·h_p$(2), $p_м=ρ_м·g·h_м$(3), где $ρ_p$ и $ρ_м$ — плотность ртути и подсолнечного масла.
Подставим (2) и (3) в (1) и найдем $h_м$: $ρ_p·g·h_p=ρ_м·g·h_м⇒h_м={ρ_p·h_p}/{ρ_м}$.
Подставим числовые значения в (4): $h_м={13600·756}/{900}=11424мм$
Ответ: 11424
Задача 18
Высота столба ртути ртутного барометра составляет 756 мм. Какова плотность жидкости жидкостного барометра, высота столба которого при данном атмосферном давлении равна 12 852 мм? Плотность ртути 13600 кг/м^3. Ответ выразите в (кг/м3).
Решение
Дано:
$h_p=756мм$
$p_p=13600{кг}/{м^3}$
$h_ж=12852мм$
$p_ж-?$
Решение:
Давление столба ртути равно давлению столба жидкости: $p_p=p_ж$(1), где $p_p=p_p·g·h_p$(2), $p_ж=p_ж·g·h_ж$(3), где $p_p$ и $p_ж$ — плотность ртути и жидкости жидкостного барометра.
Подставим (2) и (3) в (1) и найдем $p_ж$: $p_p·g·h_p=p_ж·g·h_ж⇒p_p·h_p=p_ж·h_ж$.
Подставим числовые значения в (4): $p_ж={13600·756}/{12852}=800{кг}/{м^3}$
Ответ: 800