Задание 1
Налог на доходы составляет 13% от заработной платы. Заработная плата Ивана Кузьмича равна 13000 рублей. Какую сумму он получит после вычета налога на доходы? Ответ дайте в рублях.
Ответ: 11310
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$100-13=87$$% от начальной
$$13000 — 100$$%
$$x — 87$$%
$$x=frac{13000cdot87}{100}=11310$$
Задание 2
На диаграмме показано количество посетителей сайта РИА Новости во все дни с 10 по 29 ноября 2009 года. По горизонтали указываются дни месяца, по вертикали – количество посетителей сайта за данный день. Определите по диаграмме, каково наименьшее суточное количество посетителей сайта РИА Новости за указанный период.
Ответ: 400 000
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 3
На клетчатой бумаге с размером клетки $$sqrt{10}times sqrt{10}$$ изображён четырёхугольник ABCD. Найдите его периметр.
Ответ: 40
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
a — сторона;
$$a=sqrt{3^{2}+1^{2}}cdot sqrt{10}=10Rightarrow P=4cdot10=40$$
Задание 4
В магазине стоят два платёжных автомата. Каждый из них может быть неисправен с вероятностью 0,09 независимо от другого автомата. Найдите вероятность того, что хотя бы один автомат исправен.
Ответ: 0,9919
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Противоположное событие — оба не работают: $$P=0,09^{2}=0,0081$$ $$Rightarrow$$ вероятность того, что хотя бы один работает: $$1-0,0081=0,9919$$
Задание 5
В треугольнике ABC CH – высота, AD – биссектриса, O – точка пересечения прямых CH и AD, угол BAС равен 66°. Найдите угол AOC. Ответ дайте в градусах.
Ответ: $$123^{circ}$$
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$angle BAC=66^{circ}$$ $$Rightarrow$$ $$angle OAH=frac{angle BAC}{2}=33^{circ}Rightarrow$$ $$angle AOH=90^{circ}-angle OAH=90^{circ}-33^{circ}=57^{circ}Rightarrow$$ $$angle AOC=180^{circ}-57^{circ}=123^{circ}$$
Задание 6
На рисунке изображён график $$y={f}’x$$ – производной функции f (x). На оси абсцисс отмечены семь точек: x1, x2, x3, x4, x5, x6, x7 . Сколько из этих точек лежит на промежутках возрастания функции f (x)?
Ответ: 2
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Промежутки возрастания функции там, где график производной над осью Ox: x1; x2 $$Rightarrow$$ 2 точки.
Задание 7
В цилиндрический сосуд налили 2000 см3 воды. Уровень жидкости оказался равным 12 см. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 9 см.
Чему равен объем детали? Ответ выразите в см3.
Ответ: 1500
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
V=Sосн·h $$Rightarrow$$ Sосн=$$frac{V}{h}=frac{1000}{12}=frac{500}{3}$$
Vдет=$$frac{500}{3}cdot9=1500$$
Задание 8
Найдите значение выражения: $$sqrt{8}-sqrt{32}sin^{2}frac{11pi}{8}$$
Ответ: -2
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$sqrt{8}-sqrt{32}sin^{2}frac{11pi}{8}=sqrt{8}(1-sqrt{4}sin^{2}frac{11pi}{8})=$$ $$=sqrt{8}(1-2sin^{2}frac{11pi}{8})=sqrt{8}cdot cos(2cdot frac{11pi}{8})=$$ $$=sqrt{8}cdot cos frac{11pi}{4}=sqrt{8}cdot cos(2pi+frac{3pi}{4}) =$$ $$=sqrt{8}cdot cosfrac{3pi}{4}=sqrt{8}cdot(-frac{sqrt{2}}{2})=-frac{4}{2}=-2$$
Задание 9
Высота над землёй подброшенного вверх мяча меняется по закону $$h(t)=1,4+14t-5t^{2}$$, где h – высота в метрах, t – время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее 8 метров?
Ответ: 1,6
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$1,4+14t-5t^{2}geq8$$ $$-5t^{2}+14t-6,6geq0$$ $$5t^{2}-14t+6,6leq0$$ $$D=196-132=64$$ $$t_{1}=frac{14+8}{10}=2,2$$ $$t_{2}=frac{14-8}{10}=0,6$$ $$2,2-0,6=1,6$$
Задание 10
Из одной точки круговой трассы, длина которой равна 44 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 112 км/ч, и через 48 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.
Ответ: 57
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Пусть х — скорость второго авто: $$frac{44}{112-x}=frac{48}{60}=frac{4}{5}$$ $$Leftrightarrow$$ $$44cdot5=112cdot4-4x$$ $$220-44=-4x$$ $$Leftrightarrow$$ $$x=57$$
Задание 11
Найдите наибольшее значение функции $$y=10cdot ln(x+5)-10x-21$$ на отрезке [‐4,5; 0].
Ответ: 19
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$${y}’=frac{10}{x+5}-10=0$$ $$frac{10-10x-50}{x+5}=0$$ $$Leftrightarrow$$ $$frac{-10x-40}{x+5}=0$$ $$x=4$$ $$xneq -5$$ $$y=10cdot ln(-4+5)-10cdot(-4)-21=19$$
Задание 12
Дано уравнение $$log_{2}^{2}(4cos^{2}x)-8log_{2}(2cos x)+3=0$$.
А) Решите уравнение.
Б) Укажите корни этого уравнения, принадлежащие отрезку $$left [ -frac{7pi}{2}; -2piright ]$$
Ответ: a) $$pm frac{pi}{4}+2pi k, (kin Z)$$; б) $$frac{-9pi}{4}$$
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 13
В основании пирамиды $$SABC$$ лежит равнобедренный треугольник $$ABC$$, в котором $$B=4$$, $$angle BAC=120^{circ}$$. Известно, что боковая грань $$SBC$$ перпендикулярна основанию $$ABC$$, $$SB=SC$$, а высота пирамиды, проведенная из точки $$S$$, равна $$2sqrt{11}$$ . На ребрах $$SB$$ и $$SC$$ отмечены соответственно точки $$K$$ и $$P$$ так, что $$BK:SK=CP=SP=1:3$$.
а) Докажите, что сечением пирамиды плоскостью $$APK$$ является прямоугольный треугольник.
б) Найдите объем меньшей части пирамиды, на которые её делит плоскость $$APK$$.
Ответ: $$frac{7sqrt{33}}{6}$$.
Задание 14
Решите неравенство $$frac{x+6sqrt x+28}{120}leq frac{2-sqrt x}{x-6sqrt x+8}$$.
Ответ: $$[0;4)cup (4;16)$$.
Задание 15
В параллелограмме $$ABCD$$ диагональ $$BD$$ равна стороне $$AD$$.
а) Докажите, что прямая $$CD$$ касается окружности ω, описанной около треугольника $$ABD$$.
б) Пусть прямая $$CB$$ вторично пересекает ω в точке $$K$$. Найдите $$KD:AC$$ при условии, что угол $$BDA$$ равен $$120^{circ}$$.
Ответ: $$sqrt3:sqrt7$$.
Задание 16
В начале января 2018 года планируется взять кредит в банке на 4 года на S млн. рублей, где S – целое число. Условия его возврата таковы:
‐ каждый июль долг возрастает на 10% по сравнению с началом текущего года;
— с августа по декабрь каждого года необходимо выплатить часть долга;
‐ в январе каждого года долг должен составлять часть кредита в соответствии со следующей таблицей:
| Начало года | 2018 | 2019 | 2020 | 2021 | 2022 |
| Долг (в млн. рублей) | S | 0,8S | 0,5S | 0,3S | 0 |
Найдите наименьшее значение S, при котором сумма выплат банку за все 4 года составит не менее 10 млн. рублей.
Ответ: 8
Задание 17
Найти все $$a$$, при каждом из которых система $$left{begin{matrix} y-ax=a+5,\ xy^2-x^2y-2xy+4x-4y+8=0; end{matrix}right.$$ имеет ровно два решения.
Ответ: $${-25;pm 1;0;1pm frac{4}{sqrt5}}$$.
Задание 18
Дано двузначное натуральное число.
а) Оказалось, что частное этого числа и суммы его цифр, равно 7. Найдите все такие числа.
б) Какие натуральные значения может принимать частное данного числа и суммы его цифр?
в) Какое наименьшее значение может принимать частное данного числа и суммы его цифр?
Ответ: а) 21;42;63;84; б) 2;3;4;5;6;7;8;9;10; в) 1,9.
Тренировочный вариант №204 профильного ЕГЭ
А. Ларин: Тренировочный вариант № 204.
При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
Версия для печати и копирования в MS Word
1
Дано уравнение
а) Решите уравнение.
б) Найдите корни этого уравнения, принадлежащие отрезку
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
2
В основании пирамиды SABC лежит равнобедренный треугольник АВС, в котором АВ = 4, Известно, что боковая грань SBC перпендикулярна основанию АВС, SB = SC, а высота пирамиды, проведенная из точки S, равна 112 . На ребрах SB и SC отмечены соответственно точки К и Р так, что ВК : SK = CP : SP = 1 : 3.
а) Докажите, что сечением пирамиды плоскостью АРК является прямоугольный треугольник.
б) Найдите объем меньшей части пирамиды, на которые её делит плоскость АРК.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
3
Решите неравенство:
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
4
В параллелограмме АВСD диагональ ВD равна стороне AD.
а) Докажите, что прямая СD касается окружности ω, описанной около треугольника АВD.
б) Пусть прямая СВ вторично пересекает ω в точке К. Найдите КD : AC при условии, что угол ВDA равен
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
5
В начале января 2018 года планируется взять кредит в банке на 4 года на S млн. рублей, где S — целое число. Условия его возврата таковы:
— каждый июль долг возрастает на 10% по сравнению с началом текущего года;
— с августа по декабрь каждого года необходимо выплатить часть долга;
— В январе каждого года долг должен составлять часть кредита в соответствии со следующей таблицей:
| Начало года | 2018 | 2019 | 2020 | 2021 | 2022 |
| Долг (в млн.
рублей) |
S | 0,8S | 0,5S | 0,3S | 0 |
Найдите наименьшее значение S, при котором сумма выплат банку за все 4 года составит не менее 10 млн. рублей.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
6
Найдите все значения параметра а, при каждом из которых система
имеет ровно два решения.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
7
Дано двузначное натуральное число.
а) Оказалось, что частное этого числа и суммы его цифр, равно 7. Найдите все такие числа.
б) Какие натуральные значения может принимать частное данного числа и суммы его цифр?
в) Какое наименьшее значение может принимать частное данного числа и суммы его цифр?
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
Завершить тестирование, свериться с ответами, увидеть решения.
28
Сен 2017
Категория: 14 (С3) НеравенстваТ/P A. Ларина
Елена Репина
2017-09-28
2017-09-28
Смотрите также №13; №14; №16; №17; №18; №19 Тренировочной работы №204 А. Ларина.
15. Решите неравенство
Решение:
Замечаем, что – положительная величина, и применяем метод замены множителей к знаменателю:
Ответ:
Автор: egeMax |
Нет комментариев
Чтобы не потерять страничку, вы можете сохранить ее у себя:
Печать страницы
Добавить комментарий
- Материалы для подготовки к ЕГЭ
-
- Рубрики
- 01 Геометрия (13)
- 02 Стереометрия (9)
- 03 Теория вероятностей ч.1 (1)
- 04 Теория вероятностей ч.2 (1)
- 05 Простейшие уравнения (5)
- 06 Вычисления (5)
- 07 Производная, ПО (4)
- 08 «Прикладные» задачи (5)
- 09 Текстовые задачи (7)
- 10 Графики функций (7)
- 11 Исследование функции (2)
- 12 (С1) Уравнения (78)
- 13 (С2) Стереометр. задачи (94)
- 14 (С3) Неравенства (89)
- 15 (С4) Практич. задачи (71)
- 16 (С5) Планиметр. задачи (86)
- 17 (С6) Параметры* (79)
- 18 (С7) Числа, их свойства (38)
- A1 Простейшие текст/задачи (нет в ЕГЭ-22) (3)
- A2 Читаем графики (нет в ЕГЭ-22) (1)
- Видеоуроки (44)
- ГИА (11)
- II часть (11)
- ЕГЭ (диагностич. работы) (70)
- Иррациональные выражения, уравнения и неравенства (15)
- Логарифмы (39)
- МГУ (12)
- Метод интервалов (4)
- Метод рационализации (18)
- Модуль (9)
- Параметр (40)
- Переменка (5)
- Планиметрия (60)
- Показательные выражения, уравнения и неравенства (8)
- Разложение на множители (1)
- Рациональные выражения, уравнения и неравенства (10)
- Справочные материалы (92)
- Стереометрия (52)
- Т/P A. Ларина (443)
- Текстовые задачи (12)
- Теория чисел (2)
- Тесты по темам (80)
- Тригонометрические выражения, уравнения и неравенства (43)
- Функции и графики (10)
- Дружественные сайты
Сайт А. Ларина
ЕгэТренер – О. Себедаш
Математика?Легко!
Егэ? Ок! – И. Фельдман
- Свежие записи
- Тест «Гиперболы»
- Тест. Графики функций. Комбинированные задачи
- 10. Графики функций. Комбинированные задачи
- Тест. Тригонометрические функции
- 10. Тригонометрическая функция
- Тест. Кусочно-линейная функция
- 10. Кусочно-линейная функция
- Архивы Архивы
-
Главная
-
mrMathlesson Виктор Осипов
-
Разбор Варианта Алекса Ларина №204 ЕГЭ 2018 (№16-19).
Просмотров: 3 211
Если вам понравилось бесплатно смотреть видео разбор варианта алекса ларина №204 егэ 2018 (№16-19). онлайн которое загрузил mrMathlesson Виктор Осипов 27 сентября 2017 длительностью 00 ч 33 мин 16 сек в хорошем качестве, то расскажите об этом видео своим друзьям, ведь его посмотрели 3 211 раз.
Ира Ловягина
4 года назад
Почему в 18 задании (-4/x^2)*x заменили на m^2, если должно быть 2m?
Марсэль Назиров
4 года назад
По-моему, тут что-то не так с таймингами))
AngryBroPlay
5 лет назад
В 18 задании в уравнении прямой можно было сделать так: y=a(x+1)+5. Из чего следует, что прямая проходит через точку (-1; 5) и имеет угловой коэффициент а. Остаётся её просто покрутить вокруг точки и получить ответы.
Boost
5 лет назад
Всё очень здорово, огромное спасибо. Только я 17 не совсем понял. Нельзя ли поподробнее?
Legend Innzcore
5 лет назад
Снимите пожалуйста 151 вариант.
senbonzxcura
5 лет назад
Будет ли 151 вариант?
Skip to content
Тренировочный вариант №204 профильного ЕГЭadmin2023-03-03T20:47:31+03:00
Используйте LaTeX для набора формулы
Задание 1
Налог на доходы составляет 13% от заработной платы. Заработная плата Ивана Кузьмича равна 13000 рублей. Какую сумму он получит после вычета налога на доходы? Ответ дайте в рублях.
Ответ: 11310
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Скрыть
$$100-13=87$$% от начальной
$$13000 — 100$$%
$$x — 87$$%
$$x=frac{13000cdot87}{100}=11310$$
Задание 2
На диаграмме показано количество посетителей сайта РИА Новости во все дни с 10 по 29 ноября 2009 года. По горизонтали указываются дни месяца, по вертикали – количество посетителей сайта за данный день. Определите по диаграмме, каково наименьшее суточное количество посетителей сайта РИА Новости за указанный период.
Ответ: 400 000
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 3
На клетчатой бумаге с размером клетки $$sqrt{10}times sqrt{10}$$ изображён четырёхугольник ABCD. Найдите его периметр.
Ответ: 40
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Скрыть
a — сторона;
$$a=sqrt{3^{2}+1^{2}}cdot sqrt{10}=10Rightarrow P=4cdot10=40$$
Задание 4
В магазине стоят два платёжных автомата. Каждый из них может быть неисправен с вероятностью 0,09 независимо от другого автомата. Найдите вероятность того, что хотя бы один автомат исправен.
Ответ: 0,9919
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Скрыть
Противоположное событие — оба не работают: $$P=0,09^{2}=0,0081$$ $$Rightarrow$$ вероятность того, что хотя бы один работает: $$1-0,0081=0,9919$$
Задание 5
В треугольнике ABC CH – высота, AD – биссектриса, O – точка пересечения прямых CH и AD, угол BAС равен 66°. Найдите угол AOC. Ответ дайте в градусах.
Ответ: $$123^{circ}$$
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Скрыть
$$angle BAC=66^{circ}$$ $$Rightarrow$$ $$angle OAH=frac{angle BAC}{2}=33^{circ}Rightarrow$$ $$angle AOH=90^{circ}-angle OAH=90^{circ}-33^{circ}=57^{circ}Rightarrow$$ $$angle AOC=180^{circ}-57^{circ}=123^{circ}$$
Задание 6
На рисунке изображён график $$y={f}’x$$ – производной функции f (x). На оси абсцисс отмечены семь точек: x1, x2, x3, x4, x5, x6, x7 . Сколько из этих точек лежит на промежутках возрастания функции f (x)?
Ответ: 2
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Скрыть
Промежутки возрастания функции там, где график производной над осью Ox: x1; x2 $$Rightarrow$$ 2 точки.
Задание 7
В цилиндрический сосуд налили 2000 см3 воды. Уровень жидкости оказался равным 12 см. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 9 см.
Чему равен объем детали? Ответ выразите в см3.
Ответ: 1500
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Скрыть
V=Sосн·h $$Rightarrow$$ Sосн=$$frac{V}{h}=frac{1000}{12}=frac{500}{3}$$
Vдет=$$frac{500}{3}cdot9=1500$$
Задание 8
Найдите значение выражения: $$sqrt{8}-sqrt{32}sin^{2}frac{11pi}{8}$$
Ответ: -2
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Скрыть
$$sqrt{8}-sqrt{32}sin^{2}frac{11pi}{8}=sqrt{8}(1-sqrt{4}sin^{2}frac{11pi}{8})=$$ $$=sqrt{8}(1-2sin^{2}frac{11pi}{8})=sqrt{8}cdot cos(2cdot frac{11pi}{8})=$$ $$=sqrt{8}cdot cos frac{11pi}{4}=sqrt{8}cdot cos(2pi+frac{3pi}{4}) =$$ $$=sqrt{8}cdot cosfrac{3pi}{4}=sqrt{8}cdot(-frac{sqrt{2}}{2})=-frac{4}{2}=-2$$
Задание 9
Высота над землёй подброшенного вверх мяча меняется по закону $$h(t)=1,4+14t-5t^{2}$$, где h – высота в метрах, t – время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее 8 метров?
Ответ: 1,6
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Скрыть
$$1,4+14t-5t^{2}geq8$$ $$-5t^{2}+14t-6,6geq0$$ $$5t^{2}-14t+6,6leq0$$ $$D=196-132=64$$ $$t_{1}=frac{14+8}{10}=2,2$$ $$t_{2}=frac{14-8}{10}=0,6$$ $$2,2-0,6=1,6$$
Задание 10
Из одной точки круговой трассы, длина которой равна 44 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 112 км/ч, и через 48 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.
Ответ: 57
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Скрыть
Пусть х — скорость второго авто: $$frac{44}{112-x}=frac{48}{60}=frac{4}{5}$$ $$Leftrightarrow$$ $$44cdot5=112cdot4-4x$$ $$220-44=-4x$$ $$Leftrightarrow$$ $$x=57$$
Задание 11
Найдите наибольшее значение функции $$y=10cdot ln(x+5)-10x-21$$ на отрезке [‐4,5; 0].
Ответ: 19
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Скрыть
$${y}’=frac{10}{x+5}-10=0$$ $$frac{10-10x-50}{x+5}=0$$ $$Leftrightarrow$$ $$frac{-10x-40}{x+5}=0$$ $$x=4$$ $$xneq -5$$ $$y=10cdot ln(-4+5)-10cdot(-4)-21=19$$
Задание 12
Дано уравнение $$log_{2}^{2}(4cos^{2}x)-8log_{2}(2cos x)+3=0$$.
А) Решите уравнение.
Б) Укажите корни этого уравнения, принадлежащие отрезку $$left [ -frac{7pi}{2}; -2piright ]$$
Ответ: a) $$pm frac{pi}{4}+2pi k, (kin Z)$$; б) $$frac{-9pi}{4}$$
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 13
В основании пирамиды $$SABC$$ лежит равнобедренный треугольник $$ABC$$, в котором $$B=4$$, $$angle BAC=120^{circ}$$. Известно, что боковая грань $$SBC$$ перпендикулярна основанию $$ABC$$, $$SB=SC$$, а высота пирамиды, проведенная из точки $$S$$, равна $$2sqrt{11}$$ . На ребрах $$SB$$ и $$SC$$ отмечены соответственно точки $$K$$ и $$P$$ так, что $$BK:SK=CP=SP=1:3$$.
а) Докажите, что сечением пирамиды плоскостью $$APK$$ является прямоугольный треугольник.
б) Найдите объем меньшей части пирамиды, на которые её делит плоскость $$APK$$.
Ответ: $$frac{7sqrt{33}}{6}$$.
Задание 14
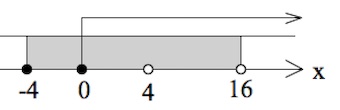
Решите неравенство $$frac{x+6sqrt x+28}{120}leq frac{2-sqrt x}{x-6sqrt x+8}$$.
Ответ: $$[0;4)cup (4;16)$$.
Задание 15
В параллелограмме $$ABCD$$ диагональ $$BD$$ равна стороне $$AD$$.
а) Докажите, что прямая $$CD$$ касается окружности ω, описанной около треугольника $$ABD$$.
б) Пусть прямая $$CB$$ вторично пересекает ω в точке $$K$$. Найдите $$KD:AC$$ при условии, что угол $$BDA$$ равен $$120^{circ}$$.
Ответ: $$sqrt3:sqrt7$$.
Задание 16
В начале января 2018 года планируется взять кредит в банке на 4 года на S млн. рублей, где S – целое число. Условия его возврата таковы:
‐ каждый июль долг возрастает на 10% по сравнению с началом текущего года;
— с августа по декабрь каждого года необходимо выплатить часть долга;
‐ в январе каждого года долг должен составлять часть кредита в соответствии со следующей таблицей:
| Начало года | 2018 | 2019 | 2020 | 2021 | 2022 |
| Долг (в млн. рублей) | S | 0,8S | 0,5S | 0,3S | 0 |
Найдите наименьшее значение S, при котором сумма выплат банку за все 4 года составит не менее 10 млн. рублей.
Ответ: 8
Задание 17
Найти все $$a$$, при каждом из которых система $$left{begin{matrix} y-ax=a+5, xy^2-x^2y-2xy+4x-4y+8=0; end{matrix}right.$$ имеет ровно два решения.
Ответ: $${-25;pm 1;0;1pm frac{4}{sqrt5}}$$.
Задание 18
Дано двузначное натуральное число.
а) Оказалось, что частное этого числа и суммы его цифр, равно 7. Найдите все такие числа.
б) Какие натуральные значения может принимать частное данного числа и суммы его цифр?
в) Какое наименьшее значение может принимать частное данного числа и суммы его цифр?
Ответ: а) 21;42;63;84; б) 2;3;4;5;6;7;8;9;10; в) 1,9.
А. Ларин: Тренировочный вариант № 204.
При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
Версия для печати и копирования в MS Word
1
Дано уравнение
а) Решите уравнение.
б) Найдите корни этого уравнения, принадлежащие отрезку
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
2
В основании пирамиды SABC лежит равнобедренный треугольник АВС, в котором АВ = 4, Известно, что боковая грань SBC перпендикулярна основанию АВС, SB = SC, а высота пирамиды, проведенная из точки S, равна 112 . На ребрах SB и SC отмечены соответственно точки К и Р так, что ВК : SK = CP : SP = 1 : 3.
а) Докажите, что сечением пирамиды плоскостью АРК является прямоугольный треугольник.
б) Найдите объем меньшей части пирамиды, на которые её делит плоскость АРК.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
3
Решите неравенство:
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
4
В параллелограмме АВСD диагональ ВD равна стороне AD.
а) Докажите, что прямая СD касается окружности ω, описанной около треугольника АВD.
б) Пусть прямая СВ вторично пересекает ω в точке К. Найдите КD : AC при условии, что угол ВDA равен
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
5
В начале января 2018 года планируется взять кредит в банке на 4 года на S млн. рублей, где S — целое число. Условия его возврата таковы:
— каждый июль долг возрастает на 10% по сравнению с началом текущего года;
— с августа по декабрь каждого года необходимо выплатить часть долга;
— В январе каждого года долг должен составлять часть кредита в соответствии со следующей таблицей:
| Начало года | 2018 | 2019 | 2020 | 2021 | 2022 |
| Долг (в млн.
рублей) |
S | 0,8S | 0,5S | 0,3S | 0 |
Найдите наименьшее значение S, при котором сумма выплат банку за все 4 года составит не менее 10 млн. рублей.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
6
Найдите все значения параметра а, при каждом из которых система
имеет ровно два решения.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
7
Дано двузначное натуральное число.
а) Оказалось, что частное этого числа и суммы его цифр, равно 7. Найдите все такие числа.
б) Какие натуральные значения может принимать частное данного числа и суммы его цифр?
в) Какое наименьшее значение может принимать частное данного числа и суммы его цифр?
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
Завершить тестирование, свериться с ответами, увидеть решения.
| Автор | Сообщение | |||
|---|---|---|---|---|
|
Заголовок сообщения: Тренировочный вариант №204
|
||||
Зарегистрирован: 10 июн 2010, 15:00 |
http://alexlarin.net/ege/2018/trvar204.html |
|||
  |
||||
|
OlG |
Заголовок сообщения: Re: Тренировочный вариант №204
|
|||
Зарегистрирован: 09 апр 2011, 14:49 |
1. Спасибо за вариант. 2. 16 б. Подробности: _________________ |
|||
  |
||||
|
ГОРЕВАВГ |
Заголовок сообщения: Re: Тренировочный вариант №204
|
|||
Зарегистрирован: 12 сен 2015, 12:09 |
Спасибо за новый вариант !!!!! _________________ Последний раз редактировалось ГОРЕВАВГ 23 сен 2017, 09:47, всего редактировалось 1 раз. |
|||
  |
||||
|
сергей королев |
Заголовок сообщения: Re: Тренировочный вариант №204
|
|||
Зарегистрирован: 13 фев 2015, 20:21 |
OlG писал(а): 2. 16 б. Подробности: Подробности: |
|||
  |
||||
|
Николай99 |
Заголовок сообщения: Re: Тренировочный вариант №204
|
|||
Зарегистрирован: 01 июл 2017, 10:12 |
Добрый день! Спасибо за новый вариант! |
|||
  |
||||
|
сергей королев |
Заголовок сообщения: Re: Тренировочный вариант №204
|
|||
Зарегистрирован: 13 фев 2015, 20:21 |
сергей королев писал(а): OlG писал(а): 2. 16 б. Подробности: Подробности: Подробности: |
|||
  |
||||
|
khazh |
Заголовок сообщения: Re: Тренировочный вариант №204
|
|||
Зарегистрирован: 23 мар 2012, 10:13 |
Николай99 писал(а): Добрый день! Спасибо за новый вариант! А у меня ещё один. |
|||
  |
||||
|
Владимир Анатольевич |
Заголовок сообщения: Re: Тренировочный вариант №204
|
|||
Зарегистрирован: 26 янв 2015, 09:06 |
khazh писал(а): Николай99 писал(а): Добрый день! Спасибо за новый вариант! А у меня ещё один. У меня тоже. |
|||
  |
||||
|
antonov_m_n |
Заголовок сообщения: Re: Тренировочный вариант №204
|
|||
Зарегистрирован: 12 июн 2016, 12:25 |
сергей королев писал(а): сергей королев писал(а): OlG писал(а): 2. 16 б. Подробности: Подробности: Подробности: Не надо Подробности: _________________ |
|||
  |
||||
|
Николай99 |
Заголовок сообщения: Re: Тренировочный вариант №204
|
|||
Зарегистрирован: 01 июл 2017, 10:12 |
khazh писал(а): Николай99 писал(а): Добрый день! Спасибо за новый вариант! А у меня ещё один. Точно! Потерял `a=1+4/sqrt(5)`. Обидно, что по невнимательности забыл про точку пересечения нижней ветви гиперболы с прямой |
|||
  |
||||
| Показать сообщения за: Сортировать по: |
Кто сейчас на форуме
|
Сейчас этот форум просматривают: нет зарегистрированных пользователей и гости: 1 |
|
Вы не можете начинать темы |
|
|
ЕГЭ 2010, Математика, 11 класс, Вариант №204.
На выполнение экзаменационной работы по математике дается 4 часа (240 мин). Работа состоит из двух частей и содержит 18 заданий.
Часть 1 содержит 12 заданий с кратким ответом (В1-В12) базового уровня по материалу курса математики. Задания части 1 считаются выполненными, если экзаменуемый дал верный ответ в виде целого числа или конечной десятичной дроби.
Часть 2 содержит 6 более сложных заданий (С1-С6) по материалу курса математики. При их выполнении надо записать полное решение и ответ.
Советуем для экономии времени пропускать задание, которое не удается выполнить сразу, и переходить к следующему. К выполнению пропущенных заданий можно вернуться, если у вас останется время.
Примеры.
Баржа в 10:00 вышла из пункта А в пункт В, расположенный в 15 км от А. Пробыв в пункте В 1 час 20 минут, баржа отправилась назад и вернулась в пункт A в 16:00 того же дня. Определите (в км/ч) скорость течения реки, если известно, что собственная скорость баржи равна 7 км/ч.
На рисунке жирными точками показана цена золота на момент закрытия биржевых торгов во все рабочие дни с 8 по 19 января 1996 года. По горизонтали указываются числа месяца, по вертикали — цена унции золота в долларах США. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку наибольшую цену золота на момент закрытия торгов в указанный период (в долларах США за унцию).
На рисунке изображены график функции у = f(x) и касательная к этому графику, проведенная в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Бесплатно скачать электронную книгу в удобном формате, смотреть и читать:
Скачать книгу ЕГЭ 2010, Математика, 11 класс, Вариант №204 — fileskachat.com, быстрое и бесплатное скачивание.
Скачать pdf
Ниже можно купить эту книгу по лучшей цене со скидкой с доставкой по всей России.Купить эту книгу
Скачать книгу ЕГЭ 2010, Математика, 11 класс, Вариант №204 — pdf — depositfiles.
Скачать книгу ЕГЭ 2010, Математика, 11 класс, Вариант №204
— pdf — Яндекс.Диск.
Дата публикации: 18.03.2013 10:22 UTC
Теги:
ЕГЭ по математике :: математика :: 11 класс
Следующие учебники и книги:
- ЕГЭ 2010, Математика, 11 класс, Вариант №208
- ЕГЭ 2010, Математика, 11 класс, Вариант №207
- ЕГЭ 2010, Математика, 11 класс, Вариант №206
- ЕГЭ 2010, Математика, 11 класс, Вариант №205
Предыдущие статьи:
- ЕГЭ 2010, Математика, 11 класс, Вариант №203
- ЕГЭ 2010, Математика, 11 класс, Вариант №202
- ЕГЭ 2010, Математика, 11 класс, Вариант №201
- ЕГЭ 2010, Математика, 11 класс, Вариант №200










 (
(