Задание 1
Стоимость проездного билета на месяц составляет 1150 рублей, а стоимость билета на одну поездку— 40 рублей. Аня купила проездной и сделала за месяц 37 поездок. На сколько рублей больше она бы потратила, если бы покупала билеты на одну поездку?
Ответ: 330
Скрыть
Стоимость 37 поездок по 40 рублей $$37cdot40=1480$$
$$1480-1150=330$$
Задание 2
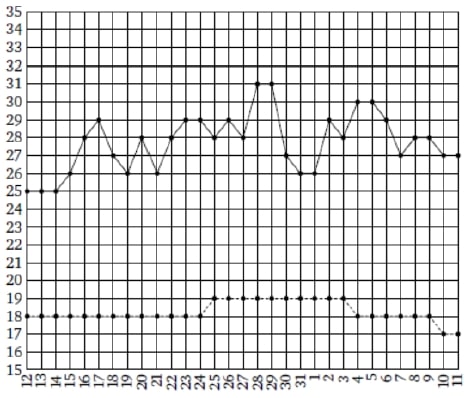
На рисунке жирными точками показаны среднесуточная температура в Москве в период с 12 июля 2010 года по 11 августа 2010 года и климатические нормы среднесуточной температуры за соответствующий период. По горизонтали указываются дни, по вертикали — температура в градусах Цельсия. Для наглядности жирные точки, соответствующие среднесуточной температуре, соединены сплошной линией, а точки, соответствующие климатической норме, — пунктирной линией.
Определите по рисунку наибольшую разность между среднесуточной температурой и климатической нормой среднесуточной температуры. Ответ дайте в градусах Цельсия.
Ответ: 12
Задание 3
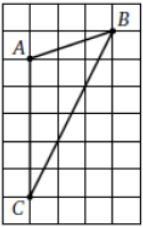
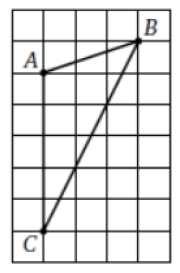
На клетчатой бумаге изображен треугольник АВС. Найдите сумму $$angle A+angle C$$. Ответ выразите в градусах.
Ответ: 135
Скрыть
$$tgβ=frac{1}{2}$$
$$tgα=frac{1}{3}$$
$$tg(α+β)=frac{tgα+tgβ}{1-tgαcdottgβ}=$$1 или $$α+β=45°$$
Но $$∠A=90+∠α$$
Значит,
$$∠A+∠B=90+45=135$$
Задание 4
На рок-фестивале выступают группы — по одной от каждой из 9 заявленных стран. Порядок выступления определяется жребием. Какова вероятность того, что группа из Дании будет выступать после группы из Швеции и после группы из Норвегии, которые выступают третьей и седьмой соответственно? Ответ округлите до сотых.
(Автор задачи Николай Журавлев)
Ответ: 0,29
Скрыть
Всего свободных мест для Дании 7 (Швеция и Норвегия свои места заняла по условию)
Места после Швеции и Норвегии – это 8,9 места (т.е. 2 благоприятных для нас места)
$$P(A)=frac{2}{7}approx0,29$$
Задание 5
Решите уравнение $$x^2+11+sqrt{x^2+11}=42$$. Если корней несколько, в ответе укажите их сумму.
Ответ: 0
Скрыть
Замена $$sqrt{x^2+11}=t$$, $$tgeq0$$
$$t^2+t=42$$
$$t=−7$$ – не подходит
$$t=6$$
$$sqrt{x^2+11}=6$$
$$x^2+11=36$$ (можно смело возводить в квадрат никакого ОДЗ не надо, т.к по условию уже корень положительный и равен $$6>0$$)
$$x=pm5$$
$$-5+5=0$$
Задание 6
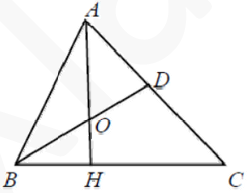
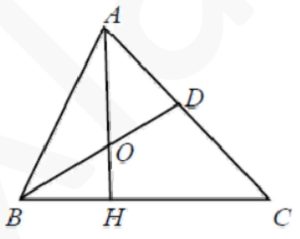
В треугольнике АВС проведены высота АН и биссектриса BD, которые пересекаются в точке О. Найдите угол АВС, если $$angle AOB = 126^{circ}$$.
Ответ: 72
Скрыть
$$∠BOH=180−126=54°$$
$$∠OBH=180−90−54=36°$$
$$∠B=2∠OBH=72°$$
Задание 7
Материальная точка движется прямолинейно по закону $$x(t)=frac{1}{3}t^3-t^2+5t+19$$, где $$x$$ — расстояние от точки отсчета в метрах, $$t$$ — время в секундах, измеренное с начала движения. Через сколько секунд после начала движения ускорение материальной точки будет равно нулю?
Ответ: 1
Скрыть
По физическому смыслу производной
$$a=x»(t)=2t−2$$
$$2t−2=0$$
$$t=1$$
Т.е. через 1 секунду после начала движения ускорение будет $$= 0$$
Задание 8
В треугольную пирамиду вписана сфера радиуса 1. Найдите площадь полной поверхности пирамиды, если ее объем равен 3.
Ответ: 9
Скрыть
Знатоки стереометрии сразу вспомнят формулу $$S_{п.п}=frac{3V}{R}$$, где $$R$$ – радиус вписанной сферы.
Но мы ее попробуем вывести.
$$V=frac{1}{3}S_{осн}cdot h$$
Если обозначить за т. O – центр вписанной сферы,
$$V=V_{OABC}+V_{OASC}+V_{OBSC}+V_{OASB}$$
$$V_{OABC}=frac{1}{3}S_{ABC}cdot R$$
$$V_{OASC}=frac{1}{3}S_{ASC}cdot R$$
$$V_{OBSC}=frac{1}{3}S_{BSC}cdot R$$
$$V_{OASB}=frac{1}{3}S_{ASB}cdot R$$
$$V=frac{1}{3}Rcdot S_{полн.п}$$
$$S_{полн.п}=frac{3cdot3}{1}=9$$
Задание 9
Найдите значение выражения $$8^{log_{ln2cdotlog_2e^{1/3}}sqrt[6]{9}}$$
Ответ: 0,5
Скрыть
$$ln2cdotlog_2e^{1/3}=ln2cdotfrac{ln e^{1/3}}{ln2}=frac{1}{3}$$
$$log_{frac{1}{3}}9^{1/6}=-frac{1}{3}$$
$$8^{-1/3}=0,5$$
Задание 10
Катер должен пересечь реку шириной $$L = 100$$ м так, чтобы причалить точно напротив места отправления. Скорость течения реки $$u = 0,8$$ м/с. Время в пути, измеряемое в секундах, равно $$t=frac{L}{u}cdotctgalpha$$, где $$alpha$$ — острый угол между осью катера и и линией берега. Под каким минимальным углом а к берегу нужно направить катер, чтобы время в пути было не больше 125 с? Ответ дайте в градусах.
Ответ: 45
Скрыть
$$frac{100}{0,8}cdotctg αleq125$$
$$ctg αleq1$$
Т.к. угол острый, на $$[0;frac{pi}{2}]$$ котангенс убывает, значит минимальный угол будет при $$ctg α=1$$
$$α=45$$
Задание 11
Объёмы ежемесячной добычи газа на первом, втором и третьем месторождениях относятся как 3 : 8 : 13. Планируется уменьшить месячную добычу газа на первом месторождении на 13% и на втором — тоже на 13%. На сколько процентов нужно увеличить месячную добычу газа на третьем месторождении, чтобы суммарный объём добываемого за месяц газа не изменился?
Ответ: 11
Скрыть
Составим уравнение:
$$3cdot0,87+8cdot0,87+13x=24$$
Отсюда $$x=1,11$$
Задание 12
Найдите наименьшее значение функции $$y=2^{log_3(x^2-2x+4)}$$
Ответ: 2
Скрыть
Т.к все функции возрастающие и $$x^2-2x+4$$ – ветви вверх, то минимум будет в вершине параболы
$$x_0=-frac{-2}{2}=1$$
$$y(1)=2^{log_3 3}=2$$
Задание 13
А) Решите уравнение $$(cos x-sin x)^2+sqrt{2}sin(frac{3pi}{4}-2x)+sqrt{3}cos x=0$$
Б) Укажите корни этого уравнения, принадлежащие отрезку $$[-frac{4pi}{3};-frac{2pi}{3}]$$
Ответ: А)$$frac{pi}{2}+pi n;pmfrac{5pi}{6}+2pi n,nin Z$$ Б)$$-frac{7pi}{6};-frac{5pi}{6}$$
Задание 14
В основании прямой призмы АВСА1В1С1 лежит прямоугольный треугольник АВС с прямым углом С. Точка М — середина ребра В1С1, точка N лежит на ребре АС, причем AN:NC=15:1. Катет АС в четыре раза больше бокового ребра АА1 призмы.
А) Докажите, что прямая MN перпендикулярна прямой СА1
Б) Найдите расстояние между прямыми MN и CA1, если $$AC = 16, BC = 2sqrt{17}$$
Ответ: $$sqrt{frac{17}{2}}$$
Задание 15
Решите неравенство $$frac{log_{6-x}(x^2-2x+1)}{log_3(x-1)-2}geq0$$
Ответ: (1;2],(5;6)
Задание 16
Две окружности касаются внешним образом в точке А, через которую проведена их общая касательная, на которой отмечена точка В. Через точку В проведены две прямые: одна пересекает первую окружность в точках К и L (точка К находится между В и L), а другая — вторую окружность в точках М и N ( точка М находится между В и N). Прямые KN и LM пересекаются в точке Р.
А) Докажите, что точки K, L, M, N лежат на одной окружности.
Б) Найдите отношение площадей треугольников KLP и MNP, если BL=9, BM=5, AB=6.
Ответ: $$frac{625}{121}$$
Задание 17
Георгий приобрёл ценную бумагу за 7 тыс. рублей. Цена бумаги каждый год возрастает на 2 тыс. рублей. В любой момент Георгий может продать бумагу и положить вырученные деньги на банковский счёт. Каждый год сумма на счёте будет увеличиваться на 10%. В течение какого года после покупки Георгий должен продать ценную бумагу, чтобы через тридцать лет после покупки этой бумаги сумма на банковском счёте была наибольшей?
Ответ: В течение 8-го года
Задание 18
Найдите все значения параметра $$a$$, при каждом из которых уравнение
$$(x^2+x+2a^2+1)^2=8a^2(x^2+x+1)$$
имеет ровно один корень.
Ответ: $$pmsqrt{frac{3}{8}}$$
Задание 19
Имеются зелёные и жёлтые карточки, всего их 80 штук. На каждой карточке написано натуральное число, а среднее арифметическое всех чисел равно 31. Все числа на жёлтых карточках разные. При этом любое число на жёлтой карточке больше любого числа на зелёной карточке. Числа на жёлтых карточках увеличили в 3 раза, после этого среднее арифметическое всех чисел стало равно 88.
А) Может ли быть ровно 50 жёлтых карточек?
Б) Может ли быть ровно 15 зелёных карточек?
В) Какое наибольшее количество жёлтых карточек может быть?
Ответ: А) да, Б) нет, В) 57
Решение и ответы заданий № 1–12 варианта №343 Александра Ларина. Разбор ЕГЭ 2020 по математике (профильный уровень).
Задание 1.
Стоимость проездного билета на месяц составляет 1150 рублей, а стоимость билета на одну поездку – 40 рублей. Аня купила проездной и сделала за месяц 37 поездок. На сколько рублей больше она бы потратила, если бы покупала билеты на одну поездку?
Задание 2.
На рисунке жирными точками показаны среднесуточная температура в Москве в период с 12 июля 2010 года по 11 августа 2010 года и климатические нормы среднесуточной температуры за соответствующий период. По горизонтали указываются дни, по вертикали – температура в градусах Цельсия. Для наглядности жирные точки, соответствующие среднесуточной температуре, соединены сплошной линией, а точки, соответствующие климатической норме, – пунктирной линией.
Определите по рисунку наибольшую разность между среднесуточной температурой и климатической нормой среднесуточной температуры. Ответ дайте в градусах Цельсия.
Задание 3.
На клетчатой бумаге изображен треугольник АВС. Найдите сумму ∠А + ∠С. Ответ выразите в градусах.
Задание 4.
На рок‐фестивале выступают группы – по одной от каждой из 9 заявленных стран. Порядок выступления определяется жребием. Какова вероятность того, что группа из Дании будет выступать после группы из Швеции и после группы из Норвегии, которые выступают третьей и седьмой соответственно? Ответ округлите до сотых.
(Автор задачи Николай Журавлев)
Задание 5.
Решите уравнение х2 + 11 + = 42. Если корней несколько, в ответе укажите их сумму.
Задание 6.
В треугольнике АВС проведены высота АН и биссектриса BD, которые пересекаются в точке О. Найдите угол АВС, если ∠AOB = 126º.
Задание 7.
Материальная точка движется прямолинейно по закону x(t) = t3 – t2 + 5t + 19, где x – расстояние от точки отсчета в метрах, t – время в секундах, измеренное с начала движения. Через сколько секунд после начала движения ускорение материальной точки будет равно нулю?
Задание 8.
В треугольную пирамиду вписана сфера радиуса 1. Найдите площадь полной поверхности пирамиды, если ее объем равен 3.
Задание 9.
Найдите значение выражения
Задание 10.
Катер должен пересечь реку шириной L = 100 м так, чтобы причалить точно напротив места отправления. Скорость течения реки u = 0,8 м/с. Время в пути, измеряемое в секундах, равно , где α острый угол между осью катера и линией берега. Под каким минимальным углом α к берегу нужно направить катер, чтобы время в пути было не больше 125 с? Ответ дайте в градусах.
Задание 11.
Объёмы ежемесячной добычи газа на первом, втором и третьем месторождениях относятся как 3 : 8 : 13. Планируется уменьшить месячную добычу газа на первом месторождении на 13% и на втором – тоже на 13%. На сколько процентов нужно увеличить месячную добычу газа на третьем месторождении, чтобы суммарный объём добываемого за месяц газа не изменился?
Задание 12.
Найдите наименьшее значение функции
Источник варианта: alexlarin.net
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 4.8 / 5. Количество оценок: 4
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
А. Ларин. Тренировочный вариант № 343.
При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
Версия для печати и копирования в MS Word
1
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
2
В основании прямой призмы ABCA1B1C1 лежит прямоугольный треугольник ABC с прямым углом C. Точка M — середина ребра B1C1, точка N лежит на ребре AC, причем AN : NC = 15 : 1. Катет AC в четыре раза больше бокового ребра AA1 призмы.
а) Докажите, что прямая MN перпендикулярна прямой CA1.
б) Найдите расстояние между прямыми MN и CA1, если AC = 16,
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
3
Решите неравенство
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
4
Две окружности касаются внешним образом в точке A, через которую проведена их общая касательная, на которой отмечена точка B. Через точку B проведены две прямые: одна пересекает первую окружность в точках K и L (точка K находится между B и L), а другая — вторую окружность в точках M и N (точка M находится между B и N). Прямые KN и LM пересекаются в точке P.
а) Докажите, что точки K, L, M, N лежат на одной окружности.
б) Найдите отношение площадей треугольников KLP и MNP, если BL = 9, BM = 5, AB = 6.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
5
В таблице показано количество билетов и возможные выигрыши беспроигрышной денежной лотереи. Цена билета лотереи равна 110 рублей. Всего билетов выпущено 1000 штук. Участник покупает один случайный билет. На сколько рублей цена билета выше, чем математическое ожидание выигрыша?
| Выигрыш | 30 | 300 | 1000 | 10000 |
| Количество билетов |
960 | 30 | 9 | 1 |
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
6
Найдите все значения параметра а, при каждом из которых уравнение
имеет ровно один корень.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
7
Имеются зеленые и желтые карточки, всего их 80 штук. На каждой карточке написано натуральное число, а среднее арифметическое всех чисел равно 31. Все числа на желтых карточках разные. При этом любое число на желтой карточке больше любого числа на зелёной карточке. Числа на желтых карточках увеличили в 3 раза, после этого среднее арифметическое всех чисел стало равно 88.
а) Может ли быть ровно 50 желтых карточек?
б) Может ли быть ровно 15 зеленых карточек?
в) Какое наибольшее количество желтых карточек может быть?
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
Завершить тестирование, свериться с ответами, увидеть решения.
На чтение 1 мин Просмотров 1 Опубликовано 5 марта, 2023
Решение варианта Ларина №343 ЕГЭ Решение и ответы на задачи на официальном сайте источника онлайн.
Решение и ответы заданий № 1–12 варианта №343 Александра Ларина. Разбор ЕГЭ 2021 по математике (профильный уровень).
Варианты ответов и решение задачи ТУТ: https://ege314.ru/ege-varianty-larina/reshenie-varianta-larina-343-ege/
Ответы и решение задачи онлайн
Оставляйте комментарии на сайте, обсуждайте их решения и ответы, предлагайте альтернативные варианты ответов.
Варианты Алекса Ларина ОГЭ 2023 по математике 9 класс тренировочный вариант №343 и вариант 344 с ответами и решением, который вышел на сайте 22 января 2022 года, по новой демоверсии ОГЭ 2023 года ФИПИ усложнённая и лёгкая версия варианта.
- Скачать вариант 343
- Скачать вариант 344
Работа состоит из двух модулей: «Алгебра» и «Геометрия». Всего в работе 25 заданий. Модуль «Алгебра» содержит семнадцать заданий: в части 1 — четырнадцать заданий; в части 2 — три задания. Модуль «Геометрия» содержит восемь заданий: в части 1 — пять заданий; в части 2 — три задания. На выполнение экзаменационной работы по математике отводится 3 часа 55 минут (235 минут).
Ответы к заданиям 7 и 13 записываются в виде одной цифры, которая соответствует номеру правильного ответа. Эту цифру запишите в поле ответа в тексте работы. Для остальных заданий части 1 ответом является число или последовательность цифр, которые нужно записать в поле ответа в тексте работы. Если в ответе получена обыкновенная дробь, обратите её в десятичную.
Решения заданий части 2 и ответы к ним запишите на отдельном листе или бланке. Задания можно выполнять в любом порядке, начиная с любого модуля. Текст задания переписывать не надо, необходимо только указать его номер.
вариант343-ларин-огэ2023
На плане (см. рис. выше) изображён дачный участок. Участок имеет прямоугольную форму. Въезд и выезд осуществляются через единственные ворота. При входе на участок слева от ворот находится мастерская хозяина дома, а справа расположен виноградник, отмеченный на плане цифрой 1. Площадь, занятая виноградником, равна 32 м2. Жилой дом находится в глубине территории и обозначен на плане цифрой 4.
Помимо мастерской, жилого дома и виноградника, на участке имеется площадка для отдыха с зоной для барбекю и беседкой, расположенной справа от входа в дом. На участке также растут фруктовые деревья. Около дома высажены цветы, а также расположен декоративный пруд площадью 4 м2 с золотыми рыбками и кувшинками.
Между виноградником и площадкой для отдыха находится огород. Все дорожки внутри участка имеют ширину 1 м и вымощены тротуарной плиткой размером 50 см × 50 см. Сразу за воротами при въезде на участок расположена площадка для автомобиля площадью 36 м2, вымощенная такой же плиткой.
1. Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу. В ответе запишите последовательность четырёх цифр без пробелов, запятых и других разделительных символов.
2. Плитки для садовых дорожек продаются в упаковках по 12 штук. Сколько упаковок плиток понадобилось, чтобы выложить все дорожки и площадку для автомобиля?
3. Найдите периметр (в метрах) основания жилого дома.?
4. На сколько процентов площадь, которую занимает беседка, меньше площади, которую занимает мастерская?
5. Хозяин участка решил покрасить весь забор вокруг участка (только с внешней стороны). Площадь забора, которую необходимо покрасить, равна 244 м2. Купить краску можно в одном из двух ближайших магазинов. Цена и характеристика краски и стоимость доставки заказа даны в таблице (см. ниже). Во сколько рублей обойдётся наиболее дешёвый вариант покупки с доставкой?
10. В лыжных гонках участвуют 13 спортсменов из России, 2 спортсмена из Норвегии и 5 спортсменов из Швеции. Порядок, в котором спортсмены стартуют, определяется жребием. Найдите вероятность того, что первым будет стартовать спортсмен из России.
14. В ходе биологического эксперимента в чашку Петри с питательной средой поместили колонию микроорганизмов массой 3 мг. За каждые 20 минут масса колонии увеличивается в 3 раза. Найдите массу колонии микроорганизмов через 80 минут после начала эксперимента. Ответ дайте в миллиграммах.
18. Даны 9 попарно подобных прямоугольников ABCD , AEFG , EBPF , HIJK , LMNO , FPCQ , GHKD , ILOJ , MFQN (см. рис.). Найдите площадь прямоугольника ABCD , если известно, что сумма площадей прямоугольников EBPF , GHKD , ILOJ , MFQN равна 2 .
19. Какие из следующих утверждений верны? Если верных утверждений несколько, запишите их номера в порядке возрастания без пробелов, запятых и других разделительных символов.
- 1) Если угол равен 47°, то смежный с ним равен 153°.
- 2) Если две прямые перпендикулярны третьей прямой, то эти две прямые параллельны.
- 3) Через любую точку проходит ровно одна прямая.
21. Рыболов в 5 часов утра на моторной лодке отправился от пристани против течения реки, через некоторое время бросил якорь, 2 часа ловил рыбу и вернулся обратно в 10 часов утра того же дня. На какое расстояние (в км) от пристани он отплыл, если скорость реки равна 2 км/ч, а собственная скорость лодки 6 км/ч?
24. Дан правильный восьмиугольник. Докажите, что если его вершины последовательно соединить отрезками через одну, то получится квадрат.
Вариант 344 Ларин ОГЭ 2023
вариант344-ларин-огэ2023
На графике (см. выше) точками изображено количество минут, потраченных на исходящие вызовы, и количество гигабайтов мобильного интернета, израсходованных абонентом в процессе пользования смартфоном, за каждый месяц 2020 года. Для удобства точки, соответствующие минутам и гигабайтам, соединены сплошными и пунктирными линиями соответственно.
В течение года абонент пользовался тарифом «Популярный», абонентская плата по которому составляет 500 рублей в месяц. При условии нахождения абонента на территории РФ в абонентскую плату тарифа «Популярный» входит: – пакет минут, включающий 300 минут исходящих вызовов на номера, зарегистрированные на территории РФ; – пакет интернета, включающий 4 гигабайта мобильного интернета; – пакет SMS, включающий 100 SMS в месяц; – безлимитные бесплатные входящие вызовы. Стоимость минут, интернета и SMS сверх пакета указана в таблице (см. ниже)
Абонент не пользовался услугами связи в роуминге и не звонил на номера, зарегистрированные за рубежом. За весь год абонент отправил 98 SMS.
1. Определите, какие месяцы соответствуют указанному в таблице трафику мобильного интернета. Заполните таблицу. В ответе запишите последовательность четырёх чисел без пробелов, запятых и других разделительных символов.
2. Сколько рублей потратил абонент на услуги связи в сентябре?
3. Сколько месяцев в 2020 году абонент не превышал лимит ни по пакету минут, ни по пакету мобильного интернета?
4. Известно, что в 2019 году абонентская плата по тарифу «Популярный» составляла 400 рублей. На сколько процентов выросла абонентская плата в 2020 году по сравнению с 2019 годом?
5. В конце 2020 года оператор связи предложил абоненту перейти на новый тариф. Его условия приведены в таблице. Абонент решал, перейти ли ему на новый тариф, посчитав, сколько бы он потратил на услуги связи за 2020 год, если бы пользовался им. Если получилось бы меньше, чем он потратил фактически за 2020 год, то абонент принял бы решение сменить тариф. Если же получилось бы столько же или больше, то абонент оставил бы прежний тариф на 2019 год. Какова была ежемесячная абонентская плата (в рублях) абонента по тарифу в 2021 году?
10. Из каждых 1000 электрических лампочек 6 бракованных. Какова вероятность купить исправную лампочку?
14. Пете надо решить 333 задачи. Ежедневно он решает на одно и то же количество задач больше по сравнению с предыдущим днем. Известно, что за первый день Петя решил 5 задач. Определите, сколько задач решил Петя в последний день, если со всеми задачами он справился за 9 дней.
19. Какие из следующих утверждений верны? Если верных утверждений несколько, запишите их номера в порядке возрастания без пробелов, запятых и других разделительных символов.
- 1) Любые три прямые имеют не более одной общей точки.
- 2) Если угол равен 120°, то смежный с ним равен 120°.
- 3) Если расстояние от точки до прямой больше 3, то и длина любой наклонной, проведённой из данной точки к прямой, больше 3.
Ященко И.В ОГЭ 2023 года по математике 9 класс
Ященко скачать 36 вариантов ОГЭ 2023 по математике 9 класс с ответами
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
Шкалирование
| Первичный | Тестовый | Оценка |
|---|---|---|
| 5-6 | 27-34 | 3 |
| 7-8 | 40-46 | 4 |
| 9-10 | 52-58 | |
| 11-12-13 | 64-66-68 | 5 |
| 14-15-16 | 70-72-74 | |
| 17-18-19 | 76-78-80 | |
| 20-21-22 | 82-84-86 | |
| 23-24-25 | 88-90-92 | |
| 26-27-28 | 94-96-98 | |
| 29-30-31 | 100 |
| Первичный балл / Тестовый балл |
5/27 | 6/34 | 7/40 | 8/46 | 9/52 | 10/58 | 11/64 | 12/66 | 13/68 | 14/70 |
|---|---|---|---|---|---|---|---|---|---|---|
| 15/72 | 16/74 | 17/76 | 18/78 | 19/80 | 20/82 | X / 2X+42 | 29+ / 100 |
Регистрация Форум Текущее время: 10 мар 2023, 14:24 Сообщения без ответов | Активные темы Страница 1 из 1 [ Сообщений: 10 ] Начать новую тему»> Ответить Тренировочный вариант №343
Тренировочный вариант №343
Страница 1 из 1 [ Сообщений: 10 ] Текущее время: 10 мар 2023, 14:24 | Часовой пояс: UTC + 3 часа Удалить cookies форума | Наша команда | Вернуться наверх Кто сейчас на форуме
|


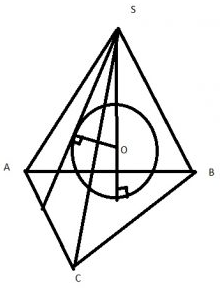
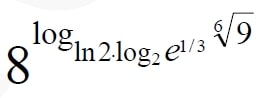



 Для печати |
Для печати |  Известить друга
Известить друга
 Предыдущая тема | Следующая тема
Предыдущая тема | Следующая тема 


