Задание 1
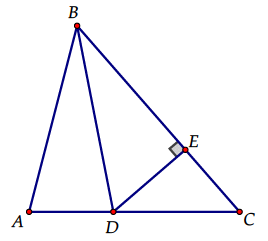
Площадь треугольника АВС равна 30. На стороне АС взята точка D так, что AD : DC = 2 : 3. Длина перпендикуляра DE, проведенного к стороне ВС, равна 9. Найдите ВС.
Ответ: 4
Скрыть
Проведенная из вершины В высота — общая для треугольников АВС, АВD и DBC, поэтому отношение их площадей равно отношению соответствующих оснований. По условию AD : DC = 2 : 3, значит DC : AC = 3 : 5 и площадь треугольника DBC равна трем пятым от площади треугольника АВС:
$$3cdotfrac{30}{5}=18$$.
Так как площадь треугольника DBC равна половине произведения длины высоты DE на длину стороны ВС, получаем, что
$$ВС=2cdotfrac{18}{9}=4$$.
Задание 2
Найдите объем правильной шестиугольной пирамиды, если ее боковое ребро равно 13, а радиус окружности, описанной около основания, равен 11.
Ответ: 726
Скрыть
Основанием данной пирамиды является правильный шестиугольник, и радиус окружности, описанной около этого шестиугольника, равен 11. Значит, длина стороны основания равна 11, и основание можно представить в виде объединения шести равносторонних треугольников со стороной 11. Соответственно, площадь S основания пирамиды равна умноженной на 6 площади равностороннего треугольника со стороной 11:
$$S = 6cdot11^2cdotfrac{3^{frac{1}{2}}}{4} = 181,5cdot3^{frac{1}{2}}$$.
Высоту h пирамиды найдем по теореме Пифагора из прямоугольного треугольника, в котором h — катет, боковое ребро пирамиды — гипотенуза, равная 13, и радиус описанной окружности — другой катет, равный 11:
$$h = (13^2-11^2)^{frac{1}{2}} = 48^{frac{1}{2}} = 4cdot3^{frac{1}{2}}$$.
Объем V данной пирамиды:
$$V = frac{Sh}{3} = 181,5cdot3^{frac{1}{2}}cdot4cdotfrac{3^{frac{1}{2}}}{3} = 181,5cdot4 = 726$$.
Задание 3
Вероятность того, что в будний день число посетителей торгового центра превысит 2000 человек, равна 0,34. Вероятность того, что число посетителей торгового центра превысит 2500 человек, равна 0,18. Найдите вероятность того, что в случайно выбранный будний день число посетителей окажется от 2001 до 2500 человек.
Ответ: 0,16
Скрыть
Вероятность того, что число посетителей превысит 2000 складывается из сумм вероятностей двух независимых событий:
Первое событие что это число будет от 2001 до 2500
Второе событие, что число посетителей будет больше 2500,а вероятность этого уже известна 0,18.
Значит, вероятность того что посетителей будет от 2001 до 2500 равна:
$$0,34-0,18=0,16$$
Задание 4
Если гроссмейстер А. играет белыми, то он выигрывает у гроссмейстера Б. с вероятностью 0,6. Если А. играет черными, то А. выигрывает у Б. с вероятностью 0,4. Гроссмейстеры А. и Б. играют две партии, причем во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет только одну партию из двух.
Ответ: 0,52
Скрыть
Итак, нам подходят результаты, когда А выигрывает только одну партию из двух. Варианты выигрыша двух партий или проигрыша обеих партий нам как раз не подходят. И мы точно знаем, что один раз А будет играть белыми и один раз чёрными. Очерёдность, по-моему, неважна.
Выигрыш двух партий $$= 0,6cdot0,4=0,24$$.
Проигрыш в двух партиях $$= (1-0,6)cdot(1-0,4)=0,24$$.
Все остальные исходы — это выигрыш в любой одной партии $$= 1- 0,24-0,24=0,52$$.
Задание 5
Решите уравнение $$9^{sqrt{x-5}}-27=6cdot3^{sqrt{x-5}}$$.
Ответ: 9
Скрыть
$$9^{sqrt{x-5}}-27=6cdot3^{sqrt{x-5}}$$
Пусть $$3^{sqrt{x-5}}=y>0$$. Тогда $$y^2-27=6yRightarrow y^2-6y-27=0Rightarrowleft[begin{matrix} y=9\ y=-3<0 end{matrix}right.$$
Получим $$3^{sqrt{x-5}}=9Rightarrow sqrt{x-5}=2Rightarrow x-5=4Rightarrow x=9$$
Задание 6
Найдите значение выражения $$4cos260^{circ}sin130^{circ}cos160^{circ}$$.
Ответ: 0,5
Скрыть
$$4cos260^{circ}sin130^{circ}cos160^{circ}=4cos(180+80)sin(90+40)cos(2cdot80)=$$
$$=-4cos80cos40cos160=frac{-4sin40cos40cos80cos160}{sin40}=$$
$$=frac{-frac{4}{2}sin80cos80cos160}{sin40}=frac{-frac{2}{2}sin160cos160}{sin40}=frac{-frac{1}{2}sin320}{sin40}=frac{frac{1}{2}sin(360-40)}{sin40}=$$
$$=frac{frac{1}{2}sin40}{sin40}=frac{1}{2}=0,5$$
Задание 7
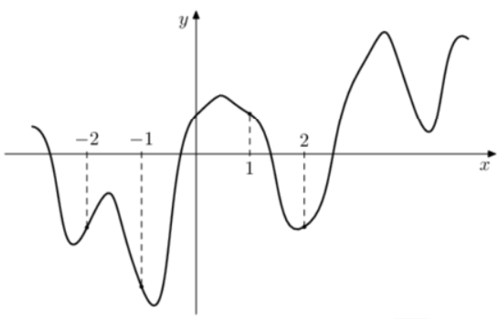
На рисунке изображен график функции $$y=f(x)$$. На оси абсцисс отмечены точки -2, -1, 1, 2. В какой из этих точек значение производной наибольшее? В ответе укажите эту точку.
Ответ: -2
Скрыть
Производная положительная, если функция возрастает $$Rightarrow -2$$ и $$2$$. Там больше, где угол между касательной, проведённой в точку, и Ox ближе к $$90^{circ}Rightarrow -2$$.
Задание 8
При адиабатическом процессе для идеального газа выполняется закон $$pV^k=1,6cdot10^5$$ $$Паcdot м^2$$, где $$p$$ — давление газа (в Па), $$V$$ — объем газа (в $$м^3$$), $$k=frac{4}{3}$$. Найдите, какой объём $$V$$ (в $$м^3$$) будет занимать газ при давлении $$p$$, равном $$6,25cdot10^6$$ Па.
Ответ: 0,064
Скрыть
Подставим данные в задании величины в формулу давления и объема, получим:
$$6,25cdot10^6cdot V^{frac{4}{3}}=1,6cdot10^5$$
$$V^{frac{4}{3}}=frac{1,6}{62,5}=frac{16}{625}$$
$$V=frac{(16)^{frac{3}{4}}}{(625)^{frac{3}{4}}}=frac{2^3}{5^3}=frac{8}{125}=0,064$$
Задание 9
Пункт С расположен в 12 км от пункта В вниз по течению. Рыбак отправился на лодке в пункт С из пункта А, расположенного выше пункта В. Через 4 часа он прибыл в С, а на обратный путь затратил 6 часов. В другой раз рыбак воспользовался моторной лодкой, увеличив тем самым собственную скорость передвижения относительно воды втрое, и дошел от А до В за 45 минут. Найдите скорость течения (в км/ч), считая ее постоянной.
Ответ: 1
Скрыть
Пусть $$v_т$$ км/ч — скорость течения; $$v_л$$ км/ч — скорость лодки; $$a$$ км/ч — расстояние между A и B. Тогда по условию:
$$left{begin{matrix} (v_л+v_т)cdot4=12+a\ (v_л-v_т)cdot6=12+a\ a=(3v_л+v_т)cdot0,75 end{matrix}right.$$
откуда $$v_т=1$$ км/ч
Задание 10
На рисунке изображен график функции $$f(x)=ksqrt{x}$$. Найдите $$f(7,84)$$.
Ответ: 9,8
Скрыть
График проходит через (4;7):
$$7=kcdotsqrt{4}Rightarrow k=3,5$$
$$f(7,84)=3,5sqrt{7,84}=3,5cdot2,8=9,8$$
Задание 11
Найдите наибольшее значение функции $$f(x)=e^{-x}-e^{-2x}$$ на отрезке [0;2].
Ответ: 0,25
Скрыть
Пусть $$e^{-x}=y$$. Получим $$f(y)=y-y^2$$.
Тогда $$f'(y)=1-2y=0Rightarrow y=frac{1}{2}$$
При этом $$y=frac{1}{2}$$ — точка максимума $$Rightarrow f_{max}(y)=frac{1}{2}-frac{1}{2}cdotfrac{1}{2}=0,25$$.
Задание 12
А) Решите уравнение $$log_{0,5sin2x}(sin x)cdotlog_{0,5sin2x}(cos x)=0,25$$
Б) Найдите все корни уравнения, принадлежащие промежутку $$(2,25pi;4,5pi]$$
Ответ: А)$$frac{pi}{4}+2pi n,nin Z$$ Б)$$frac{17pi}{4}$$
Задание 13
Точка F — середина бокового ребра SA правильной четырехугольной пирамиды SABCD, точка М лежит на стороне основания АВ. Плоскость $$beta$$ проходит через точки F и М параллельно боковому ребру SC.
А) Плоскость $$beta$$ пересекает ребро SD в точке К. Докажите, что ВМ : МА = DK : KS.
Б) Пусть ВМ : МА = 3 : 1. Найдите отношение объемов многогранников, на которые плоскость $$beta$$ разбивает пирамиду.
Ответ: $$frac{25}{39}$$
Задание 14
Решите неравенство: $$log_5 x+log_xfrac{x}{3}<frac{log_5 xcdot(2-log_3 x)}{log_3 x}$$
Ответ: $$(0;frac{sqrt{5}}{5}),(1;3)$$
Задание 15
У инвестора есть 50 млн рублей. Часть денег он планирует вложить в проект. Если он вложит в проект $$frac{5x^2}{144}$$ млн рублей, то по завершении проекта он получит $$x$$ млн рублей. Невложенные в проект деньги инвестор планирует разместить на банковском счете. По завершении проекта инвестор получит из банка сумму, увеличенную на 20%.
Инвестор собирается распределить деньги так, чтобы общая сумма полученных им денег от вложения в проект и размещения в банке оказалась наибольшей. Прибыль от проекта — это разность между полученной от проекта и вложенной в проект суммами денег.
Найдите сколько процентов составит прибыль от проекта от вложенной в него суммы денег.
Ответ: 140
Задание 16
В остроугольном треугольнике АВС на высоте AD взята точка М, а на высоте ВР — точка N так, что углы ВМС и ANC — прямые. Известно, что $$angle MCN = 30^{circ}, MN = 4 + 2sqrt{3}$$.
А) Докажите, что $$frac{MD^2}{BDcdot CD}=1$$.
Б) Найдите длину биссектрисы CL треугольника MCN.
Ответ: $$7+4sqrt{3}$$
Задание 17
Найдите все значения параметра $$a$$, при каждом из которых уравнение:
$$3cdotsqrt[5]{x+2}=16a^2cdotsqrt[5]{32x+32}+sqrt[10]{x^2+3x+2}$$
имеет единственное решение.
Ответ: $$(-infty;-frac{1}{2sqrt{2}}],[-frac{1}{4};frac{1}{4}],[frac{1}{2sqrt{2}};infty)$$
Задание 18
На доске написано $$N$$ различных натуральных чисел, каждое из которых не превосходит 33. Для каждых двух написанных чисел $$a$$ и $$b$$ таких, что $$a < b$$, ни одно из написанных чисел не делится на $$b — a$$ и ни одно из написанных чисел не является делителем числа $$b — a$$.
А) Могли ли на доске быть написаны числа 11, 12, 13?
Б) Среди написанных на доске чисел есть число 15. Может ли $$N$$ быть равным 18?
В) Найдите наибольшее значение $$N$$?
Ответ: А) нет, Б) нет, В) 11
Новый тренировочный вариант №397 Алекса Ларина ЕГЭ 2023 по математике профильный уровень 11 класс с ответами и решением, который вышел на сайте 10 сентября 2022 года, по новой демоверсии ЕГЭ 2023 года ФИПИ.
Скачать вариант с ответами
Демоверсия ЕГЭ 2023 по математике
Тренировочный вариант 397 Ларина ЕГЭ 2023 по математике профиль
ларин-егэ2023-вариант-397-ответы
Ответы для варианта
1)Около окружности, радиус которой равен 8, описан многоугольник, площадь которого равна 208. Найдите периметр этого многоугольника.
Ответ: 52
2)В прямоугольном параллелепипеде АВСDА1B1C1D1 известны длины ребер: АВ = 11, AD = 20, AA1 = 4. Найдите расстояние от вершины С до центра грани АА1D1D.
Ответ: 15
3)Из слова «максимум» случайным образом выбирается одна буква. Найдите вероятность того, что будет выбрана буква, встречающаяся в этом слове только один раз.
Ответ: 0,625
4)Куб, все грани которого окрашены, распилен на 1000 кубиков одинакового размера, которые затем тщательно перемешаны. Найти вероятность того, что извлечённый наугад кубик будет иметь хотя бы одну окрашенную грань.
Ответ: 0,488
9)Имеется три одинаковых по массе сплава. Известно, что процентное содержание никеля во втором сплаве на 25 процентных пункта больше, чем в первом, а процентное содержание никеля в третьем сплаве на 4 процентных пункта больше, чем во втором. Из этих трёх сплавов получили четвертый сплав, содержащий 64% никеля. Сколько процентов никеля содержит первый сплав?
Ответ: 46
13)В правильной шестиугольной пирамиде SABCDEF сторона основания AB = 4, а боковое ребро SA = 7. Точка M лежит на ребре BC, причем BM = 1, точка K лежит на ребре SC, причем SK = 4. А) Докажите, что плоскость MKD перпендикулярна плоскости основания пирамиды. Б) Найдите объем пирамиды CDKM.
15)В июле 2026 года планируется взять кредит на три года. Условия его возврата таковы: — каждый январь долг будет возрастать на 20% по сравнению с концом предыдущего года; — с февраля по июнь каждого года необходимо выплатить одним платежом часть долга; — платежи в 2027 и в 2028 годах должны быть по 300 тыс. руб.; — к июлю 2029 года долг должен быть выплачен полностью. Известно, что платёж в 2029 году будет равен 417,6 тыс. руб. Какую сумму (в тыс. рублей) планируется взять в кредит?
Ответ: 700
16)Две окружности пересекаются в точках Р и Q. Через точку Р проведена прямая, пересекающая вторично первую из окружностей в точке А, а вторую – в точке В. Через точку Q также проведена прямая, пересекающая вторично первую окружность в точке С, а вторую – в точке D. А) Докажите, что прямые АС и BD параллельны. Б) Найдите наибольшее возможное значение суммы длин отрезков АВ и CD, если расстояние между центрами данных окружностей равно 1.
18)Издательство на выставку привезло несколько книг для продажи (каждую книгу привезли в единственном экземпляре). Цена каждой книги — натуральное число рублей. Если цена книги меньше 100 рублей, на неё приклеивают бирку «выгодно». Однако до открытия выставки цену каждой книги увеличили на 10 рублей, из‐за чего количество книг с бирками «выгодно» уменьшилось.
А) Могла ли уменьшиться средняя цена книг с биркой «выгодно» после открытия выставки по сравнению со средней ценой книг с биркой «выгодно» до открытия выставки?
Б) Могла ли уменьшиться средняя цена книг без бирки «выгодно» после открытия выставки по сравнению со средней ценой книг без бирки «выгодно» до открытия выставки?
В) Известно, что первоначально средняя цена всех книг составляла 110 рублей, средняя цена книг с биркой «выгодно» составляла 81 рубль, а средняя цена книг без бирки — 226 рублей. После увеличения цены средняя цена книг с биркой «выгодно» составила 90 рублей, а средняя цена книг без бирки — 210 рублей. При каком наименьшем количестве книг такое возможно?
Видео решение варианта Ларина
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
А. Ларин. Тренировочный вариант № 415.
При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
Версия для печати и копирования в MS Word
1
а) Решите уравнение
б) Найдите все корни уравнения, принадлежащие отрезку
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
2
В правильной четырехугольной пирамиде SABCD с вершиной S каждое ребро равно Через середины сторон AD и DC и середину высоты пирамиды проведена плоскость α.
а) Докажите, что плоскость α параллельна ребру SD.
б) Найдите площадь сечения пирамиды плоскостью α.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
3
Решите неравенство:
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
4
В июле 2023 года планируется взять кредит в банке на 6 лет в размере S тысяч рублей. Условия его возврата таковы:
— каждый январь долг увеличивается на 16% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо одним платежом выплатить часть долга;
— в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей.
| Дата | Июль 2023 | Июль 2024 | Июль 2025 | Июль 2026 | Июль 2027 | Июль 2028 | Июль 2029 |
|---|---|---|---|---|---|---|---|
| Долг (в тыс. руб.) |
S | 0,9S | 0,8S | 0,7S | 0,6S | 0,5S | 0 |
Найдите, на сколько процентов общая сумма платежей после полного погашения кредита превысит сумму взятого кредита.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
5
B трапеции ABC боковая сторона AB перпендикулярна основаниям. Из точки A на сторону CD опустили перпендикуляр AH. На стороне AB отмечена точка E так, что прямые CD и CE перпендикулярны.
а) Докажите, что прямые BH и ED параллельны.
б) Найдите отношение BH к ED, если
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
6
Найдите все значения параметра a, для каждого из которых уравнение
имеет хотя бы одно решение.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
7
Натуральное число называется свободным от квадратов, если оно не делится ни на один квадрат натурального числа, кроме 1. Составим последовательность {an}, состоящую из чисел, свободных от квадратов: пусть и для любых натуральных n
где ai — число, свободное от квадратов.
а) Может ли число, свободное от квадратов, иметь 15 делителей?
б) Чему равно n, если an = 326?
в) Чему равно a100?
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
Завершить тестирование, свериться с ответами, увидеть решения.
Пробные и тренировочные варианты по математике профильного уровня в формате ЕГЭ 2023 из различных источников.
Варианты составлены в соответствии с демоверсией 2023 года
Тренировочные варианты ЕГЭ 2023 по математике (профиль)
| vk.com/pezhirovschool | |
| Вариант 1 | решения |
| Вариант 2 | решения |
| Вариант 3 | решения |
| Вариант 4 | решения |
| Вариант 5 (с ответами) | |
| Вариант 6 (с ответами) | |
| Вариант 7 (с ответами) | |
| Вариант 8 (с ответами) | |
| egemath.ru | |
| вариант 1 | скачать |
| вариант 2 | скачать |
| вариант 3 | скачать |
| вариант 4 | скачать |
| вариант 5 | скачать |
| вариант 6 | скачать |
| вариант 7 | скачать |
| вариант 8 | скачать |
| вариант 9 | скачать |
| вариант 10 | скачать |
| вариант 11 | скачать |
| вариант 12 | скачать |
| вариант 13 | скачать |
| вариант 14 | скачать |
| вариант 15 | скачать |
| вариант 16 | скачать |
| вариант 17 | скачать |
| вариант 18 | скачать |
| вариант 19 | скачать |
| вариант 20 | скачать |
| time4math.ru | |
| вариант 1-2 | ответы |
| вариант 3-4 | ответы |
| вариант 5-6 | ответы |
| вариант 7-8 | |
| yagubov.ru | |
| вариант 33 (сентябрь) | ege2023-yagubov-prof-var33 |
| вариант 34 (октябрь) | ege2023-yagubov-prof-var34 |
| вариант 35 (ноябрь) | ege2023-yagubov-prof-var35 |
| вариант 36 (декабрь) | ege2023-yagubov-prof-var36 |
| вариант 37 (январь) | ege2023-yagubov-prof-var37 |
| вариант 38 (февраль) | ege2023-yagubov-prof-var38 |
| math100.ru (с ответами) | |
| variant 179 | скачать |
| variant 180 | скачать |
| variant 181 | скачать |
| variant 182 | скачать |
| variant 183 | скачать |
| variant 184 | скачать |
| variant 185 | скачать |
| variant 186 | скачать |
| variant 187 | скачать |
| variant 188 | скачать |
| variant 189 | скачать |
| variant 190 | скачать |
| variant 191 | скачать |
| variant 192 | скачать |
| variant 193 | скачать |
| variant 194 | скачать |
| variant 195 | скачать |
| variant 196 | скачать |
| variant 197 | скачать |
| variant 198 | скачать |
| variant 199 | скачать |
| variant 200 | скачать |
| variant 201 | скачать |
| variant 202 | скачать |
| variant 203 | скачать |
| variant 204 | скачать |
| variant 205 | скачать |
| alexlarin.net | |
| Вариант 397 | проверить ответы |
| Вариант 398 | проверить ответы |
| Вариант 399 | проверить ответы |
| Вариант 400 | проверить ответы |
| Вариант 401 | проверить ответы |
| Вариант 402 | проверить ответы |
| Вариант 403 | проверить ответы |
| Вариант 404 | проверить ответы |
| Вариант 405 | проверить ответы |
| Вариант 406 | проверить ответы |
| Вариант 407 | проверить ответы |
| Вариант 408 | проверить ответы |
| Вариант 409 | проверить ответы |
| Вариант 410 | проверить ответы |
| Вариант 411 | проверить ответы |
| Вариант 412 | проверить ответы |
| Вариант 413 | проверить ответы |
| vk.com/ege100ballov | |
| вариант 1 | скачать |
| вариант 2 | скачать |
| вариант 3 | скачать |
| вариант 4 | скачать |
| вариант 5 | скачать |
| вариант 6 | скачать |
| вариант 7 | скачать |
| вариант 8 | скачать |
| вариант 9 | скачать |
| вариант 10 | скачать |
| вариант 11 | скачать |
| vk.com/math.studying | |
| Вариант 1 | ответы |
| vk.com/marsel_tutor | |
| Вариант 1 | разбор |
| Вариант 2 | конспект / разбор |
| Вариант 3 | конспект / разбор |
| Вариант 4 | конспект / разбор |
| Вариант 5 | конспект / разбор |
| Вариант 6 | разбор |
| vk.com/shkolkovo_easy_math | |
| Вариант 1 | решение |
| Вариант 2 | решение |
| Вариант 3 | решение |
| Вариант 5 | решение |
| Вариант 6 | решение |
| vk.com/mathlearn_ru | |
| вариант 1 | разбор |
| vk.com/ekaterina_chekmareva | |
| Вариант 1 | ответы |
| Вариант 2 | ответы |
| Вариант 3 | ответы |
| Вариант 4 | ответы |
| Вариант 5 | ответы |
| Вариант 6 | ответы |
| Вариант 7 | ответы |
| Вариант 8 | ответы |
Структура варианта КИМ ЕГЭ 2023 по математике профильного уровня
Экзаменационная работа состоит из двух частей и включает в себя 18 заданий, которые различаются по содержанию, сложности и количеству заданий:
– часть 1 содержит 11 заданий (задания 1–11) с кратким ответом в виде целого числа или конечной десятичной дроби;
– часть 2 содержит 7 заданий (задания 12–18) с развёрнутым ответом (полная запись решения с обоснованием выполненных действий).
Задания части 1 направлены на проверку освоения базовых умений и практических навыков применения математических знаний в повседневных ситуациях. Посредством заданий части 2 осуществляется проверка освоения математики на профильном уровне, необходимом для применения математики в профессиональной деятельности и на творческом уровне.
Задания части 1 предназначены для определения математических компетентностей выпускников образовательных организаций, реализующих программы среднего (полного) общего образования на базовом уровне. Задание с кратким ответом (1–11) считается выполненным, если в бланке ответов № 1 зафиксирован верный ответ в виде целого числа или конечной десятичной дроби.
Задания 12–18 с развёрнутым ответом, в числе которых 5 заданий повышенного уровня и 2 задания высокого уровня сложности, предназначены для более точной дифференциации абитуриентов вузов.
Примеры заданий:
1. Перед началом первого тура чемпионата по бадминтону участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 76 бадминтонистов, среди которых 22 спортсмена из России, в том числе Игорь Чаев. Найдите вероятность того, что в первом туре Игорь Чаев будет играть с каким-либо бадминтонистом из России.
2. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орёл не выпадет ни разу
3. На доске написали несколько не обязательно различных двузначных натуральных чисел без нулей в десятичной записи. Сумма этих чисел оказалась равной 363. Затем в каждом числе поменяли местами первую и вторую цифры (например, число 17 заменили на число 71).
а) Приведите пример исходных чисел, для которых сумма получившихся чисел ровно в 4 раза больше, чем сумма исходных чисел.
б) Могла ли сумма получившихся чисел быть ровно в 2 раза больше, чем сумма исходных чисел?
в) Найдите наибольшее возможное значение суммы получившихся чисел.
Смотрите также:
Пробные варианты по математике профильного уровня в формате ЕГЭ 2023 из различных источников.
Варианты составлены в соответствии с демоверсией 2023 года
Пробные варианты ЕГЭ 2023 по математике (профиль)
| egemath.ru | |
| вариант 1 | скачать |
| вариант 2 | скачать |
| вариант 3 | скачать |
| вариант 4 | скачать |
| вариант 5 | скачать |
| вариант 6 | скачать |
| time4math.ru | |
| вариант 1-2 | |
| yagubov.ru | |
| вариант 33 (сентябрь) | ege2022-yagubov-prof-var33 |
| вариант 34 (октябрь) | ege2022-yagubov-prof-var34 |
| вариант 35 (ноябрь) | ege2022-yagubov-prof-var35 |
| вариант 36 (декабрь) | ege2022-yagubov-prof-var36 |
| math100.ru (с ответами) | |
| variant 180 | скачать |
| variant 181 | скачать |
| variant 182 | скачать |
| variant 183 | скачать |
| variant 184 | скачать |
| variant 185 | скачать |
| variant 186 | скачать |
| variant 187 | скачать |
| variant 188 | скачать |
| alexlarin.net | |
| Вариант 400 | проверить ответы |
| Вариант 401 | проверить ответы |
| Вариант 402 | проверить ответы |
| Вариант 403 | проверить ответы |
| Вариант 404 | проверить ответы |
| Вариант 405 | проверить ответы |
| vk.com/ege100ballov | |
| вариант 1 | скачать |
| вариант 2 | скачать |
| вариант 3 | скачать |
| вариант 4 | скачать |
| вариант 5 | скачать |
| вариант 6 | скачать |
| вариант 7 | скачать |
| vk.com/shkolkovo_easy_math | |
| Вариант 1 | решение |
| Вариант 2 | решение |
| Вариант 3 | решение |
| Вариант 5 | решение |
Экзаменационная работа состоит из двух частей, включающих в себя 18 заданий.
Часть 1 содержит 11 заданий с кратким ответом базового и повышенного уровней сложности.
Часть 2 содержит 7 заданий с развёрнутым ответом повышенного и высокого уровней сложности.
На выполнение экзаменационной работы по математике отводится 3 часа 55 минут (235 минут).
Связанные страницы:
Пробные варианты ЕГЭ 2022 по математике (профильный уровень)
Сборник задач по стереометрии для 10-11 классов
Задание 10 по профильной математике — новые задачи по теории вероятностей в ЕГЭ-2022
Тест по теме «Производная» 11 класс алгебра с ответами
Основные тригонометрические тождества и формулы
Критерии
Оценивание
| № задания | 1-11 | 12, 14, 15 | 13, 16 | 17, 18 | Всего |
|---|---|---|---|---|---|
| Баллы | 1 | 2 | 3 | 4 | 31 |
Экзаменационная работа состоит из двух частей, включающих в себя 18 заданий. Часть 1 содержит 11 заданий базового уровня сложности с кратким ответом. Часть 2 содержит 7 заданий с развёрнутым ответом повышенного и высокого уровней сложности.
На выполнение экзаменационной работы по математике отводится 3 часа 55 минут (235 минут).
Ответы к заданиям 1–11 записываются в виде целого числа или конечной десятичной дроби. Числа запишите в поля ответов в тексте работы, а затем перенесите в бланк ответов № 1, выданный на экзамене!
При выполнении работы Вы можете воспользоваться справочными материалами, выдаваемыми вместе с работой.
Разрешается использовать только линейку, но можно сделать циркуль своими руками. Запрещается использовать инструменты с нанесёнными на них справочными материалами. Калькуляторы на экзамене не используются.
На экзамене при себе надо иметь документ удостоверяющий личность (паспорт), пропуск и капиллярную или гелевую ручку с черными чернилами! Разрешают брать с собой воду (в прозрачной бутылке) и еду (фрукты, шоколадку, булочки, бутерброды), но могут попросить оставить в коридоре.
| № задания | 1-11 | 12, 14, 15 | 13, 16 | 17, 18 | Всего |
|---|---|---|---|---|---|
| Баллы | 1 | 2 | 3 | 4 | 31 |
Экзаменационная работа состоит из двух частей, включающих в себя 18 заданий. Часть 1 содержит 11 заданий базового уровня сложности с кратким ответом. Часть 2 содержит 7 заданий с развёрнутым ответом повышенного и высокого уровней сложности.
На выполнение экзаменационной работы по математике отводится 3 часа 55 минут (235 минут).
Ответы к заданиям 1–11 записываются в виде целого числа или конечной десятичной дроби. Числа запишите в поля ответов в тексте работы, а затем перенесите в бланк ответов № 1, выданный на экзамене!
При выполнении работы Вы можете воспользоваться справочными материалами, выдаваемыми вместе с работой.
Разрешается использовать только линейку, но можно сделать циркуль своими руками. Запрещается использовать инструменты с нанесёнными на них справочными материалами. Калькуляторы на экзамене не используются.
На экзамене при себе надо иметь документ удостоверяющий личность (паспорт), пропуск и капиллярную или гелевую ручку с черными чернилами! Разрешают брать с собой воду (в прозрачной бутылке) и еду (фрукты, шоколадку, булочки, бутерброды), но могут попросить оставить в коридоре.
Шкалирование
| Первичный | Тестовый | Оценка |
|---|---|---|
| 5-6 | 27-34 | 3 |
| 7-8 | 40-46 | 4 |
| 9-10 | 52-58 | |
| 11-12-13 | 64-66-68 | 5 |
| 14-15-16 | 70-72-74 | |
| 17-18-19 | 76-78-80 | |
| 20-21-22 | 82-84-86 | |
| 23-24-25 | 88-90-92 | |
| 26-27-28 | 94-96-98 | |
| 29-30-31 | 100 |
| Первичный балл / Тестовый балл |
5/27 | 6/34 | 7/40 | 8/46 | 9/52 | 10/58 | 11/64 | 12/66 | 13/68 | 14/70 |
|---|---|---|---|---|---|---|---|---|---|---|
| 15/72 | 16/74 | 17/76 | 18/78 | 19/80 | 20/82 | X / 2X+42 | 29+ / 100 |
ЕГЭ по математике — Профиль 2023. Открытый банк заданий с ответами.