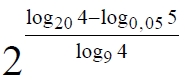Задание 1
Оплата за использование природного газа составляла 20 рублей на одного человека в месяц. С нового года она повысилась на 20%. Сколько рублей должна заплатить семья из трех человек за использование природного газа за три месяца в новом году?
Ответ: 216
Скрыть
После повышения цены на 20%, оплата стала $$20cdot1,2=24$$ рубля за 1 человека
$$24cdot3cdot3=216$$ рублей за 3 человека за 3 месяца
Задание 2
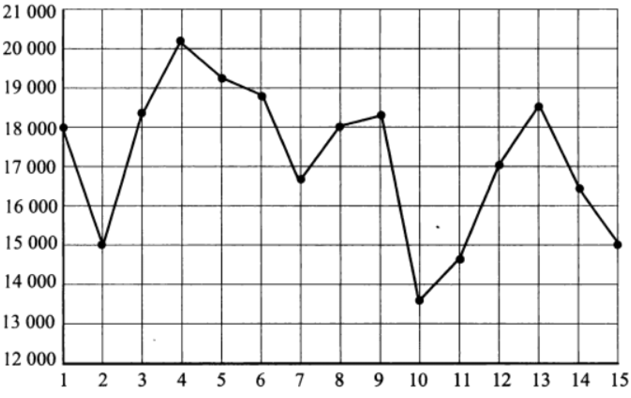
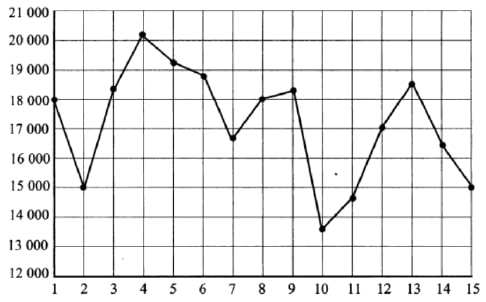
На рисунке жирными точками показана дневная аудитория некоторого сайта во все дни с 1 по 15 апреля 2020 года. По горизонтали указываются числа месяца, по вертикали — количество человек, посетивших сайт хотя бы раз за день. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, сколько суток из данного периода дневная аудитория сайта была между 16000 и 19000 человек.
Ответ: 9
Задание 3
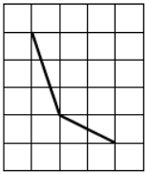
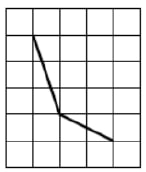
На клетчатой бумаге изображен угол. Найдите его величину.
Ответ дайте в градусах.
Ответ: 135
Скрыть
Видно, что искомый угол это $$90°+α+β$$
Легче всего работать через тангенсы, т.к. не будет корней
Определяем из прямоугольных треугольников
$$tg α=frac{1}{3}, tgβ=0.5$$
$$tg(α+β)=frac{tg α+tg β}{1-tg αcdottg β}$$ – известная формула
$$tg(α+β)=1$$
Значит $$α+β=45°$$
$$90°+45°=135°$$
Задание 4
Пресс изготавливает стеклянные тарелки. Вероятность того, что готовая тарелка будет с дефектом, равна 0,05. Перед упаковкой каждая тарелка проходит систему контроля. Вероятность того, что система забракует тарелку с дефектом, равна 0,94. Вероятность того, что система по ошибке забракует тарелку без дефектов, равна 0,01. Найдите вероятность того, что случайно выбранная изготовленная тарелка будет забраковано системой контроля.
Ответ: 0,0565
Скрыть
Вероятность, что тарелку с дефектом забракуют $$P(A)=0,94cdot0,05$$
Вероятность, что тарелку без дефекта забракуют $$P(B)=(1-0,05)cdot0,01$$
$$P(A+B)=P(A)+P(B)=0,0565$$
Задание 5
Решите уравнение $$sqrt[3]{8x+4}-sqrt[3]{8x-4}=2$$. Если корней несколько, то в ответе укажите сумму всех корней уравнения.
Ответ: 0
Скрыть
Нужно как то упростить уравнение, сделаем замену на $$8x+4=t$$
$$8x−4=(8x+4)−8=t−8$$
$$t^{frac{1}{3}}−(t−8)^{frac{1}{3}}=2$$
$$t^{frac{1}{3}}=(t−8)^{frac{1}{3}}+2$$
Возводим все в куб
$$t=t+6(t−8)^{frac{2}{3}}+12(x−8)^{frac{1}{3}}$$
$$6(t−8)^{frac{1}{3}}((t−8)^{frac{1}{3}}+2)=0$$
$$t=8$$
$$t=0$$
Делаем обратную замену и получаем ответ
$$x=0,5$$
$$x=-0,5$$
$$0,5+(-0,5)=0$$
Задание 6
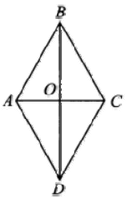
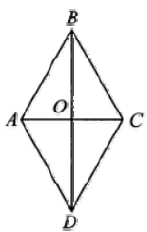
Диагонали ромба относятся как 5:12. Площадь ромба равна 30. Найдите периметр ромба.
Ответ: 26
Скрыть
$$S=frac{1}{2}d_1cdot d_2$$, $$d_1,d_2$$ — диагонали ромба
Обозначим $$d_1=12x, d_2=5x$$
$$S=120x^2=30$$
$$x=0,5$$ (сторона неотрицательна)
Тогда сторону ромба можем найти по теореме Пифагора $$sqrt{25x^2+144x^2}=13x$$
Периметр $$4cdotsqrt{25x^2+144x^2}=26$$
Задание 7
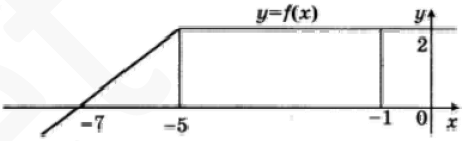
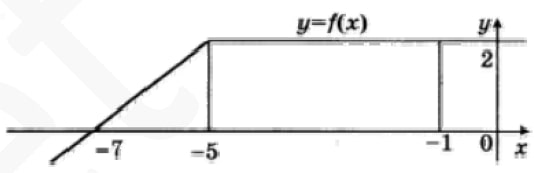
На рисунке изображен график некоторой функции $$y=f(x)$$. Пользуясь рисунком, найдите интеграл $$int^{-1}_{-7}f(x)dx.$$
Ответ: 10
Скрыть
Геометрический смысл интеграла – это площадь под графиков ф-ции, ее легко найти из рисунка как площадь трапеции.
$$S=frac{6+4}{2}cdot2=10$$
Задание 8
Найдите объём правильной шестиугольной пирамиды, если её боковое ребро равно 6, а радиус окружности, описанной около основания, равен 3.
Ответ: 40,5
Скрыть
$$V=frac{1}{3}S_{осн}cdot h$$
Помним важное свойство правильный шестиугольной пирамиды – радиус описанной окружности около основания равен стороне правильной шестиугольной пирамиды (это следует из того что все 6 треугольников, которые образуют шестиугольник – правильные, т.е. равносторонние).
$$a=R=3$$
Осталось только найти высоту пирамиды. Это легко можно сделать по теореме Пифагора, т.к. мы знаем боковую сторону и сторону основания.
$$h=sqrt{36−9}=sqrt{27}=3sqrt{3}$$
$$S_{осн}=6S_{правильных,треуг}=6cdotfrac{a^2sqrt{3}}{4}$$
$$V=frac{1}{3}cdot6cdotfrac{a^2sqrt{3}}{4}cdot3sqrt{3}=40,5$$
Задание 9
Найдите значение выражения $$2^{frac{log_{20}4-log_{0,05}5}{log_9 4}}$$
Ответ: 3
Скрыть
$$2^{frac{log_{20}4+log_{20}5}{log_9 4}}=2^{frac{1}{log94}}=2^{log_4 9}=2^{log_2 3}=3$$
Задание 10
Амплитуда колебаний маятника зависит от частоты вынуждающей силы и определяется по формуле $$A(omega)=frac{A_0^2omega^2_p}{|omega^2_p-omega^2|}$$, где $$omega$$ — частота вынуждающей силы в (с-1), $$A_0$$ — постоянный параметр, $$omega_p = 450$$ c-1 — резонансная частота. Найдите минимальную частоту $$omega$$, большую резонансной, для которой амплитуда колебаний превосходит величину $$A_0$$ не более, чем на $$frac{2}{7}A_0$$. Ответ выразите в с-1.
Ответ: 600
Скрыть
$$frac{A_0^2omega^2_p}{|omega^2_p-omega^2|}leq A_0+frac{2}{7}A_0$$
Из этого неравенство можно легко найти
$$omegageqfrac{4cdotomega_p}{3}$$ (не забываем, что частота – положительный параметр)
И модуль мы точно можем раскрыть со знаком -, т.к $$omega>omega_p$$
$$omegageq600$$
Задание 11
Петя и Вася живут в деревне в соседних домах и учатся в одной школе. Петя вышел в школу в 7:34, а Вася — в 7:40. Вася догнал Петю в 8:04 и 10 минут шли вместе. Затем Вася зашагал в своем привычном темпе. На сколько минут опоздал Петя, если урок начинается в 8:30, а Вася вошел в класс со звонком?
(Автор задачи Николай Журавлев)
Ответ: 4
Скрыть
$$S=vt$$
Из условия можно найти время движения Пети и Васи перед встречей
$$8:04−7:34=30$$ минуты шел Петя
$$8:04−7:40=24$$ минуты шел Вася
Пусть скорость Пети $$x$$, а Пети $$y$$ (размерность пусть будет м/мин). Отсюда
$$x=frac{4}{5}y$$ ($$30x=24y$$ – т.к они прошли одинаковое расстояние)
После 8:04 они 10 минут шли вместе. Мы знаем что Вася шел 16 минут (т.к. по условию он пришел в 8:30), обозначим время за которое пришел Петя в класс за $$t$$. Т.к. они прошли одинаковый путь:
$$16y=tcdotfrac{4}{5}y$$
$$t=20$$
Т.е. Петя пришел в $$8:14+20=8:34$$
Опоздал на $$4$$ минуты
Задание 12
Найдите наибольшее значение функции $$y=3cos x+frac{12}{pi}x-3$$ на отрезке $$[-frac{pi}{4};0]$$
Ответ: 0
Скрыть
Найдем критические точки:
$$y’=−3sin x+frac{12}{π}=0$$
$$sin x=frac{4}{π}>1$$ — тут нет решения, т.к. множество значений синуса $$[-1;1]$$
Значит, наибольшее значение будет достигаться на концах отрезка.
Наибольшее значение будет в точке 0.
$$y(0)=0$$
Задание 13
А) Решите уравнение $$2sin^2 x+sin xcos x+sqrt{3}(sin 2x+cos^2 x)=0$$
Б) Укажите корни этого уравнения, принадлежащие отрезку $$[frac{5pi}{6};frac{11pi}{6}]$$
Ответ: А)$$-frac{pi}{3}+pi n;-arctgfrac{1}{2}+pi n,nin Z$$ Б)$$frac{5pi}{3};pi-arctgfrac{1}{2}$$
Задание 14
Плоскость $$alpha$$ проходит через середины двух противоположных ребер треугольной пирамиды и параллельна медиане одной из ее граней.
А) Докажите, что среди медиан граней этой пирамиды в точности две являются параллельными к плоскости $$alpha$$
Б) Найдите площадь сечения данной пирамиды плоскостью $$alpha$$, если эти медианы перпендикулярны друг другу и равны 2.
(Автор задачи Николай Журавлев)
Ответ: 2
Задание 15
Решите неравенство $$((frac{1}{3})^{sqrt{x+4}}-(frac{1}{3})^{sqrt{x^2+3x+4}})cdot(|x|-5)geq0$$
Ответ: $$[-2;0],[5;infty)$$
Задание 16
В треугольнике АВС на сторонах АВ и ВС заданы соответственно точки М и N такие, что АМ=МВ, BN:NC=1:2. Отрезки СМ и AN пересекаются в точке О.
А) Докажите, что расстояние от точки О до прямой АС равно $$frac{2}{5}BH$$, где ВН высота треугольника АВС.
Б) Найдите расстояние от точки О до прямой АС, если $$angle BAC = 30^{circ}, angle BCA = 45^{circ}, AC = 8$$
Ответ: $$frac{8(sqrt{3}-1)}{5}$$
Задание 17
В июле 2026 года планируется взять кредит в банке на пять лет в размере S тыс. рублей. Условия его возврата таковы:
— каждый январь долг возрастает на 30% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;
— в июле 2027, 2028 и 2029 годов долг остаётся равным S тыс. рублей;
— выплаты в 2030 и 2031 годах равны по 338 тыс. рублей;
— к июлю 2031 года долг будет выплачен полностью.
Найдите общую сумму выплат за пять лет.
Ответ: 1090 тыс. рублей
Задание 18
При каких значениях параметра $$a$$ уравнения $$4^{x+1}+2^{x+4}=2^{x+2}+16$$ и $$|a-9|cdot3^{x-2}+acdot9^{x-1}=1$$ равносильны?
Ответ: $$left{-9right},[0;9]$$
Задание 19
В школах №1 и №2 учащиеся писали тест. Из каждой школы тест писали не меньше 2 учащихся. Каждый учащийся, писавший тест, набрал натуральное количество баллов. Оказалось, что в каждой школе средний балл за тест был целым числом, причем в школе №1 средний балл равнялся 18. Один из учащихся, писавших тест, перешел из школы №1 в школу №2, а средние баллы за тест были пересчитаны в обеих школах. В результате средний балл в школе №1 вырос на 10%.
А) Сколько учащихся могло писать тест в школе №1 изначально?
Б) В школе №1 все писавшие тест набрали разное количество баллов. Какое наибольшее количество баллов мог набрать учащийся этой школы?
В) Известно, что изначально в школе №2 писали тест более 10 учащихся и после перехода одного учащегося в эту школу и пересчета баллов средний балл в школе №2 также вырос на 10%. Какое наименьшее количество учащихся могло писать тест в школе №2 изначально?
Ответ: А) 6, Б) 89, В) 19
Решение и ответы заданий № 1–12 варианта №345 Александра Ларина. Разбор ЕГЭ 2020 по математике (профильный уровень).
Задание 1.
Оплата за использование природного газа составляла 20 рублей на одного человека в месяц. С нового года она повысилась на 20%. Сколько рублей должна заплатить семья из трех человек за использование природного газа за три месяца в новом году?
Задание 2.
На рисунке жирными точками показана дневная аудитория некоторого сайта во все дни с 1 по 15 апреля 2020 года. По горизонтали указываются числа месяца, по вертикали – количество человек, посетивших сайт хотя бы раз за день. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, сколько суток из данного периода дневная аудитория сайта была между 16000 и 19000 человек.
Задание 3.
На клетчатой бумаге изображен угол. Найдите его величину. Ответ дайте в градусах.
Задание 4.
Пресс изготавливает стеклянные тарелки. Вероятность того, что готовая тарелка будет с дефектом, равна 0,05. Перед упаковкой каждая тарелка проходит систему контроля. Вероятность того, что система забракует тарелку с дефектом, равна 0,94. Вероятность того, что система по ошибке забракует тарелку без дефектов, равна 0,01. Найдите вероятность того, что случайно выбранная изготовленная тарелка будет забраковано системой контроля.
Задание 5.
Решите уравнение Если корней несколько, то в ответе укажите сумму всех корней уравнения.
Задание 6.
Диагонали ромба относятся как 5:12. Площадь ромба равна 30. Найдите периметр ромба.
Задание 7.
На рисунке изображен график некоторой функции y = f(x). Пользуясь рисунком, найдите интеграл .
Задание 8.
Найдите объём правильной шестиугольной пирамиды, если её боковое ребро равно 6, а радиус окружности, описанной около основания, равен 3.
Задание 9.
Найдите значение выражения
Задание 10.
Амплитуда колебаний маятника зависит от частоты вынуждающей силы и определяется по формуле 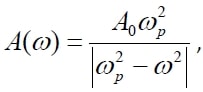
. Ответ выразите в с‐1.
Задание 11.
Петя и Вася живут в деревне в соседних домах и учатся в одной школе. Петя вышел в школу в 7:34, а Вася – в 7:40. Вася догнал Петю в 8:04 и 10 минут шли вместе. Затем Вася зашагал в своем привычном темпе. На сколько минут опоздал Петя, если урок начинается в 8:30, а Вася вошел в класс со звонком?
(Автор задачи Николай Журавлев)
Задание 12.
Найдите наибольшее значение функции y = 3cos x + – 3 на отрезке [
; 0]
Источник варианта: alexlarin.net
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 0 / 5. Количество оценок: 0
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
Тренировочный вариант №345 Алекса Ларина ОГЭ 2023 по математике 9 класс с ответами и решением, который вышел на сайте 29 января 2022 года, по новой демоверсии ОГЭ 2023 года ФИПИ усложнённая и лёгкая версия варианта.
вариант_345_ларин_огэ2023
Задания с 1 варианта
На рисунке (см. выше) изображён план местности. Длина стороны каждой клетки на плане соответствует 2 км. Антон Сергеевич живёт в деревне Котенково. В субботу он хочет съездить в районный центр Собачково. Туда можно добраться по прямой грунтовой дороге, а можно доехать по шоссе до посёлка Хомяковка и свернуть под прямым углом на другое шоссе, ведущее в Собачково.
Есть и третий путь: от Котенково по другой грунтовой дороге, идущей вдоль рощи, добраться до деревни Попугаевка, где свернуть на шоссе, ведущее в Собачково. Грунтовые дороги образуют с шоссе прямоугольные треугольники. По шоссе Антон Сергеевич едет со скоростью 72 км/ч, а по грунтовой дороге – 50 км/ч.
1. Определите, какие месяцы соответствуют указанному в таблице трафику мобильного интернета. Заполните таблицу. В ответе запишите последовательность четырёх чисел без пробелов, запятых и других разделительных символов.
2. Сколько километров проедет Антон Сергеевич, если поедет по шоссе через посёлок Хомяковка?
3. Найдите расстояние (в км) по прямой грунтовой дороге от Котенково до Собачково.
4. Сколько минут потратит Антон Сергеевич на дорогу, если поедет мимо рощи через деревню Попугаевка?
5. В таблице (см. ниже) указана стоимость в рублях некоторых товаров в четырёх магазинах, расположенных в населённых пунктах Котенково, Хомяково, Попугаевка и Собачково. Антон Сергеевич хочет купить две булки белого хлеба, 4 кг зелёных яблок и 0,5 кг сала. В каком магазине такой набор товаров будет стоить дешевле всего? В ответе укажите стоимость данного набора товаров в выбранном магазине в рублях.
10. Девятиклассники Петя, Катя, Ваня, Даша и Наташа бросили жребий, кому начинать игру. Найдите вероятность того, что жребий начинать игру Кате не выпадет.
14. Клиент взял в банке кредит в размере 50 000 р. на 5 лет под 20% годовых. Какую сумму он должен вернуть в банк в конце срока, если проценты начисляются ежегодно на текущую сумму долга и весь кредит с процентами возвращается в банк после срока?
16. Длина хорды окружности равна 64, а расстояние от центра окружности до этой хорды равно 24. Найдите диаметр этой окружности.
17. Боковая сторона равнобедренного треугольника равна 68, а основание равно 120. Найдите площадь этого треугольника.
19. Какие из следующих утверждений верны? Если верных утверждений несколько, запишите их номера в порядке возрастания без пробелов, запятых и других разделительных символов.
- 1) Диаметр делит окружность на две равные дуги.
- 2) Параллелограмм имеет две оси симметрии.
- 3) Площадь треугольника равна его основанию, умноженному на высоту.
21. Первая труба пропускает на 3 литра воды в минуту меньше, чем вторая труба. Сколько литров воды в минуту пропускает вторая труба, если резервуар объёмом 260 литров она заполняет на 6 минут быстрее, чем первая труба?
Задания с 2 варианта
Общепринятые форматы листов бумаги обозначают буквой А и цифрой: А0, А1, А2 и так далее. Лист формата А0 имеет форму прямоугольника, площадь которого равна 1 кв. м. Если лист формата А0 разрезать пополам параллельно меньшей стороне, получается два равных листа формата А1. Если лист А1 разрезать так же пополам, получается два листа формата А2. И так далее. Отношение большей стороны к меньшей стороне листа каждого формата одно и то же, поэтому листы всех форматов подобны. Это сделано специально для того, чтобы пропорции текста и его расположение на листе сохранялись при уменьшении или увеличении шрифта при изменении формата листа.
1. В таблице даны размеры (с точностью до мм) четырёх листов, имеющих форматы А3, А4, А5 и А6. Установите соответствие между форматами и номерами листов. Заполните таблицу. В ответе запишите последовательность четырёх чисел без пробелов и других разделительных символов.
2. Сколько листов формата А5 получится из одного листа формата А0?
3. Найдите длину (в мм) меньшей стороны листа бумаги формата А2.
4. Найдите площадь листа формата А3. Результат (если нужно) округлите до десятков.
5. Бумагу формата А4 упаковали в пачки по 500 листов. Найдите массу (в граммах) пачки, если плотность бумаги равна 80 г/м2. Результат (если нужно) округлите до сотен.
10. Тайное голосование – это голосование, при котором учитывается лишь число голосов, поданных за каждого кандидата, и не учитывается, кто за кого голосовал персонально. Общество из 6 членов выбирает из своего состава одного представителя. Сколькими способами может произойти тайное голосование?
14. При свободном падении тело прошло в первую секунду 5 м, а в каждую следующую на 10 м больше. Найдите глубину шахты (в метрах), если свободно падающее тело достигло его дна через 5 с после начала падения.
18. Пит на квадратном холсте нарисовал композицию из прямоугольников (см. рис.) На рисунке даны площади нескольких прямоугольников, в том числе синего и красного квадратов. Чему равна сумма площадей двух серых прямоугольников?
- Варианты математика 9 класс ОГЭ 2023 статград
- ОГЭ 2023 текстовые задачи по математике 9 класс и ответы
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
А. Ларин. Тренировочный вариант № 345.
При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
Версия для печати и копирования в MS Word
1
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
2
Плоскость α проходит через середины двух противоположных ребер треугольной пирамиды и параллельна медиане одной из ее граней.
а) Докажите, что среди медиан граней этой пирамиды в точности две являются параллельными к плоскости α.
б) Найдите площадь сечения данной пирамиды плоскостью α, если эти медианы перпендикулярны друг другу и равны 2.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
3
Решите неравенство
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
4
В треугольнике ABC на сторонах AB и BC заданы соответственно точки M и N такие, что AM = MB, BN : NC = 1 : 2. Отрезки CM и AN пересекаются в точке O.
а) Докажите, что расстояние от точки O до прямой AC равно где BH высота треугольника ABC.
б) Найдите расстояние от точки O до прямой AC, если ∠BAC = 30°, ∠BCA = 45°, AC = 8.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
5
В июле 2026 года планируется взять кредит на пять лет в размере S тыс.рублей. Условия его возврата таковы:
— каждый январь долг возрастает на 30% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;
— в июле 2027, 2028 и 2029 годов долг остается равным S тыс. рублей;
— выплаты в 2030 и 2031 годах равны по 338 тыс.рублей;
— к июлю 2031 года долг будет выплачен полностью.
Найдите общую сумму выплат за пять лет.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
6
Найдите все значения параметра а, при которых уравнения и
равносильны.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
7
В школах № 1 и № 2 учащиеся писали тест. Из каждой школы тест писали не меньше двух учащихся. Каждый учащийся, писавший тест, набрал натуральное количество баллов. Оказалось, что в каждой школе средний балл за тест был целым числом, причем в школе № 1 средний балл равнялся 18. Один из учащихся, писавших тест, перешел из школы № 1 в школу № 2, а средние баллы за тест были пересчитаны в обеих школах. В результате средний балл в школе № 1 вырос на 10%.
а) Сколько учащихся могло писать тест в школе № 1 изначально?
б) В школе № 1 все писавшие тест набрали разное количество баллов. Какое наибольшее количество баллов мог набрать учащийся этой школы?
в) Известно, что изначально в школе № 2 писали тест более 10 учащихся и после перехода одного учащегося в эту школу и пересчета баллов средний балл в школе № 2 также вырос на 10%. Какое наименьшее количество учащихся могло писать тест в школе № 2 изначально?
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
Завершить тестирование, свериться с ответами, увидеть решения.
| Автор | Сообщение | |||
|---|---|---|---|---|
|
Заголовок сообщения: Тренировочный вариант №345
|
||||
|
http://alexlarin.net/ege/2021/trvar345.html |
|||
  |
||||
|
|
||||
|
An_na |
Заголовок сообщения: Re: Тренировочный вариант №345
|
|||
|
13 Подробности: 15 Подробности: 16 Подробности: 17 Подробности: 18 Подробности: |
|||
  |
||||
|
hpbhpb |
Заголовок сообщения: Re: Тренировочный вариант №345
|
|||
|
An_na писал(а): 13 Подробности: 15 Подробности: 16 Подробности: 17 Подробности: 18 Подробности: Да. |
|||
  |
||||
|
Владимiръ |
Заголовок сообщения: Re: Тренировочный вариант №345
|
|||
|
Задача 19 Подробности: |
|||
  |
||||
|
netka |
Заголовок сообщения: Re: Тренировочный вариант №345
|
|||
|
Большое спасибо за интересный вариант! 14. Подробности: |
|||
  |
||||
|
ОГЭ_ЕГЭ |
Заголовок сообщения: Re: Тренировочный вариант №345
|
|||
|
Доброго времени суток ! 13 б) 5п/3; 2п-arctg(1/2) |
|||
  |
||||
|
khazh |
Заголовок сообщения: Re: Тренировочный вариант №345
|
|||
|
netka писал(а): Большое спасибо за интересный вариант! 14. Подробности: Да. |
|||
  |
||||
|
netka |
Заголовок сообщения: Re: Тренировочный вариант №345
|
|||
|
khazh писал(а): Да. Спасибо, Елена Ильинична! ОГЭ_ЕГЭ писал(а): 13 б) 5п/3; 2п-arctg(1/2) из второй серии корень не входит в указанный промежуток, там предыдущий корень войдёт |
|||
  |
||||
|
ОГЭ_ЕГЭ |
Заголовок сообщения: Re: Тренировочный вариант №345
|
|||
|
Спасибо, согласен ! |
|||
  |
||||
|
Raisa |
Заголовок сообщения: Re: Тренировочный вариант №345
|
|||
|
An_na писал(а): 18 Подробности: . У меня а in(-беск;9] из ур.|a-9|=9-a.В чем я неправа? |
|||
  |
||||
| Показать сообщения за: Сортировать по: |
Кто сейчас на форуме
|
Сейчас этот форум просматривают: нет зарегистрированных пользователей и гости: 1 |
|
Вы не можете начинать темы |
|
|
Шкалирование
| Первичный | Тестовый | Оценка |
|---|---|---|
| 5-6 | 27-34 | 3 |
| 7-8 | 40-46 | 4 |
| 9-10 | 52-58 | |
| 11-12-13 | 64-66-68 | 5 |
| 14-15-16 | 70-72-74 | |
| 17-18-19 | 76-78-80 | |
| 20-21-22 | 82-84-86 | |
| 23-24-25 | 88-90-92 | |
| 26-27-28 | 94-96-98 | |
| 29-30-31 | 100 |
| Первичный балл / Тестовый балл |
5/27 | 6/34 | 7/40 | 8/46 | 9/52 | 10/58 | 11/64 | 12/66 | 13/68 | 14/70 |
|---|---|---|---|---|---|---|---|---|---|---|
| 15/72 | 16/74 | 17/76 | 18/78 | 19/80 | 20/82 | X / 2X+42 | 29+ / 100 |
На чтение 1 мин Просмотров 2 Опубликовано 5 марта, 2023
Решение варианта Ларина №345 ЕГЭ Решение и ответы на задачи на официальном сайте источника онлайн.
Решение и ответы заданий № 1–12 варианта №345 Александра Ларина. Разбор ЕГЭ 2021 по математике (профильный уровень).
Варианты ответов и решение задачи ТУТ: https://ege314.ru/ege-varianty-larina/reshenie-varianta-larina-345-ege/
Ответы и решение задачи онлайн
Оставляйте комментарии на сайте, обсуждайте их решения и ответы, предлагайте альтернативные варианты ответов.