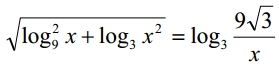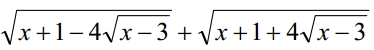Задание 1
В маршрутном такси 20 посадочных мест. Какое минимальное количество такси потребуется для того, чтобы перевезти 87 учащихся от школы до Дворца Спорта, если каждое такси будет заполнено школьниками на 90%?
Ответ: 5
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 2
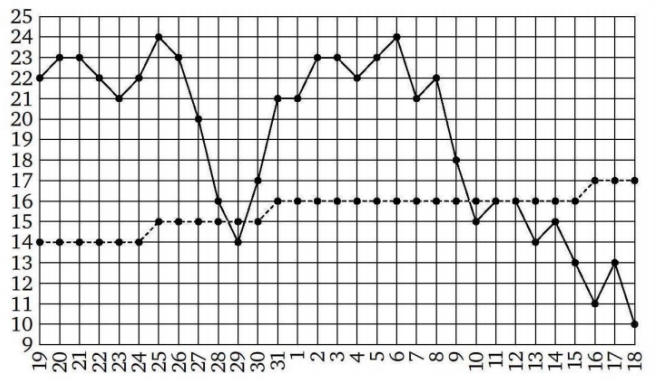
На рисунке жирными точками показаны среднесуточная температура в Москве в период с 19 мая 2014 года по 18 июня 2014 года и климатические нормы среднесуточной температуры за соответствующий период. По горизонтали указываются дни, по вертикали – температура в градусах Цельсия. Для наглядности жирные точки, соответствующие среднесуточной температуре, соединены сплошной линией, а точки, соответствующие климатической норме, ‐ пунктирной линией.
Определите по рисунку наибольшую разность между среднесуточной температурой и климатической нормой среднесуточной температуры. Ответ дайте в градусах Цельсия.
Ответ: 9
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 3
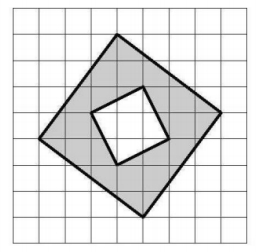
Найдите площадь закрашенной фигуры, изображенной на клетчатой бумаге со стороной клетки 1 см. Ответ выразите в квадратных сантиметрах
Ответ: 20
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 4
Игрок зажал в кулаке носовой платок так, что между пальцами торчат только четыре уголка. Второй игрок наудачу выбирает два уголка. Он выигрывает, если взял платок за диагональ, и проигрывает в противном случае. Найдите вероятность выигрыша второго игрока. Ответ округлите до соты
Ответ: 0,33
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 5
Решите уравнение, указав в ответе корень уравнения или сумму корней, если их несколько: $$sqrt{log^{2}_{9}x+log_{3}x^{2}}=log_{3}frac{9sqrt{3}}{x}$$
Ответ: 3
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 6
В треугольник ABC со сторонами AB=10 и BC=8 вписана окружность с центром O. Прямая BO пересекает сторону AC в точке K. Найдите CK, если AC=9.
Ответ: 4
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 7
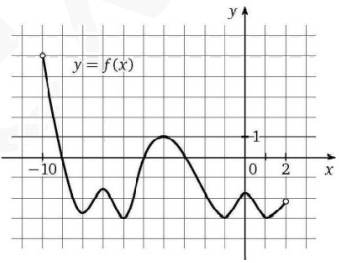
На рисунке изображен график функции $$y=f(x)$$, определенной и дифференцируемой на интервале $$(-10;2)$$. Найдите наименьшую из длин промежутков, в каждой точке каждого из которых производная этой функции неположительна.
Ответ: 1
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 8
Найдите объём треугольной пирамиды DABC, если AB=30, BC=CA=17 и все двугранные углы при основании равны 45о.
Ответ: 150
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 9
Найдите значение выражения: $$sqrt{x+1-4sqrt{x-3}}+sqrt{x+1+4sqrt{x-3}}$$, если $$x=3,185$$
Ответ: 4
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 10
Уравнение процесса, в котором участвовал газ, записывается в виде $$pV^{a}=const$$ , где $$p$$ (Па) – давление в газе, V ‐ объем газа в кубических метрах, a ‐ положительная константа. При каком наименьшем значении константы a уменьшение вдвое объема газа, участвующего в этом процессе, приводит не менее чем к четырехкратному увеличению давления?
Ответ: 2
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 11
Имеется 2 раствора кислоты. Первый раствор состоит из 1056 г кислоты и 44 г воды, а второй – из 756 г кислоты и 1344 г воды. Из этих растворов нужно получить 1500 г нового раствора, содержание кислоты в котором 40%. Сколько граммов первого раствора нужно для этого взять?
Ответ: 100
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 12
Найдите наименьшее значение функции $$y=log_{0,5}(4^{x}-2^{x+2}+8)$$ на отрезке $$[-1;2]$$.
Ответ: -3
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 13
а) Решите уравнение $$10cos^{2}frac{x}{2}=frac{11+5ctg(frac{3pi}{2}-x)}{1+tg x}$$
б) Укажите корни этого уравнения, принадлежащие промежутку $$(-2pi;-frac{3pi}{2})$$
Ответ: А)$$frac{pi}{4}pm arccos frac{3sqrt{2}}{5}+2pi n,n in Z$$ Б) $$-frac{7pi}{4}pm arccos frac{3sqrt{2}}{5}$$
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 14
В правильной четырёхугольной призме ABCDA1B1C1D1стороны основания равны 4, боковые рёбра равны 6. Точка M –середина ребра СС1, на ребре BB1отмечена точка N, такая, что BN:NB1 =1:2.
а) В каком отношении плоскость AMN делит ребро DD1?
б) Найдите угол между плоскостями ABC и AMN.
Ответ: А)1:2 Б)$$arctg frac{sqrt{5}}{4}$$
Задание 15
Решите неравенство: $$lg(7^{2+log_{70}x}+frac{2}{10^{log_{70}x}})leq 2-log_{70}x$$
Ответ: (0;2]
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 16
В остроугольном треугольнике ABC высоты BB1и CC1пересекаются в точке H.
а) Докажите, что $$angle NAH=angle BB_{1}C_{1}$$
б) Найдите расстояние от цента описанной окружности треугольника ABC до стороны BC, если B1C1=12 и $$angle BAC=60^{circ}$$.
Ответ: $$4sqrt{3}$$
Задание 17
В офисном строении 8 этажей, на каждом из которых, кроме первого, находится кабинет начальника отдела. Управляющая жилищная компания объявила, что в день профилактического ремонта лифта он сделает всего один подъем сразу всех начальников отделов на один, указанный ими этаж. После подъема начальники будут вынуждены идти в свои кабинеты по лестнице. В качестве компенсации за причиненные неудобства за каждый необходимый подъем на очередной этаж по лестнице каждому начальнику будет начислено 200 рублей. За каждый аналогичный спуск – 100 рублей. Этаж необходимо выбрать так, чтобы общая сумма компенсаций была минимальной. Определите в рублях эту сумму.
Ответ: 1600 рублей
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 18
Найдите все значения параметра параметра а, при которых система уравнений: $$left{begin{matrix} 5|x|+12|y-2|=60\ y^{2}-a^{2}=4(y-1)-x^{2} end{matrix}right.$$ имеет ровно четыре решения.
Ответ: $$(-12;-5);4frac{8}{13};(5;12)$$
Задание 19
На доске записаны числа 1, 2, 3, …, 27. За один ход разрешается стереть произвольные три числа, сумма которых меньше 31 и отлична от каждой из сумм троек чисел, стертых на предыдущих ходах.
а) Можно ли сделать 4 хода?
б) Можно ли сделать 9 ходов?
в) Какое наибольшее число ходов можно сделать?
Ответ: да,нет,5
А. Ларин. Тренировочный вариант № 332. (часть C).
При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
Версия для печати и копирования в MS Word
1
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие промежутку
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
2
В правильной четырёхугольной призме ABCDA1B1C1D1 стороны основания равны 4, боковые рёбра равны 6. Точка M — середина ребра СС1, на ребре BB1 отмечена точка N, такая, что BN : NB1 = 1 : 2.
а) В каком отношении плоскость AMN делит ребро DD1?
б) Найдите угол между плоскостями ABC и AMN.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
3
Решите неравенство
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
4
В остроугольном треугольнике ABC высоты BB1 и CC1 пересекаются в точке H.
а) Докажите, что
б) Найдите расстояние от центра описанной окружности треугольника ABC до стороны BC, если B1C1 = 12 и
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
5
В офисном строении 8 этажей, на каждом из которых, кроме первого, находится кабинет начальника отдела. Управляющая жилищная компания объявила, что в день профилактического ремонта лифта он сделает всего один подъем сразу всех начальников отделов на один, указанный ими, этаж. После подъема начальники будут вынуждены идти в свои кабинеты по лестнице.
В качестве компенсации за причиненные неудобства за каждый необходимый подъем на очередной этаж по лестнице каждому начальнику будет начислено 200 рублей. За каждый аналогичный спуск — 100 рублей. Этаж необходимо выбрать так, чтобы общая сумма компенсаций была минимальной. Определите в рублях эту сумму.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
6
Найдите все значения параметра параметра а, при которых система уравнений
имеет ровно четыре решения.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
7
На доске записаны числа 1, 2, 3, …, 27. За один ход разрешается стереть произвольные три числа, сумма которых меньше 31 и отлична от каждой из сумм троек чисел, стертых на предыдущих ходах.
а) Можно ли сделать 4 хода?
б) Можно ли сделать 9 ходов?
в) Какое наибольшее число ходов можно сделать?
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
Завершить тестирование, свериться с ответами, увидеть решения.
Решение и ответы заданий № 1–12 варианта №332 Александра Ларина. Разбор ЕГЭ 2021 по математике (профильный уровень).
Задание 1.
В маршрутном такси 20 посадочных мест. Какое минимальное количество такси потребуется для того, чтобы перевезти 87 учащихся от школы до Дворца Спорта, если каждое такси будет заполнено школьниками на 90%?
Задание 2.
На рисунке жирными точками показаны среднесуточная температура в Москве в период с 19 мая 2014 года по 18 июня 2014 года и климатические нормы среднесуточной температуры за соответствующий период. По горизонтали указываются дни, по вертикали – температура в градусах Цельсия. Для наглядности жирные точки, соответствующие среднесуточной температуре, соединены сплошной линией, а точки, соответствующие климатической норме, ‐ пунктирной линией.
Определите по рисунку наибольшую разность между среднесуточной температурой и климатической нормой среднесуточной температуры. Ответ дайте в градусах Цельсия.
Задание 3.
Найдите площадь закрашенной фигуры, изображенной на клетчатой бумаге со стороной клетки 1 см. Ответ выразите в квадратных сантиметрах.
Задание 4.
Игрок зажал в кулаке носовой платок так, что между пальцами торчат только четыре уголка. Второй игрок наудачу выбирает два уголка. Он выигрывает, если взял платок за диагональ, и проигрывает в противном случае. Найдите вероятность выигрыша второго игрока. Ответ округлите до сотых.
Задание 5.
Решите уравнение, указав в ответе корень уравнения или сумму корней, если их несколько:
Задание 6.
В треугольник ABC со сторонами AB = 10 и BC = 8 вписана окружность с центром O. Прямая BO пересекает сторону AC в точке K. Найдите CK, если AC = 9.
Задание 7.
На рисунке изображен график функции y = f(x), определенной и дифференцируемой на интервале (–10; 2). Найдите наименьшую из длин промежутков, в каждой точке каждого из которых производная этой функции неположительна.
Задание 8.
Найдите объём треугольной пирамиды DABC, если AB = 30, BC = CA= 17 и все двугранные углы при основании равны 45º.
Задание 9.
Найдите значение выражения:
если x = 3,185.
Задание 10.
Уравнение процесса, в котором участвовал газ, записывается в виде pVa = const, где p (Па) – давление в газе, V ‐ объем газа в кубических метрах, a ‐ положительная константа. При каком наименьшем значении константы a уменьшение вдвое объема газа, участвующего в этом процессе, приводит не менее чем к четырехкратному увеличению давления?
Задание 11.
Имеется 2 раствора кислоты. Первый раствор состоит из 1056 г кислоты и 44 г воды, а второй – из 756 г кислоты и 1344 г воды. Из этих растворов нужно получить 1500 г нового раствора, содержание кислоты в котором 40%. Сколько граммов первого раствора нужно для этого взять?
Задание 12.
Найдите наименьшее значение функции 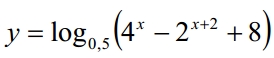
Источник варианта: alexlarin.net
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 0 / 5. Количество оценок: 0
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
| 2641 | Найдите все значения параметра а, при которых система уравнений { (5abs(x)+12abs(y-2)=60), (y^2-a^2=4(y-1)-x^2) :} имеет ровно четыре решения |
Тренировочный вариант 332 от Ларина Задание 18 | |
| 2640 | Игрок зажал в кулаке носовой платок так, что между пальцами торчат только четыре уголка. Второй игрок наудачу выбирает два уголка. Он выигрывает, если взял платок за диагональ, и проигрывает в противном случае. Найдите вероятность выигрыша второго игрока. Ответ округлите до сотых |
Игрок зажал в кулаке носовой платок так, что между пальцами торчат только четыре уголка ! Тренировочный вариант 332 от Ларина Задание 4 | |
| 2639 | Найдите значение выражения sqrt(x+1-4sqrt(x-3))+sqrt(x+1+4sqrt(x-3)) если x=3,185 |
Найдите значение выражения если x=3,185 ! Тренировочный вариант 332 от Ларина Задание 9 | |
| 2638 | Найдите объём треугольной пирамиды DABC, если AB=30, BC=CA=17 и все двугранные углы при основании равны 45^@ |
Найдите объём треугольной пирамиды DABC ! Тренировочный вариант 332 от Ларина Задание 8 | |
| 2637 | Имеется 2 раствора кислоты. Первый раствор состоит из 1056 г кислоты и 44 г воды, а второй – из 756 г кислоты и 1344 г воды. Из этих растворов нужно получить 1500 г нового раствора, содержание кислоты в котором 40%. Сколько граммов первого раствора нужно для этого взять? |
Имеется 2 раствора кислоты ! Тренировочный вариант 332 от Ларина Задание 11 | |
| 2636 | В остроугольном треугольнике ABC высоты BB1 и CC1 пересекаются в точке H. а) Докажите, что /_BAH=/_ BB1 C1. б) Найдите расстояние от цента описанной окружности треугольника ABC до стороны BC, если B1C1=12 и /_BAC=60^@ |
В остроугольном треугольнике ABC высоты BB1 и CC1 пересекаются в точке H ! Тренировочный вариант 332 от Ларина Задание 16 | |
| 2632 | а) Решите уравнение 10cos^2(x/2)=(11+5ctg((3pi)/2-x))/(1+tan(x)) б) Укажите корни этого уравнения, принадлежащие промежутку (-2pi; -(3pi)/2). |
Тренировочный вариант 332 от Ларина Задание 13 ЕГЭ | |
| 2631 | Решите неравенство lg(7^(2+log_{70}(x))+2/(10^(log_{70}(x))))<=2-log_{70}(x) |
Тренировочный вариант 332 от Ларина Задание 15 | |
| Clear |
Тренировочный вариант №332 Алекса Ларина ОГЭ 2023 по математике 9 класс с ответами и решением, который вышел на сайте 12 октября 2022 года, по новой демоверсии ОГЭ 2023 года ФИПИ.
Скачать 2 варианта с ответами
Тренировочный вариант 332 Ларина ОГЭ 2023 по математике 9 класс
вариант332-огэ2023-ларин
Пробный вариант ОГЭ 2023 состоит из двух модулей: «Алгебра» и «Геометрия». Всего в работе 25 заданий. Модуль «Алгебра» содержит семнадцать заданий: в части 1 — четырнадцать заданий; в части 2 — три задания. Модуль «Геометрия» содержит восемь заданий: в части 1 — пять заданий; в части 2 — три задания.
Задания и ответы
В горных районах, особенно в южных широтах с влажным климатом, земледельцы на склонах гор устраивают террасы (см. рис. выше). Земледельческие террасы – это горизонтальные площадки, напоминающие ступени. Во время дождя вода стекает с верхних террас вниз по специальным каналам. Поэтому почва на террасах не размывается и урожай не страдает.
Медленный сток воды с вершины склона вниз с террасы на террасу позволяет выращивать даже влаголюбивые культуры. В Юго Восточной Азии террасное земледелие широко применяется для производства риса, а в Средиземноморье – для выращивания винограда и оливковых деревьев.
Возделывание культур на террасах повышает урожайность, но требует тяжёлого ручного труда. Земледелец владеет несколькими участками, один из которых расположен на склоне холма. Ширина участка равна 40 м, а верхняя точка находится на высоте 12 м от подножия.
1.Земледелец на расчищенном склоне холма (ещё не террасированном) выращивал мускатный орех. Какова была площадь (в м2), отведённая под посевы?
Ответ: 35124
2.Затем земледелец решил устроить террасы на своём участке (см. рисунок ниже), чтобы выращивать рис, пшено или кукурузу. Строительство террас возможно, если угол склона (уклон) не больше 50% (тангенс угла наклона, умноженный на 100%). Сколько процентов составляет уклон? Ответ округлите до десятых.
Ответ: 150
3.На сколько процентов сократилась посевная площадь после того, как земледелец устроил террасы? Ответ округлите до десятых.
Ответ: 8
4.Земледелец получает 650 г бурого риса с одного квадратного метра засеянной площади. При шлифовке из бурого риса получается белый рис, но при этом теряется 16% массы. Сколько килограммов белого риса получит земледелец со всего своего участка?
Ответ: 13,5
5.В таблице дана урожайность культур, которые может засеять земледелец на своём террасированном участке. За год обычно собирается два урожая: летом и осенью. По данным таблицы посчитайте наибольшее число килограммов урожая, которое может собрать земледелец с участка за один год, если он может засевать разные культуры.
Ответ: 50
10.Для экзамена подготовили билеты с номерами от 1 до 25. Какова вероятность того, что наугад взятый учеником билет имеет номер, являющийся двузначным числом?
Ответ: 0,9
17.Найдите площадь квадрата, описанного около окружности радиуса 25.
Ответ: 30
19.Какие из следующих утверждений верны? Если верных утверждений несколько, запишите их номера в порядке возрастания без пробелов, запятых и других разделительных символов. 1) Диагонали ромба равны. 2) Отношение площадей подобных треугольников равно коэффициенту подобия. 3) В треугольнике против большего угла лежит большая сторона.
Ответ: 1
25.Вершины ромба расположены на сторонах параллелограмма, а стороны ромба параллельны диагоналям параллелограмма. Найдите отношение площадей ромба и параллелограмма, если отношение диагоналей параллелограмма равно 9 .
Ответ: 120
Варианты в формате ОГЭ 2023 по математике 9 класс
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
На чтение 1 мин Просмотров 1 Опубликовано 5 марта, 2023
Решение варианта Ларина №332 ЕГЭ Решение и ответы на задачи на официальном сайте источника онлайн.
Решение и ответы заданий № 1–12 варианта №332 Александра Ларина. Разбор ЕГЭ 2021 по математике (профильный уровень).
Варианты ответов и решение задачи ТУТ: https://ege314.ru/ege-varianty-larina/reshenie-varianta-larina-332-ege/
Ответы и решение задачи онлайн
Оставляйте комментарии на сайте, обсуждайте их решения и ответы, предлагайте альтернативные варианты ответов.
| Автор | Сообщение | |||
|---|---|---|---|---|
|
Заголовок сообщения: Тренировочный вариант №332
|
||||
|
http://alexlarin.net/ege/2021/trvar332.html |
|||
  |
||||
|
|
||||
|
Интересный вариант |
Заголовок сообщения: Re: Тренировочный вариант №332
|
|||
|
Спасибо за интересный вариант!!! |
|||
  |
||||
|
Kirill Kolokolcev |
Заголовок сообщения: Re: Тренировочный вариант №332
|
|||
|
Спасибо за интересный вариант! Подробности: 19 Подробности: Последний раз редактировалось Kirill Kolokolcev 21 ноя 2020, 14:24, всего редактировалось 2 раз(а). |
|||
  |
||||
|
100Бальник |
Заголовок сообщения: Re: Тренировочный вариант №332
|
|||
|
Спасибо за интересный вариант!!!!!!!!!!!!!!!!!!!!!!!!!! |
|||
  |
||||
|
Kirill Kolokolcev |
Заголовок сообщения: Re: Тренировочный вариант №332
|
|||
|
17 Подробности: |
|||
  |
||||
|
khazh |
Заголовок сообщения: Re: Тренировочный вариант №332
|
|||
|
Kirill Kolokolcev писал(а): Спасибо за интересный вариант! Подробности: 19 Подробности: Ответ к №18 надо проверить. |
|||
  |
||||
|
rgg |
Заголовок сообщения: Re: Тренировочный вариант №332
|
|||
|
Kirill Kolokolcev писал(а): 17 Подробности: Ответ аналогичный, Кирилл. Последний раз редактировалось rgg 21 ноя 2020, 14:32, всего редактировалось 1 раз. |
|||
  |
||||
|
Kirill Kolokolcev |
Заголовок сообщения: Re: Тренировочный вариант №332
|
|||
|
khazh писал(а): Kirill Kolokolcev писал(а): Спасибо за интересный вариант! Подробности: 19 Подробности: Ответ к №18 надо проверить. Елена Ильинична, Вы правы!) Поспешил |
|||
  |
||||
|
Kirill Kolokolcev |
Заголовок сообщения: Re: Тренировочный вариант №332
|
|||
|
16 Подробности: 15 Подробности: 14 Подробности: 13 Подробности: |
|||
  |
||||
|
Kirill Kolokolcev |
Заголовок сообщения: Re: Тренировочный вариант №332
|
|||
|
rgg писал(а): Kirill Kolokolcev писал(а): 17 Подробности: Ответ аналогичный, Кирилл. |
|||
  |
||||
| Показать сообщения за: Сортировать по: |